Дискретный - определение термина

Автоматизация расчета ОЕЕ с использованием системы мониторинга Диспетчер

Как говорилось выше, расчет показателя эффективности ОЕЕ с использованием данных, собираемых вручную, сложен и недостоверен. Данные могут быть искажены, как за счет неточного контроля времени изготовления детали (технологических операций), так и вследствие неточности идеальных (расчетных) времен. Причем проверить точность этих данных невозможно.

Для качественного формирования ОЕЕ требуется автоматический контроль времени выполнения технологических операций, что подразумевает использование системы мониторинга.

Диспетчер, как никакая другая из предлагаемых в настоящее время систем мониторинга, позволяет , и с использованием классического, и на основе альтернативного методов расчета.

Диспетчер позволяет точно проконтролировать машинное и штучно-калькуляционное время выполнения технологических операций для различного оборудования.

В Диспетчер используются различные способы подключения к оборудованию для получения информации об его работе: аппаратное, прямое, комбинированное. Дополнительно устанавливаемые на станке датчики (тока, вибрации) позволяют контролировать нагрузку станка и отличать реальную работу от холостого хода. Состояние станка, соответствующее машинному времени, может определяться при помощи формул. В таких формулах могут объединяться как дискретные, так и аналоговые сигналы. На станках с ЧПУ, контролируемых системой Диспетчер, фиксируются все остановы при отработке управляющей программы, регистрируется соответствие реальной скорости контурной подачи и заданной величины скорости, собираются данные об отклонениях выполняемой на станке УП от эталонной программы, написанной технологом. Следует отметить, что в Диспетчер поддерживаются станки с многоканальными системами ЧПУ.

В системе Диспетчер организован как автоматический режим сбора информации, так и комплексный режим, совмещающий автоматический и ручной сбор данных, при котором в работу системы включаются операторы станков. Учет времени различных видов простоев оборудования, не регистрируемых автоматически, учет вспомогательного и подготовительно-заключительного времени выполняется посредством ввода оператором соответствующих причин простоя станков. Для этого используются установленные на станках терминалы или коллективные пульты мониторинга. Оператор перед началом работы регистрируется на станке, например, при помощи RFID пропуска или сканера штрих-кода. Система осуществляет контроль за выполнением оператором возложенных на него обязанностей путем автоматического формирования состояния «Простой станка» по вине конкретного оператора, если тот не вводит вовремя причину простоя.

Модуль «Контроль производства» предоставляет возможность контролировать как время выполнения каждой технологической операции, так и время, затраченное на изготовление бракованной продукции и на исправление брака. Это позволяет точно рассчитать показатель ОЕЕ по классической формуле для дискретного многономенклатурного производства.

Для каждой технологической операции автоматически фиксируется машинное время и контролируется его отличие от идеального (расчетного). Имеется возможность корректировать расчетное машинное время по факту выполнения технологических операций и тем самым предотвращать ошибки в расчете показателя «Производительность».

В системе выполняется контроль изготовления бракованных деталей для каждой техоперации и регистрируется время на исправление брака. В результате можно точно рассчитать показатель «Качество».

В настоящее время на многих промышленных предприятиях приняты свои нормативы для расчета ключевых показателей эффективности, включая показатель ОЕЕ. Это связано с типом производства (непрерывное, серийное, дискретное), графиком работы и иными специфическими особенностями. В Диспетчер пользователь может задавать формулы для расчета KPI, группируя при этом собираемые данные согласно требованиям, принятым на данном предприятии.

Практические примеры использования дискретного способа расчета

Дискретный способ расчета имеет широкое применение в различных областях, где требуется анализ и оптимизация процессов с использованием дискретных значений или дискретных переменных. Вот несколько практических примеров использования дискретного способа расчета:

1. Оптимизация производственного процесса

В производственных системах, особенно в автоматизированных системах, дискретный способ расчета позволяет оптимизировать производственные процессы. Например, можно определить оптимальное распределение ресурсов для максимизации производительности и минимизации затрат, учитывая ограничения и требования к процессу производства.

2. Моделирование и оптимизация транспортных сетей

Дискретный способ расчета часто применяется для моделирования и оптимизации транспортных сетей. Можно анализировать различные сценарии в дискретном временном шаге и определить оптимальные маршруты, графики движения транспортных средств и распределение грузов.

3. Прогнозирование деятельности фирмы

Дискретный способ расчета может быть использован для прогнозирования деятельности фирмы на основе дискретных данных, таких как объем продаж по дням недели или временные ряды показателей. Это позволяет компаниям принимать обоснованные решения на основе численных прогнозов и планировать свои бизнес-процессы.

4. Анализ финансовых рынков

Дискретный способ расчета широко применяется в анализе финансовых рынков для прогнозирования цен на активы и определения оптимальных торговых стратегий. Можно использовать дискретные модели для изучения ценовых движений и анализа рисков с целью принятия обоснованных инвестиционных решений.

Все эти примеры демонстрируют возможности и преимущества дискретного способа расчета в различных областях. Он обеспечивает точные и надежные результаты при анализе и оптимизации процессов, основанных на дискретных значениях или переменных.

Виды дискретных распределений вероятностей

Существует несколько распространенных типов дискретных распределений вероятностей, которые часто встречаются в статистическом анализе. Давайте рассмотрим некоторые из них:

1. Биномиальное распределение

Биномиальное распределение — это дискретное распределение вероятностей, которое моделирует вероятность успеха или неудачи в фиксированном количестве независимых испытаний. Оно применимо в ситуациях, когда возможны только два исхода, например, выпадение голов или решки при подбрасывании монеты. В российском контексте биномиальное распределение может быть использовано для анализа успешности маркетинговых кампаний или вероятности наступления определенных событий в данной популяции.

2. Распределение Бернулли

Распределение Бернулли — это частный случай биномиального распределения, в котором существует только одно испытание. Оно представляет собой бинарный результат, обычно обозначаемый как успех или неудача, с определенной вероятностью успеха. В России распределение Бернулли может быть использовано для анализа успеха или неудачи инвестиционных решений или вероятности достижения определенных целей в различных контекстах.

3. Распределение Пуассона

Распределение Пуассона используется для моделирования вероятности наступления определенного количества событий в течение фиксированного интервала времени или пространства. Оно обычно используется для анализа редких событий или явлений, характеризующихся низкой вероятностью возникновения. В России распределение Пуассона можно применить для изучения частоты аварий, прихода клиентов в сервисный центр или возникновения стихийных бедствий.

Измерение информации

Для начала вспомним, что вся информация в компьютере хранится в виде двоичного кода – определенной последовательности нулей и единиц. Подробнее об этом мы рассказывали в статье «Основные понятия об информации». Храня информацию, компьютер выделяет ей место в памяти, в которое и будут записаны двоичные коды закодированных файлов.

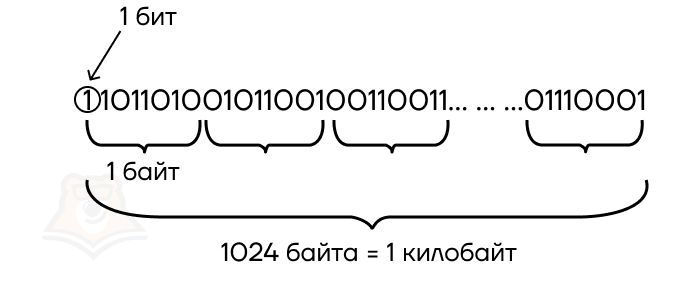
В чем измеряется информация?

Бит — наименьшая единица измерения объема информации. Ему соответствует одна цифра двоичного кода.

И по той же причине, почему нам неудобно измерять расстояние от Москвы до Владивостока линейкой, которая влезает в пенал, для измерения размера больших файлов мы будем использовать не биты, а увеличенные единицы измерения (как километры для метров):

1 байт = 8 бит1 килобайт (кбайт) = 1024 байт1 мегабайт (мбайт) = 1024 кбайт1 гигабайт (гбайт) = 1024 мбайт1 терабайт (тбайт) = 1024 гбайт

Перевод между ними происходит посредством деления и умножения. Например:

5 гбайт = 5 * 1024 мбайт = 5120 мбайт;
2048 кбайт = 2048 / 1024 мбайт = 2 мбайт;
800 бит = 800 / 8 байт = 100 байт.

Почему в килобайте 1024 байт?Мы привыкли, что, например, в 1 килограмме – ровно 1000 грамм, а в 1 метре – ровно 100 сантиметров и так далее. При измерении информации берется не ровно 1000, а 1024. Почему так?Причина в различиях систем счисления. Наша родная система счисления – десятичная, потому что нам удобно считать 10 пальцев на руках. А родная система счисления для компьютера – двоичная. Он знает всего две цифры и ему удобнее выделять в своей памяти количество места, равное степени двойки: \(2^{10}=1024\).

Поэтому нам, информатикам, неплохо бы знать степени двойки, как таблицу умножения, хотя бы до 10 степени. Это поможет избавить себя от постоянных перерасчетов одного и того же. А понадобятся они нам еще не раз:

2 = 1	21 = 2	22 = 4	23 = 8
24 = 16	25 = 32	26 = 64	27 = 128
28 = 256	29 = 512	210 = 1024	211 = 2048

Зная эти степени, мы можем гораздо удобнее оформлять промежуточные расчеты в задачах, где надо перевести большие значения величины информации в биты.

Например, 25 гбайт в битах можно представить двумя способами:

25 гбайт = 25 * 1024 мбайт = 25 * 1024 * 1024 кбайт = 25 * 1024 * 1024 * 1024 байт = 25 * 1024 * 1024 * 1024 * 8 бит = 214748364800 бит;
25 гбайт = 25 * 210 мбайт = 25 * 210 * 210 кбайт = 25 * 210 * 210 * 210 байт = 25 * 210 * 210 * 210 * 23 бит = 25 * 233 бит.

Когда это лишь промежуточная запись при решении задачи, второй вариант, очевидно, удобнее, так как со степенями работать проще, чем с огромными числами.

Примеры дискретных величин

1. Количество монет, выпавших орлом при серии подбрасываний. В данном случае, возможные значения дискретной величины — это количество монет, которые выпали орлом, то есть натуральные числа от 0 до n, где n — общее число подбрасываний.

2. Количество шариков разных цветов в урне. Если в урне находятся шарики разных цветов и нам требуется узнать, сколько шариков каждого цвета находится в урне, то это будет примером дискретной величины. Возможные значения такой величины — это натуральные числа от 0 до n, где n — общее количество шариков в урне.

3. Число студентов в аудитории. Если мы хотим узнать, сколько студентов присутствует на занятии, то это будет примером дискретной величины. Возможные значения дискретной величины в данном случае — это натуральные числа от 0 до n, где n — вместимость аудитории.

Приведенные примеры являются лишь некоторыми из множества возможных дискретных величин

Важно помнить, что дискретные величины имеют конечное или счетное множество значений, в отличие от непрерывных величин, которые могут принимать любое значение на некотором интервале

Примеры дискретных величин в ежедневной жизни

В ежедневной жизни мы сталкиваемся с множеством дискретных величин. Вот некоторые примеры:

Примеры дискретных величин	Описание
Количество детей в семье	Эта величина может принимать только целочисленные значения, так как нельзя иметь, например, 2.5 детей.
Количество студентов в классе	Точное число студентов в классе – это дискретная величина, поскольку у нас не может быть, например, 20.5 студента.
Количество машин на парковке	На парковке может быть только целое число машин. Это также является дискретной величиной.
Количество гостей на свадьбе	Количество гостей на свадьбе – это дискретная величина, так как мы не можем пригласить половину человека.

Это только некоторые примеры дискретных величин, которые мы встречаем в нашей ежедневной жизни. Изучение дискретных величин позволяет нам лучше понимать и анализировать различные явления и ситуации, с которыми мы сталкиваемся.

Примеры дискретных величин в математике

Дискретная величина в математике представляет собой счетный набор значений, то есть множество, в котором между любыми двумя элементами можно поставить биекцию. В математическом анализе и статистике дискретные величины описывают конечное или счетное число исходов. Они значения, которые можно перечислить или подсчитать.

Примеры дискретных величин включают в себя:

1. Бросок монеты: результатом может быть только орел или решка.

2. Бросок кубика: результатом может быть значения от 1 до 6.

3. Подбрасывание игральной кости: результатом может быть числа от 1 до 6.

4. Количество попаданий в цель: может быть любое целое число от 0 до бесконечности.

5. Количество побед и поражений в матче: может быть любое целое число от 0 до бесконечности.

Такие дискретные величины играют важную роль в математической моделировании, статистике и дискретной математике. Они помогают характеризовать случайные события и явления, которые могут быть представлены конечным или счетным множеством значений.

Способ определения величины показателя

Рассмотрим подробнее, как рассчитать коэффициент дисконтирования. Обычно речь идет о многошаговом расчете перспективности и экономической эффективности инвестиционного начинания, поэтому фактор дисконтирования приводит объем потока на n-м шаге к моменту приведения.

Общая формула дисконтирования потока денег имеет такой вид:

PV = FV * 1/(1+R)n

где:

PV – приведенная стоимость;
FV – будущая стоимость.

В этой формуле выделяется компонент, определяющий величину фактора приведения. Собственно, формула расчета коэффициента дисконтирования выглядит так:

КД = 1/(1+R)n

в которой:

R – установленное значение нормы дисконта;
n – количество периодов (шагов), представляющее собой число лет (месяцев) от будущего до текущего момента.

Получившийся показатель всегда имеет значение меньше единицы. Он показывает стоимость одной инвестированной денежной единицы (рубля, евро, доллара) через определенное время при соответствии условий тем, которые приняты для вычисления.

Важнейшей составной частью для расчета коэффициента является ставка дисконтирования, которую еще называют нормой дисконта. Для ее определений существует целый ряд методик, основанных на различных принципах:

дивидендный метод (модель Гордона);
стоимость капитальных активов предприятия (модель CAPM и ее многочисленные модификации);
наличие заемных и собственных средств (модель WACC);
метод значений рентабельности капитала (ROE, ROA, ROACE, ROCE);
метод вычисления рисковых премий (кумулятивный);
экспертный метод, основанный на субъективных прогнозах специалистов.

За норму дисконта можно принимать темпы инфляционных процессов, стоимость долгосрочных депозитов или кредитов, размер ставки рефинансирования Центробанка и т.д. В любом случае, каков будет этот критерий, решает на свой страх и риск инвестор. Если норма дисконта установлена неверно или в ней не учтены все основные риски, то и фактор приведения будет некорректным. Это даст инвестору неверный прогноз, который может привести к убыткам.

Другая составляющая формулы – это жизненный цикл начинания, то есть количество рассматриваемых периодов, в течение которых проект будет генерировать денежные потоки. Чем точнее, установлены эти две вводные, тем более точным будет конечный результат.

дискретный метод

Универсальный русско-английский словарь . Академик.ру . 2011 .

Смотреть что такое «дискретный метод» в других словарях:

Метод подвижных клеточных автоматов — Подвижные клеточные автоматы активно меняют своих соседей за счет разрыва существующих связей между автоматами и образования новых связей (моделирование контактного взаимодействи … Википедия

Метод дискретного элемента — (DEM, от англ. Discrete element method) это семейство численных методов предназначенных для расчёта движения большого количества частиц, таких как молекулы, песчинки, гравий, галька и прочих гранулированных сред. Метод был… … Википедия

Метод изображений — (метод зеркальных отображений) один из методов математической физики, применяемый для решения краевых задач для уравнения Гельмгольца, уравнения Пуассона, волнового уравнения и некоторых других. Суть метода изображений состоит в том, что… … Википедия

Метод Кроуноскопии — (crownscopy от англ. crown корона (свечения) и греч. scopy смотреть, наблюдать)относится к методам функциональной оценки психофизиологического состояния и адаптивных резервов организма человека. Метод основан на регистрации свечения кожного… … Википедия

Дискретный логарифм — Дискретное логарифмирование (DLOG) – задача обращения функции gx в некоторой конечной мультипликативной группе G. Наиболее часто задачу дискетного логарифмирования рассматривают в группе обратимых элементов кольца вычетов, в мультипликативной… … Википедия

ЛИННИКА ДИСКРЕТНЫЙ ЭРГОДИЧЕСКИЙ МЕТОД — специальный метод аналитич. теории чисел, использующий некоммутативную арифметику и сводящий вопросы равномерности распределения целых точек многообразия к рассмотрению потоков целых точек на этом многообразии и операторов, к рые создают эти… … Математическая энциклопедия

ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ МЕТОД — метод исследования нек рых нелинейных уравнений математическойфизики. Введён К. Гарднером (С. S. Gardner), Дж. Грином (J. М. Greene),М. Крускалом (М. D. Kruskal) и Р. Миурой (R. М. Miura) в 1967, хотя отд … Физическая энциклопедия

КАРЛСОНА МЕТОД — Sn метод, один из численных методов решения кинетического уравнения переноса нейтронов в ядерных реакторах. Первый вариант метода для сферически симметричной геометрии, предложенный Б. Карлсоном (В. Carlson, 1953), был основан на кусочно линейном … Математическая энциклопедия

ИЗОБРАЖЕНИЙ МЕТОД — один из методов решения краевых задач матем. физики (для Гелъмголъца уравнения, Пуассона уравнения, волнового уравнения и др.), заключающийся в сведении исходной задачи отыскания поля заданных (сторонних) источников в присутствии граничных… … Физическая энциклопедия

КВАНТОВАЯ МЕХАНИКА — (волновая механика), теория, устанавливающая способ описания и законы движения микрочастиц (элем. ч ц, атомов, молекул, ат. ядер) и их систем (напр., кристаллов), а также связь величин, характеризующих ч цы и системы, с физ. величинами,… … Физическая энциклопедия

автоматический — 3.3.1 автоматический пробоотборник (automatic sampler): Устройство, используемое для извлечения представительной пробы жидкости, протекающей по трубопроводу. Примечание Автоматический пробоотборник обычно состоит из зонда (щупа), экстрактора… … Словарь-справочник терминов нормативно-технической документации

Источник

Пример

Возьмём для примера контроллер системы Умный Дом EasyHomePLC 5.2.

У него 32 дискретных входа. Напряжение на входе должно быть от +9 до +60 вольт, чтобы контролер считал его единицей.

Из этих 32 входов 16 могут быть аналоговыми. Сигнал на входе от 0 до 10 вольт.

18 дискретных выходов. Из них 9 релейные (коммутация 16 ампер 230 вольт), 9 открытых коллекторов для подключения внешних реле.

6 ШИМ выходов с током коммутации до 1.4 ампера и напряжением до 30 вольт на каждый выход. Это управление светодиодной лентой, либо сигнал 0-10 вольт, если на ШИМ выход подключить RC-цепочку (резистор и конденсатор будут сглаживать сигнал ШИМ).

Интерфейсов связи у него много: Ethernet, два RS-485, два RS-232, miniUSB (для прошивки).

Подробнее про входы и выходы можно почитать здесь:

Ещё раз о входах и выходах контроллер

220, всего, сегодня

Вопросы и ответы

Каковы основные характеристики дискретного распределения вероятностей?

Дискретное распределение вероятностей характеризуется тем, что его исходы счетны или конечны. Оно представляет конкретные значения или события и приписывает вероятности каждому исходу.

Чем дискретные распределения отличаются от непрерывных?

Дискретные распределения имеют дело со счетными исходами, в то время как непрерывные распределения охватывают континуум. Дискретные распределения представляют конкретные значения, например целые числа, в то время как непрерывные распределения могут принимать любые значения в пределах диапазона.

Каковы общие примеры дискретных распределений вероятностей?

К распространенным примерам дискретных распределений вероятностей относятся биномиальное распределение, распределение Бернулли и распределение Пуассона. Эти распределения часто встречаются в статистическом анализе и находят применение в финансах, управлении рисками и демографических исследованиях.

Как дискретные распределения вероятностей могут быть использованы в финансовом анализе?

В финансовом анализе дискретные распределения вероятностей могут использоваться для моделирования вероятностей различных рыночных исходов, оценки движения цен на акции, оценки рисков инвестиционного портфеля и прогнозирования вероятности дефолта по кредиту.

Можно ли использовать дискретные распределения вероятностей при контроле качества?

Да, дискретные распределения вероятностей ценны для контроля качества. Их можно использовать для анализа вероятности брака, оценки распределения атрибутов продукции и принятия решений, основанных на данных, для оптимизации производственных процессов и обеспечения стандартов качества.

Какую роль играют дискретные распределения вероятностей в управлении рисками?

Дискретные распределения вероятностей играют важную роль в управлении рисками. Анализируя исторические данные и используя эти распределения, компании могут оценить вероятность различных рисков, таких как сбои в работе или спад на рынке, и разработать соответствующие стратегии снижения рисков.

Как дискретные распределения вероятностей используются в популяционных исследованиях?

В демографических исследованиях дискретные распределения вероятностей могут использоваться для анализа рождаемости, смертности, роста населения и вероятности наступления определенных событий в популяции, например, вероятности того, что люди имеют определенный уровень образования или дохода. Эти распределения дают представление о демографических тенденциях и закономерностях.

Ответ

1. Дискретность. Вы можете выполнить шаг только после выполнения предыдущего. Например, в алгоритме вычисления 8*3+2 (без скобок) вы сперва выполните умножение(по правилу), и только затем прибавите 2. Иначе ответ неверен.

2.Определенность. Вы не можете разделить 8 на 3, если Вам ясно сказано: умножьте. Определенность — это четкое прописывание условия задачи.

3.Результативность. После выполнения действий Вы получите ответ 26 и только 26. Результативность следует из определенности. Благодаря результативности Вы получите «среду», в которой все объекты однозначно определены.

4. Понятность. (Здесь тоже нужно объяснить? По-моему, свойство само за себя говорит.)

5.Массовость. Алгоритм может быть применен не единожды. То есть в нашем примере 8*3+2 присутствуют операции умножения и сложения, но они могут встречаться не только в нашем примере, а «пригодны» для множества других задач, в которых требуется умножить или сложить.