Шестнадцатеричная система счисления
Шестнадцатеричная система счисления – это система счисления, в которой используются 16 цифр: от 0 до 9 и от A до F. Каждая цифра обозначает определенное значение: от 0 до 15.
Эта система счисления широко применяется в программировании, особенно в компьютерных системах. В этом случае шестнадцатеричные числа используются для представления цветов, чисел IP-адресов и других параметров, связанных с управлением компьютером.
Для удобства записи шестнадцатеричных чисел перед цифрами обычно ставится префикс «0x», чтобы отличать их от десятичных чисел.
Например, число 20 в шестнадцатеричной системе записывается как «0x14», так как 1*16 + 4*1 = 20.
- Преобразование десятичного числа в шестнадцатеричное:
- Делим число на 16 и записываем остаток в конец (если остаток больше 9, то заменяем на соответствующую букву).
- Делим нацело полученное число на 16 и продолжаем до тех пор, пока не дойдем до нуля.
- Обратный процесс для преобразования шестнадцатеричного числа в десятичное: умножаем каждую цифру на соответствующую степень числа 16 и складываем результаты.
Шестнадцатеричные числа могут быть также упрощены до двоичных чисел, если каждой цифре шестнадцатеричного числа соответствует 4 бита двоичного значения. Таким образом, шестнадцатеричная система счисления может использоваться для работы с двоичными данными.
Погружение в тему
Доля единицы — это показатель, выражающий отношение числа единиц к общему числу элементов в некоторой выборке или группе. Такая доля может быть представлена в виде десятичной дроби или процента. Этот показатель является одним из важных статистических показателей и применяется в разных областях знания, включая науку, экономику и социологию.
Доля единицы часто используется для изучения пропорций в выборках и группах. Например, если мы изучаем долю студентов, которые получили высокие оценки на экзамене, мы можем определить эту долю, разделив количество студентов, получивших высокие оценки, на общее количество студентов в выборке. Эта информация может помочь нам понять, насколько высокий успех студентов в целом.
Наряду с долей единицы существует также понятие доли нулей. Доля нулей является обратным показателем к доле единицы и представляет процент или десятичную дробь из числа элементов в выборке или группе, которые равны нулю или несущественны в данном контексте. Оба этих понятия часто используются в статистике и анализе данных для более полного понимания и интерпретации результатов.
Что такое математическая доля и как она вычисляется?
Математическая доля, или просто доля, представляет собой отношение одной величины к другой в виде процента или десятичной дроби. Она позволяет выразить долю чего-либо в процентном или долевом соотношении.
Для вычисления математической доли необходимо знать две величины: числитель и знаменатель. Числитель — это количество чего-либо, которое мы хотим выразить в долях. Знаменатель — это общее количество чего-либо, относительно которого мы рассматриваем долю.
Чтобы вычислить долю в процентах, необходимо разделить числитель на знаменатель и умножить результат на 100. Например, чтобы выразить треть от 100 в процентах, нужно выполнить следующие действия:
- 100 / 3 = 33,333
- 33,333 * 100 = 33,333%
Таким образом, треть от 100 составляет 33,333% или округленно 33,33%.
Доли могут быть выражены и в виде десятичных дробей. Для этого необходимо разделить числитель на знаменатель и результат будет являться десятичной долей. Например, чтобы выразить треть от 100 в виде десятичной доли, нужно выполнить следующее вычисление:
Таким образом, треть от 100 составляет 33,333 в виде десятичной доли.
Математические доли широко применяются в различных областях, включая финансы, экономику, процентные расчеты, вероятность и статистику. Они позволяют оценивать относительные доли и процентные соотношения, что упрощает анализ данных и сравнение результатов.
Как правильно использовать кратные и дольные единицы
Когда мы измеряем физические величины, такие как длина, масса или время, мы часто сталкиваемся с большими или маленькими значениями. Для облегчения измерений используются кратные и дольные единицы, которые позволяют нам выражать значения в более удобной форме.
Кратные и дольные единицы — это единицы измерения, которые выражаются в виде множителей или делителей основной единицы. Например, когда мы измеряем длину, основной единицей является метр. Если мы хотим измерить расстояние в километрах, мы умножаем число на 1000, потому что «кило» означает «тысяча». Если мы хотим измерить в сантиметрах, мы умножаем число на 0.01, так как «санти» означает «сто». Таким образом, мы используем кратные и дольные единицы, чтобы удобно выражать значения величин.
Приведем некоторые примеры использования кратных и дольных единиц:
-
Масса: основной единицей измерения массы является килограмм. Кратные единицы: грамм (1 кг = 1000 г), тонна (1 т = 1000 кг). Дольные единицы: миллиграмм (1 г = 1000 мг), микрограмм (1 мг = 1000 мкг).
-
Время: основной единицей измерения времени является секунда. Кратные единицы: минута (1 мин = 60 сек), час (1 ч = 60 мин), сутки (1 сут = 24 часа). Дольные единицы: миллисекунда (1 сек = 1000 мс), микросекунда (1 мс = 1000 мкс).
-
Длина: основной единицей измерения длины является метр. Кратные единицы: километр (1 км = 1000 м), миллиметр (1 мм = 0.001 м). Дольные единицы: сантиметр (1 м = 100 см), микрометр (1 см = 10000 мкм).
Важно правильно использовать кратные и дольные единицы, чтобы измерения были удобными и понятными. Когда вы работаете с большими или маленькими значениями, всегда проверяйте, что вы используете правильные единицы и правильно выполняете преобразования
Это поможет избежать ошибок и позволит вам работать с данными более эффективно.
Определение доли
Представь, что ты имеешь печенье и хочешь поделить его с другими людьми. Ты можешь разделить печенье на равные части и предложить каждому получить определенное количество. В этом случае каждая часть будет представлять собой долю от общего числа печенья.
Доли выражаются в виде дробей или процентов. Например, если печенья было 10, и ты поделил его на 2 равные части, каждая часть будет составлять 1/2 (одну вторую) или 50% (пятьдесят процентов) от общего числа печенья.
Доли широко используются в различных ситуациях. Они могут представлять финансовые доли в бизнесе, доли населения в определенном регионе, а также представлять геометрические отношения в математике.
Например, в процентах, доля может быть использована для представления доли продаж товара от общего объема продаж в компании. Если процент продаж товара составляет 25%, это означает, что этот товар составляет четверть от общего объема продаж.
В математике доли могут быть сложены, вычтены, умножены и разделены друг на друга. Они также могут быть сравнены для определения, какая доля больше или меньше.
Как можно использовать математическую долю в повседневной жизни?
- Разделение общего количества на равные доли. Например, если у вас есть 10 печенек и вы хотите поделить их между троими друзьями поровну, вы можете использовать математическую долю. В данном случае, каждый получит 1/3 от общего количества печенек, то есть около 3 печенки на человека.
- Расчет скидок и наценок. Представим, что товар стоит 300 рублей, но у вас есть скидка в размере 20%. Чтобы узнать, сколько вы сэкономите, можно использовать долю. 20% от 300 рублей равно 60 рублям, поэтому вы сэкономите 60 рублей.
- Определение вероятности. Математическая доля может помочь в определении вероятности какого-либо события. Например, если вы бросаете монету, вероятность выпадения орла равна 1/2, так как есть две равновероятные стороны монеты.
- Оценка процентного соотношения. Если вы хотите оценить, какую долю составляет одно число от другого числа, вы можете использовать математическую долю. Например, если вы хотите узнать, сколько процентов составляет 25 из 100, вы можете записать это как 25/100 или 1/4.
Это лишь несколько примеров, как можно использовать математическую долю в повседневной жизни. Благодаря этому инструменту мы можем решать множество задач и делать более точные и информированные выводы в различных ситуациях.
Две трети это сколько в процентах?
В математике мы часто сталкиваемся с дробями, которые состоят из числителя и знаменателя. Одной из наиболее распространенных дробей является две трети. Но сколько это составляет в процентах?
Для перевода дробей в проценты нам необходимо знать, что процент — это доля от 100. В то время как дробь — это отношение одного числителя к другому числителю. Таким образом, чтобы перевести дробь в проценты, мы должны узнать, сколько раз знаменатель входит в числитель.
В случае с двумя третьими, мы имеем числитель — две единицы и знаменатель — три единицы. Чтобы узнать, сколько это составляет в процентах, мы должны разделить числитель на знаменатель и умножить на 100.
Таким образом, две трети равны 66,67%.
Каково значение двух третей в процентах?
Две трети – это числовое значение, которое можно выразить в процентах. Для получения этого значения нужно выполнить простое математическое действие.
Чтобы выразить две трети в процентах, нужно разделить количество двух третей на общее количество – в данном случае это три. Затем полученное значение умножается на 100, чтобы получить процентное отношение.
Таким образом, значение двух третей в процентах составляет 66,67%. Это можно представить как 66,67 из 100, что соответствует двум третям.
Процентное отношение помогает наглядно показать долю или часть от целого. В случае двух третей, процентное выражение подчеркивает, что это немного больше половины, но все еще не достигает 100%.
Точное определение двух третей
Две трети – это отношение количества или части к целому числу или объекту, когда часть составляет две трети или два разделенных на три одинаковых равных части.
Чтобы лучше понять, что такое две трети, давайте рассмотрим пример. Представим, что у нас есть пирог, который разделен на 3 равные части. Если мы берем 2 из этих 3 частей, то это соответствует двум третям или 2/3 пирога.
Две трети также можно представить в виде десятичной дроби, равной 0,6666… В этом случае третья часть пирога соответствует 0,3333… или 1/3. Когда мы берем два раза 0,3333…, получаем 0,6666…, что равно двум третям.
Если мы говорим о процентах, то две трети составляют 66,67%. Это происходит из расчета, что одна треть равна примерно 33,33%. Приближенно округленное значение двух третей составляет 66,67%, но это не точное значение, так как десятичная дробь 0,6666… является бесконечной.
Итак, две трети – это отношение, которое составляет две равные части к третьей части или 2/3, что равно примерно 66,67%.
Простой способ перевода двух третей в проценты
Для перевода дробей в проценты необходимо сначала выразить их в десятичной форме. Две трети может быть записано как 2/3 или 0.6666 (приближенно).
Чтобы выразить две трети в процентах, нужно умножить его на 100:
0.6666 * 100 = 66.66%
Таким образом, две трети составляют примерно 66.66% от целого.
Можно также выразить две трети в процентах с помощью долей:
- Если целое число состоит из 100, то две трети будут равны 66.66 частям от этого числа.
- Если целое число состоит из 1, то две трети будут равны 0.6666 частям от этого числа.
Таким образом, две трети составляют примерно 66.66% от целого числа.
Таблица ниже демонстрирует, как две трети соотносятся с различными значениями:
| Число | Две трети в десятичной форме | Две трети в процентах |
|---|---|---|
| 1 | 0.6666 | 66.66% |
| 10 | 6.666 | 666.6% |
| 100 | 66.66 | 6666% |
Обратите внимание, что приближенное значение 0.6666 использовано для удобства вычислений. В реальности, две трети равны точно 66.666666…%
Что значит две трети
Две трети – это дробь, которая означает количество, равное двум частям из трех возможных.
Это понятие широко используется в различных сферах жизни: математике, экономике, политике и т.д. Оно может быть представлено в виде числового значения или процентного соотношения.
Для выражения двух третей в процентах необходимо умножить эту дробь на 100%. Таким образом, две трети в процентах равны 66,67%.
Что такое две трети?
Две трети — это дробь, которая представляет собой две равные части из трех. Эта дробь может быть записана как 2/3 или как 0.66666666 и так далее в десятичной системе счисления.
Две трети может быть использована для выражения процентов. Для этого необходимо умножить дробь на 100%. Таким образом, две трети составляют 66,6666667% или около того.
Это популярная дробь в математике и широко используется в различных сферах, таких как промышленность, финансы, здравоохранение, строительство и т.д. Две трети также может быть использована для описания помола кофе и других ингредиентов для приготовления пищи.
- Два третих — это 66,6666667%.
- Два третих можно записать как 2/3.
- Два третих используются в различных областях, включая промышленность, финансы, здравоохранение и т.д.
Используя в своей работе две трети, важно убедиться, что вы правильно вычислили ее значение. Некоторые режимы округления могут привести к разным результатам, поэтому следует использовать точный математический расчет, особенно если речь идет о финансовых или научных расчетах
Определение и примеры
Две трети означает, что что-то разделено на три равные части, и две из этих частей составляют искомую долю. Это можно выразить математически, например, как 2/3 или 0,66666667 в десятичной форме.
Применение концепции двух третей распространено в различных сферах, включая математику, статистику, экономику и т.д.
Например, если у нас есть 12 яблок, и мы хотим поделить их на три равные группы, то каждая группа будет содержать 4 яблока. Таким образом, две трети от 12 яблок равны 8 яблокам.
Одним из примеров использования двух третей в экономике является норма выплаты дивидендов. Если компания решает выплатить дивиденды в размере двух третей чистой прибыли, то это означает, что она выплатит 2/3 от своей чистой прибыли в качестве дивидендов инвесторам.
Также, в статистике, две трети может использоваться для описания медианы распределения, где две трети значений находятся в диапазоне между первым и третьим квартилями.
В общем, понимание двух третей является важным аспектом в различных областях и помогает в лучшем понимании различных задач.
Как выразить две трети в процентах?
Две трети — это дробь, которая равна 2/3. Чтобы выразить ее в процентах, нужно выполнить следующие действия:
- Перевести дробь 2/3 в десятичную форму: 2/3 = 0,6666…
- Умножить полученное число на 100, чтобы перевести его в проценты: 0,6666… * 100 = 66,66…%
- Округлить результат до нужного количества знаков после запятой: 66,67%
Таким образом, две трети равны 66,67%.
Другой способ выразить две трети в процентах — это разделить числитель (2) на знаменатель (3) и умножить результат на 100:
- 2 ÷ 3 = 0,6666…
- 0,6666… * 100 = 66,66…%
- Округлить результат до нужного количества знаков после запятой: 66,67%
Итак, две трети можно выразить в процентах как 66,67%.
Формула и примеры расчета
Две трети (2/3) — это дробь, в которой числитель равен 2, а знаменатель равен 3. Чтобы выразить данную дробь в процентах, необходимо ее умножить на 100%:
2/3 * 100% = 66,666667%
Таким образом, две трети равны приблизительно 66,67%.
Например, если из 90 возможных ответов на экзамене студент правильно ответил на 60 вопросов, то его результат можно выразить в процентах:
60 / 90 * 100% = 66,67%
Также можно использовать таблицу эквивалентности для быстрого пересчета дробей в проценты:
| Дробь | Проценты |
|---|---|
| 1/2 | 50% |
| 1/3 | 33,33% |
| 2/3 | 66,67% |
| 1/4 | 25% |
| 3/4 | 75% |
Таким образом, используя формулу и таблицу эквивалентности, можно легко и быстро пересчитать любые дроби в проценты.
Доля и часть: определение и отличия
Доля представляет собой часть от общего целого и выражается в виде десятичной или дробной десятичной доли. Например, если у нас есть 5 яблок, а мы взяли 2 яблока, то доля взятых яблок составляет 2/5 или 0,4.
Часть, с другой стороны, представляет собой фрагмент или отдельный элемент целого, независимо от его количества. Например, если у нас есть одно яблоко и мы отрезаем от него половину, то часть, которую мы отрезали, составляет 1/2 или 0,5 яблока.
Итак, основное отличие между долей и частью состоит в том, что доля всегда выражается относительно общего целого, в то время как часть может быть самостоятельным элементом и не зависит от целого.
Применяя эти понятия в реальной жизни, можно привести такой пример: если у нас есть 10 пирожков, и мы съели 3 из них, то доля съеденных пирожков равна 3/10 или 0,3. Но если мы отрезали от одного пирожка четверть, то часть, которую мы отрезали, составляет 1/4 или 0,25 пирожка.
Таким образом, понимание разницы между долей и частью позволяет более точно описывать и измерять количественные величины.
Пример использования сотых долей в финансовой сфере
Сотые доли широко используются в финансовой сфере для обозначения процентов и долей при расчетах и анализе данных. Рассмотрим несколько примеров применения сотых долей:
-
Расчет процентных ставок:
Для определения процентной ставки по депозиту или кредиту необходимо знать, сколько процентов от суммы вклада или суммы кредита будет начислено в качестве процентов. Например, если банк предлагает годовую процентную ставку в размере 5%, то это означает, что за каждые 100 единиц валюты будет начислено 5 единиц валюты в качестве процентов. В данном случае 5 единиц валюты — это 5 сотых долей от 100 единиц, или 5%.
-
Расчет доли в портфеле инвестиций:
Определение доли определенного финансового инструмента в портфеле инвестиций также может быть выражено в сотых долях. Например, если в портфеле имеется акция компании A, которая составляет 20% от общей стоимости всех активов портфеля, то это означает, что сумма вложений в акции компании A составляет 20 сотых долей от общей стоимости портфеля.
-
Анализ финансовых показателей:
Сотые доли часто используются при анализе финансовых показателей компаний. Например, для оценки рентабельности компании используется такой показатель, как чистая прибыль от продаж в процентах. Это означает, что чистая прибыль, полученная от продажи товаров или услуг, выражена в сотых долях от общих доходов компании.
-
Расчет налогов и комиссий:
При расчете налогов и комиссий сотые доли могут использоваться для определения размера налоговой ставки или комиссии. Например, если налоговая ставка составляет 8%, то это означает, что 8 сотых долей от дохода или суммы платежа будут уплачены в качестве налога.
Все эти примеры демонстрируют, что сотые доли являются важным инструментом для математических вычислений, анализа данных и финансовых расчетов в различных областях экономики.
Примеры расчета две трети от суммы:
Для понимания того, что означает две трети от суммы, давайте рассмотрим несколько примеров:
-
Пример 1:
Предположим, у вас есть сумма в размере 1000 рублей. Чтобы найти две трети от этой суммы, вам нужно умножить ее на долю 2/3:
1000 * 2/3 = 2000/3 ≈ 666.67 рублей
Таким образом, две трети от 1000 рублей составляют около 666.67 рублей.
-
Пример 2:
Допустим, у вас есть сумма в размере 500 долларов. Чтобы найти две трети от этой суммы, вам нужно выполнить следующие шаги:
500 * 2/3 = 1000/3 ≈ 333.33 долларов
Таким образом, две трети от 500 долларов составляют около 333.33 долларов.
-
Пример 3:
Предположим, у вас имеется сумма в размере 1200 евро. Чтобы найти две трети от этой суммы, вам нужно выполнить следующие расчеты:
1200 * 2/3 = 2400/3 = 800 евро
Таким образом, две трети от 1200 евро равняются 800 евро.
Все эти примеры показывают, как вычислить две трети от суммы. Вам просто нужно умножить сумму на долю 2/3 и получить результат.
Обыкновенные дроби. Понятие дроби. Доли в дробях.
Дроби мы постоянно используем в жизни. Например, когда едим торт с друзьями. Торт можно разделить на 8 равных частей или на 8 долей. Доля – это равная часть от чего-то целого. Четыре друга съели по кусочку торта. Четыре взяли из восьми кусочков можно записать математически в виде обыкновенной дроби \(\frac{4}{8}\), читается дробь “четыре восьмых” или “четыре деленное на восемь”. Обыкновенную дробь еще называют простой дробью.
Дробная черта заменяет деление:
\(4 \div 8 = \frac{4}{8}\)
Это мы записали доли в дробях. В буквенном виде будет так:
\(\bf m \div n = \frac{m}{n}\)
4 – числитель или делимое, находится вверху над дробной чертой и показывает сколько частей или долей из общего было взято.
8 – знаменатель или делитель, находится внизу под дробной чертой и показывает общее количество частей или долей.
Если мы приглядимся внимательно, то увидим, что друзья съели половину торта или одну часть из двух. Запишем в виде обыкновенной дроби \(\frac{1}{2}\), читается “одна вторая”.
Рассмотрим еще пример:
Имеется квадрат. Квадрат разделили на 5 равных частей. Две части закрасили. Запишите дробь для закрашенных частей? Запишите дробь для не закрашенных частей?
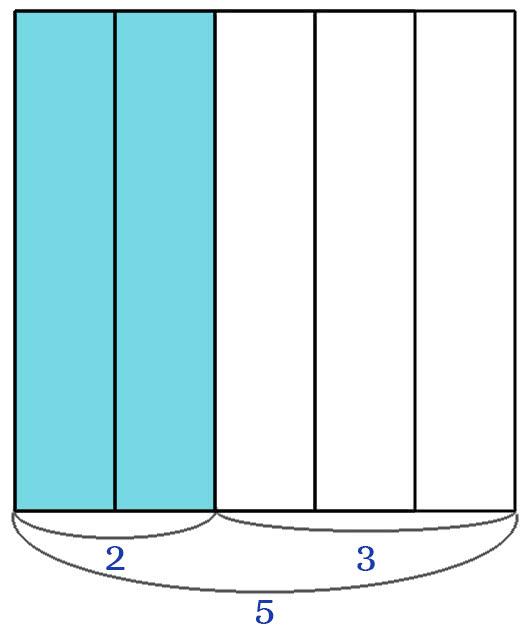
Две части закрасили, а всего частей пять, поэтому дробь будет иметь вид \(\frac{2}{5}\), читается дробь “две пятых”.
Три части не закрасили, всего частей пять, поэтому дробь запишем так \(\frac{3}{5}\), читается дробь “три пятых”.
Разделим квадрат на более мелкие квадраты и запишем дроби, для закрашенных и не закрашенных частей.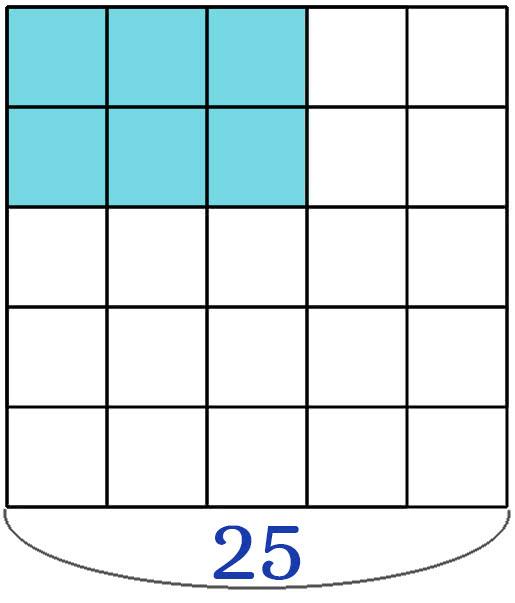
Закрашенных 6 частей, а всего 25 частей. Получаем дробь \(\frac{6}{25}\) , читается дробь “шесть двадцать пятых”.
Не закрашенных 19 частей, а всего 25 частей. Получаем дробь \(\frac{19}{25}\), читается дробь “девятнадцать двадцать пятых”.
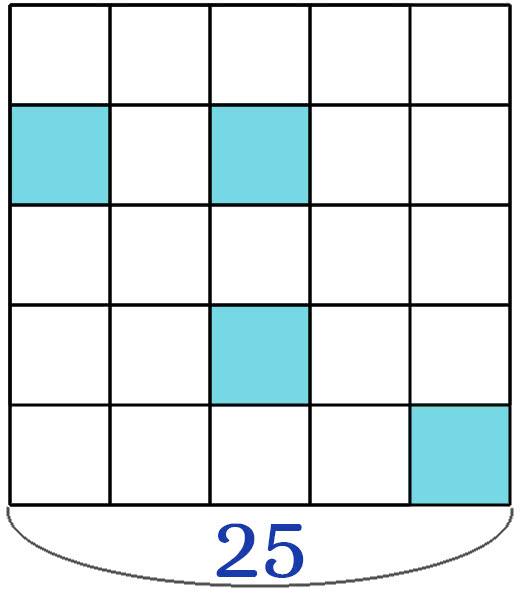
Закрашенных 4 части, а всего 25 частей. Получаем дробь \(\frac{4}{25}\), читается дробь “четыре двадцать пятых”.
Не закрашенных 21 частей, а всего 25 частей. Получаем дробь \(\frac{21}{25}\), читается дробь “двадцать один двадцать пятых”.
Любое натуральное число можно представить в виде дроби. Например:
\(5 = \frac{5}{1}\)
\(\bf m = \frac{m}{1}\)
Любое число делиться на единицу, поэтому это число можно представить в виде дроби.
Вопросы по теме “обыкновенные дроби”:Что такое доля?
Ответ: доля – это равная часть от чего-то целого.
Что показывает знаменатель?
Ответ: знаменатель показывает на сколько всего частей или долей поделено.
Что показывает числитель?
Ответ: числитель показывает сколько частей или долей было взято.
Дорога составляла 100м. Миша прошел 31м. Запишите дробью выражение сколько прошел Миша?
Ответ:\(\frac{31}{100}\)
Что такое обыкновенная дробь?
Ответ: обыкновенная дробь – это отношение числителя к знаменателю, где числитель меньше знаменателя. Пример, обыкновенных дробей \(\frac{1}{4}, \frac{3}{7}, \frac{5}{13}, \frac{9}{11}…\)
Как перевести натуральное число в обыкновенную дробь?
Ответ: любое число можно записать в виде дроби, например, \(5 = \frac{5}{1}\)
Задача №1:
Купили 2кг 700г дыни. Мише отрезали \(\frac{2}{9}\) дыни. Чему равна масса отрезанного кусочка? Сколько граммов дыни осталось?
Решение:
Переведем килограммы в граммы.
2кг = 2000г
2000г + 700г = 2700г всего весит дыня.
Мише отрезали \(\frac{2}{9}\) дыни. В знаменателе стоит число 9, значит на 9 частей разделили дыню.
2700 : 9 =300г масса одного кусочка.
В числители стоит число 2, значит надо Мише дать два кусочка.
300 + 300 = 600г или 300 ⋅ 2 = 600г столько дыни съел Миша.
Чтобы найти какая масса дыни осталась нужно вычесть от общей массы дыни съеденную массу.
2700 — 600 = 2100г осталось дыни.
Понятие «единица счета»
Единица счета это обозначение конкретной величины в числовой системе на основе которой происходят расчеты. Она является отправной точкой для определения значений других чисел и позволяет осуществлять вычисления в различных областях жизни, начиная от финансов и заканчивая наукообразными исследованиями. В математике, единицы счета являются ключевыми элементами в понимании основных математических операций.
Широко известный пример единицы счета — десятичная система, в которой любое число может быть представлено как комбинация цифр от 0 до 9, с учетом весовых коэффициентов. В этой системе, единицей счета является «1», и постепенно увеличивая значение числа на единицу, мы получаем последовательно все перед нами числа.
В других системах, используемых в математике, могут быть использованы другие единицы счета, например, в двоичной системе, используется единица и ноль. В системе измерения величин, обычно применяются стандартные единицы измерения, такие как метр, грамм, секунда и другие.
Итак, единица счета играет важную роль в математике. Она определяет весовые коэффициенты и предназначена для обозначения конкретных значений в числовых системах. Понимание понятия единицы счета является обязательным для выполнения математических расчетов
Точное понимание роли этих единиц важно для научных и технических областей, где данные должны быть точными и достоверными
Как найти процентное соотношение чисел
Также могут возникнуть ситуации, когда нам необходимо рассчитать процентнотношение двух чисел. Например, какой из двух процент число B составляет от числа А, на сколько процентов (Б) вы выполнили свою работу, исходя из определенной ставки (А), на сколько (Б) увеличилась цена товара по сравнению с первоначальной ставкой (А) и т.д.
Чтобы определить такой результат, нам нужно сделать следующее. формула:
Например, нам нужно рассчитать, что доля от числа 500 составляет число 85.
Используя вышеизложенное формулу, мы выполняем несколько простых арифметических операций:
85 / 500 * 100 = 17%
Таким образом, число 85 — это 17% от 500.
Проверьте полученные число по формуле первого способа:
500 / 100 * 17 = 85.

Важность доли равной единице в математике
В математике доля равная единице имеет особое значение и играет важную роль в различных областях этой науки. Доля, равная единице, называется также единичной долей. Она означает, что количество или величина относится к полному объему или общей сумме в качестве целой или полной части.
Единичная доля является базовым понятием в системе десятичных дробей. В десятичной записи числа, которое представлено в виде десятичной дроби, единичная доля обозначает число, которое находится справа от десятичной запятой и является последней цифрой числа. Например, в числе 3,14 единичная доля равна 4.
Доля, равная единице, также является важным понятием в вероятности и статистике. Вероятность события, равного 1, означает, что это событие обязательно произойдет. Вероятность равная единице является максимальной и гарантирует, что данное событие точно произойдет.
Единичная доля также играет роль в процентах и пропорциях. В процентах, если какая-либо величина равна 100%, это означает, что она составляет полную часть от всего. Например, если процент оперативной памяти в компьютере составляет 100%, это означает, что вся доступная память используется полностью.
В пропорциях единичная доля означает, что одна часть или одно значение относится ко всем остальным частям или значениям в пропорции. Например, если имеется пропорция 1:3, это означает, что одна часть относится к трем другим частям. Единичная доля является точкой отсчета в данной пропорции.
Таким образом, доля, равная единице, играет ключевую роль в математике и используется в различных областях этой науки. Понимание и умение работать с единичной долей позволяют более глубоко и точно анализировать и решать математические задачи.
Определение доли
Для определения доли необходимо знать количество элементов, которые входят в группу или выборку, а также количество элементов, которые являются объектом изучения. Долю можно вычислить с помощью простого математического выражения: доля = количество интересующих элементов / общее количество элементов.
Доля позволяет оценить, какая часть группы или выборки содержит определенный элемент или является объектом интереса. Например, при исследовании рынка можно определить долю рынка для конкретного продукта, чтобы понять его популярность среди конкурентов.
| Пример | Количество интересующих элементов | Общее количество элементов | Доля |
|---|---|---|---|
| Количество покупок определенного товара | 50 | 1000 | 5% |
| Количество положительных ответов на опрос | 200 | 500 | 40% |
Что такое доля в статистике
Доли в статистике широко применяются в различных областях, включая социологию, экономику, маркетинг, медицину и другие. Они позволяют оценивать долю населения с определенными характеристиками, долю продаж определенного продукта, долю случаев заболеваний, и т.д.
Для вычисления доли необходимо знать какую-либо часть и общий объем или количество. Доля обычно представляется в виде десятичной или процентной формы. Например, доля 0.5 означает половину, а доля 50% означает половину из 100.
Важно помнить, что доли в статистике являются относительными значениями и показывают соотношение или распределение частей в пределах определенного контекста или группы данных. Их использование позволяет получить более полное представление о процессах и явлениях, происходящих в исследуемом явлении или совокупности
Какую роль играет доля в статистике
Доля может быть выражена в виде десятичной дроби (от 0 до 1) или в процентах. Она позволяет нам сравнить разные группы или элементы внутри них и выявить различия или сходства.
Роль доли в статистике заключается в следующем:
1. Сравнение групп:
Доля позволяет сравнивать доли одной группы с долями других групп. Например, мы можем сравнить долю мужчин и женщин в определённой общине или выявить, какую часть рынка занимает каждая компания в отрасли.
2. Оценка изменений во времени:
Доля также может быть использована для оценки изменений во времени. Мы можем рассмотреть изменения в доле определённой группы людей, например, в пределах года или между различными периодами времени. Это может помочь нам определить тренды и понять, какие факторы могут влиять на эти изменения.
3. Принятие решений:
Доля позволяет принимать информированные решения на основе данных. Например, в бизнесе мы можем использовать долю рынка для определения, какую долю рынка у нас есть и каким образом можно увеличить нашу долю рынка.
Появление загадочного числа
Пол трети числа 100 — это числовая загадка, которая вызывает неоднозначность и споры. С одной стороны, можно подумать, что пол трети от 100 равно 50. Однако, этот ответ кажется неправильным, так как сумма трех половинок числа 100 превышает само число 100. С другой стороны, можно подумать, что пол трети от 100 равно 33,33(3), что кажется более логичным и подтверждается математическими расчетами.
Загадка пол трети числа 100 стала предметом интереса для многих ученых и математиков, и они предлагают различные теории и объяснения. Некоторые утверждают, что здесь применяется округление числа, другие говорят о том, что это является нарушением законов математики.
Безусловно, пол трети числа 100 остается загадкой, которая порождает новые вопросы и исследования. Но независимо от ответа, она напоминает нам о том, что математика может быть не такой простой, как кажется, и всегда есть место для тайны и загадок.
Примеры
Сотые доли, также называемые процентушками или процентулями, представляют собой дроби, где числитель равен числу, выраженному в процентах, а знаменатель равен 100. Например, если мы говорим о 50 процентулях, то это означает, что мы имеем в виду 50 сотых долей или 50/100.
Процентными расчетами мы пользуемся ежедневно, даже не задумываясь об этом. Например, когда мы считаем скидку на товар, мы вычисляем определенное количество сотых, чтобы узнать сумму скидки. Если у нас есть сто рублей, то 50 процентулей от этой суммы составляют 50 рублей.
Проценты также используются в финансовых расчетах, например, при вычислении процентной ставки по вкладу. Если процентная ставка составляет 5%, то сто рублей сгенерируют пять рублей в год в виде процентов.
Сотые доли являются важным понятием в математике и финансах, и понимание их позволяет нам более точно оценивать и прогнозировать различные процентные расчеты и финансовые операции.
Сотая часть (1/100) обозначается как 0.01 или 1%.
Доли в процентах, также называемые «процентучки» или «процентики», очень удобны для выражения относительных величин. Они используются во многих сферах: финансах, экономике, математике, статистике и других науках.
Проценты позволяют быстро и легко сравнивать разные величины. Например, если у вас есть 100 яблок и 1% из них имеют пятна, то это значит, что 1 яблоко имеет пятна.
Обычно в процентах используется от 0 до 100, но как видно из нашего объяснения, могут быть и доли меньше 1%. Например, если у вас есть 10 яблок и 0.1% из них имеют пятна, то это значит, что 0.01 яблока имеет пятна.
Сотая часть или 1% — это очень маленькое значение, но оно может быть важным для точного измерения и оценки данных. Например, при рассмотрении финансовых показателей, таких как процентная ставка или инфляция, даже небольшое изменение в сотых долях может иметь существенное значение.
Таблица ниже показывает, как расположены сотые доли от 0 до 1 в десятичном и процентном виде:
| Десятичное представление | Процентное представление |
|---|---|
| 0.01 | 1% |
| 0.02 | 2% |
| 0.03 | 3% |
| 0.04 | 4% |
| 0.05 | 5% |
| … | … |
| 1.00 | 100% |
Таким образом, сотая часть представляет собой небольшую, но важную составляющую целого числа или величины. Она может быть представлена как десятичная дробь или процент для удобства сравнения и измерения различных значений.
Сотые доли обычно записываются в виде десятичной дроби, где числитель представляет долю и знаменатель равен 100, что соответствует 100 процентам. Например, число 0.25 представляет 25% или «двадцать пять сотых» в виде доли. Аналогично, число 0.5 представляет 50% или «пятьдесят сотых» в виде доли.
Сотые доли могут быть использованы в различных сферах жизни для выражения процентного соотношения. Например, в финансовой сфере, сотые доли используются для представления процентных ставок, при расчете налогов и процентов по кредитам. В экономике, сотые доли используются для представления долей роста или спада величин.
В общем понимании, сотые доли помогают нам лучше понять и оценить процентное соотношение двух величин. Они предоставляют нам точку отсчета для анализа и сравнения данных, что позволяет нам принимать более информированные решения на основе процентных соотношений.






























