Симметрия фигур в пространстве

1.3. Поворотная симметрия

Предположим, что объект совмещается сам с собой при повороте вокруг некоторой оси на угол, равный 360°/n (или кратный этой величине), где n = 2, 3, 4, … В этом случае о поворотной симметрии, а указанную ось называют поворотной осью n-го порядка.

Рассмотрим примеры со всеми известными буквами «И» и «Ф». Что касается буквы «И», то у нее есть так называемая поворотная симметрия. Если повернуть букву «И» на 180° вокруг оси, перпендикулярной к плоскости буквы и проходящей через ее центр, то буква совместится сама с собой.

Иными словами, буква «И» симметрична относительно поворота на 180°. Заметим, что поворотной симметрией обладает также буква «Ф».

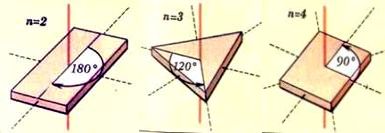
На рисунке 2.7. даны примеры простых объектов с поворотными осями разного порядка – от 2-го до 5-го.

Что такое симметрия

Наиболее часто это понятие встречается в геометрии. Объект считается симметричным, если после некоторых геометрических преобразований он смог сохранить свои первоначальные свойства.

В качестве примера стоит рассмотреть обычный круг. Если его вращать вокруг условного центра, он сохранит свою форму и первоначальные характеристики. Поэтому этот геометрический предмет смело можно назвать симметричным.

Виды симметрии определяются возможными преобразованиями для данного объекта и его свойствами, которые в результате проведенных манипуляций должны сохраниться. В случае, когда это условие не соблюдается, можно утверждать о наличии асимметрии.

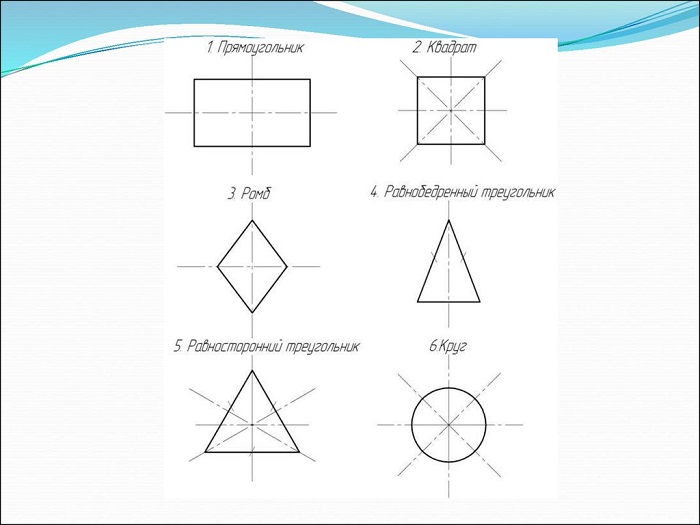
Рис. 1 Фигуры, обладающие симметричностью

1.2 Центральная симметрия

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре .

Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм (Рисунок 2.6).

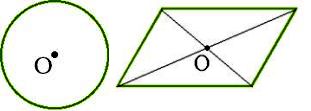
Точка О называется центром симметрии фигуры. В подобных случаях фигура обладает центральной симметрией. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма — точка пересечения его диагоналей.

Прямая также обладает центральной симметрией, однако в отличие от окружности и параллелограмма, которые имеют только один центр симметрии у прямой их бесконечно много — любая точка прямой является её центром симметрии. Примером фигуры, не имеющей центра симметрии, является треугольник.

Понятие движения

Перед тем, как ввести понятие движения в пространстве, надо ввести определение отображения пространства на себя.

Определение 1

Отображением пространства на себя будем называть такое соответствие любой точке данного пространства какой-либо точке этого же пространства, в котором участвуют все точки из этого пространства.

Введем теперь, непосредственно, определение движения.

Определение 2

Движением пространства будем называть отображением пространства на себя, которое сохраняется расстояния между соответствующими точками.

Статья: Осевая симметрия

Найди решение своей задачи среди 1 000 000 ответов

Пример – рисунок 1.

Введем теперь несколько теорем, связанных с понятием движения без доказательства.

Теорема 1

При движении отрезок будет отображаться на ему же равный отрезок.

Теорема 2

При движении треугольник будет отображаться на равный ему же треугольник.

Теорема 3

При движении пирамида будет отображаться на равную ей пирамиду.

Калькулятор оси симметрии

Этот

Калькулятор параболы

получит квадратичную функцию, упростит ее до вида ax² +b x + c и подставит значения a и b в формулу:

Но есть и другие способы поиска

Ось симметрии

параболы. Предположим, что вы

решить квадратное уравнение

ax² +b x + c = 0, и вы находите корни u и v. Как вы находите

Ось симметрии

когда вы знаете корни квадратного уравнения?

• Шаг 1: Определите заданные корни квадратных уравнений
• Шаг 2: У вас будет два корня u и v. Если есть только один корень, вы определяете u и v как одно и то же значение
• Шаг 3: Ось симметрии находится путем вычисления средней точки корней u и v: Таким образом, мы получаем формулу оси симметрии \(x = \displaystyle \frac{u+v}{2}\). Это работает как для вещественных, так и для комплексных корней

Когда у вас

сложные корни

то они будут сопряженными комплексными числами, и тогда их среднее даст действительное число.

Ось симметрии своими словами для детей

Ось симметрии — это вымышленная линия, через которую можно разделить фигуру на две одинаковые части. Когда мы отражаем фигуру относительно этой оси, она выглядит точно так же, как и до отражения.

Давай представим, что у нас есть фигура в форме буквы «А». Если мы проведем линию вдоль середины этой буквы, то она станет осью симметрии. Если мы сложим фигуру вдоль этой оси, то получим две одинаковые половины буквы «А».

Ось симметрии может быть и у других фигур. Например, у квадрата или прямоугольника есть две оси симметрии. Мы можем провести линию через середины противоположных сторон и получить две одинаковые половины фигуры.

Другой пример — круг. У круга есть бесконечное количество осей симметрии. Мы можем провести линию через центр круга и получить две одинаковые половины. Но мы также можем провести линию через любую точку на круге и получить две одинаковые половины.

Ось симметрии также может быть у букв, чисел и даже животных. Например, у буквы «В» есть ось симметрии, так как мы можем провести линию посередине и получить две одинаковые половины. У буквы «О» тоже есть ось симметрии, так как она выглядит одинаково, независимо от того, какую точку мы возьмем за ось симметрии.

Ось симметрии помогает нам видеть и понимать, что фигура симметрична. Это интересное свойство, которое можно найти во многих вещах вокруг нас.

Используемая литература:1. Белова, Т.И. Вычисление неопределенных интегралов. Обыкновенные дифференциальные уравнения. Компьютерный курс: учеб. пособие / Т.И.Белова, А.А.Грешилов, И.В.Дубограй; Ред. А.А.Грешилов. — М.: Логос, 2004. — 184 с. + 1 эл. опт. диск (CD-ROM).2. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. — 22-е изд., перераб. — СПб.: Профессия, 2006. — 432 с.3. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. — 22-е изд., перераб. — СПб.: Профессия, 2005. — 432 с.4. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. для вузов. В 2 ч. Ч.1 / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий. — 4-е изд., стереотип. — М.: Дрофа, 2004. — 725 с.5. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч. 1. Дифференциальное и интегральное исчисление / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; Ред. В.А.Садовничий. — 3-е изд., испр. — М.: ДРОФА, 2001. — 725 с.6. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч.2. Ряды, несобственные интегралы, ряды Фурье, преобразование Фурье / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; ред. В.А.Садовничий . — 3-е изд., испр. — М.: ДРОФА, 2001. — 712 с.7. Голоскоков, Д.П. Уравнения математической физики. Решение задач в системе Maple: учеб. для вузов / Д.П.Голоскоков. — СПб.: Питер, 2004. — 538с.8. Гурова, З.И. Математический анализ. Начальный курс с примерами и задачами: учеб. для втузов / З.И.Гурова, С.Н.Каролинская, А.П.Осипова; Ред. А.И.Кибзун. — М.: Физматлит, 2002. — 351 с.9. Лукьянов, А.В. Обыкновенные дифференциальные уравнения: учеб. пособие по решению задач / А.В.Лукьянов, Ю.Д.Погуляев. — Челябинск: Полиграф-Мастер, 2006.10. Математический анализ в вопросах и задачах: учеб. пособие для вузов / В.Ф.Бутузов, Н.Ч.Крутицкая, Г.Н.Медведев, А.А.Шишкин; Ред. В.Ф.Бутузов . — 5-е изд., испр. — М.: ФИЗМАТЛИТ, 2002. — 479 с.Значение термина Ось симметрии на academic.ru

Центральная симметрия

Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.

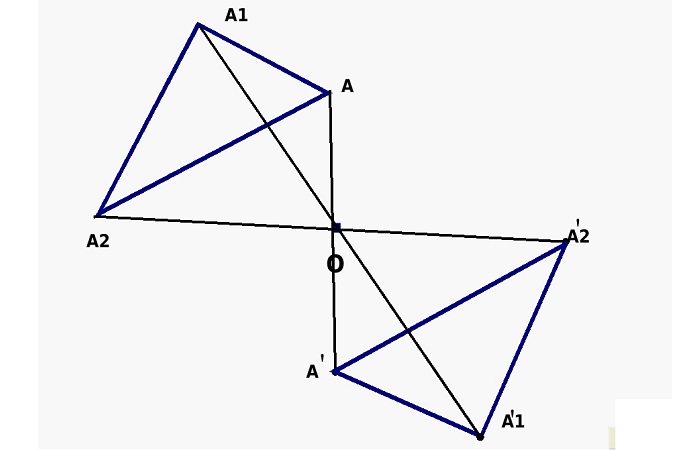
Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром. 

Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.

Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.

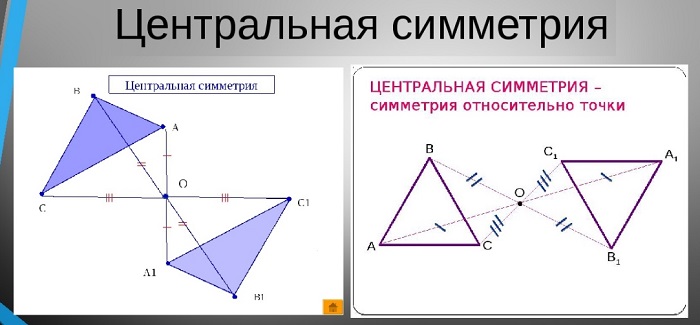
Рис. 2 Графическое представление центральной симметрии

Что такое ось симметрии?

Итак, ось симметрии — это вымышленная линия, которая делит фигуру на две равные части, как если бы она была отражена в зеркале. Представь себе, что у тебя есть прямоугольник, и ты хочешь найти его ось симметрии. Не спеши, ведь она может быть только одна!

Как найти эту ось? Для начала, проведи воображаемую линию посередине прямоугольника, от одной стороны до другой. Если обе части прямоугольника совпадут, значит, ты нашел ось симметрии! Это значит, что прямоугольник и его отражение в зеркале будут абсолютно одинаковыми. Круто, не так ли?

Ось симметрии — это что-то волшебное! Она может быть не только в прямоугольниках, но и во многих других фигурах. Например, у круга она проходит через его центр, так как круг одинаков со всех сторон.

А ты можешь найти ось симметрии вокруг себя? Попробуй оглядеться вокруг! Видишь ли ты что-то, что выглядит так же с двух сторон? Это может быть любая вещь или фигура. Попробуй провести свою воображаемую ось симметрии и увидишь, насколько все станет симметричным и гармоничным!

Симметрия — это что-то прекрасное! Она окружает нас повсюду и делает наш мир еще более удивительным. И теперь ты знаешь, что такое ось симметрии — волшебная линия, которая делит фигуру на две равные части. Используй эту информацию и разгадывай головоломки, исследуй новые фигуры и наслаждайся симметрией и красотой вокруг тебя!

Раздел 2. Как распознать симметричные фигуры

Одним из самых простых способов распознать симметричную фигуру является тест на симметрию относительно прямой. Если фигура равна самой себе после отражения от прямой, значит, она симметричная.

Еще один способ – это визуальный метод. Если копировать фигуру на бумагу, а затем повернуть бумагу на половину, чтобы одна половина оказалась поверх другой, и они совпали, то это будет означать, что фигура симметрична.

Также можно обращать внимание на следующие признаки:

• Фигура имеет одинаковую форму и размеры по обе стороны линии симметрии.
• Если на фигуре есть несколько линий симметрии, это значит, что фигура имеет повышенную степень симметрии.

Кроме того, есть фигуры, которые могут быть симметричными только при определенных условиях, например, квадрат, который симметричен только при повороте на 90 градусов.

Для более точного определения симметричности, можно использовать таблицы и сравнивать фигуры между собой:

	Симметричная	Несимметричная
Фигура 1	+
Фигура 2		+
Фигура 3	+

С помощью таких таблиц можно легко определить, какие фигуры симметричные, а какие нет. Это полезно при работе с детьми для развития их математических навыков.

Что такое ось симметрии

Ось симметрии может проходить через центр фигуры или быть расположенной в другом месте. Например, у прямоугольника или квадрата есть главная горизонтальная и вертикальная оси симметрии. У равнобедренного треугольника осью симметрии служит его высота.

Ось симметрии имеет большое значение в математике, искусстве и дизайне. Она помогает при создании симметричных и гармоничных ком

Определение оси симметрии

Ось симметрии может быть вертикальной, горизонтальной или диагональной. Вертикальная ось делит фигуру на левую и правую стороны, горизонтальная — на верхнюю и нижнюю, а диагональная — на две равные части, угол между которыми часто составляет 45 градусов.

Ось симметрии является важным понятием в геометрии и дизайне. Она помогает определить симметричность фигуры и может использоваться для создания баланса и гармонии в композиции. Например, многие логотипы и эмблемы имеют оси симметрии, что делает их эстетически привлекательными и запоминающимися.

Примеры оси симметрии

Один из самых распространенных примеров оси симметрии — это человеческое лицо. Часто наше лицо оказывается симметричным, при этом оно делится пополам горизонтальной осью, проходящей через нос. Отражая лицо относительно этой оси, мы получаем идентичное изображение.

Другим примером оси симметрии является растение. Многие цветы имеют ось симметрии, которая делит их на две равные части. Например, ромашка или подснежник имеют центральную ось симметрии, вдоль которой отражаются их лепестки.

Архитектура также полна примеров оси симметрии. Многие здания имеют фасады, которые разделены вертикальными осами симметрии. Это придает зданию баланс и гармонию.

Оси симметрии играют большую роль в искусстве. Например, многие картины имеют центральную ось симметрии, которая делит полотно на две симметричные части. Это помогает создать эстетическое равновесие и привлекательность для зрителя.

Таким образом, ось симметрии широко использована в природе, архитектуре, искусстве и повседневной жизни. Она помогает создавать баланс, гармонию и привлекательность в различных областях.

Как обучить учеников работать с осями симметрии?

Для того чтобы научить учеников работать с осями симметрии, можно использовать несколько интересных и познавательных методов.

1. Объясните концепцию оси симметрии таким образом, чтобы она была легко понятна детям. Вы можете использовать образные примеры из реальной жизни, такие как отражение лица в зеркале или симметричные фигуры в природе.

2. Предложите ученикам выполнить различные задания и игры, связанные с осями симметрии. Например, попросите их найти ось симметрии в различных фигурах или отразить фигуру относительно заданной оси.

3. Проведите практические уроки, включающие работу с настоящими зеркалами. Ученики могут использовать зеркала, чтобы создавать симметричные фигуры и проверять, являются ли они отражениями друг друга.

4. Предоставьте детям возможность создавать свои собственные симметричные фигуры. Например, они могут использовать различные материалы, чтобы сделать симметричную открытку или картину.

5. Поощряйте учеников думать креативно и искать симметричные элементы в окружающем мире

После урока с осью симметрии, попросите их обратить внимание на симметричные объекты или фигуры, которые они могут увидеть в повседневной жизни

С помощью этих методов ученики смогут легко понять и применять понятие оси симметрии, что позволит им справляться с задачами и играми, связанными с этой темой.

Осевая симметрия

Перед тем, как определить понятие осевой симметрии, введем понятие симметричности точки относительно какой-либо оси.

Определение 3

Точки $X$ и $X_1$ будем называть симметричными относительно какой-либо оси $a$, если прямая $(XX_1)$ будет перпендикулярна оси $a$ и при этом ось $a$ будет делить отрезок $$ пополам (рис. 2).

Определение 4

Осевой симметрией фигуры относительно оси будем называть отображение, при котором получается фигура, составленная из точек, симметричных относительно этой оси каждой точке начальной фигуры.

Введем следующую теорему:

Теорема 4

Осевая симметрия – движение.

Доказательство.

Пусть нам даны две точки $Z$ и $Z’$ – симметричные относительно оси $l$. Построит систему координат $O_{xyz}$, где ось $Oz$ – это прямая $l$. Пусть точка $Z$ в этой системе координат имеет координаты $(α,β,γ)$, а точка $Z’$ имеет координаты $(α’,β’,γ’)$. Так как эти точки симметричны относительно оси $Oz$, то эта ось будет делить отрезок $$ пополам, то есть

$\frac{α+α’}{2}=0$, $\frac{β+β’}{2}=0$

следовательно

$α=-α’$, $β=-β’$

Так как ось $Oz$ совпадает с нашей осью симметрии, то $γ=γ’$.

Возьмем две произвольные точки $X$ и $Y$ с координатами $(α_1,β_1,γ_1)$ и $(α_2,β_2,γ_2)$, соответственно. Расстояние между ними равно

$d=\sqrt{(α_1-α_2)^2+(β_1-β_2)^2+(γ_1-γ_2)^2 }$

По формулам выше, получим, что симметричные им точки $X’$ и $Y’$ имеют координаты $(-α_1,-β_1,γ_1)$ и $(-α_2,-β_2,γ_2)$, соответственно. Расстояние между ними равно

$d’=\sqrt{(-α_1+α_2 )^2+(-β_1+β_2 )^2+(γ_1-γ_2 )^2}=\sqrt{(α_1-α_2)^2+(β_1-β_2)^2+(γ_1-γ_2)^2}=d$

То есть осевая симметрия сохраняет расстояния, что и доказывает нашу теорему.

С понятием осевой симметрии также связано понятие симметричной фигуры:

Определение 5

Фигуру будем называть симметричной относительно какой-то своей оси, если при такой осевой симметрии фигура перейдет в себя
(рис. 3).

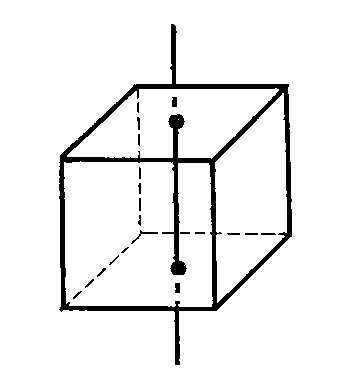
1.1. Осевая симметрия

Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему (Рисунок 2.1). Каждая точка прямой а считается симметричной самой себе.

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой a также принадлежит этой фигуре (Рисунок 2.2).

Прямая а называется осью симметрии фигуры.
Говорят также, что фигура обладает осевой симметрией.

Осевой симметрией обладают такие геометрические фигуры как угол, равнобедренный треугольник, прямоугольник, ромб (Рисунок 2.3).

Фигура может иметь не одну ось симметрии. У прямоугольника их две, у квадрата – четыре, у равностороннего треугольника – три, у круга – любая прямая, проходящая через его центр.

Если присмотреться к буквам алфавита (Рисунок 2.4)., то и среди них можно найти, имеющие горизонтальную или вертикальную, а иногда и обе оси симметрии. Объекты, имеющие оси симметрии достаточно часто встречаются в живой и неживой природе.

Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.

В своей деятельности человек создаёт много объектов (в том числе и орнаменты), имеющих несколько осей симметрии.

Примеры объектов с двумя осями симметрии

Две оси симметрии подразумевают наличие двух линий, относительно которых объект выглядит симметричным. Такие объекты могут быть найдены в различных областях, как естественных, так и искусственных. Вот несколько примеров объектов с двумя осями симметрии:

• Человеческое тело: тело человека обычно имеет две оси симметрии — вертикальную и горизонтальную. Вертикальная ось проходит по центру тела, разделяя его на левую и правую половины. Горизонтальная ось проходит через талию, разделяя тело на верхнюю и нижнюю половины.
• Лицо: лицо человека также имеет две оси симметрии. Вертикальная ось проходит по носу, разделяя лицо на левую и правую части. Горизонтальная ось проходит через глаза, разделяя лицо на верхнюю и нижнюю части.

Зооморфные объекты:

• Бабочка: у бабочки есть две оси симметрии, проходящие через ее тело. Вертикальная ось проходит по центру тела, а горизонтальная ось проходит через крылья, разделяя их на верхнюю и нижнюю половины.
• Муравей: тело муравья также имеет две оси симметрии. Вертикальная ось проходит по центру тела, а горизонтальная ось проходит через передние и задние ноги, разделяя тело на верхнюю и нижнюю части.

Объекты в природе:

• Раковина: раковина моллюска обычно имеет две оси симметрии. Вертикальная ось проходит по центру раковины, разделяя ее на две равные части. Горизонтальная ось проходит через верхнюю и нижнюю части раковины.
• Лист дерева: многие листья деревьев имеют две оси симметрии. Одна ось проходит вдоль центральной жилки листа, разделяя его на две одинаковые половины. Вторая ось проходит через лист поперек жилки, разделяя его на верхнюю и нижнюю части.

Архитектурные объекты:

• Корпус симметрии: в архитектуре существуют здания, имеющие две оси симметрии. Это могут быть симметричные здания с центральным проходом и двумя боковыми крыльями, расположенными по обе стороны.
• Украшения: некоторые украшения, такие как кулончики или серьги, могут иметь форму с двумя осями симметрии. Например, серьги в форме бабочек или с линейными элементами могут быть симметричными относительно вертикальной и горизонтальной оси.

Все эти примеры объектов с двумя осями симметрии иллюстрируют концепцию симметрии в различных контекстах, будь то естественный мир или искусство. Симметрия придает форме объекта баланс и гармонию.

Симметрия в повседневной жизни

Симметрия стала частью жизни человека уже в древние времена. Орнаменты с признаками зеркального отражения встречаются на античных зданиях, древнегреческих вазах. Свойство пропорционального расположения заимствовано в науку из природы. 

Зеркальное отражение часто встречается в живой и неживой природе. Этой характеристикой обладают снежинки. В растительном мире одинаково расположены противоположные элементы растений: большинство листьев зеркально отражаются сравнительно среднего стебля. В животном мире законы симметрии проявляются в наличии у животных правой и левой сторон. Большинство представителей фауны обладает парными частями тела: уши, лапы, глаза, крылья, рога. Ярким образцом зеркальной симметрии считается бабочка. Прямая, условно проведенная вдоль туловища насекомого по центру, является осью симметрии.

Поскольку человек – это часть природы, в своем творчестве он использует принцип симметрии. В искусстве свойство отражения применяется для создания красоты и гармонии. В архитектуре пропорциональность выполняет практическую функцию – придает зданиям устойчивость и надежность. В предметах быта можно встретить одинаковость в расположении частей узоров на коврах, принтов на ткани, рисунков обоев.

Роль осей симметрии в прямоугольниках и их применение

Горизонтальная ось симметрии делит прямоугольник на две равные части, которые отражаются друг относительно этой оси. Вертикальная ось симметрии также разделяет прямоугольник на две равные части, которые симметричны относительно оси.

Оси симметрии в прямоугольниках играют важную роль в практическом применении этой фигуры. Именно благодаря своим свойствам прямоугольники используются в различных областях нашей жизни.

Один из примеров использования прямоугольников — это строительство. Прямоугольник имеет простую форму и легко создается, поэтому часто используется при построении зданий и других сооружений. Благодаря оси симметрии прямоугольника, стены и окна могут быть размещены симметрично, что создает более гармоничный и эстетически привлекательный внешний вид.

Прямоугольник также широко применяется в дизайне и искусстве. Благодаря своей простой форме и симметричной структуре, прямоугольники используются в дизайне интерьера, создании картины или фотографии, а также в проектировании упаковки товаров. Отсутствие дополнительных осей симметрии помогает в создании уникального и эстетически привлекательного дизайна.

Оси симметрии в прямоугольниках также имеют практическое применение в математике и геометрии. Изучение свойств прямоугольников помогает усвоить понятия о симметрии и рассмотреть различные способы его применения в решении задач. Знание о двух осях симметрии прямоугольника помогает упростить расчеты и увеличивает точность результатов.

Прямоугольник	Оси симметрии	Применение
Строительство	Горизонтальная и вертикальная	Равномерное размещение окон и стен в зданиях
Дизайн и искусство	Горизонтальная и вертикальная	Создание эстетически привлекательных образов
Математика и геометрия	Горизонтальная и вертикальная	Усвоение понятий о симметрии и решении задач

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

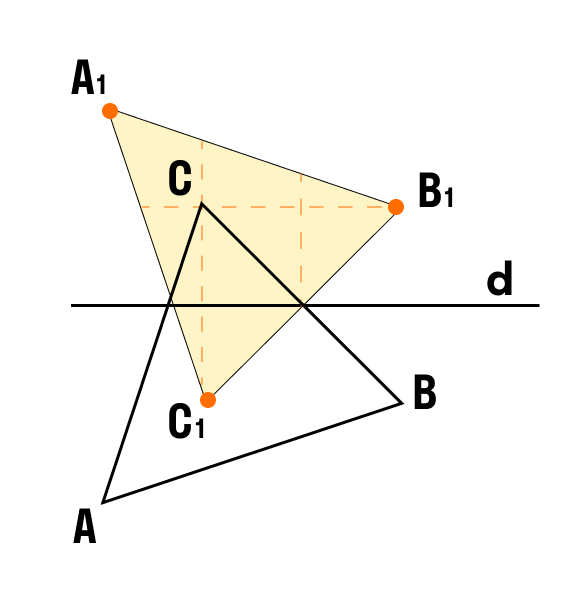
1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Проводим через точку А прямую, перпендикулярную прямой l.
2. Проводим через точку В прямую, перпендикулярную прямой l.
3. Измеряем расстояния от точек А и В до прямой l.
4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
5. Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Валы симметрии круга

Если вы наблюдаете любой круг, независимо от его радиуса, вы можете видеть, что не каждая линия, которая пересекает его, является осью симметрии..

Например, ни одна из линий, нарисованных на следующем рисунке, не является осью симметрии..

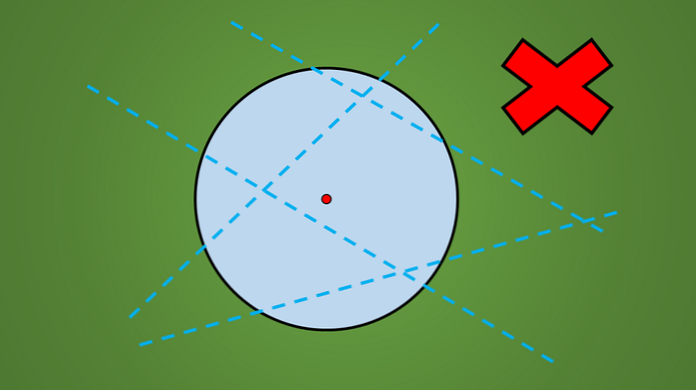
Простой способ проверить, является ли линия осью симметрии или нет, состоит в том, чтобы перпендикулярно отразить геометрическую фигуру к противоположной стороне линии..

Если отражение не соответствует исходному рисунку, то эта линия не является осью симметрии. Следующее изображение иллюстрирует эту технику.

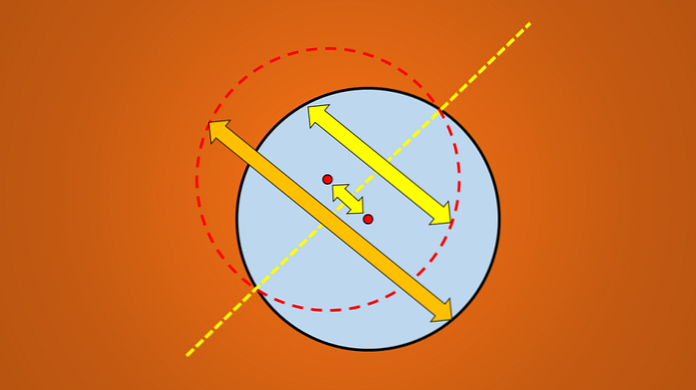
Но если рассматривается следующее изображение, хорошо известно, что нарисованная линия является осью симметрии круга.

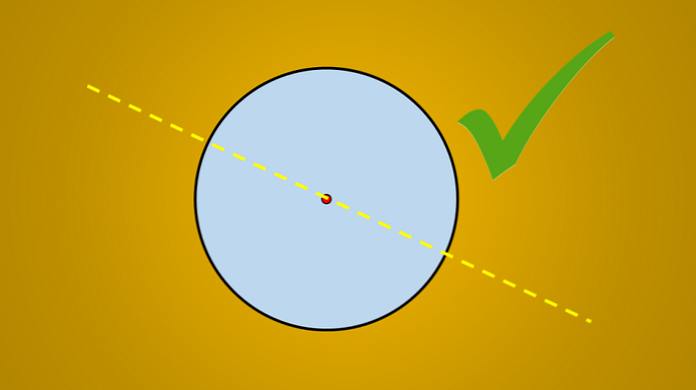
Вопрос: есть ли еще оси симметрии? Ответ — да. Если повернуть эту линию на 45 ° против часовой стрелки, полученная линия также является осью симметрии круга.

То же самое происходит, если вы поворачиваете на 90 °, 30 °, 8 ° и вообще на любое количество градусов.

Важной особенностью этих линий является не склонность, которую они имеют, но все они проходят через центр круга. Следовательно, любая линия, содержащая диаметр окружности, является осью симметрии.

Таким образом, поскольку круг имеет бесконечное число диаметров, то он имеет бесконечное количество осей симметрии.

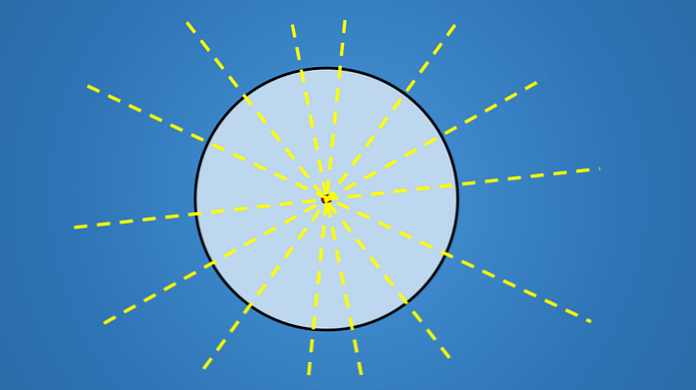
Другие геометрические фигуры, такие как треугольник, четырехугольник, пятиугольник, шестиугольник или любой другой многоугольник, имеют конечное число осей симметрии.

Причина, по которой круг имеет бесконечное число осей симметрии, заключается в том, что у него нет сторон.