Информатика

Причины двоичного кодирования в электронных вычислительных машинах

Человек для рукописного и машинописного текста применяет буквенные символы. Например, в нашем русском алфавите тридцать три буквы. Для записи чисел, как известно, мы используем всего десять цифр, от нуля до десяти. Для обработки графических изображений может потребоваться уже набор из порядка миллиона цветовых параметров. Диапазон слышимых человеком звуков простирается от, примерно, 16 до 20000 герц. Плюс ко всему вышеперечисленному, необходимо добавить осязание, способность различать запахи (обоняние), вкусовые ощущения человека, что в итоге выливается в очень большое количество самых разных потоков информации. Всё это способен анализировать, сохранять и перерабатывать мозговой центр человека.

Пока что современная техника не может воспроизвести полный аналог устройства мозга. Человеку наиболее легко проектировать устройства, которые имеют два стабильных состояния. Например, лампа включена или выключена, электрический ток протекает или нет, и тому подобное. Гораздо труднее научить ту же лампу, к примеру, при различных событиях засветиться одним, заданным заранее цветом, из большого набора цветовой палитры. Тем более, если вспомнить о примерно десяти миллионах, различаемых людьми, цветовых оттенков. В технических устройствах гораздо проще использовать много несложных модулей, чем малое количество, но очень усложнённых элементов. Для хранения и обработки информационных данных различными техническими устройствами и был создан немецким математиком Готфридом Лейбницем очень простая и очень удобная двоичная система кодирования или бинарный код. Он создал арифметику двоичных чисел и даже спроектировал вычислительную машину, работающую в двоичном коде, но довести её реально действующего устройства так и не смог.

С помощью различных комбинаций только нуля и единицы, в двоичном коде возможно сделать шифр любого числа, текста, звуков или графического изображения. Электронная вычислительная машина (компьютер), есть ни что иное, как прибор, служащий для сохранения и работы с информационными данными именно в таком формате.

Определение 1

Преобразование информации в бинарный код называют кодированием. Соответственно, обратное действие, при котором двоичный код снова преобразуется в понятный человеку формат, называют процессом декодирования.

Двоичный код алфавита: полное руководство по его пониманию

Двоичный код – это система представления информации с использованием всего двух символов: 0 и 1. Эта система широко используется в электронике и вычислительной технике, поскольку компьютеры и другие цифровые устройства внутренне работают с электрическими сигналами, которые могут иметь только два состояния.: на (1) или выключено (0). В этой статье мы объясним, как интерпретируется двоичный код и как он используется для представления букв алфавита.

Как работает двоичный код?

Двоичный код использует комбинацию нулей и единиц для представления различных значений. Каждая двоичная цифра называется битом (сокращение от двоичной цифры). Биты группируются в наборы по 8 штук, образуя байты, которые являются основной единицей хранения данных в компьютерных системах.

Для представления букв алфавита в двоичном коде используется стандарт ASCII (Американский стандартный код обмена информацией). В коде ASCII каждой букве, цифре и символу присвоено десятичное число, которое представляет его двоичный эквивалент. Например, буква «А» обозначается как 01000001, а буква «Z» — как 01011010.

Таблица двоичных кодов алфавита

A: 01000001

B: 01000010

C: 01000011

D: 01000100

E: 01000101

F: 01000110

G: 01000111

H: 01001000

I: 01001001

J: 01001010

K: 01001011

L: 01001100

M: 01001101

N: 01001110

O: 01001111

P: 01010000

Двоичный код алфавита: полное руководство по его пониманию
В мире электроники и вычислений двоичный код является фундаментальной системой представления и обработки информации. Хотя эта система в основном используется для представления чисел, ее также можно использовать для представления букв и других символов. В этой статье мы собираемся подробно изучить двоичный код алфавита и научиться говорить «привет» в двоичном формате.
Двоичный код основан на использовании двух цифр: 0 и 1. Эти цифры называются битами и являются основной единицей информации в двоичной системе. В двоичном коде каждая буква алфавита представлена ​​уникальной комбинацией битов.
Ниже приведена таблица, показывающая двоичный код, соответствующий каждой букве алфавита:
A: 01000001
B: 01000010
C: 01000011
D: 01000100
E: 01000101
F: 01000110
G: 01000111 XNUMX
H: 01001000
Я: 01001001
Дж: 01001010
К: 01001011
L: 01001100
М: 01001101
N: 01001110
О: 01001111
P: 01010000
Вопрос: 01010001
R: 01010010
S: 01010011
Т: 01010100
U: 01010101 XNUMX
V: 01010110
W: 01010111
X: 01011000
Y: 01011001
От: 01011010
Теперь, когда у нас есть двоичный код для каждой буквы, мы можем сказать «привет» в двоичном формате. Слово «здравствуйте» представлено следующим образом:
H: 01001000
О: 01001111
L: 01001100
A: 01000001
Что такое двоичная система и примеры
**Двоичный код алфавита: полное руководство по его пониманию**
Двоичная система — это способ представления информации с использованием только двух цифр: 0 и 1. Она широко используется в электронике и вычислительной технике, поскольку электронные компоненты и компьютерные программы работают с электрическими сигналами, которые могут быть включены или выключены, что представлено 1 и 0 соответственно. .
В случае алфавита каждая буква может быть представлена ​​уникальным двоичным кодом. Это означает, что каждой букве присвоена определенная комбинация 0 и 1

Например, буква А может быть представлена ​​как 01000001, буква Б — как 01000010 и так далее.
Важно отметить, что двоичный код алфавита основан на стандарте ASCII (Американский стандартный код обмена информацией). Стандарт ASCII присваивает каждому символу десятичное число, а затем преобразует это десятичное число в двоичное для получения соответствующего двоичного кода.
Вот вам таблица с двоичным кодом алфавита в ASCII:
A: 01000001
B: 01000010
C: 01000011
D: 01000100
E: 01000101
F: 01000110
G: 01000111 XNUMX
H: 01001000
Я: 01001001
Дж: 01001010
К: 01001011
L: 01001100
М: 01001101
N: 01001110
О: 01001111
P: 01010000
Вопрос: 01010001
R: 01010010
S: 01010011
Т: 01010100
U: 01010101 XNUMX
V: 01010110
W: 01010111
X: 01011000
Y: 01011001
От: 01011010
Важно отметить, что двоичный код алфавита может меняться.
Вот и всё, друг! Теперь вы знаток двоичного кода алфавита

Теперь вы можете поразить своих друзей своими знаниями о том, как компьютеры понимают наши буквы и слова. Помните, хотя на первый взгляд это может показаться сложным, двоичный код — это универсальный язык для машин. Так что продолжайте исследовать увлекательный мир электроники и узнавайте больше о двоичном коде и всех его приложениях! До новых встреч, бинарный брат!

История двоичного кода

Готфрид Лейбниц

Современная двоичная система счисления, основа двоичного кода, была изобретена Готфридом Лейбницем в 1689 году и появилась в его статье « Объяснение двоичной арифметики» в 1703 году.

Полное название — «Объяснение бинарной арифметики, в которой используются только символы O и I с замечаниями о ее полезности и о том, как она передает значение древних китайских фигур Фохи ». В системе Лейбница используются 0 и 1, как в современной двоичной системе счисления.

Лейбниц открыл И Цзин через французского иезуита Иоахима Буве и с восхищением отметил, как его гексаграммы соответствуют двоичным числам 0-111111, и пришел к выводу, что это отображение является свидетельством основных достижений Китая в области философской математики, которой он восхищался. Лейбниц видел в гексаграммах подтверждение универсальности его собственной религиозной веры.

Двоичные числа были в центре теологии Лейбница. Он считал, что двоичные числа символизируют христианскую идею creatio ex nihilo или сотворения из ничего. Лейбниц пытался найти систему, которая преобразует словесные утверждения из логики в чисто математическую систему. После того как его идеи были проигнорированы, он обнаружил классический китайский текст под названием И Цзин или «Книга перемен», в котором использовался тип двоичного кода. Книга подтвердила его теорию о том, что жизнь можно упростить или свести к ряду простых утверждений.

Он создал систему, состоящую из строк нулей и единиц. В этот период Лейбниц еще не нашел применения этой системе.

Бинарные системы до Лейбница также существовали в древнем мире. Цзин отметил , что Лейбниц обнаружил даты с IX — го  века  до нашей эры. Нашей эры в Китае. Бинарная система И Цзин , текста, посвященного гаданию, основана на двойственности Инь и Ян . Щелевые барабаны с двоичными звуками использовались для кодирования сообщений в Африке и Азии. Индийский ученый Пингала (около V — го  -  II — го  века  . До н.э. ) разработал двоичную систему для описания просодии в Chandashutram .

Джордж Буль

Жители острова Мангареву в Французской Полинезии с использованием гибридной системы десятичной, двоичной , прежде чем 1450 XI — го  века, ученый и философ Шао Юн разработал метод организации гексаграммы, который, однако невольно, в последовательности от 0 до 63, представлен в двоичном формате, где инь — 0, ян — 1, а младший бит находится вверху. Заказ также лексикографический порядок из sextuples элементов , выбранных из набора из двух элементов.

В 1605 году Фрэнсис Бэкон обсуждал систему, с помощью которой буквы алфавита можно было преобразовать в последовательности двоичных цифр, которые затем можно было закодировать как едва заметные вариации шрифта в любом тексте

Что важно в отношении общей теории двоичного кодирования, он добавил, что этот метод может использоваться с любым объектом: «при условии, что эти объекты могут иметь только двойное различие; как с колокольчиками, трубами, фонарями, факелами, мушкетами и всеми подобными инструментами»

В 1847 году Джордж Буль опубликовал статью, озаглавленную «Математический анализ логики», в которой описывается алгебраическая логическая система, в дальнейшем называемая алгеброй Буля . Система Буля была основана на бинарном подходе «да-нет», включающем три основные операции: И, ИЛИ и НЕТ. Эта система не использовалась и была забыта до тех пор , аспирант Массачусетского технологического института , Клод Шеннон , понял , что Булева алгебра он узнал , была подобна электрической цепью. Шеннон написала диссертацию в 1937 году, в которой были реализованы ее открытия. Диссертация Шеннона стала отправной точкой для использования двоичного кода в практических приложениях, таких как компьютеры, электрические схемы и т. Д.

Каковы функции переводчиков двоичного кода?

Существует несколько вариантов использования преобразователя двоичного кода в ASCII, который может преобразовывать двоичный код в удобочитаемый текст и наоборот. Давайте рассмотрим основы этого онлайн-ресурса:

№1. Преобразование двоичного кода в текст

Важно знать, что эта бесплатная веб-программа может переводить двоичный код на удобочитаемый английский язык, присваивая значение каждой последовательности двоичных чисел. Это можно сделать с соответствующими символами, которые основаны на схеме кодировки символов, такой как ASCII или Unicode

№2. Преобразование двоичных чисел в десятичные

С помощью бесплатного онлайн-декодера двоичных чисел вы теперь можете конвертировать двоичные числа в их десятичные эквиваленты. Для этого мы должны умножить каждый бит на соответствующую ему степень 2 и сложить полученные числа. Вам нужно просто добавить значения в инструмент и получить результаты через пару секунд.

№3. Преобразование десятичной системы в двоичную

Если вам нужно преобразовать десятичные данные в двоичные, то этот абсолютно бесплатный онлайн-конвертер двоичных чисел в ASCII — ваш лучший выбор. Кроме того, транслятор двоичного кода позволяет вводить десятичные целые числа, которые затем представляются в двоичном виде посредством серии делений на 2.

№4. Преобразование текста в двоичный код

Если вы хотите преобразовать текст в двоичный код, вы можете использовать этот инструмент, поскольку он позволяет вводить текст и преобразовывать его в двоичный код. Имейте в виду, что, поскольку он использует определенную схему кодирования символов, каждый символ в тексте преобразуется в соответствующее ему двоичное представление.

№5. Обнаружение и исправление ошибок

Самое лучшее в этом онлайн-переводчике с бинарного языка на английский — это то, насколько быстро он может помочь вам обнаружить и исправить ошибки. Из-за природы двоичного кода трансляторы включают процедуры обнаружения и исправления ошибок, чтобы гарантировать целостность передаваемых или хранимых данных.

Современное использование двоичного кодирования

Двоичное кодирование остается одним из основных принципов работы компьютеров и других цифровых устройств в настоящее время. Это связано с его простотой и эффективностью при хранении, передаче и обработке данных.

В современном мире двоичное кодирование используется во множестве областей, включая программирование, сетевые технологии, криптографию и многое другое. Компьютеры работают исключительно с двоичными данными, поэтому все отображение и использование символов, чисел и других типов данных основаны на их двоичном представлении.

В программировании двоичное кодирование используется для представления и хранения чисел, текстов, изображений и других типов данных. В сетевых технологиях двоичное кодирование используется для передачи данных по сети, а также для управления и обмена информацией между компьютерами.

Криптография является еще одной областью, где двоичное кодирование играет важную роль. Шифрование и дешифрование данных основаны на преобразовании информации в двоичную форму и обратно. Это позволяет обеспечить безопасность при передаче и хранении данных.

Несмотря на то, что двоичное кодирование может сложно выглядеть для неспециалистов, оно остается неотъемлемой частью нашей цифровой жизни. Знание основ двоичного кодирования помогает понять, как работают компьютеры и обеспечить эффективное использование цифровых технологий.

Итак, почему компьютеры используют двоичные файлы?

Короткий ответ: аппаратное обеспечение и законы физики. Каждый номер вашего компьютера является электрическим сигналом, и в первые дни вычислений электрические сигналы были намного сложнее измерить и контролировать очень точно. Было более разумно различать только «включенное» состояние, представленное отрицательным зарядом, и «выключенное» состояние, представленное положительным зарядом. Для тех, кто не знает, почему «выключено» представлено положительным зарядом, это связано с тем, что электроны имеют отрицательный заряд, а больше электронов — больше тока с отрицательным зарядом.

Таким образом, ранние компьютеры размером с комнату использовали двоичные файлы для создания своих систем, и хотя они использовали гораздо более старые, более громоздкие аппаратные средства, мы придерживались одних и тех же основополагающих принципов. Современные компьютеры используют так называемый транзистор для выполнения расчетов с двоичным кодом. Вот схема того, как выглядит полевой транзистор (FET):

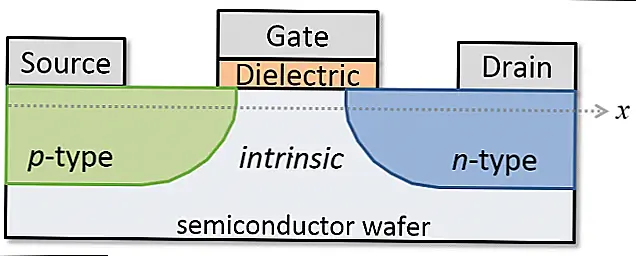По сути, он позволяет только ток течь от источника к стоку, если в воротах есть ток. Это формирует двоичный ключ. Производители могут строить эти транзисторы невероятно малыми — вплоть до 5 нанометров или размером с две нити ДНК. Это то, как работают современные процессоры, и даже они могут страдать от проблем, различающих состояние включения и выключения (хотя это в основном связано с их нереальным молекулярным размером, подверженным странности квантовой механики).

Подсчет в двоичном формате

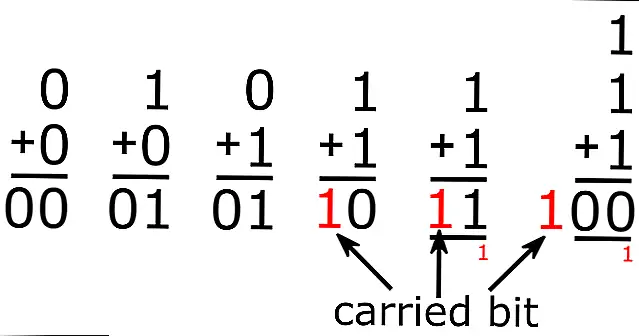В двоичном выражении первая цифра стоит 1 в десятичной системе. Вторая цифра стоит 2, третья — 4, четвертая — 8, и так далее — удваивается каждый раз. Добавление всех этих значений дает вам число в десятичном формате. Так,

Учет 0, это дает нам 16 возможных значений для четырех двоичных битов. Переместитесь на 8 бит, и вы получите 256 возможных значений. Это занимает намного больше места для представления, поскольку четыре цифры в десятичной форме дают нам 10 000 возможных значений. Может показаться, что мы преодолеем всю эту проблему, чтобы заново изобрести нашу систему подсчета, чтобы сделать ее clunkier, но компьютеры понимают двоичные файлы намного лучше, чем они понимают десятичную. Конечно, бинарный занимает больше места, но мы сдерживаем аппаратное обеспечение. И для некоторых вещей, таких как логическая обработка, двоичный код лучше десятичного.

Есть еще одна базовая система, которая также используется в программировании: шестнадцатеричная. Хотя компьютеры не работают в шестнадцатеричном формате, программисты используют его для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры шестнадцатеричного числа могут представлять собой целый байт, восемь цифр в двоичном формате. Шестнадцатеричный использует 0-9, как десятичный, а также буквы от A до F, чтобы представить дополнительные шесть цифр.

Эволюция двоичного кодирования

Первые шаги в развитии двоичного кодирования были сделаны еще в Древнем Китае и Индии. Например, в Китае двоичные числа были использованы для представления дат и времени еще в III веке до н.э.

Однако наибольшее развитие двоичное кодирование получило в XIX веке. В 1801 году французский математик Готфрид Бине внес значительный вклад в развитие двоичной системы с помощью своей работы «Теория алгебры». Он впервые предложил использовать двоичные числа для представления чисел и выполнения арифметических операций.

Дальнейшее развитие двоичного кодирования было связано с развитием коммуникационных систем и электронных устройств. Первыми шагами в этом направлении стали исследования американского инженера Томаса Эдисона в области телеграфии и изобретение им телеграфного аппарата, который использовал двоичный код для передачи сообщений.

Затем, в 1947 году, появился транзистор — небольшое электронное устройство, которое стало основой для создания компьютеров. Он позволял создавать электронные устройства, которые могли работать с двоичными кодами.

Таким образом, двоичное кодирование продолжало развиваться и расширять свои возможности с появлением новых технологий и открытий. Сегодня эта система кодирования стала неотъемлемой частью многих сфер деятельности, особенно в области компьютерной науки и информационных технологий.

Важно отметить, что с развитием двоичного кодирования возникли другие системы кодирования, такие как шестнадцатеричная и восьмеричная, которые используются для более компактного представления двоичных данных

Раздел 3: Эффективность работы с двоичными числами

Почему в ЭВМ используется двоичная система счисления? Ответ на этот вопрос связан с эффективностью работы с двоичными числами.

Двоичная система счисления состоит из двух цифр: 0 и 1. Компьютеры работают с электрическими сигналами, которые могут принимать только два состояния: включено (1) или выключено (0). Таким образом, использование двоичной системы счисления позволяет компьютерам легко представлять и обрабатывать данные.

Использование двоичной системы счисления в ЭВМ обеспечивает следующие преимущества:

• Простота представления данных: Двоичные числа легко представляются в виде последовательности 0 и 1, что упрощает их хранение и обработку.
• Меньшие затраты ресурсов: Использование двоичных чисел позволяет сократить объем используемой памяти и уменьшить количество переключений состояний в электрических схемах, что значительно экономит ресурсы ЭВМ.
• Более надежная передача данных: Двоичные числа менее чувствительны к помехам и искажениям сигнала, что повышает надежность передачи данных между устройствами.

Кроме того, двоичная система счисления также обладает простой и легко интерпретируемой структурой, что позволяет программистам и инженерам более эффективно разрабатывать и отлаживать программное и аппаратное обеспечение. Большинство алгоритмов и операций в компьютерах строятся на основе двоичной логики, что делает их более эффективными и быстрыми.

В результате, использование двоичной системы счисления в ЭВМ является необходимым для обеспечения оптимальной эффективности работы компьютеров во всех областях: от арифметических операций до обработки сигналов и передачи данных.

Простота реализации и исполнения операций

Двоичная система счисления является основой для работы с данными в электронно-вычислительной машине (ЭВМ). Почему именно двоичная система выбрана для этой цели?

Простота реализации и исполнения операций является одной из основных причин использования двоичной системы счисления в ЭВМ. В двоичной системе счисления всего две цифры — 0 и 1. Это делает ее легкой для понимания и использования в микроэлектронике, где используются только два электрических состояния — высокий и низкий уровень напряжения.

Использование двоичной системы счисления позволяет создавать простые и надежные логические схемы, основанные на применении логических элементов, таких как И, ИЛИ и НЕ. Такие схемы легко реализуются на базе транзисторов, которые являются основными строительными блоками современных компьютеров.

Одной из особенностей двоичной системы счисления является то, что любая ее операция можно представить с помощью логических операций. Например, сложение двоичных чисел сводится к применению операций И, ИЛИ и ИСКЛЮЧАЮЩЕЕ ИЛИ, а умножение — к циклическому сдвигу и сложению. Это упрощает исполнение арифметических и логических операций в современных процессорах.

Поэтому двоичная система счисления выбрана для использования в ЭВМ, так как она обеспечивает простоту реализации и исполнения операций, а также легко совмещается с принципом работы электронных устройств и логики компьютерных систем.

Минимизация потребления ресурсов

Почему в электронно-вычислительных машинах (ЭВМ) используется двоичная система счисления? Одной из главных причин является минимизация потребления ресурсов.

Двоичная система счисления основана на двух цифрах — 0 и 1. Использование двух цифр вместо десяти или другого количества цифр значительно упрощает процесс обработки информации в ЭВМ. Переключение между двумя состояниями — включено (1) или выключено (0) — легче и быстрее, чем переключение между большим числом состояний.

Это позволяет сократить количество ресурсов, необходимых для работы ЭВМ. В случае использования других систем счисления, требовалось бы больше электрических сигналов и более сложные устройства для их обработки. Также, использование двоичной системы счисления обеспечивает более надежную передачу информации, так как два состояния легче различать, чем множество состояний.

Кроме того, двоичная система позволяет использовать простые логические операции, основанные на применении алгоритмов с двумя состояниями. Это позволяет сокращать время выполнения программ и повышать эффективность работы ЭВМ.

Все это делает двоичную систему счисления наиболее подходящим выбором для использования в электронно-вычислительных машинах, так как она помогает минимизировать потребление ресурсов, упрощает обработку информации и обеспечивает надежность передачи данных.

Преимущества и недостатки использования двоичного кода

Преимущества использования двоичного кода:

1. Простота и надежность: Двоичный код прост в понимании и реализации. Он использует только два символа, что облегчает его передачу и хранение. Кроме того, двоичный код более устойчив к ошибкам, поскольку любые искажения информации могут быть обнаружены и исправлены с помощью специальных алгоритмов.

2. Система иерархического представления: Двоичный код удобен для организации больших объемов информации. Он позволяет построить иерархическую систему представления данных, где каждый уровень может быть разделен на два подуровня, и так далее. Это позволяет эффективно хранить и передавать информацию.

3. Совместимость с цифровыми устройствами: Практически все цифровые устройства работают на основе двоичного кода. Поэтому использование этого кода помогает обеспечить совместимость с широким спектром устройств и обеспечивает плавную передачу информации между ними.

Недостатки использования двоичного кода:

1. Информационная плотность: Двоичный код имеет низкую информационную плотность, поскольку каждый байт данных требует 8 бит для представления. Это может привести к неэффективному использованию ресурсов памяти и пропускной способности.

2. Сложность человеческого восприятия: Двоичный код может быть сложен для понимания и интерпретации человеком. Его использование требует обучения и специализированных знаний, что может быть ограничивающим фактором для пользователей.

3. Время обработки информации: При работе с двоичным кодом обычно требуется больше времени на обработку информации. Это связано с необходимостью выполнения множества операций для перевода и интерпретации кода в понятный вид для пользователя.

Несмотря на некоторые недостатки, использование двоичного кода остается основным и необходимым компонентом в области цифровых технологий и информационных систем. Он обеспечивает надежность и эффективность функционирования множества устройств и позволяет реализовывать сложные вычисления и обработку данных.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.Брукшир Д.Ж. Информатика и вычислительная техника. 7-ое издание. Питер 2004 год. 620 страниц;

2.Гуда А.Н., Бутакова М.А., Нечитайло Н.М, Чернов А.В. Информатика. Общий курс. Ростов на Дону 2008 год. 400 страниц;

3.Мобилев А.В. Информатика. Учебное пособие для студентов педагогических вузов. Москва 1999 год. 816 страниц;

4.Пачкин С.Г. Вычислительные машины, системы и сети. Кемерово 2009 год. 196 страниц;

5.Степанов А.Н. Информатика. Учебник для вузов. 5-ое издание. Питер 2007 год. 756 страниц;

6.Соболь Б.В. Информатика. Учебник. Ростов на Дону 2006 год. 448 страниц.

7. https://www.sites.google.com/site/setiinformatika/home/predstavlenie-informacii

• Жизненный цикл организации..
• Новая экономика: ее суть и факторы развития
• Понятие дипломатических привилегий и иммунитетов
• Современное мировое хозяйство: понятие и сущность; структура, субъекты и тенденции развития
• Правовые основы использования информационных систем
• История химии
• Дипломатия. Принципы. Задачи. Методы
• Российский фондовый рынок: проблемы и перспективы
• Законодательство в сфере защиты информации
• Понятие и разновидности спора
• деловой этикет
• Личность И.В.Сталина

Другие формы двоичного кода

Даосский багуа

Битовая строка — не единственный тип двоичного кода. В общем, двоичная система — это система, которая допускает только два выбора, например, переключатель в электронной системе или простой тест на истинность или ложь.

Шрифт Брайля

Шрифтом Брайля является тип бинарного кода широко используется слепым людям читать и писать на ощупь, названный в честь его создателя, Луи Брайля. Эта система состоит из сеток по шесть точек в каждой, по три на столбец, в которых каждая точка имеет два состояния: высокое или невысокое. Различные комбинации выпуклых и плоских точек могут представлять любую букву, цифру и знак препинания.

Багуа

В Багуа представлены диаграммы , используемые в исследованиях фэн — шуй , в космологии даосской и цзин . Ба гуа состоит из 8 триграмм; bā означает 8, а guà означает фигуру гадания. То же слово используется для 64 гуа (гексаграмм). Каждая фигура объединяет три линии ( yáo ), которые либо прерваны ( инь ), либо не прерваны ( янь ). Отношения между триграммами представлены в двух формах: изначальное багуа , «Старое небо» или «Фуси», и проявленное багуа , «Позднее небо» или «Король Вэнь» . (См. Также последовательность 64 гексаграмм короля Вэня ).