Содержание
- Для использования в других целях, см Сфера (значения).
А сфера симметричный геометрический объект. В нематематическом использовании этот термин используется для обозначения круглого шара или его двумерной поверхности. В математике сфера — это совокупность всех точек в трехмерном пространстве (р3) которые находятся на расстоянии р из фиксированной точки этого пространства, где р положительное действительное число, называемое радиус сферы. Таким образом, в трех измерениях математическая сфера считается сферической поверхностью, а не объемом, содержащимся в ней. Неподвижная точка называется центр, и не является частью самой сферы. Частный случай р = 1 называется единичная сфера.
В этой статье рассматривается математическая концепция шара. В физике сфера — это объект (обычно идеализированный для простоты), способный сталкиваться или складываться с другими объектами, занимающими пространство.
Обобщение на метрические пространства
В более общем смысле, в метрическом пространстве (E,d), сфера центра Икс и радиус Шаблон: Ambox — это набор точек у такой, что d(Икс,у) = р.
Если центр является выделенной точкой, рассматриваемой как начало E, как и в нормированном пространстве, он не упоминается в определении и обозначениях. То же самое относится и к радиусу, если он принимается равным единице, как в случае единичной сферы.
В отличие от шара, сфера может быть пустым множеством даже для большого радиуса. Например, в Zп с евклидовой метрикой сфера радиуса р непусто, только если р2 можно записать как сумму п квадраты целых чисел.
Применение единичной сферы в физике и геометрии
Единичная сфера — это сфера радиусом 1, центр которой находится в начале координат. Она является одним из основных объектов в физике и геометрии и находит широкое применение в различных областях науки.
Физика
- Единичная сфера используется в физических моделях для описания тел и их взаимодействия. Она может представлять атом, молекулу, элементарную частицу или другую физическую систему.
- В механике единичная сфера может быть использована для моделирования вращательного движения объектов. Она помогает определить оси вращения и угловые скорости.
- В квантовой механике единичная сфера используется для представления состояний спина частицы. Она позволяет описать различные направления спина и его квантовые состояния.
Геометрия
- Единичная сфера является основным объектом изучения в сферической геометрии. Она позволяет рассматривать свойства и отношения на сфере, такие как длины дуг, углы, площади и объемы.
- Сферическая геометрия находит применение в навигации и астрономии, где рассматриваются движения и расположение объектов на поверхности Земли или на небесной сфере.
- Единичная сфера также используется в компьютерной графике для создания 3D-моделей и визуализации объектов. Она служит основой для расчета освещения, отражения и преломления света.
Применение единичной сферы в физике и геометрии демонстрирует ее важность и универсальность в научных и практических исследованиях. Благодаря единичной сфере мы можем лучше понимать и описывать мир вокруг нас, от микро- и макрообъектов до географических и космических явлений
Сферические объекты в космосе
В космосе можно наблюдать множество сферических объектов, которые имеют важное значение для нашего изучения Вселенной. Вращение единого тела вокруг своей оси опережает формирование плоских систем, таких как диски или кольца
Знание геометрических фигур, которые получаются при вращении сферы, позволяет нам лучше понять структуру и форму различных космических объектов.
| Объект | Описание |
|---|---|
| Планета | Множество планет в нашей Солнечной системе являются сферическими объектами. Их форма определяется их собственной гравитацией, которая пытается сделать их самыми симметричными. |
| Луна | Луны, которые обращаются вокруг планеты, также имеют сферическую форму. Например, Луна Земли представляет собой близкую к сфере форму, хотя небольшие аномалии в ее форме вызываются ее неоднородностью и гравитационными эффектами. |
| Кометы | Кометы, пролетающие через нашу Солнечную систему, часто имеют сферическую форму. Это связано с давлением солнечного ветра и образованием атмосферной оболочки вокруг ядра кометы, которая защищает ее от высоких температур. |
| Звезды | Хотя звезды имеют форму сферы из-за внутреннего давления и гравитационного сжатия, некоторые из них могут иметь неравномерную форму из-за гравитационного взаимодействия с другими звездами или вращения. |
| Галактики | Множество галактик имеют сферическую форму, но эта форма может быть значительно искажена из-за гравитационных сил и динамических процессов внутри галактик. |
Исследование и наблюдение этих сферических объектов в космосе помогает нам расширить нашу картину Вселенной и лучше понять ее форму и структуру.
Круглые тела в математике: все, что вам нужно знать
Круглые тела — это тела, которые могут быть описаны круговой или эллиптической поверхностью. Эти фигуры имеют большое значение в геометрии, физике и инженерных науках.
Одним из наиболее известных круглых тел является сфера. Сфера — это круглое тело, у которого каждая точка на поверхности находится на одинаковом расстоянии от центра. Объем сферы можно вычислить по формуле V = (4/3)πr³, где r — радиус сферы, π — число пи.
Другие примеры круглых тел включают конус, тор, шарнир и т.д. Круглые тела широко используются в производстве и конструировании для создания деталей, машин и сооружений, таких как мосты и здания. Некоторые известные строения, такие как Эйфелева башня и Гуггенхайм-музей, используют круглые формы и круглые тела в своем дизайне.
Суммируя, круглые тела — это важная тема в математике и инженерии. Их формулы и свойства не только позволяют рассчитывать объемы и площади поверхности, но и дают возможность создавать красивые и эффективные конструкции. Поэтому, знание круглых тел является необходимым и полезным для всех, кто занимается наукой и технологией.
Единичные шары в нормированных векторных пространствах
Точнее, открытый шар в нормированное векторное пространство V{ displaystyle V}, с норма ‖⋅‖{ displaystyle | cdot |}, является
- {Икс∈V‖Икс‖<1}{ Displaystyle {х в V: | х |
Это интерьер из закрытый шар из (V,||·||):
- {Икс∈V‖Икс‖≤1}{ Displaystyle {х в V: | х | Leq 1 }}
Последнее представляет собой несвязанный союз первых и их общую границу, единичная сфера из (V,||·||):
- {Икс∈V‖Икс‖=1}{ Displaystyle {х в V: | х | = 1 }}
«Форма» единичный мяч полностью зависит от выбранной нормы; он вполне может иметь «углы» и, например, может выглядеть как п, в случае max-нормы в рп. Естественно получается круглый мяч как единичный шар, относящийся к обычному Гильбертово пространство нормы, основанной в конечномерном случае на Евклидово расстояние; его граница — это то, что обычно подразумевается под единичная сфера.
Позволять Икс=(Икс1,…Иксп)∈рп.{ displaystyle x = (x_ {1}, … x_ {n}) in mathbb {R} ^ {n}.} Определите обычный ℓп{ displaystyle ell _ {p}}-норма для п ≥ 1 как:
- ‖Икс‖п=(∑k=1п|Иксk|п)1п{ Displaystyle | х | _ {p} = ( sum _ {k = 1} ^ {n} | x_ {k} | ^ {p}) ^ {1 / p}}
потом ‖Икс‖2{ Displaystyle | х | _ {2}} это обычный Гильбертово пространство норма.‖Икс‖1{ Displaystyle | х | _ {1}} называется нормой Хэмминга, или ℓ1{ displaystyle ell _ {1}}-norm. состояние п ≥ 1 необходимо в определении ℓп{ displaystyle ell _ {p}} норма, поскольку единичный шар в любом нормированном пространстве должен быть выпуклый как следствие неравенство треугольника.Позволять ‖Икс‖∞{ Displaystyle | х | _ { infty}} обозначим max-норму или ℓ∞{ displaystyle ell _ { infty}}-норма x.
Обратите внимание, что для окружностей Cп{ displaystyle C_ {p}} двумерных единичных шаров (n = 2) имеем:
- C1=42{ displaystyle C_ {1} = 4 { sqrt {2}}} — минимальное значение.
- C2=2π.{ Displaystyle C_ {2} = 2 пи ,.}
- C∞=8{ displaystyle C _ { infty} = 8} — максимальное значение.
Значение в естествознании
Совершенство сферической формы издавна привлекало внимание мыслителей и учёных, которые с помощью сфер пытались объяснить гармонию окружающего мира. Древнегреческий учёный Пифагор вместе с шарообразной Землёй в центре Вселенной ввёл окружающую Землю удалённую хрустальную сферу, к которой прикреплены звёзды, и семь более близких вращающихся хрустальных сфер, к которым прикреплены Солнце, Луна и пять известных к тому времени планет (исключая Землю)
Эта модель впоследствии усложнялась: Евдокс Книдский рассматривал уже 27 подобных сфер, а Аристотель — 55 хрустальных сфер. Представления о вращающихся небесных сферах господствовали по крайней мере до средних веков и даже вошли в гелиоцентрическую систему мира Николая Коперника, который назвал свой основной труд «О вращении небесных сфер» (лат. De revolutionibus orbium coelestium).
Небесные сферы со времён Древней Греции были частью более общей концепции гармонии сфер о музыкально-астрономическом устройстве мира, куда также входило понятие «музыка сфер». Эта концепция также существовала как минимум до средневековья. У одного из известнейших астрономов, Иоганна Кеплера, сфера занимала центральное место во всей его системе религиозно-мистических представлений, он писал: «Образ триединого бога есть сферическая поверхность, а именно: бог-отец в центре, бог-сын — на поверхности и святой дух — в симметричном отношении между центром и описанной вокруг него сферической поверхностью». Одно из первых значительных сочинений Кеплера, «Тайна мироздания» (лат. Mysterium Cosmographicum), было посвящено параметрам небесных сфер, Кеплер считал, что он открыл замечательную связь между правильными многогранниками, которых только пять, и небесными сферами шести известных к тому времени планет (включая Землю), являвшимися, по Кеплеру, описанными и вписанными сферами этих многогранников. Представления о гармонии сфер сыграли большую роль при открытии Кеплером третьего закона движений небесных тел (во всяком случае, могут рассматриваться как стимул к поиску астрономических соотношений). Однако у Кеплера небесные сферы являлись уже чисто математическими объектами, а не физически существующими телами. К тому времени Тихо Браге показал, что движение комет, в частности, Большой кометы 1577 года, несовместимо с существованием твердых небесных сфер. Как удобная математическая модель, осталась одна небесная сфера, с помощью которой астрономы по сей день представляют видимые положения звезд и планет.
Ключевые особенности единичной сферы
Единичная сфера — это геометрическая фигура, представляющая собой сферу радиусом 1 и центром в начале координат. Она является одной из фундаментальных фигур в математике и имеет несколько ключевых особенностей:
Радиус 1: Единичная сфера имеет фиксированный радиус, который равен 1. Это означает, что все точки на поверхности сферы находятся на одном и том же расстоянии от центра.
Симметрия: Единичная сфера обладает сферической симметрией. Это означает, что она выглядит одинаково независимо от направления, из которого на нее смотреть. Например, если повернуть единичную сферу на 180 градусов вокруг любой оси, она все равно будет выглядеть идентично.
Площадь поверхности: Площадь поверхности единичной сферы составляет 4π
Это важное свойство, которое используется в различных математических и физических рассуждениях.
Интегральные сферические координаты: Единичная сфера играет ключевую роль в интегральных сферических координатах, которые широко используются в математическом анализе и физике. Они позволяют описывать трехмерное пространство с помощью угловых и радиальных координат.
Единичная сфера имеет множество приложений в различных областях математики и физики. Она используется в геометрии, алгебре, теории вероятностей, теории управления, гравитации и других науках. Понимание ключевых особенностей единичной сферы позволяет математикам и исследователям проводить сложные вычисления и получать новые знания о пространстве и его свойствах.
Единичные сферы и шары в евклидовом пространстве
В Евклидово пространство из п размеры, (п−1)-мерная единичная сфера — это множество всех точек (Икс1,…,Иксп){ displaystyle (x_ {1}, ldots, x_ {n})} которые удовлетворяют уравнению
- Икс12+Икс22+⋯+Иксп2=1.{ displaystyle x_ {1} ^ {2} + x_ {2} ^ {2} + cdots + x_ {n} ^ {2} = 1.}
В п-мерный единичный открытый шар — это множество всех точек, удовлетворяющих неравенство
- Икс12+Икс22+⋯+Иксп2<1,{ displaystyle x_ {1} ^ {2} + x_ {2} ^ {2} + cdots + x_ {n} ^ {2}
и п-мерный замкнутый единичный шар — это множество всех точек, удовлетворяющих неравенство
- Икс12+Икс22+⋯+Иксп2≤1.{ displaystyle x_ {1} ^ {2} + x_ {2} ^ {2} + cdots + x_ {n} ^ {2} leq 1.}
Общие формулы площади и объема
Классическое уравнение единичной сферы — это уравнение эллипсоида с радиусом 1 и без изменений Икс-, у-, или же z— оси:
- ж(Икс,у,z)=Икс2+у2+z2=1{ displaystyle f (x, y, z) = x ^ {2} + y ^ {2} + z ^ {2} = 1}
Объем единичного шара в п-мерное евклидово пространство и площадь поверхности единичной сферы появляются во многих важных формулах анализ. Объем единичного шара в п размеры, которые мы обозначим Vп, можно выразить с помощью гамма-функция. это
- Vп=πп2Γ(1+п2)={πп2(п2)!яж п≥ яs еvеп, π⌊п2⌋2⌈п2⌉п!!яж п≥ яs оdd,{ displaystyle V_ {n} = { frac { pi ^ {n / 2}} { Gamma (1 + n / 2)}} = { begin {case} { pi ^ {n / 2}} / {(n / 2)!} & mathrm {if ~} n geq 0 mathrm {~ ~ четное,} ~ { pi ^ { lfloor n / 2 rfloor} 2 ^ { lceil n / 2 rceil}} / {n !!} & mathrm {если ~} n geq 0 mathrm {~ ~ нечетное,} end {case}}}
куда п!! это двойной факториал.
Гиперобъем (п−1) -мерная единичная сфера (т.е., «площадь» границы п-мерный единичный шар), который обозначим Ап, можно выразить как
- Ап=пVп=пπп2Γ(1+п2)=2πп2Γ(п2),{ displaystyle A_ {n} = nV_ {n} = { frac {n pi ^ {n / 2}} { Gamma (1 + n / 2)}} = { frac {2 pi ^ {n / 2}} { Gamma (n / 2)}} ,,}
где последнее равенство выполняется только для п > 0.
Площади поверхности и объемы для некоторых значений п{ displaystyle n} являются следующими:
| п{ displaystyle n} | Ап{ displaystyle A_ {n}} (площадь поверхности) | Vп{ displaystyle V_ {n}} (объем) | ||
|---|---|---|---|---|
| (1!)π{ displaystyle 0 (1/0!) pi ^ {0}} | (1!)π{ displaystyle (1/0!) pi ^ {0}} | 1 | ||
| 1 | 1(211!!)π{ displaystyle 1 (2 ^ {1} / 1 !!) pi ^ {0}} | 2 | (211!!)π{ displaystyle (2 ^ {1} / 1 !!) pi ^ {0}} | 2 |
| 2 | 2(11!)π1=2π{ Displaystyle 2 (1/1!) pi ^ {1} = 2 pi} | 6.283 | (11!)π1=π{ Displaystyle (1/1!) pi ^ {1} = pi} | 3.141 |
| 3 | 3(223!!)π1=4π{ Displaystyle 3 (2 ^ {2} / 3 !!) pi ^ {1} = 4 pi} | 12.57 | (223!!)π1=(43)π{ Displaystyle (2 ^ {2} / 3 !!) pi ^ {1} = (4/3) pi} | 4.189 |
| 4 | 4(12!)π2=2π2{ Displaystyle 4 (1/2!) pi ^ {2} = 2 pi ^ {2}} | 19.74 | (12!)π2=(12)π2{ Displaystyle (1/2!) pi ^ {2} = (1/2) pi ^ {2}} | 4.935 |
| 5 | 5(235!!)π2=(83)π2{ Displaystyle 5 (2 ^ {3} / 5 !!) pi ^ {2} = (8/3) pi ^ {2}} | 26.32 | (235!!)π2=(815)π2{ Displaystyle (2 ^ {3} / 5 !!) pi ^ {2} = (8/15) pi ^ {2}} | 5.264 |
| 6 | 6(13!)π3=π3{ Displaystyle 6 (1/3!) pi ^ {3} = pi ^ {3}} | 31.01 | (13!)π3=(16)π3{ Displaystyle (1/3!) pi ^ {3} = (1/6) pi ^ {3}} | 5.168 |
| 7 | 7(247!!)π3=(1615)π3{ Displaystyle 7 (2 ^ {4} / 7 !!) pi ^ {3} = (16/15) pi ^ {3}} | 33.07 | (247!!)π3=(16105)π3{ displaystyle (2 ^ {4} / 7 !!) pi ^ {3} = (16/105) pi ^ {3}} | 4.725 |
| 8 | 8(14!)π4=(13)π4{ Displaystyle 8 (1/4!) pi ^ {4} = (1/3) pi ^ {4}} | 32.47 | (14!)π4=(124)π4{ Displaystyle (1/4!) pi ^ {4} = (1/24) pi ^ {4}} | 4.059 |
| 9 | 9(259!!)π4=(32105)π4{ displaystyle 9 (2 ^ {5} / 9 !!) pi ^ {4} = (32/105) pi ^ {4}} | 29.69 | (259!!)π4=(32945)π4{ Displaystyle (2 ^ {5} / 9 !!) pi ^ {4} = (32/945) pi ^ {4}} | 3.299 |
| 10 | 10(15!)π5=(112)π5{ Displaystyle 10 (1/5!) pi ^ {5} = (1/12) pi ^ {5}} | 25.50 | (15!)π5=(1120)π5{ Displaystyle (1/5!) pi ^ {5} = (1/120) pi ^ {5}} | 2.550 |
где десятичные расширенные значения для п ≥ 2 округляются до отображаемой точности.
Рекурсия
В Ап значения удовлетворяют рекурсии:
- А={ displaystyle A_ {0} = 0}
- А1=2{ displaystyle A_ {1} = 2}
- А2=2π{ displaystyle A_ {2} = 2 pi}
- Ап=2πп−2Ап−2{ displaystyle A_ {n} = { frac {2 pi} {n-2}} A_ {n-2}} за п>2{ displaystyle n> 2}.
В Vп значения удовлетворяют рекурсии:
- V=1{ displaystyle V_ {0} = 1}
- V1=2{ displaystyle V_ {1} = 2}
- Vп=2πпVп−2{ displaystyle V_ {n} = { frac {2 pi} {n}} V_ {n-2}} за п>1{ displaystyle n> 1}.
Дробные размеры
Формулы для Ап и Vп можно вычислить для любого действительного числа п ≥ 0, и есть обстоятельства, при которых целесообразно искать площадь сферы или объем шара, когда п не является целым неотрицательным числом.
Это показывает гиперобъем (Икс–1) -мерная сфера (т.е., «площадь» поверхности Икс-мерный единичный шар) как непрерывная функцияИкс.
Это показывает объем шара в Икс размеры как непрерывная функцияИкс.
Другие радиусы
Площадь поверхности (п-1) -мерная сфера радиусом р является Ап рп−1 и объем п-мерный шар с радиусом р является Vп рп. Например, площадь А = 4π р 2 для поверхности трехмерного шара радиуса р. Объем V = 4π р 3 / 3 для трехмерного шара радиусар.
Значение единичной сферы в компьютерной графике и моделировании
Единичная сфера — это математический объект, который имеет радиус равный единице и центр в начале координат. В компьютерной графике и моделировании единичная сфера играет важную роль и широко используется для различных задач.
Одним из основных применений единичной сферы является создание и отображение трехмерных объектов. Путем масштабирования и трансформаций единичная сфера может быть использована для создания различных форм и моделей. Например, путем вытягивания и сжатия единичной сферы по определенным осям можно получить форму тела человека или животного.
Также единичная сфера используется для аппроксимации сложных геометрических форм. Многие объекты в реальном мире имеют сложную форму, которую сложно представить в компьютерной графике. Поэтому для упрощения моделирования используются аппроксимации с помощью единичной сферы. В таком случае объект разбивается на множество маленьких сферических участков, что значительно упрощает вычисления и обработку данных.
Единичная сфера также используется для освещения трехмерных объектов и создания эффектов отражения и преломления света. Сферическая форма единичной сферы позволяет более точно определить направление источников света, а также учитывать их взаимодействие с другими объектами.
Для удобства работы с единичной сферой в компьютерной графике и моделировании часто используются специальные алгоритмы и библиотеки. Они позволяют легко создавать, трансформировать и отображать сферические объекты, а также реализовывать различные эффекты и аппроксимации.
Таким образом, единичная сфера является важным и универсальным инструментом в компьютерной графике и моделировании. Она позволяет создавать и визуализировать различные трехмерные объекты, упрощать моделирование и вычисления, а также создавать эффекты света и отражения.
Определение и особенности
Единичная полуокружность — это геометрическая фигура, представляющая собой половину окружности радиусом 1, расположенную в единичном круге с центром в начале координат.
Особенностью единичной полуокружности является то, что она является границей для множества точек в окружности, у которых x-координата положительна или равна нулю. Другими словами, все точки на единичной полуокружности удовлетворяют уравнению x^2 + y^2 = 1, где x и y — координаты точки на плоскости.
Единичная полуокружность широко применяется в математике, особенно в геометрии, тригонометрии и анализе. Она используется для изучения геометрических свойств окружностей и их взаимодействия с другими фигурами, а также для решения различных задач, связанных с тригонометрическими функциями и аналитической геометрией.
Единичная полуокружность также является основой для построения графиков тригонометрических функций, таких как синус, косинус и тангенс. Они определяются как y-координата точки на полуокружности, соответствующая определенному углу, измеренному в радианах. Например, синус угла θ определяется как y-координата точки на полуокружности под углом θ.
Части шара
Сегмент шара – это часть шара, отсекаемая плоскостью. Иногда называется шаровым сегментом. На рисунке ниже окрашен в зеленый цвет.
Срез шара – часть шара между двумя параллельными плоскостями, пересекающими его. Также может называться шаровым слоем. На рисунке ниже закрашен желтым.
Сектор шара – состоит из шарового сегмента и конуса, вершина которого находится центре шара, а основание совпадает с основанием сегмента. На рисунке ниже сектор залит оранжевым.
Секущая, хорда, секущая плоскость сферы и их свойства
Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).
Секущая плоскость — это плоскость, которая пересекает сферу.
Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).Любая хорда, проходящая через центр сферы (шара) является диаметром.Хорда является отрезком секущей прямой.Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:
d < R
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m < R
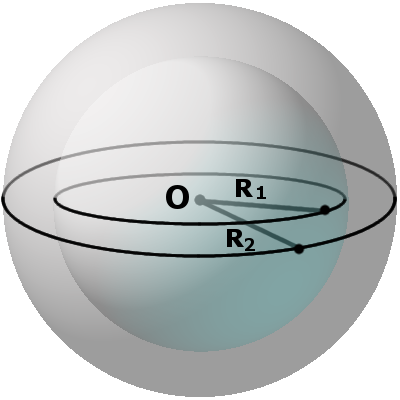
Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:
r = √R2 — m2,
где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.Определение.Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновенияРасстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.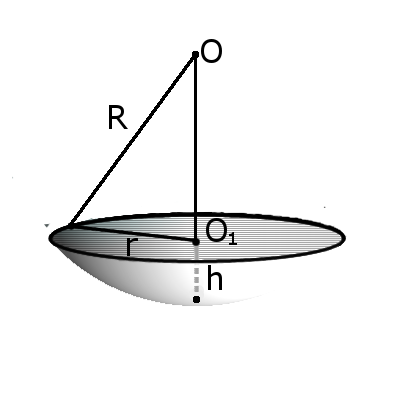
Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегментаh называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента. Формула.Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:
S = 2πRh
Формула.Объём сегмента сферы с высотой h через радиус сферы R:
| V = | h2π | (3R — h) |
| 3 |

Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.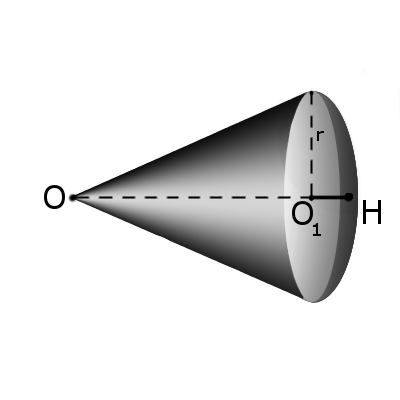
Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.
Площадь поверхности сектора S с высотой O1H (h) через радиус шара OH (R):
S = πR(2h + √2hR — h2)
Объём сектора V с высотой O1H (h) через радиус шара OH (R):
| V = | 2πR2h |
| 3 |
Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.
Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.
Геометрическое определение единичной сферы
Единичная сфера — это геометрическое тело в трехмерном пространстве, образованное всеми точками, находящимися на одинаковом расстоянии от центра сферы. Радиус единичной сферы равен единице.
Геометрическое определение единичной сферы также может быть представлено с использованием формулы: x^2 + y^2 + z^2 = 1. Здесь x, y и z — координаты точки на сфере.
Единичная сфера является примером поверхности в трехмерном пространстве, в отличие от объемного тела. Запрещается деление на 0 при расчетах или использовании формул, связанных с этим геометрическим объектом.
Единичная сфера имеет множество приложений в физике, математике, компьютерной графике и других областях. Она используется в моделировании трехмерных объектов, сферической геометрии и величинах, связанных с расстоянием или мерой.
Важно отметить, что единичная сфера является частным случаем более общего понятия сферы, где радиус может быть любым числом
Единичные шары в нормированных векторных пространствах
Точнее, открытый шар в нормированное векторное пространство V{ displaystyle V}, с норма ‖⋅‖{ displaystyle | cdot |}, является
- {Икс∈V‖Икс‖<1}{ Displaystyle {х в V: | х |
Это интерьер из закрытый шар из (V,||·||):
- {Икс∈V‖Икс‖≤1}{ Displaystyle {х в V: | х | Leq 1 }}
Последнее представляет собой несвязанный союз первых и их общую границу, единичная сфера из (V,||·||):
- {Икс∈V‖Икс‖=1}{ Displaystyle {х в V: | х | = 1 }}
«Форма» единичный мяч полностью зависит от выбранной нормы; он вполне может иметь «углы» и, например, может выглядеть как п, в случае max-нормы в рп. Естественно получается круглый мяч как единичный шар, относящийся к обычному Гильбертово пространство нормы, основанной в конечномерном случае на Евклидово расстояние; его граница — это то, что обычно подразумевается под единичная сфера.
Позволять Икс=(Икс1,…Иксп)∈рп.{ displaystyle x = (x_ {1}, … x_ {n}) in mathbb {R} ^ {n}.} Определите обычный ℓп{ displaystyle ell _ {p}}-норма для п ≥ 1 как:
- ‖Икс‖п=(∑k=1п|Иксk|п)1п{ Displaystyle | х | _ {p} = ( sum _ {k = 1} ^ {n} | x_ {k} | ^ {p}) ^ {1 / p}}
потом ‖Икс‖2{ Displaystyle | х | _ {2}} это обычный Гильбертово пространство норма.‖Икс‖1{ Displaystyle | х | _ {1}} называется нормой Хэмминга, или ℓ1{ displaystyle ell _ {1}}-norm. состояние п ≥ 1 необходимо в определении ℓп{ displaystyle ell _ {p}} норма, поскольку единичный шар в любом нормированном пространстве должен быть выпуклый как следствие неравенство треугольника.Позволять ‖Икс‖∞{ Displaystyle | х | _ { infty}} обозначим max-норму или ℓ∞{ displaystyle ell _ { infty}}-норма x.
Обратите внимание, что для окружностей Cп{ displaystyle C_ {p}} двумерных единичных шаров (n = 2) имеем:
- C1=42{ displaystyle C_ {1} = 4 { sqrt {2}}} — минимальное значение.
- C2=2π.{ Displaystyle C_ {2} = 2 пи ,.}
- C∞=8{ displaystyle C _ { infty} = 8} — максимальное значение.
История возникновения Сферы
История Сферы имеет давнее происхождение и связана с древними цивилизациями. Еще в древности люди заметили, что небесные тела имеют сферическую форму. Веками астрономы изучали характеристики и движение звезд, планет и других небесных тел, и пришли к выводу, что они имеют форму сферы.
В Индии и Греции сфера была символом солнца и мудрости. В греческой мифологии, Зевс держал в руках сферу, олицетворяющую весь мир. В этот период сфера была использована в декоративных искусствах, а также в качестве инструмента для измерений и навигации.
Временем специалисты стали изучать геометрию сферы и ее свойства. Развитие математики и физики привело к тому, что сфера стала одной из ключевых геометрических фигур. Ее уникальные характеристики, такие как равенство длин любых двух дуг и радиусов, делают ее незаменимой в научных и технических расчетах.





























