Команда chattr в linux (атрибуты файлов)

Запись прав доступа с помощью чисел

Записывать права доступа можно не только с помощью букв. Если положительное значение права (когда доступ есть) обозначать единицей, а отрицательное (доступа нет) – нулем, то получим такую картину для файла, который могут все читать, но изменять только владелец:

110100100

Именно с помощью нулей и единиц хранятся данные в памяти компьютера, в том числе атрибуты доступа. Под права выделяются 9 бит в атрибутах файла, каждый бит хранит ноль или единицу.

Однако запись из девяти символов достаточно длинная. Чтобы ее сократить, используют преобразование двоичных чисел в восьмеричные. Триады нулей и единиц двоичной системы как раз составляют значения от 0 до 7 в восьмеричной системе счисления. Поэтому права доступа трех категорий (владельца, группы, остальных) можно выразить как три независимых друг от друга числа от 0 до 7-ми.

Не все числа имеют смысл. Трудно представить файл, который можно изменять, но нельзя прочитать. Часто используемые числа, которые полезно запомнить: 4 – только чтение, 5 – чтение и выполнение, 6 – чтение и запись, 7 – все права.

Алгоритмы перевода в системы счисления по разным основаниям

Алгоритм перевода чисел из любой системы счисления в десятичную

1. Представить число в развернутой форме. При этом основание системы счисления должно быть представлено в десятичной системе счисления.
2. Найти сумму ряда. Полученное число является значением числа в десятичной системе счисления.

Алгоритм перевода целых чисел из десятичной системы счисления в любую другую

1. Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, меньше делителя.
2. Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
3. Составить число в новой системе счисления, записывая его, начиная с последнего остатка.

Алгоритм перевода правильных дробей из десятичной системы счисления в любую другую

1. Последовательно умножаем данное число и получаемые дробные части произведения на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равна нулю или будет достигнута требуемая точность представления числа.
2. Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
3. Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.

Алгоритм перевода произвольных чисел из десятичной системы счисления в любую другую

Перевод произвольных чисел, т.е. содержащих целую и дробную часть, осуществляется в два этапа:

1. Отдельно переводится целая часть.
2. Отдельно переводится дробная.
3. В итоговой записи полученного числа целая часть отделяется от дробной запятой.

Перевод чисел из двоичной системы счисления в систему счисления с основанием q=2n

Для облегчения решения задач заполним следующую таблицу: 

Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

Если основание q-ричной системы счисления является степенью числа 2, то перевод чисел из q-ричной систему счисления в 2-ичную и обратно можно проводить по более простым правилам.

1. Двоичное число разбить справа налево на группы по n в каждой.
2. Если в левой последней группе окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов.
3. Рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой в системе счисления с основанием q=2n

Двоичная арифметика

Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным правилам. 

Сложение

Рассмотрим сложение чисел в двоичной системе счисления

В основе лежит таблица сложения одноразрядных двоичных чисел: 
0+0=00+1=11+0=11+1=101+1+1=11

Важно обратить внимание на то, что при сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или больше основания системы счисления. Для двоичной системы счисления эта величина равна двум. Сложение многоразрядных двоичных чисел происходит в соответствие с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов с старшие. 

Для двоичной системы счисления эта величина равна двум. Сложение многоразрядных двоичных чисел происходит в соответствие с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов с старшие. 

Вычитание

Рассмотрим вычитание двоичных чисел. В основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда. В таблице заем обозначается 1 с чертой. 
0-0=00-1=111-0=11-1=0

Умножение

В основе умножения лежит таблица умножения одноразрядных двоичных чисел: 
0*0=00*1=01*0=01*1=1

Умножение многоразрядных двоичных чисел происходит в соответствии с приведенной таблицей умножения по обычной схеме, применяемой в десятичной системе счисления, с последовательным умножением множимого на очередную цифру множителя. 

Деление

Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.

Неполные квадратные уравнения

Неполное квадратное уравнение — это уравнение, в котором один из коэффициентов \(b\) или \(c\) равен нулю, \(a\neq0\).

Как решать квадратное уравнение \(ax^2+bx=0\)?

Рассмотрим уравнение, в котором \(c=0\), оно будет иметь вид:
$$ax^2+bx=0;$$
Чтобы его решить, нужно вынести общий множитель \(x\) за скобки:
$$x(ax+b)=0;$$
И вспомнить правило, что произведение равно нулю, когда хотя бы один из множителей равен нулю. Здесь два множителя: \(x\) и \((ax+b)\). Приравниваем их к нулю и решаем каждое по-отдельности:
$$x=0;$$
Тут решать-то нечего, сразу дан корень.
Второе:
$$ax+b=0;$$
Обычное линейное уравнение:
$$ax=-b;$$
$$x=\frac{-b}{a};$$

Получили, что уравнение имеет сразу два корня:\(x=0\) и \(x=\frac{-b}{a}\).

Разберем на примере:

Пример 7
$$2x^2+8x=0;$$
Выносим общий множитель \(x\):
$$x(2x+8)=0;$$
$$\quad x_1=0 \quad и \quad 2x+8=0;$$
$$2x+8=0;$$
$$2x=-8;$$
$$x_2=-4.$$
Ответ: \(x_1=0 \quad и \quad x_2=-4.\)

Как решать квадратное уравнение \(ax^2+с=0\)?

Вот с такими уравнениями надо быть очень внимательными

Важно помнить, что любое число (выражение), возведенное в квадрат, всегда больше или равно нуля, оно не может быть отрицательным

Общая схема решения уравнений вида \(ax^2+с=0\):

• Выражаем \(x^2\) из уравнения:
  $$ax^2+c=0;$$
  $$ax^2=-c;$$
  $$x^2=\frac{-c}{a};$$
• Если \(-\frac{c}{a} \geq 0\):
  $$x_1=\sqrt{-\frac{c}{a}};$$
  $$x_2=-\sqrt{-\frac{c}{a}};$$
• Если \(-\frac{c}{a} \lt 0\):
  РЕШЕНИЙ НЕТ.

Пример 8
$$2x^2-8=0;$$
$$2x^2=8;$$
$$x^2=\frac{8}{2};$$
$$x^2=4;$$
$$x=\pm\sqrt{4};$$
$$x_1=2;$$
$$x_2=-2;$$
Ответ: \(x_1=2 \quad и \quad x_2=-2.\)

Пример 9
$$4x^2+36=0;$$
$$2x^2=-36;$$
$$x^2=\frac{-36}{2}=-18;$$
Так как \(-18
Ответ: Нет корней.

Чем отличаются Chmod файлов и папок

«Права»	«Файл»	«Папка»
—	Ничего нельзя делать	Доступ к каталогу и его подкаталогам запрещен
r—	Можно читать содержимое	Можно прочитать содержимое папки
rw-	Можно видеть и изменять содержимое	Можно добавить, удалить, изменить файл папки
rwx	Читать, изменять и выполнять файл	Можно читать, удалять, изменять файлы, сделать каталог текущим, т.е. “войти” в этот каталог.
r-x	Можно прочитать, либо выполнить	Можно зайти в каталог и прочитать его содержимое, удалять или добавлять файлы нельзя.
—x	Выполнить, если файл двоичный	Пользователь может выполнить двоичный файл о существовании которого ему известно, зайти или прочитать каталог запрещено

Как разбить текст по ячейкам по маске (шаблону).

Эта опция очень удобна, когда вам нужно разбить список схожих строк на некоторые элементы или подстроки. Сложность состоит в том, что исходный текст должен быть разделен не при каждом появлении определенного разделителя (например, пробела), а только при некоторых определенных вхождениях. Следующий пример упрощает понимание.

Предположим, у вас есть список строк, извлеченных из некоторого файла журнала:

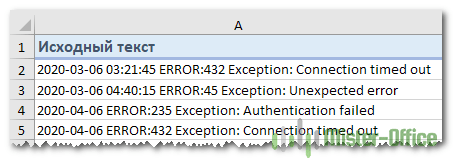
Вы хотите, чтобы дата и время, если таковые имеются, код ошибки и поясняющие сведения были размещены в 3 отдельных столбцах. Вы не можете использовать пробел в качестве разделителя, потому что между датой и временем также есть пробелы. Также есть пробелы в тексте пояснения, который также должен весь находиться слитно в одном столбце.

Решением является разбиение строки по следующей маске: * ERROR: * Exception: *

Здесь звездочка (*) представляет любое количество символов.

Двоеточия (:) включены в разделители, потому что мы не хотим, чтобы они появлялись в результирующих ячейках.

То есть в данном случае в качестве разделителя по столбцам выступают не отдельные символы, а целые слова.

Итак, в начале ищем позицию первого разделителя.

Затем аналогичным образом находим позицию, в которой начинается второй разделитель:

Итак, для ячейки A2 шаблон выглядит следующим образом:

С 1 по 20 символ – дата и время. С 21 по 26 символ – разделитель “ERROR:”. Далее – код ошибки. С 31 по 40 символ – второй разделитель “Exception:”. Затем следует описание ошибки.

Таким образом, в первый столбец мы поместим первые 20 знаков:

Обратите внимание, что мы взяли на 1 позицию меньше, чем начало первого разделителя. Кроме того, чтобы сразу конвертировать всё это в дату, ставим перед формулой два знака минус

Это автоматически преобразует цифры в число, а дата как раз и хранится в виде числа. Остается только установить нужный формат даты и времени стандартными средствами Excel.

Далее нужно получить код:

Думаю, вы понимаете, что 6 – это количество знаков в нашем слове-разделителе «ERROR:».

Ну и, наконец, выделяем из этой фразы пояснение:

Аналогично добавляем 10 к найденной позиции второго разделителя «Exception:», чтобы выйти на координаты первого символа сразу после разделителя. Ведь функция говорит нам только то, где разделитель начинается, а не заканчивается.

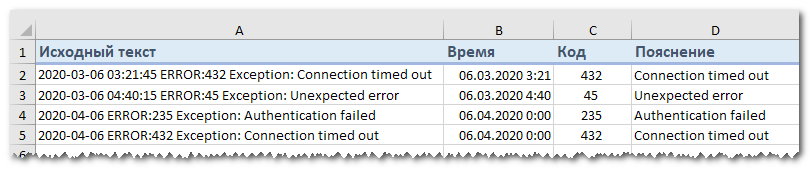
Таким образом, ячейку мы распределили по 3 столбцам, исключив при этом слова-разделители.

Если выяснение загадочных поворотов формул Excel — не ваше любимое занятие, вам может понравиться визуальный метод разделения ячеек в Excel, который демонстрируется в следующей части этого руководства.

What is xxd?#

• What is xxd?

• Syntax

• Examples

• How to print the first 20 bytes of a file.

• How to print the last 20 bytes of a file.

• How to print the first 5 bytes of a file as bits.

• How to inspect a text file for nonprinting characters.

• How to edit binary.

• How to create a text file.

• How to use xxd in vim.

• How to convert the whole file.

• How to convert the current line.

• How to convert between marked locations.

• Related commands

• Linux commands help

• How to print the first 20 bytes of a file.

• How to print the last 20 bytes of a file.

• How to print the first 5 bytes of a file as bits.

• How to inspect a text file for nonprinting characters.

• How to edit binary.

• How to create a text file.

• How to convert the whole file.

• How to convert the current line.

• How to convert between marked locations.

Примеры использования команды chmod в абсолютном режиме

Разрешение чтения, записи, выполнения файла file всеми пользователями и группами (полный доступ):

$ chmod 777 file        (rwxrwxrwx)

Установка разрешений на чтение и запись для владельца, группы и остальных пользователей:

$ chmod 666 file        (rw-rw-rw-)

Установка полного доступа к файлу для владельца и лишь чтения для группы и остальных пользователей:

$ chmod 744 file        (rwxr–r–)

Установка полного доступа к файлу владельцу файла и запрет доступа группе и другим пользователям:

$ chmod 700 file        (rwx——)

Установка разрешений на чтение и запись для владельца файла и лишь чтения для группы и остальных:

$ chmod 644 file        (rw-r–r–)

Установка разрешений на чтение и запись владельцу файлу и его группе и запрет доступа для других:

$ chmod 640 file        (rw-r—–)

Установка доступа к файлу с разрешением чтения для всех пользователей и групп:

$ chmod 444 file        (r–r–r–)

Права доступа к файлу для чтения, записи, выполнения владельцем и чтения, выполнения группе и другим:

$ chmod 755 file        (rwxr-xr-x)

Разрешение доступа к файлу на чтение и выполнение пользователю и остальным и запрет доступа для группы:

$ chmod 505 file        (r-x—r-x)

Если вы хотите назначить права доступа на все файлы в текущем каталоге,
просто поставьте после назначаемых прав доступа знак * (звездочка):

$ chmod 755 *

В результате выполнения этой команды владелец получит полные права
(чтение, изменение, выполнение) на все файлы текущего каталога, а группа
и другие пользователи – только чтение и выполнение.
Если вы хотите, чтобы ваши действия распространились рекурсивно (включая
все подкаталоги), воспользуйтесь опцией -R:

$ chmod -R 777 *

Результатом выполнения вышеприведенной команды будет рекурсивный “обход”
всех подкаталогов текущего каталога и назначение полного доступа для
всех пользователей и групп.
В этой статье рассмотрены лишь некоторые примеры применения команды
chmod

Если вы хотите узнать подробнее о работе команды chmod и правах
доступа в Linux, обратите внимание на эту статью.

Смена прав только у директорий (рекурсивно)

$ find /path/to/base/dir -type d -exec chmod 755 {} +

или

$ chmod 755 $(find /path/to/base/dir -type d)

или

$ chmod 755 `find /path/to/base/dir -type d`

или

$ find /path/to/base/dir -type d -print0 | xargs -0 chmod 755

Смена прав только у файлов (рекурсивно)

$ find /path/to/base/dir -type f -exec chmod 644 {} +

или

$ chmod 644 $(find /path/to/base/dir -type f)

или

$ chmod 0755 `find ./ -type f`

или

$ find /path/to/base/dir -type f -print0 | xargs -0 chmod 644

Взаимосвязь параметра

Объяснение дискриминанта имеет и графическое обоснование. Физически задача заключается в комплексном подходе установления взаимосвязи. Фактически это фиксирование нулей параболы уравнения, то есть точек, в которой она пересекает ось абсциссы. Знак при переменной в квадрате будет определять положение веток параболы. Они будут идти вверх при a > 0, и вниз, если a < 0.

Исходя из этого, дискриминант равняется отношению суммы или разности числового коэффициента, стоящего возле неизвестного в первой степени с корнем квадратным из b 2 — 4 ac к удвоенному произведению первого коэффициента в уравнениях x1 = (- b + √ b 2 — 4 ac) / 2a; x2 = (- b — √ b 2 — 4 ac) / 2a. Подкоренное выражение называют формулой сокращённого дискриминанта.

Дискриминант при нахождении корней уравнения может принимать три значения:

1. Отрицательное. В случае, когда он меньше нуля, точный квадрат должен равняться числу с минусом, чего не может быть из-за свойств квадратной степени. Поэтому при таком положении вещей решений или действительных корней у уравнения нет. График уравнения не пересекает ось абсциссы.
2. Равное нулю. Это состояние характеризуется уравнением вида: (2 am + b)2 = 0. Так как квадрат числа может быть равен нулю, только если это число нулевое, то рассматриваемое уравнение можно переписать как m = — b / 2a. Это и есть упрощённая формула при дискриминанте, равному 0. На графике существует лишь одна точка пересечения с осью абсциссы.
3. Положительное. Это наиболее распространённый случай и самый тяжёлый для проведения расчётов. При нём из обеих частей уравнения теоремы (2 am + b) 2 = b 2 — 4 ac надо извлечь квадратный корень. В итоге получится 2am + b =± √D. Тут следует отметить следующее: минус возникает из-за того, что возводимое в квадрат число может быть как положительное, так и отрицательное. Например, 92 = 81 и -92 = 81. Из этого выражения можно выразить неизвестное. Оно будет равняться половинному значению m = (-b ± √D) / 2a. Парабола пересекает ось абсцисс в двух точках.

Последнее выражение является формулой корней квадратного уравнения. Именно с её помощью могут решаться равенства, в степени которых стоит двойка. Через дискриминант можно вычислять корни и уравнений больших порядков. Для этого используются приёмы понижения степени до квадратного. Но эти операции учащиеся начинают изучать на уроках в выпускном классе, когда проходят решение уравнений n-го порядка.

https://youtube.com/watch?v=bYLGJMyJypM

Использование с препроцессорами

Я привык использовать CSS-препроцессор Sass. Одна из его лучших возможностей — управление цветами.

Используя HSL, мы управляем цветами как в «ванильном» CSS.

Что здесь происходит. В CSS-переменных есть небольшие «цветовые фрагменты», и мы собираем из них полноценные цвета.

Функция позволяет изменять эти фрагменты. Например, вот цвет :

Мы используем обычный оттенок и насыщенность для нашего красного цвета, но уменьшаем освещённость на 20%. И цвет превращается из  в .

Это может показаться сложнее, чем в Sass, да и кода побольше. Но ведь это всё происходит в чистом CSS.

В отличие от функций и переменных Sass, которые компилируются в конкретные значения, «зашитые» в код, CSS-переменные легко изменить. Мы можем настроить любую из них с помощью JavaScript, и тогда все остальные цвета автоматически изменятся.

Это очень удобно для вещей вроде автоматической тёмной темы, определённых пользователем цветовых схем и всякого такого.

Что такое двусложные слова, и какие существуют правила переноса для них

Прежде чем думать, как правильно переносится слово, нужно определить, относится ли оно вообще к двусложным. В русском языке за слогообразование «ответственны» гласные. В слове насчитывается именно столько слогов, сколько оно содержит гласных. Число согласных, «ь», «ъ», «й», на их число никак не влияют.

Для взрослого разделить слово на слоги фонетически не составляет проблем. В процессе произношения четко выделяются два «толчка» выдыхаемого воздуха, один из них – более акцентированный (ударный).

Справка!  В русском языке фонетический слог – один или несколько звуков, произносимых слитно, «на одном дыхании».

Чтобы объяснить процесс деления ребенку, можно предложить ему простое упражнение: развернув раскрытую ладонь параллельно полу, подставить ее к подбородку снизу так, чтобы оставалось 2-3 см свободного пространства и, четко артикулируя, произнести несколько двусложных слов. Одновременно ведется подсчет – сколько раз подбородок стукнется о ладонь. Это и будет искомым числом слогов.

Согласные при делении слова «прилипают» к гласным, «окружая» их. Так формируются закрытые слоги. Когда слог начинается или заканчивается на гласную, он называется открытым. Двусложные слова могут состоять из двух закрытых, двух открытых, открытого и закрытого слогов. Во всех случаях они переносятся исключительно по слогам:

• пар-тер; прин-тер, мос-тик, фан-тик, кор-пус;
• ут-ро, ед-ва, ро-ща, пра-во, ли-па;
• фор-ма, ве-чер, солн-це, мес-то, руч-ка.

Возможен и еще один вариант – гласная сама по себе становится «самодостаточным» слогом. В этом случае двусложное слово не переносится.

Почему не все двусложные слова можно переносить

Двусложные (и многосложные) слова, начинающиеся или заканчивающиеся слогом, состоящим из одной гласной, входят в перечень тех, которые нельзя перенести со строки на строку. К этой же категории относятся односложные слова (том, стол, взгляд, мост, сон). Запрет на их перенос обусловлен тем, что при написании страдает стройность письменной речи.

И если слова из четырех и более слогов можно перенести, соблюдая фонетические нормы (а-ва-ри-я – ава-рия, а-ка-ци-я – ака-ция, ре-во-лю-ци-я – револю-ция, мо-ти-ва-ци-я – моти-вация), то для двух или трехсложных (а-ри-я) таких вариантов их деления просто не существует. Поэтому их нужно писать полностью на одной строке, не допуская переноса.

Перенос двусложных слов с буквами ь, ъ, й в составе слова

Деление на слоги слов с «ь», «ъ», «й» традиционно вызывает трудности. Чтобы не допустить ошибку, нужно помнить, что их наличие никак не влияет на число слогов, всегда учитываются только гласные. Буквы «ь», «ъ», «й» их не образуют ни самостоятельно, ни вместе с согласными:

• моль, рай, съесть, знай, явь, вьюн – односложные слова;
• улей, майка, съела, тикай, икать, окунь – двусложные слова.

Внимание! Согласно правилам русского языка, при переносе многосложных слов «ь», «ъ» и «й» запрещается отделять от предшествующей им гласной или согласной (медаль-он, объ-явление, стай-ка).

Примеры двусложных слов, которые нельзя переносить

Большинство двусложных слов, начинающихся или заканчивающихся слогом, состоящим из одной гласной – существительные. Число букв при этом может быть любым:

• ива, эра, шея, яма, ухо, еда, туя, очи, аир, эхо;
• стая, якут, эфес, обоз, иней, угол, азот, ибис, араб, идол;
• окунь, олень, анонс, эмаль, струя, обувь, изюбр, арест, яхонт;
• участь, ярость.

В категорию «непереносимых» попадают многие двусложные имена собственные:

• Ева;
• Аня;
• Оля;
• Юля;
• Лия;
• Ира
• Ада;
• Яков;
• Егор;
• Юрий.

Только существительными перечень двусложных слов, которые нельзя перенести с одной строки на другую не ограничивается. В него входят и иные части речи:

• прилагательные (юный, злая, алый, ярый);
• глаголы (юлить, осесть, ушить, унять, опасть, орать, учить, иметь, умыть, ехать);
• местоимения (мое, твоя, ее, оно, его, свое, это, иной);
• деепричастия (стоя, упав, рея, тая, моя, осев, воя, брея);
• числительные (один, двое, трое, оба);
• наречия (оземь, еле, еще, уже, вдвое).

Деление слов на слоги – простая и понятная процедура. Но и здесь бывают сложности. Их вызывают двусложные слова, которые нельзя перенести. Их очень много, поэтому запоминать нет необходимости. Нужно только запомнить соответствующее правило.

Именованные цвета

Технически это не совсем цветовой формат. В HTML доступны 140 именованных цветов. Это специальные ключевые слова вроде , или .

Разработчик Энтони Лиеуаллен создал демо со всеми 140 именованными цветами в одном круге:

Именованные цвета можно использовать, когда вам нужна цветная плашка вместо картинки — например, при создании прототипов сайта. Или если вы создаёте обучающие материалы, потому что нет ничего понятнее, чем .

Об этом редко говорят, но именованные цвета чаще всего не используют при реальной разработке сайтов. 140 цветов — очень мало, это даже меньше, чем в восьмибитной цветовой палитре на NES.

С миру по нитке

Вот два именованных цвета:

Как вышло, что тёмно-серый светлее, чем серый?!

Дело в том, что эти 140 цветов собирали с миру по нитке. Среди источников были спецификация HTML4, оконная система X11 Unix и цвета, которые добавлены в память о конкретных людях.

В итоге получилась не всегда логичная солянка из разных палитр.

Высокая эффективность работы с файлами

Одно из главных преимуществ использования утилиты xxd — это ее высокая эффективность. Благодаря своей оптимизированной структуре и алгоритмам, xxd способна работать с файлами различных размеров и типов с высокой скоростью и максимальной производительностью.

Утилита xxd также обладает широким набором возможностей для работы с файлами. Она позволяет просматривать содержимое файла в шестнадцатеричном, десятичном и восьмеричном форматах, а также в ASCII и Unicode кодировках. Таким образом, xxd обеспечивает гибкость и удобство при работе с различными типами файлов и кодировок.

Кроме того, xxd позволяет изменять содержимое файлов и выполнять различные операции с данными. Например, с помощью утилиты xxd можно изменять значения отдельных байтов в файле, копировать и объединять содержимое нескольких файлов, а также преобразовывать данные из одного формата в другой.

Благодаря своей эффективности и многофункциональности, утилита xxd является неотъемлемой частью инструментария любого системного администратора или разработчика в операционной системе Linux. Она позволяет удобно и эффективно работать с файлами, обеспечивая высокую производительность и гибкость в обработке данных.

Позиционная система счисления: что это

— 2 0 умножить на 2. Коэффициент равен a

— 2 n-2 + … + a

• Простота запоминания и изображения чисел.
• Удобство совершения математических и логических операций.
• Миниатюрная запись огромных значений.

а остаток равен

• Обладает минимальными таблицами умножения, сложения.
• Представит любое число посредством двух состояний: единица и ноль.
• Помехоустойчивая по причине всего пары состояний.
• Проста в выполнении арифметических операций.

Полученный коэффициент снова делится на 2, а остаток является a

1.1.2. Двоичная система счисления

Если продолжить этот процесс деления, то на n-ом шаге мы получим набор цифр

которые являются частью двоичного представления исходного числа и соответствуют остатку от последовательного деления на 2.

100112Итак, чтобы перевести десятичное целое число в двоичную систему счисления, нужно разделить данное число и получившиеся целые части последовательно на 2, пока не получится часть, равная нулю. Исходное число в двоичной нотации составляется путем записи получающихся остатков один за другим, начиная с последнего.10.

Пример 4. Переведем десятичное число 11 в двоичную систему счисления. Описанная выше последовательность операций (алгоритм перевода) может быть представлена следующим образом:

Если мы запишем остаток от деления в направлении, указанном стрелкой, то получим: 11

= 1011_n-1Пример 5. Если десятичное число достаточно велико, то более подходящей является следующая нотация вышеприведенного алгоритма:_n-2= 101101011Восьмеричная система счисления — это позиционная система счисления, основанная на числе 8. Цифры восьмеричной системы счисления — 0, 1, 2, 3, 4, 5, 6, 7._n-1= 101101011₁Например: 1063..

= 1 — 8 3 + 0 — 8 2 + 6 — 8 1 + 3 — 8 0 = 563₁.

Таким образом, чтобы перевести восьмеричное целое число в десятичную систему счисления, мы должны перейти к расширенной системе счисления и вычислить значение полученного выражения.

Чтобы перевести целое десятичное число в восьмеричную систему счисления, необходимо разделить это число и полученные целые части на 8 последовательно, пока целая часть не будет равна нулю. Исходное число в новой нотации дополняется путем последовательной записи получившихся остатков, начиная с последнего.

Пример 6. Переведем десятичное число 103 в восьмеричную систему счисления.

База: q = 16.

Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, C, C, D, E, F.₁₀Здесь только десять из шестнадцати цифр имеют условное обозначение 0,…, 9. Первые пять букв латинского алфавита обычно используются для записи цифр с десятичными эквивалентами 10, 11, 12, 13, 14, 15.₂.

Поэтому обозначение 3AF

36310означает:2

1.1.3. Восьмеричная система счисления

= 3 — 16 2 + 10 — 16 1 + 15 — 16 0 = 768 + 160 + 15 = 943

Пример 7. Переведем десятичное число 154 в шестнадцатеричную систему счисления.

Система, на которой основаны компьютеры, была изобретена гениальным немецким ученым Г.В. Лейбницем (до 19 века!). Он изобрел и описал СС, в которой все расчеты производятся с использованием d₈Объяснение. Расширенная форма символики 579: 5*10 2 +7*10 1 +9*10 0 = 579₁₀.

Источник

Обычно мы используем сокращенную нотацию чисел, т.е. без деления и умножения оснований.

А чтобы было проще, мы используем готовую таблицу коэффициентов, равных 2.

1.1.4. Шестнадцатеричная система счисления

Сначала запишите числа, равные двум, начиная с наибольшего:

Затем нужно вычесть из числа максимальную степень двойки и поставить 1, если в основании есть единица, или 0, если ее нет. Перевод 579

Обратный путь еще проще. Посчитайте количество цифр — это мощность от 2 д о-1. И так далее. И проще использовать одну и ту же таблицу:

Если оно на 1 больше, то число начинается и заканчивается 1, а внутри — сплошной 0.₁₆Основание этой системы — 8, а числа в восьмеричной системе — 0-7. Эта система счисления является тематической и целочисленной. Он используется в областях, связанных с цифровыми технологиями, особенно с программным обеспечением Linux (права доступа, исполнение).

3AF16Это 16-ричная система целых чисел (шестнадцатеричные цифры 0-9 и буквы от A до F), используемая в приложениях низкоуровневого компьютерного программирования и документирования, поскольку она представляет собой 8-битный байт и для записи требуется 2 шестнадцатеричные цифры.10.

В стандарте Unicode используется 4 или более 16 символов SS.

How to use the XXD command in Linux

Once you are done with the installation, you have to follow the given command syntax to use the xxd command:

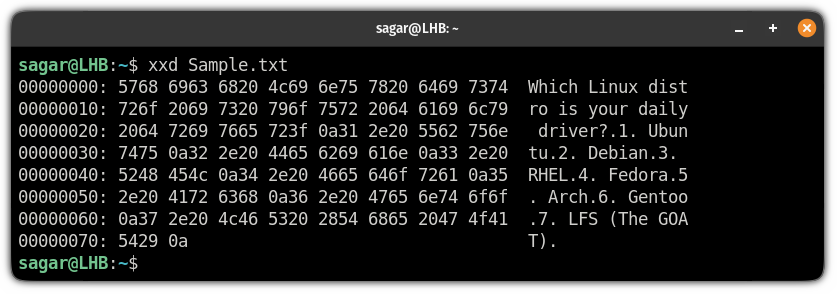
To make things easy to understand, I will be using the file named throughout the tutorial, which contains the following:

To create a hex dump of the file, I will be using the following command:

Sure, you can use different options to tweak the default behavior of the xdd command. Let me show you how.

Trim lines in xxd output

The xxd command allows you to trim down lines from your output.

To do so, you will have to use the flag and append how many initial lines you want to skip:

So let’s say you want to start the hex dumping from the 5th line, which means you need to trim down the first 4 lines:

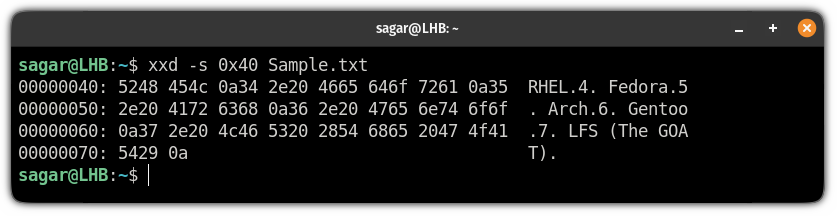
And as you can see, it trimmed the first 4 lines and gave me the hex dump starting from the 5th line.

But if you want to get the hex dump of the last few lines, you can do that too!

To get the hex dump of the last n number of the lines, you will have to execute the xxd command in the following manner:

So let’s say I want to get the hex dump of the last 3 lines, then, I will be using the following:

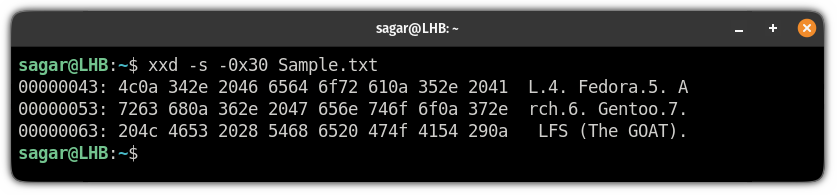
Specify the column length

You may want to specify how many columns should be shown instead of what xxd gets you by default (10).

To do so, you will need to use the flag and append how many columns should be displayed on the output:

Let’s say I want the output in 4 columns, then I will be using the following:

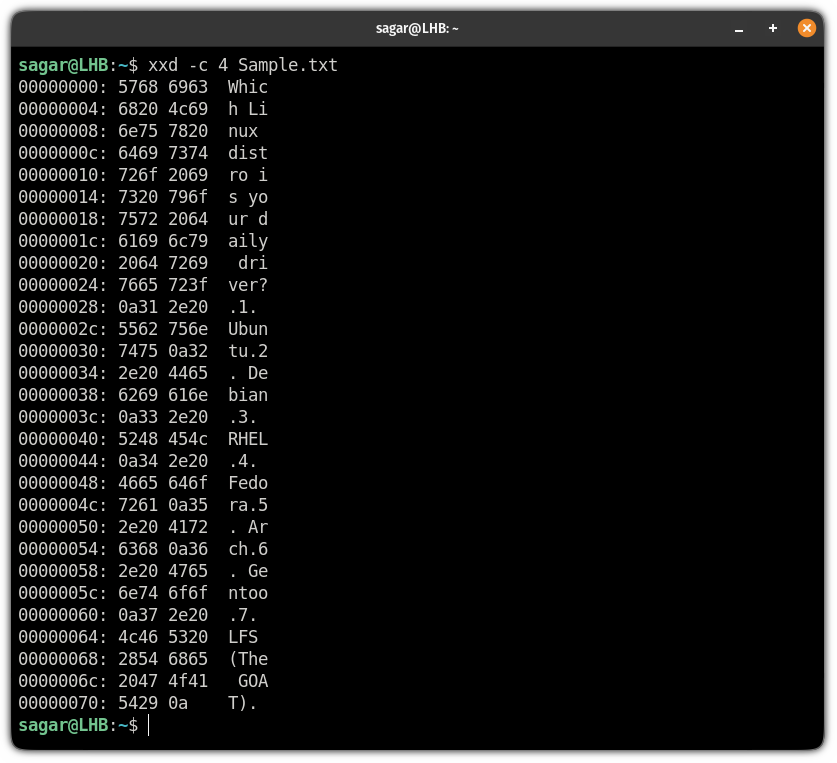
Specify the output length

It is similar to what I explained in how you can trim the output but here, you can specify how many lines of the output you want from the first line.

To specify the output length, all you have to do is use the flag and specify how many lines of output you want:

So let’s say I only want the first 5 lines of the hex dump, then I will be using the following:

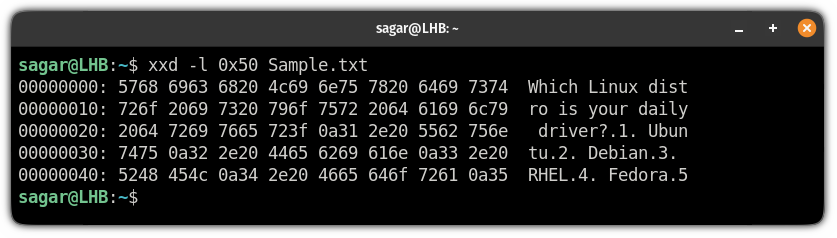
Get binary output instead of hexadecimal

The xxd command also allows you to get output in binary instead of hexadecimal!

It is quite simple and the binary output can be achieved using the flag:

Here, I converted my text file to binary:

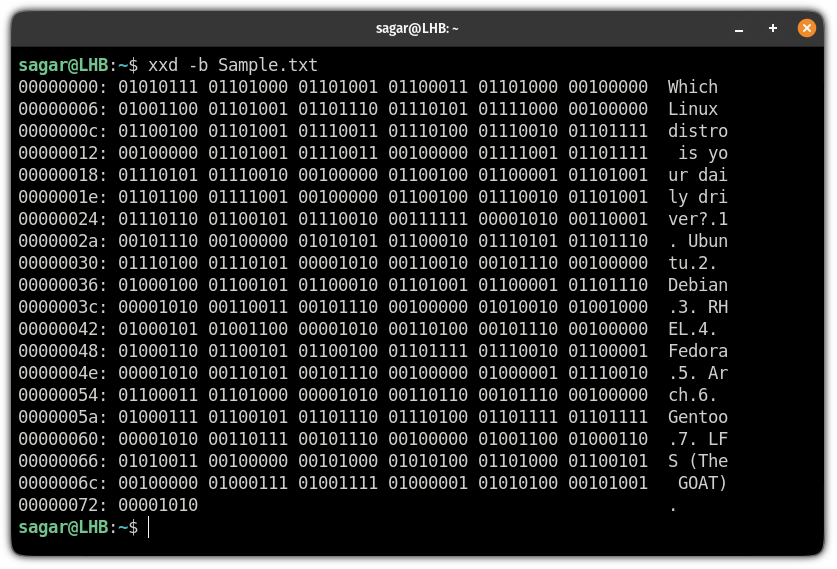
Get hex output in capital letters

You may find situations where you want the output in capital letters.

And you can easily get the hex output in capital letters using the flag as shown:

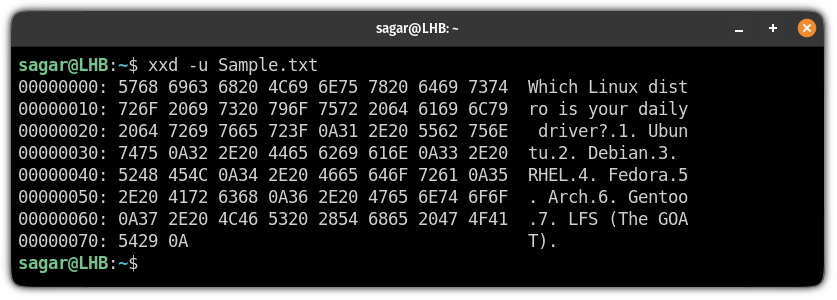
Convert hex to the normal text again

So if you redirected the output of the hex to a file, there is a way to get back to normal quite easily.

For your reference, I’m redoing the whole process of how you can redirect the output of the hex dump to the text file first:

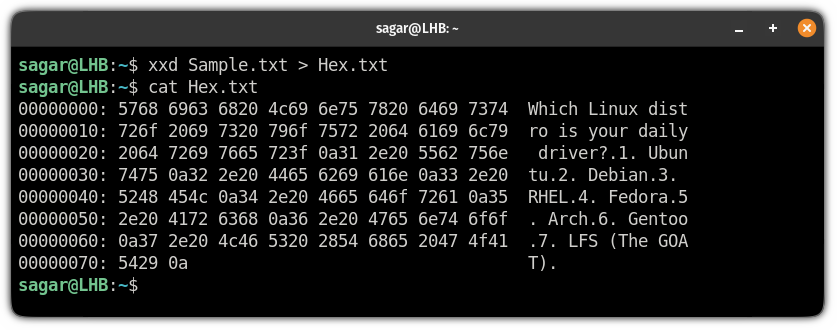
So I saved the hex dump output to the .

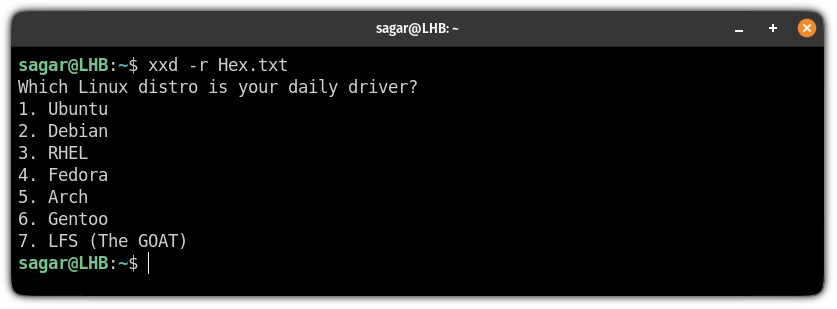
Now, if I want to read the content of the , I will have to perform the conversion. Otherwise, it is just a pain in the head.

To reverse this effect, you will have to use the flag in shown manner:

Что такое динамический диск в Windows 10

Чтобы начать обработку данных, необходимо проверить тип устройства. Для этого необходимо выполнить следующие действия:

• одновременно нажать сочетание горячих клавиш «Win» и «R»;
• в открытое поле ввести команду diskmgmt.msc, подтвердить запрос кнопкой «Enter»;

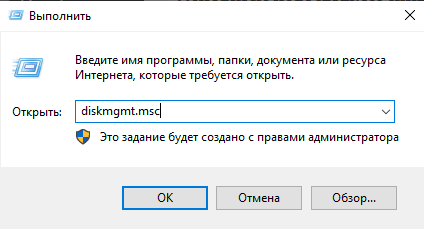
откроется дополнительное окно «Управление накопителями».

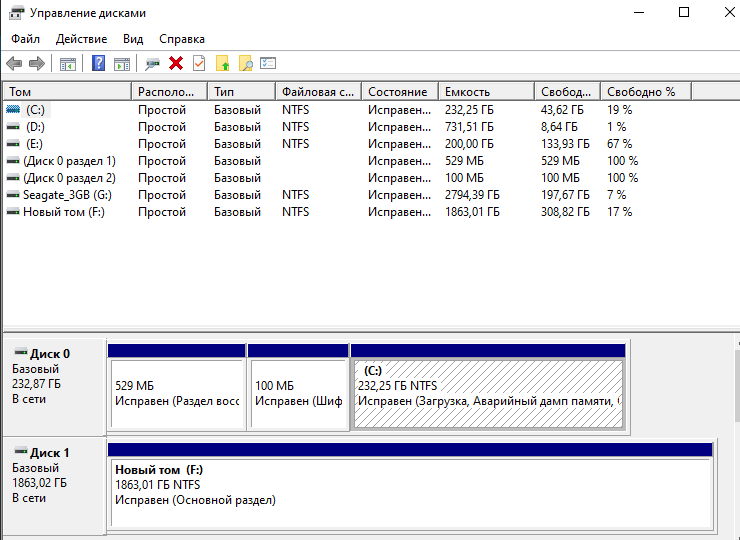
Одна из колонок называется «Тип». Напротив каждого носителя указывается значение – базовый или динамический. Особенности второго варианта:

допускается внесение изменений (например, размер базового носителя корректировать недопустимо);

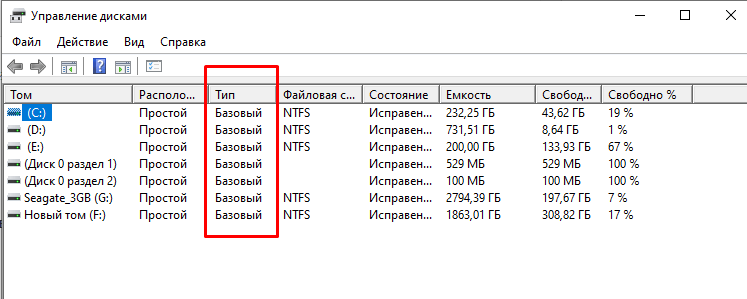
• специальные накопители могут быть смежными;
• накопители пластичны (имеется в виду отношение к дополнительным настройкам).

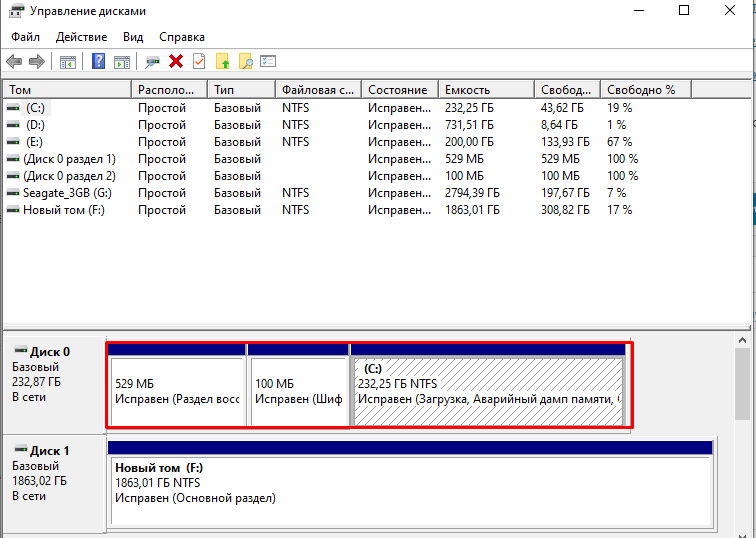
Основным недостатком считается невозможность применения мультизагрузки – установки нескольких операционных систем на один персональный компьютер (стационарный или ноутбук).

Использование встроенных функций Python для перевода чисел

Python предлагает удобные встроенные функции, которые облегчают перевод чисел из двоичной системы в десятичную. Эти функции предоставляют готовые инструменты для выполнения операций перевода без необходимости реализации алгоритмов вручную.

Функция

Функция может быть использована для перевода числа из двоичной системы в десятичную. Она принимает два аргумента: строку представляющую число в двоичной системе и базу, в которую нужно выполнить перевод. Для перевода в десятичную систему, база устанавливается равной 2. Пример использования функции :

Функция преобразует строку в число 11 в десятичной системе.

Функция

Функция может быть также использована для перевода числа из двоичной системы в десятичную. Она вычисляет значение выражения, переданного в виде строки. Пример использования функции :

В этом примере мы добавляем префикс к строке , чтобы указать, что число представлено в двоичной системе счисления. Функция вычисляет это выражение и возвращает результат, равный 11 в десятичной системе.

Функция

Функция может быть использована для получения двоичного представления числа. Она принимает число в десятичной системе и возвращает его строковое представление в двоичной системе. Пример использования функции :

Функция преобразует число 11 в его двоичное представление .

Использование этих встроенных функций Python упрощает перевод чисел из двоичной системы в десятичную. Они предоставляют готовые инструменты для выполнения операций перевода и устраняют необходимость реализации алгоритмов вручную.