Таблица математических символов

Различные стили вертикальной черты

Толщина

Вертикальная черта может иметь различную толщину, в зависимости от шрифта и его параметров. Она может быть тонкой и незаметной, или же более толстой и выразительной.

Длина

Вертикальная черта может быть разной длины в разных шрифтах. Она может достигать определенной высоты в пределах линий текста, либо охватывать весь блок текста.

Прерывистая черта

В некоторых стилях и шрифтах вертикальная черта может быть прерывистой, то есть состоять из набора небольших горизонтальных линий. Этот стиль добавляет ощущение движения и динамики в тексте.

Украшения и декорации

Вертикальная черта может быть украшена или иметь некоторые декоративные элементы, такие как стрелки, цветные полоски, точки и т. д. Это придает тексту стильный и оригинальный вид.

Эмоциональное значение

Вертикальная черта может использоваться не только для разделения текста, но также для передачи определенного эмоционального значения. Например, в некоторых стилях вертикальная черта может символизировать силу, уверенность или границу между различными идеями.

Стилистическое применение

Вертикальная черта может быть использована для создания разных стилистических эффектов в тексте. Например, она может быть использована для выделения определенного блока текста, создания колонок или создания таблицы.

Заметка: стиль вертикальной черты может быть установлен с помощью CSS и HTML-кода. Можно изменять ее толщину, длину, цвет, а также добавлять различные украшения и декорации.

Извлечение корней

Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.

Таблица квадратов

Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:

1. Извлеките квадратный корень: √289

Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.

Влево — 1, вверх — 7.

2. Извлеките квадратный корень: √3025

Ищем в таблице число 3025. Влево — 5, вверх — 5.

3. Извлеките квадратный корень: √7396

Ищем в таблице число 7396.

Влево — 8, вверх — 6.

4. Извлеките корень: √9025

Ищем в таблице число 9025.

Влево — 9, вверх — 5.

5. Извлеките корень √1600

Ищем в таблице число 1600.

Влево — 4, вверх — 0.

Извлечением корня называется нахождение его значение.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Обелюс — Википедия

Материал из Википедии — свободной энциклопедии

О́белюс, обел (÷) (лат. obelus — от греч. ὀβελός, тот же корень, что и обелиск) — небуквенный символ, внешне напоминающий объединение знаков минуса и двоеточия.

Был введён древнегреческим филологом, александрийским библиотекарем Зенодотом Эфесским для обозначения сомнительности слова или утверждения. Символ мог выглядеть либо как обычная горизонтальная черта, либо как та же черта, но с добавлением точек по одной сверху и снизу. Ставился на полях напротив тех частей текста, которые вызывали сомнения в ходе проверки поступавших в библиотеку рукописей.

В 1659 году немецкий математик Йоханн Ран в своей работе Teutsche Algebra применил обелюс для обозначения деления. Некоторые авторы использовали этот символ как знак вычитания, что стало нормой в ряде стран Европы (например, в Норвегии и Дании). В польской типографской традиции обелюс использовался для обозначения диапазонов, например, запись 3÷7 эквивалентна выражению «от трёх до семи».

В англоязычных странах, а также на клавишах микрокалькуляторов, обелюс используется в качестве знака деления. В языке TeX кодируется сочетанием: \div.

Плюс (+) Минус (−) Знак умножения (· или ×) Знак деления ( или ) Обелюс (÷) Знак корня (√) Факториал (!) Знак интеграла (∫) Набла (∇) Знак равенства (=, ≈, ≡ и др.) Знаки неравенства (≠, >, < и др.) Пропорциональность (∝) Скобки (( ), , ⌈ ⌉, ⌊ ⌋, { }, ⟨ ⟩) Вертикальная черта (|) Косая черта, слеш () Обратная косая черта, бэкслеш (\) Знак бесконечности (∞) Знак градуса (°) Штрих (′, ″, ‴, ⁗) Звёздочка (*) Процент (%) Промилле (‰) Тильда (~) Карет (^) Циркумфлекс (ˆ) Плюс-минус (±) Знак минус-плюс (∓) Десятичный разделитель (, или .) Символ конца доказательства (∎)

Определение и основные принципы использования вертикальной черты

Вертикальная черта, обозначаемая символом «|», является одним из важных символов в математике. Ее применение распространено в различных областях, включая логику, комбинаторику, теорию множеств и другие.

Основными принципами использования вертикальной черты являются:

1. Разделение элементов в множествах:

В математике множество представляет собой совокупность уникальных элементов. Вертикальная черта используется для разделения элементов множества внутри фигурных скобок. Например, множество натуральных чисел можно представить таким образом: {1, 2, 3, 4, …}.

Перечисление условий в определении:

Вертикальная черта используется для разделения условий или свойств элементов при задании определения. Например, определение простого числа может быть записано следующим образом: «Простое число — это натуральное число, большее 1, которое не имеет делителей, кроме 1 и самого себя».

Обозначение альтернативы:

Вертикальная черта также используется для указания альтернативных вариантов или условий в логических выражениях. Например, для обозначения «или» можно использовать символ «|». Такое выражение можно сформулировать следующим образом: «если х > 0, то x может быть равен 1 или 2 | x

Обозначение абсолютной величины:

Вертикальная черта может использоваться для обозначения абсолютной величины числа. Например, |x| обозначает модуль числа x, то есть расстояние от x до нуля на числовой прямой.

Отображение последовательностей:

Вертикальная черта может быть использована для обозначения последовательностей или матриц. Например, в матричной форме система линейных алгебраических уравнений может быть записана так: |a11*x1 + a12*x2 = b1, a21*x1 + a22*x2 = b2|.

Вертикальная черта является мощным инструментом в математике, который позволяет компактно и ясно выражать различные математические концепции и отношения.

Применение в информатике

Специалисты, которые работают с такими системами как DOS и UNIX, знают, что такое вертикальная линия, поскольку часто с ней работают. Подобное объясняется тем, что именно это обозначение используется для Stdout. А что же представляет собой Stdout? Все просто – это процесс, который обозначает перенаправление стандартного потока вывода определенной программы в другой конвейер.

Чтобы было более понятно, рассмотрим такую сложную формулу: cat fruits.txt | grev –v ^bad | sort. Но сразу отметим, что она сложная только на первый взгляд. В действительности программист задал простой алгоритм. С его помощью можно вывести на экран список фруктов, который содержится в файле под названием fruits.txt.

Но при этом можно будет увидеть только те фрукты, в названии которых в первых 3-х символах нет «bad». Более того, выведенный список будет сразу отсортирован по алфавиту. Все просто, не так ли? Но какая же формула натолкнула программистов на мысль сравнить вертикаль с трубопроводом?

Та, что приведена выше. На примере этой формулы можно понять, почему же российским программистам пришло в голову сравнить данный символ с трубопроводом. Описанный метод передачи информации направляет поток данных по тому же принципу работы, что и обычный трубопровод. Именно поэтому программисты из Советского Союза посчитали, что термин «pipe», пришедший с Запада, можно заменить на другой «трубопровод». Ведь по вертикали это значит и вниз, и вниз.

Пример программы в информатике с использованием вертикальных линий

Символы вероятности и статистики

Символ	Название символа	Значение / определение	пример
P ( А )	функция вероятности	вероятность события A	P ( A ) = 0,5
P ( A ⋂ B )	вероятность пересечения событий	вероятность того, что событий A и B	P ( A ⋂ B ) = 0,5
P ( A ⋃ B )	вероятность объединения событий	вероятность того, что событий A или B	P ( A ⋃ B ) = 0,5
P ( A | B )	функция условной вероятности	вероятность события A данное событие B произошло	P ( A | B ) = 0,3
f ( x )	функция плотности вероятности (pdf)	P ( a ≤ x ≤ b ) = ∫ f ( x ) dx
F ( х )	кумулятивная функция распределения (cdf)	F ( х ) = Р ( Х ≤ х )
μ	Средняя численность населения	среднее значение совокупности	μ = 10
E ( X )	ожидаемое значение	ожидаемое значение случайной величины X	E ( X ) = 10
E ( X | Y )	условное ожидание	ожидаемое значение случайной величины X с учетом Y	E ( X | Y = 2 ) = 5
var ( X )	отклонение	дисперсия случайной величины X	var ( X ) = 4
σ 2	отклонение	дисперсия значений совокупности	σ 2 = 4
std ( X )	стандартное отклонение	стандартное отклонение случайной величины X	std ( X ) = 2
σ X	стандартное отклонение	значение стандартного отклонения случайной величины X	σ X = 2
	медиана	среднее значение случайной величины x
cov ( X , Y )	ковариация	ковариация случайных величин X и Y	cov ( X, Y ) = 4
корр ( X , Y )	корреляция	корреляция случайных величин X и Y	корр ( X, Y ) = 0,6
ρ X , Y	корреляция	корреляция случайных величин X и Y	ρ X , Y = 0,6
∑	суммирование	суммирование — сумма всех значений в диапазоне ряда
∑∑	двойное суммирование	двойное суммирование
Пн	Режим	значение, которое чаще всего встречается в популяции
MR	средний диапазон	MR = ( x макс + x мин ) / 2
Мкр	медиана выборки	половина населения ниже этого значения
Q 1	нижний / первый квартиль	25% населения ниже этого значения
2 квартал	медиана / второй квартиль	50% населения ниже этого значения = медиана выборки
3 квартал	верхний / третий квартиль	75% населения ниже этого значения
х	выборочное среднее	среднее / среднее арифметическое	х = (2 + 5 + 9) / 3 = 5,333
с 2	выборочная дисперсия	оценщик дисперсии выборки населения	s 2 = 4
с	стандартное отклонение выборки	Оценка стандартного отклонения выборки населения	s = 2
z x	стандартная оценка	z x = ( x — x ) / s x
X ~	распределение X	распределение случайной величины X	X ~ N (0,3)
N ( μ , σ 2 )	нормальное распределение	гауссово распределение	X ~ N (0,3)
U ( а , б )	равномерное распределение	равная вероятность в диапазоне a, b	Х ~ U (0,3)
ехр (λ)	экспоненциальное распределение	f ( x ) = λe — λx , x ≥0
гамма ( c , λ)	гамма-распределение	f ( x ) = λ cx c-1 e — λx / Γ ( c ), x ≥0
χ 2 ( к )	распределение хи-квадрат	f ( x ) = x k / 2-1 e — x / 2 / (2 k / 2 Γ ( k / 2))
F ( k 1 , k 2 )	F распределение
Корзина ( n , p )	биномиальное распределение	f ( k ) = n C k p k (1 -p ) nk
Пуассон (λ)	распределение Пуассона	е ( К ) знак равно λ К е — λ / К !
Геом ( p )	геометрическое распределение	f ( k ) = p (1 -p ) k
HG ( N , K , n )	гипергеометрическое распределение
Берн ( p )	Распределение Бернулли

Черточка над буквой в информатике: значение и применение

Черточка над буквой – это один из важных символов, используемых в информатике. Она играет значительную роль в различных аспектах программирования и языковой обработке текста. Черточка над буквой представляет собой оверлей, надеваемый на букву, который изменяет ее значение или дает ей дополнительные характеристики.

В информатике черточка над буквой имеет разные названия и функции в разных языках программирования. Она может использоваться как для обозначения управляющих команд, так и для написания специальных символов или акцентов в языках, использующих нестандартные символы.

Например, в языке программирования C черточка над буквой используется для обозначения типов данных, таких как указатели или длинные целые числа. В языке Python она может использоваться для указания на особый смысл переменной, например, что она является локальной или глобальной. В HTML черточка над буквой может использоваться для создания специальных символов, таких как символ копирайта или торговой марки.

Использование черточки над буквой для обозначения производных величин

В информатике черточка над буквой часто используется для обозначения производных величин. Производная является основной понятием в математическом анализе и науке о данных, и ее обозначение с помощью черточки значительно упрощает и ускоряет запись и чтение формул и уравнений.

Обычно черточку над буквой ставят после буквы, обозначающей переменную, или перед буквой, если она обозначает функцию. Например, если величина обозначается буквой «x», то ее производная обозначается как «х черта». Если величина обозначается другой буквой, например «y», то производная обозначается как «y черта». Если же величина обозначает функцию, то производная обозначается черточкой перед буквой, например «f черта».

Производные величины играют важную роль в информатике. Они позволяют вычислять скорость изменения функции, определять экстремумы, находить точки перегиба, а также решать уравнения и задачи оптимизации. Удобное обозначение производных величин с помощью черточки над буквой делает математические выкладки и программирование более легкими и понятными для специалистов в области информатики и анализа данных.

Символьное представление черточки над буквой в формате Unicode

Черточка над буквой, также известная как диакритическая черта, является специальным символом, который используется для изменения звуковой или смысловой характеристики буквы. В информатике черточка над буквой представляется с помощью символов Unicode.

Символ черточки над буквой можно представить в HTML с помощью специального кода символа. Например, для черточки над буквой «а» код символа Unicode составляет U+0304. Чтобы вставить этот символ в HTML, используйте код ̄ или ̄. Это позволит отобразить черточку над буквой «а».

Если требуется использовать черточку над другой буквой, нужно выбрать соответствующий код символа Unicode. Например, для черточки над буквой «е» код составляет U+0305. Подобным образом можно использовать различные коды символов Unicode для представления черточки над любой буквой.

Unicode предлагает различные варианты черточек над буквами, такие как прямая, косая, волнистая и другие. Кроме того, есть возможность комбинировать черточки над буквой с другими символами Unicode для создания сложных символов. Для этого комбинируются коды символов в правильном порядке.

Использование символов Unicode для представления черточки над буквой позволяет создавать более гибкие и универсальные текстовые элементы

Это особенно полезно при отображении текста в различных языках и системах письма, где черточка над буквой имеет важное значение для правильного произношения или смысла слова

Как на клавиатуре поставить прямую вертикальную палочку?

Как на клавиатуре сделать прямую вертикальную палочку?

Где находится прямая палочка на клавиатуре?

Прямую вертикальную палочку на клавиатуре можно набрать так:

1.Переходим на английскую раскладку, для этого набираем сочетание клавиш » Shift » + » Alt «, либо » Shift » + » Ctrl «, так же можно это сделать в панели задач.

2.Дальше над клавишей » Enter » находим клавишу в изображением нескольких палочек, зажимаем клавишу » Shift » и печатаем нужную нам палочку » | «.

Для того, чтобы на клавиатуре поставить прямую вертикальную палочку, достаточно проделать эти самые наипростейшие шаги:

во — вторых, необходимо нажать на палочку с клавишей, но при этом нужно удерживать клавишу Shift.

Черта сверху в математике: смысл и применение

Черта сверху над числом в математике имеет различные значения и применения в разных областях математики. Она может добавить дополнительную информацию к числу или изменить его значение.

Одним из наиболее распространенных применений черты сверху является обозначение возведения числа в степень. Например, число «a» с чертой сверху «b» (a^b) означает, что число «a» умножается само на себя «b» раз. Это позволяет удобно записывать и вычислять числа в степенной форме.

Черта сверху также часто используется для обозначения корней чисел. Например, символ «√» с чертой сверху означает квадратный корень, а символ «∛» означает кубический корень. Это помогает указать, какой именно корень извлекается из числа. Например, число «16» с чертой сверху «√» означает квадратный корень из числа «16», что равно «4».

Другим применением черты сверху является обозначение векторов. Векторные величины обычно обозначаются буквами с чертой сверху, чтобы выделить их отдельное значение. Например, вектор «v» с чертой сверху (v̂) означает единичный вектор – вектор с длиной равной единице.

В некоторых случаях черта сверху может использоваться для обозначения других математических операций или функций, в зависимости от предметной области. Она может иметь дополнительные значения, которые специфичны для конкретного контекста или области математики.

Обозначение	Описание	Пример
a^b	Возведение числа в степень	2^3 = 8
√a	Квадратный корень числа	√16 = 4
∛a	Кубический корень числа	∛8 = 2
û	Единичный вектор	û = (1, 0)

Извлечение квадратного корня из большого числа

Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

1. Определить «сотни», между которыми оно стоит.
2. Определить «десятки», между которыми оно стоит.
3. Определить последнюю цифру в этом числе.

Извлечь корень из большого числа можно разными способами — вот один из них.

Извлечем корень из √2116.

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

Мы видим что, 2116 больше 1600, но меньше 2500.

Это значит, что число 2116 находится между 40 2 и 50 2 .

41, 42, 43, 44, 45, 46, 47, 48, 49.

Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.

Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей

4 2 = 16 ⇒ 6

5 2 = 25 ⇒ 5

6 2 = 36 ⇒ 6

7 2 = 49 ⇒ 9

8 2 = 64 ⇒ 4

9 2 = 81 ⇒ 1

Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.

Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.

Число 43, возведенное в квадрат, даст число, на конце которого — 9.

Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.

Таким образом, у нас остаются два варианта: 44 2 и 46 2 .

Далее вычисляем: 44 * 44 = 1936.

Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.

Еще пример. Извлечем корень из числа √11664

Разложим число 11664 на множители:

Запишем выражение в следующем виде:

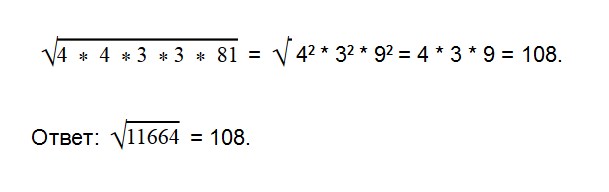
Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.

Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.

• 1. Вычислите значение квадратного корня: √36
• 2. Вычислите значение квадратного корня: √64*36
• 3. Вычислите значение квадратного корня:
• 4. Вычислите значение квадратного корня:
• 5. Вычислите значение квадратного корня:
• 6. Вычислите значение выражения: 4√16 — 12
• 7. Вычислите значение выражения: 5√9 — 8
• 8. Вычислите значение выражения: 7√25 — 10
• 9. Вычислите значение квадратного корня:
• 10. Вычислите значение квадратного уравнения:
• 11. Вычислите значение квадратного уравнения:

• 12. Извлеките квадратный корень из числа √7056 удобным вам способомКак решаем:

• 13. Вычислите значение квадратного корня √0,81Ответ: √0,81 = 0,9
• 14. Вычислите значение квадратного корня: Как решаем: = 0,09
• 15. Вычислите значение выражения: 8√81 — 20Как решаем: 8√81 — 20 = 8 * 9 — 20 = 72 — 20 = 52 Ответ: 8√81 — 20 = 52.
• 16. Вычислите значение выражения: 13√100 — 15Как решаем: 13√100 — 15 = 13 * 10 — 15 = 130 — 15 = 115 Ответ: 13√100 — 15 = 115.
• 17. Вычислите значение выражения: √16 + 5√4Как решаем: √16 + 5√4 = 4 + 5 * 4 = 4 + 20 = 24 Ответ: √16 + 5√4 = 24.
• 18. Вычислите значение выражения: √36 + 2√9Как решаем: √36 + 2√9 = 6 + 2 * 3 = 6 + 6 = 12 Ответ: √36 + 2√9 = 12.
• 19. Вычислите значение выражения: 2√16 — 3√25Как решаем: 2√16 — 3√25 = 2 * 4 — 3 * 5 = 8 — 15 = -7 Ответ: 2√16 — 3√25 = -7.
• 20. Вычислите значение выражения: 3√81 — 5√9Как решаем: 3√81 — 5√9 = 3*9 — 5 * 3 = 27 — 15 = 12 Ответ: 3√81 — 5√9 = 12.
• 21. Вынесите множитель из-под знака корень: √60Как решаем: √60 = √15 * √4 = 2√15 Ответ: √60 = 2√15.
• 22. Вынесите множитель из-под знака корень: √160Как решаем: √160 = √16 * √10 = 4√10 Ответ: √160 = 4√10.
• 23. Внесите множитель под знак корня: 6√7Как решаем: √6 2 * 7 = √36 * √7 = √252 Ответ: 6√7 = √252.
• 24. Внесите множитель под знак корня: 8√2Как решаем: 8√2 = √8 2 * 2 = √64 * √2 = √128 Ответ: 8√2 = √128.
• 25. Внесите множитель под знак корня: 9√5

  Как решаем: 9√5 = √9 2 * 5 = √81 * √5 = √405 Ответ: 9√5 = √405.

• 26. Упростите выражение: (5 — √2) 2Как решаем: (5 — √2) 2 = 5 2 — 2 * 5 * √2 + (√2) 2 = 25 — 10√2 + 2 = 27 — 10√2. Ответ: (5 — √2) 2 = 27 — 10√2.
• 27. Вычислите значение выражения: 3√49 — 3√25Как решаем: 3√49 — 3√25 = 3 * 7 — 3 * 5 = 21 — 15 = 6 Ответ: 3√49 — 3√25 = 6.
• 28. Вычислите значение квадратного корня: √484 * √576Как решаем: √484 * √576 = 22 * 24 = 528 Ответ: √484 * √576 = 528.
• 29. Вычислите значение квадратного корня: √625 * √81Как решаем: √625 * √81 = 25 * 9 = 225 Ответ: √625 * √81 = 225.
• 30. Найдите значение выражения: 3√100 — √144Как решаем: 3100 — 144 = 3 * 10 — 12 = 18 Ответ: 3√100 — √144 = 18.

• 0 0 0 0 0 0

Вебинар : Гаджеты: как вернуть ребёнка в реальность среда, 23 февраля в 19:00 МСК

использовать

Математика

Вертикальная черта используется в таблице математических символов  :

• Абсолютное значение  : считывает «  на абсолютное значение (или модуль ) х  »;|Икс|{\ Displaystyle \, | х |}
• Делимость  : читается как «  делится  » или «  делится на  ».б|в{\ displaystyle b | a}б{\ displaystyle b}в{\ displaystyle a}в{\ displaystyle a}б{\ displaystyle b}
• Норма  : читает «  в норму из й индексных один х подстрочных два  »‖(Икс1,Икс2)‖{\ Displaystyle \, \ | (х_ {1}, х_ {2}) \ |}
• Разделитель в наборах: читает «  набор x таких, что x меньше трех  » (часто определение записывается с двоеточием ( :), а не с вертикальной чертой).{Икс∣Икс<3}{\ Displaystyle \ {х \ середина х <3 \}}
• Эффект в логике:

в|бзнак равно¬(в∧б){\ Displaystyle а | b: = \ neg (а \ клин b)}, то есть «  нет ( а и б )» или по-английски «  а нанд б  ».

в||бзнак равнов+б{\ displaystyle a || b = a + b}, то есть сказать «  a или b  » или по-английски «  a или b  ».

Указатель мыши

В тексте, который нельзя редактировать, но который можно выбрать, например на веб-странице , указатель мыши часто представляет собой вертикальную полосу (иногда с засечками вверху и внизу).

Язык разметки вики

На сайтах, использующих программное обеспечение MediaWiki ( например, Википедия ), вертикальная полоса используется (среди прочего) в синтаксисе внутренних ссылок вики для отделения ссылки от отображаемого текста. Например, «]» отображается как «текст», но ссылается на «статью». Этот символ также используется для написания таблиц и как разделитель при написании моделей.

Форма Бэкуса-Наура

В этой форме выражения состоят из последовательностей символов и / или последовательностей, разделенных символами «| », Обозначающий альтернативу , каждый из которых может быть заменен символом слева. Например,

<имя пользователя> :: = <имя> | <инициалы>

UNIX

Труба представляет собой функциональность определенных операционных систем используются , в частности , в системе UNIX , и что делает возможным , чтобы перенаправить стандартный вывод одного процесса со стандартным вводом другого. В командных интерпретаторах труба представлена ​​вертикальной полосой. Эта функция также присутствует в DOS и Windows.

Регулярные выражения

В регулярных выражениях вертикальная черта обозначает альтернативу (выбранный оператор). Например, grep «foo | bar» вернет «foo» или «bar».

Угловой

Angular предлагает множество каналов в стандартной комплектации для обработки дат, валют, интернационализации, регистра символов, чисел.

Оболочка

В оболочках UNIX канал используется для направления вывода команды (например, dmesg) другой команде (например, grep). Напримерdmesg | grep firewire перенаправит вывод dmesg на grep, который будет выводить только строки, содержащие слово «  firewire  ».

Дизъюнкция

Во многих языках программирования это относится к функции логического ИЛИ , будь то побитовое или или логическое или .

Таким образом, в языке программирования C и других языках, использующих синтаксис C, таких как Perl и Java , (a | b) означает или побитовое , а двойная вертикальная черта (a || b) означает или логическое .

Делимитация

Хотя символ «|» встречается реже, чем запятые или табуляторы. Может использоваться в текстовом файле, представляющем табличные данные, например в формате LEDES 1998B.

Тот же символ может использоваться в диалектах Лиспа для ограничения начала и конца символов, имен переменных и т. Д. который может содержать различные символы (даже непечатаемые).

Кодировка символов

Фамилия	глиф	Юникод	codePage 1252	МакРоман	HTML- объект
Вертикальная полоса	|	007C	7C	7C
Латинская буква clic стоматологическая	ǀ	01C0
Пунктуация на иврите paseq, pési, legarméh	׀	05C0
Делитель	∣	2223
Тонкая вертикальная полоса	❘	2758
Непрерывный вертикальный стержень, разделительный стержень, стержень с отверстиями	¦	00A6	A6
Слэш	002F	2 F	2 F
Латинские буквы бокового щелчка	ǁ	01C1
Параллельно	∥	2225
Двойная вертикальная линия	‖	2016 г.
Восклицательный знак, факториал	!	0021	21 год	21 год

Что значит черта над числом в математике?

В теории чисел: обозначает, что под чертой все вместе считается числом, например, ¯abcde,efg и с чертой над всеми этими символами — говорит о том, что каждая буква — это цифра, а вместе они образуют десятичное число. В функциональном анализе так может обозначаться замыкание множества.

Как поставить черту над буквой?

поставить черточку над буквой. Выделите текст, который требуется подчеркнуть. Потом На вкладке Начальная страница в группе Шрифт выберите команду Подчеркнутый. Или нажмите сочетание клавиш CTRL+U.

Что значит черта над вектором?

Это когда-то раньше использовали черточку в обозначении вектора. Сейчас черточка над буквой обозначает среднюю величину, но не вектор! Кроме того, часто вектор обозначают парой букв (обычно заглавных), причём первая буква обозначает начало вектора, а вторая — его конец (рис. 1).

Что означает х с черточкой сверху?

Сре́днее арифмети́ческое (в математике и статистике) — разновидность среднего значения. Определяется как число, равное сумме всех чисел множества, делённой на их количество.

Как в Excel сделать верхнее подчеркивание?

Выделите текст, который вы хотите подчеркнуть. Перейдите на вкладку Главная и нажмите кнопку вызова диалогового окна » Шрифт » . Совет: Вы также можете использовать сочетание клавиш CTRL + D. С помощью раскрывающегося списка стиль подчеркивания выберите стиль подчеркивания.

Как поставить верхнюю точку на клавиатуре?

Для этого зажмите клавишу «Alt» и наберите «0146», после этого отпустите «Alt» и в том месте, где был установлен курсор, должна появиться одинарная верхняя запятая.

Как в ворде сделать верхнее подчеркивание?

Изначально необходимо напечатать нужный текст. Далее перейти во вкладку «Вставка» в области «Иллюстрации» выбрать кнопку «Фигуры». В новом окне кликнуть по фигуре «Линия». Поставить крестик над словом в начале, нажать и протянуть линию до конца слова, двигая вверх или вниз выровнять линию и отпустить.

Как называется значок над буквой?

р.). Система диакритических знаков какой-либо письменности или текста также называется диакри́тикой. В некоторых случаях с одной буквой могут употребляться одновременно два, три или даже четыре диакритических знака: ặ, ṩ, ᶑ, ᾧ.

Как в ворде сделать штрих над буквой?

Наведите указатель мыши на нужный документ, щелкните появившуюся стрелку, а затем выберите команду Изменить для названия программы Office (например, изменить в Microsoft Office Word). Поместите курсор в то место документа, куда вы хотите вставить штрихкод. На вкладке Вставка в группе штрихкод нажмите кнопку штрихкод.

Что называют вектором в пространстве?

Другими словами, вектором называется отрезок, для которого указано, какой из его концов является началом, а какой концом. На рисунках направление вектора обозначается стрелкой от начала к концу.

Что значит стрелка над буквой в физике?

Связано это с тем, что обозначения этих величин (особенно — скорости) в учебниках по математике и физике можно увидеть различные: с чертой над буквой v (читается: ), со стрелкой над буквой v, а также буквы v, выделенные курсивом или жирным шрифтом. …

Что называется вектором примеры?

Например, длина, площадь, масса, температура и т. д. Вектором называется направленный отрезок ¯AB; точка A — начало, точка B — конец вектора (рис. 1).

Что означает черта над х?

Черта́ све́рху — типографический знак горизонтальной линии, нарисованной сразу над текстом. В математической нотации черта сверху долгое время используется для vinculum, объединения определённых символов.

Для чего используется среднее гармоническое?

Среднее гармоническое помогает нам вычислить среднее арифметическое в рядах чисел, заданных обратными значениями. Это бывает чаще, чем можно подумать. Например, если я еду со скоростью 30 км/ч, это значит, что я получаю определённый результат (30 км) за какую-либо единицу времени (1 час).

Чем отличается среднее значение от математического ожидания?

Мат. ожидание — это среднее значение, но не среднее арифметическое, а среднее взвешенное (для дискретного распределения).

Примеры использования черты в математических задачах

Черта над буквой в математике имеет различные значения в разных контекстах. Рассмотрим несколько примеров использования черты в математических задачах:

Пример	Значение
AB̄	Черта над двумя буквами, например AB̄, может обозначать отрезок AB, то есть расстояние между точками A и B.
x̄	Черта над переменной, например x̄, обозначает среднее арифметическое данной переменной в наборе значений.
P̄Q̄	Черта над двумя буквами, например P̄Q̄, может также обозначать отрезок PQ, то есть расстояние между точками P и Q.
ā	Черта над переменной, например ā, может обозначать среднее арифметическое данной переменной в наборе значений.

Это лишь несколько примеров использования черты в математических задачах. В математике черта может иметь и другие значения в зависимости от контекста использования.

Черта над буквой в математике имеет свое значение в различных областях математики и наук, где используются символы, формулы и уравнения.

Одной из основных областей применения черты над буквой является алгебра, где она обозначает переменную, отличную от остальных переменных в системе. Например, если у нас есть система уравнений, в которых есть переменные x, y и z, то черта над буквой x может указывать на особую переменную в этой системе.

В геометрии черта над буквой может обозначать отрезок или вектор. Она может быть использована для обозначения отрезка на плоскости или в пространстве, например, AB или CD. Также вектор может быть обозначен с помощью черты над буквой, например, вектор AB или вектор CD.

В математическом анализе черта над буквой может обозначать производную или дифференциал. Она может указывать на то, что буква является переменной, по которой берется производная или дифференциал. Например, если у нас есть функция f(x), то производная этой функции по переменной x может быть обозначена как f'(x) или df/dx.

Черта над буквой также может использоваться в теории вероятностей и статистике для обозначения условной вероятности. Она показывает, что вероятность зависит от какого-то условия. Например, P(A|B) обозначает условную вероятность события A при условии, что произошло событие B.

Таким образом, черта над буквой в математике имеет различные значения и области применения в зависимости от контекста и области математики или науки, где она используется.

Использование в физике и химии

Черта сверху над числом, также известная как экспонента или показатель степени, используется в физике и химии для обозначения различных величин и физических явлений. Эта математическая концепция играет важную роль в описании и анализе законов природы.

В физике черта сверху над числом обозначает степень, в которую необходимо возвести данное число. Например, скорость света в вакууме обычно обозначается как «с = 3 × 10^8 м/с» — это значит, что число 3 умножается на 10 в степени 8, т.е. 3 с перемещением десятой точки вправо на 8 позиций. Такое представление облегчает запись больших и малых чисел и позволяет сравнивать их между собой.

В химии черта сверху над числом используется для обозначения числа атомов элемента в химической формуле. Например, формула воды — H2O — означает, что в каждой молекуле воды содержится 2 атома водорода (H) и 1 атом кислорода (O). Это позволяет установить соотношение между различными элементами в химическом соединении и определить его состав и свойства.

Черта сверху над числом также используется для обозначения степени ионизации в химических реакциях. Например, в реакции образования соляной кислоты из хлороводорода и воды: HCl + H2O → H3O+ + Cl-, символы H3O+ и Cl- означают ионы гидроксония и хлорида соответственно, а значок «+» означает, что ион положительно заряжен, а «-» — отрицательно. Это позволяет описывать ионные реакции и анализировать химические процессы.

Физика	Химия
10^2	H2O
10^3	H2SO4
10^4	NaCl
10^5	C6H12O6