Предел функции

Методы и примеры

Существует несколько методов, которые можно применять для доказательства того, что предел последовательности не существует. Некоторые из них включают:

• Метод предельного перехода: для доказательства отсутствия предела можно попытаться найти две различные подпоследовательности, сходящиеся к разным пределам. Если такие подпоследовательности найдены, то предел не существует.
• Метод Больцано-Вейерштрасса: если ограниченная последовательность содержит две различные сходящиеся подпоследовательности, то она не имеет предела.
• Метод зажатой последовательности: если можно найти две ограниченные последовательности, сходящиеся к одному и тому же пределу, и наша последовательность находится между ними, то предел не существует.
• Метод расходимости: если последовательность имеет тенденцию расти или убывать неограниченно, то предел не существует.

Давайте рассмотрим примеры:

1. Последовательность {n}, где каждый элемент равен своему индексу. Мы можем заметить, что подпоследовательность четных чисел будет сходиться к нечетному пределу именно их индексов, а подпоследовательность нечетных чисел будет сходиться к четному пределу именно их индексов. Поскольку две различные подпоследовательности имеют разные пределы, предел для всей последовательности не существует.
2. Последовательность {(-1)^n}, где каждый элемент чередуется между -1 и 1. В этом случае мы видим, что последовательность не сходится к одному пределу, поскольку она постоянно меняет свое значение между -1 и 1.
3. Последовательность {\frac{n+1}{n}}. Если мы берем подпоследовательность элементов с четными индексами, то предел этой подпоследовательности будет равен 1. Если мы берем подпоследовательность элементов с нечетными индексами, то предел будет равен 1. В итоге, у нас существуют две различные сходящиеся подпоследовательности, и поэтому предел для всей последовательности не существует.

Это только некоторые из методов и примеров, которые можно использовать для доказательства отсутствия предела

Важно понимать, что доказательство отсутствия предела требует тщательного анализа последовательности и поиска различных подпоследовательностей или характеристик, которые указывают на отсутствие предела

Понятие предела.

Важную роль в курсе математического анализа играет понятие предела, связанное с поведением функции в окрестности данной точки. Напомним, что \(\delta\) — окрестностью точки \(a\) называется интервал длины \(2\delta\) с центром в точке \(a\), то есть множество
$$
U_{\delta}(a)=\{x:|x-a| < \delta\}=\{x:a-\delta < x < a+\delta\}.\nonumber
$$

Если из этого интервала удалить точку \(a\), то получим множество, которое называют проколотой \(\delta\)-окрестностью точки \(a\) и обозначают \(\dot{U}_{\delta}(a)\), то есть
$$
\dot{U}_{\delta}(a)=\{x:|x-a|<\delta,\ x\neq a\}=\{x:0<|x-a|<\delta\}.\nonumber
$$

Предваряя определение предела функции, рассмотрим два примера.

Пример 1

Исследуем функцию \(f(x)=\displaystyle \frac{x^2-1}{x-1}\) в окрестности точки \(x=1\).

\(\triangle\) Функция \(f\) определена при всех \(x\in\mathbb{R}\), кроме \(x=1\), причем \(f(x)=x+1\) при \(x\neq 1\). График этой функции изображен на

Рис. 10.1

Из этого рисунка видно, что значения функции близки к 2, если значения \(x\) близки к 1 (\(x\neq 1)\). Придадим этому утверждению точный смысл.

Пусть задано любое число \(\varepsilon>0\) и требуется найти число \(\delta>0\) такое, что для всех \(x\) из проколотой \(\delta\)-окрестности точки \(x=1\) значения функции \(f(x)\) отличаются от числа 2 по абсолютной величине меньше, чем на \(\varepsilon\).

Иначе говоря, нужно найти число \(\delta>0\) такое, чтобы для всех \(x\in\dot{U}_{\delta}(a)\) соответствующие точки графика функции \(y=f(x)\) лежали в горизонтальной полосе, ограниченной прямыми \(y=2-\varepsilon\) и \(y=2+\varepsilon\) , то есть чтобы выполнялось условие \(f(x)\in U_{\varepsilon}(2)\). В данном примере можно взять \(\delta=\varepsilon\).

В этом случае говорят, что функция \(f(x)\) стремится к двум при \(x\), стремящемся к единице, а число 2 называют пределом функции \(f(x)\) при \(x\rightarrow 1\) и пишут \(\displaystyle \lim{x\rightarrow 1}f(x)=2\) или \(f(x)\rightarrow 2\) при \(x\rightarrow 1.\quad\blacktriangle\)

Пример 2

Исследуем функцию
$$
f(x)=\left\{\begin{array}{ll}
1-x,\ \mbox{если}\ x < 0,\\
0,\ \mbox{если}\ x=0,\\
1-x^{2},\ \mbox{если}\ x>0,
\end{array}\right.\nonumber
$$
в окрестности точки \(x=0.\)

Рис. 10.2

\(\triangle\) Из графика этой функции видно, что для любого \(\varepsilon>0\) можно найти \(\delta>0\) такое, что для всех \(x\in\dot{U}_{\delta}(0)\) выполняется условие \(f(x)\in U_{\varepsilon}(1)\). В самом деле, прямые \(y=1+\varepsilon\) и \(y=1-\varepsilon\) пересекают график функции \(y=f(x)\) в точках, абсциссы которых равны \(x_{1}=-\varepsilon,\ x_2=\sqrt{\varepsilon}\). Пусть \(\delta\) — наименьшее из чисел \(|x_{1}|\) и \(x_2\), т.e. \(\displaystyle \delta=\min(\varepsilon,\sqrt{\varepsilon})\). Тогда если \(|x|<\delta\) и \(x\neq 0\), то \(|f(x)-1|<\varepsilon\), то есть для всех \(x\in\dot{U}_{\delta}(0)\) выполняется условие \(f(x)\in U_{\varepsilon}(1)\). В этом случае говорят, что функция \(f(x)\) стремится к единице при \(x\), стремящемся к нулю и пишут,
$$
\displaystyle \lim_{x\rightarrow 0}{f(x)}=1.\quad\blacktriangle\nonumber
$$

В первом примере функция не определена в точке \(x=1\), а во втором функция определена в точке \(x=0\), но значение функции в точке \(x=0\) не совпадает с ее пределом при \(x\rightarrow 0\).

Предел по Коши

Формально, предел по Коши определяется через понятие окрестности. Говорят, что последовательность чисел имеет предел по Коши, если для любого положительного числа ε существует такой номер N, начиная с которого все элементы последовательности находятся в ε-окрестности предела.

Предел по Коши обладает некоторыми свойствами, которые могут быть использованы для доказательства его существования. Например, если есть две последовательности, сходящиеся к одному пределу по Коши, то их сумма также сходится к тому же пределу. Аналогично, произведение и отношение сходящихся последовательностей также имеют предел по Коши.

Доказательство предела по Коши требует строгой формализации и логической работы. Оно включает в себя выбор подходящего ε, нахождение соответствующего N и проверку выполнения условий определения.

Предел по Коши играет важную роль в анализе функций и последовательностей. Он позволяет понять и описать поведение последовательности или функции в окрестности определенной точки или значения аргумента. Доказательство предела по Коши является одним из основных инструментов для анализа и изучения математических объектов.

Определение предела по Коши

Определение предела по Коши гласит:

Для любого положительного числа ε (эпсилон) существует такое положительное число δ (дельта), что для любого значения x, отличного от точки a и удовлетворяющего условию |x — a| < δ, выполняется неравенство |f(x) — L| < ε, где L – предельное значение функции f(x) при x, стремящемся к a.

То есть, если мы можем найти такое положительное число δ, что для всех значений x, отличных от точки a и находящихся в интервале (δ, +∞), разность f(x) — L будет меньше, чем любое положительное число ε, то говорят, что предел функции f(x) при x, стремящемся к a, равен L. В этом случае мы записываем lim_{x → a} f(x) = L.

Определение предела по Коши позволяет формализовать и ригорозно определить понятие предела функции, что является основой многих математических и физических теорий и методов, например, дифференциального исчисления.

Сходимость последовательности по Коши

Последовательность чисел называется сходящейся по Коши, если для любого положительного числа ε существует такой номер N, начиная с которого все члены последовательности находятся на расстоянии меньше ε друг от друга.

Формально, последовательность {an} сходится по Коши, если для любого ε>0 найдется натуральное число N, такое что для всех n, m>N выполняется |an — am|

Из определения следует, что если последовательность сходится по Коши, то она ограничена, то есть существует такое число M, что |an| ≤ M для всех n.

Сходимость по Коши является одним из понятий, которое используется при доказательстве пределов последовательностей и рядов. Она представляет собой более строгое понятие сходимости, чем просто ограниченность последовательности.

Сходимость последовательности по Коши является важным понятием в анализе, так как позволяет определить сходимость последовательностей и рядов, что является базовым для многих математических теорем и концепций.

На практике, для доказательства сходимости последовательности по Коши используются различные методы, включая арифметические свойства чисел и неравенства, а также понятия такие как пределы и ограниченность.

Таким образом, сходимость последовательности по Коши позволяет формально задать понятие предела последовательности и является важной частью математического анализа

Свойства предела по Коши

Уникальность предела: Если последовательность или функция имеют предел по Коши, то этот предел единственный. Другими словами, если последовательность или функция сходятся к двум разным значениям, то предел не существует.

Арифметические свойства предела:

1. Сумма: Предел суммы двух последовательностей или функций равен сумме пределов этих последовательностей или функций.
2. Разность: Предел разности двух последовательностей или функций равен разности пределов этих последовательностей или функций.
3. Произведение: Предел произведения двух последовательностей или функций равен произведению пределов этих последовательностей или функций.
4. Частное: Предел частного двух последовательностей или функций равен отношению пределов этих последовательностей или функций, при условии, что предел делителя отличен от нуля.

Пример:

Рассмотрим последовательность a_n = n + 1 и последовательность b_n = n — 1. Сумма этих последовательностей будет равна c_n = (n + 1) + (n — 1) = 2n. Пределы последовательностей a_n и b_n равны A = +∞ и B = +∞ соответственно. Сумма последовательности c_n будет равна C = +∞ + +∞ = +∞. Из этого примера следует, что предел суммы равен сумме пределов.

Определение, что число a не является пределом

Теперь рассмотрим обратное утверждение, что число a
не является пределом последовательности.

Число a
не является пределом последовательности
,
если существует такое ,
что для любого натурального n
существует такое натуральное m >
n
,
что.

Запишем это утверждение с помощью логических символов.(2)
.

Утверждение, что число a
не является пределом последовательности
, означает, чтоможно выбрать такую ε
— окрестность точки a
,
за пределами которой будет находиться бесконечное число элементов последовательности
.

Рассмотрим пример
. Пусть задана последовательность с общим элементом(3)
Любая окрестность точки содержит бесконечное число элементов. Однако эта точка не является пределом последовательности, поскольку и любая окрестность точки также содержит бесконечное число элементов. Возьмем ε
— окрестность точки с ε = 1

.
Это будет интервал (-1, +1)

.
Все элементы, кроме первого, с четными n
принадлежат этому интервалу. Но все элементы с нечетными n
находятся за пределами этого интервала, поскольку они удовлетворяют неравенству x n > 2

.
Поскольку число нечетных элементов бесконечно, то за пределами выбранной окрестности будет находиться бесконечное число элементов. Поэтому точка не является пределом последовательности.

Теперь покажем это, строго придерживаясь утверждения (2). Точка не является пределом последовательности (3), поскольку существует такое ,
так что, для любого натурального n
,
существует нечетное ,
для которого выполняется неравенство.

Также можно показать, что любая точка a
не может являться пределом этой последовательности. Мы всегда можем выбрать такую ε
— окрестность точки a
,
которая не содержит либо точку 0, либо точку 2. И тогда за пределами выбранной окрестности будет находиться бесконечное число элементов последовательности.

Что такое предел функции

Сначала вспомним, что такое функция и аргумент.

Функция — это математическое правило, которое получает на вход число и возвращает какой-то результат. Например, в функции y = x2 число умножается на само себя. Передали 2, получили 4.

Аргумент — это число, которое мы передаём, то есть подставляем в функцию. В нашем примере аргумент равен 2.

В общем виде функция записывается так:

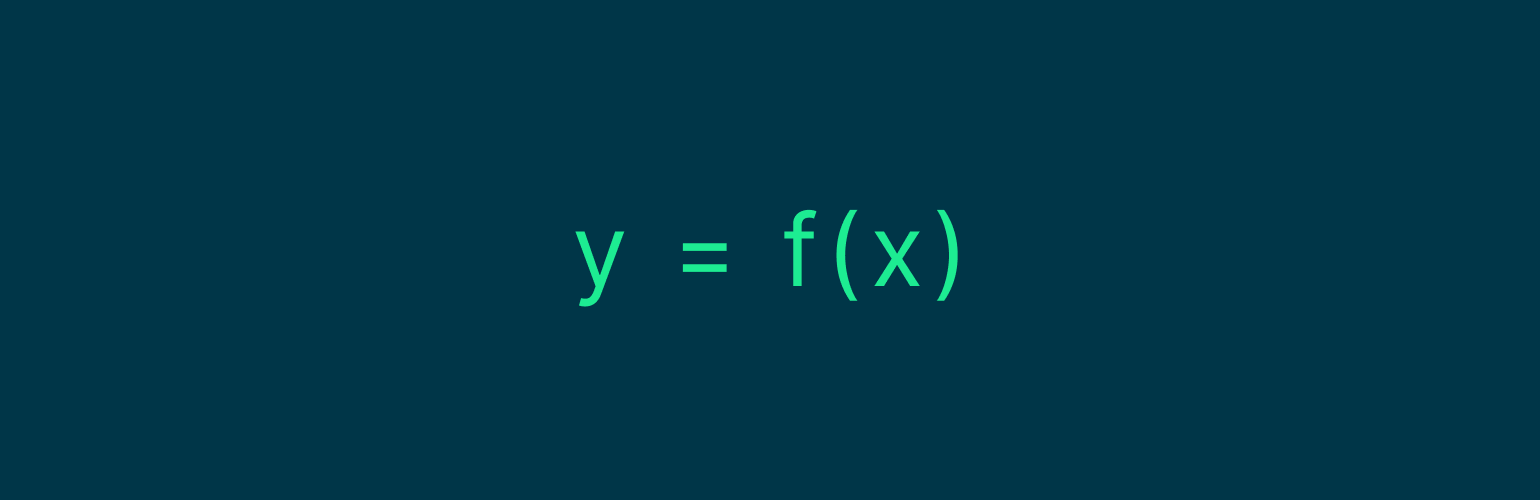
Изображение: Skillbox Media

Здесь f — это функция, x — её аргумент, y — результат её выполнения.

Предел функции — это значение, к которому стремится функция, когда её аргумент приближается к определённому значению. Проще всего разобраться в этом на примере.

Напишем простую функцию:

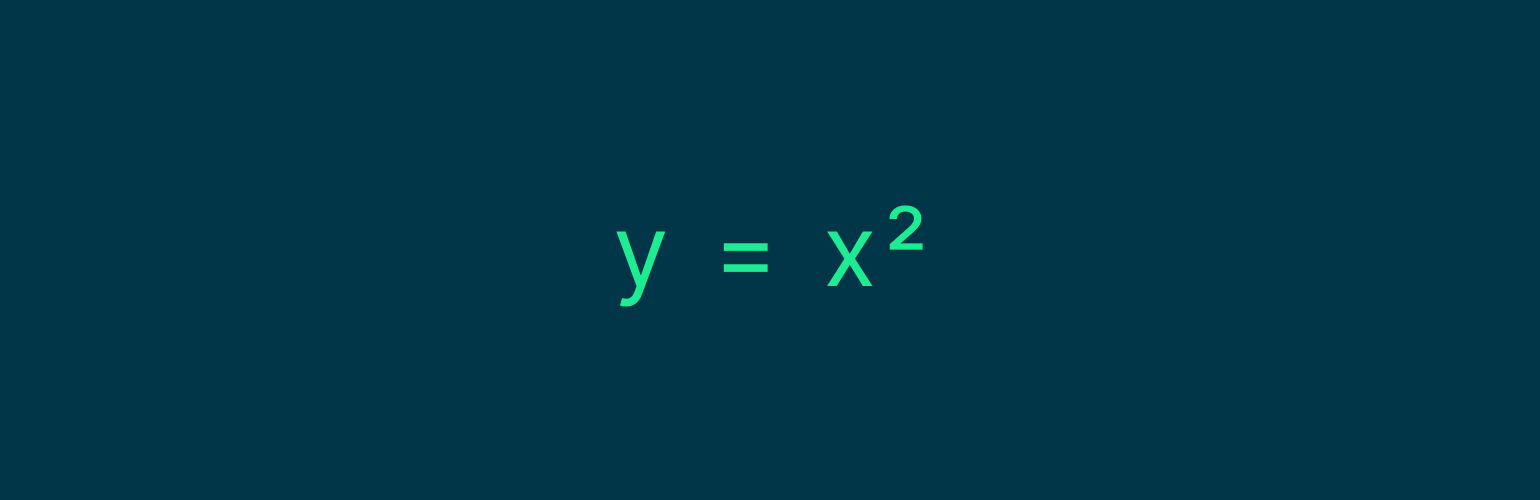
Изображение: Skillbox Media

Представим, что x стремится к числу 2, но не достигает его:

1,9; 1,99; 1,999…1,99999.

Тогда y будет стремиться к 4:

3,61; 3,9601; 3,996001…3,9999600001.

Число будет всё больше и больше, но никогда не достигнет числа 4, а только приблизится к нему.

Получается, что предел для функции при x, стремящемся к 2, равен 4.

Предел в математике обозначается с помощью lim:

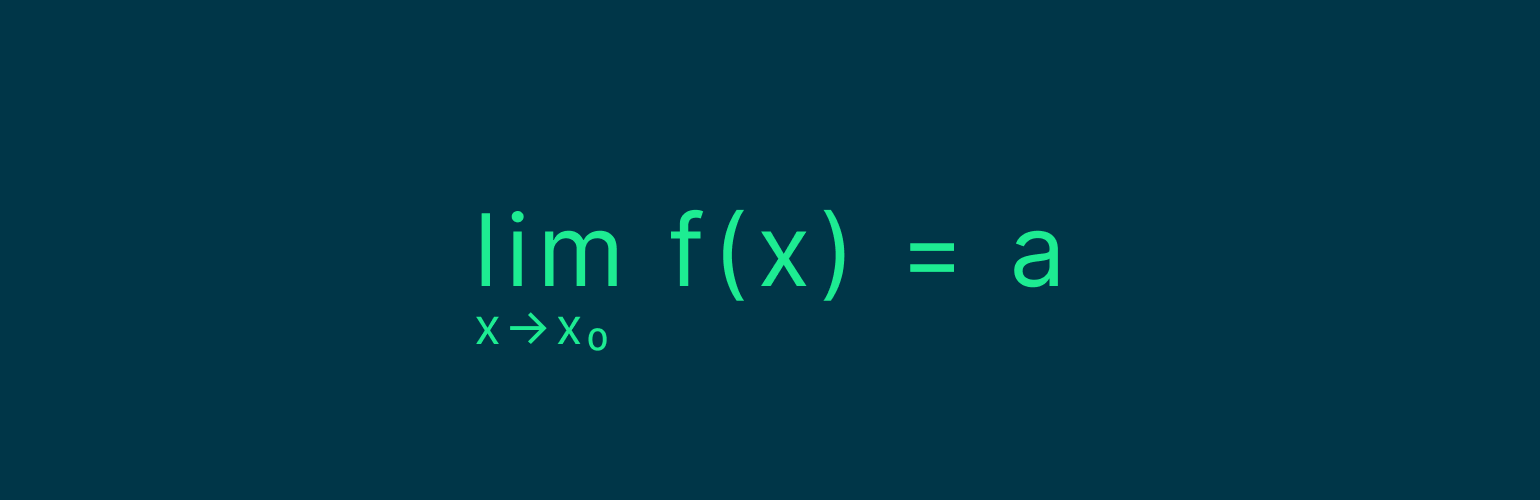
Изображение: Skillbox Media

Читается выражение так: для функции y = f(x) пределом называется такое число a, к которому приближается y при x, стремящемся к определённой точке x. Стремление обозначается стрелкой.

Слово «стремится» означает, что переменная приближается к пределу на сколь угодно малую величину, но никогда не достигает его.

Посмотрим на другую формулу:

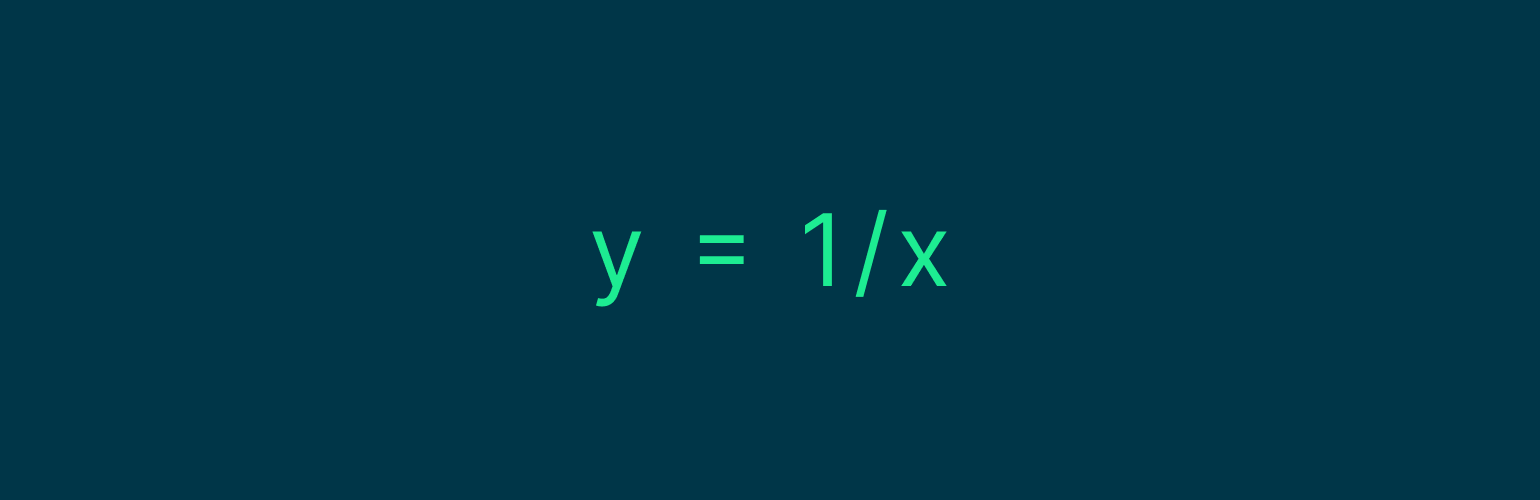
Изображение: Skillbox Media

И сразу построим для неё график:

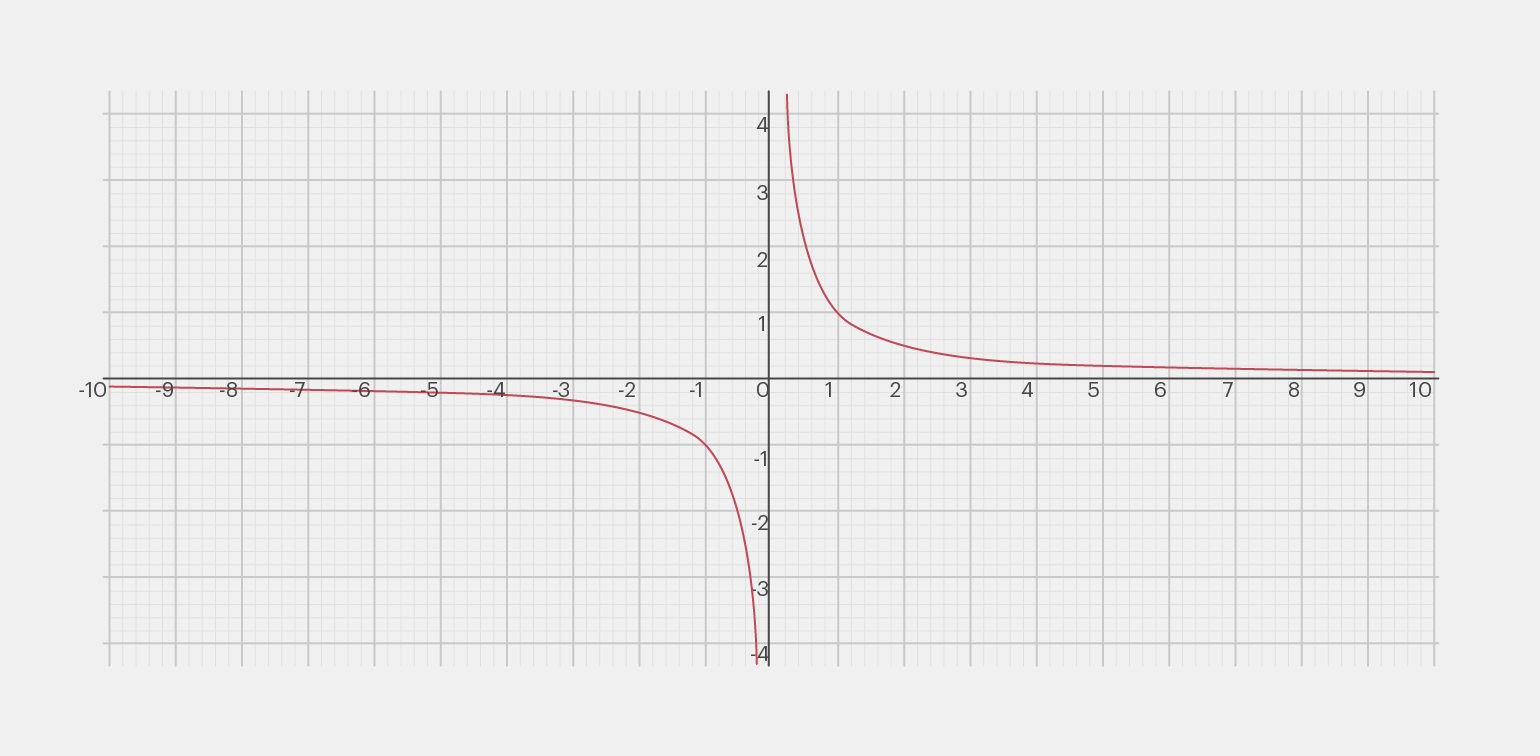
Инфографика: Майя Мальгина для Skillbox Media

Операторы и применение лимитов

В математике существует большое количество операторов, которые позволяют вычислять различные значения и свойства функций. Один из самых важных операторов в алгебре — это оператор предела, обозначаемый символом lim.

Оператор лимита позволяет установить, к какому числу стремится функция при приближении ее аргумента к некоторому значению. Понимание и применение лимитов является важным для анализа функций и решения различных задач в математике и физике.

Применение лимитов в математике позволяет решать такие задачи, как нахождение точки разрыва функции, нахождение асимптот и определение поведения функции в окрестности некоторой точки.

Для вычисления предела функции необходимо определить точку, к которой аргумент функции стремится, и исследовать поведение функции в этой точке. Если функция определена на интервале и в окрестности этой точки, то она может иметь как конечный, так и бесконечный предел.

Оператор лимита может применяться к различным типам функций, таким как полиномы, рациональные функции, тригонометрические функции и другие. При нахождении предела функции можно использовать различные приемы, такие как арифметические действия с пределами, приведение подобных дробей и замена переменных.

Применение лимитов также позволяет решать задачи с использованием правила Лопиталя, которое позволяет вычислить предел отношения двух функций, имеющих вид неопределенности 0/0 или ∞/∞. Правило Лопиталя основано на нахождении производных функций и может существенно упростить вычисления пределов.

Примеры операторов и применения лимитов:
Функция
Предел

lim{x → 0}(sin x / x)
1

lim{x → ∞}(1 + 1/x)x
e

lim{x → 1}(x2 — 1) / (x — 1)
2

Использование оператора лимита позволяет проводить анализ функций и выявлять их особенности, такие как точки разрыва, асимптоты, поведение в окрестности некоторой точки и т. д. Это очень важный инструмент в математике, который находит свое применение в широком спектре дисциплин и областях знаний.

Свойства и особенности предела функции

1. Единственность предела: Для каждой функции существует только один предел в каждой точке.

2. Определение предела с помощью окрестностей: Предел функции определяется через понятие окрестности точки и произвольно малого числа. Существуют формальные определения предела функции, основанные на окрестностях.

3. Предел функции в точке и на бесконечности: Функция может иметь предел как в конкретной точке, так и на бесконечности. Предел функции в точке определяется приближением аргумента к данной точке, а предел функции на бесконечности – приближением аргумента к бесконечности.

4. Арифметические операции с пределами функций: Существуют особые правила для вычисления пределов функций при их арифметических операциях, таких как сложение, вычитание, умножение и деление.

5. Односторонние пределы: Функция может иметь односторонний предел в точке, который определяется приближением аргумента справа или слева от данной точки.

6. Существование предела: Не все функции имеют пределы во всех точках. Существуют функции, у которых предел существует только для определенного множества значений аргумента или для некоторых точек.

7. Границы пределов: Если функция имеет предел в точке, то ее значения в этой точке и в некоторой окрестности этой точки ограничены. В некоторых случаях границы предела могут быть достигнуты или нет, в зависимости от характера функции.

8. Значение функции и предел: Предел функции является значением, к которому функция стремится при приближении аргумента к определенной точке или бесконечности. Интуитивно, предел функции можно рассматривать как «предсказание» значения функции в данной точке, основанное на значениях функции в ее окрестности.

Эти свойства и особенности предела функции являются важными для понимания и применения математического анализа в различных областях науки и инженерии.

Арифметическая прогрессия как часть последовательностей

Прежде чем искать пределы последовательностей, целесообразно поглубже окунуться в само понятие подобного числового ряда, с которым все сталкивались, будучи в средних классах. Арифметическая прогрессия — это ряд чисел, в котором разница между соседними членами постоянна.

Задача: «Пусть а 1 =15, а шаг прогрессии числового ряда d=4. Постройте первые 4 члена этого ряда»

Решение: а 1 = 15 (по условию) — первый член прогрессии (числового ряда).

а 2 = 15+4=19 — второй член прогрессии.

а 3 =19+4=23 — третий член.

а 4 =23+4=27 — четвёртый член.

Однако подобным методом трудно добраться до крупных значений, например до а 125. . Специально для таких случаев была выведена удобная для практики формула: а n =a 1 +d(n-1). В данном случае а 125 =15+4(125-1)=511.

Эквивалентность определений предела по Гейне и по Коши

Теорема
Определения предела функции по Гейне и по Коши эквивалентны.

Доказательство

При доказательстве мы предполагаем, что функция определена в некоторой проколотой окрестности точки (конечной или бесконечно удаленной). Точка a
также может быть конечной или бесконечно удаленной.

Доказательство Гейне ⇒ Коши

Пусть функция имеет в точке предел a
согласно первому определению (по Гейне). То есть для любой последовательности ,
принадлежащей окрестности точки и имеющей предел(1)
,
предел последовательности равен a
:
(2)
.

Покажем, что функция имеет предел в точке по Коши. То есть для любого существует ,
что для всех .

Допустим противное. Пусть условия (1) и (2) выполнены, но функция не имеет предела по Коши. То есть существует такое ,
что для любого существует ,
так что.

Возьмем ,
где n
— натуральное число. Тогда существует ,
причем.
Таким образом мы построили последовательность ,
сходящуюся к ,
но предел последовательности не равен a
.
Это противоречит условию теоремы.

Первая часть доказана.

Доказательство Коши ⇒ Гейне

Пусть функция имеет в точке предел a
согласно второму определению (по Коши). То есть для любого существует ,
что(3)
для всех .

Покажем, что функция имеет предел a
в точке по Гейне. Возьмем произвольное число .
Согласно определению Коши, существует число ,
так что выполняется (3).

Возьмем произвольную последовательность ,
принадлежащую проколотой окрестности и сходящуюся к .
По определению сходящейся последовательности, для любого существует ,
что при .
Тогда из (3) следует, что при .
Поскольку это выполняется для любого ,
то.

Теорема доказана.

Использованная литература: Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.

Сегодня на уроке мы разберём строгое определение последовательности
и строгое определение предела функции
, а также научимся решать соответствующие задачи теоретического характера. Статья предназначена, прежде всего, для студентов 1-го курса естественнонаучных и инженерно-технических специальностей, которые начали изучать теорию математического анализа, и столкнулись с трудностями в плане понимания этого раздела высшей математики. Кроме того, материал вполне доступен и учащимся старших классов.

За годы существования сайта я получил недобрый десяток писем примерно такого содержания: «Плохо понимаю математический анализ, что делать?», «Совсем не понимаю матан, думаю бросить учёбу» и т.п. И действительно, именно матан часто прореживает студенческую группу после первой же сессии. Почему так обстоят дела? Потому что предмет немыслимо сложен? Вовсе нет! Теория математического анализа не столь трудна, сколько своеобразна
. И её нужно принять и полюбить такой, какая она есть =)

Начнём с самого тяжёлого случая. Первое и главное – не надо бросать учёбу. Поймите правильно, бросить, оно всегда успеется;-) Безусловно, если через год-два от выбранной специальности будет тошнить, тогда да – следует задуматься (а не пороть горячку!)
о смене деятельности. Но пока стОит продолжить. И, пожалуйста, забудьте фразу «Ничего не понимаю» – так не бывает, чтобы СОВСЕМ ничего не понимать.

Что делать, если с теорией плохо? Это, кстати, касается не только математического анализа. Если с теорией плохо, то сначала нужно СЕРЬЁЗНО налечь на практику. При этом решаются сразу две стратегические задачи:

– Во-первых, значительная доля теоретических знаний появилась благодаря практике. И поэтому многие люди понимают теорию через… – всё верно! Нет-нет, вы не о том подумали =)

– И, во-вторых, практические навыки с большой вероятностью «вытянут» вас на экзамене, даже если…, но не будем так настраиваться! Всё реально и всё реально «поднять» в достаточно короткие сроки. Математический анализ – это мой любимый раздел высшей математики, и поэтому я просто не мог не протянуть вам ноги руку помощи:

В начале 1-го семестра обычно проходят пределы последовательностей и пределы функций. Не понимаете, что это такое и не знаете, как их решать? Начните со статьи Пределы функций
, в которой «на пальцах» рассмотрено само понятие и разобраны простейшие примеры. Далее проработайте другие уроки по теме, в том числе урок о пределах последовательностей
, на котором я фактически уже сформулировал строгое определение.

Какие значки помимо знаков неравенств и модуля вы знаете?

– длинная вертикальная палка читается так: «такое, что», «такая, что», «такой, что» либо «такие, что»
, в нашем случае, очевидно, речь идёт о номере – поэтому «такой, что»;

– для всех «эн», бОльших чем ;

– знак модуля означает расстояние
, т.е. эта запись сообщает нам о том, что расстояние между значениями меньше эпсилон.

Ну как, убийственно сложно? =)

После освоения практики жду вас в следующем параграфе:

Предел монотонной последовательности

Предел у такой последовательности может быть, а может и не быть. Сначала полезно понять, когда он есть, отсюда можно оттолкнуться при доказательстве отсутствия предела.

Среди монотонных последовательностей выделяют сходящуюся и расходящуюся. Сходящаяся — это такая последовательность, которая образована множеством х и имеет в данном множестве действительный или комплексный предел. Расходящаяся — последовательность, не имеющая предела в своём множестве (ни действительного, ни комплексного).

Причём последовательность сходится, если при геометрическом изображении её верхний и нижний пределы сходятся.

Предел сходящейся последовательности во многих случаях может быть равен нулю, так как любая бесконечно малая последовательность имеет известный предел (ноль).

Какую сходящуюся последовательность ни возьми, они все ограничены, однако далеко не все ограниченные последовательности сходятся.

Сумма, разность, произведение двух сходящихся последовательностей — также сходящаяся последовательность. Однако частное может быть также сходящейся, если оно определено!

Понятие противоречия и его применение в доказательствах

Рассмотрим пять практических способов применения понятия противоречия в доказательствах неравенства пределов функций.

1. Противоречие с определением предела. Если предел функции в точке существует, то он единственный. Предположим, что предел функции равен заданному числу, но при этом нарушается свойство единственности предела. Такое противоречие показывает, что предел не может быть равен заданному числу.
2. Противоречие с использованием отрицания определения предела. Отрицание определения предела позволяет найти параметры, при которых предел функции не существует или не равен заданному числу. Противоречие возникает, когда существуют значения параметров, при которых предел функции не соответствует заданному числу.
3. Противоречие с использованием основных арифметических операций. При выполнении арифметических операций с функциями есть некоторые правила, которые необходимо соблюдать. Предположим, что предел функции равен заданному числу, но при выполнении операций с этой функцией получается невозможный результат или нарушается известное правило. Такое противоречие свидетельствует о том, что предел не равен заданному числу.
4. Противоречие с использованием числовых свойств. Числовые свойства, такие как сравнение чисел, сумма, произведение и прочие, могут быть использованы для доказательства противоречия. Предположим, что предел функции равен заданному числу, но при сравнении этого числа с другими значениями или при выполнении числовых операций возникает противоречие. Это свидетельствует о том, что предел не равен заданному числу.
5. Противоречие с использованием логических операций. Логические операции, такие как отрицание, конъюнкция, дизъюнкция и импликация, могут быть использованы в доказательствах неравенства пределов функций. Предположим, что предел функции равен заданному числу, но при использовании логических операций получается ложное утверждение или противоречие с уже известными фактами. Такое противоречие показывает, что предел не равен заданному числу.

Таким образом, понятие противоречия является мощным инструментом в математических доказательствах, позволяющим опровергнуть утверждения о равенстве предела функции заданному числу. Правильное использование противоречия требует внимательного анализа и понимания определений и правил математического аппарата.

Свойства пределов функций.

Локальные свойства функции, имеющей предел.

Покажем, что функция, имеющая конечный предел в заданной точке, обладает некоторыми локальными свойствами, то есть свойствами, которые справедливы в окрестности этой точки.

Если функция \(f(x)\) имеет предел в точке \(a\), то существует такая проколотая окрестность точки \(a\), в которой эта функция ограничена.

\(\circ\) Пусть \(\displaystyle \lim_f(x)=A\). В силу определения предела по заданному числу \(\varepsilon=1\) можно найти число \(\delta>0\) такое, что для всех \(x\in\dot_(a)\) выполняется неравенство \(|f(x)-A| Свойство 2

Свойство сохранения знака предела.

Если \(\displaystyle \lim_f(x)=A\), причем \(A\neq 0,\) то найдется такая проколотая окрестность точки \(a\), в которой значения функции \(f\) имеют тот же знак, что и число \(A\).

\(\circ\) Согласно определению предела по заданному числу \(\varepsilon = \frac>0\) можно найти такое число \(\delta>0\), что для всех \(x\in\dot_(a)\) выполняется неравенство \(\displaystyle |f(x)-A| 0\), то из левого неравенства \eqref следует, что $$ f(x)>\frac>0\ для\ x\in\dot_(a).\nonumber $$ Если \(A Свойство 3

Если \(\displaystyle \lim_g(x)=B\), причем \( B\neq0\), то существует число \(\delta>0\) такое, что функция \(\displaystyle\frac\) ограничена на множестве \(\dot_(a).\)

\(\circ\) В силу определения предела по заданному числу \(\varepsilon=\frac\) можно найти число \(\delta>0\), такое, что для всех \(x\in\dot_\delta(a)\) выполняется неравенство $$ |g(x)-B| \frac\),и поэтому \(\displaystyle \frac Свойство 1

Если существует число \(\delta>0\) такое, что для всех \(\dot_(a)\) выполняются неравенства $$ g(x)\leq f(x)\leq h(x),\label$$ и если $$ \lim_g(x)=\lim_h(x)=A,\label$$ то существует \(\displaystyle \lim_f(x)=A.\)

\(\circ\) Воспользуемся определением предела функции по Гейне. Пусть \(\\>\) — произвольная последовательность такая, что \(x_n\in\dot_(a)\) для \(n\in\mathbb\) и \(\displaystyle \lim_f(x)=a\). Тогда в силу условия \eqref \(\displaystyle \lim_g(x_)=\lim_h(x_)=A.\)

Так как, согласно условию \eqref, для всех \(n\in\mathbb\) выполняется неравенство $$ g(x_)\leq f(x_)\leq h(x_),\nonumber $$ то в силу свойств пределов последовательностей \(\displaystyle \lim_f(x_)=A\). Следовательно, \(\displaystyle \lim_f(x)=A.\ \bullet\)

\(\circ\) Для доказательства этого свойства достаточно воспользоваться определением предела функции по Гейне и соответствующими свойствами пределов последовательностей. \(\bullet\)

Бесконечно малые функции обладают следующими свойствами:

Эти свойства легко доказать, используя определения бесконечно малой и ограниченной функции, либо с помощью определения предела функции по Гейне и свойств бесконечно малых последовательностей. Из свойства 2) следует, что произведение конечного числа бесконечно малых при \(x\rightarrow a\) функций есть бесконечно малая при \(x\rightarrow a\) функция.

Из определения предела функции и определения бесконечно малой функции следует, что число \(A\) является пределом функции \(f(x)\) в точке \(a\) тогда и только тогда, когда эта функция представляется в виде $$ f(x)=A+a(x),\nonumber $$ где \(a(x)\) — бесконечно малая при \(x\rightarrow a\) функция.

Свойства пределов, связанные с арифметическими операциями.

Если функции \(f(x)\) и \(g(x)\) имеют конечные пределы в точке \(а\), причем \(\displaystyle \lim_f(x)=A,\ \lim_g(x)=B\), то:

\(\circ\) Для доказательства этих свойств достаточно воспользоваться определением предела функции по Гейне и свойствами пределов последовательностей. \(\bullet\)

Отметим частный случай утверждения \eqref: $$ \lim_(C f(x))=C\lim_f(x),\nonumber $$ то есть постоянный множитель можно вынести за знак предела.