Распределение пуассона дискретной случайной величины

Решение примеров с распределением Пуассона

Пример 1. Менеджер телекоммуникационной компании
решил рассчитать вероятность того, что в некотором небольшом городе в течении пяти
минут поступят 0, 1, 2, … вызовов. Выбраны случайные интервалы в пять минут, подсчитано
число вызовов в каждый их интервалов и рассчитано среднее число вызовов:
.

Вычислить вероятность того, что в течении пяти минут поступят 6 вызовов.

Решение. По формуле Пуассона получаем:

Тот же результат получим, используя функцию MS Excel ПУАССОН.РАСП (значение интегральной величины — 0):

P(6) = ПУАССОН.РАСП(6; 4,8; 0) = 0,1398.

Вычислим вероятность того, что в течение пяти минут поступят не более 6 вызовов (значение интегральной величины — 1):

P(≤6) = ПУАССОН.РАСП(6; 4,8; 1) = 0,7908.

Решить пример самостоятельно, а затем посмотреть решение

Пример 2. Производитель отправил в некоторый город 1000 проверенных,
то есть исправных телевизоров. Вероятность того, что при транспортировке телевизор выйдет из строя,
равна 0,003. То есть в этом случае действует закон распределения Пуассона. Найти вероятность того, что
из всех доставленных телевизоров неисправными будут:
1) два телевизора;
2) менее двух телевизоров.

Продолжаем решать примеры вместе

Пример 3. В центр звонков клиентов поступает поток
звонков с интенсивностью 0,8 звонков в минуту. Найти вероятность того, что за 2 минуты:
а) не придёт ни одного звонка; б) придёт ровно один звонок; в) придёт хотя бы один звонок.

Решение. Случайная величина X — число звонков за 2 минуты с параметром
— распределена
по закону Пуассона. У нас есть всё, чтобы вычислить
требуемые в условии задачи вероятности:

а) (так
как ).

б) .

в) .

Пример 4. Поток грузовых железнодорожных составов, прибывающих
на сортировочную горку, имеет интенсивность 4 состава в час. Найти вероятности
того, что за полчаса на горку прибудет: а) ровно один состав; б) хотя бы один состав; в) не менее трёх составов.

Решение. Случайная величина X — число составов за 0,5 часа с параметром
— распределена по
закону Пуассона. Вычисляем требуемые в условии задачи вероятности:

а) .

б) .

в) .

Назад

Листать

Вперёд>>>

Начало темы «Теория вероятностей»

Условия возникновения распределения Пуассона

Рассмотрим условия, при которых возникает распределение Пуассона.

Во-первых, распределение Пуассона является предельным для биномиального распределения,
когда число опытов n неограниченно увеличивается (стремится к бесконечности) и одновременно
вероятность p успеха в одном опыте неограниченно уменьшается (стремится к нулю), но так, что
их произведение np сохраняется в пределе постоянным и равным
(лямбде):

.

В математическом анализе доказано, что распределение Пуассона с параметром
можно приближенно применять вместо
биномиального, когда число опытов n очень велико, а вероятность p очень мала, то есть
в каждом отдельном опыте событие A появляется крайне редко.

Во-вторых, распределение Пуассона имеет место, когда есть поток событий, называемым простейшим
(или стационарным пуассоновским потоком). Потоком событий называют последовательность таких моментов,
как поступление вызовов на коммуникационный узел, приходы посетителей в магазин, прибытие составов на
сортировочную горку и тому подобных. Пуассоновский поток обладает следующими свойствами:

• стационарность: вероятность наступления m событий в определённый период времени постоянна
  и не зависит от начала отсчёта времени, а зависит только от длины участка времени;
• ординарность: вероятность попадания на малый участок времени двух или более событий
  пренебрежимо мала по сравнению с вероятностью попадания на него одного события;
• отсутствие последствия: вероятность наступления m событий в определённый период времени не зависит
  от того, сколько событий наступило в предыдущий период.

Распределение Пуассона: формула вероятности редких событий

Распределение Пуассона — случай биномиального распределения, когда
число испытаний n достаточно большое, а вероятность p события
A мала ().

Распределение Пуассона называют также распределением редких событий.
Например, рождение за год трёх или четырёх близнецов, тот же закон распределения имеет
число распавшихся в единицу времени атомов радиоактивного вещества и др.

Вероятность наступления редких событий вычисляется по формуле Пуассона:

,

где m число наступления события A;

—
среднее значение распределения Пуассона;

e=2,7183 — основание натурального логарифма.

Закон Пуассона зависит от одного параметра —
(лямбда), смысл которого в следующем: он является одновременно математическим ожиданием и дисперсией
случаной величины, распределённой по закону Пуассона.

Формулы Муавра-Лапласа

Если в схеме Бернулли наряду с числом испытаний п велики также значения то следует применять формулы Муавра-Лапласа — локальную или интегральную. При этом локальную формулу Муавра-Лапласа, как следует из самого названия, необходимо применять в том случае, когда нас интересует вероятность получить ровно m успехов в п испытаниях, а интегральную — если определяется вероятность получить число успехов, заключенное в пределах от

Так же, как и теорема Пуассона, локальная и интегральная теоремы Муавра-Лапласа приводятся в «инженерной» трактовке.

Локальная теорема Муавра-Лапласа:

Если в схеме Бернулли число испытаний п велико, то для всех m справедлива приближенная формула (локальная формула Муавра-Лапласа)

где а

Одно из первых доказательств теоремы было основано на известной из курса математического анализа формуле Стирлинга

Не вдаваясь в математические подробности доказательства, изложим основную его суть. Считая, что n и достаточно велики, и подставляя в формулу Бернулли вместо их приближенные значения, вычисленные по формуле Стирлинга, получаем

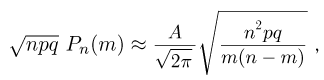
где

Положим Тогда Логарифмируя теперь А, имеем

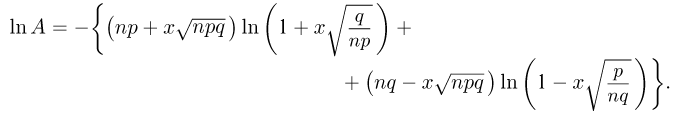
Поскольку малы при больших п, разложим логарифмы в ряд Маклорена по степеням x до второго члена. Тогда

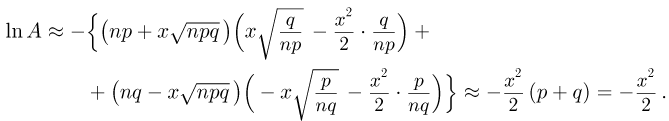
Следовательно,

Наконец, учитывая, что при фиксированном х и больших п, получаем

откуда и вытекает утверждение теоремы.

Значения функции которую называют плотностью стандартного нормального, или гауссова, распределения, для некоторых х приведены в табл.2 приложения. Поскольку функция является четной, то при определении для отрицательных х нужно воспользоваться равенством

Интегральная теорема Муавра-Лапласа:

Если в схеме Бернулли число испытаний п велико, то для вероятности того, что число успехов заключено в пределах от справедливо приближенное соотношение (интегральная формула Муавра-Лапласа)

где

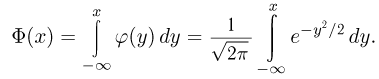
Доказательство теоремы проведем, опираясь на локальную теорему Муавра-Лапласа (здесь мы также опускаем отдельные технические детали доказательства). Если то в силу теоремы о среднем и равномерной непрерывности функции

равномерно по х. Поэтому, полагая из локальной теоремы Муавра-Лапласа находим

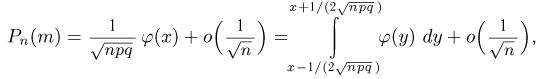
где Суммируя по всем окончательно получаем

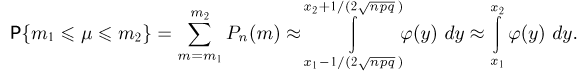
Тем самым утверждение теоремы доказано.

Отметим, что интегральная теорема Муавра-Лапласа является следствием более общей центральной предельной теоремы, которую мы докажем другим, более простым способом в гл. 8.

Функция фигурирующая в интегральной формуле Муавра-Лапласа, носит название функции стандартного нормального, или гауссова, распределения. В силу четности функция стандартного нормального распределения обладает свойством Поэтому в табл. 3 приложения приведены значения не а интеграла Лапласа и только для положительных х. Ясно, что является нечетной функцией, т.е. и, кроме того, В терминах интеграла Лапласа интегральная формула Муавра-Лапласа имеет вид

Именно этой формулой мы будем пользоваться при расчетах в примерах следующего параграфа.

Замечание. Распределение Пуассона, плотность и функция стандартного нормального распределения играют в приложениях столь существенную роль, что таблицы их значений содержатся практически в любом справочнике, учебнике или задачнике по теории вероятностей или математической статистике (см. также приложение)

Однако следует еще раз обратить внимание на то, что довольно часто в таблицах приводятся не значения функции стандартного нормального распределения, а значения интеграла Лапласа или даже функции Поэтому, прежде чем пользоваться таблицей, необходимо внимательно посмотреть, значения какой функции даны в этой таблице

Задача Коши для уравнения теплопроводности[править | править код]

Однородное уравнение

Рассмотрим задачу Коши для однородного уравнения теплопроводности:

∂u∂t−a2Δu=,x∈Rn,t>,u(x,)=φ(x),x∈Rn,{\displaystyle {\begin{array}{l}\displaystyle {\frac {\partial u}{\partial t}}-a^{2}\Delta u=0,\quad x\in \mathbb {R} ^{n},\;t>0,\\{}\qquad u(x,\;0)=\varphi (x),\quad x\in \mathbb {R} ^{n},\\\end{array}}}

где φ(x){\displaystyle \varphi (x)} — начальная функция, непрерывная и ограниченная на всём пространстве, и искомая функция u=u(x,t){\displaystyle u=u(x,t)} является непрерывной и ограниченной при t≥{\displaystyle t\geq 0} и всех значениях аргумента x{\displaystyle x}.

Фундаментальным решением или ядром уравнения теплопроводности называется решение задачи Коши для однородного уравнения теплопроводности с начальным условием φ(x)=δ(x){\displaystyle \varphi (x)=\delta (x)}, где δ(x){\displaystyle \delta (x)} — дельта-функция Дирака. Оно имеет вид:

Φ(x,t)=1(2aπt)nexp⁡(−|x|24a2t),  x∈Rn, t>{\displaystyle \Phi (x,t)={\frac {1}{(2a{\sqrt {\pi t}})^{n}}}\exp {\biggl (}-{\frac {|x|^{2}}{4a^{2}t}}{\biggr )},\ \ x\in \mathbb {R} ^{n},\ t>0.}

где |x|2=x12+⋯+xn2{\displaystyle |x|^{2}=x_{1}^{2}+\cdots +x_{n}^{2}} — стандартный скалярный квадрат вектора x∈Rn{\displaystyle x\in \mathbb {R} ^{n}}.

Интеграл Пуассона задает единственное непрерывное и ограниченное решение данной задачи Коши по следующей формуле:

u(x,t)=∫RnΦ(x−y,t)φ(y)dy=1(2aπt)n∫Rnexp⁡(−|x−y|24a2t)φ(y)dy.{\displaystyle u(x,t)=\int \limits _{\mathbf {R} ^{n}}\Phi (x-y,t)\,\varphi (y)\,dy={\frac {1}{(2a{\sqrt {\pi t}})^{n}}}\int \limits _{\mathbf {R} ^{n}}\exp {\biggl (}-{\frac {|x-y|^{2}}{4a^{2}t}}{\biggr )}\,\varphi (y)\,dy.}

Неоднородное уравнение

Рассмотрим задачу Коши для неоднородного уравнения теплопроводности:

∂u∂t−a2Δu=f(x,t),x∈Rn,t>,u(x,)=φ(x),x∈Rn.{\displaystyle {\begin{array}{l}\displaystyle {\frac {\partial u}{\partial t}}-a^{2}\Delta u=f(x,t),\quad x\in \mathbb {R} ^{n},\;t>0,\\{}\qquad u(x,\;0)=\varphi (x),\quad x\in \mathbb {R} ^{n}.\\\end{array}}}

В этом случае интеграл Пуассона имеет вид:

u(x,t)=1(2aπt)n∫Rnexp⁡(−|x−y|24a2t)φ(y)dy+{\displaystyle u(x,t)={\frac {1}{(2a{\sqrt {\pi t}})^{n}}}\int \limits _{\mathbf {R} ^{n}}\exp {\biggl (}-{\frac {|x-y|^{2}}{4a^{2}t}}{\biggr )}\,\varphi (y)\,dy+}

+∫t∫Rn1(2aπ(t−s))nexp⁡(−|x−y|24a2(t−s))f(y,s)dyds.{\displaystyle +\int \limits _{0}^{t}\int \limits _{\mathbf {R} ^{n}}{\frac {1}{(2a{\sqrt {\pi (t-s)}})^{n}}}\exp {\biggl (}-{\frac {|x-y|^{2}}{4a^{2}(t-s)}}{\biggr )}\,f(y,s)\,dy\,ds.}

Обобщения[править | править код]

По теореме Римана об области, связная односвязная область в C{\displaystyle \mathbb {C} } конформно эквивалентна диску с метрикой Пуанкаре, то есть плоскости Лобачевского. Она допускает описание как однородное пространство, а именно SO(2,1)SO(2){\displaystyle \mathrm {SO} (2,1)/\mathrm {SO} (2)}. Его ближайшими родственниками служат многомерное пространство Лобачевского Λn+1=SO(n+1,1)SO(n+1){\displaystyle \Lambda ^{n+1}=\mathrm {SO} (n+1,1)/\mathrm {SO} (n+1)}, а также комплексное ΛCn+1=SU(n+1,1)SU(n+1){\displaystyle \Lambda _{\mathbb {C} }^{n+1}=\mathrm {SU} (n+1,1)/\mathrm {SU} (n+1)} и кватернионное ΛHn+1=Sp(n+1,1)Sp(n+1){\displaystyle \Lambda _{\mathbb {H} }^{n+1}=\mathrm {Sp} (n+1,1)/\mathrm {Sp} (n+1)} пространства Лобачевского.

В случае вещественного пространства Лобачевского аналог преобразования Пуассона для внешних форм Картана был найден П.-И. Гэйяром. Оно сопоставляет внешней форме, определённой на абсолюте, гармоническую козамкнутую форму на пространстве Лобачевского. Именно, пространство Λn+1×Sn{\displaystyle \Lambda ^{n+1}\times S^{n}}, где Sn=∂Λn+1{\displaystyle S^{n}=\partial \Lambda ^{n+1}} — абсолют, является однородным пространством для группы SO(n+1,1)SO(n+1){\displaystyle \mathrm {SO} (n+1,1)/\mathrm {SO} (n+1)}. На нём имеются инвариантные внешние формы πk∈Ωk,n−k(Λn+1×Sn){\displaystyle \pi _{k}\in \Omega ^{k,n-k}(\Lambda ^{n+1}\times S^{n})} (то есть такие, которые, быть может, принимают ненулевые значения только при подстановке в них k{\displaystyle k} векторных полей, касающихся сомножителя Λn+1{\displaystyle \Lambda ^{n+1}} и n−k{\displaystyle n-k} векторных полей, касающихся сомножителя-абсолюта). Если α∈Ωk(Sn){\displaystyle \alpha \in \Omega ^{k}(S^{n})}, то интеграл Пуассона от неё определяется как послойный интеграл внешнего произведения pSn∗α∧πk{\displaystyle p_{S^{n}}^{*}\alpha \wedge \pi _{k}}, где pSnΛn+1×Sn→Sn{\displaystyle p_{S^{n}}\colon \Lambda ^{n+1}\times S^{n}\to S^{n}} — проекция на сомножитель. Эти формы, в сущности, являются высшими ядрами Пуассона. Инвариантные формы на однородном пространстве могут быть заданы в одной точке, и взаимно однозначно соответствуют тривиальным подпредставлениям внешней степени соответствующего присоединённого представления группы, относительно которой пространство однородно; в случае вещественного пространства Лобачевского такие формы единственны с точностью до пропорциональности в силу одномерности соответствующего тривиального подпредставления.

В случае комплексного и кватернионного пространств Лобачевского эти подпредставления уже не одномерны, поэтому определить подобным образом какое-либо каноническое преобразование Пуассона не представляется возможным. Это, однако, возможно с учётом более тонкой геометрической структуры на абсолюте: именно, абсолют S2n+1{\displaystyle S^{2n+1}} комплексного пространства Лобачевского ΛCn+1{\displaystyle \Lambda _{\mathbb {C} }^{n+1}} (как и вообще граница всякого комплексного многообразия) имеет КР-структуру, то есть вполне неинтегрируемое распределение (которое, если реализовать сферу S2n+1{\displaystyle S^{2n+1}} как единичную сферу в пространстве Cn+1{\displaystyle \mathbb {C} ^{n+1}} можно определить в каждой точке x∈S2n+1{\displaystyle x\in S^{2n+1}} как максимальное комплексное подпространство, содержащееся в касательном пространстве TxS2n+1{\displaystyle T_{x}S^{2n+1}} к сфере). В случае кватернионного пространства Лобачевского аналогичную роль играет так называемая кватернионно-контактная структура. Со всяким вполне неинтегрируемым распределением связан комплекс Рюмина, аналогичный комплексу де Рама гладкого многообразия. Его аналог, который может быть определён чисто в алгебраических терминах теории представлений, называется комплексом Бернштейна — Гельфанда — Гельфанда. В нём имеются естественные операции, родственные элементу Казимира. Дополнительные условия на то, как должно себя вести ядро Пуассона относительно таких операций, позволяют выбрать его однозначно с точностью до пропорциональности.

Применение формулы Пуассона в реальной жизни

Формула Пуассона, разработанная французским математиком Симеоном Дени Пуассоном, используется для рассчета вероятности того, что определенное событие произойдет определенное число раз в заданном промежутке времени или пространства.

Применение формулы Пуассона находит свое применение в различных областях. Вот несколько примеров:

1. Теория вероятностей: Формула Пуассона позволяет рассчитать вероятность того, что определенное событие произойдет в заданном временном или пространственном интервале. Например, с помощью этой формулы можно оценить вероятность того, что определенное количество автомобилей пройдет по определенной дороге за определенный период времени.

2. Телекоммуникации: В области телекоммуникаций формула Пуассона используется для оценки потока данных или трафика. Например, с ее помощью можно определить вероятность возникновения коллизий в сети или предсказать количество запросов, поступающих на сервер в определенный период времени.

3. Физика: Формула Пуассона находит применение при моделировании случайных процессов, таких как распад радиоактивного изотопа или число частиц, сработавших в детекторе.

4. Финансы: В финансовой сфере формула Пуассона может быть использована для анализа риска или предсказания количества событий, таких как количество заявок на кредит в банке или число клиентов, посетивших магазин в определенный день.

Применение формулы Пуассона позволяет моделировать и анализировать различные случайные процессы, что помогает принимать обоснованные решения в различных областях деятельности.

Примеры

В этом разделе приведены некоторые примеры вычисления интеграла Пуассона.

Пример 1:

Вычислим интеграл Пуассона для функции f(x) = e^(-x^2):

1. Данная функция является чётной, поэтому можно вычислять интеграл на положительной полуоси и умножить результат на 2.
2. Интеграл Пуассона для данной функции записывается следующим образом: I = 2 * ∫ e^(-x^2) dx.
3. Для вычисления данного интеграла используются различные методы, например, метод Симпсона или численные методы.
4. Используем метод Симпсона для вычисления: I ≈ 2 * (e^(-0^2) + 4e^(-(0.5^2)) + 2e^(-(1^2)) + 4e^(-(1.5^2)) + 2e^(-(2^2)) + … + 2e^(-(∞^2))).
5. Вычисляем сумму числового ряда и получаем приближенное значение интеграла.

Пример 2:

Вычислим интеграл Пуассона для функции f(x) = sin(x):

1. Данная функция является нечётной, поэтому нужно вычислять интеграл на всей числовой оси и умножить результат на 2.
2. Интеграл Пуассона для данной функции записывается следующим образом: I = 2 * ∫ sin(x) dx.
3. Для вычисления данного интеграла также используются различные методы.
4. Используем численные методы для вычисления: I ≈ 2 * (sin(-∞) + sin(-5) + sin(-4) + sin(-3) + … + sin(3) + sin(4) + sin(5) + sin(∞)).
5. Вычисляем сумму числового ряда и получаем приближенное значение интеграла.

Пример 3:

Вычислим интеграл Пуассона для функции f(x) = 1/x:

1. Данная функция не является чётной или нечётной, поэтому нужно вычислять интеграл на интервале, где функция положительна.
2. Интеграл Пуассона для данной функции записывается следующим образом: I = ∫ 1/x dx, где a и b — границы интервала, где функция положительна.
3. Для вычисления данного интеграла также используются различные методы.
4. Используем численные методы для вычисления: I ≈ (1/a + 1/(a + Δx) + 1/(a + 2Δx) + … + 1/(b — Δx) + 1/b), где Δx — шаг.
5. Вычисляем сумму числового ряда и получаем приближенное значение интеграла.

Пример 4:

Вычислим интеграл Пуассона для функции f(x) = x^2:

1. Данная функция является чётной, поэтому можно вычислять интеграл на положительной полуоси и умножить результат на 2.
2. Интеграл Пуассона для данной функции записывается следующим образом: I = 2 * ∫ x^2 dx.
3. Для вычисления данного интеграла также используются различные методы.
4. Используем численные методы для вычисления: I ≈ 2 * (0 + 0.5^2 + 1^2 + 1.5^2 + 2^2 + … + (∞^2)).
5. Вычисляем сумму числового ряда и получаем приближенное значение интеграла.

Формула Бернулли

Вычислим вероятность получить в n испытаниях ровно m успехов. Событие — в n испытаниях произошло ровно m успехов — состоит из тех элементарных исходов, в которых буква У появляется ровно m раз. Для того чтобы подсчитать число таких исходов, заметим, что оно совпадает с числом способов, которыми можно расставить m букв У на n местах. Поскольку порядок, в котором мы расставляем буквы, нас не интересует то мы имеем дело с со четаниями и число способов равно С другой стороны, каждый элементарный исход, в котором интересующая нас буква У встречается ровно m раз, как мы знаем, имеет вероятность Окончательно получаем для вероятности наступления m успехов в n независимых испытаниях формулу Бернулли:

Данное выражение носит также название биномиального закона, поскольку можно получить как коэффициент при разложения по степеням z бинома Заметим, что последнее выражение представляет собой производящую функцию (z-преобразование) для биномиального закона (см. параграф 3 гл. 8); аппарат производящих функций широко используется в теории вероятностей.

Пример:

В шаре радиусом R находится n молекул идеального газа. Вычислим вероятность того, что ровно т из них будут находиться на расстоянии, меньшем от центра этого шара. Поскольку каждая из п молекул может находиться в любой точке шара независимо от остальных, искомая вероятность определяется с помощью формулы Бернулли. При этом для вычисления вероятности р попадания одной молекулы в шар радиусом р (успех) можно воспользоваться схемой геометрической вероятности, т. е.

Тогда по формуле Бернулли окончательно получаем

Пример:

Частица пролетает последовательно мимо 6 счетчиков. Каждый счетчик независимо от остальных отмечает ее пролет с вероятностью р = 0,8. Частица считается зарегистрированной (событие А), если она отмечена не менее чем двумя счетчиками. Найдем вероятность зарегистрировать частицу. В соответствии с аксиомой сложения искомую вероятность Р(A) можно представить в виде

где — событие, заключающееся в том, что частица отмечена ровно i счетчиками. Теперь для определения можно было бы воспользоваться формулой Бернулли, однако мы предварительно перейдем к дополнительному событию — частица либо не отмечена ни одним счетчиком, либо отмечена только одним. Тогда

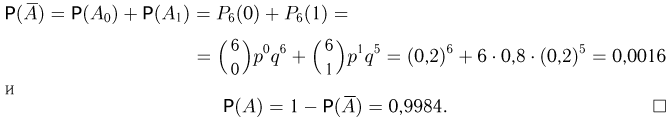
Что такое интеграл Пуассона?

Интеграл Пуассона — это математический инструмент, который используется для вычисления вероятности того, что случайная величина примет определенное значение или попадет в определенный интервал. Он был предложен французским математиком Симеоном Дени Пуассоном в начале 19 века.

Интеграл Пуассона часто применяется в статистике, особенно при анализе распределения Пуассона, которое описывает случайные события, происходящие с постоянной интенсивностью в течение фиксированного периода времени или в пространственном объеме.

Применение интеграла Пуассона включает решение задач о вероятности встречи определенного числа событий или величины в заданном временном интервале или пространственном объеме. Интеграл Пуассона также может использоваться для определения вероятности появления определенного числа успехов в серии независимых испытаний.

Итак, интеграл Пуассона является мощным инструментом для статистического анализа случайных событий и вероятностей. Он позволяет нам получать предсказуемые результаты и делать выводы о вероятностях на основе имеющихся данных.