Урок 1: стереометрия

Символы вероятности и статистики

Символ	Название символа	Значение / определение	пример
P ( А )	функция вероятности	вероятность события A	P ( A ) = 0,5
P ( A ⋂ B )	вероятность пересечения событий	вероятность того, что событий A и B	P ( A ⋂ B ) = 0,5
P ( A ⋃ B )	вероятность объединения событий	вероятность того, что событий A или B	P ( A ⋃ B ) = 0,5
P ( A \| B )	функция условной вероятности	вероятность события A данное событие B произошло	P ( A \| B ) = 0,3
f ( x )	функция плотности вероятности (pdf)	P ( a ≤ x ≤ b ) = ∫ f ( x ) dx
F ( х )	кумулятивная функция распределения (cdf)	F ( х ) = Р ( Х ≤ х )
μ	Средняя численность населения	среднее значение совокупности	μ = 10
E ( X )	ожидаемое значение	ожидаемое значение случайной величины X	E ( X ) = 10
E ( X \| Y )	условное ожидание	ожидаемое значение случайной величины X с учетом Y	E ( X \| Y = 2 ) = 5
var ( X )	отклонение	дисперсия случайной величины X	var ( X ) = 4
σ 2	отклонение	дисперсия значений совокупности	σ 2 = 4
std ( X )	стандартное отклонение	стандартное отклонение случайной величины X	std ( X ) = 2
σ _X	стандартное отклонение	значение стандартного отклонения случайной величины X	σ _X = 2
	медиана	среднее значение случайной величины x
cov ( X , Y )	ковариация	ковариация случайных величин X и Y	cov ( X, Y ) = 4
корр ( X , Y )	корреляция	корреляция случайных величин X и Y	корр ( X, Y ) = 0,6
ρ _{X , Y}	корреляция	корреляция случайных величин X и Y	ρ _{X , Y} = 0,6
∑	суммирование	суммирование — сумма всех значений в диапазоне ряда
∑∑	двойное суммирование	двойное суммирование
Пн	Режим	значение, которое чаще всего встречается в популяции
MR	средний диапазон	MR = ( x _макс + x _мин ) / 2
Мкр	медиана выборки	половина населения ниже этого значения
Q ₁	нижний / первый квартиль	25% населения ниже этого значения
₂ квартал	медиана / второй квартиль	50% населения ниже этого значения = медиана выборки
₃ квартал	верхний / третий квартиль	75% населения ниже этого значения
х	выборочное среднее	среднее / среднее арифметическое	х = (2 + 5 + 9) / 3 = 5,333
с 2	выборочная дисперсия	оценщик дисперсии выборки населения	s 2 = 4
с	стандартное отклонение выборки	Оценка стандартного отклонения выборки населения	s = 2
z _x	стандартная оценка	z _x = ( x — x ) / s _x
X ~	распределение X	распределение случайной величины X	X ~ N (0,3)
N ( μ , σ 2 )	нормальное распределение	гауссово распределение	X ~ N (0,3)
U ( а , б )	равномерное распределение	равная вероятность в диапазоне a, b	Х ~ U (0,3)
ехр (λ)	экспоненциальное распределение	f ( x ) = λe — λx , x ≥0
гамма ( c , λ)	гамма-распределение	f ( x ) = λ cx c-1 e — λx / Γ ( c ), x ≥0
χ 2 ( к )	распределение хи-квадрат	f ( x ) = x k / 2-1 e — x / 2 / (2 k / 2 Γ ( k / 2))
F ( k ₁ , k ₂ )	F распределение
Корзина ( n , p )	биномиальное распределение	f ( k ) = _n C _k p k (1 -p ) nk
Пуассон (λ)	распределение Пуассона	е ( К ) знак равно λ К е — λ / К !
Геом ( p )	геометрическое распределение	f ( k ) = p (1 -p ) k
HG ( N , K , n )	гипергеометрическое распределение
Берн ( p )	Распределение Бернулли

Виды альфа в геометрии

В геометрии существует несколько видов альфа, которые играют важную роль при решении различных задач.

Первый вид альфа — это угол между двумя прямыми. Изучение этого вида альфа позволяет понять, какие прямые пересекаются, параллельны или перпендикулярны друг другу.

Второй вид альфа связан с углами при треугольниках. Знание этого вида альфа помогает решать задачи о нахождении площади треугольника, длины его сторон и углов.

Третий вид альфа — это угол поворота. Он определяет, насколько фигура повернута относительно начальной позиции. Изучение этого вида альфа помогает решать задачи о симметрии фигур и преобразованиях в координатной плоскости.

И, наконец, четвертый вид альфа связан с расстоянием между точками на плоскости. Он показывает, насколько две точки удалены друг от друга. Изучение этого вида альфа позволяет решать задачи о построении графиков функций и нахождении расстояний в пространстве.

Все эти виды альфа взаимосвязаны и помогают развивать логическое мышление, умение анализировать и решать геометрические задачи.

Альфа-угол в геометрии: особенности и свойства

Основным свойством альфа-угла является его размер, который может быть различным в зависимости от конкретной геометрической фигуры или соответствующего объекта. Альфа-угол может быть как остроугольным, так и тупоугольным.

Однако, независимо от размера, альфа-угол всегда является основным элементом при определении других характеристик геометрической фигуры. Например, при решении задач на построение или вычисление площади, периметра и других параметров фигур, знание альфа-угла позволяет получить более точные и надежные результаты.

Кроме того, альфа-угол играет важную роль в геометрических преобразованиях и симметриях. Он является мерой отношения между сторонами или углами фигуры и может быть использован для определения ее геометрических свойств и характеристик.

Таким образом, знание альфа-угла в геометрии является необходимым для более глубокого понимания структуры и свойств геометрических фигур. Оно помогает проводить точные вычисления и строить точные модели, что в свою очередь полезно для решения разнообразных задач в различных областях науки и техники.

Углы с альфа-параметром в геометрии: классификация

Альфа-параметр в геометрии указывает на угол, который имеет определенные характеристики, необходимые для его классификации. Угол с альфа-параметром может быть разделен на несколько категорий, в зависимости от своего положения и взаимоотношений с другими углами.

Вот некоторые из основных категорий углов с альфа-параметром:

Резкий угол с альфа-параметром: это угол, который меньше 90 градусов и имеет острые стороны. Он характеризуется малым значением альфа-параметра.
Прямой угол с альфа-параметром: это угол, который равен 90 градусов. Он имеет одну прямую сторону и характеризуется альфа-параметром, равным 1.
Тупой угол с альфа-параметром: это угол, который больше 90 градусов и имеет тупую сторону. Альфа-параметр такого угла может быть больше 1, но всегда меньше 2.
Полный угол с альфа-параметром: это угол, который равен 180 градусов. У него две противоположные прямые стороны и альфа-параметр, равный 2.

Знание классификации углов с альфа-параметром в геометрии является важной основой для понимания свойств и взаимодействий углов в различных геометрических конструкциях. Это помогает решать задачи, связанные с измерением углов, а также использовать их в других областях, таких как физика, инженерия и архитектура

Проверь себя

Задание 1. Выберите верное утверждение.

Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом все линейные углы двугранного угла равны между собой;
Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом линейные углы двугранного угла не равны между собой;
Грань двугранного угла — это общая прямая плоскостей, которые его образуют;
Ребра двугранного угла — это плоскости, которые его образуют.

Задание 2. Угол между плоскостями — это…

Тупой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
Острый или прямой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
Тупой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей;
Острый или прямой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей.

Задание 3. Что такое проекция прямой на плоскость?

Это любая прямая, проведенная из точки пересечения прямой и плоскости;
Это перпендикуляр, опущенный из любой точки на плоскость;
Это всегда точка пересечения прямой и плоскости;
Это прямая, образованная проекциями всех точек прямой на плоскость.

Задание 4. Какой будет проекция прямой, перпендикулярной к плоскости, на эту плоскость?

Проекция будет равна этой прямой и параллельна ей;
Проекция будет меньше прямой и образовывать с ней угол;
Проекция будет точкой пересечения прямой и плоскости;
Проекция будет больше прямой и образовывать с ней угол.

Задание 5. Как доказать, что прямая перпендикулярна плоскости?

Достаточно доказать, что прямая перпендикулярна одной любой прямой в плоскости;
Достаточно доказать, что прямая перпендикулярна двум параллельным прямым в плоскости;
Достаточно доказать, что угол между прямой и любой прямой в плоскости равен 90°;
Достаточно доказать, что прямая перпендикулярна к двум пересекающимся прямым в этой плоскости.

Ответы: 1. — 1 2. — 2 3. — 4 4. — 3 5. — 4

Измерение угла альфа

Угол альфа является одним из важных понятий в геометрии, который используется для измерения отклонения направления двух прямых или плоскостей друг относительно друга.

Измерение угла альфа проводится с использованием основных единиц измерения углов: градусов, минут и секунд.

Градусы: градус — это единица измерения угла, которая равна 1/360 части полного оборота.
Минуты: минута — это единица, равная 1/60 части градуса. В одном градусе содержится 60 минут.
Секунды: секунда — это единица, равная 1/60 части минуты. В одной минуте содержится 60 секунд.

Измерение угла альфа может быть представлено в виде записи в градусах, минутах и секундах. Например, если угол альфа равен 45 градусов, 30 минутам и 15 секундам, то его запись будет выглядеть следующим образом: 45° 30′ 15″.

Единица измерения	Обозначение
Градусы	°
Минуты	‘
Секунды

В геометрии также используется измерение угла альфа в радианах. Радиан — это другая единица измерения угла, которая связана с длиной дуги окружности. Между градусами и радианами существует простое соотношение: 180° = π радиан, где π (пи) — математическая константа, приближенно равная 3,14159.

Таким образом, измерение угла альфа является важным аспектом геометрии, который позволяет определить относительное направление прямых или плоскостей и выразить его в угловых единицах: градусах, минутах, секундах или радианах.

Аксиомы стереометрии с рисунками

Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Аксиома 2. Если две точки прямой лежат в плоскости, то все точки данной прямой лежат в этой плоскости. В этом случае говорят, что прямая лежит в плоскости или что плоскость проходит через прямую.

Аксиома 3. Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей. В этом случае говорят, что плоскости пересекаются по прямой.

Аксиома 4. В любой плоскости пространства выполняются все аксиомы планиметрии. Таким образом, в любой плоскости пространства можно использовать все доказанные теоремы и формулы из планиметрии.

Следствия из аксиом

Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.

Следствие 2. Через две пересекающиеся прямые проходит плоскость и притом только одна.

Следствие 3. Через две параллельные прямые проходит плоскость и притом только одна.

Следствие 4. Из аксиомы (математическое утверждение не требующее доказательства) 2 следует, что прямая, не лежащая в плоскости, не может иметь с плоскостью более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость.

Формулы сложения и вычитания углов

Перейдем к сложению и вычитанию аргумента. В записи задания это обычно выглядит, например, так: \(tg(\alpha+\beta)\) или \(ctg(\alpha-\beta)\). Если повезет, выражение в аргументе может прийти к обычному углу, который достаточно легко посчитать. Однако, не всегда все так просто.

Например, попробуем посчитать \(sin(45+60)\). В скобках получаем угол в 105 градусов, что не является табличным значением. Что же делать? Считать через аркфункцию? Подробнее про аркфункцию мы поговорим чуть дальше.

На самом деле, мы можем воспользоваться формулами сложения и вычитания углов. Рассмотрим их.

\(sin(\alpha\pm\beta)=sin\alpha*cos\beta \pm cos \alpha*sin\beta\) \(cos(\alpha\pm\beta)=cos \alpha*cos\beta \mp sin \alpha*sin\beta\)\(tg(\alpha\pm\beta)=\frac{tg \alpha \pm tg\beta}{ 1\pm tg \alpha*tg\beta}\)\(ctg(\alpha\pm\beta)=\frac{ctg \alpha*ctg\beta\mp1}{ctg\beta\mp ctg\beta \pm \alpha}\)

Заметим, что в этих формулах у нас появился знак \(\mp\). Знаки \(\pm\) и \(\mp\) отличаются друг от друга и эту разницу мы сейчас обсудим.

Знак \(\mp\) означает, что нам нужно использовать противоположный знак тому, который стоит в аргументе. Например, у нас в аргументе стоит +, тогда при преобразовании формулы мы должны поменять его на минус. Например, \(cos(a+\beta)=cos a*cos\beta -sin a*sin\beta\).Точно так же с этим знаком минус меняется на плюс.

Если в аргументе стоит привычный \(\pm\), то знаки мы не меняем и используем те же, что даны изначально. Например, \(sin(a+\beta)=sin a*cos \beta+cos a*sin \beta\).

Чтобы точно не запутаться в преобразовании знаков, нужно ориентироваться по одной стороне. Например, если в примере у нас стоит знак сверху, то и все остальные знаки для преобразований мы берем сверху.

Рассмотрим \(tg(a-\beta)\). Заметим, что в изначальной формуле минус стоит снизу, значит, для преобразований берем только нижние знаки. Получаем:

\(tg(a-\beta)=\frac{tg a-tg\beta}{1+tg a*tg \beta}\)

Теперь попробуем решить наше выражение sin(45+60). Применим формулу и получим:

\(sin(45+60)=sin 45*cos 60+cos 45*sin 60\)

Далее нам просто нужно подставить табличные значения синусов и косинусов. Саму таблицу мы приложили ниже, а подробнее про работу с ней рассказывали в статье «Тригонометрическая окружность. Часть 1».

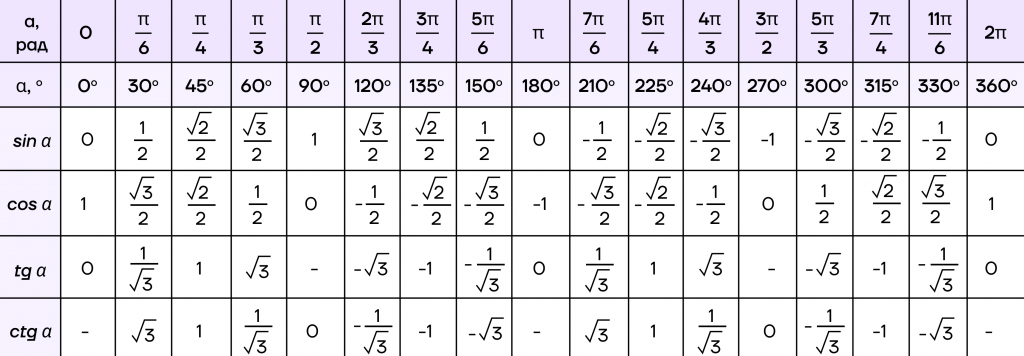
По таблице получаем:

\(sin 45*cos 60+cos 45*sin 60=\frac{\sqrt2}{2}*\frac{1}{2}+\frac{\sqrt2}{2}*\frac{\sqrt3}{2}\)

Осталось посчитать выражение и найти ответ:

\(\frac{\sqrt2}{2}*\frac{1}{2}+\frac{\sqrt2}{2}*\frac{\sqrt3}{2}=\frac{\sqrt2}{4}+\frac{\sqrt6}{4}=\frac{\sqrt2+\sqrt6}{4}\)

Аргументы мы меняли различными способами. Можем ли как-то поменять саму тригонометрическую функцию? Конечно! Например, возведем ее в квадрат.

Углы образованные при пересечении двух прямых

При пересечении двух прямых образуются два вида углов:

смежные;
вертикальные.

Смежные углы

Определение

Два угла называются смежными, если они имеют общую вершину и одну общую сторону, а две другие стороны расположены на одной прямой и образуют развернутый угол. Смежные углы между собой дополняемые, так как являются продолжением один другого.

Свойства смежных углов

Сумма смежных углов равна 180°
Если оба смежных угла равны между собой, то они являются прямыми.
В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
Синусы смежных углов равны.
Косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.

Вертикальные углы

Определение

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Пример:

Пары углов 1 и 3; 2 и 4 – являются вертикальными

По свойству вертикальных углов:

Пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1 — являются смежными

По свойству смежных углов:

Смежные углы	Вертикальные углы
Два угла с общей стороной и вершиной называются смежными.	Когда две прямые пересекаются друг с другом, то пары противоположных углов, образованных при вершине, называются вертикальными углами.
Имеют общую сторону и общую вершину.	Имеют общую вершину, но не имеют общую сторону
Смежные углы не всегда равны по величине	Вертикально противоположные углы равны по величине

Разница между смежными и вертикальными углами

Способы вставки в Word

Рассмотрим несколько вариантов:

Переведите раскладку клавиатуры на английский язык. Напечатайте букву « a » или « b ». Выделите её и установите шрифт «Symbol». Буква « a » автоматически преобразуется в альфа, а « b » — в бета.

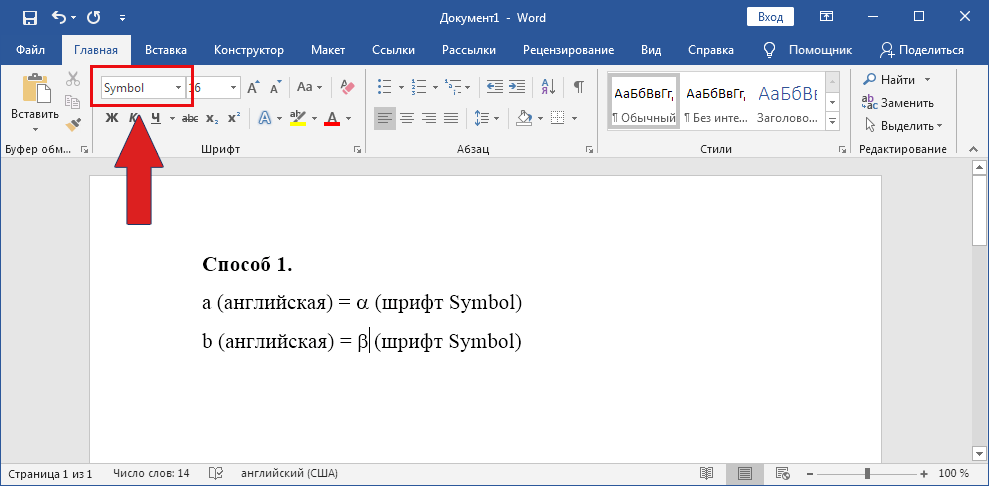
Другой вариант — использовать коды знаков. Напишите последовательность цифр « 03B1 » или « 03B2 ». Нажмите одновременно Alt и X на английской раскладке клавиатуры.

0 3 B 1 ➟ Alt + X = α 0 3 B 2 ➟ Alt + X = β

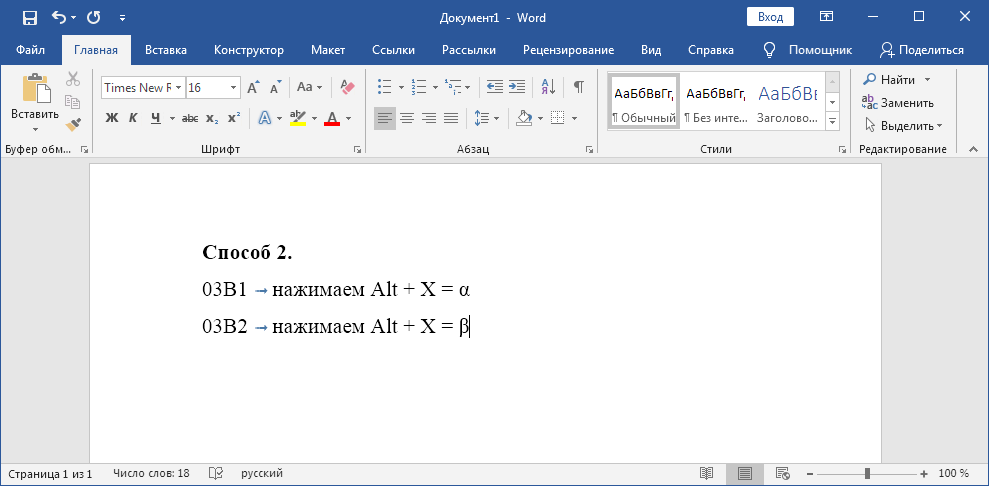
Для обладателей полноценных клавиатур с цифровым блоком клавиш справа, могу порекомендовать запомнить более короткие коды — « 945 » или « 946 ». Зажимаем Alt и вводим цифрами справа нужный код. Отпускаем Alt и цифры автоматически преобразуются в нужный символ.

Alt + 9 4 5 = α Alt + 9 4 6 = β

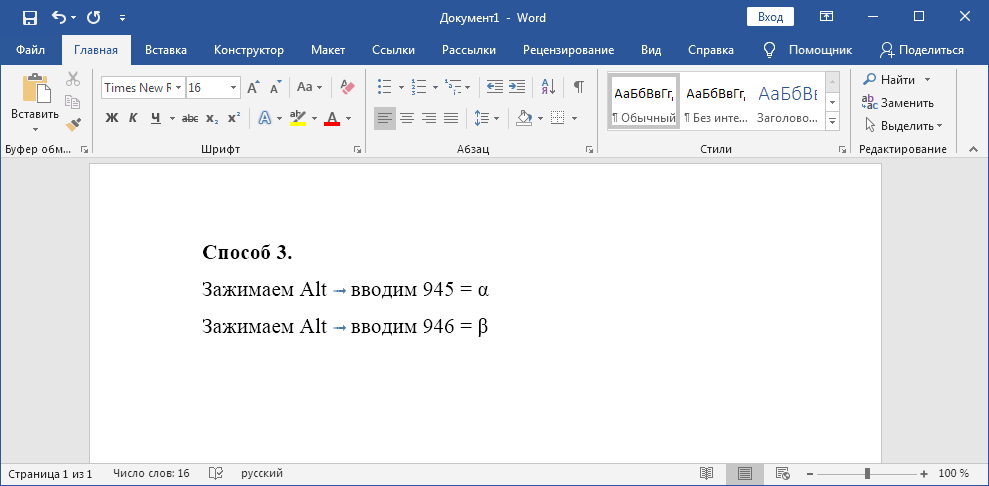
Заглавные буквы выглядят как « A » и « B », поэтому их написание не рассматривается.

В Word есть возможность вставить любую букву только мышью через пункт « Вставка ». Но такой подход отнимает больше времени. При частом использовании специальных символов, рекомендую держать под рукой таблицу с их кодами.

Равнобедренные треугольники: параллельность боковых сторон

Параллельность боковых сторон равнобедренного треугольника имеет место быть по определению равнобедренности. Если две стороны треугольника равны по длине, то они также параллельны и имеют одинаковую ориентацию. Боковые стороны равнобедренного треугольника, которые соответствуют равным сторонам, являются параллельными между собой и имеют одинаковую ориентацию.

Свойство	Описание
Равные стороны	Две стороны треугольника равны по длине.
Параллельность боковых сторон	Боковые стороны равнобедренного треугольника параллельны и имеют одинаковую ориентацию.
Равные углы	Углы, противолежащие равным сторонам, равны между собой.

Основные свойства равнобедренных треугольников

Основные свойства равнобедренных треугольников:

Базы равнобедренного треугольника — это две равные стороны, которые образуют основание треугольника.
Медиана равнобедренного треугольника, проведенная из вершины, которая не лежит на основании, делит основание на две равные части.
Биссектриса равнобедренного треугольника, проведенная из вершины угла, который соответствует основанию, делит противоположную сторону на две равные части.
Высота равнобедренного треугольника, опущенная из вершины, которая лежит на основании, перпендикулярна основанию и делит его на две равные части.
Точка пересечения медиан, биссектрис и высот равнобедренного треугольника называется центром симметрии.
Углы основания равнобедренного треугольника равны между собой, то есть они являются смежными углами.
Они также равны половине величины третьего угла треугольника.

Критерий параллельности боковых сторон треугольников

Для того чтобы боковые стороны двух треугольников были параллельными, необходимо и достаточно, чтобы соответствующие им стороны были пропорциональными и лежали на параллельных прямых. Этот критерий называется критерием параллельности боковых сторон треугольников.

Формально, если а, b и с – это стороны первого треугольника, а а’, b’ и с’ – это стороны второго треугольника, то условием параллельности будет равенство:

а/а’ = b/b’ = c/c’

Если данное равенство выполняется, то боковые стороны треугольников являются параллельными. Если же равенство не выполняется, то боковые стороны не являются параллельными.

Знание критерия параллельности боковых сторон треугольников позволяет определить, являются ли два треугольника параллельными или нет, и совершать соответствующие геометрические преобразования.

Углы между прямой и плоскостью

Если нарисовать две прямые на листе бумаги, мы с легкостью можем измерить угол между ними с помощью транспортира. А если провести прямую к плоскости, как точно измерить угол между ними?

И в этом вопросе к нам снова на помощь приходит стереометрия. Но для начала рассмотрим, что такое угол между прямой и плоскостью.

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.

Что такое проекция? Предположим, мы проткнем лист бумаги (плоскость) очень длинной иглой.

А теперь сделаем этот рисунок ближе к чертежу. Пусть плоскость а пересекает прямая а в точке О.

Начнем строить проекцию. Прежде чем разобраться, что такое проекция прямой на плоскость, найдем проекцию точки на плоскость.

Возьмем на нашей прямой а точку А и опустим из нее перпендикуляр к плоскости а. Точка, в которой перпендикуляр пересечет плоскость, будет называться проекцией точки на плоскость. На рисунке обозначим ее как А₁.

Проекция точки на плоскость — это основание перпендикуляра, опущенного из этой точки на плоскость.

Теперь, если мы будем брать каждую точку на прямой и проектировать ее на плоскость а, то получим проекцию этой прямой на плоскость. Но поскольку на прямой бесконечное множество точек, достаточно соединить точки А₁ и О, получаем, что А₁О — проекция прямой а на плоскость а.

Заметим, что если мы проведем из любой точки прямой проекцию к плоскости, то попадем на прямую А₁О.

Проекция прямой а на плоскость — это прямая а₁, образованная проекциями всех точек прямой а на плоскость.

Таким образом можно построить проекции не только прямой, но и любой фигуры.

Мы построили угол из определения. Тогда углом между прямой а и плоскость а будет угол А₁ОА.

В этом случае мы также берем острый угол, образованный прямой и плоскостью.

Алгоритм нахождения угла между прямой и плоскостьюШаг 1. Построить проекцию прямой на плоскость.Шаг 2. Найти угол между прямой и построенной проекцией.

Если прямая параллельна плоскости угол будет равен 0.

Проекция прямой на плоскость будет этой же прямой, просто лежащей в плоскости.

Когда прямая перпендикулярна плоскости, проекцией прямой на плоскость будет точка пересечения прямой и плоскости. Угол между прямой и плоскостью будет равен 90°.

Чуть подробнее остановимся на случае, когда прямая перпендикулярна плоскости.

Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости.

А что делать, если прямая будет перпендикулярна только одной прямой из плоскости? По определению обязательно, чтобы она была перпендикулярна всем прямым из плоскости. Как тогда проверить перпендикулярность?

Для этого существует признак перпендикулярности прямой и плоскости:

Если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.

Следовательно, если необходимо в задаче доказать перпендикулярность прямой и плоскости, достаточно доказать, что прямая будет перпендикулярна всего двум пересекающимся прямым в этой плоскости, а не всему множеству прямых, лежащий в данной плоскости.

Рассмотрим несколько интересных свойств, связанных с прямой, перпендикулярной к плоскости.

Свойство 1. Через любую точку пространства можно провести единственную прямую, перпендикулярную плоскости.

Попробуйте подставить уголок к стене из любой точки. Получится ли у вас сделать так, что из одной и той же точки уголок встанет перпендикулярно стене несколько раз? Нет.

Свойство 2. Если две прямые перпендикулярны одной и той же плоскости, то такие прямые параллельны.

Здесь тоже просто все доказать. Достаточно построить в плоскости прямую, которая пересечет две данные прямые и посмотреть на рисунок “сбоку”. Заметим, что соответственные углы равны, а значит, прямые параллельны.

Подробнее про соответственные углы и параллельные прямые можно прочитать в статье “Основы планиметрии”.

Свойство 3. Если к одной прямой перпендикулярны две плоскости, то такие плоскости параллельны.

Тут такие же рассуждения, как и в предыдущем свойстве: достаточно построить прямые, принадлежащие плоскостям, и посмотреть на них “сбоку”.

Свойство 4. Если через перпендикулярную к плоскости прямую проходит плоскость, то данные плоскости будут перпендикулярны.

Это легко проверить, если найти любой двугранный угол между построенными плоскостями.

Выводы о значении альфы в геометрии

Альфа (α) представляет собой угол, который может быть измерен или задан в геометрии. Он имеет несколько значений и особенностей, которые служат основой для изучения и решения различных геометрических задач.

1. Выражение угла:

Альфа может быть выражена в градусах (°) или радианах (rad). Градус — это наиболее распространенная система измерения углов, в которой полный оборот равен 360°, а половина оборота — 180°. Радиан — это альтернативная система измерения, в которой полный оборот равен 2π радиан, а половина оборота — π радиан.

2. Значение угла:

Угол альфа может быть острый, тупой или прямой в зависимости от его величины. Острый угол имеет значение меньше 90°, прямой угол равен 90°, а тупой угол больше 90°, но меньше 180°.
Альфа также может быть отрицательным, если он измеряется в направлении против часовой стрелки, и положительным, если он измеряется в направлении по часовой стрелке.
Еще одной особенностью альфы является то, что ее значения могут быть кратными другим углам. Например, если угол β равен 60°, то угол α может быть 30°, 60°, 90° и т.д.

3. Значение в геометрических конструкциях:

Альфа играет важную роль в геометрических конструкциях. В треугольниках, например, сумма всех углов равна 180°. Это позволяет использовать альфу для определения неизвестных углов или сторон треугольника.

4. Значение в тригонометрии:

Альфа также находит свое применение в тригонометрии. С помощью геометрических отношений и тригонометрических функций, таких как синус, косинус и тангенс, можно определить значения углов и сторон треугольника на основе известных данных.

В конечном счете, альфа является важным элементом геометрии, который содействует пониманию и решению различных геометрических задач. Знание его значений и особенностей поможет строить геометрические модели и сделать точные вычисления в этой области.