Язык и позиция субъекта: лакановская структурно-семиотическая концепция субъективности

Практическое применение концепции безусловности:

Концепция безусловности имеет широкое практическое применение в различных сферах жизни. Ниже приведены некоторые примеры:

• Психология: В клинической психологии концепция безусловности используется в рамках терапии групповой поддержки. Безусловная поддержка и понимание со стороны группы могут способствовать эмоциональному восстановлению и росту участников.

• Воспитание: Родители и педагоги часто применяют концепцию безусловности в процессе воспитания детей. Они стараются выражать свою любовь и принятие ребенка независимо от его поступков и ошибок, тем самым помогая ему развиваться и чувствовать себя безопасно.

• Межличностные отношения: Предоставление безусловной поддержки и уважения в отношениях может помочь создать гармоничные и здоровые взаимоотношения. Это означает быть способным принять другого человека таким, какой он есть, с его качествами и недостатками.

• Бизнес: В корпоративной среде принцип безусловности может применяться к руководству и командной работе. Руководители, демонстрирующие безусловное принятие своих сотрудников, могут создать благоприятную рабочую атмосферу и повысить работоспособность коллектива. Также безусловность может быть применена при оценке результатов работы, разделяя успехи и неудачи.

Это лишь несколько примеров практического применения концепции безусловности. В целом, идея безусловного принятия и поддержки является важным элементом на пути к гармоничным взаимоотношениям и достижению личного и профессионального роста.

Определение неявности

Неявность в логике относится к понятию, которое не явно или неявно определено в тексте высказывания или аргументации. Она может быть связана с необходимостью предположений, которые не явно указаны, но считаются подразумеваемыми в контексте.

Неявные определения являются важным уровнем логического анализа текстов и помогают раскрыть скрытые предположения, которые влияют на доказательства и выводы. Они могут включать логические правила, значения терминов или факты, которые авторы предполагают известными читателю.

Отсутствие явного определения может привести к неоднозначности и недостаточной ясности в аргументации

Поэтому важно распознавать и анализировать неявные определения, чтобы получить полное понимание контекста и сделать точные логические выводы

Неявные определения могут быть выявлены путем внимательного анализа текста, выявления доступной информации и разбора содержательных аргументов. Это помогает избежать логических ошибок, противоречий и недостаточных логических выводов в процессе дедукции и анализа.

Безусловность в отношениях между людьми:

Безусловность в отношениях между людьми — это способность и готовность принимать и ценить другого человека независимо от его поступков, мнений, качеств или поведения. Это основа здоровых и гармоничных межличностных отношений.

Когда мы оказываем безусловность другому человеку, мы проявляем уважение к его индивидуальности и право на собственное мнение. Мы признаем его ценность и позволяем ему быть самим собой, не прилагая усилий для изменения его внешности, поведения или убеждений.

Безусловность приводит к тому, что взаимные отношения становятся более открытыми и искренними. Когда мы чувствуем, что нас принимают такими, какие мы есть, мы становимся более комфортными и свободными в выражении себя.

В отношениях, где присутствует безусловность, люди чувствуют себя значимыми и важными для других. Это способствует развитию благоприятной атмосферы в общении и способствует укреплению взаимоотношений.

Безусловность требует от нас открытости, терпимости и готовности к принятию других людей такими, какие они есть

Важно помнить, что каждый человек уникален и имеет право на проявление своей индивидуальности

Однако важно отметить, что безусловность не означает безграничной поддержки и одобрения всех поступков другого человека. Мы можем не соглашаться с чьим-то мнением или действиями, но при этом все равно сохранять уважение к нему как личности

Безусловность в отношениях между людьми способствует гармонии и взаимопониманию. Это помогает нам построить качественные и полноценные взаимоотношения, основанные на взаимном уважении и любви.

Определение понятия и способы объяснения значения слова

Лексическое значение слова – это то, что оно обозначает. При этом значение может быть абстрактным и конкретным, что проще всего рассмотреть на примере слова “лес”. Так, в общем случае оно означает некую совокупность деревьев, расположенную на определенной территории, где также обитают животные. Но при этом слово может конкретизироваться, обозначая какой-то определенный лес.

Как определить его значение? Для этого используются разные способы. Первый и самый простой – это заглянуть в толковый словарь. Там же можно найти и контекст – цитаты, где оно употребляется. Это делает расшифровку значения еще более понятной.

Самый распространенный толковый словарь русского языка составлен С. И. Ожеговым – в нем около 80 тысяч слов. Школьники также используют словарь, предназначенный специально для них – он так и называется – школьный. И, конечно, нельзя не упомянуть словарь, собранный Владимиром Ивановичем Далем, хотя в нем уже довольно много устаревших на сегодня слов.

Существуют и другие способы лексического значения слова. Так, можно самостоятельно понять, что оно означает, если подобрать однокоренные конструкции. Например, если вы уже знаете значение слова “лес”, то “лесник” и “лесной” понятны интуитивно.

Подбор синонимов и антонимов также помогает понять, что означает то или иное слово.

Противоречивость категории основание[]

Теоретически нагруженный научный факт (факт совместно с его интерпретацией) может не укладываться в рамки либо парадигмы, либо подвергать верификации (фальсификации) закон науки. Такая ситуация и двигает вперёд науку…
Теоретически нагруженный научный факт, проинтерпретированный в соответствии с приятой логической парадигмой, внутренне противоречив, так как содержит “результаты измерения”, полученные на основе исторически обусловленного знания, которое встроено в измерительный инструмент. Следовательно, имея приоритет перед логической парадигмой и исторически обусловленными законами науки, он, тем не менее, содержит, по умолчанию, и то и другое в своём составе!!!
Если же новый научный факт никак не укладывается в логическую парадигму (“элементарная частица” – корпускула и волна одновременно) или противоречит общепринятому закону науки, то «старая» модель явления начинает вызывать подозрения в своей неточности и недостаточности. В эту область науки начинают устремляться ресурсы и на определённом этапе исследований «старая» модель заменяется «новой», более точной…

Следует, одновременно, отметить, что ОСНОВАНИЕ может содержать по умолчанию и недостоверные допущения, которые традиция превратила в предрассудок: например, отказавшись от принятого по умолчанию ошибочного допущения об изоморфности течения времени в любой системе отсчёта, Эйнштейн построил специальную теорию относительности! Альберт Эйнштейн противопоставил этому молчаливому допущению явно прописанный тезис о зависимости течения времени от скорости движения системы отсчёта.

Отсюда следует однозначный вывод:

1) применимость выбранной парадигмы (точнее, формализма) должна быть обоснована (при этом исследователь всегда должен отдавать себе отчёт в том, что любой формализм носит принципиально становящийся характер и не является “истиной в последней инстанции”);

2) для всех используемых законов науки должны быть явно указаны граничные условия (ГУ), в которых интерсубъективно удостоверена их адекватность реальности;

3) все допущения должны быть явно прописаны;

4) все привлекаемые научные факты должны быть проинтерпретированы в рамках применяемой логической парадигмы и используемых законов науки, то есть никакая эклектика не допустима.

Как уже отмечалось выше, З.д.о. собственно законом ФЛ не является, это закон металогики. Все остальные аксиомы, даже закон тождества, могут входить или не входить в систему аксиом.

Что можно сказать о достаточности основания произвольного философского утверждения? Причём под подобным утверждением мы в данном конкретном случае понимаем достаточно широко известное утверждение, разделяемое многими философами.

Например, «Сущность является» или «Явление существенно». В определённом выше смысле у этих утверждений вообще нет никаких оснований. Почему?

Потому, что:

1) эти утверждения представляют собой нарратив (неформализованный текст), то есть каждый из философов понимает их по-своему (вкладывает свой оттенок смысла). Логическая парадигма, в рамках которой мы должны интерпретировать смысл этих утверждений, явно не задана. То, что эти суждения были порождены Гегелем в ответ на кантовскую “вещь-в-себе”, сути дела не меняет;

2) никакие законы науки для выдвижения этих положений не используются и, таким образом, не заданы ГУ истинности этих утверждений — они безусловны, тотальны, то есть предполагаются истинными “везде и всегда” (в любой координате пространства-времени);

3) никакие научные факты для обоснования этих утверждений не приводятся — мыслитель просто взывает к «здравому смыслу» читателя (Ох уж этот “здравый смысл” – путь и преграда одновременно!).

Если отталкиваться от сформулированного выше смысла достаточного основания, то философия, взятая как целое за всю историю своего развития, представляет собой набор необоснованных спекуляций… Но так ли это?

Когда является членом предложения

Как краткое прилагательное оно может быть в предложении сказуемым, а как наречие ― обстоятельством образа действия. В обоих случаях к ним удаётся задать вопрос от другого члена предложения.

Значение здесь будет наиболее близкое к первоначальному смыслу понятия «безусловность»: «без условий», независимо от них, однозначно, несомненно:

• Чувство матери к ребёнку безусловно. То есть, «слепо, неизменно». Оно отвечает на вопрос «каково?», относится к существительному («чувство») и выражено кратким прилагательным, значит это сказуемое. Убрать сказуемое из фразы и не нарушить её структуру невозможно.
• Разве можно безусловно доверять всему, что написано в интернете? Доверять (как?), то есть, это обстоятельство, выраженное наречием. Оно имеет значение «безоговорочно», и без него смысл всего предложения будет неполным.

Не играет роли для пунктуации, но полезно знать, что когда данное слово выделено в отдельное предложение, то это не что иное, как утвердительная частица: «Вы с нами, сударь?» ― «Безусловно!» Она означает «да» или «само собой».

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Пусть есть предел:

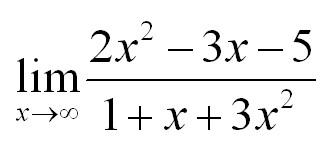
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

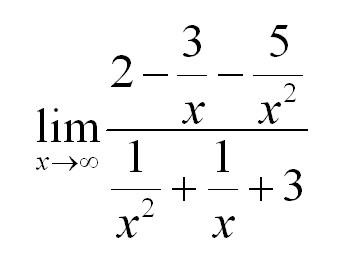
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

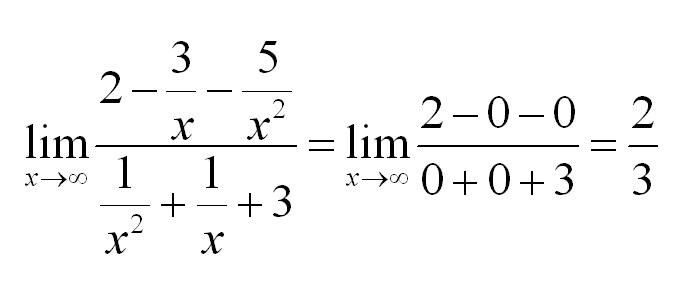
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

 

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:

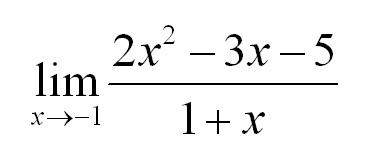
Как всегда, подстановка в функцию значения х=-1 дает в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

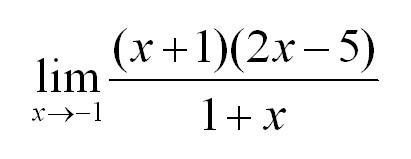
Сократим и получим:

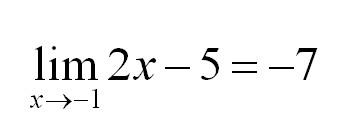
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

 

Виды толкования по объему

Толкование по объему (результат толкования) связано с толкованием-интерпретацией. Основной целью толкования при этом является раскрытие содержания правовой нормы применительно к конкретной ситуации, связанной с квалификацией юридических фактов. Результаты толкования выражаются в юридических оценках и интерпретационных нормах. Интерпретационные акты являются результатом толкования органов, имеющих право на официальное толкование. Результат толкования характеризуется не только по содержанию, но и по объему, который определяется его соотношением с текстом нормы.

По объему толкование может быть буквальным, распространительным и ограничительным.

Буквальное толкование означает толкование нормы права в точном соответствии со смыслом текста нормативно-правового акта. Действительное содержание нормы права, установленное в результате толкования, соответствует результату, полученному на основе простого прочтения текста нормативного акта (буква закона и дух закона (смысл) полностью совпадают). Такое толкование можно назвать адекватным.

Распространительное (расширительное) толкование означает, что действительное содержание нормы права шире ее текстуального выражения, т.е. расширяется смысл нормы права до желаемого или действительного содержания (дух закона шире буквы закона). Норма права при этом толкуется несколько шире ее текста.

Ограничительное толкование – это толкование, при котором действительное содержание нормы права несколько уже ее текстуального выражения.

Расширительное и ограничительное толкование является исключением из общего правила толкования, при котором смысл закона и текст закона полностью совпадают. Ограничительное или распространительное толкование возможно лишь в случаях обнаружения несоответствия между предполагаемым содержанием нормы права и ее текстом. В остальных случаях подобное толкование является отступлением от принципа и режима законности. Например, при расширительном толковании смысл нормы в целом исходит из ее текста, т.е. данный смысл предполагается, но он не выражен прямо, непосредственно. Этим отличается толкование от аналогии закона, когда делается отсылка к другой норме. Аналогия необходима в силу того, что юридические факты не охватываются ни текстом, ни смыслом нормы права. Ограничительное и распространительное толкование норм права связано в целом с системностью права, когда смысл толкуемой нормы раскрывается на основе содержания других норм права. Например, ограничительное толкование может быть основано на наличии специальной нормы права, которая применяется в случае конкуренции с общей нормой (специальная норма ограничивает сферу действия общей нормы).

Распространительно толкуются незавершенные положения норм, связанные с аналогичными условиями, обстоятельствами или с определенными предполагаемыми категориями субъектов (например, перечень законных представителей лица, перечень условий, сопутствующих заключению договора и т.д.). Нельзя расширительно толковать завершенные нормой права перечни или наоборот – ограничительно толковать незавершенные перечни. Нельзя ограничительно или расширительно толковать легальные дефиниции. Во всех случаях подобного толкования задача субъекта толкования состоит в правильном раскрытии содержания нормативно-правового акта с учетом прежде всего воли законодателя, выраженной в тексте нормы права.

Безусловность в профессиональной сфере:

Безусловность в профессиональной сфере означает выполнение задач и обязанностей на высоком уровне без каких-либо оговорок или условий.

В профессиональной деятельности безусловность проявляется в следующих аспектах:

Полное и своевременное выполнение рабочих задач. Безусловные профессионалы всегда доводят свою работу до конца, не оставляя задачи наполовину выполненной.
Ответственность за свои действия

Безусловные специалисты осознают важность своей роли и принимают на себя полную ответственность за результаты своей работы.
Профессиональная этика. Безусловные специалисты соблюдают этические нормы и правила поведения как на рабочем месте, так и в общении с коллегами и клиентами.
Стремление к саморазвитию

Безусловные профессионалы постоянно совершенствуют свои навыки и знания, следят за новыми тенденциями в своей отрасли и готовы к профессиональному росту.

Безусловность в профессиональной сфере является ключевым качеством для достижения успеха и развития в карьере. Безусловные специалисты востребованы на рынке труда и пользуются доверием со стороны коллег и работодателей.

Ключевые слова: безусловность, профессиональная сфера, выполнение задач, ответственность, профессиональная этика, саморазвитие.

Безусловность в воспитании детей

Безусловность в воспитании детей – это педагогический подход, основанный на принципе безусловной любви и поддержки ребенка. В рамках этого подхода родители и педагоги придерживаются принципа уважения к индивидуальности и самоопределению ребенка.

Основной идеей безусловности в воспитании является принятие ребенка таким, какой он есть, с его достоинствами и недостатками. В безусловном воспитании отсутствует критика и наказания, а вместо этого используются методы обратной связи и конструктивного диалога.

Применение безусловности в воспитании дает ребенку возможность развивать свои навыки и умения, искать свои интересы и предпочтения, а также принимать ответственность за свои действия. Безусловность помогает ребенку чувствовать себя уверенно и защищенно, формирует у него позитивное самооценку и позволяет строить гармоничные отношения с окружающими.

Однако безусловность в воспитании не означает отсутствия границ и правил. Важным аспектом безусловности является постановка четких границ и предоставление ребенку возможности проявления своей самостоятельности в рамках этих границ. Такие ограничения помогают ребенку ориентироваться во взаимодействии с окружающим миром, формировать навыки самоконтроля и саморегуляции.

Следует отметить, что безусловность в воспитании не означает отсутствие родительской ответственности и ребенка. Родители всегда остаются руководителями и наставниками для своих детей, однако они применяют мягкие и конструктивные методы взаимодействия, а не авторитарные или строгие.

В целом, безусловность в воспитании создает условия для гармоничного развития ребенка, помогает ему реализовать свой потенциал и стать уверенным и самостоятельным человеком.

Понятие числового ряда

В общем виде числовой ряд можно записать так: .
Здесь:– математический значок суммы; – общий член ряда (запомните этот простой термин); – переменная-«счётчик». Запись обозначает, что проводится суммирование от 1 до «плюс бесконечности», то есть, сначала у нас , затем , потом , и так далее – до бесконечности. Вместо переменной  иногда используется переменная  или . Суммирование не обязательно начинается с единицы, в ряде случаев оно может начинаться с нуля , с двойки либо с любого натурального числа.

В соответствии с переменной-«счётчиком» любой ряд можно расписать развёрнуто: – и так далее, до бесконечности.

Cлагаемые  – это ЧИСЛА, которые называются членами ряда. Если все они неотрицательны (больше либо равны нулю), то такой ряд называют положительным числовым рядом.

Пример 1

Записать первые три члена ряда
Это уже, кстати, «боевое» задание – на практике довольно часто требуется записать несколько членов ряда.

Сначала , тогда:
Затем , тогда:
Потом , тогда:

Процесс можно продолжить до бесконечности, но по условию требовалось написать первые три члена ряда, поэтому записываем ответ:

Обратите внимание на принципиальное отличие от числовой последовательности,в которой члены не суммируются, а рассматриваются как таковые. Пример 2

Пример 2

Записать первые три члена ряда

Это пример для самостоятельного решения, ответ в конце урока

Даже для сложного на первый взгляд ряда не составляет трудности расписать его в развернутом виде:

Пример 3

Записать первые три члена ряда

На самом деле задание выполняется устно: мысленно подставляем в общий член ряда сначала , потом  и . В итоге:

Ответ оставляем в таком виде, полученные члены ряда лучше не упрощать, то есть не выполнять действия: ,  , . Почему? Ответ в виде  гораздо проще и удобнее проверять преподавателю.

Иногда встречается обратное задание

Пример 4

Записать сумму в свёрнутом виде с общим членом ряда
Здесь нет какого-то четкого алгоритма решения, закономерность нужно просто увидеть.
В данном случае:
Для проверки полученный ряд  можно «расписать обратно» в развернутом виде.

А вот пример чуть сложнее для самостоятельного решения:

Пример 5

Записать сумму в свёрнутом виде с общим членом ряда
Выполнить проверку, снова записав ряд в развернутом виде

Акты толкования

В процессе толкования норм права практическое значение имеют акты толкования (интерпретационные акты). Акт толкования права – это правовой акт, содержащий разъяснение смысла юридических норм.

Акты толкования не просто разъясняют смысл норм права, но содержат прежде всего конкретизирующие предписания. Это не нормативные предписания, так как они не имеют самостоятельного значения и действуют на основе толкуемых норм права. Так как субъекты толкования не являются субъектами правотворчества, «предписания общего характера, содержащиеся в интерпретационных актах, следует считать не нормами права, а правоположениями. В отличие от норм они не имеют юридической силы, но имеют юридическое значение. Последнее проявляется в том, что правоприменительные органы (нижестоящие суды) должны при решении конкретных вопросов учитывать содержание правоположений. Однако при этом они не могут составлять основу правоприменительных решений».

Различаются следующие виды актов толкования:

• в зависимости от типов официального толкования они делятся на акты нормативного и казуального толкования;
• в зависимости от юридической природы различают интерпретационные акты правотворческих и правоприменительных органов;
• в зависимости от конкретных органов, осуществляющих толкование, различают акты суда, прокуратуры, администрации и др.;
• в зависимости от формы – это постановления, разъяснения, приказы, инструкции и т.д.;
• в зависимости от предмета правового регулирования – акты толкования конституционного, гражданского, административного, уголовного права и др.;
• в зависимости от характера – на материальные и процессуальные интерпретационные акты.

Самостоятельное значение прежде всего имеют интерпретационные акты правотворчества и интерпретационные акты правоприменения. Акты толкования не подменяют собой акты правотворчества и правоприменения, они имеют дополнительное (субсидиарное) значение к названным нормативно-правовым и индивидуальным актам.

показать содержание

Принципы неявных определений

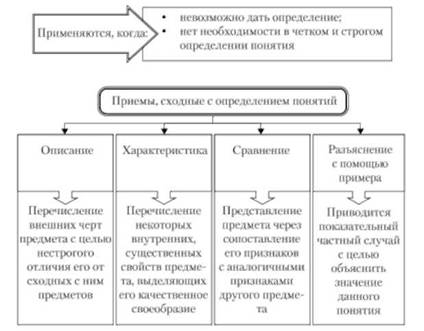
1. Конкретность: Определение должно быть ясным и однозначным, чтобы не вызывать недоразумений и разночтений. Неявные определения должны быть предметными и конкретными, чтобы избежать размытости и неопределенности в их интерпретации.

2. Контекстуальность: Неявные определения должны учитывать контекст, в котором они используются

Многозначность может возникнуть из-за разных контекстов, поэтому необходимо принимать во внимание окружение и обстоятельства, в которых происходит употребление определения

3. Список отношений: Определение может включать в себя список связанных понятий или отношений, чтобы дать более полное представление о его значении. Это может помочь уточнить и расширить его смысл, а также установить связи между различными понятиями.

4. Логическое следование: Определение должно быть логически связанным с определяющим понятием. Оно должно следовать из основной идеи или сути определяемого понятия, чтобы не вызывать противоречий или непонимания.

5. Ясность и краткость: Неявные определения должны быть ясными и лаконичными, чтобы не перегружать текст излишней информацией. Они должны быть выражены в достаточной мере, чтобы передать необходимую суть, но при этом быть краткими и легко запоминающимися.

6. Доступность: Определение должно быть доступным для понимания широкого круга лиц. Оно не должно содержать сложные термины или специфическую терминологию, которая может быть непонятна для обычных пользователей. Оно должно быть сформулировано простым и понятным языком.

7. Источники и авторитетность: Неявные определения должны быть основаны на достоверных и авторитетных источниках. Они должны быть подкреплены доказательствами и ссылками на исследования, эксперименты или другие источники информации. Такие определения имеют большую степень надежности и весомости.

Принцип суждений

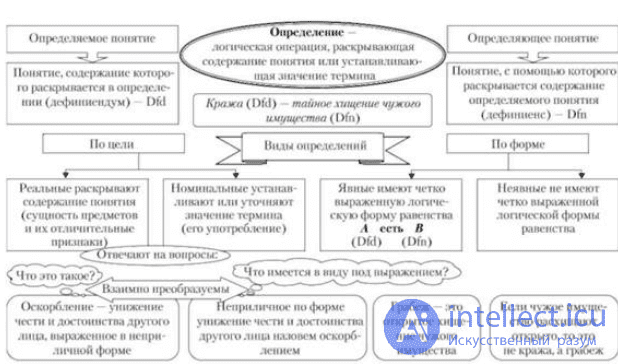
Принцип суждений является фундаментальным принципом в логике и философии. Он утверждает, что все высказывания, предположения или утверждения должны быть явно или неявно суждениями. Суждение — это выражение, которое имеет истинностное значение и может быть истинным или ложным.

Принцип суждений важен, чтобы ясно и однозначно определять содержание высказывания и его истинностное значение. Суждение имеет форму «A есть B» или «A характеристика B» и используется для выражения отношений между объектами или свойствами мира.

Примеры суждений могут быть: «Солнце светит», «Морская вода соленая», «Мясо красное». Все эти высказывания содержат суждения о фактах или свойствах.

Принцип суждений позволяет нам анализировать и оценивать высказывания с точки зрения их истинности или ложности. Он является основой для построения логических выводов и аргументаций.

Принцип суждений также связан с понятием квази-суждений, которые содержат в себе неявные суждения. Квази-суждение — это выражение, которое содержит в себе неявное суждение, например, «Погода хорошая», где предполагается неявное суждение «Солнце светит».

В целом, принцип суждений является фундаментальным принципом в логике и философии, он помогает нам определять и анализировать высказывания, основываясь на их суждениях и истинности.

Принцип предикатов

Принцип предикатов является одним из основных принципов в логике и используется для определения и описания свойств и качеств объектов. Предикаты — это выражения, которые связывают объекты с определенными свойствами или отношениями.

Принцип предикатов гласит, что для описания любого объекта или явления мы можем использовать предикаты, которые устанавливают какие-либо свойства или отношения между объектами. Предикаты могут быть простыми или составными, и они определяются с помощью логических операторов и кванторов.

Одним из примеров принципа предикатов является так называемое «кванторное определение». Например, мы можем определить понятие «студент» с помощью предиката «учится в университете». Таким образом, мы можем сказать, что «студент — это человек, который учится в университете». Здесь предикат «учится в университете» связывает объект «студент» с его свойством «учиться в университете».

Принцип предикатов позволяет нам более точно и ясно описывать объекты и явления с помощью логических конструкций. Он является одним из основных инструментов логики и используется в различных областях знания, таких как математика, философия, компьютерная наука и др.

Примеры неявных определений

Неявные определения в логике имеют множество примеров, которые могут быть полезными для понимания и применения этого концепта. Одним из примеров является ситуация, когда мы говорим о классическом примере овоща — моркови. Мы можем применить неявное определение, чтобы объяснить, что морковь — это овощ, который широко используется в кулинарии и содержит много витаминов и питательных веществ.

Другим примером является определение цвета. Мы можем сказать, что синий — это цвет, который ассоциируется с небом или морем, без явного указания причины этой ассоциации. Это неявное определение позволяет нам понять цвет синий и использовать его в контексте различных областей, таких как дизайн или искусство.

Еще одним примером неявного определения может быть обсуждение понятия «дружба». Мы можем сказать, что дружба — это отношение, основанное на взаимной привязанности, доверии и поддержке, без ссылки на конкретные действия или ситуации. Это позволяет нам понять, что дружба может проявляться по-разному в различных ситуациях, но иметь общие основы и характеристики.

Для наглядности можно привести еще один пример неявного определения, связанный с понятием «успех». Мы можем сказать, что успех — это достижение поставленных целей и выполнение задач, без указания конкретной сферы жизни или критериев успеха. Это позволяет нам понимать, что успех может быть разным для разных людей и зависеть от их индивидуальных целей и ценностей.

Неявное определение в математике

В математике существует понятие неявного определения, которое используется для задания объектов или свойств без явного указания их характеристик. Неявное определение позволяет описывать объекты или отношения на основе некоторых свойств или условий, которые могут быть неявно предположены.

Одним из примеров неявного определения в математике является уравнение эллипса. Уравнение эллипса задается в виде: x2/a2 + y2/b2 = 1, где a и b являются полуосями эллипса. В данном случае, объектом является эллипс, а его характеристики (полуоси) не указываются явно, а задаются через уравнение.

Другим примером неявного определения является определение функции как отображения, которое может быть записано следующим образом: f: X -> Y, где X — множество аргументов (область определения), Y — множество значений (область значений). В данном случае, объектом является функция, а её характеристики (аргументы и значения) не указываются явно, а задаются через обозначение отображения.

Неявное определение в математике широко используется для описания различных объектов и отношений, а также для формулировки условий и свойств. Такое определение позволяет более гибко описывать математические объекты и рассматривать их различные свойства без явного указания всех характеристик.

Неявное определение в философии

Неявное определение, одно из ключевых понятий в философии, является основой для анализа истинности утверждений и понятий. Оно предполагает скрытое или подразумеваемое определение, которое не является явным или ясным для всех. Неявные определения могут быть неявными связями или предпосылками, которые не упоминаются напрямую, но при этом влияют на наше понимание и оценку концепта или аргумента.

Принцип неявного определения в философии заключается в том, что для полного и точного понимания какого-либо понятия или идеи необходимо учитывать не только явные определения, но и скрытые возможности, которые могут влиять на их смысл и интерпретацию

Важно осознавать, что неявные определения могут быть неоднозначными и различными для разных людей и культур

Примером неявного определения в философии может служить понятие «свобода». Вроде бы это простое и понятное понятие, но оно имеет много разных трактовок. Каждый человек может воспринимать свободу по-своему, иметь свои неявные представления о том, что значит быть свободным. Эти неявные представления могут проистекать из предыдущего жизненного опыта, культурных норм или субъективных ожиданий. Поэтому, при обсуждении свободы, необходимо учесть и неявные определения, чтобы полноценно понять, о чем идет речь.

Раскрытие неявных определений является важным инструментом в философии, помогающим более глубоко понять, анализировать и критически оценивать концепты и аргументы. Благодаря разбору неявных определений, мы можем расширить свое понимание и быть более гибкими в интерпретации различных философских понятий.

Виды толкования по субъектам

Такое толкование является толкованием-разъяснением, даваемое официальными или неофициальными органами, отдельными гражданами. Оно зависит от правового положения субъектов, которые осуществляют толкование норм права. Толкование по субъектам делится на официальное и неофициальное.

Официальное толкование дается уполномоченными (компетентными) государственными органами. Оно содержится в специальном акте, является обязательным и имеет юридические последствия.

Официальное толкование по объему делится на нормативное и казуальное. Нормативное толкование распространяется на всех лиц, на все случаи, предусмотренные толкуемой правовой нормой. Нормативным данное толкование является в силу того, что носит общий характер, является обязательным при рассмотрении всех дел, которые разрешаются на основе истолкованной нормы. Нормативность такого толкования выражается также в специальных актах толкования (интерпретационных актах). Эти акты не являются источниками права, но являются основой для понимания и применения норм права (например, постановления пленумов высших судов). Кроме высших судебных инстанций официальное толкование могут осуществлять исполнительные органы в пределах своей компетенции (Президент, Правительство и др.), но специальных актов толкования эти органы не издают. Например, различные министерства и ведомства принимают акты разъяснительного характера (указания, информационные письма и т.д.). Субъекты Федерации также имеют право официального толкования актов на своей территории.

Нормативное толкование в свою очередь делится на аутентичное (дается тем же органом, который издал нормативно-правовой акт) и на легальное (даваемое специально уполномоченным органом). При аутентичном толковании специального полномочия на толкование не надо в отличие от легального толкования. При легальном толковании акт-разъяснение имеет силу в том случае, если определенный орган наделен специальной компетенцией.

Казуальное толкование – это такое разъяснение содержания правовой нормы, которое дается в связи с рассмотрением конкретного юридического дела (в процессе правоприменения). Такое толкование имеет силу лишь для определенного конкретного случая (казуса). Оно формально обязательно только для конкретного разрешения дела. В ряде случаев действительное значение актов казуального толкования, которое дается вышестоящими инстанциями, распространяется и на другие случаи, например, на аналогичные дела, рассматриваемые нижестоящими судебными инстанциями (правоприменительное толкование). В этом случае эти акты приобретают значение прецедентов судебного толкования, которые не являются прецедентами в собственном смысле слова, так как формально их не обязательно применять к сходным случаям.

В некоторых случаях имеет место – делегированное толкование, которое дается органом, получившим на это специальное полномочие в силу закона.

Неофициальное толкование – это толкование нормативных актов субъектами, которые не имеют на это официального права. Оно не является юридически обязательным и может исходить как от отдельного гражданина, так и от организации. Значение такого толкования зависит от авторитета толкователя (ученого, адвоката, нотариуса, следователя и др.).

Неофициальное толкование по видам делится в целом на доктринальное (научное), профессиональное (компетентное толкование юристов-практиков) и обыденное (толкование любым человеком).