Развитие логического мышления и абстрактного мышления
Математика, особенно тематика групп, колец и полей, играет важную роль в развитии логического мышления и абстрактного мышления у человека. Уже со школьных лет дети начинают изучение этих понятий, а в дальнейшем, при изучении высшей математики, более глубоко и систематически разбираются в них.
Изучение групп, колец и полей требует аналитического подхода, активного применения логики и построения математических доказательств. Это развивает умение мыслить последовательно и логически, а также научает абстрагироваться от конкретных ситуаций и рассматривать общие закономерности и свойства.
Абстрактное мышление в математике позволяет видеть общие законы и связи между объектами, а также уметь работать с абстрактными понятиями и символами. Именно эти навыки и умения часто требуются для решения сложных математических задач и проблем. Стремление к абстракции помогает видеть большую картину, а не застревать в деталях, что часто бывает в реальных жизненных ситуациях.
Разбираться в группах, кольцах и полях также требует умения мыслить ассоциативно и понимать взаимосвязи. Представление сложных структур в виде групп и колец помогает увидеть взаимосвязи между элементами и определить их свойства. Это развивает аналитическое мышление и способность видеть скрытые закономерности.
Итак, изучение групп, колец и полей в математике способствует развитию логического мышления и абстрактного мышления. Оно помогает формировать умение анализировать, абстрагироваться, уловить закономерности и взаимосвязи. Эти навыки хорошо себя проявляют не только в математике, но и в решении сложных задач и проблем в различных сферах жизни.
Примеры множеств, основанных на теоремах
Еще один пример о способах задания бесконечных множеств. Теорема: серединный перпендикуляр к отрезку есть геометрическое место точек, равноудаленных от его концов.
Возьмем отрезок , его центр – точка . Перпендикуляр, проведенный через точку к отрезку () – это серединный перпендикуляр, любая его точка равноудалена от концов отрезка (рис. 3). Точка принадлежит перпендикуляру () тогда и только тогда, когда . Смысл этой теоремы в том, что есть множество, которое задано характеристическим свойством, то есть равноудаленностью от концов отрезка, то есть множество задано неявно. Теорема утверждает, что это множество совпадает с серединным перпендикуляром к отрезку, то есть может быть задано явно – в том смысле, что может быть указан способ его построения, в данном случае построение циркулем и линейкой.
Рис. 3. Пример к теореме о серединном перпендикуляре к отрезку
Еще один пример: при изучении вписанных окружностей доказывают такую теорему – биссектриса есть геометрическое место точек, равноудаленных от сторон угла.
Имеем угол с вершиной , биссектриса , точка на биссектрисе. Опускаем перпендикуляры на стороны угла, к точкам и (рис. 4). Эти перпендикуляры, а значит, и расстояние от точки до лучей угла равны между собой. Точка принадлежит биссектрисе () тогда и только тогда, когда .
Рис. 4. Пример для теоремы о биссектрисе угла
Смысл этой теоремы в том, что есть множество с заданным характеристическим свойством: геометрическое место точек, равноудаленных от сторон угла, то есть множество задано неявно. Теорема утверждает, что это множество может быть задано явно, то есть может быть указан способ его построения, в данном случае построение циркулем и линейкой. Оно совпадает с биссектрисой. В данном случае мы опять сталкиваемся с тем, что задача перехода от одного описания множества к другому, может быть содержательной математически. Обратим внимание на то, что для бесконечных множеств, задание множества перечислением невозможно, а явное построение служит заменой этого способа.
Примеры и свойства главных подгрупп
В химии главные подгруппы представляют собой шесть главных блоков таблицы Менделеева. Каждая главная подгруппа имеет свои особенности и характерные свойства. Рассмотрим некоторые из них:
- 1-я главная подгруппа (IA) — щелочные металлы: представители данной подгруппы, такие как литий, натрий, калий и другие, обладают большой реакционной способностью, особенно с водой. Они образуют щелочные растворы, обладают низкой плотностью и низкой температурой плавления. Главными свойствами щелочных металлов является высокая активность и способность образовывать ионы с положительным зарядом.
- 2-я главная подгруппа (IIA) — щелочноземельные металлы: представители данной подгруппы, такие как магний, кальций, барий и другие, обладают меньшей реакционной способностью по сравнению с щелочными металлами. Они образуют щелочноземельные растворы, обладают большей плотностью и температурой плавления. Главными свойствами щелочноземельных металлов является желтоватый оттенок в пламени и способность образовывать ионы с двояким положительным зарядом.
- 3-я главная подгруппа (IIIB) — скандий-группа: представители данной подгруппы, такие как скандий, иттрий, лантан и другие, обладают средней реакционной способностью. Они образуют растворы средней щелочности, обладают средней плотностью и температурой плавления. Главное свойство группы — способность образовывать ионы с тройным положительным зарядом.
- 4-я главная подгруппа (IVB) — титан-группа: представители данной подгруппы, такие как титан, цирконий, гафний и другие, отличаются высокой температурой плавления и высокой плотностью. Они образуют соединения с различными степенями окисления и имеют свойства полупроводников.
- 5-я главная подгруппа (VB) — ванадий-группа: представители данной подгруппы, такие как ванадий, ниобий, тантал и другие, обладают высокой твердостью и плотностью. Имеют переменные степени окисления и свойства полупроводников.
- 6-я главная подгруппа (VIB) — хром-группа: представители данной подгруппы, такие как хром, молибден, вольфрам и другие, отличаются высокой температурой плавления и высокой плотностью. Имеют разные степени окисления и широкое применение в промышленности.
Это лишь некоторые примеры свойств главных подгрупп. Каждая главная подгруппа имеет свою уникальную химическую активность и свойства.
Кольца и поля
Кольцом называется (непустое) множество K, на котором определены две операции (сложение и умножение), обладающие следующими свойствами:
1) множество K относительно сложения образует коммутативную группу;
2) умножение ассоциативно: для любых а, b, с ∈ K
3) сложение и умножение подчиняются дистрибутивному закону:
для любых а, b, с ∈ K.
При этом множество K, рассматриваемое лишь относительно операции сложения, называется аддитивной группой кольца.
Приведем некоторые примеры колец.
Читателю предлагается проверить выполнимость аксиом кольца в каждом из примеров. Остановимся подробнее на примере 3.
Поскольку операции над классами вычетов сводятся к операциям над числами из этих классов, то свойства ассоциативности и коммутативности этих операций вытекают из аналогичных свойств числового сложения и умножения. То же замечание относится к свойству дистрибутивности. Роль нулевого элемента при сложении играет класс 0‾. Противоположным элементом для класса вычетов r‾ ≠ 0‾ является класс n-r‾. Из определения сложения классов следует, что
В общем определении кольца не содержится требование коммутативности умножения. В том случае, если умножение обладает этим дополнительным свойством, кольцо называется коммутативным. В примерах 1-3 мы имеем как раз коммутативные кольца, а позднее (в приложении 5) познакомимся с важным примером некоммутативного кольца.
Рассмотрим таблицы умножения ненулевых элементов в кольцах вычетов Z4 и Z5.
Таблица 19 показывает, что в кольце могут существовать ненулевые элементы, произведение которых равно нулю: в Z4 2‾ · 2‾ = 0‾. Из этой же таблицы видно, что класс 2‾ необратим. Вообще, можно доказать, что ненулевые элементы, произведение которых равно нулю (называемые делителями нуля), всегда необратимы. С другой стороны, таблица 20 показывает, что в кольце Z5 всякий ненулевой элемент обратим. Кольца с этим свойством имеют особое значение. Примем такое определение.
Коммутативное кольцо с единицей, в котором всякий ненулевой элемент обратим, называется полем.
Множество ненулевых элементов поля относительно умножения образует в силу определения поля коммутативную группу, которая называется мультипликативной группой поля.
Простейшими примерами числовых полей являются поле рациональных чисел Q и поле действительных чисел R (разумеется, относительно операций сложения и умножения чисел). Полем, как ясно из предыдущего, является и кольцо Z5. Вообще, можно доказать, что при любом простом р (и только в этом случае) кольцо вычетов Zp является полем. Оно называется полем вычетов по модулю р. В таблице 21 указаны элементы, обратные к ненулевым элементам поля вычетов Z7.
Конечные поля часто называют полями Галуа (их обозначают GF(g)); важное их свойство, используемое, в частности, и в теории кодирования, состоит в следующем:
Мультипликативная группа поля Галуа является циклической группой порядка q-1.
Образующий элемент мультипликативной группы поля Галуа называют примитивным элементом. Так, в поле Z7 примитивным элементом является класс вычетов 3‾. Действительно, его степени
исчерпывают все ненулевые элементы поля.
Заметим, что класс 2 не является примитивным элементом в Z7, так как среди его степеней нет, например, класса В. В то же время имеется очень много простых чисел р, для которых элемент ‾2 примитивен в Zр. Так обстоит дело в полях Z3, Z5, Z11 и т. д. В теории чисел известна следующая до сих пор не решенная задача:
Бесконечно ли множество тех простых чисел р, для которых ‾2 является примитивным элементом в Zp?
Интересно, что с ответом на этот вопрос связано решение некоторых проблем теории кодирования.
Подмножество I кольца K называется его (двусторонним) идеалом, если оно само является кольцом относительно операций на K и если для любых элементов а ∈ K и b ∈ I оба произведения аb и bа принадлежат I.
Так, множество четных чисел есть идеал кольца Z. Читатель легко проверит, что и вообще всякое множество чисел, кратных какому-нибудь числу k, является идеалом кольца Z.
Рекомендуем читателю найти идеалы колец вычетов Z5, Z6, Z8 и кольца многочленов R.
Алгебраические структуры: поля
Числовое кольцо называется числовым полем, если оно содержит частное любых двух своих чисел
(делитель предполагается отличным от нуля). Следовательно, можно говорить о поле рациональных чисел, поле
действительных чисел, поле комплексных чисел, в то время как кольцо целых чисел полем не является.
Поле можно определить и следующим образом. Множество называют полем, если в этом множестве по меньшей мере два
элемента и для них
1) определена операция сложения;
1′) определена операция умножения;
2) для сложения выполняется сочетательный (ассоциативный) закон;
2′) для умножения выполняется сочетательный (ассоциативный) закон;
3) для сложения выполнятся переместительный (коммутативный) закон;
3′) для умножения выполняется переместительный (коммутативный) закон;
4) выполнима операция вычитания;
4′) выполнима операция деления, кроме деления на нуль.
Для любых элементов поля и
найдётся такой элемент ,
что .
Для любых элементов поля и
найдётся такой элемент ,
что ,
если .
Для поля в силе распределительный (дистрибутивный) закон умножения (относительно сложения): .
Алгебраические структуры часто называют просто «алгебрами». Их используют
в абстрактном моделировании. В частности, они могут быть применены в программировании.
Например, когда нужно определить свойства и правила какой-либо структуры и установить запрет
на добавление в эту структуру элемента, которое (добавление) нарушило бы свойства и правила
для этой структуры.
| Назад | Листать | Вперёд>>> |
Универсальность и общность понятий
Группа – это множество элементов, для которого задана операция, обладающая определенными свойствами. Эта абстрактная структура позволяет исследовать различные универсальные законы и свойства, которые присутствуют не только в арифметике, но и в других областях науки и техники.
Кольцо – это расширение понятия группы, в котором заданы две операции: сложение и умножение. Кольцо образует более общую и богатую структуру, которая позволяет рассматривать такие алгебраические свойства, как ассоциативность, коммутативность и дистрибутивность.
Поле – это еще более широкое понятие, чем кольцо. В поле, помимо операций сложения и умножения, определена операция деления. Более того, в поле выполняются все основные арифметические свойства, такие как коммутативность, ассоциативность, дистрибутивность, а также свойства нуля и единицы.
С помощью групп, колец и полей математики исследуют универсальные законы и принципы, которые применимы в самых разных областях. Например, группы используются для исследования симметрий и преобразований в физике и химии, колец – для алгоритмов и шифрования, поля – для построения геометрических моделей и компьютерных графиков.
Таким образом, группы, кольца и поля являются универсальными инструментами, позволяющими описывать и анализировать различные абстрактные структуры и их свойства. Они не только являются основой для многих математических теорий, но и находят применение во многих практических областях человеческой деятельности.
Изоморфизм и гомоморфизм
Гомоморфизм
Одна группа гомоморфна другой группе, если любым двум элементам A и B из первой группы можно однозначно сопоставить два элемента A’ и B’, соответственно, из второй группы
так, что если AB=C, а A’B’=C’, то элементу C из первой группы однозначно сопоставляется элемент C’ из второй группы.
Фактически, это означает, что существует какая-то однозначная операция отображения всех элементов первой группы на все элементы второй группы так, что при этом сохраняются все отношения между элементами,
задаваемые групповыми операциями. Такое отображение называется гомоморфизмом.
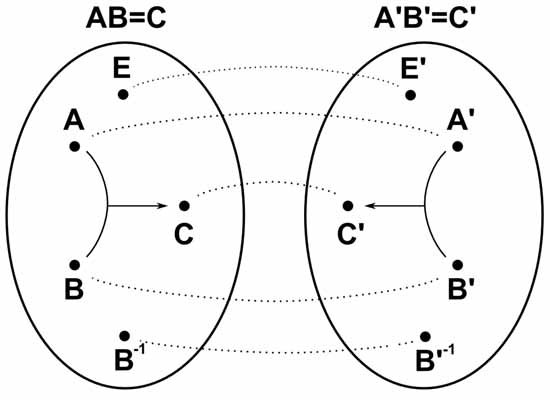
Из этого понятно, что единичный элемент первой группы при гомоморфизме всегда соответствует единичному элементу второй группы. А все пары взаимно обратных элементов первой группы всегда соответствуют
парам взаимно обратных элементов второй группы.
Простой пример гомоморфизма. Группу целых четных чисел с операцией сложения можно однозначно отобразить на группу всех целых чисел с операцией умножения. При этом числу 0 первой группы
соответствует число 0 второй группы. Числу 2 первой группы соответствует число 1 второй группы. Числу 4 первой группы соответствует число 2 второй группы. И т.д. То же самое и с отрицательными числами. В
общем случае число n из второй группы является соответствием числа 2n из первой группы.
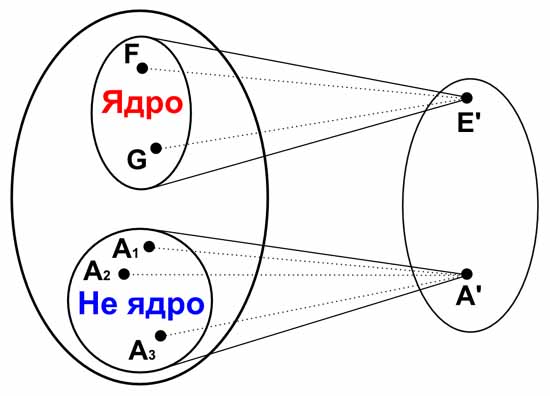
Гомоморфизм требует однозначности такого отображения, но не требует при этом взаимности этого отображения. То есть элемент A из первой группы имеет только один соответствующий ему элемент A’
из второй группы. Во второй группе нет никакого другого элемента, который соответствует элементу A из первой группы. Но вот для двух разных элементов A1 и A2 из
первой группы (A1≠A2) допускается иметь только один соответствующий им элемент A’ из второй группы.

В этом смысле вторая группа может не только иметь меньше элементов, чем первая группа, но и быть более простой, чем первая группа. Ядром гомоморфизма первой группы называется такая подгруппа первой
группы, которая при гомоморфизме переходит в единичный элемент второй группы.
Изоморфизм
Изоморфизм, это взаимно однозначный гомоморфизм.
То есть, когда элементу A первой группы не только соответствует один элемент A’ второй группы, но и элементу A’ соответствует только один элемент A из первой группы.
Если между двумя группами существует изоморфизм, то данные группы называются изоморфными. Изоморфные группы не отличаются друг от друга с точки зрения теории групп. С точки зрения теории групп изоморфные
группы являются совершенно одинаковыми. Элементы таких групп могут иметь разную математическую природу, операции таких групп также могут быть разными, но в теории групп, это одна и та же группа.
Рассмотрим пример изоморфизма. Пусть одна группа представляет собой 4 числа, 1, i, -1, -i, где i, это мнимая единица, а групповой операцией будет умножение этих чисел.
Данная группа изоморфна группе вращений плоскости, которые совмещают квадрат с самим собой при поворотах квадрата вокруг своего центра с групповой операцией последовательного применения двух вращений.
Соответствуют друг другу число 1 и поворот на 0 градусов, число i и поворот на 90 градусов, число (-1) и поворот на 180 градусов, число (-i) и поворот на 270 градусов. Можно
убедиться, что операция умножения в первой группе точно соответствует операции сочетания двух соответствующих поворотов из второй группы.
Изоморфизм в теории групп полезен тем, что позволяет перенести многие доказанные математиками вещи из одной области математики в другую, когда удается доказать изоморфизм основных групп в этих разных
областях математики.
Примеры использования главной и побочной подгрупп в различных областях науки
Химия:
- В органической химии главная подгруппа может определять, насколько карбонильная группа сильно влияет на свойства молекулы, тогда как побочная подгруппа может показать, как изменения в цепи могут повлиять на реакционную способность молекулы.
- В неорганической химии главная подгруппа может указывать на металлические ионные группы, а побочная подгруппа может описывать содержание других элементов, таких как кислород, сера или азот, в молекуле.
Биология:
- В молекулярной биологии главная подгруппа может указывать на полностью функционирующий ген, тогда как побочная подгруппа может указывать на различные варианты генов, некоторые из которых могут также играть важную роль в биологических процессах.
- В нейробиологии главная подгруппа может относиться к сигнальным молекулам, рецепторам или другим ключевым компонентам нервной системы, а побочная подгруппа может относиться к специфическим белкам или генам, которые связаны с определенными патологиями, такими как болезни Альцгеймера или Паркинсона.
Физика:
- В физике элементарных частиц главная подгруппа может относиться к фундаментальным частицам, таким как кварки или лептоны, тогда как побочная подгруппа может относиться к частицам, которые образуются в результате взаимодействия между главными частицами.
- В оптике главная подгруппа может относиться к различным видам света, тогда как побочная подгруппа может относиться к другим формам электромагнитного излучения, таким как радиоволны или рентгеновские лучи.
Математика:
- В алгебре главная подгруппа может относиться к группе, которая содержит все основные свойства группы, тогда как побочная подгруппа может относиться к произведению групп или к подгруппе, которая не включает в себя некоторые элементы группы.
- В топологии главная подгруппа может указывать на те множества, которые являются открытыми, тогда как побочная подгруппа может указывать на те множества, которые являются замкнутыми.
Что такое главная подгруппа в таблице Менделеева?
Главная подгруппа в таблице Менделеева — это верхняя часть каждой группы, обозначающая общую химическую активность элементов группы. В главной подгруппе находятся элементы, которые имеют схожие свойства и входят в одну группу. Элементы в главной подгруппе обычно образуют ионы с положительными зарядами (катионы).
Определить, является ли элемент частью главной подгруппы в таблице Менделеева, можно, посмотрев на номер группы и расположение элемента в таблице. Главная подгруппа обычно простирается от первого элемента группы до элемента, у которого номер группы совпадает с номером подгруппы (например, для главной подгруппы 1A, это будет кислород во втором периоде и литий в первом периоде).
Важно знать, что главная подгруппа в таблице Менделеева имеет свою нумерацию и определенные обозначения. Например, главная подгруппа 1А включает элементы литий (Li), натрий (Na), калий (K), рубидий (Rb), цезий (Cs) и франций (Fr)
Главная подгруппа 2А включает элементы бериллий (Be), магний (Mg), кальций (Ca), стронций (Sr), барий (Ba) и радий (Ra).
Определение и классификация
Одна из основных характеристик элементов в таблице Менделеева — это их принадлежность к главным и побочным подгруппам. Главные подгруппы расположены в вертикальных колонках под таблицей, а побочные — в диагональных строках, которые сопровождают главные подгруппы.
Главные подгруппы обычно обозначаются римскими цифрами I-VIII, а побочные подгруппы — буквами a и b. Каждая главная подгруппа содержит несколько элементов и имеет свои общие химические свойства, которые отличают их от элементов других подгрупп или групп.
Определение, к какой подгруппе относится данный элемент, осуществляется на основе его положения в таблице Менделеева. По атомному номеру элемента можно определить его место в таблице и, соответственно, его принадлежность к главной или побочной подгруппе.
Таким образом, таблица Менделеева позволяет систематизировать и классифицировать элементы по их химическим свойствам и принадлежности к определенным подгруппам.
| № | Элемент | Подгруппа |
|---|---|---|
| 1 | Водород | Главная подгруппа I |
| 2 | Гелий | Главная подгруппа VIII |
| 3 | Литий | Главная подгруппа I |
| 4 | Бериллий | Главная подгруппа II |
| 5 | Бор | Главная подгруппа III |
| … | … | … |
Свойства и особенности
В таблице Менделеева химических элементов подгруппы разделены на главные и побочные. Главные подгруппы обозначаются цифрами от 1 до 18, а побочные подгруппы обозначаются буквами. Определение, относится ли элемент к главной или побочной подгруппе, зависит от его электронной конфигурации и расположения в таблице Менделеева.
Главные подгруппы в таблице Менделеева представлены вертикальными столбцами. Элементы в каждой главной подгруппе имеют схожие общие свойства. Главные подгруппы также называются группами элементов. Изначально главные подгруппы были разделены на шесть блоков: s, p, d, f, g и h. Однако в настоящее время используется разделение на 18 главных подгрупп по номерам.
Побочные подгруппы в таблице Менделеева представлены горизонтальными строками и обозначаются буквами от A до H. Элементы в каждой побочной подгруппе имеют схожие химические свойства и образуют ряды элементов. Побочные подгруппы также называются периодами элементов.
| 1A | 2A | 3B | 4B | 5B | 6B | 7B | 8B | 1B | 2B | 3A | 4A | 5A | 6A | 7A | 8A | |
| H | He | Li | Be | B | C | N | O | F | ||||||||
| Na | Mg | K | Ca | Sc | Ti | V | Cr | Mn | ||||||||
| Rb | Sr | Cs | Ba | La |
Таблица Менделеева является основополагающим инструментом для изучения химии. Определение главной и побочной подгруппы элементов в таблице Менделеева позволяет классифицировать элементы по их свойствам и расположению в таблице.
Что такое множество в математике и как оно обозначается
Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.
В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.
Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.
Границы совокупности обозначаются фигурными скобками { }.
Пример:
-
А = {а, в, с, у} – А состоит из четырех элементов.
-
Записать совокупность Z согласных букв в слове «калькулятор»:
Z = {к, л, т, р}, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.
Принадлежность элементов множеству обозначается знаком – Є.
Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.
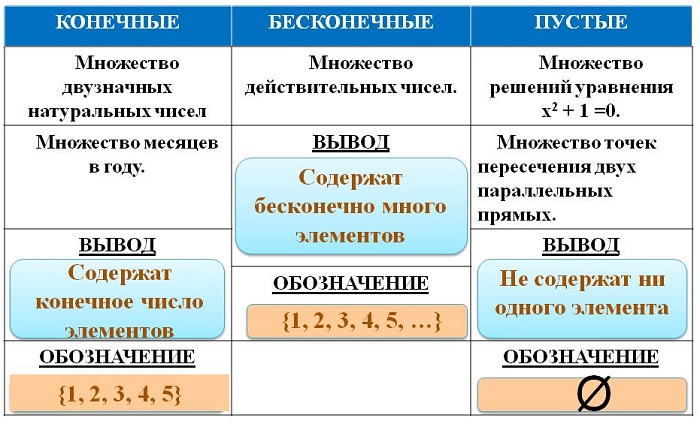
Выделяют три вида множеств:
-
конечные — совокупности, имеющие максимальный и минимальный предел (например, отрезок);
-
бесконечные — не являющиеся конечными (например, числовые);
-
пустые (обозначаются Ø) – не имеющие элементов.
Если две разные совокупности содержат одинаковые элементы, то одна из них (со всеми своими элементами) является подмножеством другой и обозначается знаком — ⊆.
Пример: А = {а, в, с, у} и В = {а, в, с, е, к} – все элементы А являются элементами совокупности В, следовательно А ⊆ В.
Если множества состоят из одинаковых элементов, их называют равными.
Пример: А = {23, 29, 48} и В = {23, 29, 48}, тогда А = В.
В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.
Группы
Вертикальные столбики элементов в периодической таблице — группы состоят из подгрупп: главной и побочной, они иногда обозначаются буквами А и Б соответственно.
В состав главных подгрупп входят s- и р-элементы, а в состав побочных — d- и f-элементы больших периодов.
Главная подгруппа — это совокупность элементов, которая размещается в периодической таблице вертикально и имеет одинаковую конфигурацию внешнего электронного слоя в атомах.
Как следует из приведенного определения, положения элемента в главной подгруппе определяется общим количеством электронов (s- и р-) внешнего энергетического уровня, равным номеру группы. Например, сера (S — 3s2 3p4 ), в атоме которого на внешнем уровне содержится шесть электронов, относится к главной подгруппе шестой группы, аргон (Ar — 3s2 3p6 ) — к главной подгруппе восьмой группы, а стронций (Sr — 5s2 ) — к ІІА-подгруппе.
Элементы одной подгруппы характеризуются сходством химических свойств. В качестве примера рассмотрим элементы ІА и VІІА подгрупп (табл.2). С ростом заряда ядра увеличивается количество электронных слоев и радиус атома, но количество электронов на внешнем энергетическом уровне остается постоянной: для щелочных металлов (подгруппа IА) — один, а для галогенов (подгруппа VIIА) — семь. Поскольку именно внешние электроны наиболее существенно влияют на химические свойства, то понятно, что каждая из рассмотренных групп элементов-аналогов имеет подобные свойства.
Но в пределах одной подгруппы наряду с подобием свойств наблюдается их некоторое изменение. Так, элементы подгруппы ІА все, кроме Н — активные металлы. Но с ростом радиуса атома и количества электронных слоев экранирующих влияние ядра на валентные электроны, металлические свойства усиливаются. Поэтому Fr более активный металл, чем Сs, a Cs — более активный, чем R в и т.д. А в подгруппе VIIA по той же причине ослабляются неметаллические свойства элементов при росте порядкового номера. Поэтому F — более активный неметалл по сравнению с Cl, a Cl — более активный неметалл сравнению с Br и т.д.
Таблица 2 — Некоторые характеристики элементов ІА и VІІА-подгрупп
| период | Подгруппа IA | Подгруппа VIIA | ||||||
|---|---|---|---|---|---|---|---|---|
| Символ элемента | Заряд ядра | Радиус атома, нм | Внешняя электронная конфигурацiя | Символ элемента | Заряд ядра | Радиус атома, нм | Внешняя электронная конфигурацiя | |
| II | Li | +3 | 0,155 | 2 s 1 | F | +9 | 0,064 | 2 s 2 2 p 5 |
| III | Na | +11 | 0,189 | 3 s 1 | Cl | +17 | 0,099 | 3 s 2 3 p 5 |
| IV | K | +19 | 0,236 | 4 s 1 | Br | 35 | 0,114 | 4 s 2 4 p 5 |
| V | Rb | +37 | 0,248 | 5 s 1 | I | +53 | 0,133 | 5 s 2 5 p 5 |
| VI | Cs | 55 | 0,268 | 6 s 1 | At | 85 | 0,140 | 6 s 2 6 p 5 |
| VII | Fr | +87 | 0,280 | 7 s 1 | — | — | — | — |
Побочные подгруппа — это совокупность элементов, размещаемых в периодической таблице вертикально и имеют одинаковое количество валентных электронов за счет застройки внешнего s- и втором снаружи d-энергетических подуровней.
Все элементы побочных подгрупп относятся к d-семейству. Эти элементы иногда называют переходными металлами. В побочных подгруппах свойства изменяются более медленно, поскольку в атомах d-элементов электроны застраивают второй извне энергетический уровень, а на внешнем уровне находятся только один или два электрона.
Положение первых пяти d-элементов (подгруппы IIIБ- VIIБ) каждого периода можно определить с помощью суммы внешних s-электронов и d-электронов второго снаружи уровня. Например, из электронной формулы скандия (Sc — 4s2 3d1 ) видно, что он размещается в побочной подгруппе (поскольку является d-элементом) третьей группы (поскольку сумма валентных электронов равна трем), а марганец (Mn — 4s2 3d5 ) размещается в побочной подгруппе седьмой группы.
Положение последних двух элементов каждого периода (подгруппы IБ и IIБ) можно определить по количеству электронов на внешнем уровне, поскольку в атомах этих элементов предыдущий уровень является полностью завершенным. Например, Ag ( 5s1 5d10 ) размещается в побочной подгруппе первой группы, Zn ( 4s2 3d10 ) — в побочной подгруппе второй группы.
Триады Fe-Co-Ni, Ru-Rh-Pd и Os-Ir-Pt размещены в побочной подгруппе восьмой группы. Эти триады образуют две семьи: железа и платиноидов. Кроме указанных семей отдельно выделяют семью лантаноидов (четырнадцать 4f-элементов) и семью актиноидов (четырнадцать 5f-элементов). Эти семьи принадлежат к побочной подгруппе третьей группы.
Рост металлических свойств элементов в подгруппах сверху вниз, а также уменьшение этих свойств в пределах одного периода слева направо обусловливают появление в периодической системе диагональной закономерности. Так, Be очень похож на Al, B — на Si, Ti — на Nb. Это ярко проявляется в том, что в природе эти элементы образуют подобные минералы. Например, в природе Те всегда бывает с Nb, образуя минералы — титанониобаты.
Примеры групп[править | править код]
| 1 | |
|---|---|
| 1 | 1 |
Следующий простой пример — группа с обычной арифметической операцией умножения, которая состоит из элементов (1, −1). Элемент 1 является единичным элементом группы, оба элемента группы обратны самим себе:
| 1 | −1 | |
|---|---|---|
| 1 | 1 | -1 |
| -1 | -1 | 1 |
Группой относительно обычной арифметической операции умножения является множество, состоящее из четырёх элементов (1, −1, i, -i). Единичным элементом здесь является 1, обратными элементами для 1 и −1 являются они сами, а элементы i и -i являются обратными друг для друга.
| 1 | −1 | i | -i | |
|---|---|---|---|---|
| 1 | 1 | -1 | i | -i |
| -1 | -1 | 1 | -i | i |
| i | i | -i | -1 | 1 |
| -i | -i | i | 1 | -1 |
Группой является два поворота пространства на 0° и 180° вокруг одной оси, если произведением двух поворотов считать их последовательное выполнение. Эта группа обычно обозначается C2. Она изоморфна (то есть тождественна) приведённой выше группе с элементами 1 и −1. Поворот на угол 0°, поскольку он является тождественным, обозначен в таблице буквой E.
| C2 | E | R180 |
|---|---|---|
| E | E | R180 |
| R180 | R180 | E |
Группу вместе с тождественным преобразованием E образует операция инверсии I, которая меняет направление каждого вектора на обратное. Групповой операцией является последовательное выполнение двух инверсий. Эта группа обычно обозначается S2. Она изоморфна приведённой выше группе C2.
| S2 | E | I |
|---|---|---|
| E | E | I |
| I | I | E |
По аналогии с группой C2 можно построить группу C3, состоящую из поворотов плоскости на углы 0°, 120° и 240°. Можно сказать, что группа C3 является группой поворотов, переводящих правильный треугольник сам в себя.
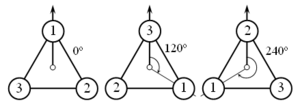
Элементы группы C3
| C3 | E | R120 | R240 |
|---|---|---|---|
| E | E | R120 | R240 |
| R120 | R120 | R240 | E |
| R240 | R240 | E | R120 |
Если к группе C3 прибавить отражения треугольника относительно трёх его осей симметрии (R1, R2, R3), то мы получим полную группу операций, которая переводит треугольник сам в себя. Эта группа называется D3.
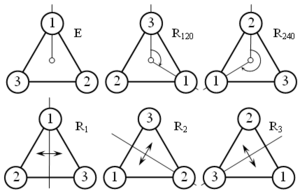
Элементы группы D3
| D3 | E | R120 | R240 | R1 | R2 | R3 |
|---|---|---|---|---|---|---|
| E | E | R120 | R240 | R1 | R2 | R3 |
| R120 | R120 | R240 | E | R2 | R3 | R1 |
| R240 | R240 | E | R120 | R3 | R1 | R2 |
| R1 | R1 | R3 | R2 | E | R240 | R120 |
| R2 | R2 | R1 | R3 | R120 | E | R240 |
| R3 | R3 | R2 | R1 | R240 | R120 | E |
Совокупность всех вращений относительно одной оси образуют непрерывную группу, называемую R2. Её элементы обозначим символами R(a), где a — угол поворота, находящийся в пределах 0 ≤ a
- R(a)⋅R(b)=R(a+b | mod 360∘).{\displaystyle R(a)\cdot R(b)=R(a+b~|~{\bmod {~}}360^{\circ }).}
Поскольку результат двух последовательных поворотов вокруг одной оси не зависит от порядка поворотов, группа R2 является коммутативной. Обратный элемент в группе определяется формулой
- R−1(a)=R(360∘−a).{\displaystyle R^{-1}(a)=R(360^{\circ }-a).}
Группа R3 представляет собой группу всевозможных вращений трёхмерного пространства относительно осей, проходящих через одну точку. Эта группа является группой симметрии сферы. Каждый элемент группы R(α,β,a) задаётся тремя параметрами: α и β — эйлеровы углы, задающие положение оси, a — угол поворота.
Группа Sn или симметрическая группа порядка n — это совокупность n! всевозможных перестановок n элементов. Перестановку удобно обозначать символом
- P=(123…np1p2p3…pn),{\displaystyle P={\begin{pmatrix}1&2&3&\dots &n\\p_{1}&p_{2}&p_{3}&\dots &p_{n}\end{pmatrix}},}
указывающим, что элемент n при перестановке заменяется на элемент pn. Обратным элементом для элемента P будет элемент
- P−1=(p1p2p3…pn123…n).{\displaystyle P^{-1}={\begin{pmatrix}p_{1}&p_{2}&p_{3}&\dots &p_{n}\\1&2&3&\dots &n\end{pmatrix}}.}
Интересно, что группа S3 изоморфна группе D3, так как последняя содержит всевозможные преобразования, переводящие треугольник сам в себя, а преобразование треугольника можно задать различными перестановками трёх его вершин:
- E=(123123); R120=(123312); R240=(123231);{\displaystyle E={\begin{pmatrix}1&2&3\\1&2&3\end{pmatrix}};~~R_{120}={\begin{pmatrix}1&2&3\\3&1&2\end{pmatrix}};~R_{240}={\begin{pmatrix}1&2&3\\2&3&1\end{pmatrix}};}
- R1=(123132); R2=(123321); R3=(123213).{\displaystyle R_{1}={\begin{pmatrix}1&2&3\\1&3&2\end{pmatrix}};~R_{2}={\begin{pmatrix}1&2&3\\3&2&1\end{pmatrix}};~~~R_{3}={\begin{pmatrix}1&2&3\\2&1&3\end{pmatrix}}.}
Мультипликативная группа кольца вычетов G(n){\displaystyle G(n)} (где n{\displaystyle n} — натуральное число) — группа, образованная взаимно простыми с n{\displaystyle n} вычетами (Zn=Z/nZ{\displaystyle \mathbb {Z} _{n}=\mathbb {Z} /n\mathbb {Z} }) по модулю n.{\displaystyle n.} Например, G(2)={1},G(3)≈Z2,G(4)≈Z2,G(5)≈Z4,G(6)≈Z2,G(7)≈Z6,G(8)≈Z2×Z2.{\displaystyle G(2)=\{1\},\quad G(3)\approx \mathbb {Z} _{2},\quad \quad G(4)\approx \mathbb {Z} _{2},\quad \quad G(5)\approx \mathbb {Z} _{4},\quad \quad G(6)\approx \mathbb {Z} _{2},\quad \quad G(7)\approx \mathbb {Z} _{6},\quad \quad G(8)\approx \mathbb {Z} _{2}\times \mathbb {Z} _{2}.}
Сочетание множества и операции
Таким образом, для группы нам необходимо и множество и какая-то операция между элементами этого множества. По отдельности множество без операции не может быть группой. И операция без множества тоже не
может быть группой.
Например, множество всех рациональных чисел, это множество, но не группа, так как не сказано, какая операция задана на этом множестве. Точно также множествами, но не группами являются множество всех
треугольников или множество всех поворотов вокруг точки в трехмерном пространстве, так как мы еще не задали операцию между элементами этого множества.
Если мы говорим просто об операциях без конкретизации множества, то это тоже не группа. Например, такие операции, как сложение или параллельный перенос не являются группой, так как не задано, с элементами
каких множеств они работают.
Еще одна особенность группы заключается в том, что в качестве группы рассматривается только одно сочетание множества и операции. Например, на множестве вещественных чисел можно определить много разных
операций (сложение, вычитание, умножение и т.д.). Но в группе рассматривается только одна из этих операций. Другая операция на этом же множестве может представлять собой совсем другую группу.
То же самое можно сказать и относительно операции. Например, операция сложение может быть определена и на множестве целых чисел и на множестве рациональных чисел и на множестве вещественных чисел и т.д.
На каждом из этих множеств операция сложения даёт свои группы.






























