Квадратный корень

§ 4. Физические величины. Измерение физических величин

Так, например, измерить длину стола — значит сравнить её с другой длиной, которая принята за единицу длины, например с метром.

Для каждой физической величины приняты свои единицы.

Для удобства все страны мира стремятся пользоваться одинаковыми единицами физических величин. С 1963 г. в России и других странах применяется Международная система единиц — СИ (система интернациональная). В этой системе основной единицей длины является метр (1 м), единицей времени — секунда (1 с), единицей массы — килограмм (1 кг).

Часто применяют единицы, которые в 10, 100, 1000 и т. д. раз больше принятых единиц (кратные). Эти единицы получили наименования с соответствующими приставками, взятыми из греческого языка. «Дека» — 10, «гекто» — 100, «кило» — 1000 и др.

Если используются единицы, которые в 10, 100 и 1000 и т. д. раз меньше принятых единиц (дольные), то применяют приставки, взятые из латинского языка. «Деци» — 0,1, «санти» — 0,01, «милли» — 0,001 и др.

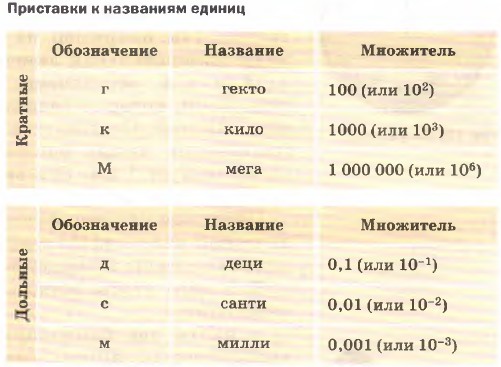
Пример. Длина теннисной ракетки 60 см. Выразите её длину в метрах (м).

Для проведения опытов необходимы приборы. Одни из них очень просты и предназначены для простых измерений. К таким приборам можно отнести: измерительную линейку, рулетку (рис. 6), измерительный цилиндр (рис. 7) и др.

По мере развития физики приборы усложнялись и совершенствовались. Появились амперметры (рис. 8), вольтметры (рис. 9), секундомеры (рис. 10), термометры (рис. 11), электронные весы, шагомеры (рис. 12).

Измерительные приборы, как правило, имеют шкалу. Это значит, что на приборе нанесены штриховые деления, а рядом написаны значения величин, соответствующие делениям.

Расстояния между двумя штрихами, возле которых написаны значения физической величины, могут быть дополнительно разделены ещё на несколько делений. Эти деления иногда не обозначены числами.

Определить, какому значению величины соответствует каждое самое малое деление, нетрудно. Так, например, на рисунке 6, а изображена измерительная линейка. Цифрами 1, 2, 3, 4 и т. д. обозначены расстояния между штрихами, которые разделены на 10 одинаковых делений. Следовательно, каждое деление (расстояние между ближайшими штрихами) соответствует 1 мм. Эта величина называется ценой деления шкалы прибора.

Перед тем как приступить к измерению физической величины, следует определить цену деления шкалы используемого прибора.

Для того чтобы определить цену деления, необходимо:

— найти два ближайших штриха шкалы, возле которых написаны значения величины;

— вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

Определим цену деления шкалы термометра, изображённого на рисунке 11, б.

Возьмём два штриха, около которых нанесены значения измеряемой величины (температуры).

Например, штрихи с обозначениями 10 °С и 20 °С. Расстояния между этими штрихами разделены на 10 делений. Таким образом, цена каждого деления будет равна

Следовательно, термометр показывает 29 °С.

Измерять физические величины в повседневной жизни приходится каждому из вас. Например, чтобы вовремя прийти в школу, приходится измерять время, которое вы тратите на дорогу.

Метеорологи для предсказания погоды измеряют температуру, атмосферное давление, скорость ветра. Врачи при исследовании пациентов измеряют его артериальное давление, температуру, вес. Модельеры, разрабатывая модели одежды, измеряют рост человека, длину рук и пр. Астрономы, изучая планеты, должны знать их температуру, расстояние, на которое они удалены от Земли, и др.

Sqrt в физике: математическая формула и примеры приложений

Sqrt (квадратный корень) является математическим оператором, который встречается во многих физических уравнениях. Формулой для квадратного корня является:

Sqrt(x) = √x

Корень позволяет решать уравнения, в которых необходимо найти значение переменной, возведенной в степень 2. Это может быть полезно в различных областях физики, таких как механика, электричество и магнетизм, оптика и термодинамика.

Примеры приложений Sqrt в физике:

1. Определение длины вектора: В физике вектор представляет собой величину, имеющую как направление, так и величину. Длина вектора вычисляется с использованием квадратного корня. Например, длина вектора, обозначенного как (x, y, z), вычисляется как Sqrt(x^2 + y^2 + z^2).
2. Вычисление силы: В механике Sqrt используется для вычисления силы, действующей на объект. Формула силы может содержать квадратные корни, например, когда вычисляется сила гравитации между двумя объектами.
3. Расчет энергии: Квадратный корень может использоваться для вычисления энергии в различных физических системах. Например, в электрической цепи формула для энергии может содержать квадратный корень.

Как видно из этих примеров, использование квадратного корня в физике позволяет решать различные задачи, связанные с измерением и вычислением физических величин.

Способы извлечения корня

В языке программирования Python 3 существует три способа извлечения корней:

• Использование функции sqrt из стандартной математической библиотеки math.
• Операция возведения в степень **
• Применение функции pow(x, n)

Чтобы воспользоваться первым способом, необходимо вначале импортировать sqrt из модуля math. Это делается с помощью ключевого слова import: . При помощи этой функции можно извлекать только квадратный корень из числа. Приведем пример:

from math import sqrt
x = sqrt(4)
print(x)

2.0

Если же нам нужно вычислить в Python корень квадратный из суммы квадратов, то можно воспользоваться функцией hypot из модуля math. Берется сумма квадратов аргументов функции, из нее получается корень. Аргументов у функции два.

from math import hypot
x = hypot(4,3)
print(x)

5.0

Еще одним, чуть более универсальным методом, будет использование возведения в степень. Известно, что для того, чтобы взять корень n из числа, необходимо возвести его в степень 1/n. Соответственно, извлечение квадратного корня из числа 4 будет выглядеть так:

n = 2
x = 4**(1./n)
print(x)

2.0

Обратите внимание, что в Python 2 необходимо ставить точку после единицы, иначе произойдет целочисленное деление, и 1/n == 0, а не нужной нам дроби. В Python 3 можно не ставить точку.. Последний метод использует функцию pow(value, n)

Эта функция в качестве аргумента value возьмет число, которое необходимо возвести в степень, а второй аргумент будет отвечать за степень числа. Как и в предыдущем методе, необходимо использовать дробь, для того, чтобы получить корень числа

Последний метод использует функцию pow(value, n). Эта функция в качестве аргумента value возьмет число, которое необходимо возвести в степень, а второй аргумент будет отвечать за степень числа. Как и в предыдущем методе, необходимо использовать дробь, для того, чтобы получить корень числа.

x = pow(4, 0.5)
print(x)

2.0

Какой метод быстрее?

Для того, чтобы определить какой же метод предпочтительнее использовать, напишем программу. Замерять время выполнения будем с помощью метода monotonic библиотеки time.

from time import monotonic
from math import sqrt
iterations = 1000000
start = monotonic()
for a in range(iterations):
    x = sqrt(4)
print("sqrt time: {:>.3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
    x = 4 ** 0.5
print("** time: {:>.3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
    x = pow(4, 0.5)
print("pow time: {:>.3f}".format(monotonic() - start) + " seconds")

sqrt time: 0.266 seconds
** time: 0.109 seconds
pow time: 0.453 seconds

Как видно, самое быстрое решение — использовать **. На втором месте метод sqrt, а pow — самый медленный. Правда, метод sqrt наиболее нагляден при вычислении в Python квадратных корней.

Таким образом, если критична скорость, то используем **. Если скорость не критична, а важна читаемость кода, то следует использовать sqrt.

Примеры использования sqrt

Функция sqrt (квадратный корень) широко применяется в физике для решения различных задач, связанных с измерениями и вычислениями. Вот некоторые примеры использования этой функции:

1. Вычисление длины гипотенузы треугольника:

Для нахождения длины гипотенузы прямоугольного треугольника можно использовать теорему Пифагора: a^2 + b^2 = c^2, где a и b – длины катетов, а c – длина гипотенузы. Если известны длины катетов, можно использовать функцию sqrt, чтобы найти значение квадратного корня и получить длину гипотенузы.

2. Вычисление модуля вектора:

Векторы широко используются в физике для описания движения и сил. Модуль вектора – это его длина. Часто комбинируются несколько векторов, и для вычисления общей длины используется функция sqrt.

3. Расчет времени свободного падения:

В физике свободное падение – это падение тела под воздействием только силы тяжести. При вычислении времени свободного падения можно использовать формулу t = sqrt(2h/g), где t – время падения, h – высота падения и g – ускорение свободного падения.

4. Расчет энергии фотона:

Энергия фотона может быть связана с его частотой или длиной волны. В этом случае функция sqrt может использоваться для вычисления энергии, например, энергии фотона света с известной частотой.

Это только некоторые примеры использования функции sqrt в физике. Эта функция является важным инструментом для проведения различных вычислений и анализа данных в физических науках.

Механика: расчет падения свободного тела

В физике существует много различных формул и уравнений, которые помогают решать различные задачи. Одно из таких уравнений используется для расчета падения свободного тела.

Уравнение падения свободного тела выглядит следующим образом:

h = 1/2 * g * t^2

Где:

• h — высота падения тела (в метрах)
• g — ускорение свободного падения (около 9.8 м/с^2)
• t — время падения тела (в секундах)

Данная формула позволяет найти высоту падения тела при известном времени. Например, если у нас есть информация о времени падения тела, то мы можем легко определить высоту, с которой оно упало.

Допустим, у нас есть время падения t = 2 секунды. Подставим это значение в уравнение:

h = 1/2 * 9.8 м/с^2 * (2 секунды)^2

h = 1/2 * 9.8 м/с^2 * 4 секунды^2

h = 1/2 * 9.8 м/с^2 * 4

h = 19.6 метров

То есть, при времени падения равном 2 секундам, высота падения свободного тела будет составлять 19.6 метров.

Такой подход к решению задач связанных с падением тела, позволяет упростить процесс расчетов и получить точные значения высоты падения.

Оптика: расчет фокусного расстояния линзы

Существует несколько способов расчета фокусного расстояния линзы, в зависимости от ее формы и характеристик. Один из простейших способов — использование формулы тонкой линзы:

1/f = (n — 1) * (1/R1 — 1/R2)

где f — фокусное расстояние линзы, n — показатель преломления среды, R1 — радиус кривизны первой поверхности линзы, R2 — радиус кривизны второй поверхности линзы.

Если известны значения n, R1 и R2, то подставив их в формулу, можно определить фокусное расстояние линзы.

Также существуют другие методы расчета фокусного расстояния линзы, например, с помощью определения фокусного расстояния с помощью оптического стола или методом измерения картинка, образующейся при прохождении света через линзу.

Зная фокусное расстояние линзы, можно определить, какой тип линзы использовать для конкретной задачи. Например, положительные линзы (с фокусным расстоянием больше нуля) используются для сбора света и фокусировки его в одной точке, а отрицательные линзы (с фокусным расстоянием меньше нуля) используются для разбирания и рассеивания света.

Видео:Функция y=√x, ее свойства и график. 8 класс.Скачать

Метод нахождения корня извлечением

Метод нахождения корня извлечением, или метод Герона, является одним из классических методов численного анализа, используемых для вычисления квадратного корня из числа.

Основная идея метода Герона заключается в построении последовательности приближений к корню извлечаемого числа и последующем уточнении этой последовательности до заданной точности.

Для применения метода Герона необходимо задать начальное приближение к корню извлекаемого числа. Чаще всего начальное приближение выбирают равным половине извлекаемого числа.

После задания начального приближения вычисляют следующее приближение с помощью формулы:

1. Положим $x_0$ равным начальному приближению.
2. Положим $x_1$ равным среднему арифметическому между $x_0$ и $\frac{A}{x_0}$: $$x_1 = \frac{1}{2} \left(x_0 + \frac{A}{x_0} ight)$$
3. Положим $x_2$ равным среднему арифметическому между $x_1$ и $\frac{A}{x_1}$: $$x_2 = \frac{1}{2} \left(x_1 + \frac{A}{x_1} ight)$$
4. Продолжаем вычислять приближения до достижения необходимой точности или заданного количества итераций.

В результате применения метода Герона мы получаем последовательность приближений, которая приближается к корню извлекаемого числа с заданной точностью.

Основное преимущество метода Герона заключается в том, что он сходится очень быстро. Параметры метода, такие как начальное приближение и точность, должны быть выбраны с учетом конкретной задачи.

Квадратные уравнения

a*x^2 + b*x + c = 0,

• где a, b и c — это коэффициенты уравнения.
• Квадратный корень (sqrt) используется для нахождения решений таких уравнений.
• Корни квадратного уравнения можно найти с помощью формулы дискриминанта:

D = b^2 — 4*a*c

• Если D больше нуля, то уравнение имеет два различных корня:
  • x1 = (-b + sqrt(D))/(2*a),
  • x2 = (-b — sqrt(D))/(2*a).
• Если D равно нулю, то уравнение имеет один корень:

  x = -b/(2*a).

• Если D меньше нуля, то уравнение не имеет действительных корней, а имеет два комплексных корня:
  • x1 = (-b + i*sqrt(|D|))/(2*a),
  • x2 = (-b — i*sqrt(|D|))/(2*a).

Квадратные уравнения широко применяются в математике, физике, инженерии и других областях, где требуется решение задач с квадратной зависимостью.

Как определить среднюю квадратичную скорость движения молекул

Определение 2

Средней квадратичной скоростью молекул идеального газа называют величину равную квадратному корню из среднего арифметического величины квадратов скоростей каждой из молекул.

Средняя скорость молекул равна:

Если обе её части возвести в квадрат и проинтегрировать, то получим выражение:

\

Ещё одно выражение для среднеквадратичной скорости:

\

Именно она присутствует в уравнении, именуемом основным уравнением молекулярно-кинетической теории

P = (1/3)nm*<Vкв>

Где n – концентрация молекул, которая вычисляется делением их общего числа на объём.

Пример. 1.

Рассмотрим простейший случай, чтобы использование интегрирования не затруднило понимание сути явления и помогло лучше понять материал. Вычислим как меняется средняя скорость движения молекул в идеальном газе при линейном увеличении его давления. График следующий:

Где P — давление, ρ — плотность

Напомним, что средняя скорость частиц:

\

Если присмотреться к представленному графику, то можно заметить, что P приблизительно равно ρ‎. Эти две величины можно связать соотношением

P=C*ρ‎

Где С – некоторая постоянная величина, константа.

Далее считаем m= ρ/n, p = n*k*T = C* ρ. Отсюда следует, что k*T = (C*ρ)/n.

Нужно лишь подставить эти значения в формулу для средней скорости:

\[V c p=\sqrt{8 \mathrm{kT} / \pi \mathrm{m}}=\sqrt{(8 \mathrm{C} \rho / \pi \mathrm{n})(\mathrm{n} / \rho)}=\sqrt{8 \mathrm{C} / \pi}\]

В полученном выражении нет ни одной переменной величины, т. е. при увеличении давления, вопреки ожиданиям, скорость оказалась неизменной.

Ответ: В процессе, который был дан нам на графике, при увеличении давления средняя скорость молекул никак не меняется.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Пример. 2.

Определим среднюю квадратичную скорость молекул газа при условии, что нам известны его давление (P), молярная масса (M) и концентрация частиц (n).

Воспользуемся формулой:

\

Также нам потребуется уравнение Менделеева-Клайперона

Здесь мы воспользовались тем, что:

m/μ = N/N_a

PV = (m/μ)*RT = (N/N_a)*RT

Если обе части этого уравнения поделить на V и принять во внимание, что

(N/V) = n, то можно получить

P = (n/N_a)*RT. Отсюда находим, что RT = (p*N)/n

Если мы это подставим в выражение для среднеквадратичной скорости \[\left\langle V_{K B}\right\rangle=\sqrt{3 \mathrm{kT} / \mathrm{m}_{0}}=\sqrt{3 \mathrm{RT} / \mu}\], получим, что средняя квадратичная скорость движения молекул газа: \[\left\langle V_{K B}\right\rangle=\sqrt{\left(3 \rho N_{a}\right) /(\mu \mathrm{n})}\]

Ответ: Формула средней квадратичной скорости молекул исходя из данный нам условий следующая:

\[\left\langle V_{K B}\right\rangle=\sqrt{\left(3 \rho N_{a}\right) /(\mu \mathrm{n})}\]

Что такое арифметический квадратный корень

А почему же число  \( a\) (число под корнем) должно быть обязательно неотрицательным?

Например, чему равен \( \sqrt{-9}\)?

Так-так, попробуем подобрать. Может, три?

Проверим: \( {{3}^{2}}=9\), а не \( -9\).

Может, \( \left( -3 \right)\)? 

Опять же, проверяем: \( {{\left( -3 \right)}^{2}}=9\).

Ну что же, не подбирается?

Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число! Это надо запомнить!

Однако ты наверняка уже заметил, что не только число под корнем должно быть неотрицательным, но и само значение тоже должно быть неотрицательным!

 Ведь в определении сказано, что «квадратным корнем из числа\( a\)называется такое неотрицательное число, квадрат которого равен\( a\)».

Но подождите!  В самом начале мы разбирали пример \( {{x}^{2}}=4\) и один из ответов был отрицательным числом! 

 Мы подбирали числа, которые можно возвести в квадрат и получить при этом \( \displaystyle 4\). Ответом были \( \displaystyle 2\) и \( \displaystyle -2\)

А тут говорится, что квадратным корнем должно быть «неотрицательное число»! Почему?

Такой вопрос вполне уместен. Здесь необходимо просто разграничить понятия квадратного уравнения и арифметического квадратного корня.

К примеру, \( \displaystyle {{x}^{2}}=4\) (квадратное уравнение) не равносильно выражению \( x=\sqrt{4}\) (арифмитический квадратный корень).

Из \( {{x}^{2}}=4\) следует, что

\( \left| x \right|=\sqrt{4}\), то есть \( x=\pm \sqrt{4}=\pm 2\) или \( {{x}_{1}}=2\); \( {{x}_{2}}=-2\)

(не помнишь почему так? Почитай тему «Модуль числа»!)

А из \( x=\sqrt{4}\) следует, что \( x=2\).

Конечно, это очень путает, но это необходимо запомнить, что знаки «плюс-минус» являются результатом решения квадратного уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.

В наше квадратное уравнение подходит как \( 2\), так и \( x=-2\).

Способы вычисления среднего значения

Среднее значение — это показатель, который используется для определения типичного значения в наборе данных. В физике среднее значение часто используется для вычисления средней скорости, среднего времени реакции и других параметров.

Существует несколько способов вычисления среднего значения:

1. Арифметическое среднее — самый распространенный способ вычисления среднего. Для его определения необходимо сложить все значения в наборе и разделить их на количество значений. Например, для набора чисел 5, 7, 10 арифметическое среднее будет равно (5 + 7 + 10) / 3 = 7.
2. Среднее гармоническое — это обратное арифметическому среднему. Для его определения необходимо сложить все обратные значения в наборе, разделить их на количество значений и затем взять обратное значение полученной суммы. Например, для набора чисел 2, 4, 8 среднее гармоническое будет равно 3 / ((1/2) + (1/4) + (1/8)) = 4.
3. Среднее квадратическое — это показатель, который вычисляется как квадратный корень из среднего значения квадратов всех значений в наборе. Для его определения необходимо возвести каждое значение в наборе в квадрат, сложить полученные значения, разделить их на количество значений и затем извлечь квадратный корень из полученной суммы. Например, для набора чисел 2, 4, 6 среднее квадратическое будет равно sqrt((2^2 + 4^2 + 6^2) / 3) ≈ 4.27.

Выбор способа вычисления среднего значения зависит от конкретной задачи и типа данных, с которыми вы работаете

Важно помнить, что каждый способ имеет свои особенности и может давать разные результаты в разных ситуациях

История возникновения

Первые упоминания о корне числа относятся к древнегреческой математике, в частности, к диалогам Платона и Евклида.

В Древнем Египте примерно в 1600 году до нашей эры были разработаны методы нахождения квадратных корней. Древние египтяне использовали геометрический подход и строили прямоугольники, стороны которых соответствовали числам, корня которых они искали. Затем они пытались найти сторону квадрата, равную этому корню.

Однако идея использования символа для обозначения корня возникла значительно позже. В 16 веке итальянский математик Раффаеле Бомбелли предложил использовать латинскую букву «r» снизу и над числом, чтобы обозначить корень.

На протяжении веков знак корня развивался и становился все более удобным и компактным. В 16-17 веках введение знака корня было главным шагом в развитии математики и алгебры. В настоящее время знак корня широко используется во всех областях математики и играет важную роль в решении различных задач.

Применение sqrt в физике

В физике функция sqrt (корень квадратный) широко используется для решения различных задач и расчета значений.

Прежде всего, в физике sqrt применяется для нахождения длины стороны треугольника по формуле Пифагора. Если известны длины двух сторон треугольника, можно использовать sqrt для определения длины третьей стороны:

С = sqrt(A^2 + B^2), где С — длина третьей стороны, A и B — известные длины сторон треугольника.

Также sqrt применяется для нахождения среднеквадратичного значения (средней величины) величин с различными значениями. Например, в физике часто используется среднеквадратичное значение для оценки колебаний, шума или энергии:

Среднеквадратичное значение (RMS) = sqrt((x1^2 + x2^2 + … + xn^2) / n), где x1, x2, …, xn — значения, n — количество значений.

Таким образом, sqrt является важной функцией в физике, позволяющей решать задачи и рассчитывать значения, опираясь на математические принципы

Вычисление корня известной величины

Для вычисления корня известной величины можно использовать функцию sqrt во многих языках программирования. Например, в языке Python вы можете написать:

import math
x = 16
sqrt_x = math.sqrt(x)
print(sqrt_x)

Результатом выполнения кода будет число 4, так как корень квадратный из 16 равен 4.

Использование корня в физике может быть полезным, например, при нахождении скорости тела при однородном движении. Формула для вычисления скорости v может быть записана следующим образом:

v = sqrt(2 * a * s)

где a — ускорение тела, s — пройденное расстояние. Таким образом, если ускорение и расстояние известны, можно легко вычислить скорость, используя функцию sqrt.

Решение квадратных уравнений

ax2 + bx + c = 0

Здесь a, b и c – это коэффициенты, где a не равно нулю. Чтобы найти решения квадратного уравнения, можно использовать формулу дискриминанта:

D = b2 — 4ac

Если дискриминант больше нуля (D > 0), то уравнение имеет два различных корня. Если дискриминант равен нулю (D = 0), то уравнение имеет один корень. Если дискриминант меньше нуля (D < 0), то уравнение не имеет решений в вещественных числах.

Решение квадратного уравнения можно получить с помощью формулы:

x_1,2 = (-b ± sqrt(D)) / (2a)

Здесь x_1,2 – это решения уравнения, а sqrt(D) – квадратный корень из дискриминанта.

Например, рассмотрим уравнение x2 — 5x + 6 = 0. Здесь a = 1, b = -5 и c = 6. Для нахождения решений подставим значения в формулу дискриминанта:

D = (-5)2 — 4 * 1 * 6 = 25 — 24 = 1

Так как дискриминант больше нуля, уравнение имеет два различных корня. Теперь найдем значения решений:

x₁ = (-(-5) + sqrt(1)) / (2 * 1) = (5 + 1) / 2 = 3

x₂ = (-(-5) — sqrt(1)) / (2 * 1) = (5 — 1) / 2 = 2

Таким образом, решения данного квадратного уравнения равны x₁ = 3 и x₂ = 2.

Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Запись иррациональных чисел с помощью квадратного корня

А теперь попробуй решить такое уравнение \( {{x}^{2}}=3\).

Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?

Начнем с самого начала – с нуля: \( {{0}^{2}}=0\) – не подходит.

Двигаемся дальше \( \displaystyle x=1\); \( \displaystyle {{1}^{2}}=1\) – меньше трех, тоже отметаем.

А что если \( \displaystyle x=2\)? 

Проверим: \( \displaystyle {{2}^{2}}=4\) – тоже не подходит, т.к. это больше трех.

С отрицательными числами получится такая же история.

И что же теперь делать? Неужели перебор нам ничего не дал?

Совсем нет, теперь мы точно знаем, что ответом будет некоторое число между \( \displaystyle 1\) и \( \displaystyle 2\), а также между \( \displaystyle -2\) и \( \displaystyle -1\).

Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными.

И что дальше?

Давай построим график функции \( \displaystyle y={{x}^{2}}\) и отметим на нем решения.

Попробуем обмануть систему и получить ответ с помощью калькулятора (как мы это делали в начале)!

Извлечем корень из \( \displaystyle 3\), делов-то!

Ой-ой-ой, выходит, что \( \sqrt{3}=1,732050807568\ldots \) Такое число никогда не кончается.

Как же такое запомнить, ведь на экзамене калькулятора не будет!?

Все очень просто, это и не надо запоминать, необходимо помнить (или уметь быстро прикинуть) приблизительное значение. \( \sqrt{3}\) и \( -\sqrt{3}\) уже сами по себе ответы.

В каких задачах можно использовать функцию корень из х?

Функция корень из х имеет широкое применение в различных областях математики и естественных наук. Она может быть использована для решения следующих задач:

1. Моделирование физических процессов Функция корень из х может быть использована для моделирования различных физических явлений, таких как движение тела, распространение звука, электромагнитные поля и т.д. В этих задачах функция корень из х помогает описать зависимость между переменными и предсказать результаты экспериментов.

2. Решение уравнений и систем уравнений Функция корень из х может быть использована для решения уравнений и систем уравнений, в которых присутствуют квадратные корни. Она помогает найти значения переменных, для которых уравнения выполняются. Такие задачи встречаются в различных областях, включая физику, экономику, инженерные науки и другие.

3. Геометрия и тригонометрия Функция корень из х может быть использована для решения геометрических и тригонометрических задач. Например, она может быть использована для вычисления расстояния между двумя точками в пространстве, определения площади треугольника, нахождения длины стороны прямоугольника и т.д.

4. Анализ данных Функция корень из х может быть использована для анализа данных. Например, она может быть использована для вычисления среднеквадратического отклонения, корреляции или других статистических метрик. Такой анализ помогает понять закономерности в данных, выявить аномалии и сделать предсказания.