Алгебра

Расстояние между точками в пространстве, формула.

Введем прямоугольную систему координат Оxyz
в пространстве. Получим формулу для нахождения расстояния от точки до точки .

В общем случае, точки А
и В
не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки А
и В
плоскости, перпендикулярные координатным осям Ох
, Оу
и Oz
. Точки пересечения этих плоскостей с координатными осями дадут нам проекции точек А
и В
на эти оси. Обозначим проекции .

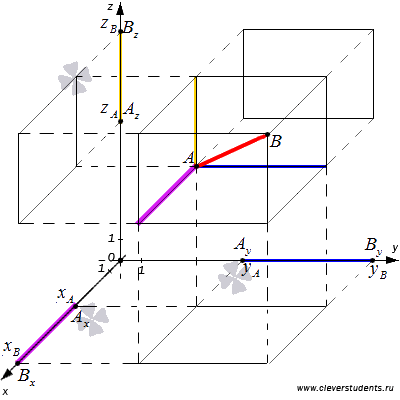
Искомое расстояние между точками А
и В
представляет собой диагональ прямоугольного параллелепипеда, изображенного на рисунке. По построению, измерения этого параллелепипеда равны и . В курсе геометрии средней школы было доказано, что квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений, поэтому, . Опираясь на информацию первого раздела этой статьи, мы можем записать следующие равенства , следовательно,
откуда получаем формулу для нахождения расстояния между точками в пространстве
.

Эта формула также справедлива, если точки А
и В

• совпадают;
• принадлежат одной из координатных осей или прямой, параллельной одной из координатных осей;
• принадлежат одной из координатных плоскостей или плоскости, параллельной одной из координатных плоскостей.

Преобразование выражений с модулями

Модуль, входящий в выражение, можно рассматривать как полноценный множитель. Его можно сокращать и выносить за скобки. Если модуль входит в многочлен, то его можно сложить с подобным ему модулем.

Как и у обычного буквенного множителя, у модуля есть свой коэффициент. Например, коэффициентом модуля |x| является 1, а коэффициентом модуля −|x| является −1. Коэффициентом модуля 3|x+1| является 3, а коэффициентом модуля −3|x+1| является −3.

Пример 1. Упростить выражение |x| + 2|x| − 2x + 5y и раскрыть модуль в получившемся выражении.

Решение

Выражения|x| и 2|x| являются подобными членами. Слóжим их. Остальное оставим без изменений:

Раскроем модуль в получившемся выражении. Если x ≥ 0, то получим 3x − 2x + 5y, откуда x + 5y.

Если x < 0, то получим −3x − 2x + 5y, откуда −5x + 5y. Вынесем за скобки множитель −5, получим −5(x − y)

В итоге имеем следующее решение:

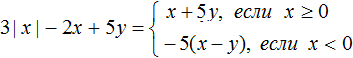
Пример 2. Раскрыть модуль в выражении: −|x|

Решение

В данном случае перед знаком модуля стоит минус. Его можно понимать как минус единицу перед знаком модуля. Если x ≥ 0, то модуль раскроется со знаком плюс, и тогда исходное выражение примет вид −x

Если x < 0, то модуль раскроется со знаком минус, и тогда исходное выражение примет вид −(−x) откуда получим просто x

Модуль комплексного числа

Дадим Определение модуля комплексного числа. Пусть нам дано Комплексное число, записанное в алгебраической форме , где x и y – некоторые действительные числа, представляющие собой соответственно действительную и мнимую части данного комплексного числа z, а – мнимая единица.

Модулем комплексного числа z=x+i·y называется арифметический квадратный корень из суммы квадратов действительной и мнимой части данного комплексного числа.

Модуль комплексного числа z обозначается как , тогда озвученное определение модуля комплексного числа может быть записано в виде .

Данное определения позволяет вычислить модуль любого комплексного числа в алгебраической форме записи. Для примера вычислим модуль комплексного числа . В этом примере действительная часть комплексного числа равна , а мнимая – минус четырем. Тогда по определению модуля комплексного числа имеем .

Геометрическую интерпретацию модуля комплексного числа можно дать через расстояние, по аналогии с геометрической интерпретацией модуля действительного числа.

Модуль комплексного числа z – это расстояние от начала комплексной плоскости до точки, соответствующей числу z в этой плоскости.

По теореме Пифагора расстояние от точки O до точки с координатами (x, y) находится как , поэтому, , где . Следовательно, последнее определение модуля комплексного числа согласуется с первым.

Данное определение также позволяет сразу указать, чему равен модуль комплексного числа z, если оно записано в тригонометрической форме как Или в показательной форме . Здесь . Например, модуль комплексного числа Равен 5 , а модуль комплексного числа Равен .

Можно также заметить, что произведение комплексного числа На комплексно сопряженное число Дает сумму квадратов действительной и мнимой части. Действительно, . Полученное равенство позволяет дать еще одно определение модуля комплексного числа.

Модуль комплексного числа z – это арифметический квадратный корень из произведения этого числа и числа, комплексно сопряженного с ним, то есть, .

В заключение отметим, что все свойства модуля, сформулированные в соответствующем пункте, справедливы и для комплексных чисел.

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера»

Модуль числа — это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности.

А между тем она проста как апельсин. Но чтобы ее понять, давай сначала разберемся зачем нужен модуль.

Вот смотри, ситуация первая.

В жизни, часто встречаются ситуации, Где отрицательные числа не имеют никакого практического смысла.

Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, неважно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными

Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.

Ситуация вторая.

Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.

И что, можно идти судиться с компанией Lays, если они тебе недовесили?

Нет. Потому что Lays устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» — это и есть модуль.

Ситуация третья.

В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч — это и есть модуль.

А вообще для простоты запомни, что модуль это Расстояние от нуля в любую сторону.

Ну вот, ты уже почти все знаешь. Давай теперь подробнее.

Символы вероятности и статистики

Символ	Название символа	Значение / определение	пример
P ( А )	функция вероятности	вероятность события A	P ( A ) = 0,5
P ( A ⋂ B )	вероятность пересечения событий	вероятность того, что событий A и B	P ( A ⋂ B ) = 0,5
P ( A ⋃ B )	вероятность объединения событий	вероятность того, что событий A или B	P ( A ⋃ B ) = 0,5
P ( A | B )	функция условной вероятности	вероятность события A данное событие B произошло	P ( A | B ) = 0,3
f ( x )	функция плотности вероятности (pdf)	P ( a ≤ x ≤ b ) = ∫ f ( x ) dx
F ( х )	кумулятивная функция распределения (cdf)	F ( х ) = Р ( Х ≤ х )
μ	Средняя численность населения	среднее значение совокупности	μ = 10
E ( X )	ожидаемое значение	ожидаемое значение случайной величины X	E ( X ) = 10
E ( X | Y )	условное ожидание	ожидаемое значение случайной величины X с учетом Y	E ( X | Y = 2 ) = 5
var ( X )	отклонение	дисперсия случайной величины X	var ( X ) = 4
σ 2	отклонение	дисперсия значений совокупности	σ 2 = 4
std ( X )	стандартное отклонение	стандартное отклонение случайной величины X	std ( X ) = 2
σ X	стандартное отклонение	значение стандартного отклонения случайной величины X	σ X = 2
	медиана	среднее значение случайной величины x
cov ( X , Y )	ковариация	ковариация случайных величин X и Y	cov ( X, Y ) = 4
корр ( X , Y )	корреляция	корреляция случайных величин X и Y	корр ( X, Y ) = 0,6
ρ X , Y	корреляция	корреляция случайных величин X и Y	ρ X , Y = 0,6
∑	суммирование	суммирование — сумма всех значений в диапазоне ряда
∑∑	двойное суммирование	двойное суммирование
Пн	Режим	значение, которое чаще всего встречается в популяции
MR	средний диапазон	MR = ( x макс + x мин ) / 2
Мкр	медиана выборки	половина населения ниже этого значения
Q 1	нижний / первый квартиль	25% населения ниже этого значения
2 квартал	медиана / второй квартиль	50% населения ниже этого значения = медиана выборки
3 квартал	верхний / третий квартиль	75% населения ниже этого значения
х	выборочное среднее	среднее / среднее арифметическое	х = (2 + 5 + 9) / 3 = 5,333
с 2	выборочная дисперсия	оценщик дисперсии выборки населения	s 2 = 4
с	стандартное отклонение выборки	Оценка стандартного отклонения выборки населения	s = 2
z x	стандартная оценка	z x = ( x — x ) / s x
X ~	распределение X	распределение случайной величины X	X ~ N (0,3)
N ( μ , σ 2 )	нормальное распределение	гауссово распределение	X ~ N (0,3)
U ( а , б )	равномерное распределение	равная вероятность в диапазоне a, b	Х ~ U (0,3)
ехр (λ)	экспоненциальное распределение	f ( x ) = λe — λx , x ≥0
гамма ( c , λ)	гамма-распределение	f ( x ) = λ cx c-1 e — λx / Γ ( c ), x ≥0
χ 2 ( к )	распределение хи-квадрат	f ( x ) = x k / 2-1 e — x / 2 / (2 k / 2 Γ ( k / 2))
F ( k 1 , k 2 )	F распределение
Корзина ( n , p )	биномиальное распределение	f ( k ) = n C k p k (1 -p ) nk
Пуассон (λ)	распределение Пуассона	е ( К ) знак равно λ К е — λ / К !
Геом ( p )	геометрическое распределение	f ( k ) = p (1 -p ) k
HG ( N , K , n )	гипергеометрическое распределение
Берн ( p )	Распределение Бернулли

Функция y = sign(x)

Функция y = sign(x) обозначает знак числа x и определяется следующим образом:

y = sign(x) = {
-1, x 0
}

Свойства функции y = sign(x):

Функция является ступенчатой и постоянна на интервалах (-∞, 0), (0, +∞).
Функция не является непрерывной и не дифференцируемой в точке x = 0.

Построение графика функции y = sign(x):
График функции y = sign(x) представляет собой две горизонтальные линии: y = -1 на интервале (-∞, 0) и y = 1 на интервале (0, +∞). В точке x = 0 график функции имеет разрыв.

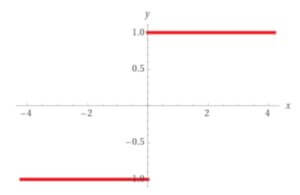
Примеры применения функции y = sign(x):

Использование в физике для определения направления силы или скорости.
Использование в анализе данных для определения направления изменения значения переменной.

В заключении можно отметить, что функции y = |x|, y = , y = {x} и y = sign(x) являются важными и широко используемыми математическими функциями. Знание и понимание свойств их графиков позволяет более глубоко понимать многие явления и процессы, которые возникают в нашей жизни и в различных областях знаний.

Неравенство треугольника

В геометрии у треугольников есть замечательное свойство, заключающееся в том, что длина любой стороны треугольника меньше суммы длин двух оставшихся. Это свойство называется «неравенством треугольника».

Например, пусть у нас есть какой-то треугольник ABC. Тогда длина стороны AC меньше суммы длин сторон AB и BC:

AC≤AB+BCAC \leq AB + BCAC≤AB+BC

В некоторых учебниках по геометрии различают сам отрезок (например, AB) и его длину ∣AB∣|AB|∣AB∣. Если пользоваться этими обозначениями, неравенство треугольника примет следующий вид:

∣AC∣≤∣AB∣+∣BC∣|AC| \leq |AB| + |BC|∣AC∣≤∣AB∣+∣BC∣

Оказывается, в алгебре есть очень похожее неравенство, но связано оно не с отрезками и их длинами, а с числами и их модулями. Из-за внешнего сходства это неравенство тоже называют неравенством треугольника.

С геометрией и треугольниками все понятно. А в чем смысл неравенства треугольника с модулями? А смысл в том, что оно задает максимально возможный результат, который можно получить с помощью сложения или вычитания двух чисел.

Например, пусть у нас есть два числа: 2 и -3. Какой максимальный результат можно получить из этих двух чисел, пользуясь только сложением и вычатнием? Проверим все 4 возможных варианта напрямую:

2+(−3)=−3+2=−12−(−3)=5−3−2=−52 + (-3) = -3 + 2 = -1 \\ 2 — (-3) = 5 \\ -3 — 2 = -52+(−3)=−3+2=−12−(−3)=5−3−2=−5

Видим, что максимальное значение равно 5. Такое же значение получаем и по доказанному выше неравенству. Итак, максимально возможное значение равно сумме модулей этих двух чисел. На самом деле, это кажется вполне логичным.

Есть также похожее неравенство, но с разностью модулей. Его называют обратным неравенством треугольника.

По аналогии с предыдущим доказанным неравенством, обратное неравенство треугольника дает нам минимальное возможное значение, которое можно получить, рассматривая сумму или разность двух чисел.

Оба доказанных неравенства можно объединить в одно цепное. Так его проще запомнить и использовать:

∣x∣−∣y∣≤∣x±y∣≤∣x∣+∣y∣|x| — |y| \leq |x \pm y| \leq |x| + |y|∣x∣−∣y∣≤∣x±y∣≤∣x∣+∣y∣

Основные свойства модуля

Вот мы и приблизились к первому свойству модуля:

Модуль не может быть выражен отрицательным числом.

То есть, если – число положительное, то его модуль будет равен этому же числу:

Если extMathbf,»> то.

Если – отрицательное число, то его модуль равен противоположному числу:

А если? Ну, конечно! Его модуль также равен :

Из этого следует, что модули противоположных чисел равны, то есть:

А теперь потренируйся:

Ответы: 9; 3; 16; 8; 17.

Довольно легко, правда?

А если перед тобой вот такое число:

Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.

Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль :

• если значение выражения больше нуля, то просто выносим его из-под знака модуля, если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.

Ну что, попробуем? Оценим :

Если, то какой знак имеет? Ну конечно, !

А, значит, знак модуля раскрываем, меняя знак у выражения:

Разобрался? Тогда попробуй сам:

Какими же ещё свойствами обладает модуль?

А что, если нам нужно разделить два числа (выражения) под знаком модуля?

Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:

При условии, что (так как на ноль делить нельзя).

Стоит запомнить ещё одно свойство модуля:

Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:

Почему так? Всё очень просто!

Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное. Допустим, что числа и оба положительные. Тогда левое выражение будет равно правому выражению.

Рассмотрим на примере:

Выражения также равны, если оба числа отрицательны:

Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:

Вроде с этим свойством все ясно, рассмотрим еще парочку полезных свойств модуля.

Что если перед нами такое выражение:

Что мы можем сделать с этим выражением? Значение x нам неизвестно, но зато мы уже знаем, что, а значит.

Число больше нуля, а значит можно просто записать:

Вот мы и пришли к другому свойству, которое в общем виде можно представить так:

А чему равно такое выражение:

Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак?

Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему степень и ее свойства. И что же получается? А вот что:

Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:

Ну, и почему сомнения? Действуем смело!

Во всем разобрался? Тогда вперед тренироваться на примерах!

1. Найдите значение выражения, если.

2. У каких чисел модуль равен?

3. Найдите значение выражений:

Если не все пока ясно и есть затруднения в решениях, то давай разбираться:

Итак, подставим значения и в выражение

Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное имеют два числа: и.

Все уловил? Тогда пора перейти к более сложному!

Попробуем упростить выражение

Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.

Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).

Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.

Получается, значение первого выражения под модулем.

, следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.

Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:

Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:

Во втором случае просто отбросим знак модуля:

Упростим данное выражение целиком:

Ориентация и рука

В двух измеренийх

правой руки

Фиксация или выбор оси x определяет ось y до направления. А именно, ось y обязательно представляет собой , перпендикуляр оси x через точку, отмеченную 0 на оси x. Но есть выбор, какую из двух половинных линий на перпендикуляре обозначить как положительную, а какую как отрицательную. Каждый из этих двух вариантов определяет различную ориентацию (также называемую хиральностью) декартовой плоскости.

Обычный способ ориентирования плоскости с положительной осью X, направленной вправо, и положительной осью Y, направленной вверх (причем ось X является «первой», а ось Y — «второй» ось) признанной положительной или стандартной ориентацией, также называемой правой ориентацией.

Обычно используемый мнемоник для определения положительной ориентации — это правило правой руки. Поместите несколько сжатую правую руку на плоскость с большим пальцем вверх, указав от оси x к оси y в положительно ориентированной системе координат.

Другой способ ориентировать — это следовать правилам левой руки, положив левую руку на плоскость большим пальцем вверх.

Когда большой палец направлен от начала оси вдоль оси в положительную сторону, кривизна пальцев указывает на положительное вращение вдоль оси.

Независимо от правил, используемой для ориентации плоскости, вращение системы координат сохранит ориентацию. Переключение любых осей изменит ориентацию на обратную, но переключение оставит ориентацию сохранить.

В трех измеренийх

После задания осей x и y они определяют линию , вдоль которой должна лежать ось z, но есть две возможные ориентации для этой линии. Возникающие в результате двух возможных систем координат называются «правая» и «левая». Стандартная ориентация, при которой плоскость xy горизонтальна, а ось z направлена ​​вверх (а ось x и y образуют положительно ориентированную двумерную систему координат в плоскости xy, если смотреть сверху на плоскость xy) называется правосторонней или положительной .

. Название происходит от правой руки. Если указательный палец правой руки направлен вперед, средний палец согнут под прямым углом к ​​нему, а большой палец расположен под прямым углом для обоих пальца указывает относительную ориентацию осей x, y и z в правой системе. Большой палец указывает ось x, указательный палец — ось y, средний палец — ось z. И, если то же самое проделать левой рукой, получится наоборот левосторонняя система.

На рисунке 7 изображены левая и правая системы координат. Отображение трехмерного объекта на двухмерном изображении показано на рисунке. Ось, направленная вниз (и вправо), также есть для направления на наблюдателя, тогда как «средняя» ось для направления в сторону от наблюдателя. Красный круг параллелен горизонтальной плоскости xy и указывает вращение от оси x к оси y (в обоих случаях). Следовательно, красная стрелка проходит перед осью z.

Рисунок 8 — еще одна попытка изобразить правую систему координат. Опять же, возникает неоднозначность, вызванная проецированием трехмерной системы координат на плоскость. Многие наблюдатели видят рисунок 8 как «переворот» между выпуклым кубом и вогнутым «углом». Это соответствует двум возможным ориентациям пространства. Если смотреть на фигуру как выпуклую, это дает левую систему координат. Таким образом увидеть «правильный» способ просмотра рисунка 8 — представить ось x как указывающую в сторону наблюдателя и, таким образом, в изогнутом углу.

Прямоугольная декартова система координат

Французский математик Рене Декарт предложил использовать математические вычисления вместо геометрических построений. Так появился координатный метод, о котором мы сейчас и поговорим.

Координатами можно назвать номер таблицы в полосе, широту и долготу на географической карте, расположение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем объект набором букв, цифр или других символов, тем самым мы устанавливаем его координаты.

Прямоугольная система координат — это система координат, изобретенная математиком Рене Декартом, также называемая «декартовой системой координат». Представляет собой два взаимно перпендикулярных луча с началом в точке их пересечения.

Чтобы узнать координаты, нужны ориентиры, с которых начнется обратный отсчет. На одном уровне эту роль будут играть две числовые оси.

Рисунок начинается с горизонтальной оси, называемой осью абсцисс, и обозначается латинской буквой x (x). Ось пишется так: Ох. Положительное направление оси абсцисс указано стрелкой слева направо.

Затем проводится вертикальная ось, которая называется осью y и обозначается y (зазор). Ось Oy зарегистрирована. Положительное направление оси ординат показано стрелкой, направленной снизу вверх.

Оси взаимно перпендикулярны, а значит, угол между ними составляет 90 °. Точка пересечения является исходной точкой для каждой из осей и обозначается как: O. Исходная точка делит оси на две части: положительную и отрицательную.

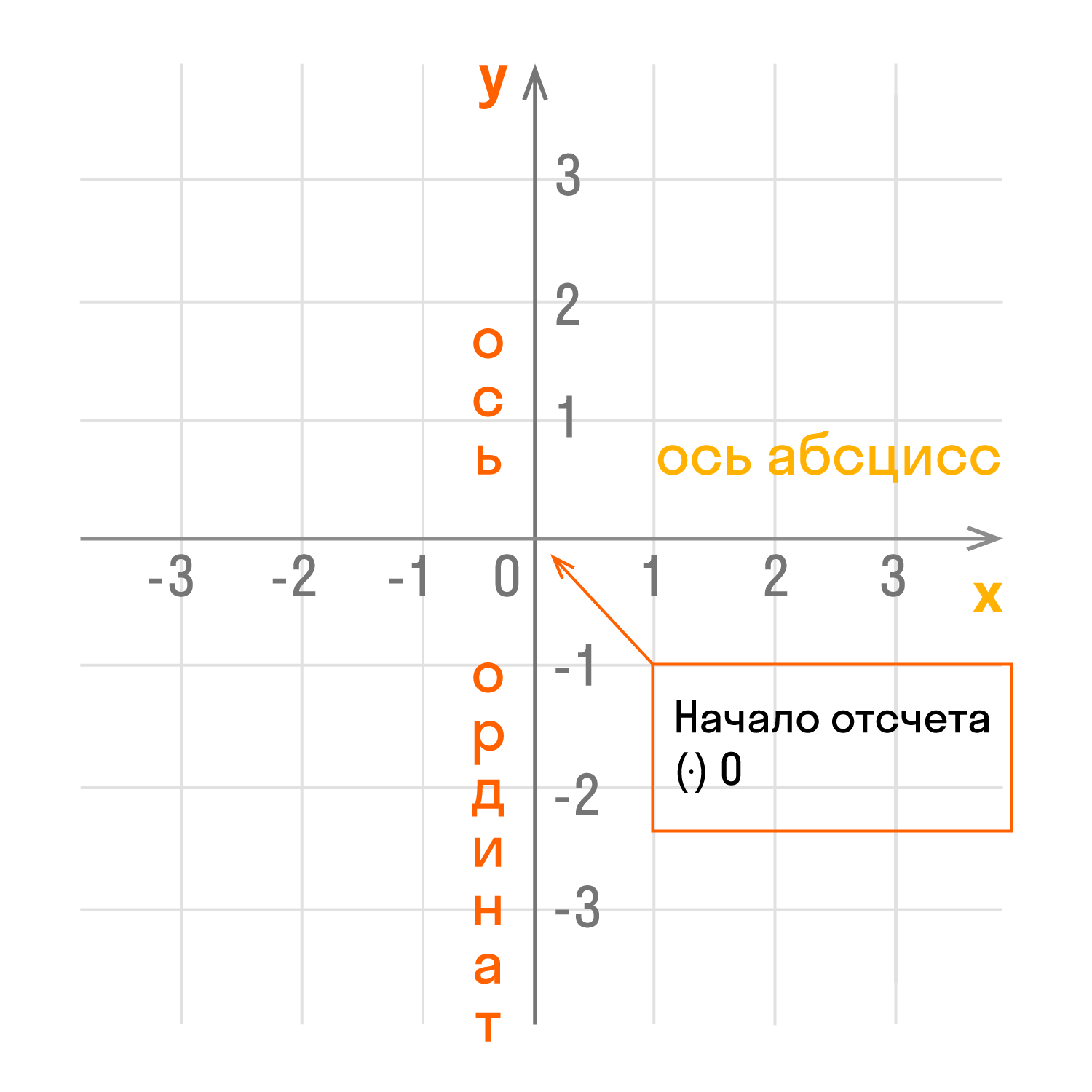
• Оси координат — это прямые линии, образующие систему координат.
• Ось абсцисс Ox — горизонтальная ось.
• Ось ординат Oy — это вертикальная ось.
• Координатная плоскость — плоскость, в которой расположена система координат. Обозначается это так: x0y.
• Единичный сегмент — это величина, которая принимается за единицу в геометрических конструкциях. В декартовой системе координат на каждой оси нанесена единичная линия. Длина сегмента показывает, сколько раз отдельный сегмент и его части помещаются в данный сегмент.

Единичные линии расположены слева и справа от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy расположены слева или справа, на оси Oy — под ней. Чаще всего единичные сегменты двух осей соответствуют друг другу, но есть задачи, в которых они не равны.

Оси координат делят плоскость на четыре угла — четыре четверти координат.

Каждая из согласованных кварталов имеет свой номер и обозначение в виде римской цифры. Обратный отсчет идет против часовой стрелки:

• верхний правый угол — первая четверть I;
• левый верхний угол — вторая четверть II;
• левый нижний угол — третья четверть III;
• нижний правый угол — четвертая четверть IV;

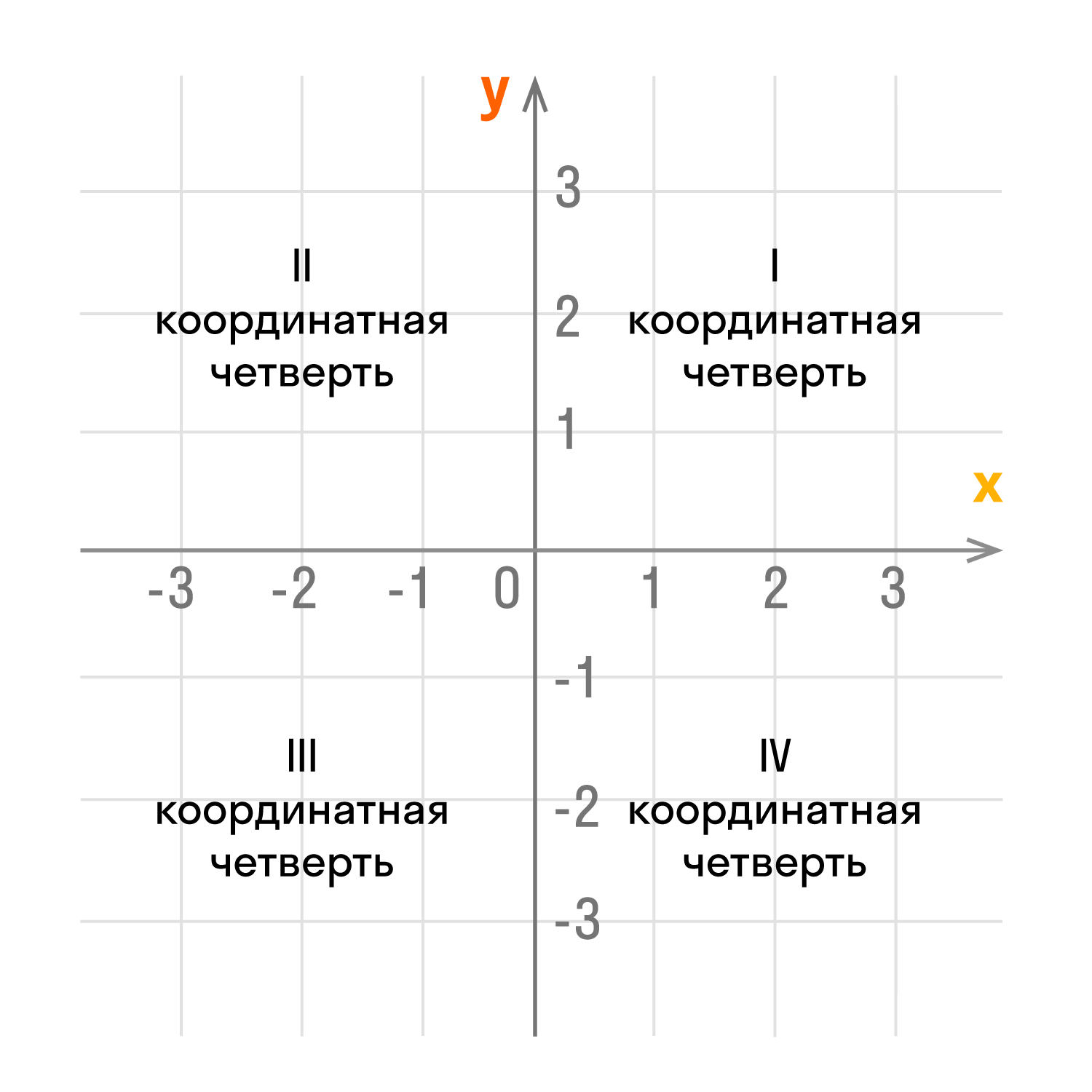
Чтобы узнать координаты точки в прямоугольной системе координат, необходимо опустить перпендикуляр от точки к каждой оси и посчитать количество единичных сегментов от нулевой отметки до освобожденного перпендикуляра. В скобках записаны координаты, первая по оси Ox, вторая по оси Oy.

Согласованные правила:

• Если обе координаты положительны, точка находится в первой четверти координатной плоскости.
• Если координата x отрицательна, а координата y положительна, то точка находится во второй четверти.
• Если обе координаты отрицательны, число находится в третьей четверти.
• Если координата x положительна, а координата y отрицательна, точка находится в четвертой четверти.

Примеры решения задач на нахождение расстояния между точками

Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами A (1 — 2) и B (11 + 2) . Необходимо найти расстояние от точки начала отсчета O до точки A и между точками A и B .

Решение

1. Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно O A = 1 — 2 = 2 — 1
2. Расстояние между точками A и B определим как модуль разности координат этих точек: A B = 11 + 2 — (1 — 2) = 10 + 2 2

Ответ: O A = 2 — 1 , A B = 10 + 2 2

Пример 2

Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней A (1 , — 1) и B (λ + 1 , 3) . λ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние А В будет равно 5 .

Решение

Чтобы найти расстояние между точками A и B , необходимо использовать формулу A B = (x B — x A) 2 + y B — y A 2

Подставив реальные значения координат, получим: A B = (λ + 1 — 1) 2 + (3 — (- 1)) 2 = λ 2 + 16

А также используем имеющееся условие, что А В = 5 и тогда будет верным равенство:

λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3

Ответ: А В = 5 , если λ = ± 3 .

Пример 3

Исходные данные: задано трехмерное пространство в прямоугольной системе координат O x y z и лежащие в нем точки A (1 , 2 , 3) и B — 7 , — 2 , 4 .

Решение

Для решения задачи используем формулу A B = x B — x A 2 + y B — y A 2 + (z B — z A) 2

Подставив реальные значения, получим: A B = (- 7 — 1) 2 + (- 2 — 2) 2 + (4 — 3) 2 = 81 = 9

Ответ: | А В | = 9

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Пусть задана прямоугольная система координат.

Теорема 1.1.
Для любых двух точек М 1 (х 1 ;у 1) и М 2 (х 2 ;у 2) плоскости расстояние d между ними выражается формулой

d = . (3)

Доказательство.
Опустим из точек М 1 и М 2 перпендикуляры М 1 В и М 2 А соответственно на оси Оу и Ох и обозначим через К точку пересечения прямых М 1 В и М 2 А (рис.1.4). Возможны следующие случаи:

1)Точки М 1 , М 2 и К различны. Очевидно, что точка К имеет координаты (х 2 ;у 1). Нетрудно заметить что М 1 К = ôх 2 – х 1 ô, М 2 К = ôу 2 – у 1 ô. Т.к. ∆М 1 КМ 2 прямоугольный, то по теореме Пифагора d = М 1 М 2 = = =.

2) Точка К совпадает с точкой М 2 , но отлична от точки М 1 (рис.1.5). В этом случае у 2 = у 1 и

d = М 1 М 2 = М 1 К = ôх 2 – х 1 ô= = =.

3) Точка К совпадает с точкой М 1 , но отлична от точки М 2 . В этом случае х 2 = х 1 и

d =М 1 М 2 = КМ 2 = ôу 2 — у 1 ô= =.

4) Точка М 2 совпадает с точкой М 1 . Тогда х 1 = х 2 , у 1 = у 2 и

d = М 1 М 2 = О =.

—

Пусть задана прямоугольная система координат.
Теорема 1.1.Для любых двух точек М1(х1;у1) и М2(х2;у2) плоскости расстояние d между ними выражается формулой
d = . (3)
Доказательство.Опустим из точек М1 и М2 перпендикуляры М1В и М2А соответственно на оси Оу и Ох и обозначим через К…

— Расстояние между двумя точками

— Расстояние между двумя точками

Определение расстояний
Лекция № 6. МЕТРИЧЕСКИЕ ЗАДАЧИ
(определение расстояний, определение величины части плоскости,
определение величины угла)
План лекции
1. Определение расстояний.
1.1. Расстояние между двумя точками:
а) без преобразования чертежа;
б)…

— Модуль вектора. Расстояние между двумя точками

Дан вектор в пространстве

Модуль вектора вычисляется по формуле: .
Важной задачей является нахождение расстояния между двумя точками:
1) расстояние между точками и на прямой равно длине вектора:
;
2) расстояние между двумя точками и на плоскости равно длине вектора:
;
…

— Теорема Шаля для отрезков. Координата направленного отрезка, заданного двумя точками декартовой оси координат. Расстояние между двумя точками, лежащими на оси координат

Теорема (1) Шаля. (Для отрезков). Если А, В, С три любые точки оси, то. (Число число числу).
Доказательство. (1). Предположим, что точки А, В, С попарно различны. Если точки В лежит между точками А и С, то длина отрезка АС равна сумме длин отрезков АВ и ВС:
;
но так как в…

Расстояние от точки до точки
— это длина отрезка, соединяющего эти точки, в заданном масштабе. Таким образом, когда речь идет об измерении расстояния, то требуется знать масштаб (единицу длины), в котором будут проводиться измерения. Поэтому, задачу нахождения расстояния от точки до точки обычно рассматривают либо на координатной прямой, либо в прямоугольной декартовой системе координат на плоскости или в трехмерном пространстве. Другими словами, наиболее часто приходится вычислять расстояние между точками по их координатам.

В этой статье мы, во-первых, напомним, как определяется расстояние от точки до точки на координатной прямой. Далее получим формулы для вычисления расстояния между двумя точками плоскости или пространства по заданным координатам. В заключении, подробно рассмотрим решения характерных примеров и задач.

Навигация по странице.

Координаты своими словами для детей

Координаты — это способ описать положение точки на плоскости или в пространстве с помощью чисел. Представь себе, что ты находишься на большом листе бумаги или в комнате со множеством игрушек. Если тебе нужно сказать другу, где находится какая-то игрушка или ты хочешь указать место, где находишься сам, ты можешь использовать координаты.

Для удобства, мы можем представить, что у листа бумаги или комнаты есть оси. Ось X идет горизонтально, а ось Y — вертикально. Точка с координатами (0,0) будет находиться в середине листа бумаги или комнаты. Если ты хочешь указать точку, которая находится правее середины листа бумаги или комнаты, ты используешь положительные числа для координаты X. Если точка находится левее середины, ты используешь отрицательные числа для координаты X. Аналогично, если точка находится выше середины, используются положительные числа для координаты Y, а если точка ниже середины — отрицательные числа.

Таким образом, каждая точка на плоскости или в пространстве имеет свои координаты, которые состоят из чисел. Ты можешь представить, что координаты — это адрес точки, который позволяет нам найти ее местоположение среди других точек. Например, если мы говорим, что точка находится в координатах (3,2), это означает, что она находится на трех шагах вправо от середины листа бумаги или комнаты и на два шага вверх от середины.

Таким образом, координаты позволяют нам описывать положение объектов и точек на плоскости или в пространстве с помощью чисел. Это очень полезно, потому что позволяет нам легко общаться о местоположении и перемещении объектов.

Используемая литература:1. Белова, Т.И. Вычисление неопределенных интегралов. Обыкновенные дифференциальные уравнения. Компьютерный курс: учеб. пособие / Т.И.Белова, А.А.Грешилов, И.В.Дубограй; Ред. А.А.Грешилов. — М.: Логос, 2004. — 184 с. + 1 эл. опт. диск (CD-ROM).2. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. — 22-е изд., перераб. — СПб.: Профессия, 2006. — 432 с.3. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. — 22-е изд., перераб. — СПб.: Профессия, 2005. — 432 с.4. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. для вузов. В 2 ч. Ч.1 / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий. — 4-е изд., стереотип. — М.: Дрофа, 2004. — 725 с.5. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч. 1. Дифференциальное и интегральное исчисление / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; Ред. В.А.Садовничий. — 3-е изд., испр. — М.: ДРОФА, 2001. — 725 с.6. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч.2. Ряды, несобственные интегралы, ряды Фурье, преобразование Фурье / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; ред. В.А.Садовничий . — 3-е изд., испр. — М.: ДРОФА, 2001. — 712 с.7. Голоскоков, Д.П. Уравнения математической физики. Решение задач в системе Maple: учеб. для вузов / Д.П.Голоскоков. — СПб.: Питер, 2004. — 538с.8. Гурова, З.И. Математический анализ. Начальный курс с примерами и задачами: учеб. для втузов / З.И.Гурова, С.Н.Каролинская, А.П.Осипова; Ред. А.И.Кибзун. — М.: Физматлит, 2002. — 351 с.9. Лукьянов, А.В. Обыкновенные дифференциальные уравнения: учеб. пособие по решению задач / А.В.Лукьянов, Ю.Д.Погуляев. — Челябинск: Полиграф-Мастер, 2006.10. Математический анализ в вопросах и задачах: учеб. пособие для вузов / В.Ф.Бутузов, Н.Ч.Крутицкая, Г.Н.Медведев, А.А.Шишкин; Ред. В.Ф.Бутузов . — 5-е изд., испр. — М.: ФИЗМАТЛИТ, 2002. — 479 с.Значение термина Координаты на academic.ru

Модуль числа — теория и решение задач

Модуль числа – это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности

А между тем она проста как апельсин. Но, чтобы ее понять, давай сначала разберемся, зачем и кому он нужен.

Ситуация первая

В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.

Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными

Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.

Ситуация вторая

Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.

И что, можно идти судиться с компанией «Lay’s», если они тебе недовесили?

Нет. Потому что «Lay’s» устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» – это и есть модуль.

Ситуация третья

В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч – это и есть модуль.

А вообще для простоты запомни, что модуль это расстояние от точки отсчета в любую сторону.

Ну вот, ты уже почти все знаешь. Давай теперь подробнее…

Основные теоретические сведения

Базовые сведения о модуле

Определение модуля может быть дано следующим образом: Абсолютной величиной числа a (модулем) называется расстояние от точки, изображающей данное число a на координатной прямой, до начала координат. Из определения следует, что:

Таким образом, для того чтобы раскрыть модуль необходимо определить знак подмодульного выражения. Если оно положительно, то можно просто убирать знак модуля. Если же подмодульное выражение отрицательно, то его нужно умножить на «минус», и знак модуля, опять-таки, больше не писать.

Основные свойства модуля:

Некоторые методы решения уравнений с модулями

Существует несколько типов уравнений с модулем, для которых имеется предпочтительный способ решения. При этом данный способ не является единственным. Например, для уравнения вида:

Предпочтительным способом решения будет переход к совокупности:

А для уравнений вида:

Также можно переходить к почти аналогичной совокупности, но так как модуль принимает только положительные значения, то и правая часть уравнения должна быть положительной. Это условие нужно дописать в качестве общего ограничения для всего примера. Тогда получим систему:

Оба этих типа уравнений можно решать и другим способом: раскрывая соответствующим образом модуль на промежутках где подмодульное выражение имеет определённый знак. В этом случае будем получать совокупность двух систем. Приведем общий вид решений получающихся для обоих типов уравнений приведённых выше:

Для решения уравнений в которых содержится более чем один модуль применяется метод интервалов, который состоит в следующем:

• Сначала находим точки на числовой оси, в которых обращается в ноль каждое из выражений, стоящих под модулем.
• Далее делим всю числовую ось на интервалы между полученными точками и исследуем знак каждого из подмодульных выражений на каждом интервале. Заметьте, что для определения знака выражения надо подставить в него любое значение x из интервала, кроме граничных точек. Выбирайте те значения x, которые легко подставлять.
• Далее на каждом полученном интервале раскрываем все модули в исходном уравнении в соответствии с их знаками на данном интервале и решаем полученное обычное уравнение. В итоговый ответ выписываем только те корни этого уравнения, которые попадают в исследуемый промежуток. Еще раз: такую процедуру проводим для каждого из полученных интервалов.