Спектр

Определения простыми словами

Все природные сигналы — непрерывные. В эту категорию попадают все звуки, запахи, изображения, которые человек извлекает из окружающего мира. Пение птиц и звуки музыкальных инструментов, пролетающая птица и проезжающая машина — все это примеры аналогового способа передачи данных.

Информация, которую получает мозг, поступает в него плавно и непрерывно. Постепенно затухают краски заката, нарастает шум колес приближающегося автомобиля и т.д.

Изначально, человек научился воспроизводить именно аналоговые сигналы. Первое радио и телевидение были созданы, опираясь на естественные методы распространения информации.

На графике ниже, разница показана наглядно.

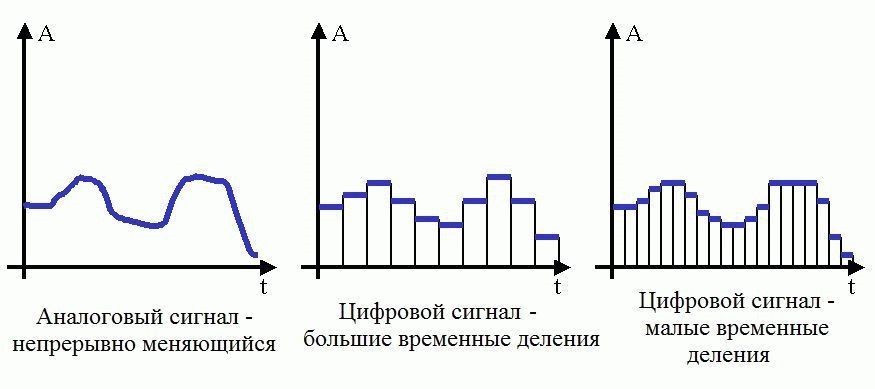
Отличие дискретного наращения от непрерывного в том, что оно происходит ступенчато. И чем больше промежуток времени между пакетами сигналов, тем больше искажение информации.

Аналоговые и дискретные процессы в природе

Абсолютное большинство процессов в природе протекают непрерывно, (изменение температуры воздуха на улице, давления, влажности, изменение скорости ветра, колебание электрического тока в проводнике, сияние Солнца). Почему все эти процессы непрерывны? Нам кажется, что время течет непрерывно, а значит в каждый момент времени должно существовать какое-то значение температуры воздуха или значение силы тока в проводнике, или значение интенсивности света Солнца. Непрерывные процессы, функции или сигналы называют аналоговыми (от слова аналог – нечто сходное, подобное чему-то, т.е. функция как модель является аналогом какому-то физическому процессу). Можно наблюдать множество непрерывных процессов в природе, например, непрерывный поток воды в источнике. Струя воды при падении вниз сужается как раз в силу поддержания непрерывности потока.

Аналоговый сигнал даже на конечном временном промежутке подразумевает набор бесконечного числа значений. Однако регистрирующие устройства, как правило фиксируют конечное число значений, поэтому мы получаем дискретные сигналы (дискретный от лат. discretus означает раздельный, состоящий из отдельных частей).

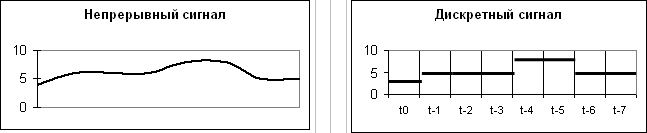
Представление непрерывного и дискретного сигналов.

Дискретные процессы также многочисленны в природе, как и аналоговые состояния. Дискретные процессы не могут находиться в каком-то промежуточном состоянии между определенными значениями. Придумаем несколько примеров из жизни:

Из квантовой физики 1-й постулат Бора: электрон в атоме может двигаться только по определенным (можно сказать по дискретным) орбитам, находясь на которых, он не излучает и не поглощает энергию. Электроны в атоме, находясь на определенных стационарных (т.е. дискретных) орбитах, имеет вполне определённые дискретные значения энергии Е1, Е2, Е3 и т.д.
Если вы играете на пианино, то звучащая музыка во времени представляет собой перескоки с одной дискретной ноты на другую, то есть ноты – это отдельно выбранные дискретные звуки.
Когда мы поднимаемся по лестнице, ступня в пространстве оси высот находится только на определенной дискретной координате (ступеньке)

Поскольку человек не может оперировать с бесконечными числами и величинами, обычно все округляем до ближайших целых чисел – в результате получаем цифровые сигналы. Например, мы наносим цифровую шкалу на столбик термометра и фиксируем округленное значение температуры. Непрерывное время мы разбиваем на секунды минуты, часы – наносим цифры на циферблат часов. Все символьные и знаковые системы, созданные человечеством для обмена информацией, использует конечное число возможных элементов.

Поскольку все вычислительные информационные устройства могут работать лишь с дискретными символьными системами и с цифровыми сигналами, постоянно возникает необходимость в переходе от существующих в природе непрерывных процессов, к дискретным и цифровым. С развитием цифровой связи и цифровых устройств (микроконтроллеров, компьютеров) постоянно и повсеместно на каждом шагу выполняется аналого-цифровое преобразование сигналов, неотъемлемой частью которого является дискретизация сигналов

Но здесь важно следующее: перейти от непрерывного сигнала к дискретному дело нехитрое – здесь удачно подходит выражение “ломать не строить”. По аналогии можно сказать “ломать аналоговый сигнал – не восстанавливать его”, здесь все просто реализовать, но главное при этом выполнить дискретизацию правильно

Одно дело просто произвести выборку отдельных значений сигнала, но есть еще другое дело – потом надо будет по этим значениям снова восстановить исходный непрерывный сигнал. Как правильно дискретизировать сигналы говорится в теореме о дискретизации сигналов, или ее можно называть в честь автора – теоремой Котельникова.

Спектральный анализ и его применение в науке и технике

Спектральный анализ – это метод исследования и анализа сигналов, основанный на разложении сигнала на различные частотные компоненты. Он широко применяется в научных и технических областях для изучения физических явлений, анализа данных, обработки сигналов и многого другого.

Спектр представляет собой графическое изображение зависимости амплитуды или интенсивности сигнала от частоты. Частоты, на которых происходят изменения сигнала, называются его спектральными компонентами. Спектральный анализ помогает раскрыть скрытые особенности и характеристики сигнала.

Применение спектрального анализа в науке и технике очень широко. Вот некоторые из его основных областей применения:

Физика и астрономия: спектральный анализ позволяет исследовать электромагнитные волны, определять состав и свойства веществ, анализировать дальность световых и радиоволн, изучать спектры звезд и галактик.
Связь и телекоммуникации: спектральный анализ используется для анализа и обработки сигналов, устранения шумов и помех, определения пропускной способности каналов связи.
Медицина: спектральный анализ широко применяется в медицинской диагностике и исследованиях, позволяя анализировать и классифицировать биомедицинские сигналы, такие как ЭЭГ, ЭКГ, рентгеновские снимки и др.
Анализ данных: спектральные методы используются для анализа временных рядов, обработки аудио и видео данных, обнаружения шаблонов и аномалий, а также для прогнозирования временных последовательностей.
Радиофизика и радиотехника: спектральный анализ применяется в радиофизике для измерения параметров радиоволн, определения спектральной плотности радиосигналов, синхронизации систем связи.

Это только некоторые области, где спектральный анализ находит применение. Все больше и больше отраслей науки и техники используют его методы и инструменты для решения различных задач и исследований.

Спектральный анализ является мощным инструментом для изучения сигналов и анализа данных. Он позволяет нам получить информацию о частотном составе и характеристиках сигналов, которые иначе остались бы незамеченными. Благодаря спектральному анализу мы можем получать глубокое понимание физических явлений и использовать его для развития науки и техники.

Что такое дискретный сигнал

В цифровой системе хранения и передачи данных, отсутствие сигнала, также является формой обмена информацией. В какой-то момент времени он равен нулю, в другой принимает какое-либо значение. Поэтому дискретным называют сигнал прерывный, отсюда и название discretus или разделённый. Аналоговые данные разбиваются на отдельные блоки, обрабатываются и передаются в виде цифрового кода.

Дискретность не подразумевает разрыв связи. В цифровых системах широко используется двоичная система обработки и обмена информацией. Двоичная подразумевает кодировку данных с помощью единицы и нулей. В доли секунды сигнал прерывисто принимает значение 1 или 0. Вместо непрерывной кривой имеем отдельные дискретные значения. Определенный набор нулей и единичек уже несёт в себе какую либо информацию. Примитивный набор это бит или двоичный разряд. Сам по себе он ничего не значит. Данные могут кодироваться только при объединении восьми битов в следующую по сложности комбинацию – байт. Чем больше объединённых байтов, тем больше и точнее можно описать передаваемую информацию.

На качество генерируемых данных влияет не только количество объединённых битов, но и скорость передачи. Непрерывная аналоговая кривая должна быть разбита на как много больше мини участков прерывного сигнала. Полученный таким образом звук и цвет будут соответствовать оригиналу. Качественный дискретный сигнал формирует точную копию аналогового. Например, звуковая дорожка MP3 закодированная со скоростью 320 000 бит в секунду (320 kbps) значительно лучше кодированной в 128 kbps. Дорожки скоростью меньше 128 слушать вообще невозможно.

Чем отличается непрерывный сигнал от дискретного

На первый взгляд отличия в сигналах можно не различить. Оба передаются в виде электрических импульсов по проводам или электромагнитными волнами в эфире. Преобразовываются в звук и изображение, выводятся на динамики и экран. Но разница существенна. Отличие аналогового сигнала от цифрового обусловлено особенностями обработки и передачи данных.

Казалось бы, природное происхождение, простота генерации, передачи и приёма благоприятствуют использованию аналогового сигнала. Но в дело вмешиваются электрические и электромагнитные помехи. Это могут быть электромагнитные наводки от электрических сетей, работающих механизмов, рельеф местности, грозы, бури на солнце, шумы создаваемые работой передающего и принимающего оборудования, прочие. Они изменяют плавную кривую. На приёмник информация поступает с изменениями. Шипение, хрипы и искаженное изображение обычная история для аналоговой связи.

Дискретный сигнал как азбука Морзе, только вместо точек и тире — чёткие биты. Ничего более, шумы и помехи им не мешают. Цифровой информации главное дойти до цели. Цифры без примесей передадут данные и без изменений перевоплотятся в звук и цвет. Но слабый сигнал может не донести полную картину. Как пример — пропадание слов или изображения полностью. Поэтому сотовые передатчики, устанавливают как можно ближе друг от друга, также используют повторители.

Примером непрерывных и дискретных сигналов могут служить старая проводная и новая сотовая связь. Через старые АТС иногда невозможно было разговаривать с соседним домом. Шумы и плохое усиление сигнала мешали слышать друг друга. Что бы вести полноценную беседу, приходилось громко кричать самому и прислушиваться к собеседнику. Другое дело сотовая связь основанная на цифровой технологии. Звук закодирован и хорошо передаётся на далёкие расстояния. Отчетливо слышно собеседника даже с другого континента.

Оба вида связи не лишены недостатков, а ключевыми отличиями являются:

Аналоговый подвержен помехам и поступает с искажениями. В то время как цифровой доходит полностью без искажений или отсутствует вовсе.
Принять или перехватить аналоговое вещание может любой приёмник такого принципа. Дискретная передача адресована конкретному адресату, кодируется и мало доступна к перехвату.
Объём передаваемых данных у аналоговой связи конечен, поэтому она практически исчерпала себя в передаче теле сигнала. Напротив с развитием технологии преобразования аналоговой информации в цифровой код растут объемы и качество трансляции. Например, главным отличием цифрового от аналогового телевидения является превосходное качество изображения.

Цифровая технология выигрывает по всем показателям. Споры идут только среди любителей музыки. Многие меломаны и звукорежиссеры утверждают, что могут различить аналоговый оригинал и цифровую копию. Однако большинство слушателей этого сделать не в состоянии. Да и с развитием цифровых систем аналоговые данные кодируются точнее. Оригинальное звучание и цифровая копия делаются практически неразличимым.

Теория дискретного спектра:

Дискретный спектр — это спектр, который состоит из набора дискретных, отдельных значений. Наиболее распространенным примером дискретного спектра является спектр частот, который может быть получен с помощью преобразования Фурье.

Преобразование Фурье — это метод математического преобразования, который позволяет выразить сигнал в виде суммы синусоидальных компонентов разных частот. Преобразование Фурье применяется во многих областях, таких как обработка сигналов, сжатие данных, анализ временных рядов и многое другое.

Когда применяется преобразование Фурье к некоторому сигналу, результатом является спектр. Спектр — это представление сигнала в частотной области. В непрерывном спектре частоты принимают все возможные значения, амплитуды в этих точках являются непрерывными функциями.

Однако в случае дискретного спектра частоты принимают только определенные дискретные значения. Это означает, что спектр состоит из набора точечных значений, имеющих определенную амплитуду.

Дискретный спектр имеет много практических применений. Например, он может быть использован для анализа звуковых сигналов, чтобы определить частоты, присутствующие в звуке, или для анализа временных рядов, чтобы исследовать поведение процессов во времени.

Применение	Описание
Анализ звуковых сигналов	Определение частотных компонентов звука
Астрономия	Анализ электромагнитного излучения от космических объектов
Обработка сигналов	Фильтрация и усиление сигналов
Криптография	Анализ и шифрование сообщений

В заключение, дискретный спектр является важным инструментом для анализа и обработки различных типов сигналов. Он позволяет представить сигнал в виде набора дискретных частотных компонентов, что позволяет анализировать и использовать сигналы в различных областях.

Анализ и синтез дискретного спектра

В процессе анализа дискретного спектра используется преобразование Фурье, которое позволяет разложить сигнал на сумму гармонических компонент, отображая их амплитуды и фазы. Преобразование Фурье можно применить к любому дискретному сигналу, не зависящему от его происхождения и формы.

Синтез дискретного спектра осуществляется путем комбинирования различных гармонических компонент. Для этого можно использовать прямое преобразование Фурье, которое позволяет преобразовать сигнал из временной области в частотную. Затем набор комбинаций частотных компонент можно складывать или умножать с различными амплитудами и фазами, чтобы создать желаемый сигнал.

Следует отметить, что анализ и синтез дискретного спектра требуют точных вычислений и специальных алгоритмов, так как они основаны на математической теории преобразования Фурье

Также важно учитывать ограничения по разрешению частоты сигнала и длине анализируемого временного отрезка

В итоге, анализ и синтез дискретного спектра играют важную роль в множестве областей, включая цифровую обработку сигналов, коммуникации, акустические и радиосистемы. Правильное применение этих методов позволяет получить полезные сведения о сигнале и создать новые уникальные сигналы для различных приложений.

Преимущества анализа спектра:	Преимущества синтеза спектра:
1. Выявление частотных компонентов сигнала	1. Создание новых сигналов со специфическими свойствами
2. Изучение амплитуд и фаз каждой компоненты	2. Комбинирование различных частотных компонент для получения желаемых результатов
3. Определение сигналов на фоне шума	3. Генерация сигналов для испытаний и исследований

Дискретное преобразование Фурье.

Если сигнал ограничен во времени значением
tu , а его спектр — частотой wв , то он полностью характеризуется
конечным числом отсчетов N как во временной, так и в частотной областях (Рис.
1.7, а, б) :

N = tu/T — во временной
области, где T = 1/fд ,

N = fд/f1 — в
частотной области, где f1 = 1/tu .

Дискретному сигналу соответствует
периодический спектр, дискретному спектру будет соответствовать периодический
сигнал. В этом случае отсчеты X(nT) = {X0 ; X1 ; … XN-1}
являются коэффициентами ряда Фурье периодической последовательности X(jkw1), период, который равен wд. Соответственно, отчеты X(jkw1) = {X0 ; X1
; … XN-1} являются коэффициентами ряда Фурье периодической
последовательности X(nT), период, который равен tu.

Связь отсчетов сигнала и спектра
устанавливается формулами дискретного преобразования Фурье (ДПФ). Формулы ДПФ
следуют из формул Фурье для дискретных сигналов (1.5), если непрерывную переменную
w заменить дискретной переменной kw1, то есть

w kw1 , dw w1.

После замены переменной в (1.5) получим

X(jkw1) = x(nT),

x(nT) =X(jkw1).

Отсюда после подстановки w1 = wд/N, T = 2p/wд формулы ДПФ принимают
окончательный вид

X(jkw1) =x(nT)- прямое ДПФ ,

x(nT) =X(jkw1)- обратное ДПФ (1.10)

Сигнал с ограниченным спектром имеет,
строго говоря, бесконечную протяженность во времени и, соответственно
бесконечное число отсчетов и непрерывный спектр. Спектр останется непрерывным,
если число отсчетов сигнала ограничить конечным числом N. Формулы (1.10) в этом
случае будут выражать связь между N отсчетами дискретного сигнала и N отсчетами
его непрерывного спектра, который можно полностью восстановить по его отсчетам.

Пример. Определить отсчеты спектра сигнала
на Рис. 1.5, а.

Здесь N = 2 поэтому X(jkw1) =x(nT) e-jpkn следовательно

X(j0w1) =x(nT)e-j0 = x(0T) + x(1T) = a + b

X(j1w1) =x(nT)e-jpn =
x(0T) e-j0 + x(1T) e-jp = a — b

график отсчетов спектра приведен на Рис.
1.5, б, где w1 = wд/N = 0,5wд.

Сигнал с конечным числом отсчетов N имеет
спектр, который повторяет с конечной погрешностью спектр сигнала с бесконечным
числом отсчетов : спектры совпадают на отсчетных частотах kw1 и отличаются на других
частотах. Отличие спектров тем меньше, чем больше N. В самом деле, реальные
сигналы обладают конечной энергией и, следовательно, начиная с некоторого
номера отсчета остальными номерами можно пренебречь ввиду их малости, что не
окажет заметного влияния на спектр сигнала.

Пример. Осуществить дискретизацию
экспоненциального импульса X(t) = Ae-at = 1 e-10t и сравнить спектры исходного и дискретного
сигналов.

Решение.

График сигнала X(t) представлен на Рис.
1.8

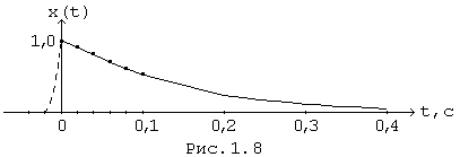
Пусть T = 0,02с. В этом случае плавным
соединением отсчетов сигнала (штриховая линия на Рис. 1.8) сигнал
восстанавливается удовлетворительно хотя заметны искажения в окрестности точки
t = 0, поэтому ошибки наложения будут некоторым образом влиять на спектральные
характеристики.

Пусть tu = 0,4с. В этом случае

N = tu/T = 20.

Расчет спектра по формуле прямого ДПФ в
точке w = 0 (k = 0) запишется так

X(j0w1) = 1,0 + 0,8187 + 0,6703 +
05488 + 0,4493 + 0,368 + 0,3012 + 0,2466 + 0,2019 + 0,1653 + 0,1353 + 0,1108 +
0,09072 + 0,07427 + 0,06081 + 0,04979 + 0,04076 + 0,03337 + 0,02732 + 0,02237 =
5,41

Истинное значение спектра в точке w = 0 можно определить зная спектр
аналогового экспоненциального импульса

Xa(jw) =, следовательно Xa(j0) == 0,1.

чтобы сравнить спектры дискретного и
непрерывного сигналов, дискретный спектр необходимо денормировать умножением на
T, так как формулы Фурье для дискретных сигналов применяются в нормированном
виде. Поэтому

X(jow1) = 5,41 T = 5,42Ч0,02 = 0,1082.

Таким образом совпадение спектров Xa(jw) и X(jw) в точке w = 0 вполне удовлетворительное. Некоторая
неточность объясняется влиянием ошибок наложения.

Уместно заметить, что выбор шага
дискретизации достаточно контролировать в точках максимальной крутизны исходной
функции X(t). В рассмотренном примере такой точкой является момент времени t =
0.

В заключение отметим, что формулы ДПФ
упрощают расчетные процедуры по взаимному преобразованию сигналов и их
спектров, что особенно важно для технических систем, функционирующих В реальном
масштабе времени. В этих случаях применяется алгоритм быстрого преобразования
Фурье (БПФ), основанный на формулах ДПФ

Ускоренная процедура расчетов по
алгоритму БПФ достигается за счет исключения повторных арифметических операций,
характерных для расчетов по формулам ДПФ.

Определение дискретного спектра

Определение дискретного спектра включает в себя дискретизацию аналогового сигнала, путем его разбиения на последовательные отсчеты в дискретных моментах времени. Затем применяется дискретное преобразование Фурье (ДПФ), которое переводит сигнал из временной области в частотную.

Дискретный спектр описывается набором дискретных отсчетов, каждый из которых соответствует определенной частоте и соответствующей амплитуде в спектре сигнала. Частоты могут быть равномерно распределены или иметь разную ширину полосы, в зависимости от спецификации сигнала и выбранного метода анализа.

Анализ дискретного спектра позволяет определить частотные характеристики сигнала, такие как основная частота, гармонические составляющие, шумы и прочие спектральные компоненты. Это особенно полезно для анализа сигналов в области цифровой обработки сигналов и телекоммуникации, где частотное разложение сигнала играет важную роль в понимании и обработке данных.

Что такое спектр сигнала?

Сигнал может быть представлен в виде дискретного или непрерывного спектра. Дискретный спектр возникает, когда сигнал оцифрован и представлен в виде последовательности значений, измеренных в разных моментах времени. Непрерывный спектр возникает, когда сигнал представлен в виде функции, определенной на непрерывном интервале времени.

Спектр сигнала может быть одномерным или многомерным, в зависимости от числа переменных, по которым сигнал разложен. В одномерном случае спектр представляет собой график зависимости интенсивности сигнала от частоты. В многомерном случае спектр представляет собой поверхность или объем, в котором на каждой точке задана амплитуда или фаза сигнала.

Спектр сигнала имеет много применений в различных областях, таких как радиосвязь, обработка сигналов, медицина, астрономия и т. д. Анализ спектра сигнала позволяет определить его характеристики, такие как частота, амплитуда, фаза, ширина спектра и т. д. Это помогает в понимании и улучшении качества сигнала, а также в решении различных задач и проблем, связанных с обработкой сигналов.

Различия дискретного спектра от аналогового

Дискретный спектр сигнала отличается от аналогового спектра в нескольких основных аспектах. Эти различия важны для понимания обработки и анализа дискретных сигналов. Рассмотрим некоторые из них:

Отсутствие бесконечного числа частот

В аналоговом спектре сигнала существует бесконечное число различных частотных компонент. Это означает, что сигнал может содержать даже очень высокие или низкие частоты. В то время как в дискретном спектре, компоненты имеют ограниченное число дискретных частот. Это связано с тем, что дискретизация сигнала происходит только в определенные моменты времени.

Возможность точного анализа и обработки

Дискретный спектр позволяет проводить точный анализ и обработку сигнала. Так как спектр представляет собой набор отдельных точек (частотных компонент) с известными значениями, возможно применять различные алгоритмы обработки и извлекать нужную информацию из каждой точки спектра. Например, можно определить амплитуду или фазу каждой частотной компоненты.

Безопасная передача и хранение

Дискретный спектр сигнала имеет преимущество перед аналоговым при передаче и хранении информации. В дискретной форме сигнал может быть представлен в цифровом виде и передан по каналам связи без искажений. Кроме того, цифровой сигнал легче хранить и воспроизводить, чем аналоговый сигнал.

Работа с дискретными системами

Дискретный спектр сигнала позволяет производить анализ и моделирование дискретных систем. Для таких систем, как цифровая обработка сигналов, речь о работе с аналоговыми спектрами сигналов с помощью дискретных методов. Дискретный спектр исходного аналогового сигнала может быть использован для создания модели системы и дальнейшего анализа ее свойств.

Изложенные различия позволяют лучше понять и осознать важность дискретного спектра сигнала. Это обеспечивает надежность передачи и хранения информации, а также возможность точного анализа и обработки, что важно для различных областей науки и техники

Дискретный спектр

Дискретный спектр представляет собой менее грубую структуру, чем существенный. Его наличие, конечность или бесконечность определяются, как правило, более тонкими свойствами потенциалов, чем свойства, ответственные за локализацию и структуру существенного спектра. Поэтому успехи в исследовании дискретного оператора, несмотря на большое число работ ему посвященных, значительно скромнее, чем успехи в исследовании существенного спектра. В то же время за последние годы получен ряд результатов о конечности и бесконечности дискретного спектра, имеющих относительно законченный характер. Именно они и составляют основное содержание данного дополнения.

Дискретный спектр такого излучения состоит из множества гармоник, чем отличается от обеих предыдущих случаев.

Дискретный спектр имеет шумы с ярко выраженными тонами, непрерывный спектр наблюдается у шумов машин со случайными неустановившимися процессами.

Изображение дискретных спектров.

Дискретные спектры можно изображать графически на временной диаграмме, как показано на рис. 5.1, а. Однако это неудобно и громоздко, особенно при большом числе спектральных составляющих. Поэтому принят другой, способ изображения дискретных спектров.

Дискретный спектр напоминает линейчатый оптический спектр. Он состоит из электронов с определенными дискретными скоростями. Тщательные ис — следования показали, что эти электроны вылетают вовсе не из ядра, а образуются как вторичный эффект у-излучения.

Дискретный спектр гамильтониана Н означает периодическое движение. При непрерывном спектре характер движения становится иным. Выясним поэтому, каким образом переход к непрерывному спектру сказывается па эволюции системы во времени. Вместо суммы-в (3.21) необходимо рассматривать интеграл.

Дискретный спектр собственных волн экранированной открытой щелевой лнннн.

Дискретные спектры ионов РЗЭ обусловлены квазизапрещенными. Сплошное, поглощение в ультрафиолетовой области следует отнести к энергетическим переходам электронов с 4 / — оболочки на внешние оболочки, подверженные сильному влиянию окружающей среды.

Отсюда соответствующий дискретный спектр коэффициентов cv называется обобщенным спектром.

Дискретный спектр сшитого бутадиенметилстирольного эластомера СКМС-30 ( рис. 7.4) показывает, что вклад в релаксацию напряжения б — процесса очень велик по сравнению с вкладом — процессов, число которых больше трех благодаря микроблочиому строению цепей сополимеров.

Относительно дискретного спектра, по-видимому, еще ничего не доказано, за исключением результата Мак-Леннана для случая твердых сфер.

Дискретным спектром стационарной случайной функции X ( t) вида () называют совокупность дисперсий всех составляющих ее гармоник.

Дискретным спектром стационарной случайной функции вида (7.4.5) называют совокупность дисперсий всех составляющих ее гармоник. Спектр можно изобразить графически: по оси абсцисс откладывают частоты, а по оси ординат — соответствующие дисперсии.

Имеется только дискретный спектр.

Дискретное излучение: понятие и основные принципы

Основными принципами дискретного излучения являются:

Квантовая теория: Дискретное излучение основано на принципе квантовой теории, которая утверждает, что энергия передается в виде дискретных порций, называемых фотонами. Фотоны имеют определенную энергию, которая является кратной некоторому фиксированному значению, называемому квантом.
Дискретность спектра: Дискретное излучение имеет дискретный спектр частот или волновых длин, что означает, что возможны только определенные значения энергии.
Интерференция и дифракция: Дискретное излучение подчиняется принципу интерференции и дифракции, что означает, что его волны могут взаимно усиливать или ослаблять друг друга при перекрестном воздействии.
Взаимодействие с веществом: Дискретное излучение может взаимодействовать с веществом, вызывая различные явления, такие как поглощение, отражение или преломление.
Эффекты на электроны: Дискретное излучение может вызывать перемещение электронов в атомах или молекулах, что приводит к эффектам, таким как фотоэффект, флюоресценция или люминесценция.

Примеры дискретного излучения включают электромагнитное излучение от атомов, молекул или других квантовых систем, таких как лазерный свет, свет от светодиодов (Light Emitting Diode — LED) или флуоресцентные лампы.