Последовательный колебательный контур

Электрический конденсатор

Ёмкость колебательного контура определяется ёмкостью электрического конденсатора. О его внешнем виде было написано выше. Теперь разберём физику процессов, которые протекают в нём.

Так как обкладки конденсатора сделаны из проводника, то по ним может течь электрический ток. Однако между двумя пластинами есть препятствие: диэлектрик (им может быть воздух, дерево или другой материал с высоким сопротивлением. Благодаря тому что заряд не может перейти от одного конца провода к другому, происходит накопление его на обкладках конденсатора. Тем самым возрастает мощность магнитного и электрического полей вокруг него. Таким образом, при прекращении поступления заряда вся электроэнергия, скопившаяся на обкладках, начинает передаваться в цепь.

Каждый конденсатор имеет номинальное напряжение, оптимальное для его работы. Если долго эксплуатировать этот элемент при напряжении выше номинального, срок его службы значительно сокращается. Конденсатор колебательного контура постоянно подвержен влиянию токов, и поэтому при его выборе следует быть предельно внимательным.

Кроме обычных конденсаторов, о которых шла речь, есть также ионисторы. Это более сложный элемент: его можно описать как нечто среднее между аккумулятором и конденсатором. Как правило, диэлектриком в ионисторе служат органические вещества, между которыми находится электролит. Вместе они создают двойной электрический слой, который и позволяет накапливать в этой конструкции в разы больше энергии, чем в традиционном конденсаторе.

Применение катушек индуктивности

Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.

Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.

Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.

По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.

Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.

Что такое добротность колебательного контура? как измерить добротность в радиолюбительских условиях.

«Добротность обозначается символом Q (от английского quality factor) и является тем параметром колебательной системы, который определяет ширину резонанса и характеризует, во сколько раз запасы энергии в системе больше, чем потери энергии за время изменения фазы на 1 радиан.

При подключении к контуру внешних цепей, параллельно Rш добавляется дополнительное сопротивление Rн, вносимое этими внешними цепями.

По большому счёту, на Рис.1 не хватает ещё одной ёмкости, равной сумме паразитных ёмкостей катушки индуктивности, внешних цепей и паразитной ёмкости монтажа. На высоких частотах эти привнесённые ёмкости могут иметь существенные величины, соизмеримые с ёмкостью самого контурного конденсатора. На добротность эти ёмкости существенного влияния не оказывают, но при расчёте резонансной частоты их необходимо учитывать и суммировать со значением основной ёмкости С.

Теперь давайте разберёмся, что такое «скорость затухания собственных колебаний в системе» и, каким боком она связана с добротностью.

Конденсатор С зарядится до уровня, равного напряжению питания.

Теперь перещёлкнем переключатель в правое по схеме положение.

Число периодов свободных колебаний в контуре можно подсчитать счётчиком импульсов и таким образом узнать добротность колебательного контура, генератор сигналов в этом случае не нужен.

Собственно говоря, на таком принципе и строится большинство промышленных измерителей добротности.

Вспоминаем дальше: «Добротность является тем параметром колебательной системы, который определяет ширину резонанса».

Рисуем резонансную кривую (амплитудно частотную характеристику) колебательного контура.

А как измерить добротность контура, не прибегая к изготовлению специальных устройств, в домашней лаборатории?

1. Если речь идёт о низких (звуковых) частотах, то тут всё просто. В этом случае, Q равна отношению реактивного сопротивления индуктивного или ёмкостного характера (характеристического сопротивления) к полному последовательному сопротивлению потерь в резонансном контуре. В виду того, что конденсаторы на данных частотах практически не вносят потерь, то добротность контура равна добротности катушки индуктивности, величина которой напрямую зависит от активного сопротивления катушки. А поскольку данное сопротивление можно легко измерить обычным омметром, то имеет полный смысл проделать эту не сильно замысловатую манипуляцию, после чего перейти на страницу ссылка на страницу и в первой таблице произвести расчёт добротности. Естественным образом, подразумевается, что катушка намотана на соответствующем для данных частот сердечнике, не вносящих существенных потерь в работу колебательного контура.

2. На высоких частотах (радиочастотах) значение активного сопротивления катушки может составлять доли ома, к тому же возможно проявление влияния добротности конденсатора на общую добротность цепи, поэтому такими же примитивными методами, как в случае НЧ обойтись не удастся

Рискну сделать осторожное предположение, что в радиолюбительской лаборатории у нас затерялся высокочастотный генератор с 50-омным выходом и такой же высокочастотный осциллограф, или, на худой конец, измеритель ВЧ напряжений

В этом случае мы воспользуемся ещё одним определением Q. Добротность резонансного контура равна фактору увеличения напряжения и может быть выражена отношением напряжения, развиваемого на реактивных элементах к входному напряжению, поданному последовательно с контуром.

Так как в случае высокодобротных элементов, сопротивление контура на резонансной частоте может превышать значение в сотню килоом, для корректного измерения добротности, входные импедансы измерителя ВЧ напряжений, либо осциллографа должны превышать это значение как минимум на порядок.

А на следующей странице порассуждаем на тему: что надо сделать, чтобы намотать катушку с максимально-возможной добротностью.

Архив записей

Архив записейВыберите месяц Ноябрь 2022 (1) Сентябрь 2022 (1) Январь 2022 (2) Сентябрь 2021 (1) Июль 2021 (1) Июнь 2021 (2) Май 2021 (1) Апрель 2021 (1) Март 2021 (1) Сентябрь 2020 (1) Август 2020 (2) Июль 2020 (2) Июнь 2020 (2) Декабрь 2019 (3) Ноябрь 2019 (4) Октябрь 2019 (3) Сентябрь 2019 (2) Май 2019 (1) Октябрь 2018 (1) Июнь 2018 (1) Апрель 2018 (1) Январь 2018 (1) Ноябрь 2017 (1) Октябрь 2017 (1) Сентябрь 2017 (2) Август 2017 (4) Июль 2017 (5) Июнь 2017 (4) Май 2017 (5) Апрель 2017 (2) Март 2017 (1) Февраль 2017 (1) Январь 2017 (3) Декабрь 2016 (1) Ноябрь 2016 (2) Октябрь 2016 (3) Сентябрь 2016 (4) Август 2016 (6) Июль 2016 (9) Июнь 2016 (4) Май 2016 (5) Апрель 2016 (6) Март 2016 (5) Февраль 2016 (8) Январь 2016 (8) Декабрь 2015 (9) Ноябрь 2015 (4) Июль 2015 (1) Март 2015 (1) Февраль 2015 (1) Январь 2015 (1) Июль 2014 (1) Июль 2013 (1) Март 2013 (2) Декабрь 2012 (1) Ноябрь 2012 (1) Сентябрь 2012 (3) Август 2012 (4) Июль 2012 (4) Июнь 2012 (4) Май 2012 (4) Апрель 2012 (5) Март 2012 (7) Февраль 2012 (8) Январь 2012 (7) Декабрь 2011 (5) Ноябрь 2011 (1)

Как найти резонанс параллельного колебательного контура на практике

Ладно, ближе к делу. Берем паяльник в руки и спаиваем катушку и конденсатор параллельно. Катушка на 22 мкГн, а конденсатор на 1000пФ.

Итак, реальная схема этого контура будет вот такая:

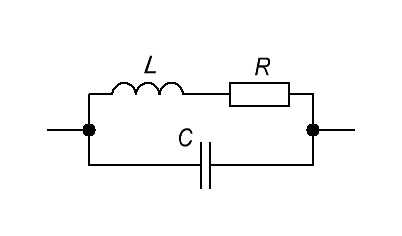
Для того, чтобы все показать наглядно и понятно, давайте добавим к контуру последовательно резистор на 1 КОм и соберем вот такую схему:

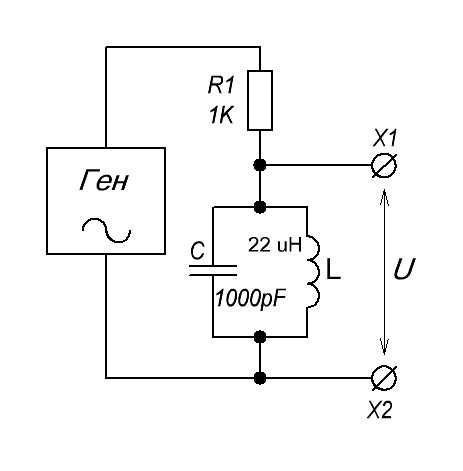
На генераторе мы будет менять частоту, а с клемм X1 и X2 мы будем снимать напряжение и смотреть его на осциллографе.

Нетрудно догадаться, что у нас сопротивление параллельного колебательного контура будет зависеть от частоты генератора, так как в этом колебательном контуре мы видим два радиоэлемента, чьи реактивные сопротивления напрямую зависит от частоты, поэтому заменим колебательный контур эквивалентным сопротивлением контура R_кон.

Упрощенная схема будет выглядеть вот так:

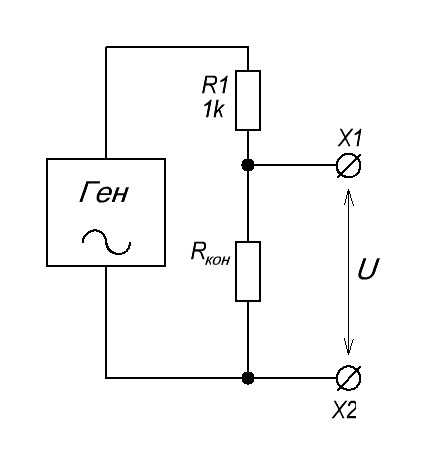
Интересно, на что похожа эта схема? Не на делитель ли напряжения? Именно! Итак, вспоминаем правило делителя напряжения: на меньшем сопротивлении падает меньшее напряжение, на бОльшем сопротивлении падает бОльшее напряжение. Какой вывод можно сделать применительно к нашему колебательному контуру? Да все просто: на резонансной частоте сопротивление R_конбудет максимальным, вследствие чего у нас на этом сопротивлении «упадет» бОльшее напряжение.

Начинаем наш опыт. Поднимаем частоту на генераторе, начиная с самых маленьких частот.

200 Герц.

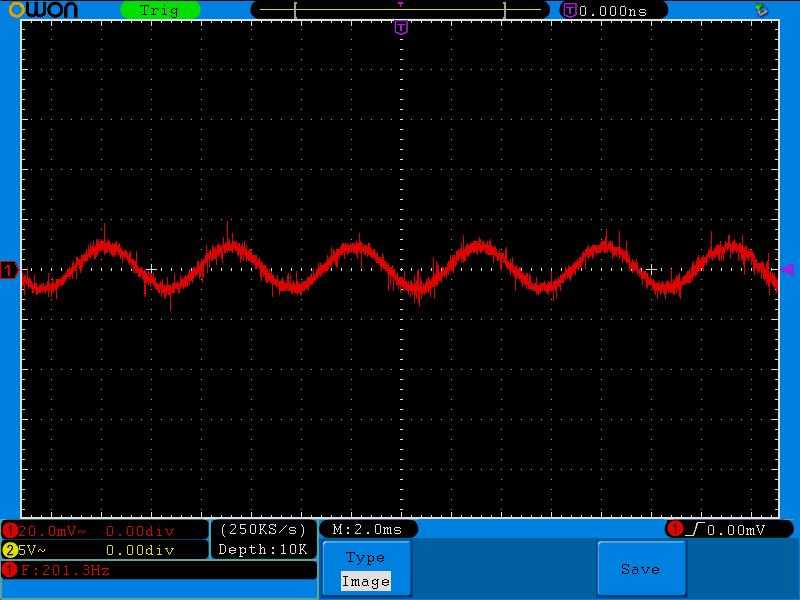
Как вы видите, на колебательном контуре «падает» малое напряжение, значит, по правилу делителя напряжения, можно сказать, что сейчас у контура малое сопротивление R_кон

Добавляем частоту. 11,4 Килогерца

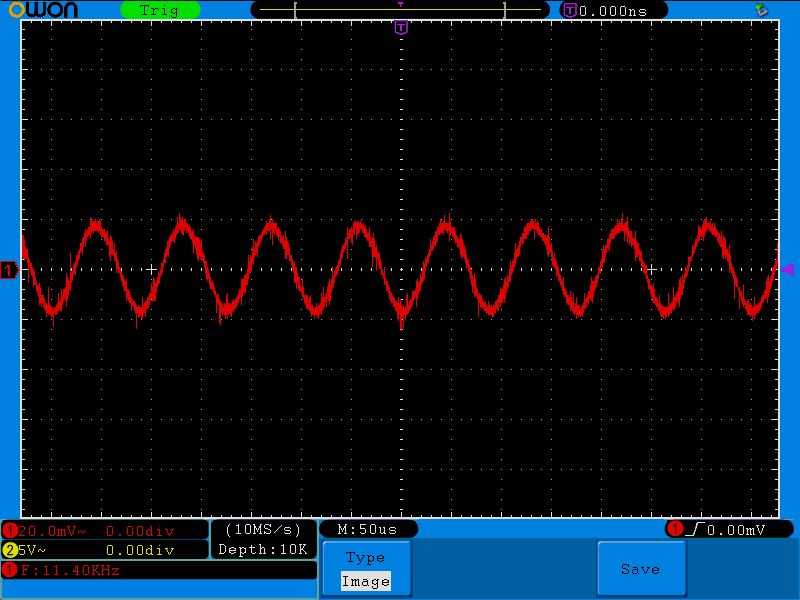
Как вы видите, напряжение на контуре поднялось. Это значит, что сопротивление колебательного контура увеличилось.

Добавляем еще частоту. 50 Килогерц

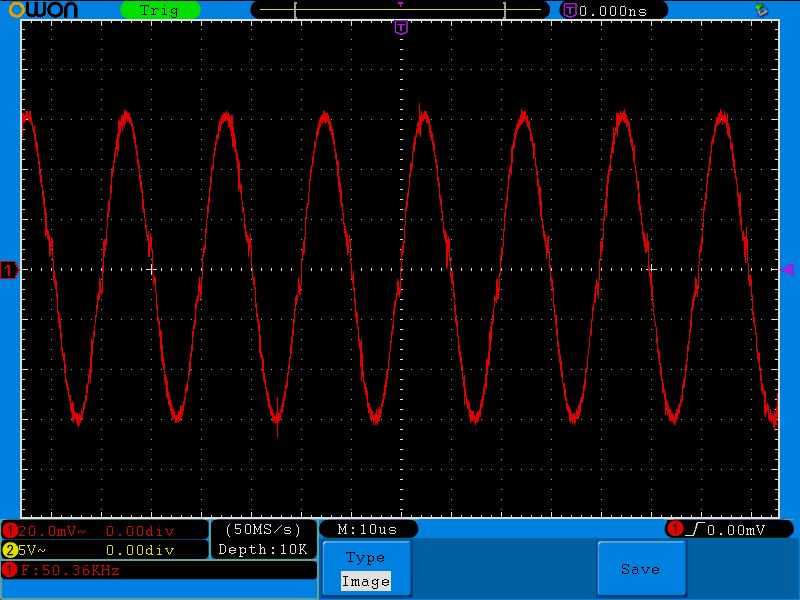
Заметьте, напряжение на контуре повысилось еще больше. Значит его сопротивление еще больше увеличилось.

723 Килогерца

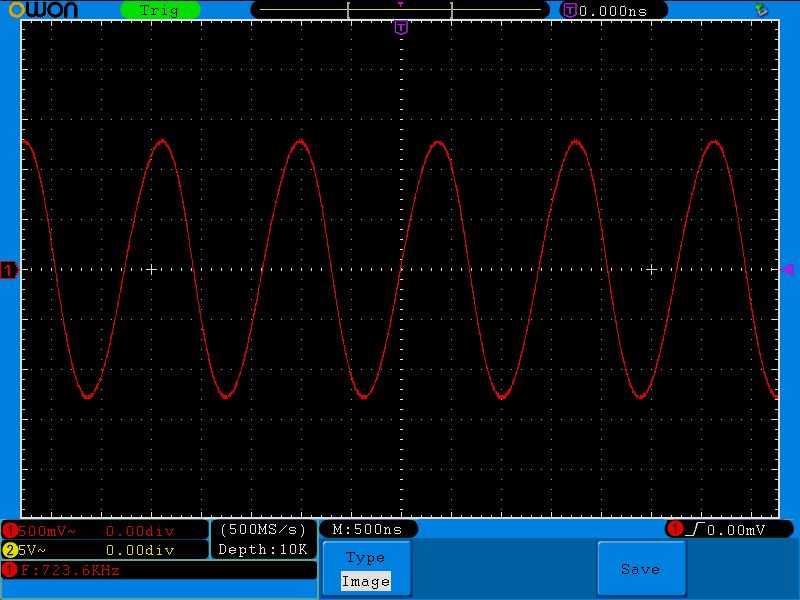
Обратите внимание на цену деления одного квадратика по вертикали, по сравнению с прошлым опытом. Там было 20мВ на один квадратик, а сейчас уже 500 мВ на один квадратик. Напряжение выросло, так как сопротивление колебательного контура стало еще больше

Напряжение выросло, так как сопротивление колебательного контура стало еще больше.

И вот я поймал такую частоту, на которой получилось максимальное напряжение на колебательном контуре

Обратите внимание на цену деления по вертикали. Она равняется двум Вольтам

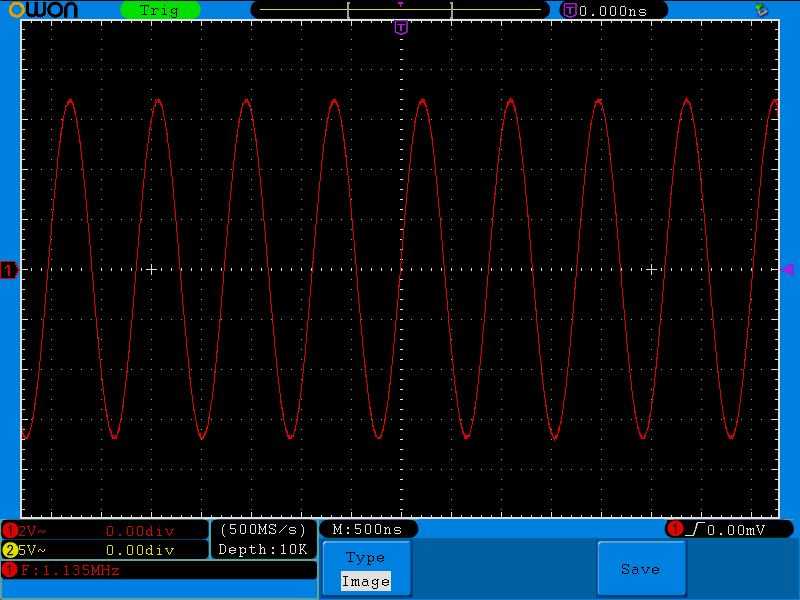
Дальнейшее увеличение частоты приводит к тому, что напряжение начинает падать:

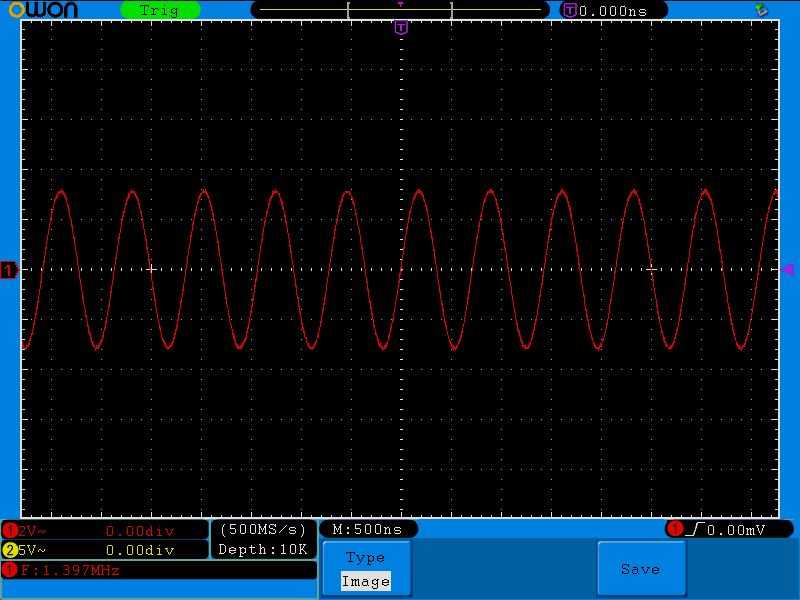
Снова добавляем частоту и видим, что напряжение стало еще меньше:

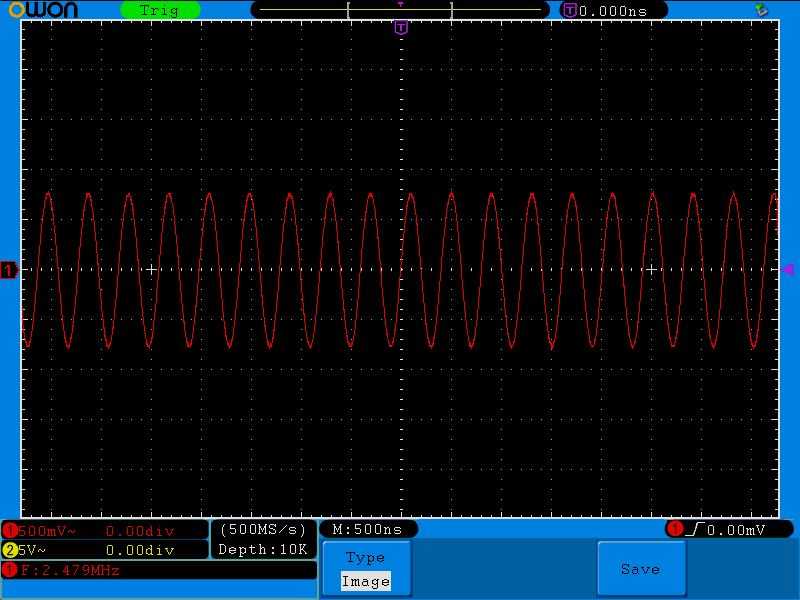
Параллельный контур

Добротность любого параллельного колебательного контура предполагает наличие цепи, в которой имеется емкость, нагрузка и индуктивность, соединенные параллельно. Они образуют так называемую RLC-схему.

Определяющая величина для такой схемы — это проводимость конденсатора с катушкой. Именно она суммируется при расчетах и является реактивной проводимостью параллельного колебательного контура. На резонансной частоте проводимость катушки с конденсатором будут равны, а общая разница при этом равняется 0. Для расчета такой цепи используется формула:

При этом стоит учитывать следующее:

Не принимается во внимание емкостная паразитная характеристика катушки индуктивности, но учитывается добротность индуктивного элемента. Она соответствует выражению:

Также учитывается добротность конденсатора, использующегося в такой электроцепи

Потери в конденсаторе связаны с наличием диэлектрика в его конструкции. Добротность конденсатора вместе с имеющимися потерями, напрямую связаны с потерями энергии на его диэлектрике tgδ. Данный коэффициент определяем с помощью такого выражения:

На резонансной частоте к переменному току прилагается бесконечное сопротивление.
В реальной RLC-цепи отсутствует бесконечное сопротивление, но этот параметр при увеличении сопротивления контура значительно снижается.

В параллельном колебательном контуре резонансная частота является той частотой, при которой реактивное сопротивление равняется 0, а величина входящего сопротивления является активным. Отсюда можно сделать вывод, что отсутствует фазовый сдвиг между током и напряжением.

Важность добротности контура

Важность добротности контура заключается в нескольких аспектах. Во-первых, высокая добротность контура позволяет распространять сигналы на большие расстояния без значительных потерь энергии

Это особенно важно в современных телекоммуникационных системах, где сигналы передаются на значительные расстояния.

Во-вторых, добротность контура определяет его частотные характеристики. Контур с высокой добротностью имеет более узкий спектр частот, что позволяет лучше фильтровать сигналы и снижать уровень помех

Это особенно важно в радиоприемниках и передатчиках, где необходимо получать или передавать сигналы определенных частот

В-третьих, добротность контура влияет на его временные характеристики. Контур с высокой добротностью имеет большую временную длительность колебаний и более плавный переход от одного состояния к другому. Это позволяет лучше синхронизироваться с другими устройствами и обеспечивать стабильную работу системы.

В целом, добротность контура играет важную роль в электронике и связи, обеспечивая эффективную передачу сигналов, фильтрацию помех и стабильную работу систем. Поэтому, при проектировании и настройке контуров, необходимо учитывать и оптимизировать добротность для достижения требуемых характеристик и результатов работы.

Преимущества высокой добротности контура:	Преимущества низкой добротности контура:
Большая эффективность передачи сигналов	Большая ширина полосы пропускания
Лучшая фильтрация помех	Более быстрое время нарастания и спада сигнала
Стабильная работа системы	Более широкий спектр частот

Зачем нужна добротность контура?

В простых словах, добротность контура показывает, насколько эффективно контур может накапливать и хранить энергию. Чем выше добротность, тем меньше потери энергии в контуре.

Добротность контура имеет решающее значение во многих приложениях. Например, в радиосвязи добротность контура определяет качество передачи сигнала. Чем выше добротность контура в радиопередатчике или радиоприемнике, тем лучше качество звука или изображения.

Добротность контура также важна при проектировании электронных фильтров. Высокая добротность позволяет более точно фильтровать сигналы разных частот и отделять полезный сигнал от помех.

Еще одним примером применения добротности контура является резонанс. Когда контур настроен на резонансную частоту, его добротность определяет, насколько быстро контур переходит в резонансное состояние и насколько долго он может поддерживать резонанс при отсутствии внешних возмущений.

Таким образом, понимание и учет добротности контура позволяют создавать более эффективные и надежные электрические и электромагнитные системы.

Как влияет добротность на эффективность работы контура?

Чем выше значение добротности, тем более эффективно работает контур. Высокая добротность позволяет контуру иметь малые потери энергии и сохранять колебания наиболее длительное время.

Эффективность работы контура определяется его способностью осуществлять требуемую функцию. Например, в электронных устройствах, высокая добротность контура позволяет увеличить дальность передачи сигнала или улучшить качество передаваемого сигнала.

Для повышения добротности контура можно использовать специальные элементы, такие как катушки с высоким коэффициентом самоиндукции и конденсаторы с низким потерями. Также важным аспектом является правильная настройка контура на резонансную частоту.

В целом, добротность контура играет значительную роль в эффективной работе различных систем и устройств, где требуется сохранение и передача энергии с минимальными потерями.

Принцип работы

Принцип работы контура состоит в поочередном обмене электрической энергией между элементами емкости и индуктивности. Происходит превращение емкостной в индуктивную и обратно. Процессы следует рассмотреть подробнее. Для этого нужно зарядить конденсатор до величины напряжения Uc. Энергия будет определяться по формуле Wс = (C * U2) / 2. Если к конденсатору подсоединить катушку индуктивности, то это вызовет в ней ЭДС самоиндукции.

При этом энергия электромагнитного поля станет рассчитываться по такому соотношению: Wl = (L * I2) / 2. Из-за нее будет постепенно уменьшаться ток в электрической цепи контура. Векторы токов конденсатора и катушки направлены в разные стороны. Следовательно, они компенсируют друг друга по I закону Кирхгофа и не выходят за пределы системы.

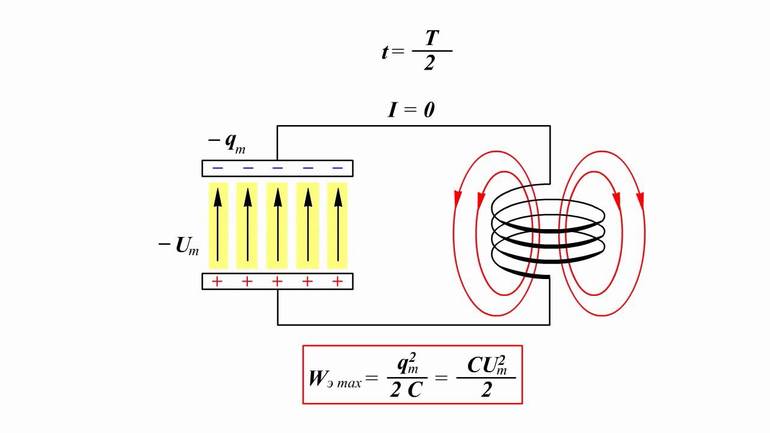
При постоянной работе генератора (источника питания) результирующий ток в системе начнет возрастать. Энергия Wc будет полностью переходить в катушку, пока не разрядится полностью конденсатор (Wc = 0). Далее в ней появляется электромагнитное поле за счет ЭДС самоиндукции, и обкладки конденсатора будут снова заряжаться до тех пор, пока Wl не будет равна 0. Такая особенность обмена энергиями порождает колебания. Их длительность зависит от коэффициента затухания контура.

Собственная частота

Когда дети становятся старше, им надоедает просто качаться на качелях и они раскачавшись прыгают с них, стараясь подлететь повыше и подальше приземлиться (хорошо что детские площадки посыпают песком). После такого прыжка на качелях не остаётся источника внешней толкающей силы, да и отцу становится «не очень интересно » толкать пустые качели. Постепенно амплитуда качения уменьшается и качели останавливаются. Интервал времени между двумя ближайшими моментами отклонения качелей (маятника, резонатора, сигнала и т.д.) называется периодом собственных колебаний, а обратная ему величина — частотой собственных колебаний.

Одни колебательные системы останавливаются быстро, всего за пару тройку колебаний (большинство качелей во дворе останавливаются не более чем за 7 колебаний), а колебания других могут затухать очень долго (колокола — это тоже колебательные системы). Скорость, с которой колебания затухают, очень важный параметр. Он называется декремент затухания.

2.2. RLC-контур. Свободные колебания window.top.document.title = «2.2. RLC-контур. Свободные колебания»;

В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур (рис. 2.2.1).

Рисунок 2.2.1.Последовательный RLC-контур

Когда ключ K находится в положении 1, конденсатор заряжается до напряжения . После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер.

Закон Ома для замкнутой RLC-цепи, не содержащей внешнего источника тока, записывается в виде

qqtRLC

Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0). Тогда

Здесь принято обозначение: Уравнение (*) описывает свободные колебания в LC-контуре в отсутствие затухания. По виду оно в точности совпадает с уравнением свободных колебаний груза на пружине в отсутствие сил трения (ч. I, § 2.2). Рис. 2.2.2 иллюстрирует аналогию процессов свободных электрических и механических колебаний. На рисунке приведены графики изменения заряда q (t) конденсатора и смещения x (t) груза от положения равновесия, а также графики тока J (t) и скорости груза υ (t) за один период колебаний.

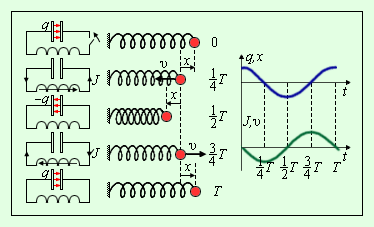Рисунок 2.2.2.Аналогия процессов свободных электрических и механических колебаний

Сравнение свободных колебаний груза на пружине и процессов в электрическом колебательном контуре позволяет сделать заключение об аналогии между электрическими и механическими величинами. Эти аналогии представлены в таблице 1.

Электрические величины	Механические величины
Заряд конденсатора	q (t)	Координата	x (t)
Ток в цепи		Скорость
Индуктивность	L	Масса	m
Величина, обратная электроемкости		Жесткость	k
Напряжение на конденсаторе		Упругая сила	kx
Энергия электрического поля конденсатора		Потенциальная энергия пружины
Магнитная энергия катушки		Кинетическая энергия
Магнитный поток	LI	Импульс	mυ

Таблица 1

В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону

Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний

Амплитуда q и начальная фаза φ определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия. В частности, для процесса колебаний, который начнется в контуре (рис. 2.2.1) после переключения ключа K в положение 2, q = C, φ = 0.

При свободных колебаниях происходит периодическое превращение электрической энергии W_э, запасенной в конденсаторе, в магнитную энергию W_м катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:

Все реальные контуры содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рис. 2.2.3).

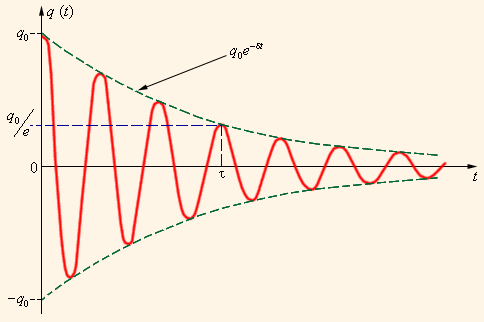Рисунок 2.2.3.Затухающие колебания в контуре

Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: F_тр = – βυ. Коэффициент β в этой формуле аналогичен сопротивлению R электрического контура. Уравнение свободных колебаний в контуре при наличии затухания имеет вид

Физическая величина δ = R / 2L называется коэффициентом затухания. Решением этого дифференциального уравнения является функция

exp (–δt)Re ≈ 2,7 разавременем затухания

Для RLC-контура добротность Q выражается формулой

Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен.

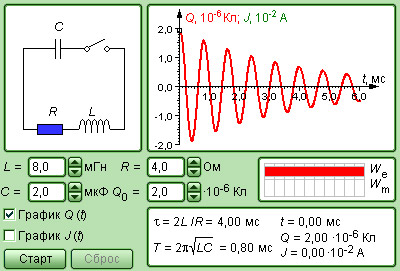
Следует отметить, что собственная частота ω свободных колебаний в контуре с не очень высокой добротностью несколько меньше собственной частоты ω идеального контура с теми же значениями L и C. Но при Q ≥ (5÷10) этим различием можно пренебречь.

Модель.
Свободные колебания в RLC-контуре

Резонанс напряжений

Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:

и конденсатор в 1000 пФ

Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.

Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!

Ну что же, приступим ;-). Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.

Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:

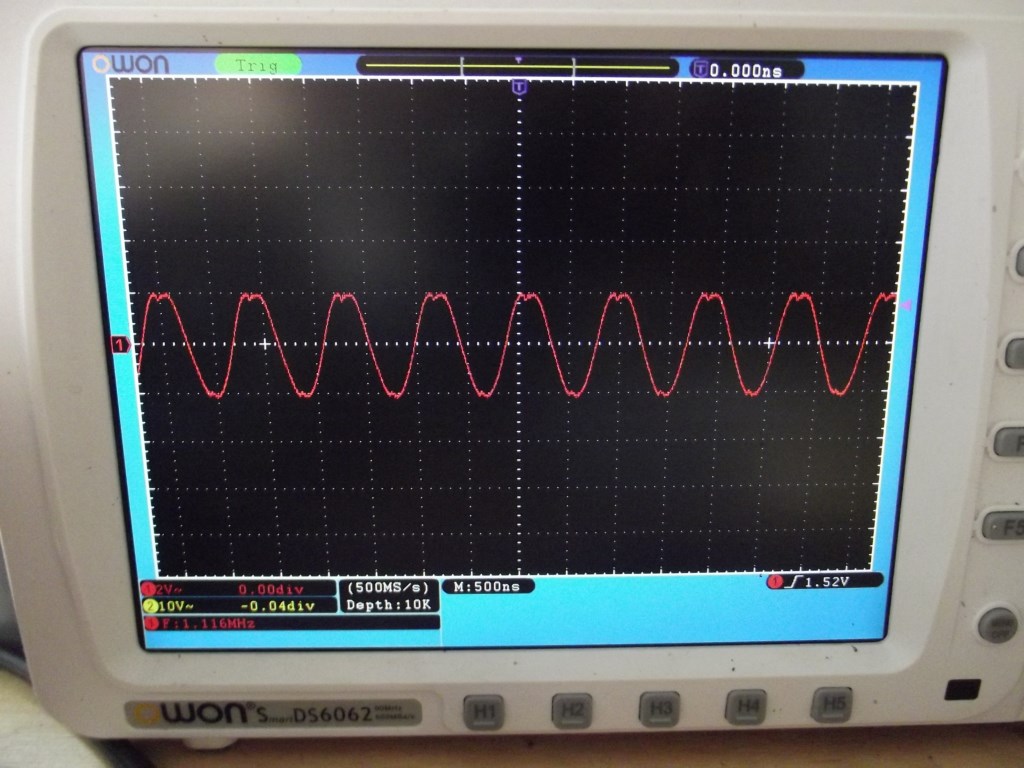
Размах амплитуды 4 Вольта

Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.

Теперь небольшой прикол

Вот этот сигнал мы подаем на наш последовательный колебательный контур:

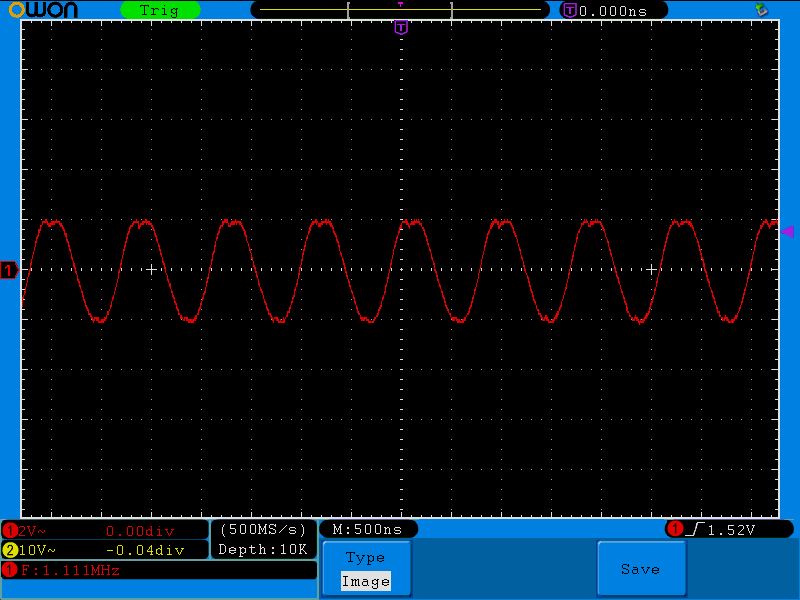
Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.

Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:

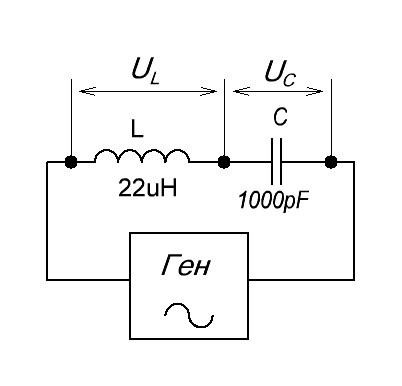
Смотрим напряжение на конденсаторе:

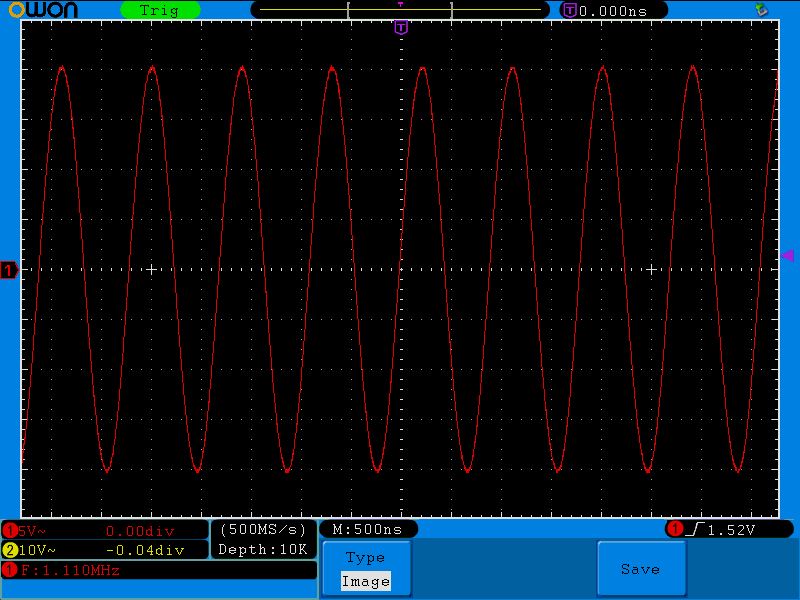
Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!

Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:

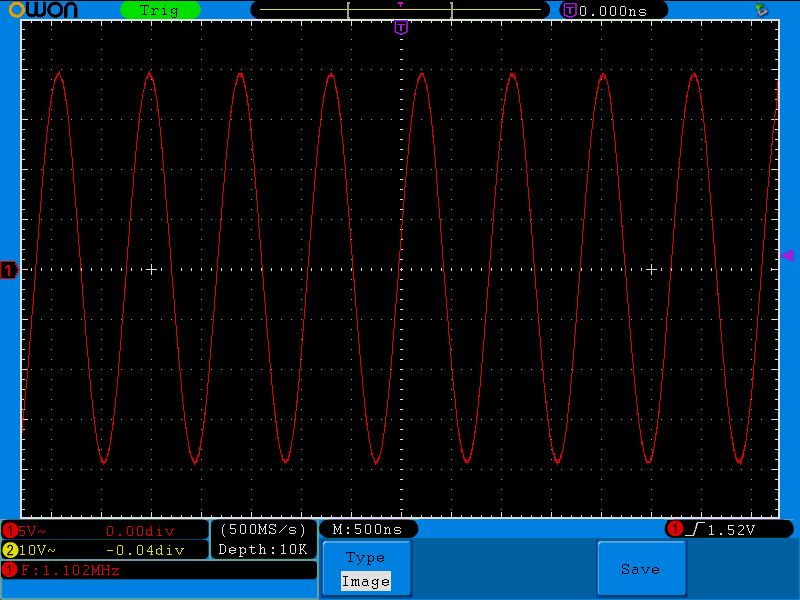
Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!

Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:

Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!

Объяснение резонанса напряжения

При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.

При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение U_L = IX_L, а на конденсаторе U_C = IX_C. А так как при резонансе у нас X_L= X_C, то получаем что U_L= U_C , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.

Электрическая добротность динамика.

Интересный момент, когда динамик пытается вернуть диффузор в своё первоначальное состояние, после снятия электрического сигнала, катушка динамика вырабатывает ЭДС, двигаясь в магнитном поле. Динамики, в свою очередь, непосредственно подключены к усилителю, аудиопроводом.

Усилитель имеет практически нулевое сопротивление. И когда сигнал от усилителя пропадает, а динамик «на ходу», то он (динамик) работает как генератор. Причем, работает как генератор, с максимальной нагрузкой (выходы катушки практически закорочены сопротивлением усилителя). Эта нагрузка создает достаточно мощную тормозящую силу, вынуждающую катушку и диффузор быстро останавливаться.

Среднее значение электрической добротности (Qes), для низкочастотного динамика – от 0,2 до 0,9, но чаще – близкий к единице. И если сравнивать параметры электрической добротности со значениями механической добротности, то получается вывод – гашение колебаний (потеря энергии) происходит, в основном, из-за электрической составляющей.

Принцип работы параллельного колебательного контура

Давайте подцепим к генератору частоты реальный параллельный колебательный контур

Что будет, если мы подадим на контур ток с частотой в ноль Герц, то есть постоянный ток? Он спокойно побежит через катушку и будет ограничиваться лишь сопротивлением потерь R самой катушки. Через конденсатор ток не побежит, потому что конденсатор не пропускает постоянный ток. Об это я писал еще в статье конденсатор в цепи постоянного и переменного тока.

Давайте тогда будем добавлять частоту. Итак, с увеличением частоты у нас конденсатор и катушка начнут оказывать реактивное сопротивление электрическому току.

Что такое — добротность динамика?

Пожалуй, сначала вопрос. А для чего вам вообще нужно знать этот параметр? Что он вам даст? Ведь этот параметр не скажет о том, на сколько хорошо или плохо сделан ваш динамик? На сколько хорошо он будет играть? Но когда возникает вопрос о доработке акустики, параметры добротности динамиков могут многое рассказать о технических возможностях будущей системы.

Но для полной картины возможностей динамика нужно будет собрать кучу параметров. В кругах «продвинутых» меломанов эти параметры называют — «параметры Тиля-Смолла».

Измерением этих параметров точно не будем заниматься, по крайней мере — не в этот раз. Но о таком параметре как — добротность, поговорим немного. Без научных выкладок и «глубокой физики». Порассуждаем по простому, что бы стало немного понятнее — какая добротность динамика лучше и почему?

Если проще, то речь идет про затухающие колебания. Так как разговор идет относительно динамика, то как он (динамик) ведет себя после подачи на него сигнала, как быстро затухают колебания диффузора при прекращении подачи сигнала на динамик.

Что такое — «запасы энергии в системе»?