Кинетическая и потенциальная энергия — определение, теоремы и формулы расчетов

Потенциальная энергия

Помимо кинетической энергии, которая представляет собой энергию движения существует потенциальная энергия. Она присуща телам, обладающим потенциалом к совершению работы, взаимодействию друг с другом. Поднятое над Землей тело обладает потенциалом к взаимодействию с гравитационными силами. Чем больше оно отдаляется от поверхности, тем сильнее возрастает потенциальная энергия. Если кинетическая энергия зависит от скорости и массы, потенциальная энергия обусловлена взаимным расположением объектов или их частей.

Во время падения тела, сила тяготения совершает работу, на которую влияет только начальное и конечное положение движущегося объекта. Форма траектории значения не имеет. Если она замкнутая, значение работы потенциальной силы будет равным нулю. Среди потенциальных сил можно выделить силу тяготения, упругости и др. Еще их называют консервативными. При упругой деформации тело наделяется энергией взаимодействия между его разными частями.

При перемещении тела вверх, работа силы тяжести будет иметь отрицательное значение.

Примеры

Подробно разберем пример с вертикальным перемещением шара из точки высота, которой обозначена \ на отметку с высотой с \.

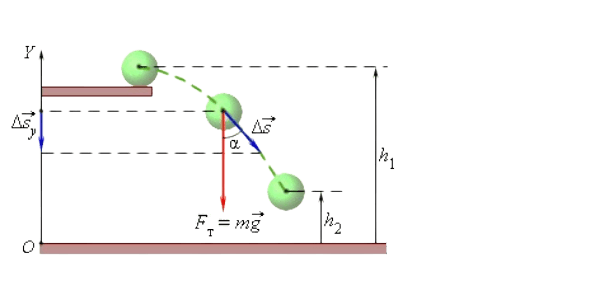
Работа, совершенная силой тяжести равна отрицательному значению \:

\

В следующем примере происходит перемещение тела по наклонной поверхности. Во время движения вниз, на него действует сила тяжести F равная mg. Работа, совершаемая этой силой равна:

\

В данной формуле, h служит для обозначения высоты наклонной плоскости, S – модуля перемещения, равного длине этой плоскости.

В следующем примере рассмотрим перемещение объекта из точки B в точку C по траектории любой формы. Тело движется по фрагментам наклонной плоскости, с разными высотами \ и т.д. Работа A представлена в виде суммы работ, совершаемой силой тяжести на каждом из участков пути.

\

\ и \ являются высотами относительно земной поверхности, на которых находятся точки B и C.

Равенство демонстрирует нам отсутствие влияния траектории пути, по которому движется тело, на работу силы тяжести. Если объект перемещается вниз, значение работы, выполняемой силой тяжести будет положительным, в противном случае – отрицательным. Тогда равенство будет выглядеть следующим образом:

Формулировка и доказательство теоремы

Теорема о кинетической энергии утверждает, что кинетическая энергия тела пропорциональна квадрату его скорости и массе, т.е.

Кинетическая энергия K тела равна половине произведения его массы m на квадрат скорости v, то есть:

K = ½ * m * v^2

Данная формула является основным математическим выражением, описывающим зависимость кинетической энергии от массы и скорости тела.

Доказательство данной теоремы основывается на законах динамики и принципах работы силы.

Из второго закона Ньютона следует, что сумма сил, действующих на тело, равна произведению массы тела на его ускорение:

ΣF = m * a

Кинетическая энергия тела определяется как работа силы, противодействующей его движению. По определению, работа силы W равна перемножению модуля силы на путь, по которому сила приложена:

W = F * s

Так как а = s/t, где t — время движения, то сила F можно выразить через ускорение и массу тела:

F = m * a = m * (s / t)

Тогда работу силы можно записать в виде:

W = m * (s / t) * s = (m * s^2) / t

С другой стороны, работа силы F также может быть записана через изменение кинетической энергии тела:

W = ΔK = K2 — K1

где K1 и K2 — кинетические энергии тела в начальный и конечный моменты времени соответственно.

Из уравнения работы силы и изменения кинетической энергии тела, получаем:

(m * s^2) / t = K2 — K1

Так как сила, действующая на тело, не зависит от времени, то t можно сократить с обеих сторон. Получаем:

m * s^2 = 2 * (K2 — K1)

Определяем разницу кинетических энергий как ΔK = 2 * (K2 — K1):

m * s^2 = ΔK

Таким образом, получаем формулу, связывающую массу тела, перемещение и изменение кинетической энергии:

m * s^2 = ΔK

Разделив обе части уравнения на 2, получаем формулировку теоремы о кинетической энергии:

½ * m * s^2 = ΔK

Что эквивалентно формуле кинетической энергии K = ½ * m * v^2.

Дельта в физике атома

В атомной физике дельта-энергия обычно обозначается как ΔE и представляет собой разницу между двумя энергетическими уровнями атома. Эта разность энергии может быть вызвана воздействием внешнего поля, переходом электрона на другой энергетический уровень или другими процессами.

Дельта-время (Δt) в атомной физике относится к изменению времени. Оно может быть использовано для измерения длительности отдельных событий или переходов в атоме.

Дельта-квант (ΔQ) может быть использован для обозначения разницы между двумя квантовыми состояниями атома. Он относится к изменению энергии, связанному с переходом между этими состояниями.

Формула для вычисления дельта k

Для вычисления дельта k в физике используется следующая формула:

Формула:

∆k = kконечное — kначальное

Здесь ∆k обозначает изменение величины k, а k_{конечное} и k_{начальное} представляют собой начальное и конечное значения величины k соответственно.

Формула для вычисления дельта k может использоваться в различных физических задачах, где требуется определить изменение некоторой физической величины. Например, она может применяться при вычислении изменения кинетической энергии тела или изменении уровня некоторой физической величины в ходе физического процесса.

При использовании этой формулы нужно учитывать, что значения k_{конечное} и k_{начальное} должны быть выражены в одних и тех же единицах измерения. Иначе результат будет некорректным.

Также следует отметить, что формула для вычисления дельта k предполагает, что изменение величины k происходит только в одном направлении, то есть от k_{начальное} к k_{конечное}. Если требуется учесть и обратное изменение, то нужно использовать другую формулу или добавить соответствующий знак перед результатом.

Дельта в электромагнетизме

В электромагнетизме понятие «дельта» может иметь несколько значений и использоваться в различных контекстах.

• Дельта-функция или функция Дирака — это математическая функция, используемая для описания идеализированных точечных зарядов или источников поля. Она является обобщением понятия дельта-функции в математическом анализе и имеет массу применений в электродинамике.
• Дельта вектор или вектор Дирака — это векторное поле, описывающее распределение электрического заряда или магнитного поля в пространстве. Он используется для описания точечных источников магнитного и электрического поля и является интуитивным способом представления электромагнитных полей.
• Дельта-метод или метод переменного параметра — это метод приближенного решения уравнений электромагнетизма на основе линеаризации этих уравнений вокруг точки равновесия. Он используется для анализа линейных систем и предоставляет простой способ определения приближенного решения электромагнитных задач.

Все эти понятия «дельта» имеют важное значение в электромагнетизме и нашли широкое применение в различных областях физики, включая электродинамику, радиофизику, теорию антенн, электрические цепи и другие

Почему приращение кинетической энергии важно?

Приращение кинетической энергии имеет большое значение в физике и механике. Оно позволяет измерить изменение энергии, которое происходит при движении тела. Кинетическая энергия определяет возможность работы и передачи энергии от одного объекта к другому.

Приращение кинетической энергии позволяет оценить эффективность работы силы, влияющей на движение. Если кинетическая энергия изменяется, это означает, что работа была совершена и произошло изменение скорости или массы объекта.

Контроль приращения кинетической энергии важен в различных сферах науки и техники. Например, в автомобильном производстве при разработке безопасных систем торможения и амортизации необходимо знать, как изменится кинетическая энергия при движении автомобиля.

Приращение кинетической энергии также используется при рассмотрении различных физических явлений, таких как удары, искры или взрывы. Измерение и анализ приращения кинетической энергии позволяет предсказывать результаты воздействия и определять возможные последствия.

Понимание приращения кинетической энергии позволяет обнаруживать потенциальные опасности и разрабатывать меры предосторожности для защиты людей и окружающей среды. Оно также помогает в создании более эффективных и безопасных технологий передвижения, производства и энергетики

Вывод: Таким образом, приращение кинетической энергии является важным показателем изменения энергии в физических системах. Оно имеет большое значение в практических применениях, помогает определить работу силы и предсказывать последствия различных физических явлений.

Понятие КПД (коэффициента полезного действия)

Термин «КПД» широко используется не только среди профессионалов, но и в быту. Под ним понимают, насколько совершенная работа превышает полезную, т.е. ту, ради которой механизм или прибор приобретается.

Учеными разработана специальная формула, из которой следует, что КПД всегда меньше единицы. Чтобы рассчитать коэффициент, нужно полезную работу, выраженную в Джоулях, разделить на энергию, которая затрачена на эту работу. Поскольку энергия также выражается в Джоулях, конечная расчетная величина безразмерна.

Объяснить бытовым языком данное понятие можно так: энергия, выделяемая от плиты, на которой должен закипеть чайник, расходуется не только на его нагревание. Она должна нагреть саму посудину, воздух вокруг нее, сам нагревательный элемент. И только ее часть будет расходоваться на передачу воде. Чтобы сориентироваться, насколько долго будет закипать чайник одного объема на различного вида печах, нужно знать их КПД.

В поисках наиболее эффективного прибора не стоит стремиться к единице. Такого не бывает. Например, КПД атомной электростанции примерно равно 35%.

Происходит это по двум причинам:

1. Исходя из закона сохранения энергии, получить больше работы, чем затрачено энергии, невозможно.
2. Любая работа сопровождается определенными потерями, будь-то нагревание тары или преодоление сил трения при движении по поверхности.

Формула кинетической энергии

Раз тело движущееся и энергией обладает именно за счет движения, можно выдвинуть кое-какое предположение. Логично, что при формула кинетической энергии «завязана» со значением скорости.

Во-вторых, неглупо предположить, что масса также связана с количеством энергии в системе. Если кинуть в соседа бумажный самолетик, это будет называться шалостью — величина кинетической энергии несущественная. А вот если кинуть в соседа кирпич… Не шалость. Целое покушение!

Понятие о том, что совершенная работа равна изменению энергии, остается неизменным. Просто на этот раз будем иметь в виду энергию кинетическую. Условимся обозначать ее как $E_к$. Заранее обозначим связь работы и кинетической энергии:$A=\Delta{E_к}$.

Продолжим выяснять, как выглядит формула кинетической энергии. Для этого предположим, что на тело с массой $m$ действует постоянная сила $F$. В результате тело проходит некоторое расстояние $s$. По второму закону Ньютона значение силы равно произведению массы на ускорение:$F=ma$.

Перемещение при равноускоренном движении, при условии, что тело начинает движение из состояния покоя, равно:$s=\frac{\upsilon^2}{2a}$.

Связывая две обозначенных формулы с формулой работы, находим:$A=F\cdot s=F\cdot \frac{\upsilon^2}{2a}=\frac{ma\cdot \upsilon^2}{2a}=\frac{mv^2}{2}$.

Полученное в результате подстановок полупроизведение массы на квадрат скорости — это и есть формула кинетической энергии $E_к$.

Экспериментально формула кинетической энергии была подкреплена нидерландским ученым Вильгельмом Гравезандом в XVIII веке. Он обнаружил, что мячик, брошенный в стену с удвоенной скоростью, оставляет в четыре раза большее углубление. Следовательно энергия пропорциональна квадрату скорости. Это мы непосредственно и наблюдаем в формуле, выведенной от работы и перемещения.  

Формула кинетической энергии: задача на расчет

Условие. Автомобиль массой $1~т$ тянет буксир с постоянной силой. Определите кинетическую энергию автомобиля в момент времени $4~с$ на основе предложенного графика зависимости скорости от времени.

Решение. Формула кинетической энергии:$E_к=\frac{m \upsilon^2}{2}$.

Опираясь на график, находим, что в момент времени $4~с$ скорость автомобиля составляла $8~м/с$. Масса автомобиля указана в тоннах, переведем ее в СИ: $m=1~т=1000~кг$. Подставим значения с формулу и посчитаем кинетическую энергию.

Получается:$E_к=\frac{1000~кг \cdot (8\frac{м}{с})^2}{2}=32000~Дж=32~кДж$.

Если бы мы каким-нибудь образом придумали устройство, которое бы позволяло переводить кинетическую энергию нашего автомобиля из задачи в электроэнергию, мы бы здорово удивились. $32~кДж$ хватило бы максимум на час работы двух энергосберегающих лампочек мощностью $20~Вт$.

Формула для вычисления дельта k

Для вычисления дельта k в физике используется следующая формула:

Формула:

∆k = kконечное — kначальное

Здесь ∆k обозначает изменение величины k, а k_{конечное} и k_{начальное} представляют собой начальное и конечное значения величины k соответственно.

Формула для вычисления дельта k может использоваться в различных физических задачах, где требуется определить изменение некоторой физической величины. Например, она может применяться при вычислении изменения кинетической энергии тела или изменении уровня некоторой физической величины в ходе физического процесса.

При использовании этой формулы нужно учитывать, что значения k_{конечное} и k_{начальное} должны быть выражены в одних и тех же единицах измерения. Иначе результат будет некорректным.

Также следует отметить, что формула для вычисления дельта k предполагает, что изменение величины k происходит только в одном направлении, то есть от k_{начальное} к k_{конечное}. Если требуется учесть и обратное изменение, то нужно использовать другую формулу или добавить соответствующий знак перед результатом.

Что такое работа в физике?

В физике работа \(W\) определяется как энергия, получаемая объектом от внешней силы, вызывающей перемещение работа вызовет не только изменение перемещения, но и изменение скорости.

Что такое реакции конденсации? Типы и примеры (Биология)

Уравнение для работы вдоль прямой линии имеет вид

\

где объект перемещается с перемещением \(s\) под действием силы \(F\) в том же направлении, что и перемещение. Как видно из этого уравнения, работа увеличивается независимо от того, увеличивается ли сила или перемещение. Она имеет единицы измерения \(\text{сила}\times\text{перемещение} = 1\text{ N}\cdot\text{m} = 1\text{ J}\).

Рис. 1 — Ящик массой \(m\) на поверхности без трения испытывает силу \(F\), направленную вправо.

Допустим, у нас есть неподвижный ящик с массой \(m\) на поверхности без трения. Если посмотреть на действующие на него силы, то вес \(w\) направлен вниз, а нормальная сила \(n\) — вверх. Если мы толкнем его силой \(F\) вправо, то ящик начнет скользить вправо. Это произойдет потому, что ящик будет подчиняться второму закону Ньютона и будет иметь ускорение в направлениисайт чистая сила . Потому что ускорение это скорость, с которой скорость изменяется со временем, ящик начнет ускоряться. Это также означает, что работа, совершенная над объектом, положительна, поскольку направление перемещения и чистая сила одинаковы.

Рис. 2 — На рисунке коробка движется вправо. По мере движения на нее действует чистая сила в противоположном направлении, и объект замедляется.

Однако если вы приложите силу слева, в то время как ящик будет двигаться вправо, то чистая сила будет направлена влево, что означает, что ускорение также будет направлено влево. Если скорость и ускорение противоположны, это означает, что объект будет замедляться! Также, если вы понимаете, что направление чистой силы и смещения противоположны, вы можете сделать вывод, что общая выполненная работа на объекте является отрицательным.

Что можно сказать о работе, совершенной над блоком, если сила была приложена под углом к перемещению? В нашем случае с блоком, перемещение все еще лежит вдоль прямой линии. Работа будет положительной, отрицательной или нулевой в зависимости от угла между силой \(\vec F\) и перемещением \(\vec s\). Работа является скаляром и дается векторным произведением \(\vec F\) и \(\vec s\).s\).

\

Где \(\phi\) — угол между силой \(\vec F\) и перемещением \(\vec s\).

Напомним, что скалярное произведение дается \(\vec A \cdot \vec B = AB\cos \phi\).

Рис. 3 — На ящик массой \(m\), движущийся со скоростью \(v\), действует вертикальная сила.

Если коробка движется вправо, а к ней вертикально вниз приложена постоянная сила, то чистая сила равна нулю, и работа, совершаемая этой силой, равна нулю. Это видно из скалярного произведения \(\vec F \cdot \vec s = Fs\cos 90^{\circ} = 0\). Ускорение также будет равно нулю, поэтому изменение скорости будет нулевым. Поэтому, в отсутствие трения, коробка продолжает двигаться.с одинаковой скоростью в одном направлении.

Это может показаться нелогичным, но помните из нашего первого рисунка: постоянная сила, направленная вниз на рисунке выше, приведет к нормальной силе той же величины, но в противоположном направлении. Чистой силы, направленной вниз, не будет, и, хотя существует смещение \(s\), произведение \(W = Fs = 0\). Но если бы существовало трение между коробкой и поверхностью, сила трения была бы равнаувеличивается, так как она пропорциональна нормальной силе (\(f = \mu N\)). Сила трения совершает работу в направлении, противоположном перемещению, и блок замедляется. Это происходит потому, что, согласно уравнению (2),

\

Вы увидите примеры теоремы о работе-энергии с трением в одном из последующих разделов этой статьи.

Если сила, действующая на объект, вызывает смещение этого объекта, то будет происходить проделанная работа силой, действующей на объект, и ему будет передана энергия. Скорость объекта изменится: он ускорится, если работа, совершенная над объектом, положительна, и замедлится, если работа, совершенная над объектом, отрицательна.

Дополнительные примеры работы см. в статье о работе, а также о случаях, когда на тело действует несколько сил.

Кинетическая энергия

Каждое движущееся тело, наделено кинетической энергией. Когда объект пребывает в состоянии покоя этот показатель равен нулю. На него влияет масса тела (m) и скорость (v) перемещения.

Формула 1

Для вычисления кинетической энергии применяют формулу:

\

Кинетическая энергия (Ек) находится в прямой пропорциональной зависимости от массы и квадрата скорости тела.

Пример

Скорость тела, движущегося под воздействием определенных сил, изменилась с \  на \. Это говорит о том, что этими силами была совершена конкретная работа  A.

Работа комплекса сил, оказывающих воздействие на тело, равна по значению той работе, которую совершает равнодействующая сила.

\

\

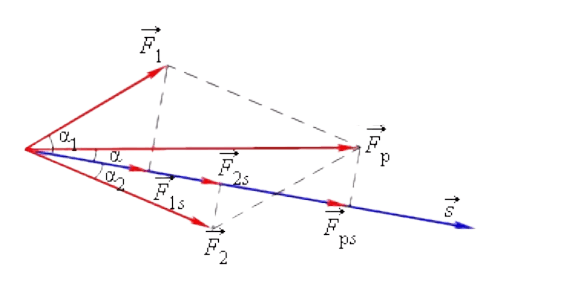
Определим взаимозависимость увеличения или уменьшения скорости тела и работы, совершаемой силами, воздействующими на объект.

Представим, что тело движется под воздействием одной силы \, направленной вдоль определенной прямой. Сила действует на тело таким образом, что его движение становится равноускоренным и прямолинейным.

Таким образом направление векторов \ является одинаковым. Следовательно, эти значения можно представить в качестве алгебраических величин.

\

Исходя из этого:

\

Это подтверждает предположение, что работа, совершенная под воздействием силы, прямо пропорциональна изменения значения квадрата скорости движения тела.

Влияние кинетической энергии на движение тел

К = ½mv²,

где К – кинетическая энергия, m – масса тела, v – скорость тела. Таким образом, чем больше масса тела и скорость его движения, тем больше его кинетическая энергия.

Влияние кинетической энергии на движение тела заключается в следующем:

1. Кинетическая энергия определяет скорость тела. Чем выше кинетическая энергия, тем больше скорость тела. Это объясняется тем, что часть энергии, превращаясь в кинетическую, увеличивает скорость тела.

2. Кинетическая энергия определяет расстояние, которое пройдет тело. Чем больше кинетическая энергия, тем больше расстояние, которое тело сможет пройти. Это связано с тем, что часть энергии, превращаясь в работу, перемещает тело.

3. Кинетическая энергия является важным показателем для определения количества работы, совершенной телом. Чем больше кинетическая энергия, тем больше работы совершает тело.

Таким образом, кинетическая энергия играет важную роль в движении тела. Она определяет скорость и расстояние, которые тело способно пройти, а также количество работы, которое оно может совершить.

Ускорение и изменение кинетической энергии

Кинетическая энергия (обозначается символом Е) – это энергия, связанная с движением тела. Она зависит от его массы и скорости и определяется формулой Е = ½mv², где m – масса тела, v – его скорость.

Когда тело движется с постоянным ускорением, его ускорение и изменение кинетической энергии тесно связаны. Чем больше ускорение тела, тем быстрее оно изменяет свою кинетическую энергию. Например, если два тела имеют одинаковую массу, но одно из них имеет большее ускорение, то оно будет иметь большую кинетическую энергию.

Ускорение и изменение кинетической энергии влияют на движение тела и его способность совершать работу. При ускорении тело приобретает энергию, которая может быть использована для совершения работы или преодоления силы трения.

Определение ускорения и понимание его связи с изменением кинетической энергии помогает улучшить наши знания о физических процессах и предсказать результаты различных движений тел.

Изменение скорости и изменение кинетической энергии

Кинетическая энергия тела определяется его массой и скоростью. Таким образом, изменение скорости тела может привести к изменению его кинетической энергии.

При изменении скорости тела происходит изменение его кинетической энергии в соответствии с законом сохранения энергии. Если тело движется с постоянной скоростью, то его кинетическая энергия остается неизменной. Однако, если скорость тела меняется, то меняется и его кинетическая энергия.

Изменение кинетической энергии тела связано с величиной прикладываемой силы, действующей на него. В соответствии со вторым законом Ньютона, сила равна произведению массы тела на ускорение. Используя это выражение, можно вывести формулу для изменения кинетической энергии:

Формула	Обозначение
ΔK = F · Δx = m · a · Δx	ΔK — изменение кинетической энергииF — сила, действующая на телоm — масса телаa — ускорение телаΔx — изменение координаты тела

Таким образом, изменение кинетической энергии тела пропорционально прикладываемой силе, изменению координаты и массе тела.

Изменение скорости и изменение кинетической энергии тесно связаны друг с другом. Величина кинетической энергии зависит от квадрата скорости тела. Поэтому, небольшое изменение скорости может привести к значительному изменению кинетической энергии.

Знание о закономерностях изменения скорости и изменения кинетической энергии позволяет более точно описывать и прогнозировать движение тел в физике.

Зависимость расстояния торможения от кинетической энергии

Кинетическая энергия тела определяется его массой и скоростью. Чем больше масса и скорость тела, тем больше его кинетическая энергия. При торможении, часть этой энергии преобразуется в другие формы энергии, такие как тепло и звук.

Зависимость расстояния торможения от кинетической энергии объясняется законом сохранения энергии. При торможении, энергия тела передается тормозам и в результате снижается его кинетическая энергия. Чем больше кинетическая энергия, тем больше энергии нужно передать тормозам, чтобы полностью остановить тело. Следовательно, расстояние торможения будет больше для тел с более высокой кинетической энергией.

Также стоит учитывать, что зависимость расстояния торможения от кинетической энергии может быть разной для разных типов транспортных средств и условий дороги. Например, на сухой асфальтовой дороге автомобиль с большей кинетической энергией будет иметь большее расстояние торможения, чем на мокрой или грязной дороге.

Кинетическая энергия – понятие и определение

Определение

Кинетическая энергия – это способность движущегося тела совершать определенную работу.

Например, движущийся автомобиль способен снести находящееся перед ним препятствие, а падающий камень – оставить вмятину на металлической пластинке.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Кинетическая энергия зависит от скорости движения и массы тела. Она описывается формулой:

\(E_k=\frac{m\nu^2}2\)

Единицей измерения кинетической энергии является Джоуль (Дж).

Проведя простые преобразования, легко вывести формулы для вычисления массы тела и скорости движения:

\(m=\frac{2E_k}{\nu^2}\)

\(\nu=\sqrt{\frac{2E_k}m}\)

Из основной формулы видно: во сколько раз изменяется масса тела, во столько раз изменяется и величина кинетической энергии. Например, если масса будет уменьшена или увеличена в 5 раз, то и величина кинетической энергии станет соответственно меньше или больше в 5 раз.

При увеличении скорости кинетическая энергия увеличивается в квадратичной зависимости. Допустим, скорость движения тела стала в 6 раз больше. Соответственно его кинетическая энергия возросла в 36 раз.

Формула кинетической энергии тела справедлива только для скоростей значительно меньших, чем скорость света. Если же скорость движения приближается к 300 000 км/с, то тут начинает действовать теория относительности, созданная Альбертом Эйнштейном.

Кинетическая энергия зависит от особенностей рассмотрения системы. Если тело принимают как макроскопический объект, то оно будет обладать внутренней энергией. В этом случае кинетическая энергия возникнет только в момент его движения.

Это же тело можно рассматривать и с микроскопической точки зрения. Тепловое движение атомов и молекул обуславливает внутреннюю энергию тела. В то же время средняя кинетическая энергия этого движения пропорциональна абсолютной температуре тела. Коэффициент этой пропорциональной зависимости называется постоянной Больцмана.

Кинетическая энергия атомов и молекул при рассмотрении тела на микроскопическом уровне описывается формулой:

\(E_k=\frac32kT\)

где \(k\) – это постоянная Больцмана.

Применение дельта л силы упругости

В инженерии и конструкционных науках, знание дельты л силы упругости позволяет предсказать, как объект будет реагировать на приложение силы. Это может быть полезно при проектировании механизмов, строительстве зданий и разработке новых материалов.

В медицине дельта л силы упругости может быть использована для измерения деформаций тканей и оценки их эластичности

Это важно для диагностики и лечения различных заболеваний

В физике и материаловедении знание дельты л помогает понять, как материалы деформируются под действием силы упругости. Это может быть полезно при исследовании свойств материалов и разработке новых технологий.

Дельта л силы упругости также широко применяется в спорте и фитнесе. В спортивной экипировке (например, в спортивной обуви и одежде) использование материалов с определенной дельтой л может повысить комфорт и производительность спортсменов.

Кроме того, понимание дельты л силы упругости может быть полезно в повседневной жизни. Например, при выборе матраца или подушки, знание и использование дельты л может помочь найти оптимальную поддержку и комфорт.

Таким образом, дельта л силы упругости имеет широкий спектр применения в различных областях и может быть полезна для понимания и оптимизации различных процессов и систем.

Использование дельта л силы упругости в инженерии

Одно из основных применений дельты л силы упругости в инженерии – определение деформаций материалов. Путем измерения дельты л исходной длины и зная коэффициент упругости материала, можно определить деформацию. Это позволяет инженерам проанализировать поведение материала под нагрузкой и предотвратить возможные поломки или разрушения конструкций.

Другое применение дельты л силы упругости заключается в расчете напряжений. Поскольку деформация и напряжение в материале связаны между собой, зная деформацию и коэффициент упругости, можно рассчитать напряжение в материале. Это помогает инженерам определить, насколько надежна конструкция и какие силы она может выдержать без поломки.

Также дельта л силы упругости используется для определения упругих модулей материалов. Коэффициент упругости позволяет выразить зависимость силы упругости от деформации и определить упругий модуль материала

Это особенно важно при выборе материалов для конструкций, так как упругий модуль определяет их прочность и долговечность

Использование дельты л силы упругости в инженерии позволяет предотвратить различные проблемы и повысить надежность конструкций. Зная деформацию и напряжение, можно проектировать более безопасные и эффективные системы. Поэтому понимание и умение использовать дельту л силы упругости является важным навыком для инженеров.

Роль дельта л силы упругости в физике

Упругие материалы обладают свойством возвращаться в исходное состояние после применения к ним какой-либо внешней силы. Это свойство называется упругостью. Дельта л силы упругости представляет собой изменение длины материала под действием внешней силы.

Под действием внешней силы упругий материал может испытывать деформацию. Дельта л силы упругости определяется как разница между исходной длиной материала и его длиной после деформации.

Размер дельта л силы упругости зависит от ряда факторов, включая свойства материала и величину приложенной силы. Определение дельта л силы упругости позволяет исследователям измерять и сравнивать упругие свойства различных материалов.

Дельта л силы упругости также играет важную роль в различных приложениях. Например, в инженерии она помогает предсказывать и оценивать поведение конструкций под действием внешних нагрузок. В медицинской технике знание дельта л силы упругости позволяет разработать и оптимизировать протезы и другие медицинские изделия.

Как вычислить дельту

Греческой буквой Δ в науке принято обозначать разность между конечным и начальным значениями некой величины. Например, Δt – разность температур в начале и конце реакции или время, за которое выполнена работа. В некоторых случаях четвертую букву греческого алфавита заменяют прописной или строчной латинской d

Но латиницей в данном случае необходимо пользоваться осторожно, поскольку этой же буквой обозначаются и другие понятия

Вам понадобится

• — измерительные приборы;
• — калькулятор.

Инструкция

Чтобы узнать, на сколько изменилась та или иная величина, нужно в первую очередь узнать начальное и конечное значение. Если речь идет о практической задаче, нужные параметры можно измерить. Нужный вам параметр можно в принципе назвать любой буквой, но лучше использовать принятые в науке обозначения. Допустим, вам нужно найти, насколько изменился объем вещества при нагревании. Результат первого измерения запишите как V1

Проведите второе измерение. Например, после того, как закончите нагревать объект. Определите его объем и обозначьте его как V2. Вычислите дельту по формуле ΔV = V2-V1. Может получиться так, что второй результат будет меньше первого. Посчитайте модуль числа так же, как и в любом другом случае, и поставьте знак «-». Не забудьте, что оба измерения должны быть в одних и тех же единицах. Если нужно, переведите их.

Нередки задачи, когда необходимо вычислить дельту между фактическим и средним значением. Например, вам дана точка, которая поменяла свои координаты по двум осям. Обозначьте координаты как x1,x2, x3 и т. д. Найдите среднее значение. Затем вычислите разницу между полученным результатом и значением каждой координаты.

Если вам нужно вычислить приращение функции f(x), определите ее значение в жестко заданной точке — пусть это будет, например, х0. Чтобы вычислить дельту, вам необходимо сравнить значение функции в этой точке с ее же значением в любой другой точке по заданной оси. Для этого вычтите значение функции в точке х1 из ее же значения в точке х0. Это и будет Δf. Чтобы найти приращение аргумента, определите его значения в заданных точках и вычислите разность.

Буквой Δ обозначают и абсолютную погрешность. Она тоже представляет собой разность. За начальное и конечное значение принимаются истинное и приближенное значения. Величина дельты в данном случае соответствует классу точности прибора.

• Как делить матрицы
• Как найти n в арифметической прогрессии
• Как решать комплексные числа

Добавить комментарий к статье Похожие советы

• Что такое дельта
• Что такое модуль
• Как найти абсолютную и относительную погрешность
• Как рассчитать дельту
• Как найти дельта t
• Как вычислить пределы функций, не пользуясь средствами дифференциального исчисления
• Имеет ли функция частные производные
• Как рассчитать определитель
• Как раскрывать модули
• Как вычислить определитель второго порядка
• Как найти знаменатель прогрессии
• В чем заключается геометрический смысл определенного интеграла
• Как найти вероятность события

Выводы

В данной статье мы рассмотрели, как найти дельта k в физике и разобрали примеры, которые помогли нам лучше понять этот процесс.

Выводы, которые мы можем сделать:

• Дельта k — это изменение кинетической энергии объекта;
• Для расчета дельта k необходимо знать начальное значение кинетической энергии и конечное значение;
• Формула для расчета дельта k: дельта k = конечное значение — начальное значение;
• Дельта k может быть как положительной, так и отрицательной величиной, в зависимости от изменения кинетической энергии объекта;
• Изменение кинетической энергии связано с работой и силой, действующей на объект.

Понимание процесса нахождения дельта k позволяет нам анализировать изменение кинетической энергии объекта и связывать его с внешними факторами, такими как силы, работа и др.

Определение дельта k помогает углубить наше понимание физических процессов и использовать это знание в решении задач и анализе физических явлений.