Площадь сферы

Возможные проблемы и пути их решения

При поиске сечения шара через площадь могут возникнуть некоторые проблемы, которые могут затруднить или повлиять на точность результатов. Ниже представлены некоторые возможные проблемы и пути их решения:

Проблема
Путь решения
Неизвестная площадь сечения
Определение площади сечения шара можно выполнить с помощью различных методов, таких как вычисление по формуле, использование технологий сканирования или использование специальных инструментов и аппаратуры.
Необходимость точного измерения
Для достижения более точных и надежных результатов измерения площади сечения шара рекомендуется использовать электронные измерительные инструменты с высокой точностью.
Сложность в подготовке образца
Перед измерением необходимо правильно подготовить образец шара, чтобы избежать искажений результатов

Важно учитывать факторы, такие как чистота поверхности, отсутствие дефектов и правильное крепление.
Влияние окружающих условий
Окружающие условия, такие как температура, влажность и давление, могут оказывать влияние на площадь сечения шара. При выполнении измерений необходимо учитывать и компенсировать эти факторы.
Ошибки алгоритма расчета
При использовании программных алгоритмов для расчета площади сечения шара могут возникать ошибки

Важно внимательно проверять и верифицировать результаты, а также обновлять программное обеспечение при необходимости.

Учитывая эти возможные проблемы и следуя рекомендациям по их решению, можно повысить точность и надежность результатов при поиске сечения шара через площадь.

В ходе исследования мы применили практические методы для нахождения сечения шара через площадь. Для этого мы использовали следующий алгоритм:

1. Начальные данные: заданная площадь сечения шара.
2. Рассчитываем радиус шара по формуле: r = √(S / π).
3. Путем подстановки данного радиуса в формулы для объема и площади шара, проверяем, что площадь сечения соответствует заданной площади.

Таким образом, мы успешно применили практические методы для нахождения сечения шара через заданную площадь. Полученный результат может быть полезен в различных областях, где требуется работа с геометрическими фигурами.

Разница между шаром и сферой

Когда людям задают вопрос, чем отличается сфер от шара, многие попросту пожимают плечами, думая, что фактически это одно и то же (аналогия с кругом и окружностью).

В повседневной жизни мы редко говорим сфера, чаще шар или шарик. И не все понимают какая разница между этими двумя геометрическими понятиями. Наверное можно сказать, что сфера это внешняя оболочка шара. Воздушный шарик, например, на самом деле не шар, а сфера. При условии, конечно, его абсолютной «круглости». Как я понимаю, то у шара абсолютно все точки поверхности равноудалены от его центра, а у сферф это условие не является обязательным.

Апельсин, футбольный мяч, арбуз, похожи на шар. Из всех тел заданного объёма шар имеет наименьшую поверхность. Поверхность шара называют сферой. Расстояние от точек сферы до её центра называется радиусом сферы и обычно обозначается R. Радиусом также называется любой отрезок, соединяющий точку сферы с её центром.

Определение.Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Любой диаметр соответствует 2-м радиусам. Часть шара (сферы), которая отсекается от него любой плоскостью (ABC), является шаровым (сферическим) сегментом. Круги ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота. 1/3 произведения площади поверхности шара на длину радиуса. Зачастую озвучивают так: объём шара равен 1/3 произведения поверхности шара на его радиус.

Все эти точки находятся от центра геометрического тела на расстоянии, которое не больше заданного. Само данное расстояние называется радиусом. От центра сферы все точки в пространстве равноудалены.

Образованная фигура — будет шар. Поэтому шар называют также телом вращения. Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.

По свойствам латекса шары можно разделить на три вида:1. Пастель2. Декоратор3. Металлик

Описание	Название вида в традициях фирм производителей
“ Latex Occidental ” (Мексика)	“ Latex Douro ” (Португалия)	“ Belbal ” (Бельгия)	“ Gemar ballons ”
1. Матовые непрозрачные
2. Прозрачные и полупрозрачные	Декоратор	Кристалл	Кристалл, Спешл*	Кристалл,
3. Непрозрачные с металлическим блеском.	Металлик, Перламутр***	Металлик	Металлик	Металлик

Спешл* — полупрозрачные шары.Неон** — полупрозрачные, специфичного оттенка.Перламутр*** — металлик светлых, нежных тонов.При совместном использовании разных видов, следует уделять большее внимание калибровке шаров. Это связано с тем, что латекс Пастели, Декоратора и Металлика отличаются по своим свойствам (например, латекс шаров Металлик гораздо плотнее и менее пластичен), а это сказывается на форме шаров

Объем шара

Формула для вычисления объема шара имеет вид:

где R — радиус шара.

Если нужно найти объем шарового сегмента — воспользуйтесь формулой:

V сег =πh 2 (R-h/3), h — высота шарового сегмента.

Площадь поверхности шара или сферы

Чтобы вычислить площадь сферы или площадь поверхности шара (это одно и то же):

где R — радиус сферы.

Архимед очень любил шар и сферу, он даже попросил оставить на его гробницу рисунок, на котором в цилиндр вписан шар. Архимед считал, что объем шара и его поверхность равны двум третьим от объема и поверхности цилиндра, в который вписан шар»

В главе 2 мы продолжим “строительную геометрию» и расскажем о строении и свойствах важнейших пространственных фигур — шара и сферы, цилиндров и конусов, призм и пирамид. Большинство предметов, созданных руками человека, — здания, машины, мебель, посуда и т.д., и т.п., состоит из частей, имеющих форму этих фигур.

§ 4. СФЕРА И ШАР

После прямых и плоскостей сфера и шар — самые простые, но очень важные и богатые разнообразными свойствами пространственные фигуры. О геометрических свойствах шара и его поверхности — сферы — написаны целые книги. Некоторые из этих свойств были известны еще древнегреческим геометрам, а некоторые найдены совсем недавно, в последние годы. Эти свойства (вместе с законами естествознания) объясняют, почему, например, форму шара имеют небесные тела и икринки рыб, почему в форме шара делают батискафы и футбольные мячи, почему так распространены в технике шарикоподшипники и т.д. Мы можем доказать лишь самые простые свойства шара. Доказательства других, хотя и очень важных свойств, часто требуют применения совсем не элементарных методов, хотя формулировки таких свойств могут быть очень простыми: например, среди всех тел, имеющих данную площадь поверхности, наибольший объем у шара.

4.1. Определения сферы и шара.

Определяются сфера и шар в пространстве совершенно так же, как окружность и круг на плоскости. Сферой называется фигура, состоящая из всех точек пространства, удаленных от данной

ной точки на одно и то же (положительное) расстояние.

Эта точка называется центром сферы, а расстояние — ее радиусом (рис. 4.1).

Итак, сфера с центром О и радиусом R — это фигура, образованная всеми точками X пространства, для которых

Шаром называется фигура, образованная всеми точками пространства, находящимися на расстоянии не большем данного (положительного) расстояния от данной точки. Эта точка называется центром шара, а данное расстояние — его радиусом.

Итак, шар с центром О и радиусом R — это фигура, образованная всеми точками X пространства, для которых

Те точки X шара с центром О и радиусом R, для которых образуют сферу. Говорят, что эта сфера ограничивает данный шар или что она является его поверхностью.

Определение.

Сфера
поверхность шара
центром сферы

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шар
центром шара

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.
Радиус сферы (шара)
(R) — это расстояние от центра сферы (шара) O
к любой точке сферы (поверхности шара).

Определение.
Диаметр сферы (шара)
(D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула.
Объём шара
:

V =	4	π R 3 =	1	π D 3
3	6

Формула.
Площадь поверхности сферы
через радиус или диаметр:

S = 4π
R 2 = π
D 2

РЖД проиндексируют зарплату сотрудникам с 1 марта

Порядок индексации зарплаты в 2024 году	Размер дополнительных выплат медицинским работникам будет варьироваться в диапазоне от 4,5 до 18,5 тыс.р. Цель повышения – совершенствование оплаты труда в первичном звене здравоохранения и выравнивание зарплат медицинских работников в разных регионах.
Какие дополнительные выплаты положены медикам в 2023 году. Кто и сколько будет получать	Об этом говорится в сообщении РЖД, передает ТАСС. При этом заработная плата всех остальных работников РЖД, в соответствии с коллективным договором, с этой даты будет проиндексирована на 2,9%.
Зарплата медиков в 2024 году: на сколько и когда повысят	С 1 июля 2023 года власти проиндексируют заработную плату медиков, соцработников и работников культуры в Московской области на 8-10%. Прибавка будет варьироваться от 5 до 12 тысяч рублей, сообщил губернатор Подмосковья Андрей Воробьев.

Что такое шар?

Свойство	Описание
Радиус	Расстояние от центра шара до любой точки его поверхности.
Диаметр	Удвоенное значение радиуса. Это самая длинная прямая линия, которую можно провести внутри шара, и она проходит через его центр.
Объем	Количество пространства, занимаемого шаром. Формула для вычисления объема шара: V = (4/3)πr³, где V — объем, r — радиус, π — математическая константа, примерно равная 3,14.
Площадь поверхности	Общая площадь всех поверхностей шара. Формула для вычисления площади поверхности: S = 4πr², где S — площадь поверхности, r — радиус, π — математическая константа, примерно равная 3,14.

Шары используются в различных областях, включая математику, физику, геометрию, астрономию, механику и технику. Они являются основными объектами при рассмотрении законов движения, взаимодействия и свойств материи.

В технике шары применяются в шариковых подшипниках, шариковых клапанах, а также в создании шаровых моделей и макетов для демонстрации определенных процессов и явлений. В астрономии шары используются для моделирования планет и других небесных тел, а также в исследовании структуры и эволюции Вселенной.

Кроме того, шары широко используются в различных видов спорта, таких как футбол, баскетбол, гольф и других, где они являются основными мячами для игры.

Определение шара

Параметр	Описание
Радиус	Расстояние от центра шара до любой точки его поверхности.
Диаметр	Удвоенное значение радиуса. Равен расстоянию между двумя точками на поверхности шара, проходящими через его центр.
Объем	Количество пространства, занимаемое шаром.
Площадь поверхности	Площадь внешней поверхности шара. Вычисляется по формуле S = 4πr^2, где r — радиус шара.

Шары находят широкое применение в различных областях, таких как геометрия, физика, инженерия, астрономия и технические науки. Они используются для моделирования сферических объектов, расчетов объемов, создания шаровых сегментов и сферических зон, а также для создания шарообразных конструкций в архитектуре и дизайне.

Структура шара

Основной элемент шара — сфера. Сфера представляет собой поверхность, все точки которой находятся на одинаковом расстоянии от ее центра. Она является внешней границей шара и определяет его форму.

Внутри сферы находится объем шара, который заполнен воздухом, газом или жидкостью. Этот объем представляет собой пространство, ограниченное сферической поверхностью.

Центр шара является точкой, которая находится в середине сферы. От центра до любой точки на сфере все расстояния одинаковые и равны радиусу шара — расстоянию от центра до поверхности.

Шары могут быть разных размеров и иметь разные радиусы в зависимости от их предназначения и области применения. Они широко используются в научных и технических областях, а также в различных игровых и спортивных занятиях.

Физические свойства шара

Основные физические свойства шара включают его диаметр, радиус и площадь его поверхности. Диаметр шара — это линия, проходящая через его центр и заканчивающаяся на противоположных сторонах поверхности. Радиус шара — это расстояние от центра до любой точки на его поверхности.

Площадь поверхности шара можно вычислить, используя формулу:

S = 4πr²

где S — площадь поверхности, π (пи) — математическая константа, примерное значение равно 3.14159, r — радиус шара.

Важной физической характеристикой шара является его объем. Объем шара можно определить по формуле:. V = (4/3)πr³

V = (4/3)πr³

где V — объем шара, π (пи) — математическая константа, примерное значение равно 3.14159, r — радиус шара.

Шары широко используются в различных областях, таких как геометрия, физика, астрономия и технические науки. Благодаря своим уникальным свойствам, шары могут быть использованы для моделирования и изучения различных процессов и явлений в природе и искусстве.

Определение величины

Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.

По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.

На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».

Площадь поперечного сечения

При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:

S = πR 2

При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.

Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:

a 2 + b 2 = c 2

Из нее можно вывести такую формулу:

c = S*q*r*t*(a 2 + b 2 )

Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:

S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:

используется в тех случаях, когда сечение идет параллельно двум основаниям.

При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:

где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.

Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:

где 2а – значение хорды, расчета площади поперечного сечения.

Разновидности круглых тел

Круглые тела — это геометрические фигуры, которые имеют форму сферы, шара или гемисферы. Круглые тела применяются в различных областях математики, физики, астрономии и техники. В зависимости от формы, круглые тела могут иметь различные свойства и характеристики.

Шар — это круглое тело, которое также имеет одинаковые расстояния от центра до всех точек на его поверхности. Шары используются в физике и механике для моделирования движения мячей и других объектов.

Гемисфера — это половина сферы, которая образуется плоскостью, проходящей через ее центр. Гемисферы используются в архитектуре и строительстве для создания куполов и других крышных конструкций.

Круглые тела также могут быть объединены для создания более сложных фигур, таких как цилиндры и конусы. Например, цилиндр состоит из двух параллельных круговых боковых поверхностей и одной прямой боковой поверхности. Конус состоит из круговой и одной конической боковой поверхности.

Более подробно изучить разновидности круглых тел можно в двумерной геометрии или в пространственной геометрии в рамках школьной программы. Это поможет лучше понять свойства круглых тел и применять их в практических задачах.

Архитектура

Архитекторы часто используют форму круга для создания куполов, куполообразных сводов и арок. Эти элементы строительства могут быть найдены в зданиях разных эпох и стилей, начиная от античности и заканчивая современной архитектурой. Круглое сечение шара обладает высокой прочностью и стабильностью, что позволяет создавать сложные и монументальные конструкции без необходимости использования большого количества материалов.

Кроме того, форма круга также широко использовалась в архитектуре для создания общественных и жилых зданий. Округлые фасады, закругленные углы и окна в форме круга создают гармоничный и приятный визуальный эффект. Они могут быть использованы как для декоративных целей, так и для повышения комфорта и эргономики внутреннего пространства здания.

В современной архитектуре форма круга и сечение шара также активно используются для создания инновационных и экологически устойчивых зданий. Круглые здания имеют меньшую площадь поверхности, что позволяет сэкономить на затратах на отопление и/или охлаждение. Кроме того, форма круга способствует естественной циркуляции воздуха и света внутри здания, что делает его более энергоэффективным и удобным для жильцов.

Использование сечения шара в архитектуре открывает широкие возможности для создания уникальных, функциональных и эстетически привлекательных зданий. Однако, при проектировании и строительстве таких сооружений необходимо учесть как внешние архитектурные требования, так и инженерные и конструктивные ограничения, чтобы достичь оптимального результата.

Альтернативные способы определения сечения шара

В мире существует множество методов для определения сечения шара, которые отличаются точностью и удобством использования. Некоторые из них могут быть реализованы при помощи простых инструментов и иметь практическое применение.

Одним из таких методов является использование деревянной модели шара и специального инструмента для определения площади сечения. Деревянная модель шара может быть изготовлена самостоятельно или приобретена в специализированном магазине. Специальный инструмент представляет собой небольшую линейку с отметками. Для определения площади сечения необходимо поместить модель шара на плоскую поверхность и акуратно провести инструментом через сечение. После этого, с помощью отметок на инструменте, можно измерить длину и ширину сечения и рассчитать площадь по формуле.

Еще одним способом определения сечения шара является использование программного обеспечения для визуализации и моделирования трехмерных объектов. С помощью такого программного обеспечения можно создать трехмерную модель шара и провести через нее плоскость, которая представляет собой сечение шара. Затем, при помощи инструментов программы, можно вычислить площадь сечения. Этот метод является более точным и удобным, но требует наличие соответствующего программного обеспечения и навыков работы с ним.

Также, для определения сечения шара можно использовать метод геометрического моделирования. Для этого необходимо создать физическую модель шара и провести через нее плоскость. Затем, используя инструменты геометрического моделирования, можно измерить площадь сечения. Этот метод также требует определенных навыков и специального оборудования, но может быть применен в некоторых практических ситуациях.

В итоге, определение сечения шара может быть осуществлено различными способами, от простых и доступных до более сложных и точных. Выбор метода зависит от условий и требований задачи.

Части шара

Сегмент шара – это часть шара, отсекаемая плоскостью. Иногда называется шаровым сегментом. На рисунке ниже окрашен в зеленый цвет.

Срез шара – часть шара между двумя параллельными плоскостями, пересекающими его. Также может называться шаровым слоем. На рисунке ниже закрашен желтым.

Сектор шара – состоит из шарового сегмента и конуса, вершина которого находится центре шара, а основание совпадает с основанием сегмента. На рисунке ниже сектор залит оранжевым.

Секущая, хорда, секущая плоскость сферы и их свойства

Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.

Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).

Секущая плоскость — это плоскость, которая пересекает сферу.

Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).Любая хорда, проходящая через центр сферы (шара) является диаметром.Хорда является отрезком секущей прямой.Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:

d < R

Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m < R

Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:

r = √R2 — m2,

где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.Определение.Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.

Касательная, касательная плоскость к сфере и их свойства

Касательная к сфере — это прямая, которая касается сферы только в одной точке.

Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновенияРасстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегментаh называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента. Формула.Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:

S = 2πRh

Формула.Объём сегмента сферы с высотой h через радиус сферы R:

V =	h2π	(3R — h)
3

Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.

Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.

Площадь поверхности сектора S с высотой O1H (h) через радиус шара OH (R):

S = πR(2h + √2hR — h2)

Объём сектора V с высотой O1H (h) через радиус шара OH (R):

V =	2πR2h
3

Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.

Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.

Как изменится объем шара при увеличении радиуса в 4 раза

Объем шара (V)

=

4/3 × π × (радиус шара)^3

Радиус шара является основным параметром, определяющим его размеры. Если радиус шара увеличивается в 4 раза, то это значит, что новый радиус будет равен 4 * (старый радиус).

Для вычисления нового объема шара нужно подставить новое значение радиуса в формулу объема:

Новый объем шара (V’)

=

4/3 × π × (4 * (старый радиус))^3

Упрощая выражение, получаем:

Новый объем шара (V’)

=

4/3 × π × (4^3) × (старый радиус^3)

4^3 равно 64, поэтому можно продолжить упрощение:

Новый объем шара (V’)

=

4/3 × π × 64 × (старый радиус^3)

Итак, при увеличении радиуса в 4 раза, объем шара увеличивается в 64 раза.

Необходимо отметить, что данная формула использует значение числа π (пи), которое приближенно равно 3,14159. Это значит, что вычисленный объем шара будет иметь некоторую погрешность из-за приближенного значения π.

Увеличение радиуса шара в 4 раза не просто увеличивает его размер, но и оказывает существенное влияние на его объем. Объем шара прямо пропорционален кубу его радиуса.

Пусть изначальный радиус шара равен r и его объем равен V. Тогда, при увеличении радиуса в 4 раза, новый радиус будет равен 4r. Чтобы вычислить новый объем шара, нужно вознести новый радиус в куб и умножить на константу 4/3.

Таким образом, новый объем шара (V’) будет равен: V’ = (4/3) * π * (4r)^3.

Путем упрощения данного уравнения можно увидеть, что новый объем шара (V’) будет равен 64 раза исходному объему (V).

Таким образом, увеличение радиуса шара в 4 раза приводит к увеличению его объема в 64 раза

Это заметное влияние радиуса на объем шара подчеркивает важность размера данной величины при расчетах и измерениях

Определение и примеры

Примером геометрического тела является куб. Куб имеет шесть равных равносторонних граней, восемь вершин и двенадцать ребер. Другим примером геометрического тела является цилиндр. У цилиндра есть два основания, которые представляют собой круги, и боковая поверхность, которая представляет собой плоскость, параллельную основаниям. Цилиндр также имеет ребра, вершины и высоту.

Кроме куба и цилиндра, в группу геометрических тел входят также сфера, пирамида, конус, параллелепипед, призма и многие другие.

Название	Описание	Примеры
Куб	Фигура с шестью равными равносторонними гранями	Рубикова головоломка
Цилиндр	Тело, у которого два основания представляют собой круги, а боковая поверхность — плоскость, параллельная основаниям	Банка из-под газировки
Сфера	Тело, все точки которого равноудалены от центра	Мяч для боулинга
Пирамида	Тело, у которого одно из оснований является многоугольником, а боковые грани — треугольниками, соединяющими вершины основания с одной точкой — вершиной пирамиды	Египетская пирамида Хеопса
Конус	Тело, у которого одно основание является кругом, а боковая поверхность состоит из всех линий, соединяющих точки на окружности основания с вершиной конуса	Хвойное дерево
Параллелепипед	Тело, у которого все грани прямоугольники, а противоположные грани параллельны	Книга
Призма	Тело, у которого два основания являются одинаковыми многоугольниками, а боковые грани — прямоугольники, соединяющие соответствующие стороны оснований	Дом

Что представляет собой группа геометрических тел

Группа геометрических тел состоит из различных трехмерных фигур, которые имеют определенные свойства и характеристики.

В эту группу входят следующие тела:

• Параллелепипед — трехмерная фигура, у которой все грани являются прямоугольниками.
• Пирамида — многогранник с одной вершиной и множеством граней, которые сходятся к этой вершине.
• Цилиндр — тело, ограниченное двумя параллельными плоскостями (основаниями) и боковой поверхностью, представляющей собой закругленный прямоугольник.
• Конус — геометрическое тело, имеющее одно основание и вершину, к которой сходятся все стороны этого основания.
• Шар — сферическое тело, все точки поверхности которого равноудалены от центра.
• Тор — геометрическое тело, представляющее собой поверхность, получаемую вращением окружности вокруг своей оси.

Эти геометрические тела имеют различные формы и свойства. Они широко применяются в геометрии, физике, инженерии и других науках для моделирования и решения различных задач.

Примеры из группы геометрических тел

Группа геометрических тел включает в себя разнообразные объекты с определенными геометрическими формами и свойствами. Некоторые примеры таких тел:

1. Параллелепипед — это тело, имеющее шесть прямоугольных граней. Он образуется, когда на каждой стороне прямоугольника построена грань-прямоугольник, параллельная данной стороне.
2. Сфера — это тело, все точки которого находятся на одинаковом расстоянии от центра. Сфера обладает свойством симметрии и не имеет граней.
3. Цилиндр — это тело, имеющее две круглые грани, параллельные друг другу, и боковую поверхность, состоящую из плоской кривой.
4. Конус — это тело, у которого одна грань представляет собой плоскую кривую, а вторая грань — круг.
5. Пирамида — это тело, у которого одна грань является многоугольником, а все остальные грани — треугольники, соединяющие вершины многоугольника с одной точкой.

Это лишь некоторые примеры из многообразия геометрических тел, которые существуют в математике и геометрии.

Элементы сферы

Так называются геометрические величины, знание которых позволяет описать либо всю фигуру, либо отдельные ее части. Основными ее элементами являются следующие:

• Радиус r, который уже был упомянут ранее. Он является расстоянием от центра фигуры до сферической поверхности. По сути, это единственная величина, которая описывает все свойства сферы.
• Диаметр d, или D. Это отрезок, концы которого лежат на сферической поверхности, а середина проходит через центральную точку фигуры. Диаметр сферы можно провести бесконечным числом способов, но все полученные отрезки будут иметь одинаковую длину, которая равна удвоенному радиусу, то есть D = 2*R.
• Площадь поверхности S — двумерная характеристика, формула для которой будет приведена ниже.
• Связанные со сферой трехмерные углы измеряются в стерадианах. Один стерадиан — это угол, вершина которого лежит в центре сферы, и который опирается на часть сферической поверхности, имеющей площадь R 2 .

Площадь поверхности фигуры

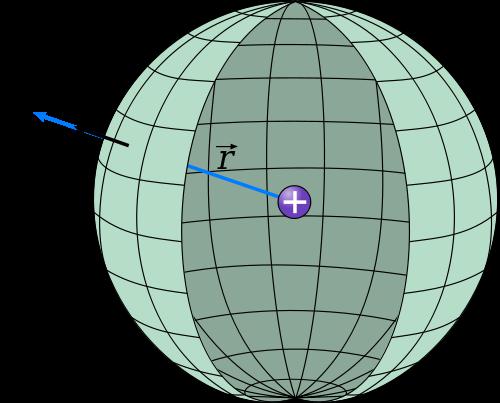
Эта величина обозначается латинской буквой S. Формула вычисления площади сферы имеет следующий вид:

Формула демонстрирует, что площадь S может быть вычислена при условии знания радиуса фигуры. Если же известен ее диаметр D, тогда формулу сферы можно записать так:

Иррациональное число pi, для которого приведены четыре знака после запятой, в ряде математических расчетов можно использовать с точностью до сотых, то есть 3,14.

Любопытно также рассмотреть вопрос, скольким стерадианам соответствует вся поверхность рассматриваемой фигуры. Исходя из определения этой величины, получаем:

Для вычисления любого объемного угла следует в выражение выше подставить соответствующее значение площади S.

Шары в природе

Шарообразная форма встречается в природе в различных объектах – от растений и грибов до камней и планет. Присутствие шаровой формы у этих объектов обусловлено разными причинами, такими как защита, сохранение энергии и оптимизация площади поверхности.

Многие растения имеют шаровидные формы. Например, хризантемы и солнцелики отлично известны своими причудливыми шарообразными соцветиями. У этих растений шарообразная форма помогает лучше распространять семена или привлекать опылителей. Порой шаровидная форма может быть необходима для защиты самих растений от ветра и других неблагоприятных факторов.

Шары также встречаются в мире грибов. Например, в семействе грибов Ascomycota есть так называемые аскомицеты – грибы, у которых репродуктивные органы, называемые асками, имеют шаровидную форму. Это облегчает распространение спор грибов и их симбиотическую жизнь с другими организмами.

Площадь поверхности фигуры

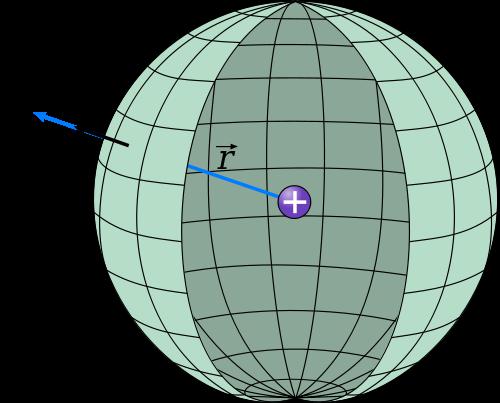
Эта величина обозначается латинской буквой S. Формула вычисления площади сферы имеет следующий вид:

Формула демонстрирует, что площадь S может быть вычислена при условии знания радиуса фигуры. Если же известен ее диаметр D, тогда формулу сферы можно записать так:

Иррациональное число pi, для которого приведены четыре знака после запятой, в ряде математических расчетов можно использовать с точностью до сотых, то есть 3,14.

Любопытно также рассмотреть вопрос, скольким стерадианам соответствует вся поверхность рассматриваемой фигуры. Исходя из определения этой величины, получаем:

Для вычисления любого объемного угла следует в выражение выше подставить соответствующее значение площади S.

Общие сведения

Площадь — это величина геометрической фигуры в двумерном пространстве. Она используется в математике, медицине, инженерных и других науках, например, в вычислении поперечного сечения клеток, атомов, или труб, таких как кровеносные сосуды или водопроводные трубы. В географии площадь используются для сравнения размеров городов, озер, стран и других географических объектов. При расчетах плотности населения также используется площадь. Плотность населения определяется как количество людей на единицу площади.

Читать также: Алюминиевый конструкционный профиль и линейные направляющие