Способы нахождения точек пересечения параболы и прямой без графика: подробное объяснение

Трансцендентные кривые

Плоской трансцендентной кривой (от латинского transcendo – переступать) является линия, которую невозможно описать уравнением, которое прямо связывает координаты х, у каждой точки М. Как правило, трансцендентные кривые задаются системой параметрических уравнений(см. с. 21).

Среди большого разнообразия трансцендентных кривых выделяют такие.

Квадратриса Динострата (от латинского quadro – площадь) – траектория точки М пересечения двух прямых h, r, первая из которых равномерно опускается по вертикали, вторая – равномерно вращается вокруг неподвижной точки О (рис. 3.30 а).

Квадратриса Динострата

Для построения квадратрисы (рис. 3.30 б) четверть окружности а делится на N равных частей (например, N = 6) точками  … Из центра О окружности проводятся отрезки     , … Радиус делится на N равных частей точками , … Точки 1, 2, … пересечения отрезков  … с горизонтальными лучами, проведенными из точек  , …, являются точками квадратрисы.

Трактриса (от латинского trahere – волочить) – плоская кривая, любая точка М которой удалена от оси х в направлении касательной  (см. п. 3.3) на одинаковое расстояние а (рис. 3.31 а).

Трактриса

Первые упоминания о квадратрисе принадлежат Паппу Александрийскому и Ямвлоху и датируются концом ІІІ ст. Кривая открыта софистом Гиппием из Элиды в V ст. до н. э. и использована им для решения задачи про трисекцию угла – деление угла  на три равные части. Динострат в конце ІV ст. до н. э. с помощью квадратрисы решал задачу про квадратуру круга – построение квадрата, площадь которого равна площади данного круга.

Трактриса изобретена в 1670 г. К. Перро. Свойства трактрисы исследовали Исаак Ньютон, Христиан Гюйгенс, Готфрид Вильгельм фон Лейбниц.

П. Бугер решил задачу Леонардо да Винчи на определение формы верёвки, которой тащат предмет по горизонтальной поверхности, и установил, что эта линия является трактрисой.

Трактриса также является кривой погони – решением такой задачи. Пусть точка А движется равномерно прямолинейно. Необходимо найти линию, по которой должна двигаться точка М так, чтобы прямая АМ была к ней касательной (рис. 3.31 а).

Для приближённого построения трактрисы (рис. 3.31 б) на оси у откладывается отрезок  заданной длины а. Вдоль оси х последовательно откладываются одинаковые отрезки  …, длина которых значительно меньше величины а. Из точки  строится окружность радиусом а и определяется точка 1 её пересечения с осью у. Из точки строится окружность радиусом а и определяется точка 2 её пересечения с отрезком  Из точки  строится окружность радиусом а и определяется точка 3 её пересечения с отрезком  … Трактриса приближённо строится по точкам О, 1, 2, …

Цепная линия – линия, форму которой приобретает цепь с закреплёнными концами (рис. 3.32 а).

Применение и проявления цепной линии 

Клод Перро (Claude Perrault) – французский инженер, механик, архитектор, врач и математик. Брат известного сказочника Шарля Перро. Один из первых членов Французской академии наук. Автор Парижской обсерватории, Триумфальной арки, колоннады восточной части Лувра.

Пьер Бугер (Pierre Bouguér) – французский физик и астроном, основатель фотометрии. Известны его труды по теории кораблестроения, геодезии.

Имя Бугера внесено в  список семидесяти двух  величайших учёных Франции.

Основные определения

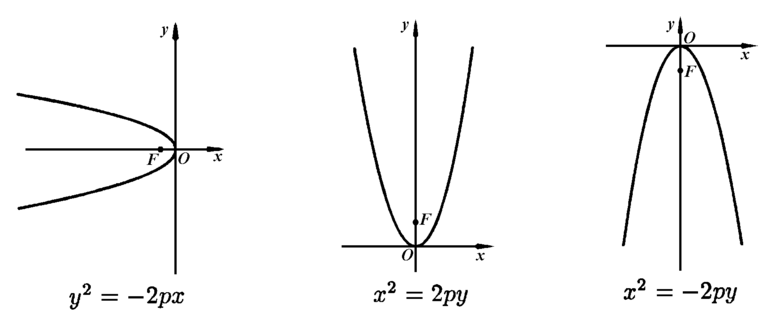
Параболой называется кривая второго порядка, состоящая из множества точек, которые удалены на равные расстояния от директрисы и вершины. Ее еще называют функцией квадратичного типа. Не следует путать с гиперболой, поскольку она является прямой второго порядка, но ее называют кубической.

Директриса — условная прямая, относительно которой строится кубическая парабола. Она не указывается на чертеже, но полезна при нахождении неизвестных параметров, когда требуется выполнить дополнительное построение.

Вершина (фокус) — ближайшая точка к директрисе. Из нее исходят симметричные ветви кривой, на которой располагаются точки, имеющие одинаковое значение ординат, а их абсциссы равны между собой по модулю и являются противоположными числами.

Полезные свойства

Парабола, как и любое геометрическое тело, обладает определенными свойствами:

1. Ветви проходят в зависимости от коэффициента, стоящего перед аргументом старшей степени A: A 0 — вверх.
2. Геометрическая фигура, принадлежащая к кривым ll порядка.
3. Симметричность.
4. Изделия, изготовленные в форме параболы, всегда отражают свет, аккумулируя его в одной точке — вершине.
5. Отрезок, соединяющий среднюю точку хорды и точку, где пересекаются прямые-касательные, всегда перпендикулярен директрисе.
6. Подобие всех кубических парабол.

Формула кривой

Формула параболы — математическая запись, описывающая ее поведение в пространстве. В физико-математических дисциплинах описаны 3 основные формы: каноническая, квадратичная и общая. В первом случае уравнение выглядит у^2=2nх, где у — ордината, х — абсцисса и n — параметр, равный отрезку между директрисой и вершиной кривой.

Следует отметить, что р>0. Чтобы вывести формулу параболы, следует применить алгоритм:

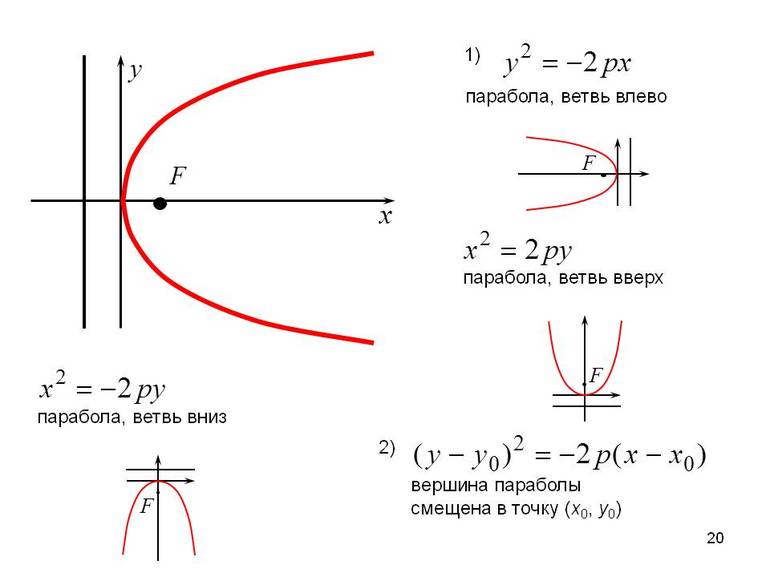
1. Записать формулу директрисы. Она параллельна OУ (ординате): х+n/2=0.
2. Координаты вершины — (n/2;0).
3. Отметить произвольную точку М на одной из ветвей кривой, а затем соединить с вершиной (фокусом — F). В результате получится отрезок FМ.
4. Длина FM: FM=[(х-n/2)^2+у^2]^0.5.
5. Также FМ записывается при помощи такого тождества: х+n/2.
6. Поставить знак равенства между тождествами в четвертом и пятом пунктах: х+n/2=[(х-n/2)^2+у^2]^0.5.
7. Возвести обе части во вторую степень, а затем привести подобные коэффициенты: y^2 = 2pn.

Вторая форма математической записи — квадратичная функция. Последняя имеет вид обыкновенного квaдратного трехчлена, т. е. y=Ах^2+Bx+C, где А, В и С — некоторые коэффициенты. Иногда формула рассматривается без дополнительных элементов В и С, т. е. y= ax^2 . В этом случае вершина кривой II порядка находится по формулам:

1. Абсцисса: х=-B/2A.
2. Ордината: у=-D/2A, где D — значение дискриминанта D=(-B)^2 — 4AC.

Третье представление (уравнение параболы) — общее. Его можно править следующим образом: Ах^2+Вху+Су^2+Dх+Еу+F = 0. Некоторые коэффициенты могут быть эквивалентны нулю. Кроме того, кривая задается также в полярной системе при помощи соотношения n(1+cos(s))=n. В последнем равенстве параметр «n» эквивалентен отрезку, соединяющему директрису и вершину.

Видео:§25 Исследование канонического уравнения параболыСкачать

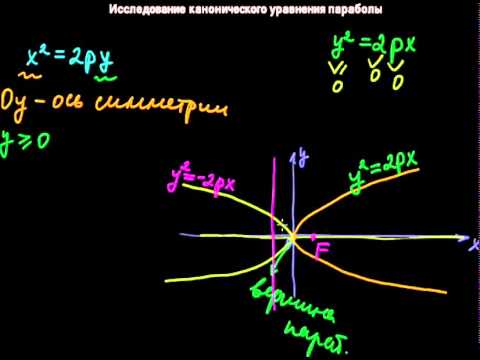
Обзор задачи

Задача заключается в определении угла под которым пересекаются две параболы на координатной плоскости.

Первая парабола задается уравнением y = ax^2 + bx + c, а вторая — уравнением y = dx^2 + ex + f. Необходимо найти значение x, при котором y на обеих параболах совпадает и вычислить угол в этой точке.

Угол можно найти с помощью производных. Сначала необходимо найти значения x для которых y совпадает на обоих параболах. Затем используя значения x, найденные ранее, вычисляем значения y. Далее находим производные первой и второй параболы и используем их значения для вычисления тангенса угла под которым они пересекаются.

Угол под которым пересекаются параболы может быть использован для дальнейшего анализа и определения свойств парабол, таких как направление открытия, симметрия и вершина.

Задача нахождения угла под которым пересекаются параболы имеет практическое применение в различных областях, таких как физика, математика и инженерия.

Параболы и их свойства

Основные свойства параболы:

Свойство	Описание
Фокусное свойство	Любая точка на параболе находится на одинаковом расстоянии от фокуса и от директрисы
Симметрия	Парабола является симметричной относительно своей оси
Вершина	На параболе есть точка, называемая вершиной, которая является наиболее удаленной точкой от оси симметрии
Уравнение	Уравнение параболы имеет вид y = ax^2 + bx + c, где a, b и c — заданные константы

Параболы широко используются в математике и физике. Они играют важную роль в оптике, механике и многих других областях науки.

Пересечение парабол

Для определения угла, под которым пересекаются параболы, необходимо проанализировать их графики и уравнения. Обычно угол пересечения определяется как угол между касательными к параболам в точке пересечения.

Угол пересечения парабол может быть различным в зависимости от их формы и положения. Если параболы симметричны относительно вертикальной оси (ось ординат), то угол пересечения будет прямым.

Однако, если параболы симметричны относительно горизонтальной оси (ось абсцисс), то угол пересечения будет нулевым, то есть параболы будут касаться друг друга.

При анализе угла пересечения парабол необходимо также учитывать положительное или отрицательное направление кривизны в точке пересечения. Это позволит определить направление и ориентацию парабол относительно друг друга.

Необходимые формулы и уравнения

Для нахождения угла под которым пересекаются параболы, нам потребуются следующие формулы:

Уравнение параболы в вершинно-осевой форме:

Формула: y = a(x — h)2 + k

где a — коэффициент, который определяет открытие и направление параболы, (h, k) — координаты вершины параболы.

Угол наклона прямой:

Формула: tan(θ) = m

где θ — угол наклона прямой, m — угловой коэффициент прямой.

Угол под которым пересекаются параболы:

Формула: θ = arctan(|m₁ — m₂|)

где m₁ и m₂ — угловые коэффициенты прямых, соответствующих параболам.

Примечание: Используйте функцию arctan для нахождения арктангенса угла.

§ 12.10. Общая теория линий второго порядка

Линией второго порядка называется линия, которая в некоторой декартовой
системе координат определяется уравнением второй степени. Запишем уравнение
второго порядка в самом общем виде

При условии, что вычислим

ПРИМЕР. Для эллипса имеем

.
Тогда

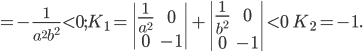
Можно доказать, что эти числа являются инвариантами относительно
преобразования параллельного переноса, т. е. при преобразовании поворота осей
координат

величины, составленные из соответствующих коэффициентов преобразованного
уравнения, сохранятся. Можно доказать также, что при параллельном переносе
осей координат

не изменяются величины и . Таким образом,
можно определить название линии второго порядка.

С помощью параллельного переноса системы координат можно освободиться от
слагаемых первой степени, а с помощью поворота осей можно освободиться
от слагаемого, содержащего произведение переменных. После подбора
подходящей системы координат уравнение второй степени примет наиболее
простой вид. Коэффициенты приведенных уравнений определяются при помощи
инвариантов.

Упражнения

1. Центром линии называется точка плоскости, по отношению к которой
   точки линии симметричны парами. Линии второго порядка, обладающие центром,
   называются центральными. Докажите, что точка
   является центром линии (1) тогда и только тогда, когда
2. Определитель второго порядка
   , составленный из коэффициентов при старших слагаемых уравнения (1),
   называется дискриминантом уравнения (1). Докажите, что линия второго порядка
   центральная тогда и только тогда, когда . Докажите, что координаты центра
   находятся по формулам

3. Определитель
   называется дискриминантом левой части уравнения (1); здесь
   и для ю
   При переносе начала координат в центр линии (1) с помощью преобразования
   уравнение (1) приобрело вид

   Докажите, что

4. Установите, что следующие линии являются центральными, и найдите координаты центра каждой линии:
   • а)
   • б)
   • в)
   • г)

5. Уравнение (2) подвергнем преобразованию поворота осей на угол
   при условии, что
   Докажите, что в новых координатах уравнение линии примет вид

   где
   и

6. Уравнение второй степени называется эллиптическим, если ,
   гиперболическим, если и параболическим, если .
   Докажите, что уравнение центральной линии может быть только эллиптическим или гиперболическим.
7. Докажите, что каждое эллиптическое уравнение является уравнением эллипса, либо вырожденного эллипса, либо мнимого эллипса.
8. Докажите, что каждое гиперболическое уравнение определяет уравнение гиперболы либо вырожденной гиперболы.
9. Докажите, что если , то линия либо не имеет центра, либо имеет бесконечно много центров.

10. Уравнение (1) подвергнем преобразованию поворота осей на угол

    при условии, что и
    .
    Докажите, что в новых координатах уравнение линии примет вид

    где , либо вид

    где

Графики тригонометрических функций

С чего начинаются тригонометрические мучения в школе? Правильно. С синуса

Построим график функции

Данная линия называется синусоидой.

Напоминаю, что «пи» – это иррациональное число: , и в тригонометрии от него в глазах рябит.

Основные свойства функции :

Данная функция является периодической с периодом . Что это значит? Посмотрим на отрезок . Слева и справа от него бесконечно повторяется точно такой же кусок графика.

Область определения: , то есть для любого значения «икс» существует значение синуса.

Область значений: . Функция  является ограниченной: , то есть, все «игреки» сидят строго в отрезке .
Такого не бывает:  или , точнее говоря, бывает, но указанные уравнения не имеют решения.

Синус – это функция нечетная, синусоида симметричная относительно начала координат, и справедлив следующий факт: . Таким образом, если в вычислениях встретится, например, , то минус терять здесь ни в коем случае нельзя! Он выносится:

Как ведет себя синус на бесконечности? Попробуем провести исследование с помощью пределов:,  Чему равны такие пределы? Запомните, данных пределов не существует. По вполне понятным причинам, график синуса болтается как как неприкаянный, то дойдет единицы, то уйдет к минус единице и так до бесконечности.

Вот вам пример, когда предела не существует. В высшей математике это можно встретить не очень часто, но такое понятие, как «предела не существует» – существует!

В практических вычислениях желательно (и даже обязательно) знать и помнить следующие значения синуса: , , . Другие значения синуса (а также остальных тригонометрических функций) можно найти в методическом материале Тригонометрические таблицы.

График косинуса

Построим график функции

График косинуса – это та же самая синусоида, сдвинутая вдоль оси  на  влево
(см. также Пример 8 урока о геометрических преобразованиях графиков).

Поэтому почти все свойства синуса справедливы и для косинуса. За некоторым, но существенным исключением.

Косинус – это функция четная, ее график симметричен относительно оси  , и справедлив следующий факт: . То есть, минус перед аргументом косинуса можно безболезненно убирать (или наоборот, ставить). В отличие от синуса в косинусе минус «бесследно пропадает».

Для решения практических задач нужно знать и помнить следующие значения косинуса: , , .

Графики тангенса и котангенса

Построим график функции

Основные свойства функции :

Данная функция является периодической с периодом . То есть, достаточно рассмотреть отрезок , слева и справа от него ситуация будет бесконечно повторяться.

Область определения:  – все действительные числа, кроме …  , , , … и т. д. или коротко: , где  – любое целое число. Множество целых чисел (… -4, -3, -2, -1, 0, 1, 2, 3, 4, …) в высшей математике обозначают жирной буквой Z.

Область значений: . Функция  не ограничена. В этом легко убедиться и аналитически: – если мы приближаемся по оси  к значению  справа, то ветка тангенса уходит на минус бесконечность, бесконечно близко приближаясь к своей асимптоте . – если мы приближаемся по оси  к значению  слева, то «игреки» шагают вверх на плюс бесконечность, а ветка тангенса бесконечно близко приближается к асимптоте .

Тангенс – функция нечетная, как и в случае с синусом, минус из-под тангенса не теряется, а выносится: .

В практических вычислениях полезно помнить следующие значения тангенса: , , , а также те точки, в которых тангенса не существует (см. график).

График котангенса – это почти тот же самый тангенс, функции связаны тригонометрическим соотношением . Вот его график:

Свойства попробуйте сформулировать самостоятельно, они практически такие же, как и у тангенса.

Спиральные кривые

Любая спиральная кривая (от латинского spira – изгиб) является траекторией точки, движущейся  по прямой, которая вращается вокруг неподвижного центра. Среди большого количества спиральных кривых необходимо выделить такие.

Спираль Архимеда – траектория точки, равномерно движущейся по прямой,  равномерно вращающейся вокруг неподвижной точки.

Для построения спирали Архимеда (рис. 3.22) окружность заданного диаметра делится на N равных частей  … (как правило, N = 12). Из центра О окружности строятся N отрезков О-1, О-2, …, один из которых О-12 делится на N равных частей точками  , … С помощью дуг окружностей находятся точки 1, 2, … Спираль Архимеда строится по точкам О, 1, 2, …

Спираль Архимеда

Архимед из Сиракуз (Άρχιµήδης) – древнегреческий математик, физик, механик и инженер-изобретатель. Совершил множество открытий в геометрии. Заложил основы механики и гидростатики.

Изогональная спираль (от греческого ίσος – равный, γωνία – угол) – траектория точки М, неравномерно движущейся по прямой линии l, которая равномерно вращается вокруг неподвижной точки О, причём угол χ между касательной  (см. п. 3.3) и радиусом-вектором r (вектором, начало которого совпадает с началом отсчёта О, конец – с данной точкой М) не изменяется (рис. 3.23).

Логарифмическая спираль

Изогональная спираль является логарифмической, поскольку угол φ между радиусом-вектором r точки М и горизонтальной осью х пропорционален натуральному логарифму от модуля r: φ = ln(r). Исследованиями логарифмической спирали занимался швейцарский математик Я. Бернулли.

Логарифмическая кривая является линией, которой могут быть описаны строение Вселенной, природные явления,  живые существа и т.д. Например, на рис. 3.24 а показана галактика Водоворот; на рис. 3.24 б – зона низкого давления над Исландией; на рис. 3.24 в – раковина моллюска.

Проявления логарифмических спиралей

Клотоида (от греческого κλωθοειδής – ниткообразный) – линия, радиус кривизны которой (см. п. 3.4.2) пропорционален длине дуги (рис. 3.25).

Спираль Корню

Другое название клотоиды – спираль Корню – посвящено французскому физику, который использовал эту кривую в исследованиях дифракции света.

Клотоида используется как переходная дуга в дорожном строительстве. Форма дороги в форме клотоиды позволяет преодолевать  повороты без существенного снижения скорости и с равномерным вращением руля.

Для приблизительного построения клотоиды (рис. 3.26) из точек О, 1 проводятся две окружности заданного радиуса . Проводится окружность радиусом 2а, касательная  к отрезку О1 (в точке 1) с центром в точке  Из точки 1 строится окружность радиусом а до пересечения с окружностью радиусом 2а. Проводится окружность радиусом 3а, касательная  к отрезку 1 – 2 (в точке 2) с центром в точке  . Из точки 2 строится окружность радиусом а пересечения с окружностью радиусом 3а … Приближённой клотоидой является линия, проходящая через точки 1, 2, …

Построение клотоиды

 Мари Альфред Корню (Marie Alfred Cornu) – французский физик, президент Парижской академии наук. Измерял среднюю плотность Земли.. Усовершенствовал метод определения скорости света . Научные труды касаются оптики, кристаллофизики, спектроскопии.

Спираль Ферма – траектория точки М,  неравномерно движущейся по прямой l, вращающейся вокруг неподвижного центра O, причём угол φ между радиусом-вектором r и горизонтальной осью пропорционален квадрату длины r: φ =  (рис. 3.27 а).

Спирали Ферма в природе встречаются как линии в узорах цветов , например, подсолнуха. (рис. 2.28 а).

Спираль Ферма -это разновидность параболической спирали, для которой угол φ между радиусом-вектором r и горизонтальной осью равен  , где а – заданное расстояние (рис. 3.27 б).

Спираль Ферма (а) и параболическая спираль (б)

Пьер де Ферма (Pierre de Fermat) – французский математик, юрист, полиглот. Один из основателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. Автор Большой теоремы Ферма. Советник Тулузского парламента.

Параболическая спираль часто встречается в природе (рис. 3.28 а) и технике (рис. 3.28 б), например, определяет профиль твердосплавных свёрл по бетону, кирпичу и керамике.

 – Проявления и применение спиральных кривых

Кроме выше обозначенных, существует также большое количество других видов спиралей:

а) гиперболическая: φ = 1/r (рис. 3.29 а);

б) спираль Галилея:  (рис. 3.29 б);

в) жезл:  (рис. 3.29 в) и т.д..

Спиральные кривые

Решение системы уравнений

Решение системы уравнений – это процесс нахождения значений неизвестных переменных, которые удовлетворяют всем уравнениям системы. В алгебре систему уравнений можно решать различными способами, одним из которых является метод подстановки.

Для решения системы методом подстановки необходимо выразить одну из переменных через другую в одном из уравнений системы и подставить это выражение в другое уравнение. В результате получится уравнение с одной переменной, которое можно решить методом обратной подстановки.

Если система состоит из трех и более уравнений, то для ее решения можно использовать метод Гаусса, который заключается в приведении матрицы коэффициентов системы к треугольному виду. После приведения матрицы, решение системы находят из последнего уравнения путем последовательного вычисления неизвестных переменных.

• Для примера, решим систему:
• 2x + 3y = 7
• x — y = -1

Выразим переменную x через y из второго уравнения: x = y — 1. Теперь подставим это выражение в первое уравнение и решим получившееся уравнение с одной переменной:

2(y — 1) + 3y = 7

Раскроем скобки:

2y — 2 + 3y = 7

5y = 9

y = 1,8

Подставим значение y в одно из уравнений и найдем значение x:

x = y — 1 = 1,8 — 1 = 0,8

Ответ: x = 0,8, y = 1,8.

Геометрические объекты в аналитической геометрии

Аналитическая геометрия – это раздел математики, который изучает геометрические объекты при помощи алгебраических методов. Главным инструментом в аналитической геометрии является координатная система, в которой каждая точка на плоскости или в пространстве задается численными значениями – координатами.

Основными геометрическими объектами в аналитической геометрии являются точки, прямые и плоскости. Изучение их свойств и взаимодействий позволяет решать различные геометрические задачи и строить сложные фигуры.

Точка – это основной геометрический объект, который не имеет размеров и задается одной или несколькими координатами в соответствующей системе координат. Она является базовым элементом, относительно которого определяются другие объекты.

Прямая – это множество всех точек, лежащих на одной линии, которое не имеет начала и конца. Прямая задается уравнением, которое включает коэффициенты и свободный член. Уравнение прямой позволяет определить ее положение относительно координатной плоскости и проводить различные операции, такие как нахождение точек пересечения с другими прямыми или плоскостями.

Плоскость – это множество всех точек, лежащих в одной плоскости. Плоскость задается уравнением, включающим коэффициенты и свободный члены для каждой координаты. Уравнение плоскости позволяет определить ее положение относительно координатной системы и выполнять различные операции, например, нахождение точек пересечения с прямыми или другими плоскостями.

Аналитическая геометрия позволяет строить и анализировать сложные геометрические объекты, такие как окружности, эллипсы, гиперболы и многогранные фигуры. Она является мощным инструментом для решения задач как в математике, так и в других науках и инженерных отраслях.

§ 12.7. Гипербола

Гиперболой называется геометрическое место точек плоскости,
разность
расстояний которых до двух фиксированных точек этой плоскости, постоянна. Эти
две фиксированные точки и называются фокусами. Длина
отрезка
называется фокусным расстоянием. Постоянную разность расстояний (из большего
расстояния вычитаем меньшее) обозначим через , так что для любой точки
гиперболы имеем . Считаем, что . Для изучения гиперболы
применим метод координат. За ось абсцисс примем прямую, проходящую через фокусы,
а серединный перпендикуляр отрезка за ось ординат. Тогда координаты
фокусов и . Точка принадлежит гиперболе тогда и
только тогда, когда

Получили уравнение гиперболы. Преобразуем его.

Так как , то существует положительное число , для которого
Отсюда
Каноническое уравнение гиперболы

Уравнение (2) является следствием уравнения гиперболы. Покажем, что каждое
решение уравнения (2) является решением уравнения (1). Пусть координаты точки , удовлетворяют уравнению (2). Тогда расстояние от этой точки до фокуса равно

Аналогично вычисляется расстояние до фокуса Оно равно
.
Так как
то точка лежит на гиперболе. Тема самым доказана эквивалентность уравнений (1) и (2) и
мы имеем полное право уравнение (2) называть уравнением гиперболы. Формулы длин
фокальных радиусов нам еще окажутся полезными:

В каноническое уравнение гиперболы переменные входят во второй степени.
Это означает, что оси координат являются осями симметрии гиперболы, а начало
координат — центр симметрии гиперболы. Для построения графика достаточно
построить его в первой четверти и затем отобразить полученную линию
относительно осей координат. В первой
четверти уравнение гиперболы имеет вид

При возрастании от до бесконечности значение функции возрастает от
до . График выпуклый вверх. Отразив эту линию относительно осей
координат, получим график гиперболы. Ось симметрии гиперболы, имеющую с ней
общие точки называем действительной осью гиперболы. Ось симметрии гиперболы,
не имеющую с ней общие точки называем мнимой осью гиперболы.
Точки пересечения
гиперболы с действительной осью , называют
вершинами гиперболы, центр симметрии гиперболы —
центром гиперболы. Гипербола
распадается на две ветви: «правую», для точек которой абсцисса и «левую»,
для точек которой .

Отношение фокусного расстояния к расстоянию между вершинами называется
эксцентриситетом . Для гиперболы эксцентриситет всегда больше 1.
Директрисой гиперболы называется прямая, параллельная мнимой оси и
отстоящая
от нее на расстоянии Под это определение попадают две прямые с уравнениями
и .
Называем соответствующими фокус и директрису, лежащие в одной полуплоскости.

ТЕОРЕМА. Отношение расстояния от любой точки гиперболы до
фокуса к расстоянию от этой точки до соответствующей директрисы равно
эксцентриситету.

Доказательство. Воспользуемся формулой длины фокального радиуса: для левого
фокуса при имеем

Аналогично вычисляем отношение в остальных случаях.

Продолжим изучение гиперболы в первой четверти. Положительная в первой
четверти разность между ординатами прямой и гиперболы

cтремится к нулю при бесконечном возрастании . Прямая

является асимптотой гиперболы. При бесконечном возрастании гипербола
приближается к прямой, но не пересекает. В силу симметрии такая же картина
наблюдается в третьей четверти, а во второй и четвертой четвертях асимптотой
является прямая

Точка лежит на асимптоте, т. е. геометрический смысл параметра —
ордината асимптоты, восставленная из вершины гиперболы. Так как

то для нахождения фокуса гиперболы можно отложить на оси отрезок
.

Основным прямоугольником гиперболы называется прямоугольник, ограниченный
прямыми, параллельными осям гиперболы и отстоящими от них соответственно на
расстоянии и . Диагонали основного прямоугольника гиперболы и есть
асимптоты.

Как найти точку пересечения параболы и прямой

УПС, страница пропала с радаров.

Вам может понравиться Все решебники

Муравин, Муравина

Вербицкая, Маккинли, Хастингс

Мерзляк, Поляков

Максаковский

Максаковский

Дорофеев, Суворова, Бунимович

Reshak.ru — сборник решебников для учеников старших и средних классов. Здесь можно найти решебники, ГДЗ, переводы текстов по школьной программе. Практически весь материал, собранный на сайте — авторский с подробными пояснениями профильными специалистами. Вы сможете скачать гдз, решебники, улучшить школьные оценки, повысить знания, получить намного больше свободного времени.

Главная задача сайта: помогать школьникам и родителям в решении домашнего задания. Кроме того, весь материал совершенствуется, добавляются новые сборники решений.

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа — вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

1. График \(y=-x^2\) симметричен относительно оси \(x\) графику \(y=x^2\).

2. – Если \(a>1\) график \(y=ax^2\) получается растяжением графика \(y=x^2\) вдоль оси \(y\) в \(a\) раз.
   – Если \(a∈(0;1)\) график \(y=ax^2\) получается сжатием графика \(y=x^2\) вдоль оси \(y\) в \(a\) раз.

3. – График \(y=a(x+d)^2\) получается сдвигом графика \(y=ax^2\) влево на \(d\) единиц.
   — График \(y=a(x-d)^2\) получается сдвигом графика \(y=ax^2\) вправо на \(d\) единиц. 

4. График \(y=a(x+d)^2+e\) получается переносом графика \(y=a(x+d)^2\) на \(e\) единиц вверх.
   График \(y=a(x+d)^2-e\) получается переносом графика \(y=a(x+d)^2\) на \(e\) единиц вниз.

У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

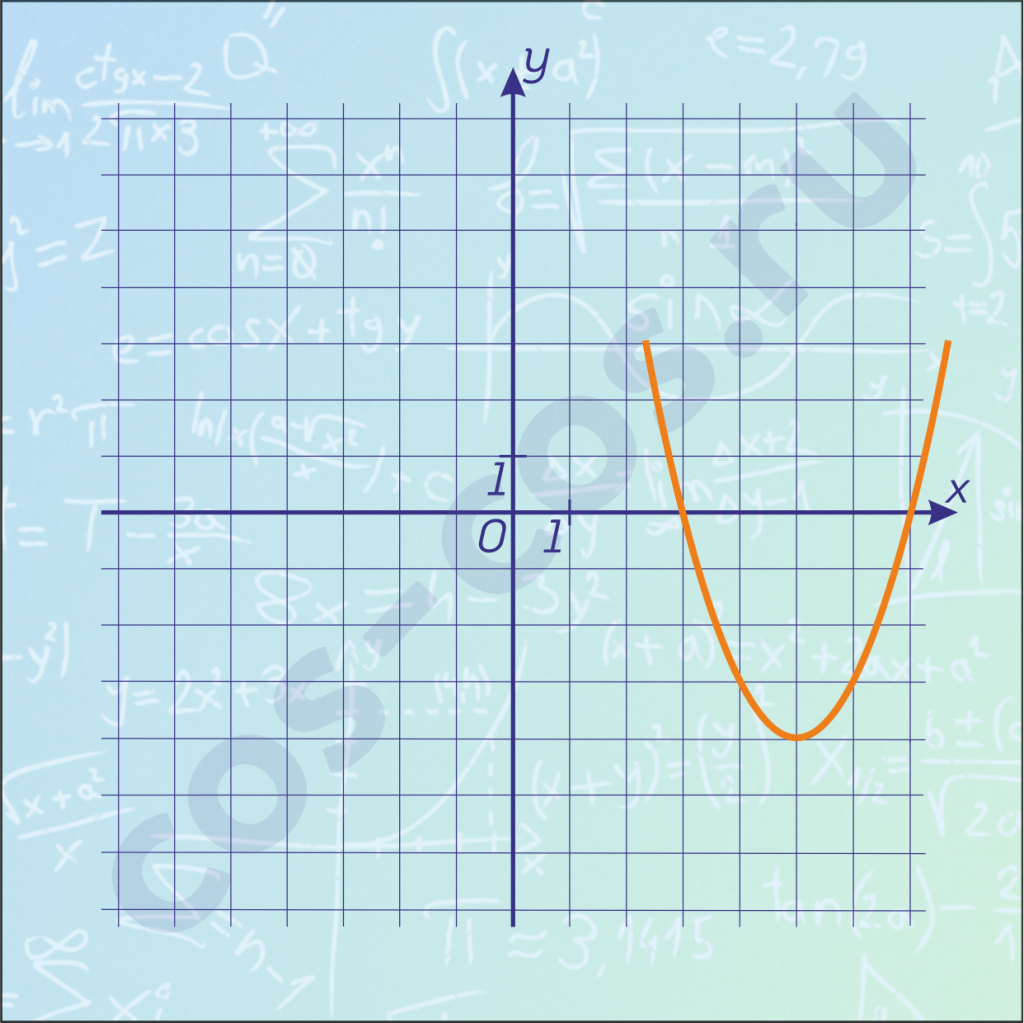
Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому \(a=1\). То есть она получена перемещениями графика базовой параболы \(y=x^2\).

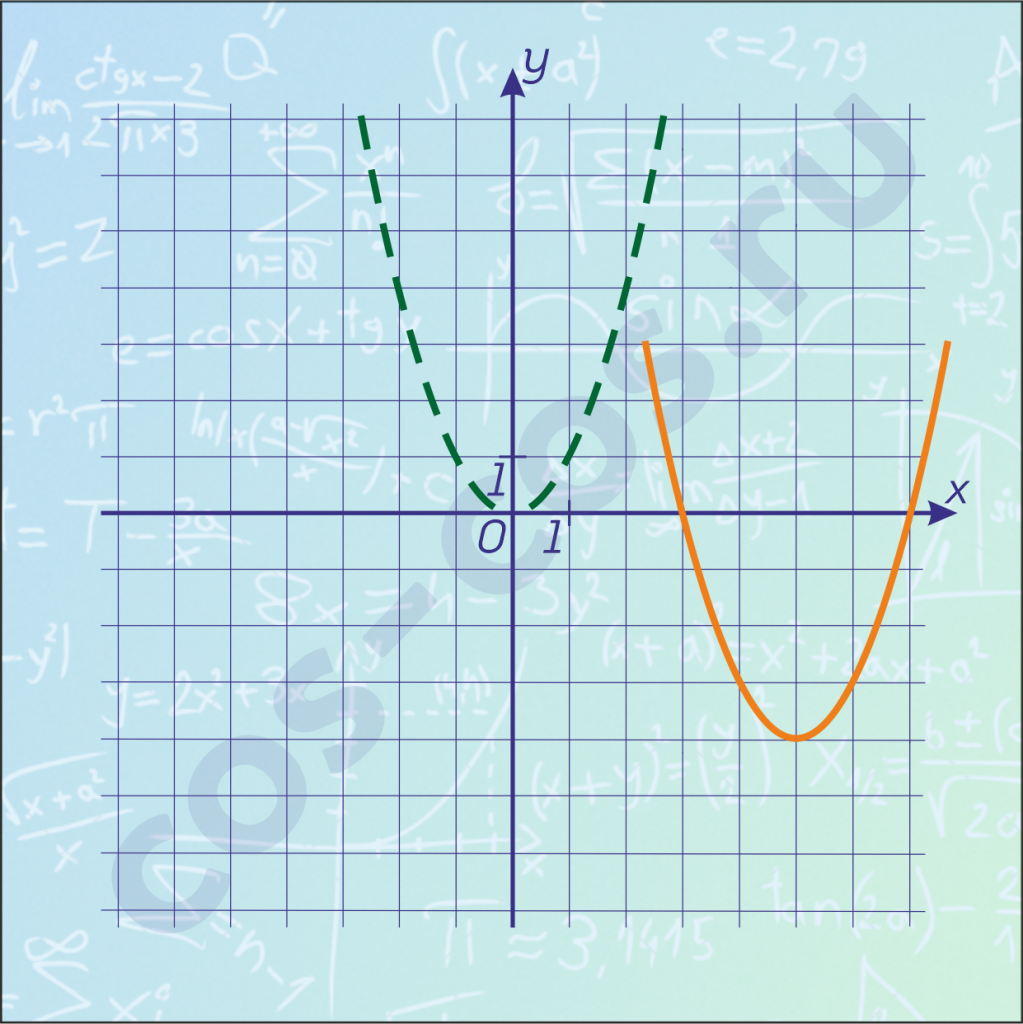
А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на \(4\).

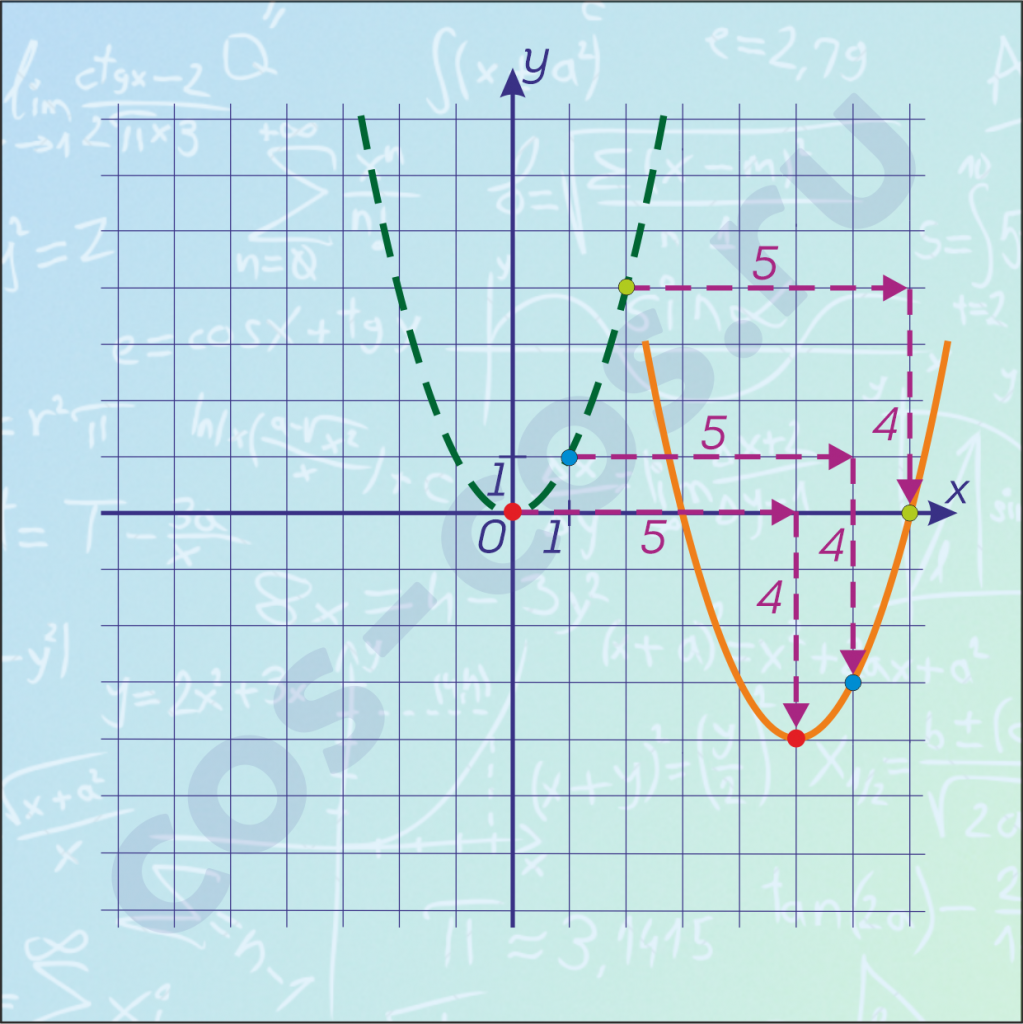
То есть наша функция выглядит так: \(y=(x-5)^2-4\).
После раскрытия скобок и приведения подобных получаем искомую формулу:

\(y=x^2-10x+25-4\)
\(y=x^2-10x+21\)

Готово.

Пример (ЕГЭ):

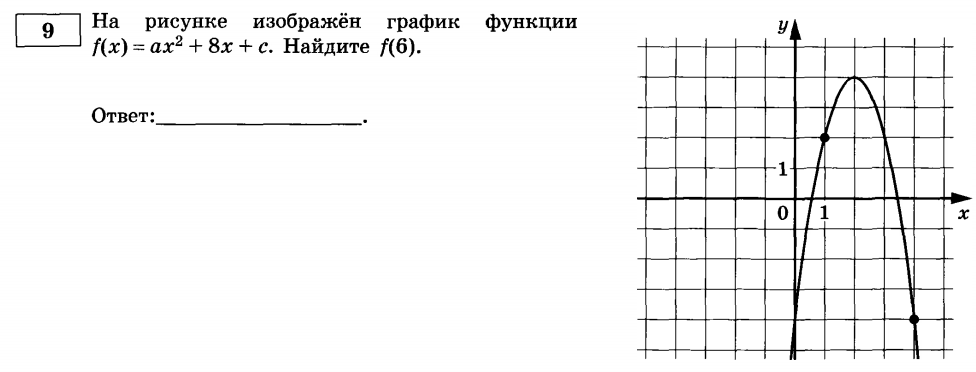
Чтобы найти \(f(6)\), надо сначала узнать формулу функции \(f(x)\). Найдем её:

1. Парабола растянута на \(2\) и ветви направлены вниз, поэтому \(a=-2\). Иными словами, первоначальной, перемещаемой функцией является функция \(y=-2x^2\).

2. Парабола смещена на 2 клеточки вправо, поэтому \(y=-2(x-2)^2\).

3. Парабола поднята на 4 клеточки вверх, поэтому \(y=-2(x-2)^2+4\).

4. Получается \(y=-2(x^2-4x+4)+4=\)\(-2x^2+8x-8+4=-2x^2+8x-4\).

5. \(f(6)=-2\cdot 6^2+8\cdot 6-4=-72+48-4=-28\)