Геометрия

Четыре замечательные точки треугольника

Точка пересечения медиан треугольника

В ней находится центр тяжести однородной треугольной пластины, также она является средним арифметическим положений всех точек треугольника.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Теорема

Медианы треугольника пересекаются в его геометрическом центре и делятся в этой точке в отношении 2:1, считая от вершин.

Доказательство

Обозначим точку пересечения медиан О и проведем среднюю линию треугольника \(А^1В^1\).

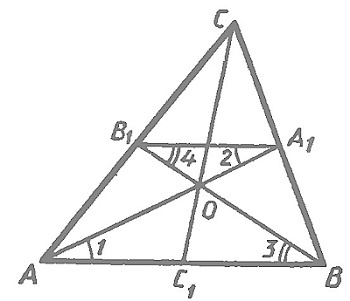
Отрезок \(А_1В_1\) параллелен \(АВ\), поэтому углы 1, 2, 3 и 4 равны друг другу. Таким образом, треугольники \(АОВ\) и \(А_1ОВ_1\) подобны по двум углам, и их стороны пропорциональны. \(АВ = 2А_1В_1\), значит, \(АО = 2А_1О\) и \(ВО = 2В_1О\), а точка О разделяет медианы на отрезки с отношением 2:1, считая от вершин. Аналогично она делит медиану \(СС_1\).

Точка пересечения биссектрис треугольника

Точка пересечения трех биссектрис расположена на равном расстоянии от всех сторон треугольника и находится в центре вписанного в треугольник круга.

Теорема

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

Следствие

Биссектрисы треугольника пересекаются в одной точке.

Доказательство

Проведем из точки пересечения биссектрис \(АА_1\) и \(ВВ_1\) отрезки \(ОК\), \(ОL\) и \(ОМ\), перпендикулярные трем сторонам треугольника.

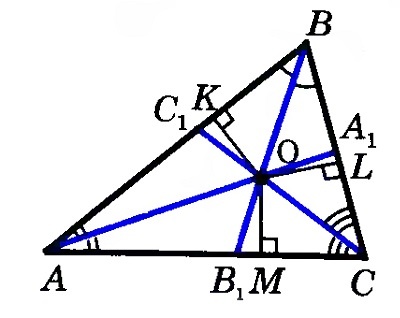
Согласно теореме о равной удаленности точек биссектрисы от сторон угла, ОК = ОМ и ОК = ОL. Соответственно, ОМ = ОL, точка О находится на равном расстоянии от сторон угла АСВ и расположена на биссектрисе. Таким образом, все три биссектрисы пересекутся в одной точке.

Точка пересечения серединных перпендикуляров треугольника

Линии, проходящие через середины сторон треугольника перпендикулярно к ним, пересекаются в центре круга, описанного вокруг треугольника. В остроугольном треугольнике точка пересечения перпендикуляров расположена внутри него, в тупоугольном — снаружи. Если треугольник прямоугольный, точка находится на гипотенузе.

Теорема

Каждая точка серединного перпендикуляра равноудалена от концов отрезка, к которому он перпендикулярен.

Следствие

Серединные перпендикуляры от сторон треугольника пересекаются в одной точке.

Доказательство

Изобразим внутри треугольника АВС перпендикуляры m и n, отметим точку их пересечения О. 

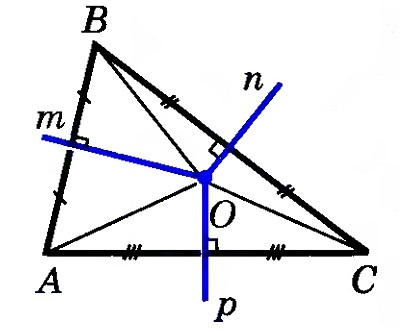
Согласно теореме о равной удаленности серединных перпендикуляров от концов отрезка, ОВ = ОА и ОВ = ОС. Соответственно, ОА = ОС, и точка О находится на одинаковом расстоянии от точек А и С. Таким образом, серединный перпендикуляр р к отрезку АС тоже будет проходить через точку О, и все три перпендикуляра пересекутся в одной точке.

Точка пересечения высот треугольника

Высоты или их продолжения могут пересекаться как внутри треугольника, если он остроугольный, так и вне его, если он тупоугольный. Если треугольник прямоугольный, тогда ортоцентр совпадает с вершиной прямого угла.

Теорема

Высоты треугольника или их продолжения пересекаются в одной точке.

Доказательство

Изобразим произвольный треугольник \(АВС\) и прямые \(AA_1\), \(BB_1\) и \(СС_1\), содержащие его высоты. Проведем через каждую вершину прямые, параллельные противоположным сторонам треугольника, получив треугольник\( A_2B_2C_2\). Точки А, В и С окажутся серединами его сторон.\( АВ = A_2C = В_2C\), так как эти отрезки являются противоположными сторонами параллелограммов \(АВА_2С\) и \(АВСВ_2\). Соответственно, \(С_2А = АВ_2\) и \(С_2В = ВА_2\).

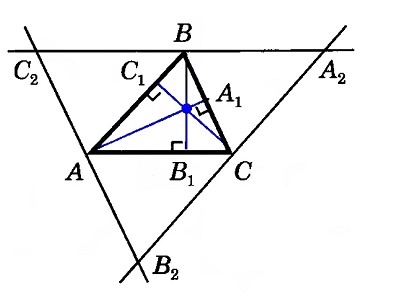
Из построения следует, что отрезок \(СС_1\) перпендикулярен \(А_2В_2\), \(АА_1 \perp В_2С_2\) и \(ВВ_1 \perp А_2С_2\). Следовательно, прямые \(АА_1\), \(ВВ_1\) и \(СС_1\) — серединные перпендикуляры сторон треугольника \(А_2В_2С_2\), которые пересекутся в одной точке.

Основные способы вписать треугольник в окружность

Окружность, вписанная в треугольник, и треугольник, вписанный в окружность, являются двумя разными геометрическими конфигурациями, но в то же время они взаимосвязаны и могут быть использованы для решения различных задач.

Существует несколько основных способов вписать треугольник в окружность:

1. Способ 1: Вписывание окружности в треугольник.
2. Способ 2: Вписывание треугольника в окружность.
3. Способ 3: Вписывание окружности в правильный треугольник.
4. Способ 4: Вписывание правильного треугольника в окружность.

Способ 1: Вписывание окружности в треугольник.

Для этого способа требуется выбрать произвольный треугольник и построить окружность, которая касается всех трех сторон треугольника. Точка касания окружности с каждой стороной треугольника называется точкой касания.

Способ 2: Вписывание треугольника в окружность.

Этот способ требует выбрать произвольную окружность и построить треугольник, вершины которого лежат на окружности. В этом случае каждая сторона треугольника будет касаться окружности в своей точке.

Способ 3: Вписывание окружности в правильный треугольник.

Для построения этого способа необходимо взять правильный треугольник – треугольник, у которого все стороны и углы равны между собой, и построить окружность, которая целиком лежит внутри треугольника. Углы треугольника будут соответствовать углам в центре окружности.

Способ 4: Вписывание правильного треугольника в окружность.

В этом способе выбирается произвольная окружность, и на ее окружности строится правильный треугольник. В этом случае каждая сторона треугольника будет лежать на окружности.

Зная основные способы вписать треугольник в окружность, можно использовать их для решения различных геометрических задач, а также для вычисления различных параметров треугольника и окружности.

[править] Определения, связанные с треугольником

Окружности

• Вписанная окружность — окружность, касающаяся всех трёх сторон треугольника. Она единственна. Центр вписанной окружности называется инцентром.
• Описанная окружность — окружность, проходящая через все три вершины треугольника. Описанная окружность также единственна.
• Вневписанная окружность — окружность, касающаяся одной стороны треугольника и продолжения двух других сторон.

Лучи, отрезки и точки

Медианой треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны (основанием медианы). Все три медианы треугольника пересекаются в одной точке. Эта точка пересечения называется центроидом или центром тяжести треугольника. Последнее название связано с тем, что у треугольника, сделанного из однородного материала, центр тяжести находится в точке пересечения медиан. Центроид делит каждую медиану в отношении 1:2, считая от основания медианы.

Высотой треугольника, проведённой из данной вершины, называется перпендикуляр, опущенный из этой вершины на противоположную сторону или её продолжение. Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.

Биссектрисой треугольника, проведённой из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам. Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности (инцентром).

Средней линией треугольника называют отрезок, соединяющий середины двух сторон этого треугольника.

В равнобедренном треугольнике биссектриса, медиана и высота, проведённые к основанию, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведённые из одной вершины, совпадают, то треугольник равнобедренный. Если треугольник разносторонний, то для любой его вершины биссектриса, проведённая из неё, лежит между медианой и высотой, проведёнными из той же вершины.

Серединные перпендикуляры(медиатриссы) к сторонам треугольника также пересекаются в одной точке, которая совпадает с центром описанной окружности.

Середины трёх сторон треугольника, основания трёх его высот и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности, называемой окружностью девяти точек.

В любом треугольнике центр тяжести, ортоцентр, центр описанной окружности и центр окружности девяти точек лежат на одной прямой, называемой прямой Эйлера.

Ортоцентр, инцентр, центроид (центр тяжести), а также некоторые другие точки называются замечательными точками треугольника.

Свойства

Определение невырожденного треугольника в геометрии основано на том, что углы треугольника суммируются в 180 градусов, каждая сторона больше нуля, и сумма двух сторон всегда больше третьей стороны. Любая грань треугольника является отрезком, соединяющим две его вершины.

Примерами невырожденных треугольников могут служить треугольник со сторонами 3, 4 и 5, а также треугольник с углами 30, 60 и 90 градусов.

Равенство суммы углов треугольника 180 градусам.

Стандартное определение треугольника в геометрии — это фигура, образованная тремя сторонами и тремя вершинами. Каждая сторона соединяет две вершины, а каждый угол образуется двумя сторонами, исходящими из одной вершины. Углы треугольника также могут быть классифицированы как острые (меньше 90 градусов), прямые (равные 90 градусам) или тупые (больше 90 градусов).

Признак невырожденного треугольника — это условие, при котором сумма длин любых двух сторон треугольника всегда больше длины третьей стороны. Иначе говоря, треугольник должен быть «закрытой» фигурой, а не прямой линией или точкой.

Важным свойством невырожденного треугольника является равенство суммы углов треугольника 180 градусам. Это значит, что сумма всех внутренних углов треугольника равна 180 градусам. Например, если у нас есть треугольник с углами 60 градусов, 70 градусов и 50 градусов, то их сумма будет равна 180 градусам.

Сумма длин двух сторон треугольника всегда больше длины третьей стороны.

В геометрии треугольник представляет собой плоскую фигуру, образованную тремя отрезками, называемыми сторонами треугольника. Каждая сторона треугольника является гранью этой фигуры, а точки их пересечения – вершинами. Сумма длин двух сторон определенного треугольника всегда больше длины третьей стороны и служит важным признаком для определения невырожденного треугольника.

Позвольте рассмотреть пример, чтобы увидеть это свойство в действии. Предположим, что у нас есть треугольник с сторонами длиной 5, 7 и 10 единиц. Чтобы проверить, выполняется ли свойство суммы длин двух сторон, необходимо сложить длины двух самых коротких сторон:

Стороны треугольника	Сумма длин двух сторон
5, 7, 10	5 + 7 = 12

Как видим, сумма длин двух сторон треугольника равна 12. Затем сравниваем эту сумму с длиной третьей стороны:

Стороны треугольника	Сумма длин двух сторон	Длина третьей стороны
5, 7, 10	12	10

Как можно заметить, сумма длин двух сторон (12) больше длины третьей стороны (10), что подтверждает наше утверждение о том, что сумма длин двух сторон треугольника всегда больше длины третьей стороны.

Сумма длин двух сторон треугольника является важным свойством, она влияет на множество других характеристик треугольника, таких как его площадь, углы и отношения между сторонами.

Высоты треугольника пересекаются в одной точке — ортоцентре.

Одним из важных свойств треугольника является то, что все высоты треугольника пересекаются в одной точке, которая называется ортоцентром. Именно ортоцентр является точкой пересечения трех высот треугольника.

Ортоцентр имеет много геометрических свойств и является ключевой точкой в задачах треугольника. Он лежит внутри или на границе треугольника, в зависимости от его типа и положения высот. Более того, ортоцентр может быть использован для определения других важных элементов треугольника, таких как окружность Эйлера и описанная окружность.

Одно из основных свойств ортоцентра заключается в том, что отрезки, соединяющие ортоцентр с вершинами треугольника, перпендикулярны соответствующим сторонам. Это означает, что углы между сторонами треугольника и этими отрезками равны 90 градусам.

Еще одним важным признаком ортоцентра является его связь с площадью треугольника. Для любого треугольника, площадь треугольника ABC равна произведению половины основания BC на высоту, проведенную из вершины A:

SABC = 0.5 * BC * HA, где SABC — площадь треугольника ABC, BC — основание треугольника, HA — высота, проведенная из вершины A.

Таким образом, ортоцентр треугольника имеет большое значение и определение его свойств позволяет углубить понимание треугольника в геометрии. Благодаря своей особенной природе, ортоцентр является важным элементом в решении задач и определении основных характеристик треугольника.

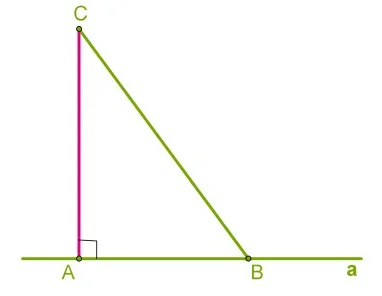
Как построить треугольник по трем элементам с помощью циркуля

Используя компас, можно изобразить треугольник с тремя известными элементами. Например, есть три аспекта в виде частей MC, OE и FG, для которых необходимо построить треугольник ABC. Должны быть выполнены следующие условия:.

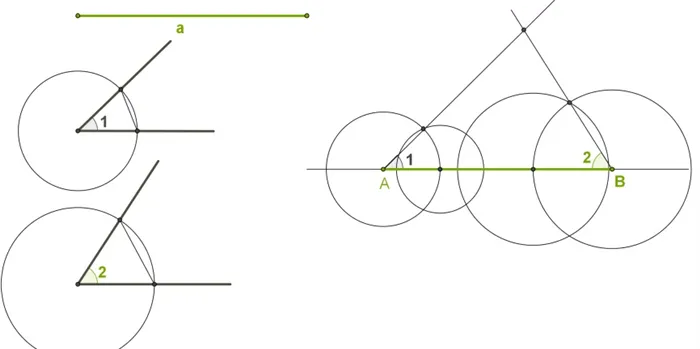
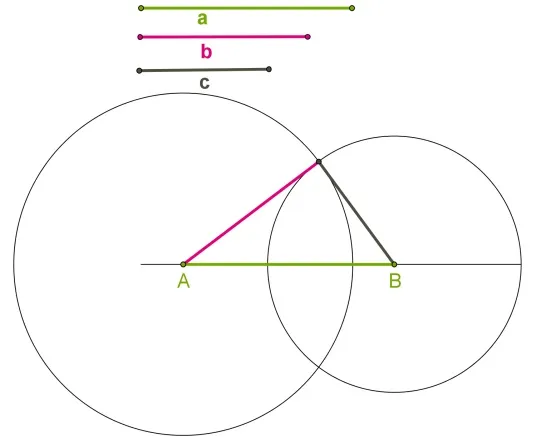
Используя линейку, проведите прямую линию a. Используя компас, проведите линию AB, соответствующую отрезку MK. В этой процедуре вы можете отметить точку A на линии A. После измерения сечения компаса MK необходимо начертить окружность с радиусом, равным центру A и MK. Не нужно рисовать весь цикл, а только лук, как показано на рисунке. Точка пересечения окружности с линией A — b.

Измерьте сечение OE с помощью компаса и начертите окружность, центр которой совпадает с точкой A, а радиус соответствует сечению OE. На изображении бант выделен синим цветом.

Следующий шаг — с помощью компаса измерить сечение FG и нарисовать окружность. Центр этого цикла совпадает с точкой B, а его радиус соответствует прямому участку FG. На рисунке лук обозначен зеленым цветом.

Точки, в которых центры A и B и окружность с лучами OE и FG определяются как C, удобно соединять с помощью линейки. В результате получается геометрическая фигура в виде треугольника ABC.

Если условия задания выполнены, то нарисованный треугольник является искомым треугольником.

Важно отметить, что такие задания не имеют решения во всех случаях. Причина в том, что неравенство треугольника должно выполняться для каждого треугольника

То есть, для каждого треугольника сумма двух сторон больше третьей стороны. Если один из отрезков, обозначенных условно, больше суммы двух других, то построить треугольник со сторонами, соответствующими этим отрезкам, невозможно.

Треугольники можно построить с помощью компаса и углов между ними, если известны обе стороны. Например, существуют секции MK и OE и углы HK. Треугольник ABC должен быть построен следующим образом.

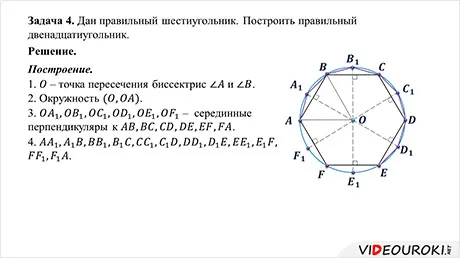
Окружность, вписанная в треугольник. Основное свойство биссектрисы угла

Определение 1. Биссектриса угла — это радиус, который делит угол на две равные части.

Теорема 1 (Основные свойства биссектрисы угла). Каждая точка биссектрисы угла находится на одинаковом расстоянии от стороны угла (рис. 1).

Доказательство Рассмотрим любую точку D на биссектрисе угла BAC и проведем перпендикулярные прямые DE и DF из D к ребру угла (рис. 1). Прямоугольные треугольники ADF и ADE равны, так как острые углы DAF и DAE равны, а косая сторона AD общая. Следовательно.

Доказательство.

Теорема 2 (обратная теорема теоремы 1). Если точки находятся на одинаковом расстоянии от сторон угла, то он лежит на биссектрисе угла (рис. 2).

Доказательство Рассмотрим любую точку D, которая лежит внутри угла BAC и находится на одинаковом расстоянии от края угла. Пусть DE и DF — перпендикуляры, проведенные из D к ребру угла (рис. 2). Прямоугольные треугольники ADF и ADE равны, так как перпендикулярные линии DF и DE равны, а косая сторона AD общая. Следовательно.

Доказательство.

Определение 2. Окружность называется вписанной в угол, если она является касательной к сторонам угла.

Теорема 3. Если окружность вписана в диагональ, то расстояние от вершины угла до точки касания окружности со стороной угла равно.

Доказательство Пусть D — центр окружности, вписанной в угол BAC, а E и F — точки касания окружности с боковыми линиями (рис. 3).

Прямоугольные треугольники ADF и ADE равны, так как кривые DF и DE равны (потому что радиус окружности — это радиус круга), а косая сторона AD — общая. Поэтому.

Доказательство.

Заявление. Теорему 3 можно сформулировать и по-другому. Отрезки касательной, проведенной по окружности из точки, равны.

Определение 3. Биссектриса треугольника — это часть биссектрисы угла треугольника, соединяющая вершины треугольника с противоположными точками.

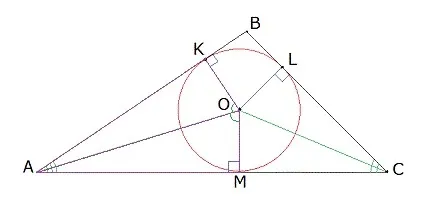
Теорема 4. В каждом треугольнике все три биссектрисы пересекаются в одной точке.

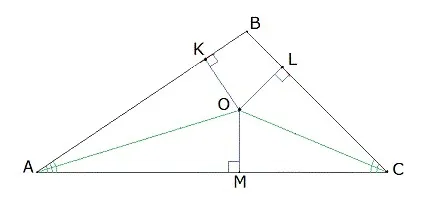
Доказательство Рассмотрите две биссектрисы A и C ABC и покажите их пересечение в точке O (рис. 4).

Из точки O оставьте перпендикуляры OD, OE и OF на сторонах треугольника. Так как O лежит на биссектрисе угла BAC, уравнение следует из Теоремы 1.

Согласно Теореме 1, если точка C лежит на биссектрисе угла ACB, то из уравнения следует.

Следовательно, уравнение верно.

Построение ортоцентра

Шаг 1: Нарисуйте треугольник ABC.

Шаг 2: Постройте высоты треугольника. Высота треугольника — это отрезок, проведенный из одного вершины до противолежащей стороны, перпендикулярно этой стороне. Проведите высоты из вершин A, B и C до противолежащих сторон BC, AC и AB соответственно.

Шаг 3: Высоты треугольника пересекаются в точке H. Результатом пересечения является ортоцентр — точка H.

Примечание: Ортоцентр может находиться внутри, на границе или вне треугольника в зависимости от его типа и формы.

Построение ортоцентра является важным шагом при решении различных геометрических задач и имеет большое практическое значение.

Формулы для радиуса окружности, вписанной в треугольник

Полезно представить типы окружностей, зарегистрированных в треугольниках, в следующей таблице, где указаны радиусы окружностей.

a, b и c — стороны треугольника, s — площадь, r — радиус коциркуля, p — полуокружность.

a — сторона равностороннего треугольника, r — внутренний радиус.

где a, b, c — стороны треугольника, s — площадь, r — эндогенный радиус и p — полуреверс.

Где a, b и c — стороны треугольника, r — внутриклеточный радиус, а p — полупинеометр.

Равнобедренный треугольник

Равносторонний треугольник

Где a — сторона правильного треугольника, r — внутриклеточный радиус

Прямоугольный треугольник

где a, b, c — стороны треугольника, s — площадь, r — эндогенный радиус и p — полуреверс.

Где a, b и c — стороны треугольника, r — внутриклеточный радиус, а p — полупинеометр.

Равнобедренный треугольник

Равносторонний треугольник

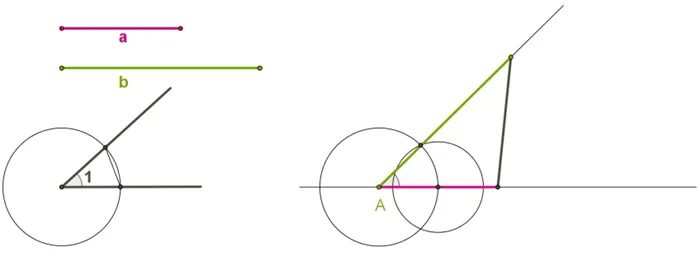
Где a — сторона правильного треугольника, r — внутриклеточный радиус

Прямоугольный треугольник

Основные линии треугольника

Ключевые слова: основные линии треугольника, медиана, биссектриса, высота, средния линия, серединные перпендикуляры

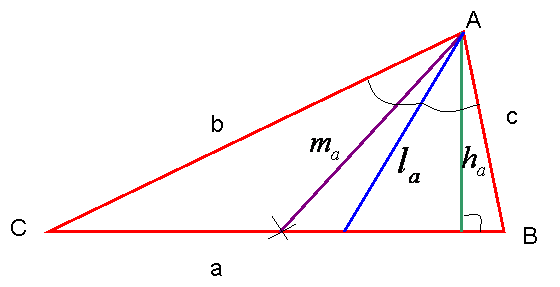
Рассмотрим произвольный треугольник ABC:

a, b, c — стороны треугольника

$$m_a$$ — медиана к стороне a угла A

$$h_a$$ — высота к стороне a угла A

$$l_a$$ — биссектриса к стороне a угла A

Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

• Медиана разбивает треугольник на два треугольника одинаковой площади.
• Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
• Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

Свойства биссектрис треугольника

• Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
• Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегажащим сторонам.
• Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.

Свойства высот треугольника

• В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
• В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
• Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон
• Три высоты в остроугольном треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.

Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.

Свойства серединных перпендикуляров треугольника

• Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
• Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Вписанный треугольник циркулем и линейкой

Для начала, возьмите лист бумаги и рисунок, на котором будете выполнять задание. Представьте, что у вас уже есть вписанная фигура, например, окружность. Нам нужно нарисовать треугольник, внутри которого лежит эта окружность.

Вот пошаговая инструкция:

Шаг	Действие
1	Найдите центр окружности и отметьте его на листе бумаги.
2	Установите один конец циркуля на одну из точек окружности и регулируйте его радиус, чтобы он пересекал другую точку окружности.
3	Опустите угол циркуля на лист бумаги и начните рисовать дугу, связывающую обе точки окружности.
4	Опустите угол циркуля на лист бумаги второй раз, на этот раз через другую пару точек окружности, и нарисуйте еще одну дугу.
5	Точка пересечения двух дуг является одной из вершин треугольника. Отметьте ее на листе бумаги.
6	Установите один конец линейки на центр окружности и проведите отрезок к вершине треугольника.
7	Установите другой конец линейки на одну из оставшихся вершин треугольника и проведите отрезок к вершине, которую вы еще не отметили.
8	Все три отрезка — это стороны нашего вписанного треугольника. Проверьте, что они все равны друг другу.

Теперь у вас есть вписанный треугольник, который был нарисован с помощью циркуля и линейки. Помните, что это только один из способов нарисовать такой треугольник, и вы можете использовать различные методы в зависимости от своих предпочтений и доступных инструментов.

Определение центра вписанного круга

Центр вписанного круга – это точка пересечения серединных перпендикуляров к сторонам вписанного треугольника. Как известно, вписанный круг касается всех сторон треугольника, а его центр расположен в точке, равноудаленной от вершин треугольника. Это полезное знание, так как центр вписанного круга имеет много применений в геометрии и решении задач.

Чтобы определить центр вписанного круга с помощью циркуля и линейки, нужно выполнить следующие шаги:

1. Нарисуйте треугольник с помощью линейки, используя три отрезка, соединяющих вершины треугольника.
2. С помощью циркуля измерьте расстояние от одной из вершин треугольника до середины противоположной стороны. Отметьте эту точку на линии стороны треугольника.
3. Повторите шаг 2 для двух других вершин треугольника.
4. Соедините отмеченные точки на сторонах треугольника. Это сделает три серединных перпендикуляра.
5. Найдите точку пересечения этих перпендикуляров. Это и будет центр вписанного круга.

Теперь вы знаете, как определить центр вписанного круга с помощью циркуля и линейки. Следуя этим инструкциям, вы сможете нарисовать вписанный треугольник и определить его центр вписанного круга без особых усилий.

Как вписывать окружность в треугольник

9 класс Оптическая геометрия. Ссылка 2 Круглые и внутренние круглые круги

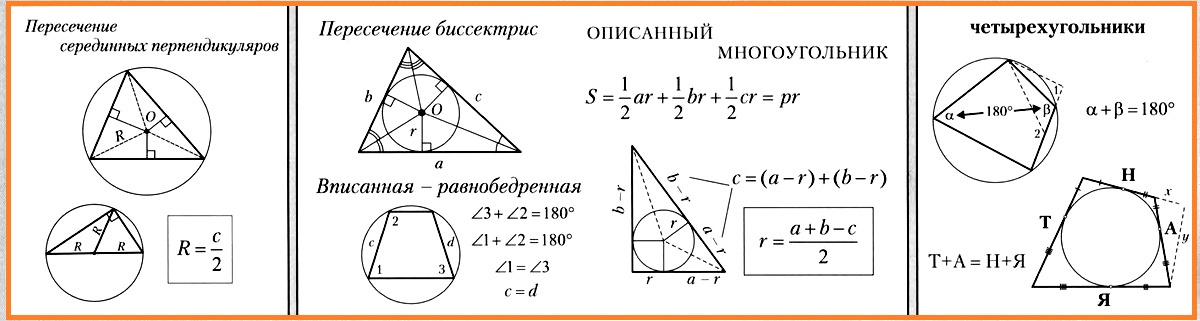
Можно сформировать круг вокруг любого треугольника. Она проходит через все вершины треугольника. Вы уже знаете, что точки пересечения середин равноудалены от вершин треугольника. Он является центром региона.

Окружность может быть вписана в любой треугольник. Он касается всех сторон треугольника. Вы также знаете, что пересечение биссектрис треугольника равноудалено от сторон треугольника. Центр круга.

Но можно ли нарисовать круг вокруг произвольного прямоугольника? Если вы попытаетесь это сделать, то обнаружите, что нарисовать круг вокруг прямоугольника можно только в том случае, если прямоугольник Вы узнаете о свойствах вписанных и описанных четырехугольников и свойствах, позволяющих определить, можно ли описать область вокруг определенного четырехугольника и можно ли вписать в него окружность.

Кроме того, вы узнаете ключевую формулу для площади треугольника S =pr.

1. Окружность, описанная около треугольника.

Если окружность проходит через все вершины, она называется очерченной вокруг треугольника.

Теорема. Круг можно нарисовать вокруг любого треугольника, но только одного. Его центр лежит на пересечении перпендикулярных линий сторон треугольника.

Доказательства.. Точка пересечения средних перпендикуляров сторон треугольника равноудалена от его вершины (доказано в седьмой степени). Поэтому точка является центром окружности, а расстояние от нее до любой вершины равно ее радиусу.

Если существует еще один круг, то его центр равноудален от трех вершин, поэтому он совпадает с пересечением перпендикулярных линий, а его радиус совпадает с радиусом первого круга. Круги совпадают.

2. Окружность, описанная около прямоугольного треугольника.

Теорема. Периферийный центр окружности, проведенной вокруг прямоугольного треугольника, находится в середине гипотенузы, а радиус окружности равен половине гипотенузы.

Доказательства.. Мы знаем, что медиана прямоугольного треугольника, образованного из вершин прямого угла, равна половине гипотенузы (это было доказано в 7 классе). Поэтому середина гипотенузы является центром окружности, а ее радиус равен половине гипотенузы. То есть, R = c/2.

3. Окружность, вписанная в треугольник.

Считается, что окружность вписана в треугольник, если она является касательной ко всем сторонам треугольника.

Теорема. В любом треугольнике можно нарисовать окружность, имеющую только один Его центр лежит на пересечении биссектрис треугольника.

Доказательства.. Пересечение биссектрис треугольника равноудалено от сторон треугольника (доказано в классе 7). Если из этой точки провести перпендикуляр к стороне и очертить окружность радиусом, равным перпендикуляру, то сторона треугольника касается окружности в точке касания.

Если существует еще один эндоцикл, то его центр равноудален от всех трех сторон, поэтому он совпадает с пересечением биссектрис, а его радиус совпадает с радиусом первой окружности. Круги совпадают.

4. Формула площади S = рr.

Теорема. Площадь треугольника S = p r, где p — полуокружность треугольника, а r — радиус вписанной окружности.

Доказательства.. Соедините центр внутренней окружности с вершиной треугольника, стороны которого равны α, β и γ. Получите три треугольника, радиусы которых являются высотами радиусов конечных циклов, выполненных в точках контакта. Площадь треугольника равна сумме площадей этих треугольников:.

где p — полуокружность треугольника.

Это уравнение применимо ко всем многоугольникам, которые могут быть вписаны в окружность, то есть ко всем окружностям. Доказательство аналогично.

Общие сведения

Треугольник — геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и отрезков, соединяющих их. Точки имеют другое название — вершины. Обозначается треугольник символом Δ, после которого идут 3 латинских буквы. Например, ΔMNO. Допускается использовать и русские литеры, но злоупотреблять этим не стоит.

В высших учебных заведениях преподаватели требуют от студентов международное обозначение. Кроме того, большинство программных продуктов и онлайн-сервисов воспринимают только латинские символы.

Классификация треугольников

Необходимо отметить, что Δ различаются между собой по некоторым критериям.

Они бывают нескольких типов:

1. Произвольные.
2. Прямоугольные.
3. Равнобедренные.
4. Равносторонние.
5. Тупоугольные.
6. Остроугольные.

В первом случае стороны фигуры не равны между собой. Чтобы идентифицировать прямоугольный треугольник, необходимо рассмотреть его углы. Если один из них является прямым (равен 90 градусам), такая фигура называется прямоугольной. В третьем виде основным критерием считается наличие двух, равных между собой сторон.

В равностороннем треугольнике все стороны равны между собой. Математики его называют «правильным». Он обладает важным свойством — вокруг него можно описать окружность. Пятый тип определяет наличие тупого угла, градусная мера которого больше 90. Если фигура является остроугольной, это значит, что все 3 его угла меньше 90, т. е. являются острыми.

Один треугольник может относиться к нескольким типам. Например, прямоугольный Δ может быть равнобедренным на основании свойства геометрии: если Δ является равнобедренным, то углы (∠), образованные боковыми сторонами с основанием, равны между собой. В этом случае их градусные меры эквивалентны 45, поскольку сумма ∠ любого Δ составляет 180. Следовательно, 180 — 90 = 2k, где неизвестная величина «к» соответствует углу при основании.

Дополнительные элементы

У любого Δ существуют определенные дополнительные элементы, необходимые при построении чертежей или схематических рисунков, доказательства теорем и решения задач по геометрии.

К ним относятся:

1. Биссектриса.
2. Медиана.
3. Высота.

Биссектриса — отрезок (прямая), проходящий через вершину Δ и делящий угол на 2 равные части. Медиана — единственный отрезок для каждой вершины, соединяющий ее с серединой стороны, на которую он опущен.

Высотой является перпендикуляр, опущенный из вершины на противоположную сторону.

В равнобедренном и равностороннем треугольниках биссектриса является медианой и высотой. В последнем случае их можно провести всего 3.

Свойства и соотношения

На основании теоремы о биссектрисах Δ были получены некоторые важные свойства, которые рекомендуется применять при решении задач и доказательства других утверждений:

1. Центр вписанной окружности соответствует точке их пересечения.
2. Точка при пересечении делит биссектрису по такому соотношению: отношение суммарного значения прилежащих к противолежащей стороне.
3. Угол между биссектрисами двух смежных углов является прямым.
4. В равнобедренном Δ равны только 2 биссектрисы, а в равностороннем — 3. Кроме того, она является медианой и высотой.

При решении задач нужно находить их длину (L).

Для удобства необходимо обозначить стороны таким образом: КМ = d, КL = e и LМ = f, чтобы воспользоваться следующими формулами через известные параметры треугольника:

1. Все стороны: Lm = / (d + e), Lк = / (d + f) и Ll = / (d + f). Параметр «р» — полупериметр, т. е. р = (d + e + f) / 2.
2. Стороны и угол: Lm = (2 * d * e * cos (∠M)) / (d + e), Lk = (2 * d * f * cos (∠K)) / (d + f) и Ll = (2 * f * e * cos (∠L)) / (f + e).

Соотношения позволяют найти не только длины Lk, Lm и Ll, но и другие параметры треугольников. Следует отметить, что углы во второй группе формул соответствуют биссектрисам, исходящим из них.

Таким образом, для решения задач на нахождение длины биссектрис необходимо знать теорию, доказательство теоремы, свойства, а также основные соотношения.