Как найти площадь неровной фигуры по клеточкам: подробное руководство

Стоит ли учить 4 классу?

Вопрос о необходимости обучения материалу, представленному в четвертом классе, довольно актуален. Некоторые могут спросить: зачем учить детей таким сложным вещам с этого возраста?

Однако, обучение в четвертом классе является важным этапом в развитии ребенка. В этом возрасте дети начинают формировать базовые навыки и знания, которые будут полезны в будущем. Они изучают основы математики, грамматики, чтения и другие предметы, которые являются фундаментом для дальнейшего образования и успешной адаптации в обществе.

Учеба в четвертом классе также помогает детям развивать логическое мышление, аналитические и проблемно-ориентированные навыки. Они научатся решать задачи, аргументировать свои мысли и работать в команде.

Кроме того, обучение в четвертом классе помогает детям развивать социальные навыки и учиться взаимодействовать с другими людьми. Они учатся быть ответственными, уважать других и сотрудничать с одноклассниками.

Поэтому, несмотря на то, что учеба в четвертом классе, возможно, кажется сложной и непонятной, она является важной частью образования и развития ребенка. Эти знания и навыки станут фундаментом для дальнейшего обучения и успешной адаптации в обществе

Простой метод для определения площади фигуры по клеточкам

Определение площади фигуры по клеточкам может быть трудной задачей для некоторых, но с использованием простого метода можно справиться с этой задачей легко и быстро.

Для начала необходимо нарисовать фигуру на клеточной бумаге или использовать программу для рисования, где клеточная сетка уже есть. Затем нужно посчитать количество клеток внутри фигуры.

Если фигура состоит только из клеток, то число клеток внутри нее и будет являться ее площадью. Достаточно просто посчитать количество этих клеток и получить результат.

Однако, если фигура имеет часть клеток, которые либо находятся не внутри фигуры, либо частично пересекаются с ее границей, то их нужно исключить из расчета. Для этого можно использовать помощь отрезков и линий, чтобы определить, какие клетки полностью находятся внутри фигуры.

Итак, чтобы определить площадь фигуры по клеточкам, мы должны:

Нарисовать фигуру на клеточной бумаге или использовать программу с клеточной сеткой.
Посчитать количество клеток, находящихся внутри фигуры. Если фигура состоит только из клеток, то это число и будет ее площадью.
Если фигура имеет несколько частей, нужно исключить из расчета клетки, которые либо находятся частично внутри фигуры, либо пересекают ее границу.

Следуя этим простым шагам, можно легко определить площадь фигуры по клеточкам и получить точный результат. Этот метод позволяет учитывать все особенности фигуры и получить правильное значение ее площади.

Важность понимания клеточной геометрии

Клеточная геометрия широко используется в различных областях, таких как архитектура, дизайн, графика и техническое черчение. Понимание клеточной структуры позволяет точно измерять и располагать объекты, а также строить сложные фигуры.

Понимание клеточной геометрии также помогает учащимся развивать свои навыки визуального анализа и пространственного мышления. Они могут видеть и понимать отношения между элементами фигур и оценивать их размеры и площади.

Кроме того, знание клеточной геометрии важно для практического применения математических знаний в повседневной жизни. Умение рассчитывать площадь фигур, изображенных на клеточной сетке, поможет учащимся в решении задач по мебельному дизайну, планированию помещений или укладке плитки

Ошибки округления при подсчете площади

При подсчете площади фигуры по клеткам в четвертом классе, важно учитывать возможные ошибки округления, которые могут влиять на точность результата. Округление – это процесс приближения числа к наиближайшему целому значению с учетом определенного правила округления

При подсчете площади фигуры по клеткам, дети должны правильно округлять значения, чтобы получить точный результат

Округление – это процесс приближения числа к наиближайшему целому значению с учетом определенного правила округления. При подсчете площади фигуры по клеткам, дети должны правильно округлять значения, чтобы получить точный результат.

Одна из распространенных ошибок округления – неправильное округление дробных чисел. Например, если площадь фигуры по клеткам равна 5,5 квадратных клеток, то правильно округлять это значение следует до 6 квадратных клеток, поскольку 5,5 больше половины клетки.

Еще одна распространенная ошибка – неправильное округление суммы площадей. Например, если у детей есть две фигуры, одна площадью 2,3 квадратных клетки, а другая площадью 4,7 квадратных клеток, то правильно округлять сумму площадей следует до 7 квадратных клеток, а не до 6 квадратных клеток, так как значения округляются отдельно перед сложением.

Ошибки округления при подсчете площади могут быть незначительными, но с накоплением они могут привести к значительным расхождениям в результатах

Поэтому важно учить детей правильному округлению и объяснять им, какие правила следует применять

Важно помнить:

Округлять дробные значения до ближайшего целого в соответствии с правилами округления.
Округлять сумму площадей отдельно, а не округлять каждую площадь перед сложением.
Объяснить детям, что ошибки округления могут накапливаться и влиять на точность результатов.

Правильное округление – важный навык, который поможет детям получить точные результаты при подсчете площади фигур по клеткам. Учителю стоит уделять достаточно времени для объяснения этого правила и проведения практических упражнений, чтобы дети научились применять его корректно.

Ход урока

Урок мы начнём вот с таких напутствующих слов:

Математика, друзья,
Абсолютно всем нужна. На уроке работай старательно,
И успех тебя ждёт обязательно!

Актуализация знаний.

а) Фронтальная работа с сигнальными карточками (у каждого ученика карточки с числами 1, 2, 3, 4; при ответе на вопрос теста ученик поднимает карточку с номером правильного ответа).

Квадратный сантиметр – это:

площадь квадрата со стороной 1 см;
квадрат со стороной 1 см;
квадрат с периметром 1 см.

Площадь фигуры, изображённой на рисунке, равна:

8 дм;
8 дм2;
15 дм2.

Справедливо ли утверждение, что равные фигуры имеют равные периметры и равные площади?

да;
нет.

Площадь прямоугольника определяется по формуле:

S = a2;
S = 2 • (a + b);
S = a • b.

Площадь фигуры изображённой на рисунке, равна:

12 см;
8 см;
16 см.

б) (Постановка проблемы). Задача. Сколько надо краски, чтобы покрасить пол, который имеет следующую форму (см. рис. ), если на 1 м2 расходуется 200 г краски?

III. Изучение нового материала.

Что же мы должны узнать, чтобы решить последнюю задачу? (Найти площадь пола, который имеет вид «сложной фигуры»

Учащиеся формулируют тему и цели урока (если необходимо учитель помогает).

Рассмотрим прямоугольник ABCD. Проведём в нем линию KPMN, разбив прямоугольник ABCD на две части: ABNMPK и KPMNCD.

Чему равна площадь ABCD? (15 см2)

Чему равна площадь фигуры ABMNPK? (7 см2)

Чему равна площадь фигуры KPMNCD? (8 см2)

Проанализируйте полученные результаты. (15= = 7 +

Вывод? (Площадь всей фигуры равна сумме площадей её частей

S = S1 + S2

Как можно применить это свойство для решения нашей задачи?(Разобьём сложную фигуру на части, найдём площади частей, затем площадь всей фигуры

S1 = 7 • 2 = 14 (м2)
S2 = (7 – 4) • (8 – 2 – 3) = 3 • 3 = 9 (м2)
S3 = 7 • 3 = 21 (м2)
S = S1 + S2 + S3 = 14 + 9 + 21 = 44 (м2)

Давайте составим план решения задач на нахождение площади «сложной фигуры»:

Разбиваем фигуру на простые фигуры.
Находим площади простых фигур.

а) Задача 1. (коллективное решение на доске и в тетрадях. ) Сколько потребуется плитки, чтобы выложить площадку следующих размеров:

S = S1 + S2
S1 = (60 – 30) • 20 = 600 (дм2)
S2 = 30 • 50 = 1500 (дм2)
S = 600 + 1500 = 2100 (дм2)

Есть ли другой способ решения? (Рассматриваем предложенные варианты

Ответ: 2100 дм2.

Задача 2. (коллективное решение на доске и в тетрадях. ) Сколько требуется м2 линолеума для ремонта комнаты, имеющей следующую форму:

S = S1 + S2
S1 = 3 • 2 = 6 (м2)
S2 = ((5 – 3) • 2) : 2 = 2 (м2)
S = 6 + 2 = 8 (м2)

Ответ: 8 м2.

А теперь, ребята, встали. Быстро руки вверх подняли. В стороны, вперед, назад. Повернулись вправо, влево. Тихо сели, вновь за дело.

б) Самостоятельная работа (обучающего характера).

Учащиеся разбиваются на группы (№ 5–8 более сильные). Каждая группа – ремонтная бригада.

Задание бригадам: определите, сколько надо краски, чтобы покрасить пол, имеющий форму фигуры, изображённой на карточке, если на 1 м2 требуется 200 г краски.

Вы эту фигуру строите своей тетради и записывая все данные, приступаете к выполнению задания. Можете обсуждать решение (но только в своей группе!). Если какая-то группа справляется с заданием быстро, то ей – дополнительное задание (после проверки самостоятельной работы).

Задания для групп:

18, № 718, № 749.

Дополнительное задание. План-схема Летнего сада (Санкт-Петербург). Вычислить его площадь.

Площадь сложных фигур — Памятки по математике — Памятки ученикам

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

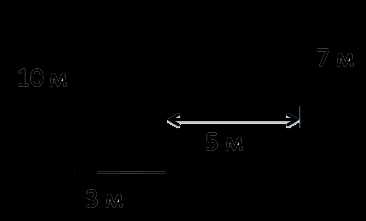
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

_ABCE_EFKL2_CDEF_CDEF2

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.

_ABCE_EFKL2

Ответ: S = 65 м2 — площадь огородного участка.

Свойство ниже может вам пригодиться при решении задач на площадь.

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

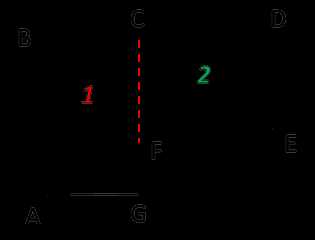
Рассмотрим прямоугольник:

АС — диагональ прямоугольника ABCD. Найдём площадь треугольников ABC и ACD.

Вначале найдём площадь прямоугольника по формуле.

_ABCD_ABCD2

S_ABC = S_ABCD : 2

S_ABC = 20 : 2 = 10 см2

S_ABC = S_ACD = 10 см2.

Задачи на площадь фигуры на координатной плоскости.

Чем отличаются задачи этого типа от предыдущих? Почти ни чем. Координатная плоскость — та же самая сетка. Только линии этой сетки
пронумеровали, а затем стерли, а на фигуре написали на каких линиях были расположены её вершины. Когда? Еще в 17-ом веке. Зачем?
Чтобы как-то, хотя бы условно, изображать большие и несоразмерные фигуры, которые не помещаются на рисунке в нормальном масштабе.

Из этих соображений, следуют два способа решения задач:Первый, самый надежный, — выучить понятия и формулы из раздела «Декартовы
координаты на плоскости и в пространстве». Второй, самый простой для тех, кто разобрался с предыдущей задачей, —
восстановить сетку.

Решение вторым способом более очевидное. Теоретически так можно решать любую задачу на координатную плоскость, но это может
оказаться значительно медленнее, чем первым способом, и потребовать «немеряного количества» бумаги. (Иначе не надо было бы
изобретать координаты.) Поэтому здесь мы рассмотрим те задачи, для которых решение восстановлением сетки достаточно быстрое и
компактное, а затем еще раз вернемся к понятию координатной плоскости в следующем разделе.

Задача 13

Найдите площадь четырёхугольника, вершины которого имеют координаты (3, 2), (7, 6), (7, 8), (3, 6).

Решение.

Оси координат — это линии сетки, с которых начинается нумерация. Ось Ox — нулевая горизонтальная линия, ось Oy — нулевая вертикальная линия. Запись «координаты (3, 2)» означает, что точка находится на 3-ей вертикальной линии сетки и на второй горизонтальной, аналогично «координаты (7, 6)» — на 7-ой вертикальной и 6-ой горизонтальной, и т. д. Рисуем нужное количество линий на заданном чертеже. Результат на рисунке слева. Видно, что этот рисунок очень похож на рисунок к условию предыдущей задачи. А, если не обращать внимания на оси, то абсолютно тот же (это потому, что для примера я специально выбрала задачу с той же самой трапецией). Значит решать можно любым из представленных выше четырёх способов. Например, разбиваем трапецию на два прямоугольных треугольника и вычисляем:S1 = 4×2/2 = 4. S2 = 4×4/2 = 8. S = S1 + S2 = 4 + 8 = 12.

Ответ: 12

Следующую задачу постарайтесь сначала решить самостоятельно, а затем проверьте своё решение.

Задача 14

Найдите площадь четырехугольника, вершины которого имеют координаты (4, 2), (8, 4), (6, 8), (2, 6).

Решение

На рисунке в условии задачи пунктиром показаны отрезки линий сетки, которые проходят через вершины четырёхугольника (здесь это 2-я, 4-я, 6-я и 8-я линии как по вертикали, так и по горизонтали). Дорисовываем весь участок сетки в окрестности заданной фигуры. Решаем задачу так, как если бы она была задана на клеточках, без координатных осей. У нашего четырёхугольника нет сторон, лежащих на линиях сетки, поэтому выберем третий метод из предыдущего раздела — метод «вырезания». Строим внешний прямоугольник, стороны которого проходят по сетке через вершины заданного. Прямым подсчетом клеточек убеждаемся в том, что красная линия на чертеже ограничивает квадрат со стороной 6 единиц, значит его площадь равна S_кв = 36 ед.2, а четыре зеленых прямоугольных треугольника равны между собой и имеют катеты 2 ед. и 4 ед., площадь каждого из них равна 2×4/2 = 4. Следовательно, искомая площадь желтого четырехугольника равна S = 36 − 4×4 = 20.

Ответ: 20

Замечания:
1) По рисунку видно, и равенством зеленых треугольников подтверждается, что заданный четырёхугольник тоже квадрат. Но нам здесь это даже не потребовалось.
2) В качестве упражнения на развитие воображения попробуйте найти эту площадь вторым методом из предыдущего раздела — методом разрезания желтого квадрата по линиям сетки на простые части.

Продолжение:Задачи на понятие координатной плоскости.Задачи на вектора.

Перейдите по стрелке, чтобы найти ссылки на другие задачи ЕГЭ по математике.

Примеры расчета площадей разных фигур

Прямоугольник:

Площадь прямоугольника можно рассчитать по формуле:

площадь = длина × ширина. Например, если у нас есть прямоугольник с длиной 6 клеток и шириной 4 клетки,

то его площадь будет равна 6 × 4 = 24 клеток.
Квадрат:

Площадь квадрата можно рассчитать по формуле:

площадь = сторона × сторона. Например, если у нас есть квадрат со стороной 5 клеток,

то его площадь будет равна 5 × 5 = 25 клеток.
Треугольник:

Расчет площади треугольника может быть сложнее, в зависимости от его формы.

Но если у нас есть прямоугольный треугольник, то его площадь можно рассчитать по формуле:

площадь = (основание × высота) / 2. Например, если у нас есть прямоугольный треугольник с основанием 4 клетки и высотой 3 клетки,

то его площадь будет равна (4 × 3) / 2 = 6 клеток.

Как найти площадь геометрической фигуры по клеточкам?

Площадь фигуры (треугольник, четырёхугольник, трапеция и др.) по клеточкам (клеткам).

Какие есть формулы?

комментировать
в избранное
10 ответов:
Алиса в Стран е
4 года назад

Есть способ, при котором надо воспользоваться формулой, основой которой будет понятие узла, узла внутреннего и узла внешнего. Узел это пересечение линий, образующих эти самые клеточки. Внешние узлы, это узлы, находящиеся на сторонах и вершинах геометрических фигур, площади которых нам надо найти. А внутренние узлы, это узлы внутри этих фигур. Клеточки у нас со сторонами равными одному сантиметру (1 см).

Формула, о которой идет речь, называется формула Пика.

Выглядит она вот так:

И по ней очень просто посчитать площадь фигуры S. В этой формуле M это количество внешних узлов, N — количество внутренних узлов.

Приведем пример, возьмем геометрическую фигуру параллелограмм:

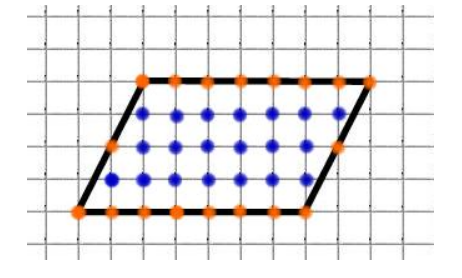
Внутренние узлы — синие — N — их у нас 20.

Внешние узлы — красные — М — их у нас 18 и их количество нам надо поделить на два, получится 18/2 = 9 узлов.

Складываем 9 + 20 и вычитаем единицу: 20 + 9 — 1 = 28 см².

Еще один пример:

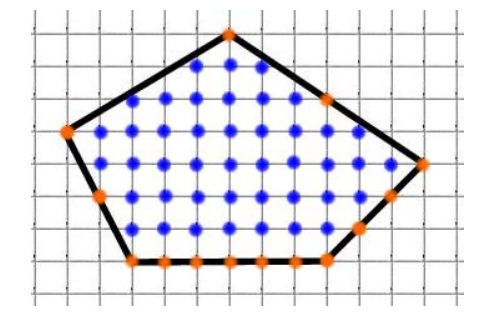
S = 14/2 + 43 — 1 = 49 см².

система выбрала этот ответ лучшим
комментировать
в избранное ссылка отблагодарить
Ксарф акс
6 лет назад

Допустим, у нас есть произвольная фигура, построенная на листе в клетку. Необходимо вычислить её площадь.

Площадь фигуры по клеточкам

Для того, чтобы найти площадь любой фигуры по клеточкам, можно использовать формулу Пика.

Данная формула основана на подсчёте количества узлов, лежащих внутри фигуры и на её границе.

Узел — это точка, которая лежит на пересечении 2 линий данной сетки: вертикальных и горизонтальных.

Площадь фигуры по клеточкам находится по формуле:

N — количество узлов, которые находятся внутри фигуры.

M — количество узлов, которые находятся на границах (на вершинах и сторонах).

Примеры нахождения площади по клеточкам

1) Найдём площадь треугольника. Будем считать, что одна клетка — это 1 см.

Отметим внутренние узлы и узлы, которые находятся на границах.

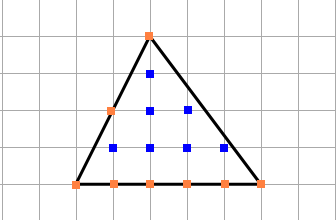
N = 7 (внутренние).

M = 8 (узлы на границах).

Площадь треугольника S = 7 + 8/2 — 1 = 10 см².

2) Найдём площадь трапеции по клеточкам, одна клетка — это 1 см. Отметим все узлы и подсчитаем их количество.

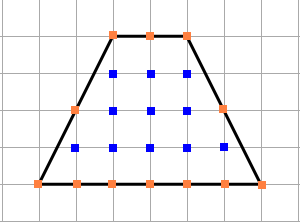
N = 11 (внутренние).

M = 12 (узлы на границах).

Площадь трапеции S = 11 + 12/2 — 1 = 16 см².

3) Найдём площадь произвольного многоугольника. Одна клетка — это 1 см.

Отметим внутренние узлы и узлы, расположенные на границах фигуры. Подсчитаем их количество.

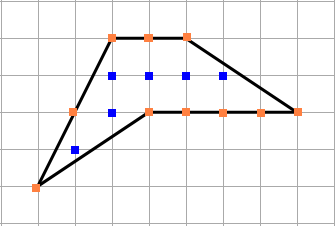
N = 6 (внутренние узлы).

M = 8 (узлы на границах).

Площадь многоугольника S = 6 + 10/2 — 1 = 10 см².

комментировать
в избранное ссылка отблагодарить
Марин а Волог да
4 года назад

Такие задачи очень часто встречаются, когда известен размер клеточки и дана фигура.

Вот пример таких задач:

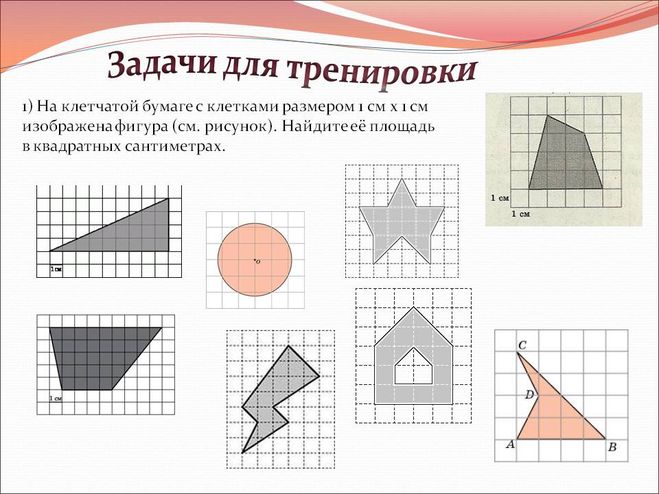
Решение зависит от того, какая фигура дана и как именно она размещена относительно клеточек.

Возьмем простой пример, необходимо вычислить площадь вот такого треугольника:

Теперь считаем, сколько клеточек треугольник в длину и сколько в высоту. У нас получается 2 в высоту и 6 в длину.

Подставляем к формуле:

S = 1/2 х 2 х 6 = 6 см2.

Считаем по клеточкам, подставляя формулу Пика:

Целых клеточек у нас 3.

Теперь считаем, сколько не целых: 6. Делим их на 2.

S = 3 + 6:2 = 6 см2.

А теперь высчитываем по формуле Пика: количество узлов сетки внутри — 2, количество узлов сетки, лежащих на границах — 10.

Подставляем к формуле и получаем — 2 + 10:2 — 1 = 6 см2.

Теперь давайте рассмотрим вот такой треугольник:

Чтобы найти площадь, вспоминаем правило:

Считаем клеточки и подставляем в формулу:

S = 1/2 х 2 х 6 = 6 см2.

А теперь находим по клеточкам: целых клеточек 2, не целых клеточек 8. Подставляем в формулу: 2 + 8:2 = 6 см2.

Пробуем сделать по формуле Пика: количество узлов сетки внутри — 3, количество узлов сетки, лежащих на границах — 8.

Подставляем к формуле и получаем — 3 + 8:2 — 1 = 6 см2.

комментировать
в избранное ссылка отблагодарить
Enot-Nina
4 года назад

Найти площадь геометрической фигуры можно самыми разными способами:

Самый простой вариант — это вручную посчитать клеточки — целые и половинки также поскладывать. Простой, хотя и не самый быстрый и может не самый точный способ, но он работает. Чтобы легче было считать, достаточно расчертить фигуру на более простые.

Есть еще один способ — это использовать давно разработанную формулу. Это так называемая формула Пика. Для нее нужно посчитать количество узлов — точек пересечения клеточек, что окружены фигурой (находятся внутри нее), а также подсчитать количество пограничных узлов — по контуру фигуры.

Вот на картинке наглядно показано, как ее можно применять, чтоб посчитать площадь любой фигуры по клеточкам:

Формула Пика

Формула Пика. Рассказ о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.

Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.

В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.

ФОРМУЛА ПИКА

Площадь искомой фигуры можно найти по формуле:

М – количество узлов на границе треугольника (на сторонах и вершинах)

N – количество узлов внутри треугольника

*Под «узлами» имеется ввиду пересечение линий.

Найдём площадь треугольника:

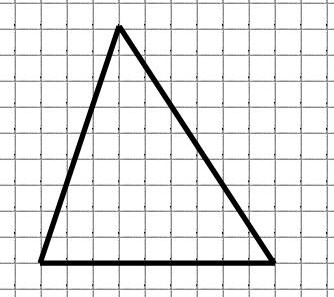
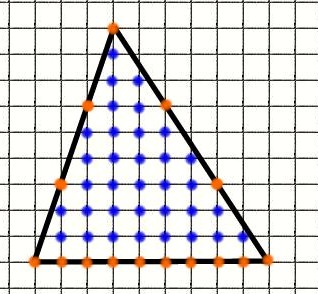
M = 15 (обозначены красным)

N = 34 (обозначены синим)

Ещё пример. Найдём площадь параллелограмма:

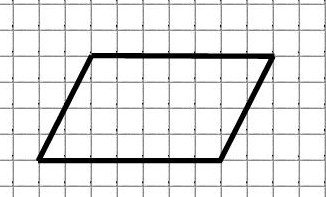
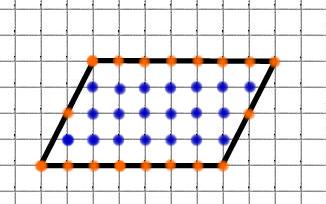
M = 18 (обозначены красным)

N = 20 (обозначены синим)

Найдём площадь трапеции:

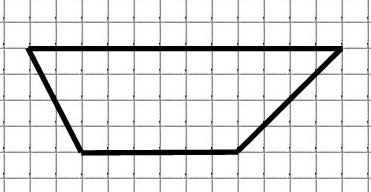
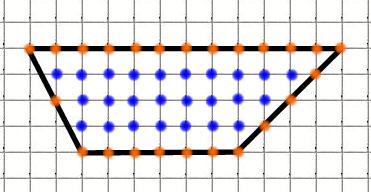
M = 24 (обозначены красным)

N = 25 (обозначены синим)

Найдём площадь многоугольника:

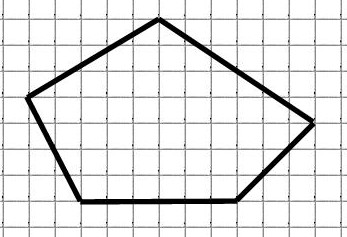
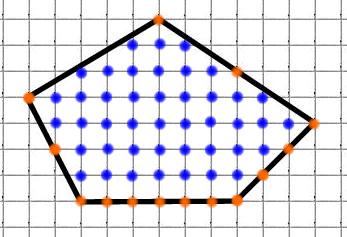
M = 14 (обозначены красным)

N = 43 (обозначены синим)

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом.

А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.

Теперь взгляните на следующие фигуры:

Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, н айдём площадь фигуры:

M = 11 (обозначены красным)

N = 5 (обозначены синим)

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.

Найдём площадь фигуры:

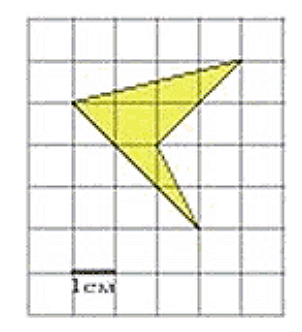
Опишем около неё прямоугольник:

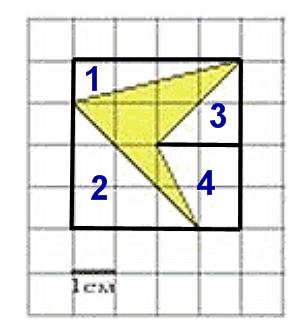
Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:

В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите! На этом всё. Успехов вам!

Для вас другие записи этой рубрики:

Объем шара
Составить пропорцию
Средняя линия треугольника. Определение
Площадь многоугольника

Пример вычисления площади пятиугольника по клеточкам

Для вычисления площади пятиугольника по клеточкам сначала нужно определить количество квадратиков, занимаемых фигурой. Затем, умножив это количество на площадь одного квадрата, получим итоговую площадь пятиугольника.

Начнем со знакомого примера. Предположим, что нам дана следующая пятиугольная фигура:

X X X
. X X X X
. . X X X X
. . . X X X
. . . . X X

Каждая точка представляет одну клеточку. Чтобы определить количество квадратиков, занимаемых фигурой, нужно просмотреть все клеточки внутри пятиугольника и посчитать их. В данном случае, у нас есть 5 символов «X», то есть пятиугольник занимает 5 квадратиков.

Допустим, площадь одного квадрата равна 1. Тогда, умножив количество квадратиков на площадь одного, получим итоговую площадь пятиугольника.

Площадь пятиугольника = 5 квадратиков * 1 квадратик = 5 квадратиков.

Таким образом, площадь данной пятиугольной фигуры равна 5 квадратикам (единицам площади).

Типы и примеры неровных фигур

1. Прямоугольник с отсеченным углом

Эта фигура представляет собой прямоугольник, у которого один угол отсечен или отрезан. Такая форма может возникнуть, например, при моделировании здания с неправильной формой.

2. Круг с булавкой

Эта фигура состоит из круга, в который вставлена или воткнута булавка. Такая форма может появиться, например, при рисовании или моделировании цветка с центральным стеблем.

Пример неровной фигуры	Изображение
Прямоугольник с отсеченным углом	!(example1.png)
Круг с булавкой	!(example2.png)

Одной из проблем при работе с неровными фигурами является определение и вычисление их площади. Это может быть сложно из-за неоднородности и сложности формы. Однако, с использованием клеточного подхода, можно разбить фигуру на более простые формы и вычислить их площади по отдельности.

Достоинства и недостатки способа №1

Достоинства:

Простота использования — для расчета площади достаточно уметь считать количество клеток внутри фигуры и умножить на размер одной клетки.
Не требует специальных инструментов — для расчета достаточно обычной линейки или мерной ленты для измерения размеров клетки.
Подходит для различных геометрических фигур — способ №1 может быть использован для расчета площади как простых, так и сложных фигур, включая прямоугольники, треугольники, круги и т.д.

Недостатки:

Точность — способ №1 не обеспечивает высокой точности расчета площади, особенно для фигур с нестандартной формой. Он лишь приближенно определяет площадь, не учитывая сложности контура фигуры и возможность вычисления «нечетких» площадей.
Неудобство для сложных фигур — при расчете площади сложных фигур с большим количеством клеток способ №1 может занять много времени и требовать много усилий. В таких случаях более точные и удобные методы могут быть предпочтительнее.
Ограниченность размеров клеток — результаты расчета площади с помощью способа №1 зависят от размеров клетки. При выборе неправильного размера клетки или неправильного масштаба изображения можно получить неточные результаты.