Алгебра

Сколько комбинаций 6-значного пароля можно составить из цифр от 0 до 10.

10 использовать нельзя, можно только цифры от 0 до 9. Тогда на первом месте любая из 10 цифр, на втором — тоже любая из 10 и т. д. всего 6 мест, следовательно, получаем 1 000 000 комбинаций, если повторения цифр в пароле возможены

возможно вы имели в виду от 0 до 9? потому как в числе 10 две цифры и оно явно не сойдёт за один символ считается это так: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 — всего 10 вариантов, и шесть полей, значит: 10 х 10 х 10 х 10 х 10 х 10 = 10^6 = 1 000 000 комбинаций то есть в данном случае ряд комбинаций 000000, 000001, 000002… 999998, 999999 ЕСЛИ ПОВТОРЯТЬ ЗНАКИ НЕЛЬЗЯ,
то каждый раз у нас будет оставаться на один вариант меньше, а считаем так же: 10 х 9 x 8 x 7 x 6 x 5 = 151 200 комбинаций

Возведите количество возможных вариантов знаков в одной ячейке пароля (10), в степень количества цифр в пароле (6).
То есть в нашем случае 10^6 = 1 000 000 ПС:
Если используются цифры от 0 до 10 включительно (то есть 0,1,2,3,4,5,6,7,8,9,10).
То так 11^6 = 1 771 561

Дробные числа от 0 до 1

Дробные числа, также известные как десятичные числа, представляют числа, которые меньше единицы, но больше нуля.

В диапазоне от 0 до 1 находится бесконечное количество дробных чисел. Некоторые из них могут быть представлены с конечным числом знаков после запятой, такие как 0,5 или 0,75. Другие дробные числа в этом диапазоне имеют бесконечное количество знаков после запятой и называются бесконечными десятичными.

Один из способов представления дробных чисел от 0 до 1 — использование обычной десятичной записи. Например, 0,25 или 0,75. Еще один способ представления — использование десятичных дробей в виде окружностей или многоугольников, где каждый отрезок представляет одну долю от всей единицы.

Примеры дробных чисел от 0 до 1:

• 0,1
• 0,2
• 0,3
• 0,4
• 0,5
• 0,6
• 0,7
• 0,8
• 0,9
• 0,10

В приведенном списке представлены примеры дробных чисел от 0 до 1. Эти числа могут быть использованы для различных вычислений или для представления точности измерения, так как они позволяют представить значения между нулем и единицей с различной степенью точности.

Сколько вариантов комбинаций из 3 цифр?

Бывают ситуации, когда может возникнуть вопрос по поводу сопоставления различных комбинаций, способных в дальнейшем помочь при решении задач любой сложно. Вопрос, на первый взгляд, может показаться достаточно легким, но на самом деле может возникнуть подвох

Важно пользоваться логическим мышлением и пытаться начать постепенно рассуждать

В данной статье можно узнать ответ и способы нахождения вариантов комбинаций из 3 цифр, возможность использовать различные методы. Главное — стараться воспользоваться каждой парой цифр по порядку, чтобы не возникло путаницы, а можно записывать по очереди, таким образом, достичь решения задачи будет проще.

Может произойти случай, когда дома находится старый чемодан или сейф, на котором стоит кодовый замок, давно забытый всеми членами семьи, но необходимо взять, что-то нужное и для этого использовать логические возможности.

Чтобы вычислить правильно количество комбинаций из 3 цифр и не ошибиться нужно применить произвольный набор способов по правилам произведения, который поможет разобраться. Например, n1*n2…*nN используя данную формулу для вычислений. К каждой позиции выбирается символ от 0 до 9, то есть 10 вариантов и так берем каждую и выбираем цифру, записываем.

10*10*10 в результате получив 1000 комбинаций и методов.

Продолжаем подставлять числа, пока не дойдем до нужного варианта и сможем решить данную задачу, при этом не прилагая особых усилий.

Размещения

Пусть в футбольном турнире участвуют 6 команд. Нам предлагают угадать те команды, которые займут призовые места (то есть первые три места). Сколько вариантов таких троек существует?

Сначала запишем ту команду, которая выиграет турнир. Здесь есть шесть вариантов, по количеству участвующих команд. Запишем эти варианты:

Далее выберем один из вариантов и для него укажем серебряного призера соревнований. Здесь есть только 5 вариантов, ведь 1 из 6 команд уже записана на 1-ом месте:

Такую пятерку можно записать для каждого из шести вариантов того, кто станет чемпионом. Получается, что всего есть 6•5 = 30 пар «чемпион – серебряный призер». Наконец, для одной такой пары можно записать 4 варианта того, кто окажется третьим (две команды писать нельзя, так как они уже записаны на первых двух строчках):

Для каждой пары можно записать 4 тройки призеров. Так как число пар «чемпион – вице-чемпион» равно 6•5 = 30, то число троек составит 6•5•4 = 120.

В данном случае из некоторого множества команд мы выбрали несколько и расположили их в каком-то порядке. То есть мы выбрали упорядоченное множество. В комбинаторике оно называется размещением.

Если общее число команд обозначить как n (в этом примере n = 6), а количество упорядочиваемых команд равно k, то количество таких размещений в комбинаторике обозначается как

В примере с командами количество размещений равнялось 120:

Читается эта запись как «число размещений из 6 по 3 равно 120».

Для нахождения этого числа мы перемножили k (3)множителей. Первый из них был равен n(6), так как каждая из n команд могла занять первая место. Второй множитель был равен (n– 1), так как после определения чемпиона мы могли поставить на вторую позицию одну из (n– 1) команд. Третий множитель был равен (n– 2). По этой логике каждый следующий множитель будет меньше предыдущего на единицу. Например, чтобы вычислить число размещений из 7 по 4, надо перемножить 4 множителя, первый из которых равен 7, а каждый следующий меньше на 1:

Однако математически удобнее представлять это произведение как отношение двух факториалов. Для этого умножим количество размещений на дробь 3!/3!, равную единице. Естественно, число размещений из-за умножения на единицу не меняется:

Число 3 в данном случае можно получить, если из 7 вычесть 4. В общем случае из числа n надо вычесть число k. Тогда формула для вычисления количества размещений примет вид:

Пример. В программе 8 «А» класса 12 различных предметов. В понедельник проводится 5 занятий подряд. Сколько существует вариантов расписаний для класса, если в течение понедельника нельзя проводить два одинаковых урока?

Решение. Для составления расписания нужно выбрать 5 предметов и расставить их по порядку. Поэтому нам необходимо найти размещение из 12 по 5:

Ответ: 95040

Пример. В вагоне 10 свободных мест. В него зашло 6 пассажиров. Сколькими способами они могут расположиться в вагоне?

Решение. Из десяти мест надо выбрать шесть и указать для каждого, какому пассажиру оно соответствует. То есть каждый вариант рассадки пассажиров – это размещение из 10 по 6. Найдем их количество:

Ответ: 151200

Заметим, что перестановка – это частный случай размещения, когда k = n. Действительно, если нам надо указать тройку призеров турнира, в котором участвуют 6 команд, то мы указываем размещение из 6 по 3. Но если мы указываем для каждой из 6 команд, какое место она займет в чемпионате, то это размещение из 6 по 6. С другой стороны, это расстановка одновременно является и перестановкой 6 команд. Убедимся, что в этом частном случае формула для подсчета количества размещений покажет тот же результат, что и формула для перестановок

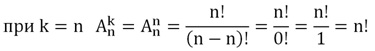
Для примера с 6 командами это будет выглядеть так:

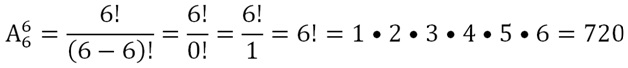
Здесь мы использовали тот факт, что факториал нуля принимается равным единице. Данное рассуждение можно, наоборот, использовать для того, чтобы доказать, что факториал нуля – это единица.

Комбинаторика: правило размещения без повторений

Подмножество, выбираемое из данного множества предметов, называют выборкой. Выборки бывают упорядоченные и неупорядоченные. Для упорядоченной выборки существенен порядок элементов. Иначе говоря, меняя порядок элементов, мы получаем другие выборки. Составим, например, из цифр 1, 2, 3, 4, 5 трехзначные числа: 123, 431, 524 и т.д. Это упорядоченные трехэлементные выборки, отличающиеся составом или порядком элементов.

Размещениями из $n$ элементов по $m$ элементов ($m$≤$n$) называют упорядоченные $m$-элементные выборки из данных $n$ элементов.

Формула размещения без повторений в комбинаторике $n$ по $m$ элементов имеет вид: $A_{n}^{m} =\frac{n!}{\left(n-m\right)!} $.

Комбинаторные задачи с решениями

Примеры всех возможных типов задач с решениями были даны выше. Здесь попробуем разобраться с более сложными случаями, встречающимися в нашей жизни.

Типы задач	Что требуется найти	Методы решения
Магический квадрат	Фигура, в которой сумма чисел в рядах и столбцах должна быть одинакова (его разновидность – латинский квадрат).	Рекуррентные соотношения. Решается подобная же задача, но с гораздо меньшим множеством элементов по известным правилам и формулам.
Задача размещения	Стандартная производственная задача (например, в лоскутной технике) найти возможные способы разложения количества продуктов в ячейки в определенном порядке.	Включения и исключения. Как правило, применяется при доказательстве различных выражений.
Задачи про торговцев	Суть найти все возможные пути прохождения людей из пункта А в пункт В.	Траектории. Для этого вида задач характерно геометрическое построение возможных способов решения.

Что почитать по комбинаторике?

Рекомендуем начать с нестареющей классики –«Комбинаторики» Н. Я. Виленкина. Книга регулярно дополняется и переиздается с 1969 года. Ее главный плюс – простой, понятный и увлекательный стиль изложения. Второй плюс – множество заданий и примеров из реальной жизни.

«Введение в комбинаторный анализ», Джон Риордан. Это тоже винтажная книга (1963 года), но она до сих пор пользуется заслуженной популярностью. Книга начинается с основных комбинаторных понятий (перестановки, сочетания и размещения), и постепенно переходит к более сложным темам – генерирующим функциям, теории вероятностей и комбинаторному анализу алгоритмов. Большой плюс книги – структурный подход к изложению материала и множество упражнений.

«Конкретная математика. Математические основы информатики», Дональд Кнут, Рональд Л. Грэхем, Орен Паташник. Книга основана на одноименном курсе лекций, который ежегодно читается в Стэнфордском университете начиная с 1970 года. Когда Кнут приступил к написанию того самого трехтомника, которым сейчас пугают всех начинающих программистов, он обнаружил, что его собственная математическая база оставляет желать лучшего. Поэтому он и создал курс, который сам хотел бы прослушать, а затем – написал эту книгу, в которой, помимо всего прочего, подробно разбираются концепции и методы комбинаторики.

«Избранные задачи комбинаторного анализа», В. К. Леонтьев. Это сборник интересных и сложных комбинаторных задач, которые можно использовать для самостоятельного изучения продвинутых тем (теории корректирующих кодов, дискретной геометрии, вероятностной комбинаторики) и для подготовки к олимпиадам и экзаменам.

«Комбинаторные алгоритмы для программистов», Н. И. Костюкова. Эта книга представляет собой сборник лекций, которые читают в Новосибирском государственном университете. Здесь компактно изложено все, что нужно знать о комбинаторике – от самых азов до алгоритмов на графах.

Размещение

Размещение — это способ выбрать и упорядочить элементы из множества. В отличие от операции сочетания, при размещении важен порядок составляющих множества.

Вопрос размещения: сколько упорядоченных наборов можно сделать из k элементов, выбранных из n?

Размещение без повторяющихся элементов

Если во множестве n ни один элемент не повторяется, то используется следующая формула:

Пример. В лототроне находится 90 шаров с номерами от 10 до 99. Ведущий последовательно достаёт три шара и кладёт их рядом так, чтобы получилось шестизначное число. Сколько вариантов шестизначных чисел может получиться?

Решение. Ведущий выбирает и упорядочивает 3 шара из 90. Подставляем числа в формулу выше и смотрим на результат:

Размещение с повторяющимися элементами

Если во множестве n один и тот же элемент можно взять несколько раз, то используется следующая формула:

Пример. В начале статьи мы писали о восьмисимвольном пароле, состоящем из латинских букв (заглавных и строчных) и цифр от нуля до девяти. Любой символ может использоваться сколько угодно раз. Сколько всего таких паролей можно составить?

Решение. Букв в латинском алфавите 26, следовательно, в пароле можно использовать 26 * 2 = 52 буквенных символа (26 для заглавных и 26 для строчных). Цифр от нуля до девяти — 10. В итоге получаем множество из 62 составляющие.

Практические приложения количества комбинаций из трех цифр

Сколько может быть комбинаций, состоящих из трех цифр? Оказывается, ответ на этот вопрос имеет множество практических применений.

Например, представим себе ситуацию, когда на двери есть кодовый замок, и чтобы его открыть, нужно ввести определенную комбинацию из трех цифр. Возможных комбинаций может быть довольно много, и злоумышленнику понадобится много времени и удачи, чтобы открыть замок методом перебора.

Количество комбинаций из трех цифр также используется в математике и статистике. В различных задачах, связанных с вероятностями, нужно знать, сколько может быть вариантов событий при определенных условиях. Например, при подбрасывании трех игральных костей, сколько может быть вариантов выпадения определенной комбинации цифр.

Другим примером применения количества комбинаций из трех цифр является лотерея. В некоторых лотерейных играх, чтобы выиграть джекпот, нужно угадать трехзначное число. Количество возможных комбинаций помогает оценить шансы на победу и определить вероятность выигрыша.

Таким образом, хотя на первый взгляд кажется, что из трех цифр может быть не так много комбинаций, на самом деле число вариантов может быть довольно значительным. Это знание находит свое применение в различных сферах жизни, связанных с безопасностью, математикой и играми, где вероятность играет важную роль.

Задачи блокировки с использованием комбинаций

Сколько может быть комбинаций из трех цифр? Данная задача часто возникает при использовании блокировки, например, на сейфе. Для ее решения необходимо учитывать, что каждая позиция в комбинации может принимать значения от 0 до 9.

Таким образом, чтобы определить сколько может быть комбинаций из трех цифр, необходимо учесть, что на первой позиции может быть любая цифра от 0 до 9, на второй позиции — любая цифра от 0 до 9 (включая возможность повторения цифр), а на третьей позиции — также любая цифра от 0 до 9.

Тогда общее количество комбинаций можно определить с помощью формулы:

Количество комбинаций = количество возможных значений на первой позиции * количество возможных значений на второй позиции * количество возможных значений на третьей позиции

В данном случае:

Количество комбинаций = 10 * 10 * 10 = 1000

Таким образом, из трех цифр может быть 1000 комбинаций.

Генерация случайных чисел с использованием комбинаций

Сколько может быть комбинаций из трех цифр? Этот вопрос может вызвать интерес у многих людей. И на самом деле ответ на него довольно прост. Если у нас есть три позиции и на каждой позиции может быть одна из десяти цифр, то общее количество комбинаций будет равно произведению возможных вариантов для каждой позиции. То есть 10 в первой степени, 10 во второй степени и 10 в третьей степени.

Итак, сколько может быть комбинаций из трех цифр? Может быть 10 * 10 * 10 = 1000 комбинаций. Каждая комбинация будет уникальной, так как порядок цифр важен. Например, число 123 и число 321 — это две разные комбинации.

Эта возможность генерировать случайные числа с использованием комбинаций может быть полезной в различных сферах. Например, в программировании, для генерации случайных чисел, которые могут быть использованы для создания уникальных идентификаторов или генерации случайных распределений данных. Также комбинации могут быть использованы в играх, лотереях или других ситуациях, где важна случайность и разнообразие.

Комбинаторика и ее основные принципы

Очень часто приходится решать задачи, в которых надо посчитать количество возможных вариантов для той или иной ситуации. Например, сколько позиций может возникнуть на шахматной доске после первого хода обоих игроков? Сколько разных паролей длиною в десять символов можно записать, если ни один символ не использовать дважды? Сколько разнообразных комбинаций чисел может выпасть при игре в лотерею «6 из 49»? На все эти вопросы помогает ответить специальный раздел математики, называемый комбинаторикой. Почти всегда комбинаторную задачу можно сформулировать так, чтобы ее вопрос начинался словами «сколькими способами…».

Очевидно, что если в конечном множестве содержится n элементов, то есть ровно n способов выбрать один из них.

Пример. В классе 15 человек. Сколькими способами учитель может назначить одного из них ответственным за чистоту доски?

Ответ. Таких способов ровно 15.

В комбинаторике существует два основных правила. Первое из них называется правилом сложения.

Несмотря на формулировку, по сути это очень простое правило.

Пример. В магазине продается 14 телевизоров Panasonic и 17 телевизоров Sony. Петя хочет купить один телевизор. Сколько у него вариантов покупки?

Решение. По правилу сложения Петя может выбрать один из 14 + 17 = 31 телевизоров.

Ответ: 31 телевизор.

Особое значение имеет второе правило, которое называют правилом умножения.

Проиллюстрируем это правило.

Пример. В секции бадминтона 15 мальчиков и 20 девочек. Тренер должен отправить на соревнования смешанную пару. Сколько вариантов действий у него?

Решение. Тренер может составить 15•20= 300 разнополых пар из своих воспитанников.

Ответ: 300

Пример. Пете нужно купить технику для компьютера. В магазине продается 20 различных клавиатур, 25 моделей геймпадов и 30 компьютерных мышей. Купить надо по одному экземпляру каждого из этих устройств. Сколько вариантов покупки есть у него?

Решение. Сначала подсчитаем число возможных пар «клавиатура-геймпад». Их количество равно 20•25 = 500. Теперь составим «тройку» из одной из 500 пар и одной из 30 мышей. Число троек равно 500•30 = 15000.

Ответ: 15000

Правила сложения и умножения можно комбинировать.

Пример. Сколько слов не более чем из трех букв можно составить, используя алфавит, содержащий ровно 30 букв?

Решение. Очевидно, что слов из одной буквы можно составить ровно 30. Количество двухбуквенных слов равно количеству пар, которые можно составить из этих букв, то есть 30•30 = 900. Трехбуквенных слов можно составить 30•30•30 = 27000. Всего же слов длиною не более 3 букв будет

30 + 900 + 27000 = 27930

Ответ: 27930

Далее мы изучим основные понятия комбинаторики – перестановки, размещения, сочетания.

Сочетания

Рассмотрим задачу, аналогичную задаче 5, но с существенным отличием.

7. Сколько существует различных вариантов выбора 4-х кандидатур из 9-ти специалистов?

В этой задаче нам нужно выбрать 4 кандидатуры, но при этом не важно, в каком порядке мы их выбираем, нас интересует только состав выбранных элементов, но не порядок их расположения. Если бы нас интересовал порядок расположения элементов, как в задаче 5, то мы могли применили бы формулу для нахождения числа размещений из 9 по 4:

Если бы нас интересовал порядок расположения элементов, как в задаче 5, то мы могли применили бы формулу для нахождения числа размещений из 9 по 4:

4 различных элемента можно расположить в определенном порядке 4! различными способами. Поскольку нас не интересует порядок расположения элементов, число способов, которыми мы можем выбрать 4 элемента, не располагая их в определенном порядке, уменьшается в 4! раза по сравнению с предыдущей задачей (так как для данной задачи различное расположение данных элементов считается одним способом), и мы получаем

способов.

В этой задаче появляется понятие сочетания.

Сочетаниями  из n элементов по k элементов называются подмножества, состоящие из k элементов множества (множества, состоящего из n элементов).

Внимание! Одно сочетание от другого отличается только составом выбранных элементов (но не порядком их расположения, как у размещений). Число сочетаний из n элементов по k элементов обозначается 

Число сочетаний из n элементов по k элементов обозначается 

и находится по формуле:

Число сочетаний из  n по k показывает, сколькими способами мы можем выбрать k элементов из n элементов, или сколькими способами мы можем расположить k объектов по n местам.

Легко заметить, что

8.  В коробке лежат 8 красных карандашей и 4 синих. Из коробки наугад вынимают 4 карандаша. Какова вероятность того, что среди них окажется 2 красных и 2 синих?

Решение.

Комбинации из трех цифр: вводная информация

Допустим, у нас есть всего три цифры — 0, 1 и 2. Мы можем использовать эти цифры для создания трехзначных комбинаций. Cколько может быть комбинаций в данном случае?

Мы можем выбрать любую цифру для первого разряда — это может быть 0, 1 или 2. После этого нам остается две цифры. Для второго разряда мы можем выбрать любую из оставшихся двух цифр, а для третьего — оставшуюся одну. Таким образом, получаем, что количество комбинаций из трех цифр равно 3 * 2 * 1 = 6.

Теперь представьте, что у нас есть больше цифр. Например, от 0 до 9. Сколько может быть комбинаций в этом случае?

Мы можем выбрать любую цифру для первого разряда — это может быть любая цифра от 0 до 9. После этого нам остается девять цифр. Для второго разряда мы можем выбрать любую из оставшихся девяти цифр, а для третьего — оставшуюся восьмую. Получаем, что количество комбинаций из трех цифр с использованием всех цифр от 0 до 9 равно 10 * 9 * 8 = 720.

Таким образом, количество возможных комбинаций из трех цифр зависит от количества доступных цифр и может быть различным.

Что такое комбинация?

• 1, 2, 3
• 1, 3, 2
• 2, 1, 3
• 2, 3, 1
• 3, 1, 2
• 3, 2, 1

Таким образом, мы можем составить 6 различных комбинаций из этих 3 цифр. Однако, если мы хотим знать сколько комбинаций может быть из заданного множества, мы можем использовать формулу для вычисления количества комбинаций. Общая формула для подсчета количества комбинаций из n элементов по k элементов выглядит следующим образом:

C(n, k) = n! / (k! * (n — k)!), где n! — факториал числа n.

Таким образом, для нашего случая с 3 цифрами, количество комбинаций будет равно:

C(3, 3) = 3! / (3! * (3 — 3)!) = 6

Таким образом, из 3 цифр может быть составлено 6 различных комбинаций.

Зачем нам нужно исследовать комбинации из трех цифр?

Исследование комбинаций из трех цифр имеет большое значение в различных областях, где требуется решение задач, связанных с числами и вероятностями. Знание сколько может быть комбинаций из трех цифр помогает нам лучше понять и анализировать данные, предсказать вероятности и проводить статистические исследования.

Сколько может быть комбинаций из трех цифр? Ответ на этот вопрос — 1000. Начиная от 000 и заканчивая 999, мы можем составить 1000 уникальных комбинаций. Каждая комбинация представляет из себя трехзначное число, где каждая позиция может быть заполнена любой цифрой от 0 до 9.

Зная, сколько может быть комбинаций из трех цифр, мы можем использовать эту информацию в различных сферах, например:

Сфера применения	Пример
Криптография	Использование комбинаций из трех цифр может помочь в защите информации, позволяя создавать сложные пароли и коды доступа.
Математика	Изучение комбинаций из трех цифр позволяет проводить исследования и доказательства в области комбинаторики и теории вероятностей.
Статистика
Игры и головоломки	Комбинации из трех цифр часто используются в играх и головоломках, где требуется логическое мышление и анализ возможных вариантов.

В общем, знание сколько может быть комбинаций из трех цифр может быть полезным во многих сферах, где требуется работа с числами и вероятностями. Это помогает нам лучше понимать и анализировать данные, принимать обоснованные решения и достигать поставленных целей.

Перестановка

Перестановка — это способ последовательно расположить составляющие множества. Например, 123, 312 и 213 — это перестановки трёх чисел: 1, 2 и 3.

Чтобы найти общее количество возможных перестановок, используют две формулы: для случаев с повторяющимися компонентами и без них. Давайте рассмотрим оба.

Перестановка без повторяющихся элементов

Если во множестве ни один элемент не повторяется, то используется следующая формула:

Пример: сколько перестановок символов можно составить из шести букв — q, w, e, r, t, y?

Решение: чтобы найти количество перестановок, нам нужно посчитать факториал числа 6 — то есть общего количества букв в наборе. Подставляем в формулу:

Перестановка с повторяющимися элементами

Если хотя бы один элемент во множестве повторяется, то используется следующая формула:

Формула выглядит довольно негуманно, поэтому объясним, в чём здесь логика. Сначала мы находим, сколько перестановок было бы, если бы все компоненты множества были разными. Потом мы делим это число на то, сколько раз можно переставить повторяющиеся элементы между собой. Это нужно, чтобы не считать одинаковые перестановки несколько раз. Дальше мы посмотрим на пример, чтобы лучше разобраться.

Пример. Допустим, у нас есть набор из восьми букв: p, a, s, s, w, o, r, d. Сколько всего перестановок символов можно составить из этих букв?

Решение. Видим, что буква s в этом наборе повторяется дважды. Значит, n = 8 и n₁ = 2. Подставляем эти значения в формулу и получаем:

Какое максимальное количество шестизначных комбинаций возможно из цифр от 0 до 9?

Нужно 10 возвести в 6-ю степень. Получится 1000000, т. е. миллион.
Это если числа повторяются. Если же они могут быть только один раз, то С = 10! / (10-6)! = 10!/4! = 151200
Ответ:
Если числа могут повторяться, то 1000000
Если числа НЕ могут повторяться, то 151200

Дохрена и более)

миллион…. 000000, 000001,000002….999999

В каждом разряде возможна любая из 10 цифр, разрядов 6, значит, 10^6 = 1000000.

Ну, главный принцип комбинатории заключается в следующем:
Если одно действие можно сделать n способами, а второе действие — m способами, то оба дела можно сделать m*n способами.
Теперь посмотрим на шестизначные комбинации:
Первую цифру шестизначной комбинации можно выбрать 10 способами (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
Вторую цифру тоже 10. И третью и четвертую, и т. д.. .
Поэтому выбрать шесть цифр можно 10*10*10*10*10*10 = 1000000 способами.
Что касается формулы, то если мы обобщим задачу следующим образом:
Имеется n различных букв, длина слова — m букв.
Умножаем m раз цифру n, получаем n в степени m.