Занимательная математика: правило гаусса

Числа от 1 до 100. Состав числа. Круглые числа

Предыдущее и последующее число

Предыдущее число — то число, которое при счете следует перед данным числом.

56, 57

Последующее число — то число, которое при счете называют сразу после данного числа.

56, 57

Однозначные и двузначные числа

Вспомни, что каждая цифра в записи занимает определенное место.

Единицы стоят на первом месте справа.

Десятки стоят на втором месте справа.

Однозначные числа записываются ОДНОЙ цифрой: 5, 9, 2, 5.

Двузначные числа записываются ДВУМЯ цифрами: 54, 91, 42, 85.

Самое маленькое однозначное число — .

Самое большое однозначное число — 9.

Самое маленькое двузначное число — 10.

Самое большое двузначное число — 99.

Состав двузначного числа

Всего на рисунке 35 палочкек.

35 = 3 дес. 5 ед.

35 = 30 + 5

Состав числа 35 — 3 дес. 5 ед.

Красных палочек 12.

12 = 1 дес. 2 ед.

12 = 10 + 2

Состав числа 12 — 1 дес. 2 ед.

Синих палочек всего 23.

23 = 2 дес. 3 ед.

23 = 20 + 3

Состав числа 23 — 2 дес. 3 ед.

Теперь научимся представлять числа в виде суммы разрядных слагаемых.

Какие разряды выделяют в двузначных числах?

В двузначных числах выделяют разряд десятков и разряд единиц, то есть двузначное число можно представить следующим образом:

десятки + единицы

В числе 35 три десятка и 9 единиц:

35 = 30 + 5

Сравнение двузначных чисел

Числа 42 и 24 похожи тем, что в их записи использованы одинаковые цифры: цифра 4 и цифра 2. Но цифра 4 для числа 42 означает десятки, а для 24 — единицы, цифра 2 для числа 42 означает единицы, а для 24 — десятки.

Число	42	24
Количество десятков	4	2
Количество единиц	2	4

42 > 24

1. Сравнение двузначных чисел всегда начинается с десятков.

2. Если количество десятков одинаково, тогда переходят к сравнению единиц.

Круглые числа

Числа, которые оканчиваются на 0, называются круглыми. — 60, 30, 20.

или

В разряде единиц у круглого числа — число 0. — 70, 90, 40.

10, 20, 30, 40, 50, 60, 70, 80, 90, 100.

10 + 40 = ?

1 дес. + 4 дес. = 5 дес.

5 дес. = 50, значит,

10 + 40 = 50

Десять любых предметов можно назвать – ОДИН ДЕСЯТОК.

Десятками можно считать:

— это 2 десятка — записываю так: 2 дес.

Действия с десятками и единицами

— это 31

Как решить пример 34 + 25?

34 — это 3 дес. и 4 ед.

25 — это 2 дес. и 5 ед.

3 дес. и 4 ед. + 2 дес. и 5 ед. = 5 дес. 9 ед.

5 дес. — 50

50 + 9 = 59

Можно записать короче:

Рассуждаю так:

Число 34 представляю в виде суммы разрядных слагаемых: 30 и 4, число 25 тоже представляю как 20 и 5. Теперь начинаю вычислять:

Сначала складываю единицы:

4 + 5 = 9

Теперь складываю десятки:

30 + 20 = 50

Запись решения выглядит так:

34 + 25 = (30 + 20) + (4 + 5) = 50 + 9 = 59

34 + 25 = 59

Десятки складываются с десятками.

Единицы складываются с единицами.

Как решить пример 38 — 16?

Число 38 — можно представить как 3 дес. и 8 ед.

Число 16 — это 1 дес. 6 ед.

3 дес. 8 ед. — 1 дес. 6 ед. = 2 дес. 2 ед.

38 — 16 = (30 — 10) + (8 — 6) = 20 + 2 = 22

38 — 16 = 22

Можно рассуждать так:

Число 38 представим в виде суммы разрядных слагаемых 30 и 8, а число 16 представим так: 10 и 6. Удобно число 6 вычесть из числа 8, получим 2. Затем число 10 вычтем из числа 30, получим 20. Теперь 2 прибавим к числу 20. Получим 22.

38 — 16 = 22

Вывод:

Десятки вычитаются из десятков.

Единицы вычитаются из единиц.

Мы рассмотрели случаи устных вычислений с двузначными числами.

Познакомиться с письменными приема вычислений (сложением в столбик и вычитанием в столбик) можно в нашем справочнике.

Правило встречается в следующих упражнениях:

2 класс

Задание 22, Моро, Волкова, Рабочая тетрадь, 1 часть

Задание 28, Моро, Волкова, Рабочая тетрадь, 1 часть

Задание 79, Моро, Волкова, Рабочая тетрадь, 1 часть

Задание 111, Моро, Волкова, Рабочая тетрадь, 1 часть

3 класс

2019 — budu5.com, Буду отличником!

Нашли ошибку?

Связаться с нами

Практическое применение знания о количестве чисел от 1 до 10

Знание о количестве чисел от 1 до 10 может быть полезным во многих практических ситуациях. Оно помогает в решении задач, связанных с подсчетом, анализом и прогнозированием данных. Рассмотрим несколько примеров применения этого знания:

1. Вероятностные расчеты

Оценка вероятности событий во многих случаях связана с подсчетом количества элементарных исходов. Зная, что между числами 1 и 10 находится 10 чисел, мы можем использовать это знание для определения вероятности различных исходов. Например, если мы хотим вычислить вероятность выбора случайного числа от 1 до 10, мы знаем, что всего возможно 10 исходов, поэтому вероятность каждого исхода будет равна 1/10 или 0,1.

2. Анализ данных

Знание о количестве чисел от 1 до 10 может быть использовано для анализа данных, особенно при решении задач классификации. Например, если у нас есть данные о людях и их возрасте, и нам нужно разделить их на группы в соответствии с возрастными категориями, мы можем использовать информацию о числе от 1 до 10 для определения количества категорий, например «дети» (1-10 лет), «подростки» (11-20 лет), «взрослые» (21-30 лет) и т. д.

3. Маркетинговые исследования

При проведении маркетинговых исследований информация о количестве чисел от 1 до 10 может быть полезна для определения размера выборки или количества респондентов, необходимых для получения достоверных результатов. Например, если мы хотим провести опрос среди случайной выборки населения, мы можем использовать информацию о количестве чисел от 1 до 10 для определения оптимального размера выборки, чтобы получить репрезентативные данные и сделать общие выводы о целевой группе.

4. Программирование и алгоритмы

Знание о количестве чисел от 1 до 10 может быть полезно при разработке программ или алгоритмов, связанных с циклами, предикатами или условиями. Например, если мы хотим, чтобы программа выполняла действие 10 раз или проверяла условие 10 раз, мы можем использовать знание о количестве чисел от 1 до 10 для контроля выполнения цикла или итераций.

5. Образовательные цели

Знание о количестве чисел от 1 до 10 может быть использовано для образовательных целей, особенно при обучении детей основам математики. Знакомство с числами от 1 до 10 позволяет детям понять базовые принципы счета, последовательность чисел и основы математических операций. Это важная основа для дальнейшего математического развития.

Итак, знание о количестве чисел от 1 до 10 имеет множество практических применений и является важным компонентом различных аспектов нашей жизни. Оно помогает нам в анализе данных, решении задач, программировании и даже в образовательных целях. Поэтому понимание этого простого концепта может быть полезным и полезным инструментом в нашем повседневном опыте и деятельности.

Решето Эратосфена

Во многих задачах все исходные данные и необходимые результаты — целые числа. При этом всегда желательно, чтобы все промежуточные вычисления тоже проводились только с целыми числами. На это есть, по крайней мере, две причины:• процессор, как правило, выполняет операции с целыми числами значительно быстрее, чем с вещественными;
• целые числа всегда точно представляются в памяти компьютера, и вычисления с ними также выполняются без погрешностей (если, конечно, не происходит переполнение разрядной сетки).

Простые числа широко используются во многих прикладных задачах, например при шифровании с помощью алгоритма RSA (вспомните материал учебника для 10 класса). Основные задачи при работе с простыми числами — это проверка числа на простоту и нахождение всех простых чисел в заданном диапазоне.

Пусть задано некоторое натуральное число N и требуется найти все простые числа в диапазоне от 2 до N. Самое простое (но неэффективное) решение этой задачи состоит в том, что в цикле перебираются все числа от 2 до N, и каждое из них отдельно проверяется на простоту. Например, можно проверить, есть ли у числа k делители в диапазоне от 2 до √k. Если ни одного такого делителя нет, то число k простое.

Описанный метод при больших N работает очень медленно. Греческий математик Эратосфен Киренский (275-194 гг. до н. э.) предложил другой алгоритм, который работает намного быстрее:1) выписать все числа от 2 до N;
2) начать с k = 2;
3) вычеркнуть все числа, кратные k (2k, 3k, 4k и т. д.);
4) найти следующее невычеркнутое число и присвоить его переменной k;
5) повторять шаги 3 и 4, пока k < N.

Покажем работу алгоритма при N = 16:

Первое невычеркнутое число — это 2, поэтому вычёркиваем все чётные числа:

Далее вычёркиваем все числа, кратные 3:

Все числа, кратные 5 и 7, уже вычеркнуты. Таким образом, получены простые числа 2, 3, 5, 7, 11 и 13.

Классический алгоритм можно улучшить, уменьшив количество операций. Заметьте, что при вычёркивании чисел, кратных трём, нам не пришлось вычёркивать число 6, так как оно уже было вычеркнуто. Кроме того, все числа, кратные 5 и 7, к последнему шагу тоже оказались вычеркнуты.

Предположим, что мы хотим вычеркнуть все числа, кратные некоторому k, например k = 5. При этом числа 2k, 3k и 4k уже были вычеркнуты на предыдущих шагах, поэтому нужно начать не с 2k, а с k2. Тогда получается, что при k2 > N вычёркивать уже будет нечего, что мы и увидели в примере. Поэтому можно использовать улучшенный алгоритм:1) выписать все числа от 2 до N;
2) начать с k = 2;
3) вычеркнуть все числа, кратные k, начиная с k2;
4) найти следующее невычеркнутое число и присвоить его переменной k;
5) повторять шаги 3 и 4, пока k2 ≤ N.

Чтобы составить программу, нужно определить, что значит «выписать все числа» и «вычеркнуть число». Один из возможных вариантов хранения данных — массив логических величин с индексами от 2 до N. Как и в учебнике 10 класса, слева будем писать программу на школьном алгоритмическом языке, а справа — на языке Паскаль.

Объявление переменных в программе будет выглядеть так (для N = 100):

Если число i не вычеркнуто, будем хранить в элементе массива A истинное значение, если вычеркнуто — ложное. В самом начале нужно заполнить массив истинными значениями:

В основном цикле выполняется описанный выше алгоритм:

Обратите внимание, что для того, чтобы вообще не применять вещественную арифметику, мы заменили условие k ≤ √N на равносильное условие k2 ≤ N, в котором используются только целые числа.

После завершения этого цикла невычеркнутыми остались только простые числа, для них соответствующие элементы массива содержат истинные значения. Эти числа нужно вывести на экран:

Следующая страница «Длинные» числа

Cкачать материалы урока

Математические задачи на логику: 1-2 класс

Но потом дети пошли в школу, буквально с первых месяцев учебы они начинают хорошо считать, ориентироваться в пространстве и времени. Домашнее задание для дошкольников уже кажется им простым и неинтересным

Поэтому для этих детей мы подготовили несколько вариантов упражнений на тренировку логики и сообразительности, акцентируя внимание на их новых навыках и способностях

1. Первоклассника попросили назвать наибольшее число. Что он ответил?
   Ответ: 31. Первые ученики каждый день записывают в тетрадь день месяца, наибольшее число для месяца — 31.
2. На доске два числа 4 и 5. Какой знак поставить между ними, чтобы получить результат больше 4 и меньше 5. Ответ: запятая.
3. По узкой дороге может проехать только машина. С одной стороны дороги есть гора. Одна машина едет под гору, другая — под гору. Как они скучают друг по другу? Ответ: Обе машины движутся в одном направлении и не должны нагреваться.
4. Сколько раз вы можете вычесть цифру 2 из числа 10? Ответ: один, потому что после первого вычитания двух остается число 8, а не 10.
5. На столе 6 стаканов: первые три были полны воды, вторые три были пустыми. Стаканы необходимо расположить так, чтобы пустые и полные стаканы чередовались, но собрать можно только один стакан. Что делать, чтобы выполнить условие? Ответ: Возьмите второй стакан и налейте из него воду в пятый стакан. Установите второй стакан в исходное положение.
6. За 10 часов 10 человек могут выкопать траншею длиной 10 метров. Сколько человек нужно, чтобы выкопать 100-метровую траншею за 100 часов? Ответ: 10 человек. За 1 час 10 человек выкопают 1 метр траншеи, за 10 часов — 10 метров траншеи, а за 100 часов — 100 метров.
7. Школьники участвуют в соревнованиях по бегу. На третьей позиции Ваня, на второй позиции Антон. Саша превосходит Антона. Какая позиция у Саши? Ответ: второе, потому что впереди Антона тоже кто-то бежит, и этот кто-то еще первый.
8. Учитель положил карандаш на пол и попросил учеников перешагнуть через него, но никто не смог. Почему? Ответ: Карандаш прислонен к стене, и детям некуда идти.
9. Таня и Алиса пошли в магазин и нашли 2 рубля. Сколько денег они нашли бы, если бы с ними поехала и Марина? Ответ: 2 рубля, потому что размер находки никак не зависит от количества найденных.
10. Кошка прошла из точки A в точку B, а мышь — из точки B в точку A. Когда они встретятся, кто из них будет ближе всего к точке A, а кто — к точке B? Ответ: Оба они будут находиться на одинаковом расстоянии от точки A и на одинаковом расстоянии от точки B.
11. На столе стояли 3 чашки чая. Папа выпил чай из чашки и поставил обратно. Мама выпила чай и тоже поставила чашку на место. Сколько чашек было на столе, когда сын пришел пить чай? Ответ: 3 стакана. Несмотря на то, что они пустые, они никуда не делись.
12. Марина ходила из дома в школу и встретила троих мужчин. У всех за спиной был мешок. У первого была кошка в мешке, у второго — кот и собака в мешке. У третьего в сумке было 2 собаки. Сколько кошек ходили в школу? Ответ: во-первых, сама Марина. Мальчики с мешками пошли в противоположном от школы направлении.
13. В классе был стол с прямоугольной столешницей. Ученики отпилили угол, что случилось со столом, сколько углов осталось на крышке? Ответ: 5. Если срезать угол, то получим на его месте 2 новых, так что углов всего 5.Примечание: на самом деле количество углов также может зависеть от того, как думает ребенок. Если он «видит» стол по углам диагонали, например разрезает его пополам, возможно, что у стола 3 угла. Если один разрез упадет на угол, а второй — на боковую часть крышки, могут остаться 4 угла. Но это нюансы, которые лучше всего учитывать при рисовании на листе бумаги, где ребенок будет «видеть» стол.
14. На тарелке 3 банана. Их нужно разделить между тремя девушками, чтобы на тарелке остался один банан. Ответ: девушке нужно подарить банан вместе с тарелкой.
15. Какое слово зашифровано: ООО? Ответ: ТРИО, т.е. ТРИ О.

Родители также могут составить для детей домашнее задание, ориентируясь на предложенные варианты. Чем чаще ребенок занимается логическими упражнениями, тем быстрее будет работать его мозг, тем выше будет его успеваемость.

Как избежать ошибок при подсчете чисел от 1 до 199?

Подсчет чисел от 1 до 199 может быть простой задачей, но иногда при выполнении этой задачи возникают ошибки и опечатки. Чтобы избежать этих ошибок, следует придерживаться нескольких рекомендаций:

1. Проверяйте внимательно границы подсчета: удостоверьтесь, что начальное и конечное значения указаны правильно. Необходимо учесть, что подсчет начинается с числа 1 и заканчивается числом 199.
2. Используйте подходящие средства для подсчета: для более точного и удобного подсчета можно воспользоваться программой, калькулятором или таблицей Excel. Такие средства помогут избежать ошибок при ручном подсчете.
3. Проверяйте результаты: после завершения подсчета необходимо проверить полученные значения. Сравните результаты с ожидаемыми значениями и удостоверьтесь, что они совпадают. В случае обнаружения расхождений, перепроверьте свои действия.
4. Будьте внимательны к деталям: при подсчете чисел от 1 до 199 необходимо быть внимательным и тщательным. Ошибки могут возникнуть из-за невнимательности к деталям, например, при переписывании чисел или при выполнении сложения.

Соблюдение этих рекомендаций поможет избежать ошибок и опечаток при подсчете чисел от 1 до 199. Тщательность, внимательность и использование подходящих средств для подсчета — гарантия правильных результатов.

Ответы на задачи

Задача 1

Ответ: 35 дней

Проще всего осознать данный ответ помогает визуальное восприятие через запись на бумаге прогрессий в обоих случаях (с одним и двумя «нулевыми» пациентами):

1 день — 1 больной;
2 день — 2 больных; 1 день — 2 больных;
3 день — 4 больных; 2 день — 4 больных;
4 день — 8 больных; 3 день — 8 больных;
5 день — 16 больных и т.д. 4 день — 16 больных и т.д.

То есть, если зараженных сразу было двое, то необходимо на один день меньше, чем было бы в случае с одним зараженным.

Задача 2

Ответ: 5 долларов

Естественно, мозг пытается подсказать очевидный и неправильный ответ – 10 долларов. Однако тогда получим цену планшета (на 100 долларов дороже стилуса) равной 110 долларам, а общая стоимость покупки тогда составит 110 + 10 = 120 долларов.

Задача 3

Ответ: $300 млрд

Проще всего решить эту задачу в лоб на бумаге, записав три простых уравнения вида: x + 200 = S, y + 140 = S и x + y = S – 40 и заменив одни переменные выражениями других.

Однако люди с гибким мышлением решают данную задачу более изящно:
Достаточно просто представить, что компания Google просто передала свои деньги на покупку Apple компании Microsoft. Последней не хватало изначально $140 млрд, а после получения денег Google стало не хватать всего 40$ млрд. Соответственно, компания Google располагала активом в размере $100 млрд и ей при этом не хватало 200 млрд для самостоятельной покупки Apple. Соответственно, цена Apple = $300 млрд.

Задача 4

Ответ: 3 минуты

Не составляет труда посчитать, что один 3D принтер печатает один треугольник за 3 минуты. Значит и 100 аппаратов произведут 100 единиц за те же 3 минуты.

Задача 5

Ответ: 40 ступенек

Подымаясь на 4 этаж, Коля преодолевает три лестничных пролета, соответственно, один лестничный пролет состоит из 120 / 3 = 40 ступенек. Поднимаясь на второй этаж, Петя проходит всего один пролет, то есть, 40 ступенек.

Примеры вычисления суммы

Подготовка к пицца-пати. Представим, что вы организуете вечеринку и решили заказать пиццу для всех гостей. Если первый гость съест 1 кусочек, второй — 2, третий — 3, и так до десятого. Сколько кусочков нужно заказать? Используя формулу, получаем сумму как 10 * (10 + 1) / 2 = 55 кусочков.

Подготовка к экзаменам. Студент решил готовиться к экзаменам, ежедневно увеличивая объём прочитанных страниц на одну. Первый день — одна страница, второй — две, и так до 30 дней. Всего он прочитает 30 * (30 + 1) / 2 = 465 страниц.

Тренировочный план бегуна. Бегун увеличивает дистанцию своих ежедневных пробежек на 1 км, начиная с 1 км в первый день и заканчивая 7 км в последний день недели. Общая дистанция будет равна 7 * (7 + 1) / 2 = 28 км.

Подготовка к дню рождения. Вы решили каждый день до своего дня рождения отложить денег: в первый день 1 рубль, во второй 2 рубля, и так до 18 дней. Сколько денег вы накопите? По формуле получается 18 * (18 + 1) / 2 = 171 рубль.

Игра в кости. Вы с друзьями решили играть в кости, где каждый следующий бросок увеличивает счёт на количество очков, равное номеру броска. Сколько очков будет после 6 бросков? Вычисляем: 6 * (6 + 1) / 2 = 21 очко.

Считать в пределах 10

Для успешного развития счета в пределах советуем разучивать с ребенком состав всех чисел от до . Учить можно как песню или стихотворение.

На первом занятии обычно разучивается состав чисел от до или (в зависимости от усидчивости ребенка).

Пишем	Проговариваем
2= 1+1
3= 1+2 3= 2+1	Три — это один и два. Три — это два и один.
4= 1+3 4= 2+2 4=3+1	Четыре — это один и три. Четыре — это два и два. Четыре — это три и один.
5 =1+4 5=2+3 5= 3+2 5= 4+1	Пять — это один и четыре. Пять — это два и три. Пять — это три и два. Пять — это четыре и один.

Проговаривая состав чисел, можно дополнительно хлопать в ладоши, отстукивать такт, бросать мячик и т. д.

Когда составы этих чисел выучены как стихи, начинаем задавать вопросы вразбивку.

Например, «Четыре это и ?», «Три это и ?» и тому подобное. После устной работы добавляем заполнение составов чисел в виде «окошек», расположенных не по порядку.

Для тренировки вы можете скачать тренажер для счет в пределах . В качестве таких фигур можно использовать елочки, самолеты, поезда и т

д.
Дома, по возможности, постарайтесь развесить эти схемы-рисунки и обращайте внимание ребенка на них как можно чаще

Одновременно с разучиванием составов чисел начинаем давать решать примеры из учебников на счет в пределах выученных чисел.

При расчетах нужно напоминать ребенку о составе числа и проговаривать примеры.

Пишем	Проговариваем
Два и три — это пять.
Четыре — это один и три.
Два — это один и один.

На следующих занятиях вводим постепенно числа от до . Лучше разучивать по одному числу за урок.

Важно! Разучивать нужно полный состав числа (все комбинации), т. е

от до

Чтобы ребенок считал уверенно и бегло, распечатайте столбики примеров и решайте их на время.

Полезно устраивать соревнования на скорость решения как между детьми, так и со взрослыми.

Если вы хотите облегчить школьную жизнь ребенка, то советуем также выучить составы чисел от до . Это вам потребуется при счете с переходом через десяток.

Подсчет чисел по условию

В отношении чисел редко случается, что нужно подсчитать количество их, равных какому-то определённому числу. Тем не менее, укажем, что записать нужно примерно следующее:

Гораздо чаще нужно высчитать количество значений, больших либо меньших определенной величины.

Чтобы посчитать значения, которые больше, меньше или равны указанному вами числу, вы просто добавляете соответствующий критерий, как показано в таблице ниже.

Обратите внимание, что математический оператор вместе с числом всегда заключен в кавычки 

Критерии		Описание
Если больше, чем	=СЧËТЕСЛИ(А2:А10;»>5″)	Подсчитайте, где значение больше 5.
Если меньше чем	=СЧËТЕСЛИ(А2:А10;»>5″)	Подсчет со числами менее 5.
Если равно	=СЧËТЕСЛИ(А2:А10;»=5″)	Определите, сколько раз значение равно 5.
Если не равно	=СЧËТЕСЛИ(А2:А10;»<>5″)	Подсчитайте, сколько раз не равно 5.
Если больше или равно	=СЧËТЕСЛИ(А2:А10;»>=5″)	Подсчет, когда больше или равно 5.
Если меньше или равно	=СЧËТЕСЛИ(А2:А10;»<=5″)	Подсчет, где меньше или равно 5.

В нашем примере

Формула подсчитывает количество крупных заказов на сумму более 10 000

Обратите внимание, что условие подсчета мы записываем здесь в виде текстовой строки и поэтому заключаем его в двойные кавычки

Вы также можете использовать все вышеприведенные варианты для подсчета ячеек на основе значения другой ячейки. Вам просто нужно заменить число ссылкой.

Замечание. В случае использования ссылки, вы должны заключить математический оператор в кавычки и добавить амперсанд (&) перед ним. Например, чтобы посчитать сколько чисел в диапазоне D2: D9, превышают значение из D3, используйте =СЧËТЕСЛИ(D2:D9,»>»&D3)

Если вы хотите сосчитать записи, которые содержат математический оператор, как часть их содержимого, то есть символ «>», «<» или «=», то употребите в условиях подстановочный знак с оператором. Такие критерии будут рассматриваться как текстовая строка, а не числовое выражение.

Например, =СЧËТЕСЛИ(D2:D9,»*>5*») будет подсчитывать все позиции в диапазоне D2: D9 с таким содержимым, как «Доставка >5 дней» или «>5 единиц в наличии».

Правила подсчета чисел в диапазоне от 1 до 10

При подсчете чисел в диапазоне от 1 до 10 обычно используются следующие правила:

• Последовательно перечисляем числа от 1 до 10: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
• Для подсчета количества чисел в этом диапазоне, можно использовать два метода: механический и математический.

Механический метод:

1. Возьмите калькулятор, переключите его в режим подсчета и запишите число 1.
2. Нажмите кнопку «+1» десять раз. Каждый раз, когда вы нажимаете эту кнопку, число на экране будет увеличиваться на 1.
3. После десяти нажатий кнопки «+1» число на экране калькулятора будет равно 10. Это означает, что вы перечислили все числа от 1 до 10.

Математический метод:

1. Число первое число диапазона — 1 и последнее число — 10.
2. Воспользуйтесь формулой для подсчета чисел в диапазоне: количество чисел = последнее число — первое число + 1.
3. Подставьте значения в формулу: количество чисел = 10 — 1 + 1 = 10.

Таким образом, в диапазоне от 1 до 10 находится 10 чисел.

Эти простые правила помогают подсчитать количество чисел в диапазоне от 1 до 10 без ошибок и упущений.

Стихотворения-считалки для обучения счету

Раз, два, три, четыре, пять — Всё могу я сосчитать: И салазки на горе, И коляски во дворе, И девчонок, и мальчишек, Их сестрёнок, и братишек, И прилавки в гастрономе, И окошки в нашем доме.

Раз, два, три, четыре, пять — Всё могу я сосчитать, Кроме звёзд и мотыльков, Кроме трав и облаков, Кроме скачущих дождинок И весенних звонких льдинок…

Мне считать их неохота: Сбиться я могу со счёта! (М. Пляцковский)

Ослика мама учила считать: «Хвостик — один, начинай повторять». Ослик упрямо кивал головой: «Что ты считаешь? Ведь, хвостик-то — мой!».

«Твой-то он — твой, но, ведь, он же, один!» «Хвостик — один», — соглашается сын. «Ну, наконец-то! А сколько ушей? Ну, не упрямься, считай поскорей!».

Ослик считает: «Вот ухо одно, Вот и второе: два уха! Смешно!». «Что ж тут смешного? Теперь посмотри: Хвост плюс два уха получится три!».

«Сколько же ног? Сосчитать помоги! Только передних одних две ноги!». «С задними быстро двумя их сложи, Сколько получится? Ну-ка, скажи!».

Ослик задумался: «Сколько же ног?» «Медленно что-то считаешь сынок! К двум своим ножкам прибавь ещё две!». “Будет четыре«,- ей ослик в ответ.

«Дальше, сынок, продолжаем считать: Ножки плюс хвостик получится…?» «Пять!». «Если же с ушками ножки сложить, Сколько получится, ослик? Скажи!».

«Ножки и ушки легко перечесть: Два плюс четыре получится шесть!». Стала тут ослика мама хвалить: «С хвостиком всё это можешь сложить?».

«Ослик, немного осталось совсем: Складывай всё! И получится…?» «Семь!». «Ослик, ну что, ж, ты упёрся опять?». «Мама, мне нечего больше считать!».

«Ноги посчитаны, уши и хвост. Что там осталось?» «Прибавь ещё нос!». «Сколько получится с носом, сынок?» «Восемь! Уж я сосчитал всё, что мог!»

«Всё ли? А глазки? Их тоже, ведь, два! И, несомненно, одна голова!». «Голову с ножками если сложить, Глазки и ушки ещё приложить,

«Девять получится!». «Верно сынок! Ты с арифметикой справится смог! Ослик, чтоб дальше нам в счёте пойти, Надо добраться нам до десяти.

«Так, продолжаем: два уха и нос, Ножки четыре, два глаза и хвост, Всё это вместе сложи, наконец!» «Десять получится!». «Вот молодец!».

«Ослик, как видишь, задачка проста. В следующий раз досчитаем до ста! (А. Гольцева)

По опушке шла лисичка: Раз — в корзинке земляничка, Два — как небо голубика, Три — румяная брусника, А четыре — вот морошка, Пять — смородины немножко, Шесть — как бусинка калина, Семь — как солнышко рябина, Восемь — в лапке ежевика, Девять — синяя черника, Десять — сочная малина. Вот и полная корзина!

Раз — рука, два — рука — Лепим мы снеговика! Три — четыре, три — четыре, Нарисуем рот пошире! Пять — найдём морковь для носа, Угольки найдём для глаз. Шесть — наденем шляпу косо. Пусть смеётся он у нас. Семь и восемь, семь и восемь — Мы сплясать его попросим. Девять, десять — снеговик Через голову — кувырк! Ну и цирк!

Танграм

Согласно легенде, головоломка была создана несколько тысяч лет назад тремя древними китайскими мудрецами для сына императора. Правитель хотел, чтобы его сын понял истоки математики с помощью простой игры, научился видеть мир вокруг себя глазами художника, стал терпеливым, как философ, и понял, что сложные вещи состоят из простых вещей.

Вот как появился «Ши-Чао-Ту», квадрат, разрезанный на семь частей:
5 треугольников (2 больших, 2 маленьких, 1 средний), квадрат и параллелограмм.

Суть «бесплатной» игры танграм состоит в том, чтобы собрать по принципу мозаики всевозможные фигурки из доступных частей: животные, птицы, люди, что угодно. Дошкольникам предлагается несложный вариант развивающей игры, в которой цифры танграм нужно просто наложить на готовый образец ответов.

Многие дети 5-7 лет кладут модели фигурок рядом с изображением ответа, даже если размеры вырезанных фигурок и деталей на изображении разные.

Танграм как пазл обычно доступен 6-7-летнему ребенку. Однако из элементов танграма нужно сложить готовую модель, а на бумаге показан только контур фигуры.

Вырежьте элементы танграма из бумаги, картона или другого квадрата, и для начала предлагаем вам собрать одну из популярных фигур — бегущего человечка, как на фото выше.

Запомните 2 правила головоломки:
1) вы должны использовать все 7 частей пазла;
2) рисунки не должны перекрываться.

Среди поклонников Танграма были Льюис Кэрролл и Наполеон Бонапарт. Считается, что американский шахматист, изобретатель «жетонов» и многих других головоломок Сэмюэл Лойд назвал игру «танграм.
В 21 веке наиболее интересные проявления танграма встречаются в дизайне мебели, одежды, ландшафтном дизайне и архитектуре.

Как решить задачу «Сколько натуральных чисел от 41 до 125» простым способом?

Чтобы решить данную задачу, можно использовать простой подход, основанный на подсчете чисел в указанном диапазоне. Нам нужно найти количество натуральных чисел, которые находятся между 41 и 125 включительно.

Для начала определим самое маленькое и самое большое число в заданном диапазоне. В данном случае, самое маленькое число — это 41, а самое большое — 125. Теперь мы можем просто пронумеровать все числа от 41 до 125 и посчитать их количество.

Натуральное число
41
42
43
…
125

Таким образом, количество натуральных чисел от 41 до 125 равно 85.

Этот метод прост и понятен даже новичкам в математике. Он может быть использован для решения подобных задач, где необходимо найти количество чисел в заданном диапазоне. Теперь вы можете использовать этот простой способ для решения других подобных задач.

Алгоритмы циклического класса

В алгоритмах циклического класса некоторая часть действий из задания повторяется до тех пор, пока не нарушится заранее определенное условие. Выполнение условия проверяется в начале. Совокупность операций, которые выполняются многократно, — это тело цикла.

В алгоритмических последовательностях этого класса выделяют ряд понятий:

• параметр цикла (с изменением этой величины связано многократное выполнение цикла);
• начальное и конечное значения циклических параметров;
• шаг цикла (речь идет о значении, на которое меняется параметр при каждом повторе).

Работу циклов организуют по специальным правилам. Алгоритмическая последовательность циклического класса включает в себя и подготовку, и тело, и условия продолжения работы.

В подготовку входят действия, которые связаны с заданием исходных значений:

• начальные значения;
• конечные значения;
• шаг.

В тело цикла входят:

• многократно повторяющиеся операции по вычислению искомых величин;
• подготовка последующего значения параметра;
• подготовка иных значений, нужных для повторного выполнения действий непосредственно в теле.

В условии продолжения цикла определяют допустимость выполнения повторяемых операций. Когда циклический параметр равен либо превышает конечное значение, выполнение прекращается.

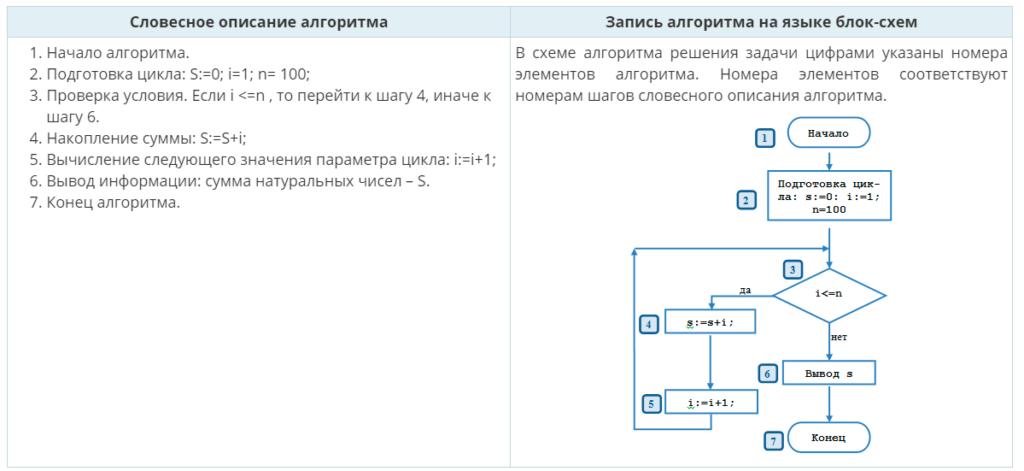
Рассмотрим задание, постановка которого связана с разработкой алгоритма вычисления суммы натуральных чисел в диапазоне от 1 до 100.

1. Математическое описание.

Сначала следует обозначить сумму натуральных чисел буквой S. В результате формулу вычисления суммы чисел от 1 до 100 можно записать следующим образом:

Здесь Xi является натуральным числом X c номером i. Этот номер меняется от 1 до n. А n=100 обозначает общее кол-во натуральных чисел.

2. Определяем входные/выходные данные.

Входные данные — это натуральные числа: 1, 2, 3, …, 99, 100.

Выходные данные представляют собой значение суммы членов последовательности натуральных чисел.

Относительно параметра цикла — речь идет о величине, определяющей число циклических повторений. В нашем задании i представляет собой номер натурального числа.

Подготовка цикла — задание начального и конечного значений циклического параметра. Тут надо пояснить следующее:

• начальное значение циклического параметра равняется единице,
• конечное значение — n,
• шаг равен 1.

Чтобы обеспечить корректность суммирования, надо, чтобы начальное значение суммы предварительно равнялось нулю.

Тело цикла. В теле станут выполняться как накопление значения суммы, так и вычисление последующего значения циклического параметра по формулам ниже:

• S=S+i;             
• I=I+1.

Циклическое повторение должно осуществляться до тех пор, пока не добавится последний член последовательности натуральных чисел, то есть до тех пор, пока циклический параметр будет меньше либо равен окончательному значению параметра.

3. Разработка.

Вводим следующие обозначения: S – это сумма последовательности, i – это значение натурального числа.

Начальное циклическое значение i=1, конечное — i =100, шаг равен 1.

По материалам: https://www.turbopro.ru/index.php/osnovy-programmirovaniya/6836-algoritmy-razrabotka-algoritma-resheniya-zadachi.