Зачем нужно знать две третьих части 4 класс
Понимание и умение работать с двумя третьими частями в математике важны для учеников 4 класса. Эта тема помогает развить навыки работы с дробями и сравнением различных частей целого.
Знание двух третьих части позволяет детям разбивать целые объекты или числа на равные части и понять, что две трети составляют большую часть, чем одна треть. Это основа для дальнейшего изучения дробей и работы с различными долями целого.
Понимание двух третьих части также помогает детям научиться сравнивать дроби и понимать их относительные величины. Например, они могут узнать, что две трети больше, чем одна треть, и использовать эту информацию для решения задач и сравнения различных значений.
Умение работать с двумя третьими частями также полезно при решении практических задач. Например, когда дети должны разделить имеющийся объем или количество на равные части, знание двух третьих помогает им справиться с этой задачей.
Важно научить детей работать с двумя третьими частями в раннем возрасте, чтобы они могли применять эти навыки в реальной жизни. Это может включать разделение пиццы на равные кусочки, распределение заданий в групповом проекте или определение процента целой суммы
Таким образом, знание двух третьих частей в 4 классе имеет множество применений и является важной основой для дальнейшего изучения дробей и математических концепций
Какую часть одно число составляет от другого
Иногда возникает необходимость узнать какую часть первое число составляет от второго. Для таких случаев предусмотрено следующее правило:
Чтобы узнать какую часть первое число составляет от второго, надо первое число разделить на второе.
Например, яблоко разделили на пять одинаковых долек. Какую часть яблока составляют две дольки?
Чтобы ответить на этот вопрос, надо первое число разделить на второе. Первое число это 2, второе — 5. Получается дробь .
Значит две дольки из пяти долек составляют две пятых. Это можно увидеть на следующем рисунке:
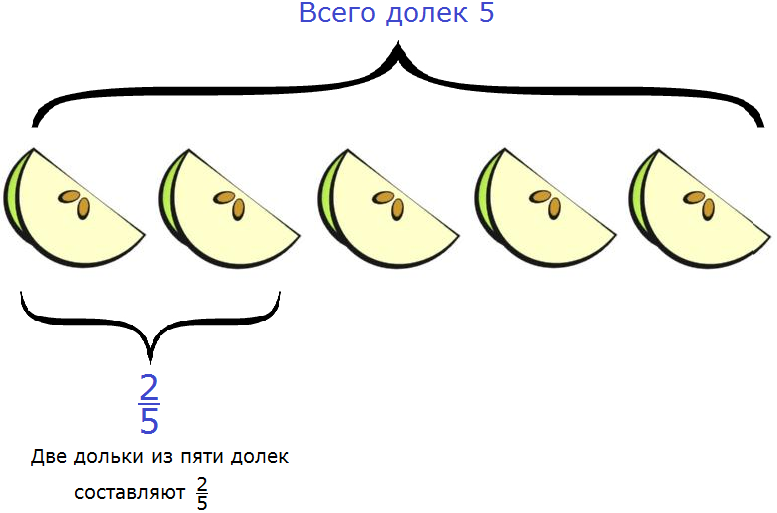
Итак, две дольки яблока из пяти составляют две пятых.
Возникает вопрос, а как узнать какое число первое, а какое второе? Для этого нужно посмотреть на вопрос, который поставлен в задаче. То число, которое указано в вопросе задачи, оно и будет первым числом. Например, в предыдущей задаче вопрос был поставлен так:
«Какую часть яблока составляют две такие дольки?»
Если внимательно присмотреться к вопросу, то можно обнаружить, что в нём указано число 2. Оно и стало первым числом.
Иногда в вопросе мелькает сразу два числа. Например: какую часть составляет число 2 от числа 10?
В этом случае первым числом будет то, которое в вопросе расположено раньше. В данном случае первое число это 2, а второе 10. Делим 2 на 10, получаем дробь . Значит число 2 от числа 10 составляет (две десятых).
Дробь означает, что число 10 разделено на десять частей, и от этих десяти частей взято две части.
Также, эту дробь можно сократить на 2. После сокращения дроби на 2 получаем дробь .
Дробь тоже может послужить ответом к задаче. Она будет означать, что число 10 разделено на пять частей, и от этих пяти частей взята одна часть.
Таким образом, число 2 составляет (одну пятую) от числа 10.
Пример 3. Какую часть составляет число 5 от числа 15?
Делим первое число на второе. Первое число 5, а второе 15. Делим 5 на 15, получаем дробь . Эту дробь можно сократить на 5
Получили аккуратную дробь . Значит ответ будет выглядеть следующим образом:
Число 5 составляет (одну третью) от числа 15.
Это можно даже проверить. Для этого нужно найти от числа 15. Если мы всё сделали правильно, то должны получить число 5.
Итак, найдём от числа 15. Как находить дробь от числа мы уже знаем
15 : 3 = 5
5 × 1 = 5
Получили ответ 5. Значит задача была решена правильно.
Пример 4. Какую часть 3 см составляют от 12 см?
Делим первое число на второе. Первое число это 3, а второе 12. Получаем дробь . Эту дробь можно сократить на 3
Получили ответ . Значит 3 см составляют (одну четвёртую) от 12 см.
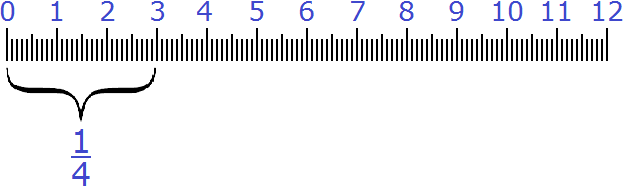
Проверим правильно ли мы решили эту задачу. Для этого найдём от 12 см. Если мы всё сделали правильно, то должны получить 3 см.
Делим 12 на знаменатель дроби
12 см : 4 = 3 см
Умножаем полученные 3 см на числитель дроби
3 см × 1 = 3 см
Получили ответ 3 см. Значит задача была решена правильно.
Мир только кажется математическим или это свойство природы?
Это, конечно же, свойство природы. Вообще, все математики — платоники. Есть такая книжка «Доказательство из книги» — она о том, что где-то есть написанные доказательства, и мы, люди, можем к ним приблизиться
И действительно, иногда берешь доказательство, оно может быть очень короткое, но доказывать что-то очень важное. Собственно, сама книга «Доказательство из книги» начинается с доказательства Евклида о существовании бесконечного числа простых чисел. Доказательство, которое уже выдержало много веков, а тем не менее действительно очень красивое, мощное и интересное! А бывает, смотришь и видишь, что мы еще чего-то не знаем и поэтому доказательство такое сложное
Доказательство, которое уже выдержало много веков, а тем не менее действительно очень красивое, мощное и интересное! А бывает, смотришь и видишь, что мы еще чего-то не знаем и поэтому доказательство такое сложное.
Математика рассеивает туман — изучает то, что мы еще не изучили в нашем мире. Она позволяет выявить сущность с помощью формализации и абстрагироваться от чего-то, что настраивается уже на эту сущность. А дальше остается применять полученные законы либо к предмету, либо к задаче — это уже зависит от того, что нужно человечеству.
Измерение и доля: ключевые понятия
Доля — это относительная величина, выражающая часть целого. Обычно доля выражается в виде десятичной или процентной дроби. Например, если у нас есть 2 предмета, а один из них занимает половину, то его доля равна 0.5 или 50%.
Ключевое понятие, объединяющее измерение и долю, — это доля измерительной величины. Доля измерительной величины представляет собой отношение значения измеренной величины к какой-то нормированной или общепринятой величине, которая служит в качестве опоры или стандарта. Например, если мы измеряем длину отрезка и получаем значение 5 сантиметров, то это значение можно интерпретировать как долю от общей длины, например, 5/10 или 50%.
Доля измерительной величины является важным показателем во многих областях, включая науку, экономику, бизнес и технику. Она позволяет сравнивать различные значения, оценивать эффективность и результативность процессов, а также принимать взвешенные решения на основе полученных данных.
Примеры:
1. В экономике доля рынка — это процентная доля компании или отрасли в общем объеме рынка. Например, если компания X продает товары на сумму 10 миллионов рублей, а весь рынок составляет 100 миллионов рублей, то доля компании X составляет 10%.
2. В физике измерение доли может использоваться для оценки эффективности эксперимента или процесса. Например, если исследователь проводит серию экспериментов и получает положительные результаты в 2 из 3 случаев, то доля успешных экспериментов составляет 2/3 или около 66.7%.
3. В медицине измерение доли может быть использовано для оценки эффективности лечения. Например, если группа пациентов имеет определенное заболевание, а после применения нового лекарства только 1 из 4 пациентов испытывает улучшение, то доля пациентов, испытывающих улучшение, составляет 1/4 или 25%.
Таким образом, понимание измерения и доли важно для получения оценок и сравнений в различных областях знания и практики
Определения
Одно из первых определений предмета математики дал Декарт :
К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера и совершенно не существенно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера. Таким образом, должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем Всеобщей математики.
В советское время классическим считалось определение из БСЭ , данное А. Н. Колмогоровым:
Математика… наука о количественных отношениях и пространственных формах действительного мира.
Это определение Энгельса ; правда, далее Колмогоров поясняет, что все использованные термины надо понимать в самом расширенном и абстрактном смысле.
Сущность математики… представляется теперь как учение об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств,— именно тех, которые в качестве аксиом положены в основание теории… Математика есть набор абстрактных форм — математических структур.
Приведём ещё несколько современных определений.
Современная теоретическая («чистая») математика — это наука о математических структурах, математических инвариантах различных систем и процессов .
Математика — наука, предоставляющая возможность исчисления моделей, приводимых к стандартному (каноническому) виду. Наука о нахождении решений аналитических моделей (анализ) средствами формальных преобразований .
Герман Вейль пессимистически оценил возможность дать общепринятое определение предмета математики:
Вопрос об основаниях математики и о том, что представляет собой в конечном счёте математика, остаётся открытым. Мы не знаем какого-то направления, которое позволит в конце концов найти окончательный ответ на этот вопрос, и можно ли вообще ожидать, что подобный «окончательный» ответ будет когда-нибудь получен и признан всеми математиками.
«Математизирование» может остаться одним из проявлений творческой деятельности человека, подобно музицированию или литературному творчеству, ярким и самобытным, но прогнозирование его исторических судеб не поддаётся рационализации и не может быть объективным .
Определение и значение
Математика — это наука, которая изучает основные законы и свойства чисел, пространства, количества и изменений. Эта наука включает широкий спектр областей, таких как алгебра, геометрия, анализ, теория вероятностей и т.д.
Основное значение математики заключается в её способности применяться к решению различных задач. Математика используется во многих областях, таких как естественные науки, экономика, компьютерные технологии, бухгалтерский учет и т.д.
Математика имеет свои принципы, которые являются основой для решения задач. Эти принципы включают, например, аксиомы, теоремы, способы рассуждения и доказательства. Изучение математики помогает развивать логическое мышление, умение решать задачи и применять математические методы в повседневной жизни и профессиональной деятельности.
- Аксиомы — это базовые утверждения, которые принимаются как самоочевидные и не доказываются.
- Теоремы — это утверждения, которые могут быть доказаны на основе аксиом и других доказанных теорем.
- Способы рассуждения, такие как индукция, дедукция и аналогия, позволяют обосновывать теоремы и решать задачи.
- Доказательства — это процесс логического вывода, который позволяет показать, что утверждение верно на основе известных фактов.
Таким образом, математика является важной наукой, которая обладает широкими приложениями и позволяет развивать умение решать сложные задачи и доказывать теоремы на основе логического вывода
Доли целого
Сначала введем понятие доли.
Предположим, что у нас есть некоторый предмет, составленный из нескольких абсолютно одинаковых (то есть, равных) частей. Для наглядности можно представить, например, яблоко, разрезанное на несколько равных частей, или апельсин, состоящий из нескольких равных долек. Каждую из этих равных частей, составляющих целый предмет, называют долей целого или просто долей.
Заметим, что доли бывают разные. Поясним это. Пусть у нас есть два яблока. Разрежем первое яблоко на две равные части, а второе – на 6 равных частей. Понятно, что доля первого яблока будет отличаться от доли второго яблока.
В зависимости от количества долей, составляющих целый предмет, эти доли имеют свои названия. Разберем названия долей. Если предмет составляют две доли, любая из них называется одна вторая доля целого предмета; если предмет составляют три доли, то любая из них называется одна третья доля, и так далее.
Одна вторая доля имеет специальное название – половина. Одна третья доля называется третью, а одна четверная доля – четвертью.
Для краткости записи были введены следующие обозначения долей. Одну вторую долю обозначают как или 1/2, одну третью долю – как или 1/3; одну четвертую долю – как или 1/4, и так далее. Отметим, что запись с горизонтальной чертой употребляется чаще. Для закрепления материала приведем еще один пример: запись обозначает одну сто шестьдесят седьмую долю целого.
Понятие доли естественным образом распространяется с предметов на величины. Например, одной из мер измерения длины является метр. Для измерения длин меньших, чем метр, можно использовать доли метра. Так можно воспользоваться, например, половиной метра или десятой или тысячной долей метра. Аналогично применяются доли других величин.
Способы рассчитать две трети
Сколько это две трети?
Две трети — это 2/3 или 0.66667 в десятичной форме. Это означает, что если у нас есть целое число или количество, то две трети этого числа составляет около 66.67% от всего.
Способы рассчитать две трети:
1. Математический расчет:
Используя математический расчет, можно узнать, сколько это две трети любого числа. Для этого необходимо взять это число и умножить на 2, затем поделить на 3. Например, если у нас есть число 9, то две трети от него будет: 9 * 2 / 3 = 6.
2. Графическое представление:
Если нам нужно визуально представить две трети чего-либо, то можно использовать графическое представление. Для этого можно нарисовать отрезок и разделить его на три равные части. Затем можно отметить две из этих равных частей, представляющие две трети.
3. Процентный расчет:
Также можно рассчитать две трети в процентах. Для этого необходимо взять число и умножить его на 0.66667. Например, если у нас есть число 100, то две трети от него в процентах будет: 100 * 0.66667 = 66.67%.
Таким образом, есть несколько способов рассчитать две трети от числа или количества. Можно использовать математический расчет, графическое представление или процентный расчет в зависимости от конкретной ситуации.
Математический подход
Математический подход позволяет выполнять расчеты и примеры с долями и процентами. Например, если у нас есть число X, а мы хотим найти две трети этого числа, мы можем воспользоваться формулой:
X * (2/3) = (2X) / 3
Таким образом, мы можем найти две трети от любого числа с помощью простых арифметических действий. При этом, умножая число на дробь 2/3, мы получим результат, который составляет две трети от исходного числа.
Графический метод
Для решения задач, связанных с двумя третями, можно использовать графический метод. При этом следует знать, что две трети это 2/3, что равняется примерно 0.67 в десятичном виде. С помощью таблицы можно произвести вычисление, используя данную долю.
| Число | Доля |
|---|---|
| 1 | 0.67 |
| 2 | 1.34 |
| 3 | 2.01 |
Из таблицы видно, что две трети (2/3) примерно равны 1.34. Таким образом, если нужно произвести расчеты и примеры, связанные с двумя третями, можно использовать значение 1.34 вместо доли.
Калькуляторы и онлайн-инструменты
Например, если вам нужно рассчитать две трети от какого-то числа, вы можете использовать калькулятор, чтобы точно узнать результат. Просто введите число, нажмите на кнопку «Умножить» и введите коэффициент 2/3. Калькулятор покажет вам результат расчета.
Также с помощью онлайн-инструментов вы можете выполнить другие математические операции с долями, такие как сложение, вычитание, умножение и деление. Это особенно удобно, если вам нужно выполнить сложные расчеты с третями или другими долями.
Кроме того, калькуляторы и онлайн-инструменты предоставляют возможность выполнить дополнительные математические операции, такие как возведение в степень, извлечение корня, нахождение процента от числа и другие. Это позволяет вам решать различные задачи и задания, связанные с математикой и статистикой.
Использование калькуляторов и онлайн-инструментов упрощает процесс выполнения математических расчетов, сокращает время и усилия, которые вы тратите на выполнение вычислений вручную. Они также позволяют избежать ошибок и получить точные результаты.
Что такое 2/3 целого?
Чтобы найти 2/3 целого числа, нам нужно умножить число на 2 и разделить на 3. Чтобы найти две трети от 18, умножьте 2/3 x 18/1, чтобы получить 36/3. 36/3 снова упрощается до 12.
Кроме того, что означает 2/3?
Две трети чего-то сумма, которая составляет две из трех равных частей.
Соответственно, что такое 2/3 в процентах?
Таблица преобразования дробей в проценты
| Доля | Процент |
|---|---|
| 2/3 | 66.67% |
| 1/4 | 25% |
| 2/4 | 50% |
| 3/4 | 75% |
Как вы рассчитываете 2/3 в процентах? Теперь мы видим, что наша доля составляет 66.666666666667 / 100, что означает, что 2/3 в процентах составляет 66.6667%.
Как мне рассчитать 2/3 моей зарплаты?
Разделение число на 3, чтобы найти «одну треть», затем умножьте на 2, чтобы найти «две трети».
Объяснение понятия «целое число»
Целое число — это число, которое не имеет дробной части и не может быть представлено в виде дроби. В математике целые числа представляются символом Z, что означает множество всех целых чисел.
Целые числа включают в себя как положительные, так и отрицательные числа, а также число 0. Например: -3, -2, -1, 0, 1, 2, 3 — все они являются целыми числами.
Целые числа используются для решения широкого спектра задач в различных областях, таких как наука, экономика, физика и математика. Они могут быть использованы для представления количественной информации, выполнения математических операций и т.д.
Понимание концепции целых чисел важно для учеников начальных классов, так как они начинают изучать основы математики. Изучение целого и его частей помогает им приобрести навыки работы с отрицательными числами и понимание базовых математических операций
Таблица ниже показывает примеры целых чисел:
Целое числоОписание
| -3 | Отрицательное целое число |
| Целое число, равное нулю | |
| 7 | Положительное целое число |
Статьи по теме вопроса
-
Основные понятия математики
Математика является одной из наиболее важных и фундаментальных наук, которая изучает структуру, свойства и отношения между различными объектами. Она является неотъемлемой частью нашей жизни и применяется во многих областях, таких как физика, экономика, биология и технические науки….
-
История развития математики
Математика – это наука, которая изучает количество, структуру, пространство и изменения. Она является одной из самых древних наук и имеет богатую и интересную историю развития.Первые шаги в математикеПервые упоминания о математике можно найти уже в древнейшей письменности,…
-
Роль математики в современном мире
Математика – это наука, которая изучает структуру, свойства и взаимосвязи чисел, пространства, структур и изменений. Она является одной из самых фундаментальных наук и играет огромную роль в различных областях жизни.Математика в технологияхСовременный мир невозможно представить без…
-
Математические методы и их применение
Математика является одной из основных наук, которая широко используется в различных областях нашей жизни. Однако, ее значение не ограничивается только теоретическими вычислениями и формулами. Математические методы имеют большое практическое применение и помогают решать сложные задачи в…
-
Математические теории и их значение
Математика – это наука, которая изучает структуру, пространство, количество и изменение. Она является одной из самых фундаментальных наук и имеет широкое применение в различных областях жизни – от ежедневных расчетов до сложных научных исследований. В своей основе математика использует…
-
Влияние математики на другие науки
Математика – это одна из старейших и наиболее важных наук, которая играет огромную роль в развитии человечества. Ее применение не ограничивается только сферой точных наук, таких как физика или химия, но также оказывает значительное влияние на другие области знаний.Развитие…
-
Задачи и проблемы, решаемые с помощью математики
ВведениеМатематика – это наука о числах, формулах и пространстве. Она является одной из основных наук и играет важную роль в различных областях человеческой деятельности. Многие люди могут думать, что математика не имеет никакого отношения к их повседневной жизни, но на самом деле она…
-
Современные достижения в области математики
Математика является одной из старейших наук и постоянно развивается, открывая новые горизонты для исследований. Сегодня мы поговорим о самых значительных достижениях в области математики за последние несколько десятилетий.Искусственный интеллект и машинное обучениеОдним из…
-
Интересные факты о математике
Математика — это наука, которая изучает структуру, пространство, количество и изменение. Она играет важную роль в нашей жизни, от повседневных расчетов до сложных научных и технических разработок. Но помимо своей практической значимости, математика также представляет собой увлекательное поле…
-
Практическое применение математики в повседневной жизни
Математика является одним из фундаментальных наук, которая изучает структуру, свойства и взаимосвязь чисел, пространства, структур и изменений. Многие люди считают ее сложной и непонятной, однако она имеет огромное практическое применение в нашей повседневной жизни.ФинансыОдно из…
Значение в математике
В математике, значение двух третей числа обозначается как x * 2/3 или 2x/3. Это значит, что числу x умножается на две трети, то есть на 2/3. Математически выражение x * 2/3 можно переписать как 2x / 3, что эквивалентно делению числа x на 3, а затем умножению результата на 2.
Для лучшего понимания, рассмотрим пример. Если дано число 9, то его значение двух третей будет: 9 * 2/3 = 18/3 = 6. Таким образом, две трети числа 9 равны 6.
Значение двух третей числа может быть использовано в различных математических расчетах и проблемах. Например, при нахождении процента от числа, можно использовать эту концепцию. Если нам нужно найти 2/3 от числа x, мы можем применить формулу: (x * 2/3) / 100. Это даст нам значение в процентах от исходного числа x.
Также, общую долю может быть представлена в виде 2/3 от целого. Например, если у нас есть 100 яблок и мы хотим узнать, сколько яблок составляет две трети от всего количества, мы можем рассчитать это, умножив 100 на 2/3. Результатом будет 66,67, что означает, что две трети от 100 яблок составляют примерно 66 яблок.
Примеры:
- Значение двух третей числа 12: 12 * 2/3 = 24/3 = 8
- Значение двух третей числа 5: 5 * 2/3 = 10/3 ≈ 3.33
- Значение двух третей числа 50: 50 * 2/3 = 100/3 ≈ 33.33
Примеры использования
Пример 1:
Допустим, у нас есть задача разделить 150 яблок поровну между двумя детьми. Мы можем использовать две трети числа для определения количества яблок, которое получит каждый ребенок:
- Делим 150 на 3: 150 / 3 = 50
- Умножаем 50 на 2: 50 * 2 = 100
- Получаем ответ: каждый ребенок получит по 100 яблок.
Пример 2:
Представим, что у нас есть группа из 30 студентов, и мы хотим определить, сколько из них можно разделить на три команды для выполнения проекта. Мы можем использовать две трети числа для этого:
- Делим 30 на 3: 30 / 3 = 10
- Умножаем 10 на 2: 10 * 2 = 20
- Получаем ответ: каждая команда будет состоять из 10 студентов, а 20 студентов будут задействованы в проекте.
Пример 3:
Предположим, что у нас есть круглый пирог, и мы хотим разделить его между троими друзьями. Мы можем использовать две трети числа, чтобы определить, сколько каждый друг получит:
- Делим пирог на 3: 1 пирог / 3 = 1/3 пирога
- Умножаем 1/3 на 2: 1/3 * 2 = 2/3 пирога
- Получаем ответ: каждый друг получит 2/3 пирога.






























