Что такое функция в алгебре?

График функции

А еще это означает, что решать уравнение для всех возможных значений х нет необходимости. Для функции можно построить график, т.е. отобразить зависимость у от х визуально. Для этого используется плоская система координат с осями х и у. Соответственно по оси х откладывается значение переменной х, а по оси у значение переменной у, определенной для этого значения х.

В простых случаях, т.е. когда между переменными существует линейная зависимость, для построения графика достаточно знать координаты 2 точек. Например для функции f(x) = 2х в пределах от 0 до 4 график будет выглядеть так:

Рисунок 538.1. График функции f(x) = 2x.

Сначала мы определяем значения функции для нижнего (х = 0) и верхнего (х = 4) пределов: f(0) = 2·0 = 0, f(4) = 2·4 = 8. Эти результаты и будут координатами точек (показаны на рисунке 538.1 красным цветом), через которые проходит график функции. Прямая, соединяющая эти точки (показана на рисунке 538.1 синим цветом) — это и есть график рассматриваемой функции.

Таким образом, для всех промежуточных значений х, а это могут быть не только натуральные (т.е. целые) числа, мы можем определять значения у по графику. Для этого достаточно провести вертикальную линию из точки, обозначающей значение х, до графика (показан на рисунке 538.1 синей линией), а затем провести горизонтальную линию из точки пересечения вертикальной линии и графика. Пересечение горизонтальной линии с осью у покажет значение переменной у для соответствующего значения х. На рисунке 538.1 подобные действия не показаны, чтобы не усложнять график.

Более того, понятие функции применимо и к простым уравнениям, содержащим только одну неизвестную, а потому постоянную величину, и для таких уравнений тоже можно построить график. Например, уравнение у = 7 — 2 можно записать так: у = f(x) = 5 и тогда графиком функции будет прямая горизонтальная линия, проходящая на высоте 5 делений от оси х.

А теперь несколько слов о том, зачем все это может понадобиться например при изучении теоретической механики или теории сопротивления материалов.

При расчете строительных конструкций, например балок, необходимо определить значение поперечных сил и моментов, действующих в различных сечениях балки, а также углы поворота и перемещения нейтральной оси балки. Для этого строятся эпюры поперечных сил, моментов, углов поворота и прогиба. Так вот эти эпюры и есть графики соответствующих функций.

При этом длина балки l измеряется по оси х, соответственно нижний предел функции х = 0, а верхний предел функции х = l.

Например уравнение моментов М(х) = qlx/2 — qx2/2 при действии на балку равномерно распределенной нагрузки в обще виде можно записать так:

у = f(x) = qlx/2 — qx2/2 (538.6)

Но на этом увлекательный мир уравнений, а также функций, их аргументов и т.п. не заканчивается, а только начинается. Следующий уровень сложности — это дифференциальные уравнения, когда одна из неизвестных величин является производной или дифференциалом второй неизвестной величины, но это уже отдельная большая тема.

Примеры ограниченной функции:

1. Функция sin(x):

График функции синус ограничен сверху и снизу горизонтальными линиями, образующими полосу шириной 2. Амплитуда синусоиды равна 1, поэтому значения функции ограничены интервалом .

2. Функция e^x:

Экспонентная функция ограничена только снизу, так как ее значения положительны и могут стремиться к нулю, но не могут превысить его. Экспонента e^x растет очень быстро, но она всегда больше 0 и не имеет верхней границы.

3. Функция tg(x):

График функции тангенс имеет периодические участки между асимптотами, где значения функции ограничены. Однако, так как тангенс функция периодическая, ее значения могут становиться очень большими и очень малыми.

4. Функция 1/x:

График функции 1/x образует гиперболу, которая имеет асимптоты по осям координат. Между этими асимптотами функция ограничена, но значения функции могут стремиться к бесконечности.

Таблица с примерами ограниченных функций:
Функция
Тип функции
Ограниченность

sin(x)
тригонометрическая
ограничена
e^x
экспонента
ограничена только снизу
tg(x)
тригонометрическая
ограничена в периодах между асимптотами
1/x
рациональная
ограничена между асимптотами

Обратная функция.

Пусть задана числовая функция $y=f(x),\;x\in D(f)$. Тогда каждому числу $x_0\in D(f)$соответствует единственное число $y_{0}=f(x_{0})\in E(f)$ . Нередко приходится по заданному значению функции $y_0$ находить соответствующее значение аргумента, то есть решать относительно $x$ уравнение
$$
f(x)=y_{0},\quad y_{0}\in E(f).\label{ref8}
$$

Это уравнение может иметь не одно, а несколько и даже бесконечно много решений. Решениями уравнения \eqref{ref8} являются абсциссы всех точек, в которых прямая $y=y_0$ пересекает график функции $y=f(x)$.

Например, если $f(x)=x^{2}$, то уравнение
$$
x^{2}=y_{0},\quad y_{0}>0,\nonumber
$$
имеет два решения: $x_{0}=\displaystyle \sqrt{y_0}$ и ${\widetilde x}_0=\sqrt{y_0}$. Если $f(x)=\sin x$, то уравнение
$$
\sin{x}=y_{0},\quad |y_{0}|\leq 1,\nonumber
$$
имеет бесконечно много решений вида $x_n=(-1)^{n}x_{0}+\pi n$, где $n\in\mathbb{Z}\;x_0$ — одно из решений этого уравнения.

Однако существуют функции, для которых уравнение \eqref{ref8} при каждом $y_{0}\in E(f)$ однозначно разрешимо, то есть имеет единственное решение $x_0\in D(f)$. Этим свойством обладают, например, следующие функции:

$f(x)=3x+4,\;D(f)=\mathbb{R}$;
$f(x)=x^{3},\;D(f)=\mathbb{R}$;
$f(x)=\displaystyle \frac{1}{x},\quad D(f)=\{x\in\mathbb{R},\;x\neq 0\}$.

Если функция $f$ такова, что при каждое значение $y_{0}\in E(f)$ она принимает только при одном значении $x_{0}\in D(f)$ , то эту функцию называют обратимой. Для такой функции уравнение
$$
f(x)=y\nonumber
$$
можно при любом $у\in Е(f)$однозначно разрешить относительно $x$, то есть каждому $y\in Е(f)$ соответствует единственное значение $x\in D(f)$.

Это соответствие определяет функцию, которую называют обратной к функции $f$ и обозначают символом $f^{-1}$.

Заметим, что прямая $y=y_0$ для каждого $y_{0}\in E(f)$ пересекает график обратимой функции $y=f(x)$ в единственной точке $(x_0,\;y_0)$, где $f(x_{0})=y_{0}$.

Обозначая, как обычно, аргумент обратной функции буквой $x$, а ее значения — буквой $y$, обратную для $f$ функцию записывают в виде
$$
y=f^{-1}(x),\quad x\in D(f^{-1}).\nonumber
$$

Для упрощения записи вместо символа $f^{-1}$ будем употреблять букву $g$.

Отметим следующие свойства, которые показывают, как связаны данная функция и обратная к ней:

если $g$ — функция, обратная к $f$, то и $f$ — функция, обратная к $g$; при этом
$$
D(g)=E(f),\quad E(g)=D(f),\nonumber
$$
то есть область определения функции $g$ совпадает с множеством значений функции $f$ и наоборот;
для любого $x\in D(f)$ справедливо равенство
$$
g(f(x))=x,\nonumber
$$
а для любого $х\in Е(f)$ справедливо равенство
$$
f(g(x))=x;\nonumber
$$
график функции $y=g(x)$ симметричен графику функции $y=f(x)$ относительно прямой $y=x$;
если нечетная функция обратима, то обратная к ней функция также является нечетной;
если $f$ — строго возрастающая (строго убывающая) функция, то она обратима, причем обратная к ней функция $g$ также является строго возрастающей (строго убывающей).

Рис. 9.9

Свойства 1) и 2) следуют непосредственно из определения обратной функции, 4) и 5) — из определений обратной и соответственно нечетной и строго монотонной функции.

Рис. 9.10

Рассмотрим свойство 3). Пусть точка $(x_{0},y_{0})$ принадлежит графику функции $y=f(x)$, то есть $y_{0}=f(x_0)$. Тогда $x_{0}=g(y_{0})$, то есть точка $(x_{0},y_{0})$ принадлежит графику обратной функции $g$. Так как точки $(x_{0},y_{0})$ и $(y_{0},x_{0})$ симметричны относительно прямой $y=x$ (рис. 9.9), то график функции $у=g(х)$ симметричен графику функции относительно этой прямой.

Рис. 9.11

На рис. 9.10 изображены графики взаимно обратных функций $y=x^{2},\;x\geq 0$, и $y=\sqrt{x}$, а на рис. 9.11 — графики взаимно обратных функций $y=x^{2},\;x\leq 0$, и $y=-\sqrt{x}$.

Действительные функции

Область определения функции и множество ее значений могут быть любыми множествами. Например, числовые последовательности – это функции, областью определения которых является множество натуральных чисел, а множеством значений – вещественные или комплексные числа. Векторное произведение тоже функция, поскольку для двух векторов и имеется только одно значение вектора . Здесь областью определения является множество всех возможных пар векторов . Множеством значений является множество всех векторов. Логическое выражение является функцией. Ее область определения – это множество действительных чисел (или любое множество, в котором определена операция сравнения с элементом “0”). Множество значений состоит из двух элементов – “истина” и “ложь”.

В математическом анализе большую роль играют числовые функции.

Числовая функция: – это функция, значениями которой являются действительные или комплексные числа.
Действительная или вещественная функция: – это функция, значениями которой являются действительные числа.

Максимум и минимум

Действительные числа имеют операцию сравнения. Поэтому множество значений действительной функции может быть ограниченным и иметь наибольшее и наименьшее значения.

Ограниченная сверху (снизу) функция: Действительная функция называется ограниченной сверху (снизу), если существует такое число , что для всех выполняется неравенство:.
Ограниченная функция: Числовая функция называется ограниченной, если существует такое число , что для всех .
Максимумом (минимумом ) функции: , на некотором множестве , называют значение функции при некотором значении ее аргумента , при котором для всех ,.

Верхняя и нижняя грани

Верхняя грань (точная верхняя граница) функции: Верхней гранью или точной верхней границей действительной, ограниченной сверху функции называют наименьшее из чисел, ограничивающее область ее значений сверху. То есть это такое число , для которого: 1) для всех ; 2) для любого , найдется такой аргумент , значение функции от которого превосходит . Верхняя грань функции может обозначаться так:.Верхней гранью неограниченной сверху функции является бесконечно удаленная точка .
Нижняя грань (точная нижняя граница) функции: Нижней гранью или точной нижней границей действительной, ограниченной снизу функции называют наибольшее из чисел, ограничивающее область ее значений снизу. То есть это такое число , для которого: 1) для всех ; 2) для любого , найдется такой аргумент , значение функции от которого меньше чем . Нижняя грань функции может обозначаться так:.Нижней гранью неограниченной снизу функции является бесконечно удаленная точка .

Таким образом, любая действительная функция, на не пустом множестве , имеет верхнюю и нижнюю грани. Но не всякая функция имеет максимум и минимум.

В качестве примера рассмотрим функцию , заданную на открытом интервале . Она ограничена, на этом интервале, сверху значением и снизу – значением для всех . Эта функция имеет верхнюю и нижнюю грани:. Но она не имеет максимума и минимума.

Если мы рассмотрим туже функцию на отрезке , то она на этом множестве ограничена сверху и снизу, имеет верхнюю и нижнюю грани и имеет максимум и минимум: для всех ;;.

Монотонные функции

Возрастающая (убывающая) функция: Пусть функция определена на некотором множестве действительных чисел . Функция называется строго возрастающей (строго убывающей), если для всех таких что выполняется неравенство:. Функция называется неубывающей (невозрастающей), если для всех таких что выполняется неравенство:.
Монотонная функция: Функция называется монотонной, если она неубывающая или невозрастающая.

Примеры функций

Линейная функция: F(x) = ax + b, где a и b – некоторые константы. Она представляет собой прямую линию на координатной плоскости и имеет постоянный наклон. Примером может быть функция y = 2x + 3.
Квадратичная функция: F(x) = ax^2 + bx + c, где a, b и c – константы. Она представляет собой параболическую кривую и имеет форму улыбки или грусти. Примером может быть функция y = x^2 — 4x + 5.
Тригонометрическая функция: F(x) = sin(x) или F(x) = cos(x), где sin и cos – тригонометрические функции. Они связывают угол с его синусом или косинусом. Примером может быть функция y = sin(x), которая описывает колебания или волны.

Это только несколько примеров функций из огромного разнообразия, которое существует. Функции играют важную роль в математике и науке, помогая описывать и понимать различные явления и процессы. Они также находят применение в различных областях, таких как экономика, физика, компьютерная графика и т.д.

Линейная функция

Формула функции f(x) = kx + b задает прямую линию на координатной плоскости. Коэффициент k называется угловым коэффициентом и определяет наклон прямой. Чем больше значение k, тем круче наклон прямой. Константа b отвечает за значение функции при x = 0 и называется свободным членом.

Линейная функция может иметь различные графики в зависимости от значений k и b. Если k > 0, то график функции будет возрастать (прямая идет вверх). Если k

Примеры линейных функций:

Функция	Уравнение	График
Прямая со степенью наклона k = 1 и свободным членом b = 0	f(x) = x
Прямая со степенью наклона k = -2 и свободным членом b = 3	f(x) = -2x + 3
Горизонтальная прямая со степенью наклона k = 0 и свободным членом b = 5	f(x) = 5

Линейная функция является одной из основных и наиболее простых функций. Она широко применяется в математике, физике, экономике и других науках для описания простых зависимостей и моделирования различных процессов.

Квадратичная функция

Основным свойством квадратичной функции является то, что ее график представляет собой параболу.

Коэффициент a определяет, какой будет открытие параболы – вверх или вниз. Если a положительно, то парабола открывается вверх, а если a отрицательно, то парабола открывается вниз.

Коэффициент b влияет на положение параболы по горизонтали. Если b положительно, то парабола смещается влево, а если b отрицательно, то парабола смещается вправо.

Коэффициент c определяет, насколько высоко или низко находится вершина параболы. Если c положительно, то вершина находится выше оси x, а если c отрицательно, то вершина находится ниже оси x.

Квадратичные функции широко применяются в математике и физике. Они используются для моделирования различных явлений, таких как траектория полета объекта или форма поверхности.

Пример квадратичной функции:

f(x) = 2x^2 — 3x + 1

В данном примере, коэффициент a равен 2, b равен -3, а c равно 1. График данной функции будет представлять собой параболу, открытую вверх, с вершиной выше оси x.

Тригонометрическая функция

Основные тригонометрические функции включают синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc). Эти функции определены для всех углов, их значения быть может как положительными, так и отрицательными, а также иметь разные периоды и амплитуды.

Синус (sin) угла в прямоугольном треугольнике определяется как отношение противолежащей стороны к гипотенузе треугольника. Косинус (cos) угла в прямоугольном треугольнике определяется как отношение прилежащей стороны к гипотенузе, а тангенс (tan) — отношение противолежащей стороны к прилежащей. Котангенс (cot), секанс (sec) и косеканс (csc) являются обратными функциями к синусу, косинусу и тангенсу соответственно.

Тригонометрические функции широко используются для решения задач, связанных с треугольниками, колебаниями и периодическими функциями. Они играют важную роль в анализе и моделировании различных физических и инженерных процессов.

Например, с помощью тригонометрических функций можно описывать движение колебательного маятника, электромагнитные волны, звуковые волны и другие периодические явления. Они также используются в геодезии, навигации, астрономии и космологии для измерения углов и расстояний.

В общем виде, тригонометрические функции могут быть представлены как графики, таблицы значений или формулы, которые позволяют вычислить значения функций для любого заданного угла. Эти функции имеют много свойств и интересных математических связей, которые изучаются в математическом анализе и теории функций.

Основные свойства функции f(x)

Функция f(x) представляет собой математическое отображение, которое сопоставляет каждому элементу из области определения значение в области значений.

Основные свойства функции f(x) включают:

Определение функции	Функция f(x) определяется правилами, с помощью которых можно выразить значение функции в зависимости от переменной x. Определение функции основано на математическом выражении, которое может быть алгебраическим, тригонометрическим, логарифмическим и т.д.
Область определения и область значений	Область определения функции f(x) — это множество всех возможных значений переменной x, при которых функция имеет определение. Область значений функции f(x) — это множество значений, которые функция может принимать.
Монотонность и экстремумы	Функция f(x) может быть монотонной, что означает, что она строго возрастает или строго убывает на определенном интервале. Экстремумы функции f(x) — это точки, в которых функция достигает максимальных или минимальных значений.

Основные свойства функции f(x) дают возможность изучать ее поведение, строить графики, решать уравнения, находить производную и интеграл, а также применять функцию в различных областях науки и техники.

Определение функции

Функцию обозначают символом f(x), где f — обозначение функции, а (x) — обозначение аргумента, для которого определена функция.

Чтобы функция была корректно определена, каждому элементу области определения должен соответствовать один и только один элемент области значений. Это означает, что функция должна быть определена для всех возможных значений аргумента.

Также важно отметить, что функция может быть представлена графически, где аргумент обычно откладывается по оси X, а значения функции — по оси Y. Определение функции в математике позволяет моделировать и анализировать различные процессы и взаимосвязи между переменными

Функции широко применяются в различных областях науки, экономики и техники

Определение функции в математике позволяет моделировать и анализировать различные процессы и взаимосвязи между переменными. Функции широко применяются в различных областях науки, экономики и техники.

Область определения и область значений функции

Область значений (ОЗ) функции — это множество значений, которые может принимать функция fx при прохождении через все точки области определения. Другими словами, это множество всех значений, которые функция fx может принимать для различных значений переменной x из области определения.

Область определения и область значений являются важными характеристиками функции, которые помогают понять её свойства и ограничения. Они могут быть представлены в виде интервалов на числовой оси или множественных условий для переменной x.

Для определения области определения и области значений функции необходимо учесть следующие факторы:

Значения, при которых функция имеет смысл: некоторые функции могут иметь ограничения на значения переменной x, например, знаменатель не может быть равен нулю в случае рациональных функций.
Ограничения на переменную x: функции могут иметь ограничения на значения переменной x, например, корень не может быть найден для отрицательного значения под корнем.
Свойства и ограничения функции: некоторые функции могут иметь специфические свойства или ограничения, которые влияют на их область определения и область значений, например, тригонометрические функции имеют периодические ограничения на значения переменной x.

Знание области определения и области значений функции помогает в решении уравнений, нахождении точек экстремума, анализе функции и её поведении на числовой оси.

Монотонность и экстремумы

Экстремумами функции называются точки, в которых функция достигает своих наибольших или наименьших значений. Экстремумы бывают двух типов: минимумы и максимумы. Минимум функции — это наименьшее значение, которое она принимает на некотором интервале, а максимум — наибольшее значение.

Монотонность и экстремумы функции могут быть определены с помощью производной функции. Монотонность определяется знаком производной: если производная положительная, то функция монотонно возрастает, если отрицательная — монотонно убывает.

Чтобы найти экстремумы функции, необходимо найти точки, где производная равна нулю или не существует. Если в окрестности этой точки производная меняет знак с «плюс» на «минус», то это будет локальный максимум, иначе — локальный минимум.

Аналитическое задание функции

Функция %%y = f(x), x \in X%% задана явным аналитическим способом, если дана формула, указывающая последовательность математических действий, которые надо выполнить с аргументом %%x%%, чтобы получить значение %%f(x)%% этой функции.

Пример

%% y = 2 x^2 + 3x + 5, x \in \mathbb{R}%%;
%% y = \frac{1}{x — 5}, x \neq 5%%;
%% y = \sqrt{x}, x \geq 0%%.

Так, например, в физике при равноускоренном прямолинейном движении скорость тела определяется формулой %%v = v_0 + a t%%, а формула для перемещения %%s%% тела при равномерно ускоренном движении на промежутке времени от %%0%% до %%t%% записывается в виде: %% s = s_0 + v_0 t + \frac{a t^2}{2} %%.

Кусочно-заданные функции

Иногда рассматриваемая функция может быть задана несколькими формулами, действующими на различных участках области ее определения, в которой изменяется аргумент функции. Например:
$$
y = \begin{cases}
x ^ 2,~ если~x < 0, \\
\sqrt{x},~ если~x \geq 0.
\end{cases}
$$

Функции такого вида иногда называют составными или кусочно-заданными. Примером такой функции является %%y = |x|%%

Область определения функции

Если функция задана явным аналитическим способом с помощью формулы, но область определения функции в виде множества %%D%% не указана, то под %%D%% будем всегда подразумевать множество значений аргумента %%x%%, при которых данная формула имеет смысл. Так для функции %%y = x^2%% областью определения служит множество %%D = \mathbb{R} = (-\infty, +\infty)%%, поскольку аргумент %%x%% может принимать любые значения на числовой прямой. А для функции %%y = \frac{1}{\sqrt{1 — x^2}}%% областью определения будет множество значений %%x%% удовлетворяющих неравенству %%1 — x^2 > 0%%, т.е. %%D = (-1, 1)%%.

Преимущества явного аналитического задания функции

Отметим, что явный аналитический способ задания функции достаточно компактен (формула, как правило, занимает немного места), легко воспроизводим (формулу нетрудно записать) и наиболее приспособлен к выполнению над функциями математических действий и преобразований.

Некоторые из этих действий — алгебраические (сложение, умножение и др.) — хорошо известны из школьного курса математики, другие (дифференцирование, интегрирование) будем изучать в дальнейшем. Однако этот способ не всегда нагляден, так как не всегда четок характер зависимости функции от аргумента, а для нахождения значений функции (если они необходимы) требуются иногда громоздкие вычисления.

Неявное задание функции

Функция %%y = f(x)%% задана неявным аналитическим способом, если дано соотношение $$F(x,y) = 0, ~~~~~~~~~~(1)$$ связывающее значения функции %%y%% и аргумента %%x%%. Если задавать значения аргумента, то для нахождения значения %%y%%, соответствующего конкретному значению %%x%%, необходимо решить уравнение %%(1)%% относительно %%y%% при этом конкретном значении %%x%%.

При заданном значении %%x%% уравнение %%(1)%% может не иметь решения или иметь более одного решения. В первом случае заданное значение %%x%% не принадлежит области определения неявно заданной функции, а во втором случае задает многозначную функцию, имеющую при данном значении аргумента более одного значения.

Отметим, что если уравнение %%(1)%% удается явно разрешить относительно %%y = f(x)%%, то получаем ту же функцию, но уже заданную явным аналитическим способом. Так, уравнение %%x + y^5 — 1 = 0%%

и равенство %%y = \sqrt{1 — x}%% определяют одну и ту же функцию.

Параметрическое задание функции

Когда зависимость %%y%% от %%x%% не задана непосредственно, а вместо этого даны зависимости обоих переменных %%x%% и %%y%% от некоторой третьей вспомогательной переменной %%t%% в виде

$$
\begin{cases}
x = \varphi(t),\\
y = \psi(t),
\end{cases} ~~~t \in T \subseteq \mathbb{R}, ~~~~~~~~~~(2)
$$то говорят о параметрическом способе задания функции;

тогда вспомогательную переменную %%t%% называют параметром.

Если из уравнений %%(2)%% удается исключить параметр %%t%%, то приходят к функции, заданной явной или неявной аналитической зависимостью %%y%% от %%x%%. Например, из соотношений
$$
\begin{cases}
x = 2 t + 5, \\
y = 4 t + 12,
\end{cases}, ~~~t \in \mathbb{R},
$$ исключением параметра %%t%% получим зависимость %%y = 2 x + 2%%, которая задает в плоскости %%xOy%% прямую.

Степенная функция с натуральным показателем

Если обозначить сторону квадрата как a, то его площадь будет являться функцией:

S = a2

Для вычисления объема куба с ребром a необходимо возводить число уже в третью степень:

V = a3

Эти выражения являются примерами степенных функций с натуральным показателем. Таковой будет являться любое уравнение y = xs, где s – это какое-то натуральное число.

При s = 1 степенная функция обращается в зависимость у = х, то есть в прямую пропорциональность. Независимая величина х может принимать любые значения, а вот область значений зависит от четности или нечетности показателя s (этот вопрос будет рассмотрен подробнее чуть позже).

Рассмотрим функцию y = x2. Ясно, что при х, равном нулю, зависимая переменная также обращается в нуль:

y(0) = 02 = 0

Следовательно, ее график проходит через точку О (0;0). Это характерное свойство степенных функций с любым натуральным показателем.

Квадрат любого числа не может быть отрицательным числом, а потому график лежит в I и II четвертях. Следовательно, областью значений будет являться всё множество неотрицательных действительных чисел.

Заметим, что противоположным значениям х соответствуют одинаковые значения y:

y(-x) = (-x)2 = x2 = y(x)

Из-за этого график обладает симметрией относительно оси у.

Найдем несколько точек, по которым можно построить график степенной функции:

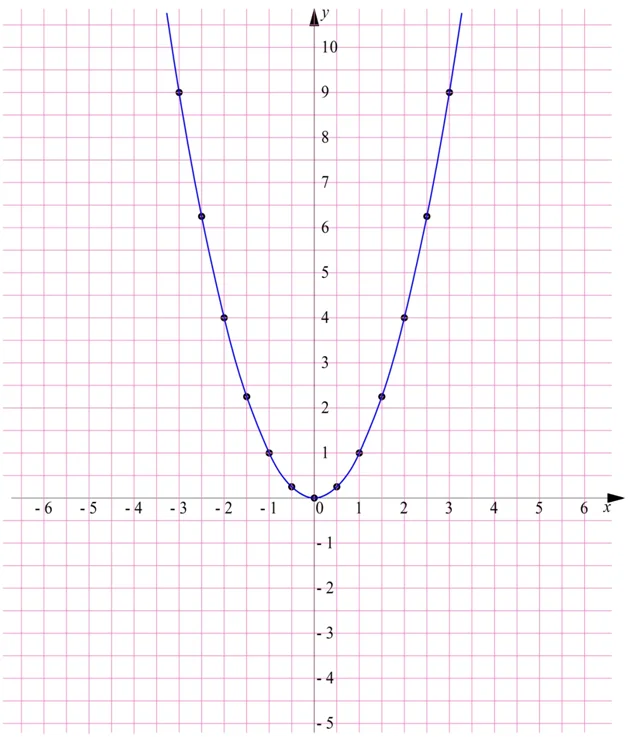
Полученную фигуру называют параболой, а точку О (0;0) – вершиной параболы. Видно, что точки параболы располагаются симметрично относительно оси ординат.

Заметим, что у степенных функций с четным показателем графики похожи. Они все симметричны относительно оси у, а также у них есть три общие точки:

(0;0);
(1;1);
(– 1;1).

Они определены на множестве всех неотрицательных чисел. Чем выше показатель степени, тем более плотно график «прижимается» к горизонтальной оси при малых х и тем более резко он поднимается вверх при больших х:

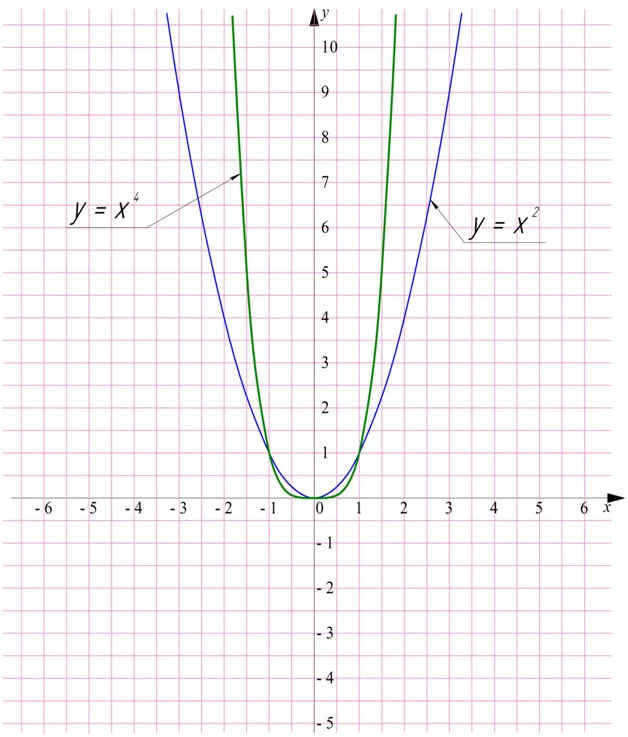
Далее изучим те степенные функции, показатель которых – нечетное число. Одной из них является

y = x3

Её график также пересекает начало координат. При положительном значении аргумента куб числа также положителен, а при отрицательном значении аргумента он будет отрицательным числом. Следовательно, график должен проходить через I и III четверти. Построим график по точкам:

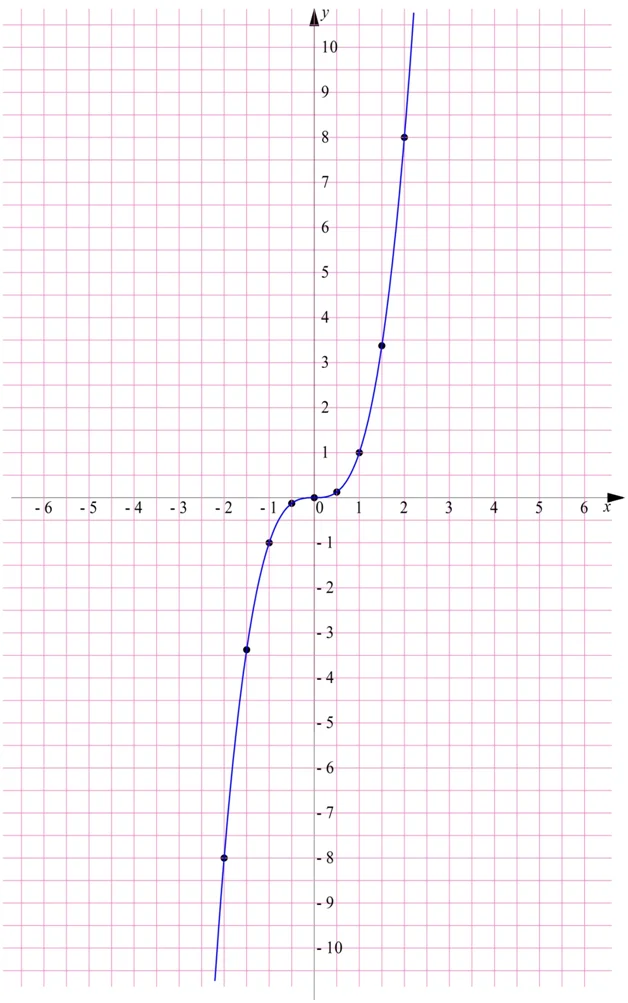
Полученный график называют кубической параболой. Графики других степенных функций (x5, x7, x9 и т.д.) похожи на этот:

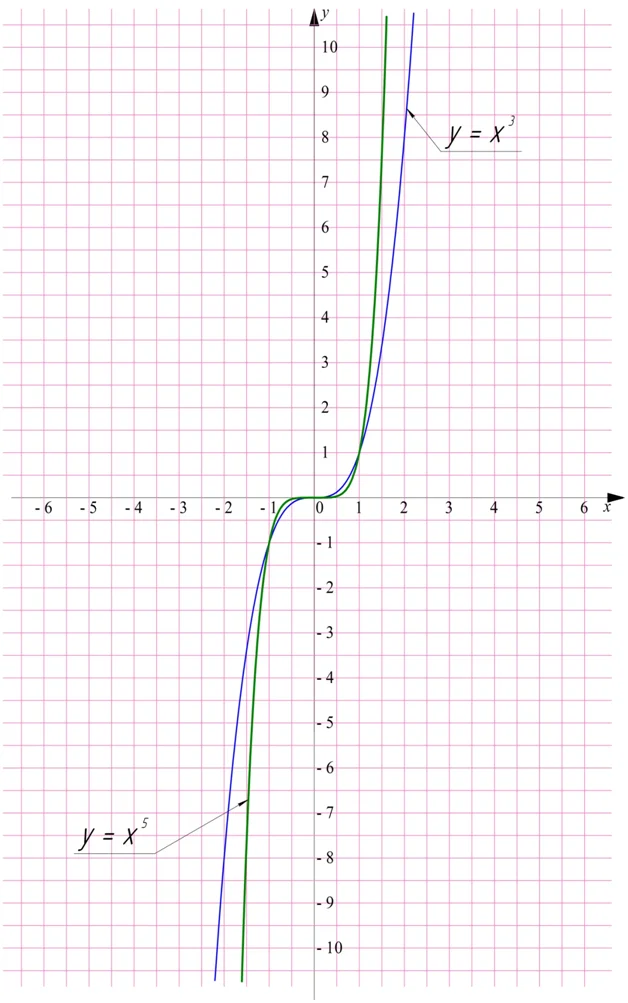
Они проходят через точки (0;0), (1;1) и (– 1; –1), лежат в I и III четвертях. У всех этих функций и в область значений, и область определений попадают все действительные числа.

Монотонные функции.

Функцию $f$ называют возрастающей (неубывающей) на множестве $X\subset D(f)$, если для любых точек $x_1 \in X, x_{2}\in X$ таких, что $x_{1}\;<\;x_{2}$, выполняется неравенство $ f(x_1)\leq f(х_2)$.Если это неравенство является строгим $(f(x_{1})\;<\;f(x_{2}))$, то функцию $f$ называют строго возрастающей на множестве $X$.

Таким образом, функция $f$ называется:

возрастающей (неубывающей) на множестве $X$, если
$$
\forall x_{1}\in X\quad \forall x_{2}\in X:\;x_{1}\;<\;x_{2}\rightarrow f(x_{1})\leq f(x_{2});\nonumber
$$
строго возрастающей на множестве $X$, если
$$
\forall x_{1}\in X\quad \forall x_{2}\in X:\;x_{1}\;<\;x_{2}\rightarrow f(x_{1})\;<\;f(x_{2}).\nonumber
$$

Аналогично функция $f$ называется:

убывающей (невозрастающей) на множестве $X$, если
$$
\forall x_{1}\in X\quad\forall x_{2}\in X:\;x_{1}\;<\;x_{2}\rightarrow f(x_{1})\geq f(x_{2});\nonumber
$$
строго убывающей на множестве $X$, если
$$
\forall x_{1}\in X\quad\forall x_{2}\in X:\;x_{1}\;<\;x_{2}\rightarrow f(x_{1})>f(x_{2}).\nonumber
$$

Убывающие и возрастающие функции объединяют названием монотонные, а строго возрастающие и строго убывающие — названием строго монотонные.

Если $X=D(f)$, то в этих определениях указание на множество $X$ обычно опускают.

Пример 9

Доказать, что функция f строго возрастает на множестве X, если:

$f(x)=x^{3},\;X=\mathbb{R}$;
$f(x)=\sin x, X=$.

Если $0\leq x_{1}\;<\;x_{2}$, то $x_{1}^{3}\;<\;x_{2}^{3}$, а если $x_1\;<\;x_{2}\leq 0$, то $0\leq-x_{2}\;<\;-x_{1}$, откуда
$$
(-x_{2})^{3}\;<\;(-x_{1})^{3}.\label{ref6}
$$
Так как $x^{3}$ — нечетная функция, то неравенство \eqref{ref6} можно записать в виде $-x_{2}^{3}\;<\;-x_{1}^{3}$, откуда $x_{1}^{3}\;<\;x_{2}^{3}$. Наконец, если $x_1\;<\;0$, а $x_{2}>0$, то $x_{1}^{3}\;<\;x_{2}^{3}$. Таким образом, неравенство $x_{1}^{3}\;<\;x_{2}^{3}$ справедливо для любых $x_{1}\in\mathbb{R},\;x_{2}\in\mathbb{R}$ таких, что $x_{1}\;<\;x_{2}$. Поэтому $x^3$ — строго возрастающая на $\mathbb{R}$ функция.
Пусть $\displaystyle -\frac{\pi}{2}\leq x_{1}\;<\;x_{2}\leq\frac{\pi}{2}$; тогда
$$
\sin x_{2}-\sin x_{1}=2\sin\frac{x_{2}-x_{1}}{2}\cos\frac{x_{2}+x_{1}}{2}>0,\nonumber
$$
так как $0\;<\;\displaystyle \frac{x_{2}-x_{1}}{2}\;<\;\frac{\pi}{2},\quad -\displaystyle \frac{\pi}{2}\;<\;\frac{x_{2}+x_{1}}{2}\;<\;\frac{\pi}{2}$.Таким образом, неравенство $\sin x_{2}>\sin x_{1}$ выполняется для $x_{1},x_{2}\displaystyle \in$, если $x_{2}>x_{1}$. Следовательно, функция $\sin x$ строго возрастает на отрезке $\displaystyle .\quad\blacktriangle$

Способы задания функции.

Числовые функции чаще всего задаются при помощи формул. Такой способ задания называют аналитическим. Например, функции $y=x^2, \ y=|x|^{3/2}, \ y=\sin^3{3x}$ заданы на множестве $\mathbb{R}$ аналитически.

Если числовая функция f задана формулой и не указана область ее определения $D(f)$ , то принято считать, что $D(f)$ — множество всех тех значений аргумента, при которых эта формула имеет смысл, и результатом каждой операции, указанной в формуле, является вещественное число. Например, если $f(x)=\sqrt{9-x^2}$, то $D(f)=$, а если $f(x)=\sqrt{\operatorname{lg} \sin{x}}$, то $D(f)$ — множество корней уравнения $\sin x=1$ то есть множество чисел $x_{k}=\pi/2.+2\pi k$, где $k\in Z$.

Следует отметить, что функция может быть задана различными формулами на разных промежутках. Например, функция
$$
f(x)=\left\{\begin{array}{l}-x,\quad если\;x\;<\;0,\\x^{2},\quad если\;0\leq x\leq1,\\2-\sqrt{x},\quad если\;x>1,\end{array}\right.\nonumber
$$
задана аналитическим способом на $\mathbb{R}$ с помощью трех различных формул.

Иногда функциональная зависимость описывается с помощью таблицы, содержащей лишь некоторые значения аргумента и соответствующие значения функции. Для значений аргумента, не содержащихся в таблице, значения функции обычно находят приближенно.

На практике часто соответствие между значениями аргумента и значениями функции задается с помощью рисунка. Например, в медицине при изучении работы сердца получают электрокардиограммы — кривые, отражающие изменение с течением времени электрических импульсов в мышце сердца. В практике физических измерений функциональная зависимость часто задается с помощью эскиза графика, снимаемого, например, с экрана осциллографа.

Свойства ограниченной функции

Ограниченная функция — это функция, которая имеет ограниченный областью значений. В противоположность ограниченным функциям, неограниченные функции имеют бесконечный областью значений.

Свойства ограниченной функции включают:

Ограниченность сверху: Ограниченная функция имеет максимальное значение, до которого она может достичь. Например, функция f(x) = sin(x) на интервале ограничена сверху значением 1.
Ограниченность снизу: Ограниченная функция имеет минимальное значение, которого она не может быть меньше. Например, функция f(x) = cos(x) на интервале ограничена снизу значением -1.
Ограниченность со всех сторон: Ограниченная функция ограничена и сверху, и снизу. То есть существуют два значения, максимальное и минимальное, которых функция не может превышать.

Ограниченные функции встречаются во многих областях математики и физики. Они играют важную роль в анализе функций и определении их свойств. Кроме того, ограниченные функции широко используются в моделировании реальных систем и являются основой для понимания различных явлений в природе.