Что такое система векторизации крутящего момента и как она работает?

Важные аспекты движения без проскальзывания

Движение без проскальзывания – это физический процесс, при котором тело перемещается без соприкосновения с другими объектами или поверхностями. Этот процесс играет важную роль в различных сферах жизни, начиная от машиностроения и инженерии, и заканчивая спортивными занятиями и интенсивными тренировками.

Существует несколько важных аспектов движения без проскальзывания, которые следует учитывать:

Коэффициент трения. Один из важных аспектов безопасности при движении без проскальзывания – это обеспечение достаточного коэффициента трения между поверхностями тела и окружающих объектов. Повышенный коэффициент трения обеспечивает лучшую устойчивость и предотвращает скольжение.

Правильный выбор обуви

Для достижения безопасного движения без проскальзывания важно выбрать правильную обувь. Она должна обладать антискользящей подошвой с хорошим амортизационным эффектом

Такая обувь обеспечит надежное сцепление с поверхностью и улучшит баланс тела.

Подготовка поверхности. Если поверхность, по которой предполагается двигаться, не обладает достаточным коэффициентом трения, то ее можно подготовить специальными антискользящими покрытиями или материалами. Применение таких покрытий позволяет существенно уменьшить риск скольжения.

Поддержание баланса и правильная техника движений. При движении без проскальзывания важно поддерживать хороший баланс тела и использовать правильную технику движений. Это позволяет распределить вес тела равномерно и избежать возможных потерь равновесия.

Регулярные тренировки. Чтобы достичь навыка движения без проскальзывания, необходима систематическая практика. Регулярные тренировки помогут развить силу и координацию мышц, улучшить баланс и устойчивость, а также повысить осведомленность о своем теле и его движениях.

Знание и применение этих важных аспектов движения без проскальзывания способствуют обеспечению безопасности, повышению эффективности движений и предотвращению возможных травм.

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ​\( S \)​ — перемещение тела относительно неподвижной системы отсчета;
​\( S_1 \)​ — перемещение тела относительно подвижной системы отсчета;
​\( S_2 \)​ — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ​\( v \)​ — скорость тела относительно неподвижной системы отсчета;
​\( v_1 \)​ — скорость тела относительно подвижной системы отсчета;
​\( v_2 \)​ — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное. Пусть \( v_1 \) — скорость первого тела, а \( v_2 \) — скорость второго тела.
Определим скорость первого тела относительно второго \( v_{12} \):

Пусть \( v_1 \) — скорость первого тела, а \( v_2 \) — скорость второго тела.
Определим скорость первого тела относительно второго \( v_{12} \):

Определим скорость второго тела относительно первого \( v_{21} \):

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ​\( \alpha \)​ друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Законы тяжести и их влияние на движение

Закон всемирного тяготения

Первый и самый известный закон тяжести, сформулированный Исааком Ньютоном, гласит, что каждое вещество во вселенной притягивается к любому другому веществу с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними. Данный закон влияет на все предметы, находящиеся на поверхности Земли, а также описывает движение планет вокруг Солнца и других небесных тел.

Закон инерции

Второй закон тяжести, также сформулированный Ньютоном, называется законом инерции. Он гласит, что тело будет оставаться в покое или двигаться равномерно прямолинейно, если на него не действуют никакие внешние силы. То есть, если на тело не действуют силы трения или другие воздействия, оно будет двигаться без изменения скорости или оставаться неподвижным.

Закон действия и противодействия

Третий закон тяжести утверждает, что на каждое действие всегда есть противоположное и равное по величине действие в противоположную сторону. Это означает, что когда взаимодействуют два тела, каждое из них оказывает на другое силу, которая направлена в противоположную сторону и имеет одинаковую величину.

Влияние законов тяжести на движение

Законы тяжести играют важную роль в объяснении и понимании различных видов движения. Например, закон всемирного тяготения объясняет, почему предметы падают на землю и как планеты перемещаются по орбитам вокруг Солнца.

Закон инерции помогает понять, почему предметы остаются на своем месте или движутся равномерно, если на них не действуют внешние силы.

Закон действия и противодействия демонстрирует, почему тела движутся в противоположных направлениях при взаимодействии.

Изучение этих законов тяжести позволяет увидеть и описать мир вокруг нас, понять, как вещи взаимодействуют друг с другом и как двигаются в пространстве.

Тяжеловесные тела и проскальзывание

При изучении движения тяжеловесных тел важно учитывать наличие трения и возможность проскальзывания. Тяжеловесные тела могут проскальзывать на горизонтальных поверхностях из-за действия силы трения

Сила трения возникает в результате взаимодействия между поверхностями тела и поверхности, на которой оно находится. Чтобы предотвратить проскальзывание тяжеловесного тела на горизонтальной поверхности, необходимо, чтобы сила трения была достаточно большой, чтобы превзойти силу, вызывающую проскальзывание (например, силу инерции)

Тяжеловесные тела могут проскальзывать на горизонтальных поверхностях из-за действия силы трения. Сила трения возникает в результате взаимодействия между поверхностями тела и поверхности, на которой оно находится. Чтобы предотвратить проскальзывание тяжеловесного тела на горизонтальной поверхности, необходимо, чтобы сила трения была достаточно большой, чтобы превзойти силу, вызывающую проскальзывание (например, силу инерции).

В случае, если между поверхностями тяжеловесного тела и поверхности, на которой оно находится, имеется достаточное сцепление, проскальзывание может быть предотвращено. Однако, если сила трения между поверхностями недостаточна, тяжеловесное тело начнет проскальзывать. В этом случае, можно применить различные методы для увеличения трения, например, использовать шероховатую поверхность или увеличить силу нажима на поверхность.

При изучении тяжеловесных тел и проскальзывания также важно учесть угол наклона поверхности. Чем больше угол наклона, тем меньше сила трения необходима для предотвращения проскальзывания

Это объясняется тем, что вместе с увеличением угла наклона поверхности, увеличивается сила нормальной реакции, которая повышает силу трения.

В целом, понимание трения и проскальзывания тяжеловесных тел имеет большое значение при решении задач в механике и применяется в различных отраслях науки и техники.

§3. Криволинейное движение. Плоскопараллельное движение твердого тела

3.6 Плоскопараллельное движение

Движение твердого тела называется плоскопараллельным, если траектории движения всех его точек являются плоскими кривыми, лежащими в параллельных плоскостях.

Плоскопараллельное движение твердого тела можно представить как суперпозицию поступательного движения и вращения вокруг оси, направление которой не изменяется. Наглядными примерами такого движения являются качение колеса, движение книги без отрыва от стола и т.д.

Для описания положения абсолютно твердого тела при плоскопараллельном движении необходимо задать две декартовые координаты какой-либо точки тела и угол его поворота, то есть плоскопараллельное движение обладает тремя степенями свободы.

Выберем внутри тела две точки A, B; зададим координаты x_A, y_A точки A и угол φ, который образует отрезок AB с направлением оси X. Три числа x_A, y_A и φ однозначно определяют положение тела на плоскости, следовательно, являются его координатами. Зная эти координаты, можно определить положение в пространстве любой другой точки твердого тела путем геометрических построений.

Покажем теперь, как можно найти скорость любой точки твердого тела при плоскопараллельном движении (рис. 36).

причем вектор скорости вращательного движения направлен перпендикулярно отрезку AB и равен по абсолютной величине V_BP = ωr, где r расстояние от точки B до оси вращения.

Рассмотрим катящееся без проскальзывания колесо радиуса R (рис. 37).

Пусть его центр движется со скоростью \(

\vec V\). Найдем скорости некоторых других точек колеса. Для этого представим движение колеса как сумму поступательного движения его центра и вращения вокруг его оси. Так как движение происходит без проскальзывания, то угловая скорость вращения определяется формулой \(

\omega = \frac\). Для точек, находящихся на ободе колеса линейная скорость вращательного движения равна по модулю скорости поступательного движения, так как для них расстояние до оси вращения равно радиусу колеса, поэтому \(

Так как разложение движения на составляющие не является однозначным, можно теперь представить качение колеса как сумму движения точки C и вращения вокруг оси, проходящей через эту точку. Мы показали, что скорость точки C равна нулю, поэтому появляется возможность рассматривать движение колеса как чистый поворот вокруг точки C. Правда, это возможно в течение только бесконечно малого промежутка времени, потому, что в следующий момент точкой касания будет другая точка колеса. Множество точек твердого тела, скорости которых в данный момент равны нулю, образуют мгновенную ось вращения тела. Такая ось существует при любом движении твердого тела. Правда положение этой оси постоянно изменяется, поэтому для вычисления координат точек такое представление движения не дает особых преимуществ. Но для вычисления скоростей точек, рассматривать плоскопараллельное движение как чистый поворот очень удобно.

Рассмотренная задача об определении скоростей точек катящегося колеса может быть легко решена, если рассматривать его движение как поворот вокруг точки C (рис. 38): точка A находится на расстоянии 2R от мгновенной оси вращения, поэтому ее скорость равна V_A = 2Rω = 2V; точка B находится на расстоянии \(

R \sqrt\) от оси, ее скорость \(

V \sqrt\). Направления векторов скоростей также совпадают с полученными ранее.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ​\( t \)​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​\( t \)​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью \( t \), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью \( t \), тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время \( t \). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​\( x=x(t) \)​.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Влияние массы и формы тела

Масса тела определяет силу трения, действующую при движении. Чем больше масса тела, тем больше трения, и тем сложнее его двигать без проскальзывания. Сила трения пропорциональна массе тела и силе, действующей на него.

Форма тела также оказывает влияние на движение без проскальзывания. У тел с определенной формой, например, шаров или колес, есть точки контакта, которые всегда остаются неподвижными при движении. Это позволяет телу перемещаться без проскальзывания по поверхности.

Некоторые тела имеют специальные формы, которые уменьшают трение и облегчают движение без проскальзывания. К примеру, сани имеют широкую площадь контакта с поверхностью, что позволяет им скользить на снегу или льду без трения и проскальзывания.

Важно учитывать массу и форму тела при планировании движения без проскальзывания, чтобы обеспечить эффективность и безопасность данного движения

Примеры движения без проскальзывания в природе и технике

Принцип движения без проскальзывания, основанный на законе трения, широко применяется в природе и технике. Вот несколько примеров:

1. Плавание рыб

Рыбы обладают специальными чешуйками на теле, которые помогают им двигаться в воде без проскальзывания. Эти чешуйки также уменьшают трение и снижают сопротивление воды. Благодаря этому рыбы могут плавать быстро и эффективно.

2. Колеса на автомобиле

Колеса автомобиля имеют резиновую поверхность с протектором, который обеспечивает хорошее сцепление с дорогой. Это позволяет автомобилю двигаться без проскальзывания, улучшает управляемость и повышает безопасность на дороге.

3. Червячная передача

Червячная передача – это механизм, используемый в многих устройствах, таких как шестеренки и винтовые прессы. Она обеспечивает надежную передачу вращения между валами, а также предотвращает проскальзывание.

4. Клешни краба

Клешни крабов обладают специальными структурами, которые позволяют им схватывать и удерживать добычу без проскальзывания. Благодаря этому крабы могут успешно охотиться и защищаться.

5. Лыжи на снегу

Лыжи имеют специальную резиновую или восковую поверхность, которая обеспечивает хороший сцеп с снегом. Это позволяет лыжнику двигаться без проскальзывания и контролировать скорость и направление.

Это лишь некоторые примеры применения принципа движения без проскальзывания. Этот принцип играет важную роль в различных аспектах нашей жизни, от техники и машиностроения до спорта и животного мира.

Трение и его влияние на движение

Существует два вида трения: сухое и вязкое. Сухое трение возникает при непосредственном контакте двух твёрдых поверхностей и зависит от типа материалов, а также от силы нажатия и площади контакта. Вязкое трение, или трение в жидкости, проявляется при движении тела в среде, такой как воздух или вода. Оно зависит от скорости движения и вязкости среды.

Трение может быть полезным или нежелательным в разных ситуациях. В некоторых случаях трение помогает удерживать тело на месте, предотвращает проскальзывание и обеспечивает сцепление между поверхностями. Например, при ходьбе трение между подошвой обуви и поверхностью позволяет нам не скользить. В других случаях трение может препятствовать движению и вызывать истощение энергии. Например, трение между колесами автомобиля и дорожной поверхностью приводит к затратам топлива.

Величина трения зависит от различных факторов, включая характеристики поверхностей, сила нажатия и наличие смазки или масла. Чтобы уменьшить трение, используются специальные смазки, снижающие силу трения между поверхностями.

Важно отметить, что трение не всегда приводит к остановке тела. При низкой площади контакта или наличии подходящей смазки, трение может быть незначительным и не препятствовать движению

Однако, в большинстве случаев трение влияет на движение тела и подчиняется законам Ньютона, которые описывают взаимодействие силы трения, силы тяжести и других сил.

Практическое применение движения без проскальзывания

Движение без проскальзывания имеет широкое практическое применение в различных областях, включая инженерию, транспорт, спорт и другие.

Одно из наиболее распространенных применений такого движения — это проектирование и строительство автомобилей и других транспортных средств. Когда автомобиль движется по дороге без проскальзывания, его колеса имеют надлежащую сцепление с дорогой, что обеспечивает безопасность и эффективность передвижения.

Еще одна область применения движения без проскальзывания — это спорт. Например, в теннисе игроки должны уметь двигаться по корту без проскальзывания, чтобы подать мяч или сделать удар эффективно. Также в беге на треке без проскальзывания участвуют специальные беговые кроссовки с противоскользящей подошвой.

В инженерии движение без проскальзывания используется при разработке и проектировании различных механизмов и машин. Например, при создании конвейерных лент, ремней передачи и ремней с различными приводами и транспортирующими устройствами.

Также движение без проскальзывания применяется при разработке и проектировании систем зажима и крепления, которые обеспечивают безопасность и надежность работы в различных областях, включая строительство, производство и медицину.

В целом, движение без проскальзывания широко используется в разных областях для обеспечения правильной работы и безопасности различных механизмов и устройств.

Как это работает — система динамической стабилизации и контроля тяги Volvo

Система стабилизации работает в три этапа:

Все начинается с датчиков. Они фиксируют скорость вращения колес и как только замечают первые признаки проскальзывания блок управления активирует трекшн-контроль. При этом «мозги» начинают принудительно давить двигатель чтобы снизить тягу, тем самым замедлив вращение колес и вернув им сцепление с дорогой.

Далее специальный модуль оценивает положение руля, при помощи оптического датчика и боковое движение авто. Если электроника поймет, что движение автомобиля не соответствует положению руля, проще говоря, что машина валит боком, внутреннее ведущее колесо начнет притормаживаться.

Система анализирует действия водителя и если он продолжает давить на тормоза, при этом машину все равно «несет», в работу включается ABS, которая не дает колесам заблокироваться и пойти юзом. Эффективность работы антиблокировочной системы ведет к тому, что колеса замедляются, не уходя в занос и не блокируясь.

Тандем двух систем, объединенных в одну, настолько эффективно работает, что водителю по большому счету не нужно тормозить или сбрасывать газ во время заноса, умная электроника сама все сделает. Она отрегулирует тягу и обороты мотора, активирует тормоз таким образом, чтобы машина эффективно и безопасно вышла из заноса, не входя в него. Другими словами, электроника пытается нивелировать пробуксовку колес и любое движение «боком», таким образом, чтобы авто следовало четко по той траектории, которую задал рулем водитель. Если же DSTC поймет, что и этого мало и авто двигается «не так или не туда», в боевую готовность приводится полный спектр функций: активируется ABS, снижаются обороты мотора, и притормаживается одно колесо. Причем первостепенной задачей системы является восстановление сцепления колес с дорогой в кратчайшие сроки.

Методика решения

Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.

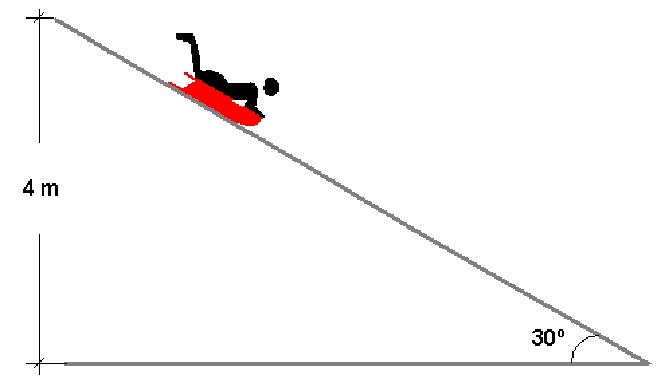
Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:

Где N — реакция опоры, µ — коэффициент трения, не имеющий размерности.

Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:

Здесь φ — это угол наклона плоскости к горизонту.

Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.

В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:

Где F_r — сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, F_r создает следующий момент:

Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.

Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.

Как рассчитать и измерить силу трения

Чтобы понять, как измеряется сила трения, нужно понять, какие факторы влияют на величину силы трения. Почему так трудно двигать холодильник?

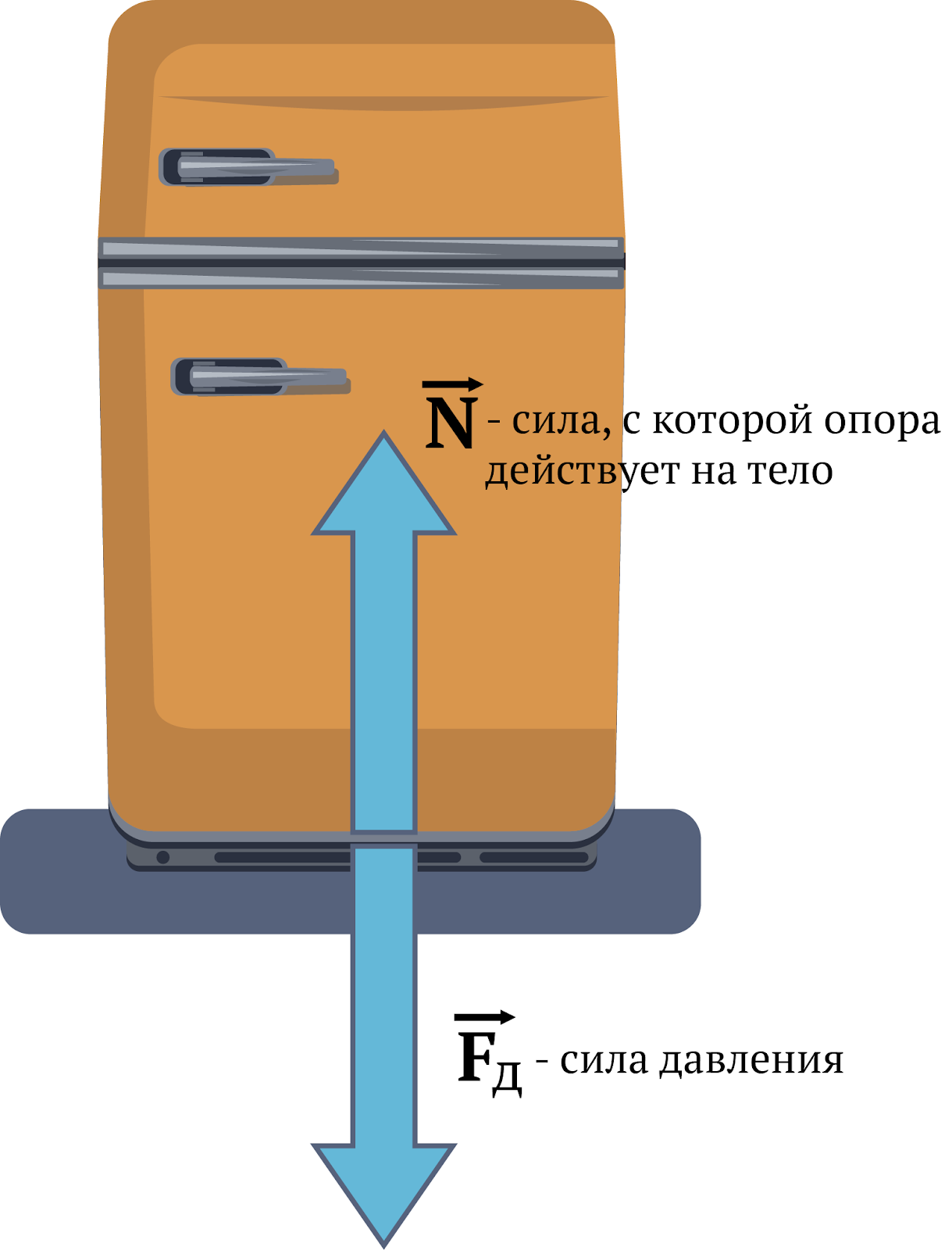
Самое очевидное — его масса играет первостепенную роль. Можно вытащить из него все продукты и тем самым уменьшить его массу, и, следовательно, силу давления холодильника на опору (пол). Пустой холодильник сдвинуть с места гораздо легче!Следовательно, чем меньше сила нормального давления тела на поверхность опоры, тем меньше и сила трения. Опора действует на тело с точно такой же силой, что и тело на опору, только направленной в противоположную сторону.

Сила реакции опоры обозначается N. Можно сделать вывод

Второй фактор, влияющий на величину силы трения, — материал и степень обработки соприкасающихся поверхностей. Так, двигать холодильник по бетонному полу гораздо тяжелее, чем по ламинату. Зависимость силы трения от рода и качества обработки материала обеих соприкасающихся поверхностей выражают через коэффициент трения.

Коэффициент трения обозначается буквой μ (греческая буква «мю»). Коэффициент определяется отношением силы трения к силе нормального давления.

Он чаще всего попадает в интервал от нуля до единицы, не имеет размерности и определяется экспериментально.

Можно предположить, что сила трения зависит также от площади соприкасающихся поверхностей. Однако, положив холодильник набок, мы не облегчим себе задачу.

Ещё Леонардо да Винчи экспериментально доказал, что сила трения не зависит от площади соприкасающихся поверхностей при прочих равных условиях.

Сила трения скольжения, возникающая при контакте твёрдого тела с поверхностью другого твёрдого тела прямо пропорциональна силе нормального давления и не зависит от площади контакта.

Этот факт отражён в законе Амонтона-Кулона, который можно записать формулой:

где μ — коэффициент трения, N — сила нормальной реакции опоры.

Для тела, движущегося по горизонтальной поверхности, сила реакции опоры по модулю равна весу тела:

Принципы движения по инерции

Первый закон Ньютона, или закон инерции, утверждает, что тело находится в состоянии покоя или движется равномерно и прямолинейно, пока на него не действует внешняя сила. Иначе говоря, тело сохраняет свое состояние движения или покоя с постоянной скоростью в отсутствие внешних воздействий.

Второй закон Ньютона, также известный как закон динамики, устанавливает, что изменение движения тела пропорционально силе, приложенной к телу, и происходит в направлении этой силы. Формула второго закона Ньютона выражает, что сила равна произведению массы тела на его ускорение.

Третий закон Ньютона, или закон взаимодействия, утверждает, что действие одного тела на другое всегда сопровождается равной по модулю и противоположно направленной противодействующей силой со стороны второго тела. То есть, если одно тело оказывает силу на другое тело, то второе тело оказывает равную по модулю, но противоположно направленную силу на первое.

Благодаря эти трем законам Ньютона, объекты сохраняют свое движение или покой без внешнего воздействия или при наличии силы с нулевой результирующей силой. Принципы движения по инерции широко применяются в науке и технологии для объяснения и расчета движения тел в различных условиях.

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ​\( a_{цс} \)​, единицы измерения – ​м/с2​.

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​\( T \)​, единицы измерения – с.

где ​\( N \)​ – количество оборотов, ​\( t \)​ – время, за которое эти обороты совершены.Частота вращения – это число оборотов за единицу времени.
Обозначение – ​\( \nu \)​, единицы измерения – с–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​\( v \)​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ​\( \omega \)​, единицы измерения – рад/с .

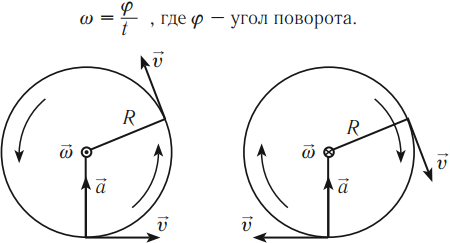
Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к

радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ​\( v_1 \)​, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью \( v_1 \), то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ​\( (m) \)​ равна нулю, мгновенная скорость в верхней точке ​\( (n) \)​ равна удвоенной скорости ​\( v_1 \)​, мгновенная скорость точки ​\( (p) \)​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​\( (c) \)​ – по теореме косинусов.

Без проскальзывания что значит физика

Когда мы говорим «абсолютно гладкая поверхность» — это значит, что между ней и телом нет трения. Такая ситуация в реальной жизни практически невозможна. Избавиться от трения полностью невероятно трудно.

Чаще при слове «трение» нам приходит в голову его «тёмная» сторона — из-за трения скрипят и прекращают качаться качели, изнашиваются детали машин. Но представьте, что вы стоите на идеально гладкой поверхности, и вам надо идти или бежать. Вот тут трение бы, несомненно, пригодилось. Без него вы не сможете сделать ни шагу, ведь между ботинком и поверхностью нет сцепления, и вам не от чего оттолкнуться, чтобы двигаться вперёд.

Трение — это взаимодействие, которое возникает в плоскости контакта поверхностей соприкасающихся тел. Сила трения — это величина, которая характеризует это взаимодействие по величине и направлению.

Основная особенность: сила трения приложена к обоим телам, поверхности которых соприкасаются, и направлена в сторону, противоположную мгновенной скорости движения тел друг относительно друга. Поэтому тела, свободно скользящие по какой-либо горизонтальной поверхности, в конце концов остановятся. Чтобы тело двигалось по горизонтальной поверхности без торможения, к нему надо прикладывать усилие, противоположное и хотя бы равное силе трения. В этом заключается суть силы трения.

Скольжение: определение и особенности

Скольжение — явление, при котором между двумя поверхностями происходит относительное перемещение с одной поверхности на другую. Оно может возникать при соприкосновении твёрдых тел, жидкостей или газов.

Основная особенность скольжения заключается в том, что на поверхности тела, вызывающей скольжение, возникают силы трения. Силы трения препятствуют скольжению и возникают вследствие взаимодействия между атомами или молекулами поверхности тела и атомами или молекулами поверхности, с которой оно соприкасается.

Скольжение может быть различным в зависимости от условий и материалов, соприкасающихся поверхностей. В ряде случаев скольжение происходит легко и практически без сопротивления, например, при скольжении между жидкостью и твердым телом. В других случаях скольжение может быть затруднено или вообще невозможно, например, при скольжении между двумя телами с однородными поверхностями.

Для определения наличия скольжения применяют различные методы, включая измерение силы трения, наблюдение относительного перемещения поверхностей и анализ их состояния после контакта.

Метод определения скольжения	Описание
Измерение силы трения	Путем применения динамометра или других средств измеряется сила, препятствующая скольжению, и на основе полученных данных делается вывод о наличии или отсутствии скольжения.
Наблюдение перемещения поверхностей	Посредством оптических или других средств наблюдается относительное перемещение поверхностей и, если оно присутствует, делается вывод о наличии скольжения.
Анализ состояния поверхностей	После соприкосновения поверхностей они могут оставлять следы или повреждения, которые могут свидетельствовать об относительном перемещении и наличии скольжения.

Выводы о наличии или отсутствии скольжения могут быть важными для понимания и оптимизации различных процессов и явлений, связанных со взаимодействием твёрдых тел, жидкостей и газов.

Определение движения без проскальзывания

Движение без проскальзывания – это физическое явление, при котором объект движется по поверхности без какого-либо скольжения или скручивания. В процессе такого движения точка на поверхности объекта, касающаяся другой поверхности, не проскальзывает и не вращается, а только скользит без усилий и сопротивления.

Чтобы уяснить эту концепцию, можно представить себе пример с автомобилем. Когда автомобиль движется насыщенно против часовой стрелки вокруг круглой дороги, все его шины движутся вперед. Однако, если автомобиль начнет совершать движение с проскальзыванием, т.е. при потере сцепления шины с дорожным покрытием, возникает скольжение, и шины начнут «перемещаться» вдоль дороги.

Движение без проскальзывания возникает при исполнении такой кондиции:

• Силы трения между поверхностями объекта и покрытием должны быть достаточно сильными, чтобы предотвратить скольжение или проскальзывание.
• Силы, воздействующие на объект в процессе его движения, должны быть правильно направлены и сбалансированы между собой.
• Сопротивление объекта вращению должно быть достаточно большим, чтобы предотвратить вращение точки на поверхности объекта.

Важно отметить, что движение без проскальзывания возможно только при выполнении определенных условий. Если сила трения снижается или воздействующие силы становятся неравномерными, может произойти проскальзывание, что может привести к потере контроля и возникновению нежелательных последствий