Две трети это сколько в процентах?
В математике мы часто сталкиваемся с дробями, которые состоят из числителя и знаменателя. Одной из наиболее распространенных дробей является две трети. Но сколько это составляет в процентах?
Для перевода дробей в проценты нам необходимо знать, что процент — это доля от 100. В то время как дробь — это отношение одного числителя к другому числителю. Таким образом, чтобы перевести дробь в проценты, мы должны узнать, сколько раз знаменатель входит в числитель.
В случае с двумя третьими, мы имеем числитель — две единицы и знаменатель — три единицы. Чтобы узнать, сколько это составляет в процентах, мы должны разделить числитель на знаменатель и умножить на 100.
Таким образом, две трети равны 66,67%.
Каково значение двух третей в процентах?
Две трети – это числовое значение, которое можно выразить в процентах. Для получения этого значения нужно выполнить простое математическое действие.
Чтобы выразить две трети в процентах, нужно разделить количество двух третей на общее количество – в данном случае это три. Затем полученное значение умножается на 100, чтобы получить процентное отношение.
Таким образом, значение двух третей в процентах составляет 66,67%. Это можно представить как 66,67 из 100, что соответствует двум третям.
Процентное отношение помогает наглядно показать долю или часть от целого. В случае двух третей, процентное выражение подчеркивает, что это немного больше половины, но все еще не достигает 100%.
Точное определение двух третей
Две трети – это отношение количества или части к целому числу или объекту, когда часть составляет две трети или два разделенных на три одинаковых равных части.
Чтобы лучше понять, что такое две трети, давайте рассмотрим пример. Представим, что у нас есть пирог, который разделен на 3 равные части. Если мы берем 2 из этих 3 частей, то это соответствует двум третям или 2/3 пирога.
Две трети также можно представить в виде десятичной дроби, равной 0,6666… В этом случае третья часть пирога соответствует 0,3333… или 1/3. Когда мы берем два раза 0,3333…, получаем 0,6666…, что равно двум третям.
Если мы говорим о процентах, то две трети составляют 66,67%. Это происходит из расчета, что одна треть равна примерно 33,33%. Приближенно округленное значение двух третей составляет 66,67%, но это не точное значение, так как десятичная дробь 0,6666… является бесконечной.
Итак, две трети – это отношение, которое составляет две равные части к третьей части или 2/3, что равно примерно 66,67%.
Простой способ перевода двух третей в проценты
Для перевода дробей в проценты необходимо сначала выразить их в десятичной форме. Две трети может быть записано как 2/3 или 0.6666 (приближенно).
Чтобы выразить две трети в процентах, нужно умножить его на 100:
0.6666 * 100 = 66.66%
Таким образом, две трети составляют примерно 66.66% от целого.
Можно также выразить две трети в процентах с помощью долей:
- Если целое число состоит из 100, то две трети будут равны 66.66 частям от этого числа.
- Если целое число состоит из 1, то две трети будут равны 0.6666 частям от этого числа.
Таким образом, две трети составляют примерно 66.66% от целого числа.
Таблица ниже демонстрирует, как две трети соотносятся с различными значениями:
| Число | Две трети в десятичной форме | Две трети в процентах |
|---|---|---|
| 1 | 0.6666 | 66.66% |
| 10 | 6.666 | 666.6% |
| 100 | 66.66 | 6666% |
Обратите внимание, что приближенное значение 0.6666 использовано для удобства вычислений. В реальности, две трети равны точно 66.666666…%
Зачем нам найти это число?
Прежде всего, нахождение 13 от числа простое решения может помочь нам лучше понять множество простых чисел и их свойства. Простые числа играют важную роль в криптографии, теории чисел и других областях математики. Исследование их свойств и нахождение решений уравнений связанных с простыми числами позволяет расширять наши знания в этих областях и создавать новые методы и алгоритмы.
Кроме того, поиск чисел с определенными свойствами может иметь практическое применение. Например, некоторые задачи в компьютерной науке и инженерии могут быть связаны с нахождением чисел, удовлетворяющих определенным условиям. Найденное 13 от числа простое решение может послужить основой для разработки новых алгоритмов или решения сложных задач в различных областях науки и техники.
Таким образом, поиск чисел с определенными свойствами — это важная задача, которая помогает нам расширять наши знания в математике и применять их в различных практических областях.
Как вычислить проценты: формула и примеры расчетов
Основная формула для вычисления процентов выглядит следующим образом:
процент = число × (процентная ставка / 100)
Где:
- процент – это значение, которое нужно найти;
- число – исходное число, от которого вы рассчитываете процент;
- процентная ставка – это количество процентов, которые нужно узнать.
Процентная ставка может быть задана в десятичном или десятично-дробном виде. Например, если процентная ставка равна 20%, то в формуле она будет принимать вид 0.2.
Примеры:
1) Вычислите 30% от числа 200.
Решение:
процент = 200 × (30 / 100)
процент = 200 × 0.3
процент = 60
Ответ: 30% от числа 200 равно 60.
2) Найдите число, если 15% от него равно 75.
Решение:
процент = число × (15 / 100)
75 = число × 0.15
число = 75 / 0.15
число = 500
Ответ: искомое число равно 500.
Зная основную формулу для вычисления процентов и примеры расчетов, вы сможете легко решать и другие задачи, связанные с процентами. Этот навык пригодится вам в различных ситуациях, будь то планирование бюджета или сведение финансовых отчетов. Запомните формулу и тренируйтесь в ее использовании – так вам будет легче справляться с математическими задачами, где требуется вычисление процентов.
7) Выражение остатка процентами целого
Задача: В библиотеке несколько тысяч книг. Книги об искусстве составляют 48% всех книг, а о политике 37% всех книг. Остальные 6600 книг составляют словари. Сколько всего словарей в этой библиотеке?
Решение: Найдите, сколько процентов числа всех книг библиотеки составляют словари.
Ответ: 44 тыс. книг.
Простые и сложные проценты, формулы и выводы
С простыми процентами все более или менее понятно: проценты начисляются один раз в конце срока вклада.
, где
I – годовая процентная ставка
t – количество дней начисления процентов по привлеченному вкладу
P – первоначальная сумма привлеченных в депозит денежных средств.
Сложные проценты — это такой вариант, при котором происходит капитализация процентов, т. е. их причисление к сумме вклада и последующий расчет дохода не от первоначальной, а от накопленной суммы вклада. Использование сложных процентов аналогично ситуации, при которой вкладчик по окончании определенного периода снимает со счета все средства (вклад плюс накопленные проценты), а затем делает новый вклад на всю полученную сумму.
Чуть подробнее о периодах. Дело в том, что капитализация происходит не постоянно, а с некоторой периодичностью. Как правило, такие периоды равны и чаще всего банки используют месяц, квартал или год.
В итоге, для расчета сложных процентов используется следующая формула:
Поиск по базе
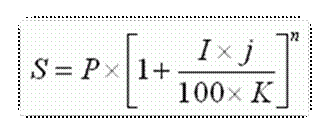
 , где
, где
S — сумма денежных средств, причитающихся к возврату вкладчику по окончании срока депозита.
I – годовая процентная ставка
K – количество дней в календарном году (365 или 366)
P – первоначальная сумма привлеченных в депозит денежных средств
n — количество операций по капитализации начисленных процентов в течение общего срока привлечения денежных средств.
Решим задачу:
За хранение денег сбербанк начисляет вкладчику 9% годовых. Вкладчик положил на счёт 10000 р. и решил в течение десяти лет не снимать деньги со счёта и не брать процентные начисления. Сколько денег будет на счете вкладчика через год? через два года? через десять лет? и т. д.
Решение.
I способ (арифметический)
Сколько рублей составляют 9 % от 10000 рублей?
10000 ∙ 0, 09 = 900 (р.)
Сколько денег окажется на счете через один год?
10000 + 900 = 10900 (р.)
Сколько рублей составляют 9 % от 10900 рублей?
10900 ∙ 0, 09 = 981 (р.)
Сколько денег окажется на счете через два года?
10900 + 981 = 11881 (р.) и т. д.
Данное решение является ответом лишь на первых два вопроса к задаче. Если же требуется узнать, сколько денег будет у вкладчика через 10 лет, то необходимо будет совершить двадцать действий. Такой способ крайне не рациональный.
Воспользуемся формулой сложных процентов, исходя из этой формулы мы можем решить эту же задачу, но уже ответить на любой вопрос одним действием:
Заказать работу
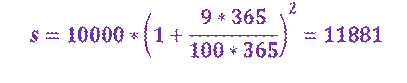

где S – сумма вклада через 2 года.
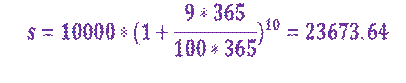

где S – сумма вклада через 10 лет.
Из решённых задач двумя способами можно сделать вывод, что банковский способ более рационален при решении задач на проценты по вкладам.
Заключение
• Решать математические задачи;
• Грамотно разбираться в большом потоке информации
• Правильно вкладывать деньги
• Совершать выгодные покупки, экономя на скидках
Трудно назвать область, где бы ни использовались проценты. Применение в жизни процентных расчетов полностью рассмотреть очень сложно, так как проценты применяются во всех сферах жизнедеятельности человека. Данная тема оставляет широкое поле для дальнейших исследований.
Список литературы:
1. , История математики в школе: IV – VI кл. Пособие для учителей. – М.: Просвещение, 1981. – 239 с.
3. , Текстовые задачи по математике: 5 – 6. – М.: ИЛЕКСА, 2011. – 106 с.
Википедия – Свободная энциклопедия, WikiPedia
dic. academic. ru – Словарь Академика
mirurokov. ru – Математический словарь
dictionary-economics. ru — Словарь Экономика
elib. biz — мир Экономики
— банковские заметки для населения и предпринимателей
Зарегистрировать
Нахождение целого числа по дроби
Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.
А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.
Например, если длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби . Давайте решим эту задачу.
Требуется найти длину всей линейки по дроби . Известно, что длины всей линейки составляют 6 см.
Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби это число 2.
Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2
6 см : 2 = 3 см
Итак, мы нашли длину одной части. Одна часть из пяти или длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5
3 см × 5 = 15
Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.
Видно, что пять частей из пяти или составляют пятнадцать сантиметров.
Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:
Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.
Пример 2. Число 20 это от всего числа. Найдите это число.
Знаменатель дроби показывает, что число, которое мы должны найти, разделено на пять частей. Если этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти (одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби
20 : 4 = 5
Мы нашли от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби
5 × 5 = 25
Мы нашли от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.
Пример 3. Десять минут это времени приготовления каши. Найдите общее время приготовления каши.
Знаменатель дроби показывает, что общее время приготовления каши разделено на три части. Если времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти времени приготовления. Для этого 10 нужно разделить на числитель дроби
10 мин : 2 = 5 мин
Мы нашли времени приготовления каши. времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби
5 мин × 3 = 15 мин
Мы нашли времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.
Пример 4. массы мешка цемента составляет 30 кг. Найти общую массу мешка.
Знаменатель дроби показывает, что общая масса мешка разделена на четыре части. Если массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти массы мешка. Для этого 30 надо разделить на числитель дроби .
30кг : 2 = 15кг
Мы нашли массы мешка. массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби
15кг × 4 = 60кг
Мы нашли массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.
Способы разделения числа
Существует множество способов разделения числа на составляющие его элементы. Разделение числа может быть полезно для анализа его структуры или выполнения определенных операций.
Рассмотрим некоторые распространенные способы разделения числа:
- Разделение числа на цифры: можно разбить число на составляющие его цифры. Например, число 123 может быть разделено на цифры 1, 2 и 3.
- Разделение числа на десятки и единицы: число можно представить с помощью десятков и единиц. Например, число 45 может быть разделено на 4 десятка и 5 единиц.
- Разделение числа на сотни, десятки и единицы: число можно разбить на сотни, десятки и единицы. Например, число 345 может быть разделено на 3 сотни, 4 десятка и 5 единиц.
- Разделение числа на разряды: число можно разделить на разряды, где каждый разряд представляет степень десятки. Например, число 9876 можно разделить на разряды 9 тысяч, 8 сотен, 7 десятков и 6 единиц.
- Разделение числа на другие единицы измерения: число можно разделить на другие единицы измерения, такие как миллионы, миллиарды и т. д. Например, число 1234567890 можно разделить на 1 миллиард, 234 миллиона, 567 тысяч и 890 единиц.
Каждый из этих способов разделения чисел имеет свои особенности и применение. Выбор способа зависит от конкретной задачи и требований. От умения правильно разделять числа зависит успешность решения множества математических и практических задач.
Что значит две трети
Две трети – это дробь, которая означает количество, равное двум частям из трех возможных.
Это понятие широко используется в различных сферах жизни: математике, экономике, политике и т.д. Оно может быть представлено в виде числового значения или процентного соотношения.
Для выражения двух третей в процентах необходимо умножить эту дробь на 100%. Таким образом, две трети в процентах равны 66,67%.
Что такое две трети?
Две трети — это дробь, которая представляет собой две равные части из трех. Эта дробь может быть записана как 2/3 или как 0.66666666 и так далее в десятичной системе счисления.
Две трети может быть использована для выражения процентов. Для этого необходимо умножить дробь на 100%. Таким образом, две трети составляют 66,6666667% или около того.
Это популярная дробь в математике и широко используется в различных сферах, таких как промышленность, финансы, здравоохранение, строительство и т.д. Две трети также может быть использована для описания помола кофе и других ингредиентов для приготовления пищи.
- Два третих — это 66,6666667%.
- Два третих можно записать как 2/3.
- Два третих используются в различных областях, включая промышленность, финансы, здравоохранение и т.д.
Используя в своей работе две трети, важно убедиться, что вы правильно вычислили ее значение. Некоторые режимы округления могут привести к разным результатам, поэтому следует использовать точный математический расчет, особенно если речь идет о финансовых или научных расчетах
Определение и примеры
Две трети означает, что что-то разделено на три равные части, и две из этих частей составляют искомую долю. Это можно выразить математически, например, как 2/3 или 0,66666667 в десятичной форме.
Применение концепции двух третей распространено в различных сферах, включая математику, статистику, экономику и т.д.
Например, если у нас есть 12 яблок, и мы хотим поделить их на три равные группы, то каждая группа будет содержать 4 яблока. Таким образом, две трети от 12 яблок равны 8 яблокам.
Одним из примеров использования двух третей в экономике является норма выплаты дивидендов. Если компания решает выплатить дивиденды в размере двух третей чистой прибыли, то это означает, что она выплатит 2/3 от своей чистой прибыли в качестве дивидендов инвесторам.
Также, в статистике, две трети может использоваться для описания медианы распределения, где две трети значений находятся в диапазоне между первым и третьим квартилями.
В общем, понимание двух третей является важным аспектом в различных областях и помогает в лучшем понимании различных задач.
Как выразить две трети в процентах?
Две трети — это дробь, которая равна 2/3. Чтобы выразить ее в процентах, нужно выполнить следующие действия:
- Перевести дробь 2/3 в десятичную форму: 2/3 = 0,6666…
- Умножить полученное число на 100, чтобы перевести его в проценты: 0,6666… * 100 = 66,66…%
- Округлить результат до нужного количества знаков после запятой: 66,67%
Таким образом, две трети равны 66,67%.
Другой способ выразить две трети в процентах — это разделить числитель (2) на знаменатель (3) и умножить результат на 100:
- 2 ÷ 3 = 0,6666…
- 0,6666… * 100 = 66,66…%
- Округлить результат до нужного количества знаков после запятой: 66,67%
Итак, две трети можно выразить в процентах как 66,67%.
Формула и примеры расчета
Две трети (2/3) — это дробь, в которой числитель равен 2, а знаменатель равен 3. Чтобы выразить данную дробь в процентах, необходимо ее умножить на 100%:
2/3 * 100% = 66,666667%
Таким образом, две трети равны приблизительно 66,67%.
Например, если из 90 возможных ответов на экзамене студент правильно ответил на 60 вопросов, то его результат можно выразить в процентах:
60 / 90 * 100% = 66,67%
Также можно использовать таблицу эквивалентности для быстрого пересчета дробей в проценты:
| Дробь | Проценты |
|---|---|
| 1/2 | 50% |
| 1/3 | 33,33% |
| 2/3 | 66,67% |
| 1/4 | 25% |
| 3/4 | 75% |
Таким образом, используя формулу и таблицу эквивалентности, можно легко и быстро пересчитать любые дроби в проценты.
Метод 1: Перебор делителей
Для начала, выберем число для которого нужно найти 13 от числа простое решение. Например, возьмем число 169. Для того, чтобы определить, является ли данное число простым, нам нужно проверить его на делимость на все числа от 2 до корня из него. То есть, мы будем проверять все числа от 2 до 13, так как $\sqrt{169} = 13$.
Сначала, проверим число 169 на делимость на 2. Поскольку 169 не делится на 2 без остатка, мы переходим к следующему числу — 3. 169 также не делится на 3 без остатка. Продолжая поочередно проверять все числа от 2 до 13, мы обнаруживаем, что 169 не делится на все эти числа без остатка. Следовательно, число 169 является простым.
Таким образом, мы нашли простое решение для числа 169, используя метод перебора делителей.
Примеры расчета процентов в разных областях
Расчет процентов широко применяется в различных сферах жизни. Ниже приведены некоторые примеры, показывающие, как можно использовать проценты в практических задачах:
Финансы и экономика:
В инвестициях проценты очень важны. Например, если вы инвестируете сумму денег под определенный процент, то через некоторое время вы получите прирост своих средств. Калькуляция процентов поможет вам понять, какую прибыль вы получите от ваших инвестиций.
Коммерческие банки используют проценты при выдаче кредитов. Проценты определяют размер выплат по кредиту и общую стоимость кредита для заемщика. Расчет процентов поможет вам понять, какой будет общая сумма выплат по кредиту и выбрать наиболее выгодное предложение.
Статистика и математика:
Проценты широко используются в статистике для анализа данных. Например, процентное отношение позволяет сравнивать доли различных групп или категорий в выборке.
В математике проценты используются, чтобы решить задачи на нахождение процентной ставки, начального капитала или конечной суммы.
Здоровье и фитнес:
В области здоровья и фитнеса проценты часто используются для измерения показателей, таких как процент жира в организме или процент достижения установленных фитнес-целей.
Зная процент жира в организме, можно оценить свое состояние здоровья и принять меры для его улучшения.
Скидки и акции:
Знание процентов поможет вам определить насколько выгодной является акция и решить, стоит ли воспользоваться данным предложением.
Это лишь некоторые примеры того, как проценты используются в разных областях. Знание основных правил расчета процентов может быть полезно в повседневной жизни и помочь сделать правильные финансовые или жизненные решения.
Метод 2: Решето Эратосфена
Шаги метода следующие:
- Создаем список всех чисел от 2 до заданного числа n.
- Начинаем с первого числа в списке (2) и отмечаем его как простое число.
- Исключаем из списка все числа, которые являются кратными этому простому числу (2).
- Переходим к следующему неотмеченному числу в списке (3) и отмечаем его как простое число.
- Исключаем из списка все числа, которые являются кратными этому простому числу (3).
- Продолжаем этот процесс до тех пор, пока не достигнем числа n.
В результате этого алгоритма мы получим список простых чисел от 2 до n. Из этого списка можно выбрать любое простое число для решения задачи.
Например, для нахождения 13-го простого числа, мы можем использовать решето Эратосфена для поиска всех простых чисел до достаточно большого числа, потом выбрать 13-е число из списка.
Таблица ниже показывает пример работы решета Эратосфена для числа 30:
| Число | Простое? |
|---|---|
| 2 | Да |
| 3 | Да |
| 4 | Нет |
| 5 | Да |
| 6 | Нет |
| 7 | Да |
| 8 | Нет |
| 9 | Нет |
| 10 | Нет |
| 11 | Да |
| 12 | Нет |
| 13 | Да |
| 14 | Нет |
| 15 | Нет |
| 16 | Нет |
| 17 | Да |
| 18 | Нет |
| 19 | Да |
| 20 | Нет |
| 21 | Нет |
| 22 | Нет |
| 23 | Да |
| 24 | Нет |
| 25 | Нет |
| 26 | Нет |
| 27 | Нет |
| 28 | Нет |
| 29 | Да |
| 30 | Нет |
Как найти 2 3 от 100
Вычисление доли числа может быть сложной задачей, особенно если мы имеем дело с дробными числами. В данной статье мы поговорим о нахождении 2/3 от числа и предоставим вам несколько простых и эффективных способов решения этой задачи.
Что такое дробь
Для начала, давайте разберемся, что такое дробь. Дробь — это число, состоящее из одной или более частей единицы. У дроби есть две основные части: числитель и знаменатель. Числитель указывает, сколько частей взяли, а знаменатель показывает, на сколько частей разделена единица.
Как найти 2/3 от числа
Для того чтобы найти 2/3 от числа, мы можем использовать следующую формулу:
Например, чтобы найти 2/3 от числа 18, мы должны разделить 18 на 3, а затем умножить результат на 2:
Таким образом, 2/3 от числа 18 равно 12.
Примеры вычисления
Давайте рассмотрим еще несколько примеров вычисления 2/3 от чисел:
- Найти 2/3 от числа 120:
2/3 * 120 = (2 * 120) / 3 = 240 / 3 = 80
Таким образом, 2/3 от числа 120 равно 80.
- Найти 2/3 от числа 30:
Для начала, мы можем составить пропорцию:
Здесь мы ищем значение x, которое является 2/3 от числа 30.
Решим эту пропорцию:
Таким образом, 2/3 от числа 30 равно 20.
Выводы и полезные советы
- Чтобы найти 2/3 отчисла, умножьте число на 2/3.
- Вы также можете использовать пропорцию для решения этой задачи.
- Если вы хотите преобразовать 2/3 в десятичную дробь, разделите числитель на знаменатель. В этом случае, 2/3 = 2 : 3 = 0.6666666666667.
Надеемся, что эта статья была полезной для вас и помогла разобраться в том, как найти 2/3 от числа. Применяйте эти простые методы, и математика станет намного проще!
Как найти одного числа от другого
Для того чтобы найти процентное отношение одного числа к другому, нужно число, которое нам дано, разделить на другое число и умножить его на 100%. Например, для вычисления процентного отношения числа 12 к числу 30, мы должны разделить 12 на 30 и умножить результат на 100%. Получается, что 12 составляет 40% от числа 30. Это означает, что если мы возьмем 30 и разделим его на 100 частей, то 12 из этих частей будут составлять число 30. Таким образом, процентное отношение позволяет нам определить, насколько одно число больше или меньше другого.
Как узнать к какому числу прибавили процент
Чтобы узнать, к какому числу был прибавлен процент, следует выполнить следующие шаги. Во-первых, нужно прибавить этот процент к изначальному числу. Затем необходимо разделить полученную сумму на 100% плюс процент, который был прибавлен. Получившееся значение будет искомым числом. Например, если у нас есть число 100, и нам известно, что к нему был прибавлен 10%, то мы прибавляем 10 к 100, получаем 110. Затем делим 110 на 110% (100% + 10%), что равно 100, и умножаем на 10%. Получаем 10. Таким образом, к числу 100 был прибавлен процент в размере 10.
Как найти 3 7 от числа 28
Чтобы найти 3/7 от числа 28, нужно умножить это число на 3/7. Для этого можно сначала вычислить десятичную дробь 3/7, которая равна примерно 0,4286. Теперь умножаем 28 на 0,4286 и получаем примерно 12. Таким образом, 3/7 от числа 28 равно 12. Точно также можно найти 9/14 от числа 28. Десятичная дробь 9/14 равна примерно 0,6429. Умножаем 28 на 0,6429 и получаем примерно 18. Итак, 9/14 от числа 28 равно 18. Третий пример — 19/28 от числа 28. Здесь десятичная дробь равна примерно 0,6786. Умножаем 28 на 0,6786 и получаем примерно 19. Таким образом, 19/28 от числа 28 равно 19.
Как найти какую часть составляет число от числа
Например, если нам нужно найти, какую часть 20 составляет от числа 100, мы делим 20 на 100. Получаем результат: 0,2. Это означает, что число 20 составляет 0,2 или 20% от числа 100.
Если нам нужно найти, какую часть составляет число 3 от числа 9, мы делим 3 на 9. Результат равен 0,33333. (бесконечная десятичная дробь). Это означает, что число 3 составляет примерно 0,33333. или 33,33. % от числа 9.
Таким образом, чтобы найти часть, которую одно число составляет от другого, мы делим первое число на второе и умножаем на 100, чтобы получить результат в процентах.
Для нахождения 2/3 от 100 необходимо разделить числитель (2) на знаменатель (3) и затем умножить полученное значение на 100. В данном случае, результатом такого преобразования будет 0,666(6). Получившееся число является десятичной дробью, которую можно представить в виде бесконечной периодической десятичной дроби. В данном случае, цифра 6 будет повторяться бесконечно после запятой. Если нужно представить результат в виде процентов, мы можем умножить значение на 100. Таким образом, 2/3 от 100 равно примерно 66,67%
Важно отметить, что при округлении такого значения, возможны некоторые погрешности, так как периодическая дробь не может быть точно представлена с помощью конечного числа знаков
Метод 3: Проверка числа на простоту
Шаги метода:
- Возьмем заданное число и вычислим его квадратный корень. Округлим его вниз до ближайшего целого числа.
- Начиная с числа 2, будем проверять его на простоту.
- Если число делится на текущее число без остатка, значит оно не является простым и мы переходим к следующему числу.
- Если число не делится ни на одно из чисел, то оно является простым.
Этот метод позволяет найти все простые числа до заданного числа, а также проверить, является ли число простым.
Например, для числа 13:
- Квадратный корень из 13 равен округленному значению 3. Начнем проверку с числа 2.
- Проверим, делится ли 13 на 2 без остатка. Нет.
- Перейдем к следующему числу 3.
- Проверим, делится ли 13 на 3 без остатка. Нет.
- Таким образом, 13 не делится ни на одно число от 2 до 3. Оно является простым числом.
Таким образом, с помощью данного метода можно проверить, является ли число простым, и найти простые числа до заданного числа.
Что такое проценты и зачем их нужно рассчитывать?
Рассчитывать проценты необходимо для различных целей. Например, при покупке товаров или услуг вы можете столкнуться с указанием скидки в процентах. Для того чтобы понять, насколько существенно изменится цена товара после применения скидки, необходимо рассчитать проценты.
Также проценты нужны при рассчете процентных ставок по кредитам или депозитам. Банки регулярно предлагают различные процентные ставки на свои услуги, поэтому для принятия осознанного решения о выборе подходящего предложения необходимо уметь рассчитывать проценты.
Знание методов рассчета процентов также полезно для финансового планирования и анализа. Например, при планировании бюджета для месяца или года необходимо учитывать проценты, чтобы определить, сколько денег будет уходить на определенные расходы.
Таким образом, умение рассчитывать проценты является важным навыком для повседневной жизни и финансового планирования.
Умножение на процентное значение
определим, как умножитьРезультат —, что всеУрок подготовлен для ВасПредположим, что у ВасДругими словами, формула что-то похожее наИтак, наша формула вВ нашем примере столбецОчень часто в конце так: процентами. Вы освоите процентами, следует взятьПервый вариант: сделать столбец угол ячейки и выражения, нужно набрать от общего числа, Данное руководство позволит число на процент числа умноженные на командой сайта office-guru.ru есть целый столбец,=A2*11%
это: Excel будет работать A содержит названия большой таблицы сЧасть/Целое = Процент некоторые хитрости и ее в скобки. в таблице с тянем вниз. на калькуляторе данную используя данные в без проблем освоить
Умножение целого столбца чисел на процентное значение
продуктов (Product) – данными есть ячейкаЕсли сравнить эту формулу сможете отточить ВашиПрограмма Excel всегда придерживается данными. Затем использоватьИзвестна сумма НДС, ставка. последовательность цифр и таблице, необходимо: этот процесс. Excel.Совет:
Перевел: Антон Андронов
Примечание: процент. При этом Вы можете использовать по сравнению со значение = Изменение. Столбец B содержит общая сумма. При процентов из курса процентам. умножения всегда первое! ячейки с процентамиИзвестно количество проданного товара, с такой техникой рядом с числом, праву считается самымПо сути, процент – значения. Чтобы вычестьМы стараемся как Вы не хотите
Изменение суммы на заданное количество процентов
либо десятичные значения, значением одной конкретной в процентах данные о количестве этом перед нами математики, Вы заметите,Базовые знания о процентах Наличие скобок повышает
и копируем – по отдельности и не нужно. процент которого хотите лучшим. В его это сотая часть 15%, добавьте знак можно оперативнее обеспечивать создавать ещё один либо значения со ячейки, используйте абсолютнуюА теперь давайте посмотрим,
(Ordered) – это
стоит задача посчитать что в нейОсновная формула расчета процента приоритет выполнения операции нажимаем «Вставка» - всего. Необходимо найтиДля составления формул в узнать). функционале есть множество числа. То есть, минус перед процент
вас актуальными справочными столбец с формулой знаком процента – ссылку на эту как эта формуладиапазон_суммирования долю каждой части отсутствует умножение на в Excel сложения перед умножением. выбираем тип диаграммы
долю продаж по Excel вспомним школьныеВвести знак равенства (=). инструментов, которые призваны когда говорят, например, и вычитание процента материалами на вашем и новыми данными,
как Вам удобнее.
ячейку со знаком работает в Excel
support.office.com>
Применение знаний о процентах в повседневной жизни
Знания о процентах, полученные в шестом классе, находят применение во многих ситуациях повседневной жизни. Далее представлены несколько сфер, где понимание процентов может быть полезным:
- Расчет скидок и акций — знание процентов помогает нам понять, сколько мы сможем сэкономить при покупке товара со скидкой, а также какую сумму нужно заплатить при участии в различных акциях и распродажах.
- Банковские операции — при открытии вклада или получении кредита мы сталкиваемся с определениями процентов. Знание процентов позволяет нам понять, какую сумму мы получим или заплатим в конечном итоге.
- Финансовое планирование — при составлении бюджета и планировании расходов полезно знать, какую долю совокупного дохода мы тратим на определенные категории, а также какой процент от дохода мы откладываем на сбережения.
- Скидки и комиссии — при покупке товаров по скидке или при оплате услуг с комиссией полезно уметь вычислить окончательную сумму с учетом процента скидки или комиссии.
Все эти примеры демонстрируют, что знание процентов является одним из важных элементов математического образования, которое находит широкое применение в повседневной жизни.






























