Работа с функциями: обнаружение максимума и минимума

5.2. Интегралы от функций с бесконечными разрывами

Если

непрерывна на

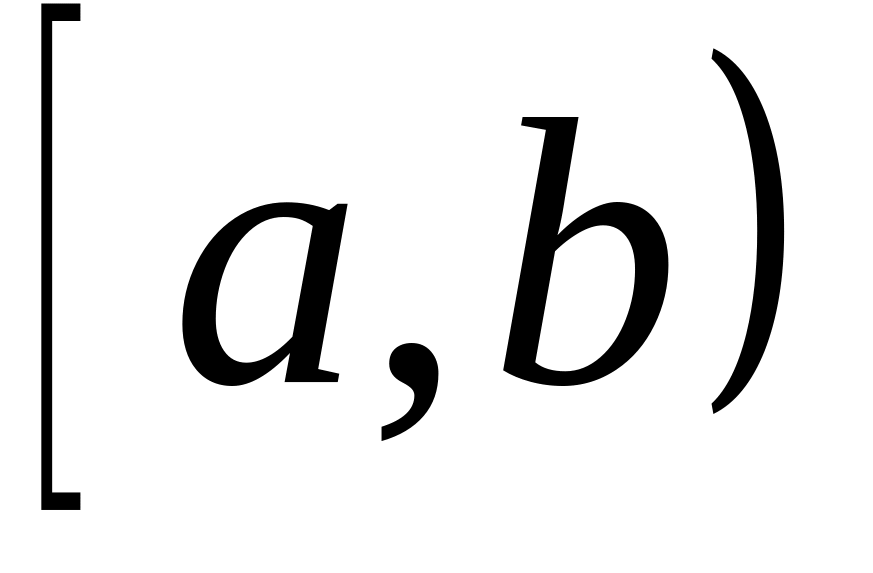
и неограниченна в любой окрестности
точки

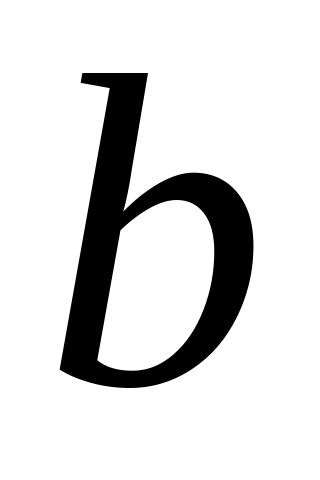
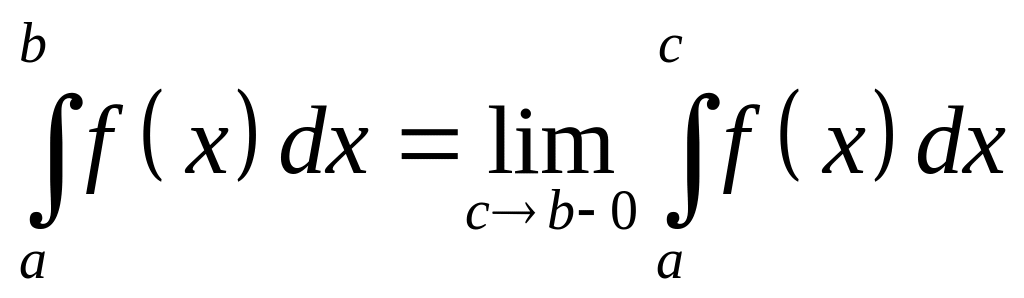
называется
несобственным интегралом от

.
Если предел существует и конечен,
интеграл называется сходящимся, если
нет, то расходящимся. Если

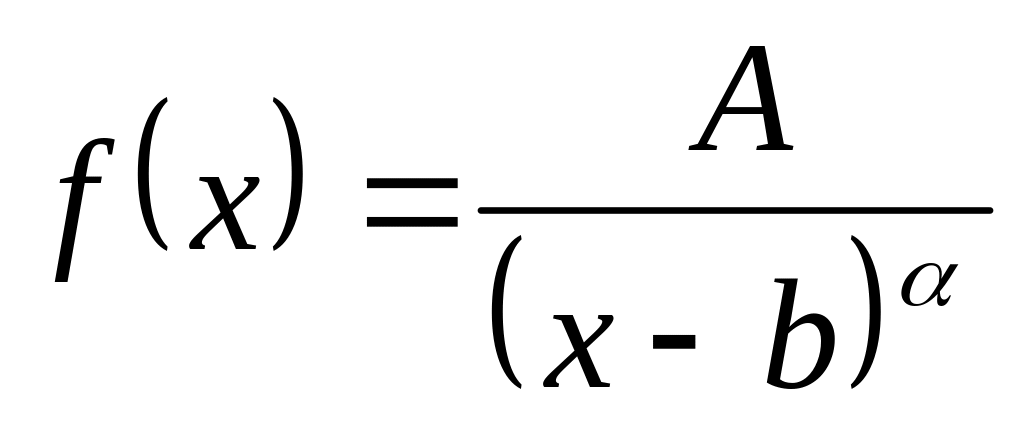
при

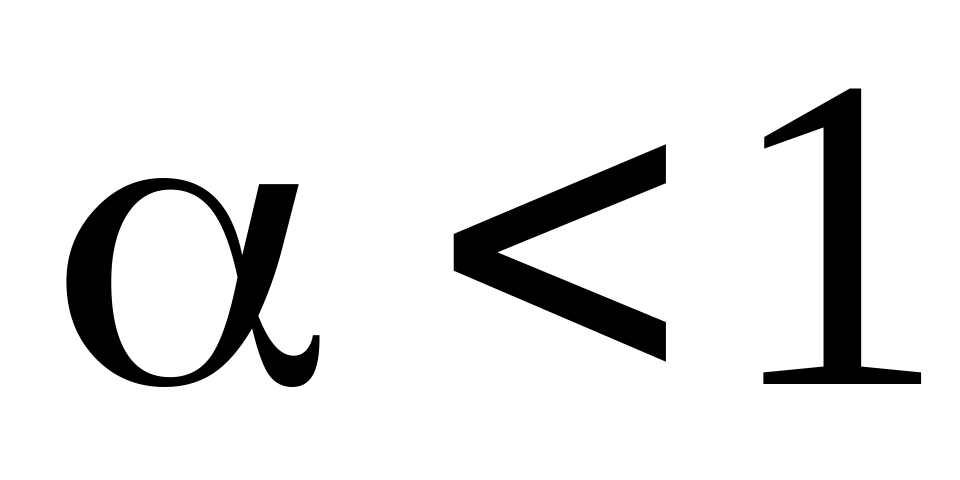
интеграл сходится, при

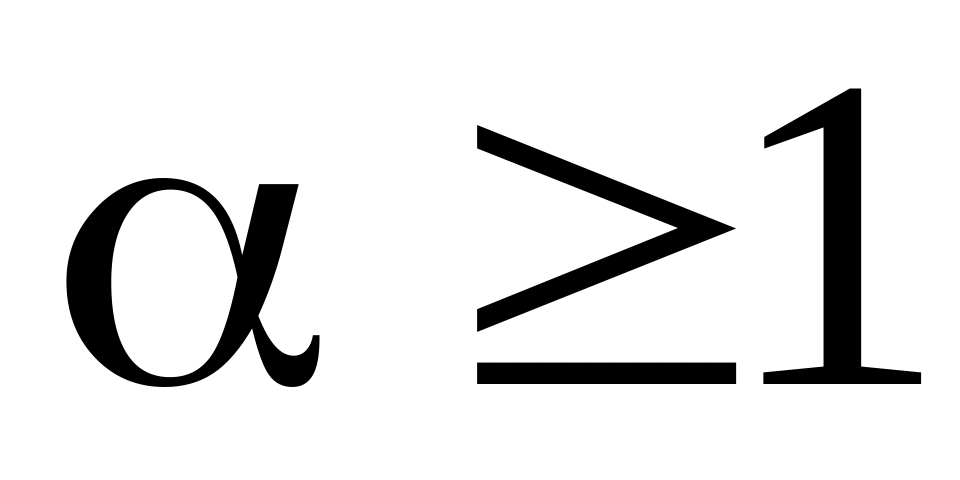
интеграл расходится.

Примеры:

5.2.1. Исследовать
на сходимость интеграл.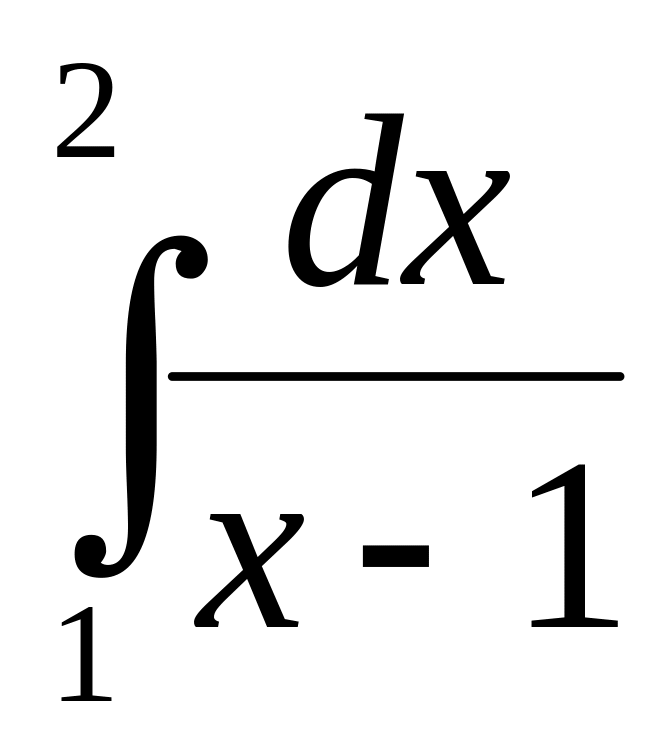

 Так как
подынтегральная функция

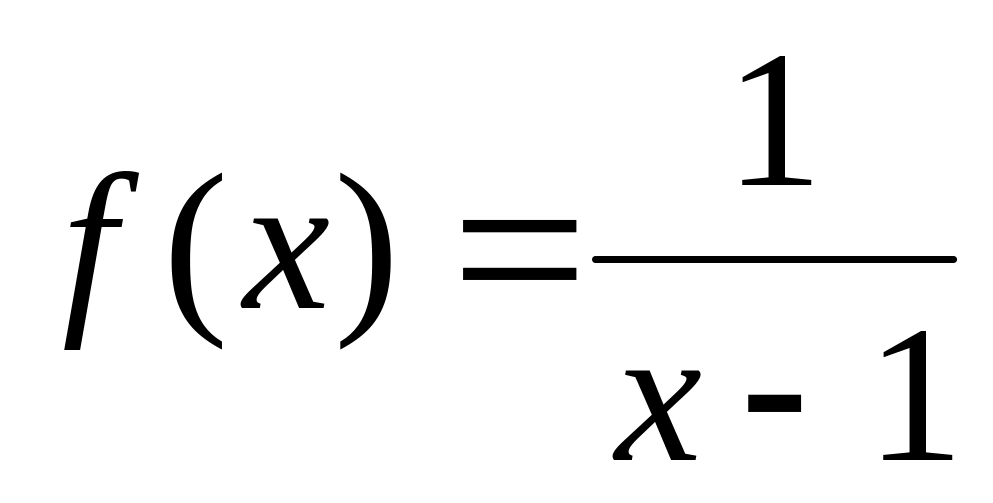
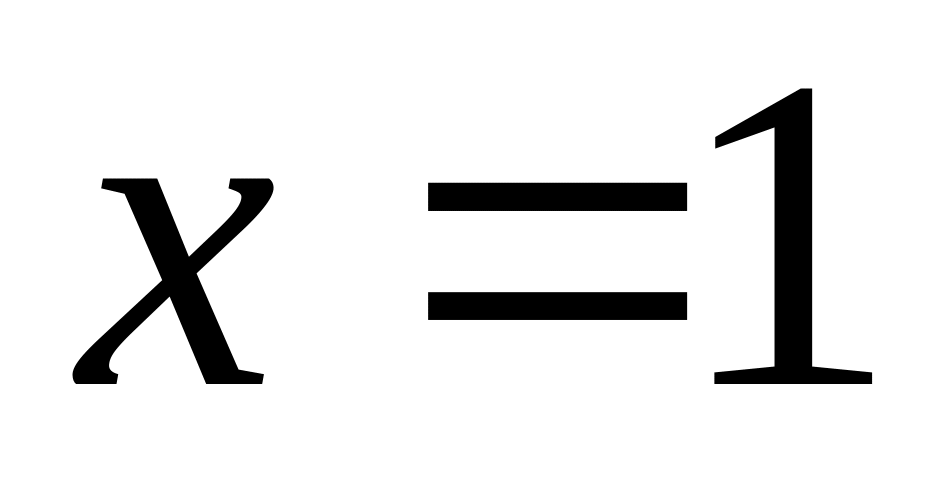
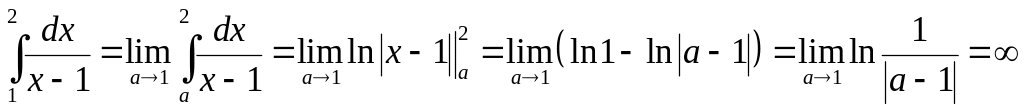
Конечного предела
не существует, значит, интеграл расходится.
◄

5.2.2.
Исследовать на сходимость интеграл

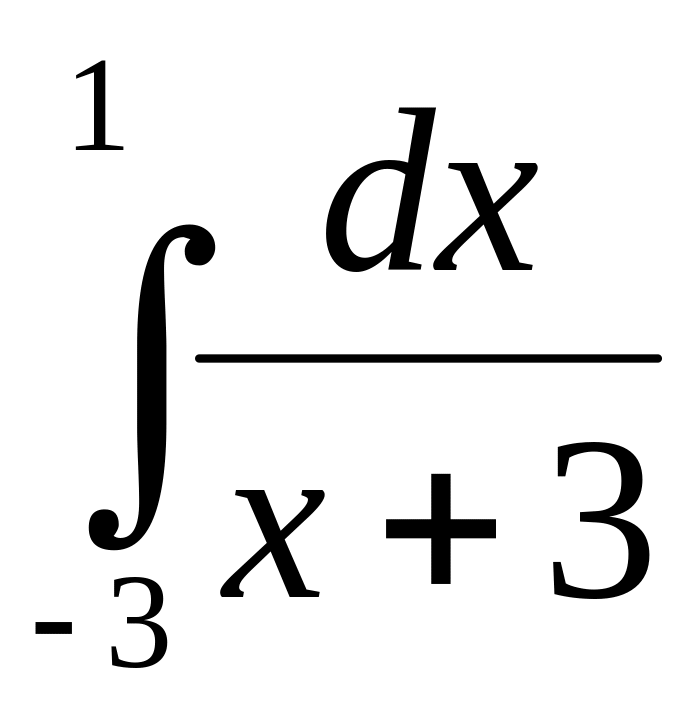
 Так как
подынтегральная функция

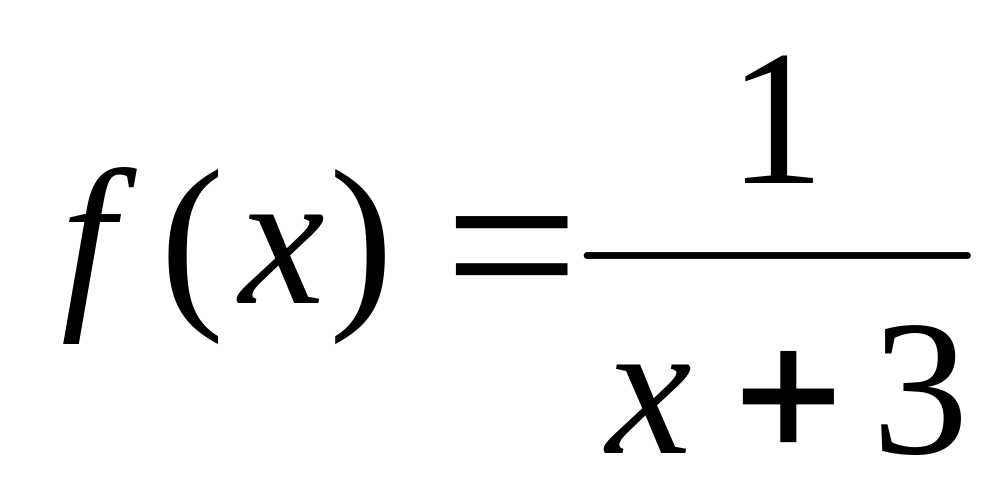
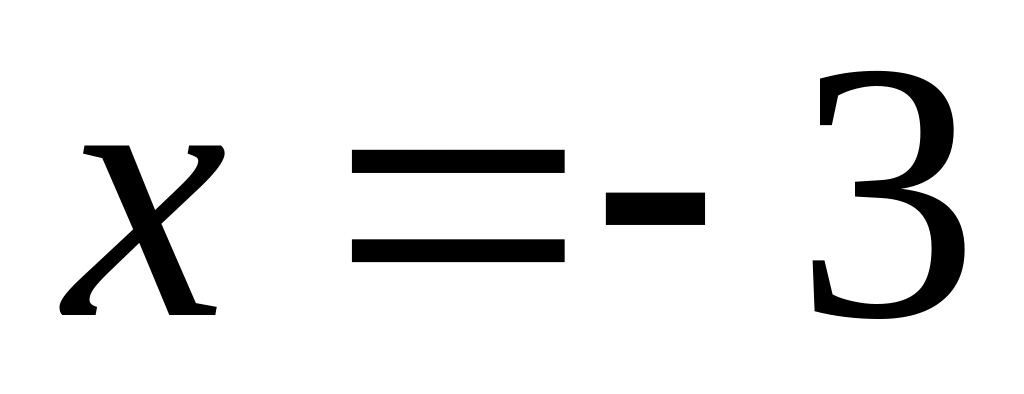
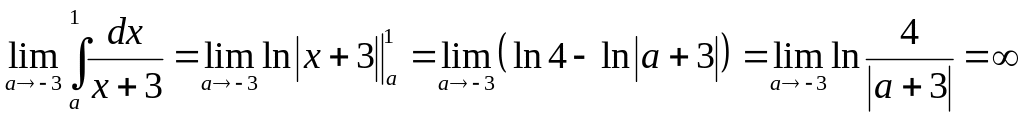
Конечный предел
равен бесконечности. Значит, интеграл
расходится. ◄

5.2.3. Исследовать
на сходимость интеграл

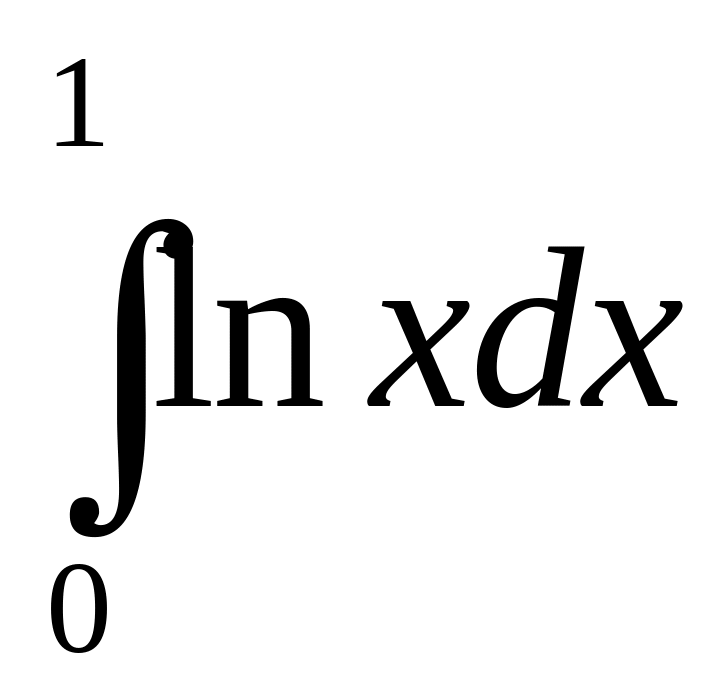
 Так как
подынтегральная функция

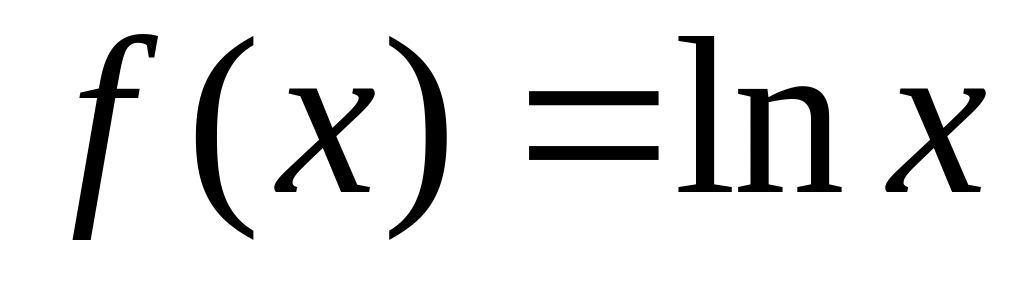
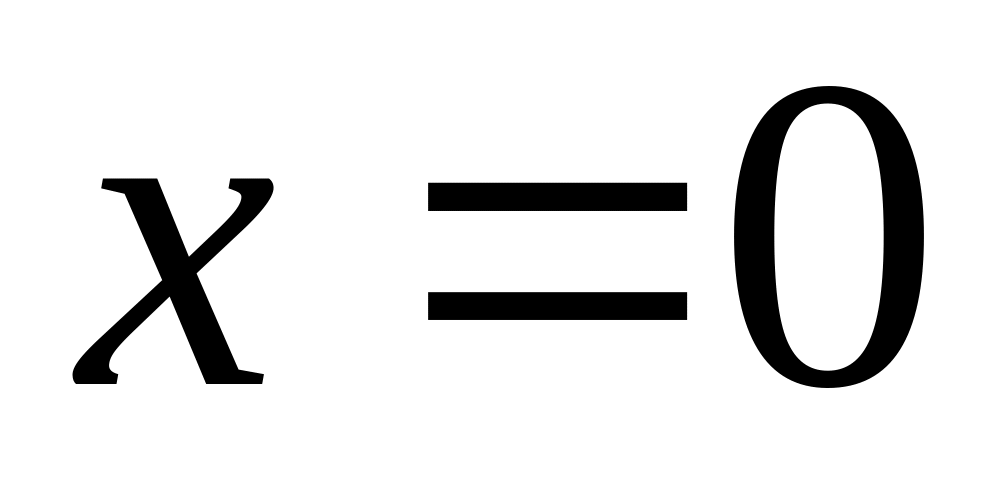
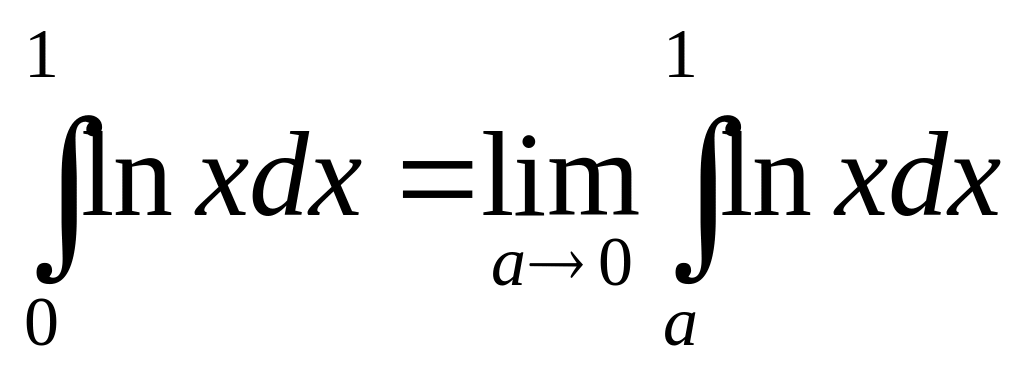
Применим
интегрирование по частям. Пусть

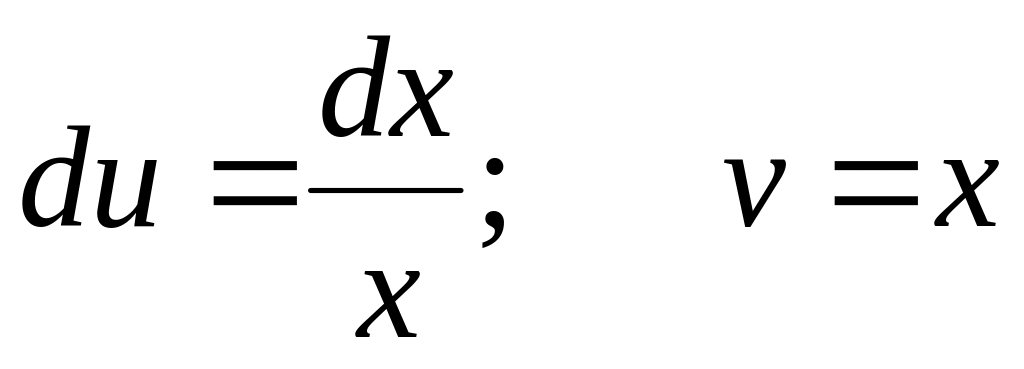
И первоначальный
интеграл примет вид:

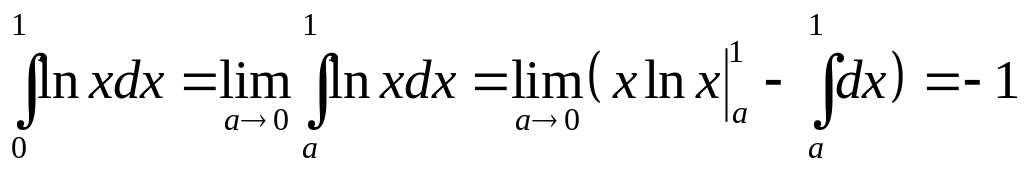
Предел конечен.
Поэтому интеграл сходится.
◄

5.2.4. Исследовать
на сходимость интеграл

 Имеем

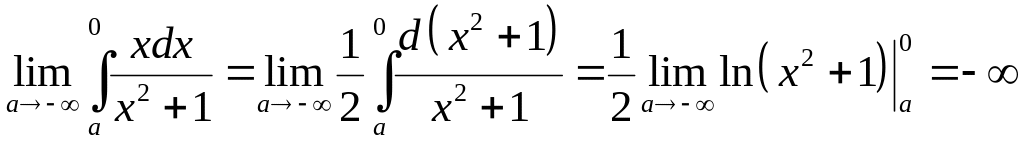
Предел бесконечен.
Следовательно, интеграл расходится.
◄

Прямоугольная и трапецеидальная формулы

Прямоугольная формула

Прямоугольная формула — это метод численного интегрирования, который использует вертикальные прямоугольники, чтобы аппроксимировать подынтегральную функцию. Этот метод называется прямоугольным, потому что каждый прямоугольник имеет одинаковую ширину и высоту на всей длине интервала интегрирования.

Преимуществом прямоугольной формулы является простота. Она легко вычисляется и может быть использована для быстрого приближенного вычисления площадей и численных интегралов.

Трапецеидальная формула

Трапецеидальная формула — это метод численного интегрирования, который использует трапеции, чтобы аппроксимировать подынтегральную функцию. Этот метод называется трапецеидальным, потому что каждая трапеция имеет разную высоту на интервале интегрирования.

Преимуществом трапецеидальной формулы является более точное приближение подынтегральной функции, поскольку каждая трапеция имеет разную высоту. Она может использоваться для решения более сложных численных интегралов и имеет более точный результат, чем прямоугольная формула.

Формула	Точность
Прямоугольная	Не очень точная
Трапецеидальная	Более точная

Вычисление определенного интеграла

Чтобы вычислить определенный интеграл, нужно:

1. Задать функцию. Функция должна быть непрерывна на заданном отрезке.
2. Задать пределы интегрирования. Определить начальную и конечную точки отрезка, на котором будет вычисляться интеграл.
3. Разбить отрезок на маленькие части. Это можно сделать, например, с помощью равномерного или неравномерного разбиения.
4. Вычислить площади прямоугольников. Для каждой части отрезка вычислить площадь прямоугольника, который полностью покрывает область под графиком функции.
5. Сложить площади прямоугольников. Полученные площади прямоугольников нужно сложить. Это и будет приближенное значение определенного интеграла.

Важно помнить, что чем меньше шаги разбиения и больше их количество, тем точнее будет значение определенного интеграла. Интегралы широко применяются в математике, физике, экономике и других науках для решения различных задач

Они помогают понять и описать различные явления и процессы в природе и обществе

Интегралы широко применяются в математике, физике, экономике и других науках для решения различных задач. Они помогают понять и описать различные явления и процессы в природе и обществе.

Метод производной

Идея метода заключается в том, что при экстремуме функции производная равна нулю, то есть точка экстремума является решением уравнения f'(x) = 0. Таким образом, для нахождения экстремума нужно найти корни производной функции.

Для применения метода производной необходимо выполнить следующие шаги:

1. Найти производную функции f'(x).
2. Решить уравнение f'(x) = 0 для нахождения корней.
3. Для каждого найденного корня проверить его тип, используя вторую производную f»(x).
4. Определить, является ли точка экстремумом и какого типа (максимум или минимум).

При применении метода производной важно учитывать, что функция должна быть непрерывной и дифференцируемой в рассматриваемом интервале. Также нужно помнить о возможности наличия точек перегиба, где производная может быть равной нулю, но не является экстремумом

Метод производной позволяет находить экстремумы функции по графику с использованием математического анализа и представляет удобный инструмент для определения максимальных и минимальных значений функции.

Как найти среднее значение функции на отрезке

«Вы, профессор, воля ваша, что-то нескладное придумали! Оно, может, и умно, но больно непонятно. Над вами потешаться будут»

«Мастер и Маргарита», Булгаков М. А.

Жизнь у всех разная и проявляется это ещё и в том, что источники информации, с которыми мы имеем дело, тоже у всех различны. Кроме этого, далеко не каждые сведения оставляют нас равнодушными, не вызывая совершенно никаких эмоций или мыслей. При этом иногда сочетание данных из двух источников может побуждать к весьма своеобразным умозаключениям.

Есть у меня одна книга – пособие для учителя информатики . Не помню, как она у меня появилась – может купил, а может мне её кто-то подарил – однако в школе она мне как-то пригодилась в освоении языка Basic, программы на котором мы тогда собственноручно набивали на болгарских машинах «Правец 8A». Именно из этой книги я когда-то впервые узнал, что помимо так называемого среднего арифметического для нескольких чисел бывает, например, ещё и среднее квадратическое.

На первом курсе (1999-2000 гг.) университета, на лекциях по высшей математике, когда мы проходили определённые интегралы, была упомянута так называемая «теорема о среднем» . И вот это-то, в комбинации с сидящими в памяти сведениями из упомянутой книги, почему-то отозвалось в мозгах вопросом: «А какое именно среднее имеется в виду в теореме: арифметическое, кубическое или какое-нибудь другое?». Ну а раз возник вопрос – можно попытаться найти и ответ. Поиск сей вскоре привёл меня к тому, что, собственно, и составляет основу материала данной заметки. Свои измышления я условно назвал «теорией средних» и достаточно долгое время они хранились у меня в виде конспекта. Теперь же результаты этой «мозговой гимнастики» я выложил в сеть по следующим соображениям. Во-первых, если на этот материал наткнётся математик, то, думается, это сможет его повеселить. Во-вторых, мне слабо верится, что никто из профессиональных математиков в своих работах не додумался до чего-то подобному тому, что изложено здесь. В связи с этим мне особенно интересно было бы узнать, чьи это результаты мной, вероятно, «переоткрыты» – к сожалению, я не располагаю возможностью и временем это выяснить самостоятельно, но буду очень благодарен за сведения об этом.

I. Типы средних (введение)

Пусть у нас имеется множество из n чисел x ₁, x ₂. x_n .

а) Среднее арифметическое этих чисел:

б) Среднее квадратическое:

в) Среднее кубическое:

г) Если ни одно из чисел рассматриваемого множества не равно нулю, то для них можно вычислить среднее гармоническое :

II. Средние значения функции на замкнутом числовом промежутке

Рассмотрим непрерывную функцию y = f ( x ), определённую на отрезке . Разобьём на n равных частей величиной Δ x_i =( b – a )/ n . Теперь внутри каждого отрезка разбиения Δ x_i произвольно выберем точку C_i () и вычислим значение функции y = f ( x ) в точке C_i : y_i = f ( C_i ) (Рисунок 1).

Для полученного таким образом множества значений по формулам (1), (2), (3) можно вычислить средние арифметическое, квадратическое и кубическое:

В случае, если f ( x ) на ни в одной точке не обращается в ноль, то по (4) можно вычислить и среднее гармоническое:

Будем теперь увеличивать неограниченно n и найдём пределы выражений (5), (6), (7) и (8) при n →∞. Если эти пределы существуют для рассматриваемой функции y = f ( x ) на отрезке , то назовём их, соответственно, средним арифметическим, средним квадратическим, средним кубическим и средним гармоническим значениями функции y = f ( x ) на отрезке . Введём обозначения:

Для удобства операторы

, , ,

назовём арифией, квадрией, кубинией и гармонией соответственно.

III. Вычисление арифии функции на замкнутом числовом промежутке

Вернёмся к Рисунку 1. Составим для функции f ( x ) интегральную сумму Римана:

Эта сумма при неограниченном возрастании n имеет предел, равный интегралу:

Величина ( b – a ) – длина отрезка – число постоянное, поэтому

Подставим (9) в (13):

Из (14) как раз и следует ответ на возникший у меня вопрос: в теореме о среднем фигурирует именно среднее арифметическое значение функции на отрезке (придуманная мной «арифия»).

IV. Свойства арифии функции на отрезке

Свойство 1 (свойство линейности оператора арифии):

( C ₁ и C ₂ – постоянные числа, f ( x ) и g ( x ) – непрерывные и определённые на функции).

Свойство 2. Если C =const, то

Свойство 3. Если a c b , то

Свойство 4. Если f ( x ) – чётная функция и a > 0, то

Так как f ( x ) – чётная, то

, &nbsp .

Свойство 5. Если f ( x ) – нечётная функция, то

Так как f ( x ) – нечётная, то

,

Домножим обе части этого неравенства на ( b – a ) ( b – a > 0):

V. Вычисление квадрии, кубинии и гармонии функции на отрезке

Пусть g ₁( x )= 2 , тогда

Пусть теперь g ₂( x )= 3 , тогда

Пусть теперь функция y = f ( x ) на ни в одной точке не принимает нулевого значения. Обозначим .

Ищем наименьшее и наибольшее значения функции вместе

Пример 1. Найти наименьшее и наибольшее значения функции на отрезке .

Решение. Находим производную (первое и второе слагаемые — табличная производная 3,
третье — табличная производная 1) данной функции .
Приравняем производную нулю ()
и, решив уравнение, получим две критические точки: и
. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на
концах отрезка и в точке ,
так как точка не
принадлежит отрезку . Эти значения функции — следующие: ,
,
. Из этого следует, что
наименьшее значение функции (на графике ниже обозначено красным), равное -7, достигается на правом конце отрезка — в точке
, а наибольшее (тоже
красное на графике), равно 9,
— в критической точке .

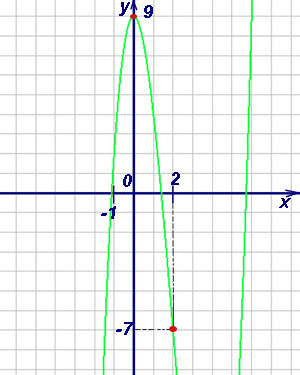
Если функция непрерывна в некотором промежутке и этот промежуток не является отрезком
(а является, например, интервалом; разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок),
то среди значений функции может и не быть наименьшего и наибольшего. Так, например, функция, изображённая
на рисунке ниже, непрерывна на и не имеет
наибольшего значения.

Однако для любого промежутка (закрытого, открытого или бесконечного) справедливо
следующее свойство непрерывных функций.

Если функция непрерывна в промежутке и имеет единственный экстремум, то он
является наименьшим значением в случае минимума и наибольшим — в случае максимума.

Как наименьшее значение функции, так и её наибольшее значение, могут быть найдены
не только в одной точке, принадлежащей заданного интервала, а, как, например, далее — в двух.

Пример 2. Найти наименьшее и наибольшее значения функции на отрезке .

Решение. Находим производную (первое и второе слагаемые — табличная производная 3,
третье — табличная производная 1) данной функции .
Привыкаем к однообразным действиям: приравниваем производную нулю ()
и решение этого уравнения даёт нам три критические точки: ,
и
. Все критические точки
принадлежат отрезку . Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке находим её значения на
концах отрезка и во всех критических точках. Эти значения следующие:

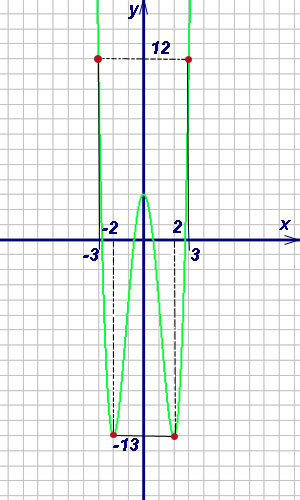
Видим, что функция достигает наименьшего значения, равного -13, в двух точках
и
и наибольшего
значения, равного 12, также в двух точках
и
(то есть на концах отрезка).

Нередки случаи, когда уравнение, полученное от приравнивания производной функции нулю,
не имеет действительных решений. Тогда наименьшее и наибольшее значения функции можно найти только
на концах отрезка. Таков следующий пример.

Пример 3. Найти наименьшее и наибольшее значения функции на отрезке .

Решение. Находим производную (первое слагаемое — табличная производная 2, второе —
табличная производная 5) данной функции .
Приравниваем производную нулю: .
Видим, что это уравнение не имеет действительных корней. Поэтому наименьшее и наибольшее значения
функции можем найти только на концах данного отрезка. Находим значения функции на
концах отрезка:

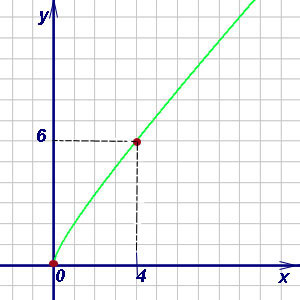
Обе точки, следуя условию, годятся, так что функция достигает наименьшего значения, равного 0, в точке
и наибольшего
значения, равного 6, в точке
.

Неплохо было бы взять и случаи, когда производная функции вычисляется не одним махом,
как в предыдущих примерах. Это мы сейчас и сделаем, решив пример, где требуется найти
производную частного.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 4. Найти наименьшее и наибольшее значения функции на отрезке .

Решение. Находим производную данной функции как :

.

Приравниваем производную нулю,
что даёт нам одну критическую точку: .
Она принадлежит отрезку . Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке находим её значения на
концах отрезка и в найденной критической точке:

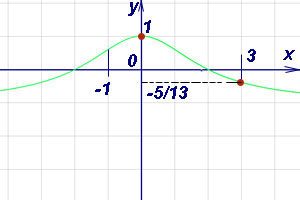
Сравниваем эти значения. Вывод: функция достигает наименьшего значения, равного -5/13,
в точке и наибольшего
значения, равного 1, в точке
.

Определения и теоремы

Функция, непрерывная на отрезке

Функция называется непрерывной на отрезке (при ), если она непрерывна во всех точках открытого интервала (при ) и в точках и , соответственно.

Первая теорема Вейерштрасса об ограниченности непрерывной на отрезке функции

Если функция непрерывна на отрезке , то она ограничена на этом отрезке.

Достижимость максимума (минимума) функции на множестве

Функция достигает своего максимума (минимума) на множестве , если существует такой аргумент , для которого для всех .

Достижимость верхней (нижней) грани функции на множестве

Функция достигает своей верхней (нижней) грани на множестве , если существует такой аргумент , для которого.

Легко заметить, что эти определения эквивалентны. Если   и   ,   то . Если   и   ,   то .

Различие между максимумом (минимумом) и верхней (нижней) гранью в том, что максимум (минимум) принадлежит множеству (в данном случае множеству значений функции), а верхняя (нижняя) грань может не принадлежать этому множеству. Пусть, например, на открытом интервале задана функция . На этом интервале функция имеет верхнюю и нижнюю грани:. Но максимума и минимума не имеет. Действительно, для любого всегда можно указать такие числа и , принадлежащие , значения функции от которых будут больше и меньше . На отрезке функция имеет как верхнюю и нижнюю грани, так максимум и минимум:. Также верхняя (нижняя) грань может равняться плюс (минус) бесконечности: , а максимум (минимум) не может быть бесконечным числом.

Любое множество, в котором определены операции сравнения, имеет верхнюю и нижнюю грани.

Вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции

Непрерывная на отрезке функция достигает на нем своих верхней и нижней граней или, что тоже самое, достигает на отрезке своего максимума и минимума.

Эта теорема означает, что существуют такие точки и , принадлежащие отрезку , значения функции в которых равны, соответственно, нижней и верхней граням:. Поскольку, исходя из определений верхней и нижней граней: при , при , и поскольку , то и являются минимумом и максимумом функции на отрезке .

Вторая теорема Больцано – Коши о промежуточном значении

Пусть функция непрерывна на отрезке . И пусть есть произвольное число, находящееся между значениями функции на концах отрезка: и . Тогда существует точка , для которой.

Следствие 1 (первая теорема Больцано – Коши)

Пусть функция непрерывна на отрезке . И пусть значения функции на концах отрезка имеют разные знаки: или . Тогда существует точка , значение функции в которой равно нулю:.

Следствие 2

Пусть функция непрерывна на отрезке . И пусть . Тогда функция принимает на отрезке все значения из и только эти значения:  при  .

Использованная литература: О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004. С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

См. также: Непрерывность функции в точке – свойства и теоремы

План действий

Пример – дана функция f(x) на отрезке . Наибольшее и наименьшее значение такой непрерывной функции достигаются в определенных местах. Это – критические точки. Там, где производная записанного выражения будет равно нулю.

Для того, чтобы найти наибольшие значения уравнения, потребуется придерживаться следующего алгоритма:

1. Узнайте, какая перед вами функция. Для этого нужно проверить ее на непрерывность. В расчет обязательно берется заданный отрезок.
2. Если запись непрерывная – ищем производную.
3. После того, как найдем производную, приравниваем ее к нулю. Это поможет найти точки экстремумов. В результате получаются корни.
4. Образовавшиеся корни – это критические точки. Нужно выбрать те «параметры», что относятся к промежутку .
5. Вычислить значения функции на концах отрезка .
6. Определить значения имеющегося выражения в критических «отметках».

Теперь понятно, как найти наибольшие функции на заданном отрезке. После произведенных подсчетов остается выбрать из результатов M (максимум) и m (минимум).

Схема решения задач B15

Если в задаче B15 требуется найти максимальное или минимальное значение функции f(x) на отрезке , выполняем следующие действия:

1. Найти производную функции: f’(x).
2. Решить уравнение f’(x) = 0. Если корней нет, пропускаем третий шаг и переходим сразу к четвертому.
3. Из полученного набора корней вычеркнуть все, что лежит за пределами отрезка . Оставшиеся числа обозначим x₁, x₂, …, x_n — их, как правило, будет немного.
4. Подставим концы отрезка и точки x₁, x₂, …, x_n в исходную функцию. Получим набор чисел f(a), f(b), f(x₁), f(x₂), …, f(x_n), из которого выбираем наибольше или наименьшее значение — это и будет ответ.

Небольшое пояснение по поводу вычеркивания корней, когда они совпадают с концами отрезка. Их тоже можно вычеркнуть, поскольку на четвертом шаге концы отрезка все равно подставляются в функцию — даже если уравнение f’(x) = 0 не имело решений.

Также следует внимательно читать условие задачи. Когда требуется найти значение функции (максимальное или минимальное), концы отрезка и точки x₁, x₂, …, x_n подставляются именно в функцию, а не в ее производную.

Для начала найдем производную: y’ = (x3 + 3×2 − 9x − 7)’ = 3×2 + 6x − 9.

Затем решаем уравнение: y’ = 0 ⇒ 3×2 + 6x − 9 = 0 ⇒ … ⇒ x = −3; x = 1.

Вычеркиваем корень x = 1, потому что он не принадлежит отрезку .

Осталось вычислить значение функции на концах отрезка и в точке x = −3:
y(−5) = (−5)3 + 4·(−5)2 − 9·(−5) − 7 = −12;
y(−3) = (−3)3 + 4·(−3)2 − 9·(−3) − 7 = 20;
y(0) = 03 + 4·02 − 9·0 − 7 = −7.

Очевидно, наибольшее значение равно 20 — оно достигается в точке x = −3.

Теперь рассмотрим случай, когда требуется найти точку максимума или минимума функции f(x) на отрезке . Если отрезок не задан, функция рассматривается на своей области определения. В любом случае, схема решения такова:

1. Найти производную функции: f’(x).
2. Решить уравнение f’(x) = 0. Если производная — дробно-рациональная функция, дополнительно выясняем, когда ее знаменатель равен нулю. Полученные корни обозначим x₁, x₂, …, x_n.
3. Отметить x₁, x₂, …, x_n на координатной прямой и расставить знаки, которые принимает производная между этими числами. Если задан отрезок , отмечаем его и вычеркиваем все, что лежит за его пределами.
4. Среди оставшихся точек ищем такую, где знак производной меняется с минуса на плюс (это точка минимума) или с плюса на минус (точка минимума). Такая точка должна быть только одна — это и будет ответ.

Вдумчивый читатель наверняка заметит, что для некоторых функций этот алгоритм не работает. Действительно, существует целый класс функций, для которых нахождение точек экстремума требует более сложных выкладок. Однако такие функции в ЕГЭ по математике не встречаются.

Внимательно отнеситесь к расстановке знаков между точками x₁, x₂, …, x_n. Помните: при переходе через корень четной кратности знак у производной не меняется. Когда ищутся точки экстремума, знаки всегда просматриваются слева направо, т.е. по направлению числовой оси.

Найдем производную:

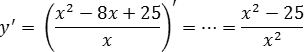
Поскольку это дробно-рациональная функция, приравниваем к нулю производную и ее знаменатель:
y’ = 0 ⇒ x2 − 25 = 0 ⇒ … ⇒ x = 5; x = −5;
x2 = 0 ⇒ x = 0 (корень второй кратности).

Отметим точки x = −5, x = 0 и x = 5 на координатной прямой, расставим знаки и границы:

Очевидно, что внутри отрезка осталась лишь одна точка x = −5, в которой знак производной меняется с плюса на минус. Это и есть точка максимума.

Еще раз поясним, чем отличаются точки экстремума от самих экстремумов. Точки экстремума — это значения переменных, при которых функция принимает наибольшее или наименьшее значение. Экстремумы — это значения самих функций, максимальные или минимальные в некоторой своей окрестности.

Помимо обычных многочленов и дробно-рациональных функций, в задаче B15 встречаются следующие виды выражений:

1. Иррациональные функции,
2. Тригонометрические функции,
3. Показательные функции,
4. Логарифмические функции.

С иррациональными функциями проблем, как правило, не возникает. Остальные случаи стоит рассмотреть более подробно.

Анализ функции

Анализ функции — это процесс изучения основных свойств функции, таких как область определения, область значений, график функции, поведение функции на различных участках, наличие экстремумов и асимптот, а также решение уравнений и неравенств, связанных с функцией.

Для проведения анализа функции нужно выполнять следующие шаги:

1. Определить область определения функции — множество значений переменной x, при которых функция определена.
2. Определить область значений функции — множество значений, которые принимает функция.
3. Построить график функции — графическое представление функции на плоскости, где по оси x откладываются значения переменной, а по оси y — значения функции.
4. Исследовать поведение функции на различных участках — определить монотонность, возрастание или убывание, наличие точек экстремума, точек разрыва и асимптот графика функции.
5. Решить уравнения и неравенства, связанные с функцией — найти значения переменной x, при которых функция принимает заданное значение или удовлетворяет заданному условию.

Анализ функции позволяет получить полное представление о ее свойствах и особенностях, что позволяет решать задачи связанные с определением экстремальных значений, нахождением корней уравнений и неравенств, а также построением математических моделей.

Принцип определения наибольших и наименьших значений функции на отрезках

Рассмотрим последовательность проведения основных операций, для определения нужных нам числовых значений для определенной функции:

1. Для начала задается область определения функции. Далее необходимо провести ее анализ и проверить входит ли в ее пределы заданный отрезок.
2. Определяем точки, на отрезках, в которых не существует первой точки. Это показательно, для функций у которых аргумент обозначается в виде модуля. А также, данную характеристику можно встретить у степенных функций, у которых показатель — простое рациональное числовое значение.
3. Вычисляем определение производной функции и приравниваем ее к нулевому значению. Составляем нужное нам уравнение и подбираем корневые значения. Если ни одна стационарная точка не попадает в заданный нами отрезок, нужно применить другие действия. Расписанные в пунктах 4 и 5.
4. Вычисляем значения в стационарных точках, если они не существуют в первой производной
5. В конечном итоге мы получаем ряд числовых значений. Далее начинаем выбирать самое максимальное и минимальное значение, для функции, которые мы хотим определить.

Весь приведенный алгоритм решения, рассмотрим на конкретном примере, для лучшего восприятия информации.

Задано условие задачи:

Функция следующего вида \

Необходимо определить значения, которые будут отражать максимальное и минимальное числовое значение на заданном отрезке. Отрезок отображает следующие значения ]-4;1].

Выполняем все необходимые действия, применяя наш уже изученный алгоритм решения.

Определяем область функции, которая равняется действительным числам, отличным от нулевого значения.

Два отрезка, определенно, будут находится в области определения. Затем по известным формулам, определяем производное значение функции.

Из уравнения мы определили, что производная значения функции, будет существовать во всех точках заданных отрезках.

Далее, при помощи определенного нами уравнения, вычислим значения стационарных точек.

\

Уравнение имеет только один корень действительного числа, он равняется значению два. Это и будет стационарная точка, которая будет попадать в отрезок

Определяем значения на концах отрезка, в данной точке.

А именно: x=1, x=2, x=4.

Мы определили максимальное значение, которое можно записать в следующем виде max y=y(2)=3. Данная запись будет актуальна, при x=1, минимальное значение min y=y(2)=3 — когда х=2.

Что касаемо второго отрезка, то ни одно стационарной точки, он в себя не включает. Поэтому вычисляем значения на концах заданного отрезка.

Следовательно: максимальное значение будет равняться трем, а минимальное будет равно — \.

Анализ функции

Анализ функции — это процесс изучения основных свойств функции, таких как область определения, область значений, график функции, поведение функции на различных участках, наличие экстремумов и асимптот, а также решение уравнений и неравенств, связанных с функцией.

Для проведения анализа функции нужно выполнять следующие шаги:

1. Определить область определения функции — множество значений переменной x, при которых функция определена.
2. Определить область значений функции — множество значений, которые принимает функция.
3. Построить график функции — графическое представление функции на плоскости, где по оси x откладываются значения переменной, а по оси y — значения функции.
4. Исследовать поведение функции на различных участках — определить монотонность, возрастание или убывание, наличие точек экстремума, точек разрыва и асимптот графика функции.
5. Решить уравнения и неравенства, связанные с функцией — найти значения переменной x, при которых функция принимает заданное значение или удовлетворяет заданному условию.

Анализ функции позволяет получить полное представление о ее свойствах и особенностях, что позволяет решать задачи связанные с определением экстремальных значений, нахождением корней уравнений и неравенств, а также построением математических моделей.

Метод прямоугольников

Идея метода заключается в следующем: для заданной функции на отрезке разбиваем этот отрезок на n равных частей, и на каждом подотрезке выбираем точку xi. Затем находим значение функции в каждой точке xi и приближенно вычисляем площадь прямоугольника, которая равна (xi+1 — xi) * f(xi), где f(xi) — значение функции в точке xi. Суммируем площади всех прямоугольников и получаем приближенное значение среднего значения функции на отрезке .

Метод прямоугольников имеет несколько вариаций, в зависимости от того, как выбираются точки xi на каждом подотрезке . Существуют три основных способа выбора точек: левые прямоугольники, правые прямоугольники и средние прямоугольники.

В случае использования левых прямоугольников, значение функции в точке xi берется равным f(xi), т.е. значение функции в левой границе подотрезка . При использовании правых прямоугольников, значение функции в точке xi берется равным f(xi+1), т.е. значение функции в правой границе подотрезка . При использовании средних прямоугольников, значение функции в точке xi берется равным f((xi+xi+1)/2), т.е. значение функции в середине подотрезка .

Метод прямоугольников прост в реализации и может быть использован для приближенного нахождения среднего значения функции на отрезке в тех случаях, когда точное решение не требуется или когда функция не может быть аналитически выражена.

Нахождение длины интервала интегрирования

Для того чтобы найти среднее значение функции через интеграл, необходимо знать длину интервала интегрирования. Длина интервала определяет границы, между которыми будет осуществляться интегрирование функции.

Для найдения длины интервала интегрирования достаточно вычислить разницу между верхней и нижней границами интервала. Данную разницу можно выразить математически:

Верхняя граница	Нижняя граница	Длина интервала
a	b	b — a

Где:

• a — нижняя граница интервала интегрирования;
• b — верхняя граница интервала интегрирования.

После нахождения длины интервала можно приступать к вычислению интеграла функции и нахождению среднего значения на данном интервале.

Поиск значения функции на отрезке: как найти x?

При поиске значения функции на определенном отрезке, наиболее распространенным методом является численное приближение. Для этого можно использовать различные алгоритмы, такие как метод половинного деления, метод Ньютона и метод секущих.

Метод половинного деления основан на принципе бисекции отрезка. Идея заключается в том, чтобы разбить отрезок на две равные части и выбрать ту часть, в которой значение функции имеет разный знак с исходным значением функции. Затем процесс повторяется для нового отрезка, пока не будет достигнута заданная точность.

Метод Ньютона и метод секущих основаны на аппроксимации функции с помощью ее касательной. Они позволяют более быстро сходиться к решению, но требуют более сложных вычислений.

Для применения любого из этих методов необходимо знать начальное приближение x0, на котором функция имеет разный знак с искомым значением функции на отрезке. Чтобы найти приближение, можно использовать график функции или применить другие методы, например, метод половинного деления.

После нахождения начального приближения, можно применить выбранный метод для приближенного нахождения значения функции на отрезке

Важно помнить, что точность результата зависит от выбранного метода и точности начального приближения

Обратите внимание, что для некоторых функций может не существовать решения на заданном отрезке. В таком случае рекомендуется проверить график функции и выбрать другой отрезок или метод для решения задачи