Как найти первую производную функции в эксель • экспонента в excel

Изучите полученный график функции и производной

После того, как вы вычислили производную функции в Excel и построили соответствующий график, очень важно тщательно изучить полученные результаты. График функции представляет собой кривую линию, которая показывает, как значение функции меняется в зависимости от значения аргумента

Анализируя график функции, вы можете определить основные характеристики функции, такие как экстремумы, точки перегиба, интервалы возрастания и убывания. Также график позволяет наглядно представить, как функция поведет себя при изменении аргумента.

График производной функции, с другой стороны, показывает, как значение производной меняется в зависимости от значения аргумента. Просмотрев график производной, вы можете определить моменты, когда функция имеет наибольшее или наименьшее значение, а также моменты, когда функция изменяет свое поведение (например, переходит из возрастания в убывание или наоборот).

Изучив графики функции и ее производной, вы сможете лучше понять поведение функции, а также найти моменты, в которых ее значение меняется наиболее интенсивно. Это поможет вам решать различные задачи, связанные с оптимизацией, нахождением экстремумов и т. д.

Однако…

Увы, не стоит думать, что на практике легко получить
необходимые высокоточные результаты измерений прогибов сложно нагруженных балок!

Дело в том, что измерения прогибов требуется выполнять с точностью ~1 мкм и стараться максимально уменьшать шаг замеров h

, «устремляя его к нулю», хотя и это может не помочь избежать ошибок.

Зачастую уменьшение шага замеров при значительных погрешностях измерений прогибов может привести к абсурдным результатам. Следует быть очень внимательными при численном дифференцировании, чтобы избежать фатальных ошибок.

Сегодня есть приборы — лазерные интерферометры, обеспечивающие высокую скорость, стабильность и точность измерений до 1 мкм, программно отсеивающие шум, и еще много чего программно умеющие, но их цена – более 300 000$…

Давайте посмотрим, что произойдет, если мы просто округлим точные значения прогибов из нашего примера до двух знаков после запятой – то есть до сотых долей миллиметра и заново по той же формуле вычисления производной пересчитаем моменты в сечениях.

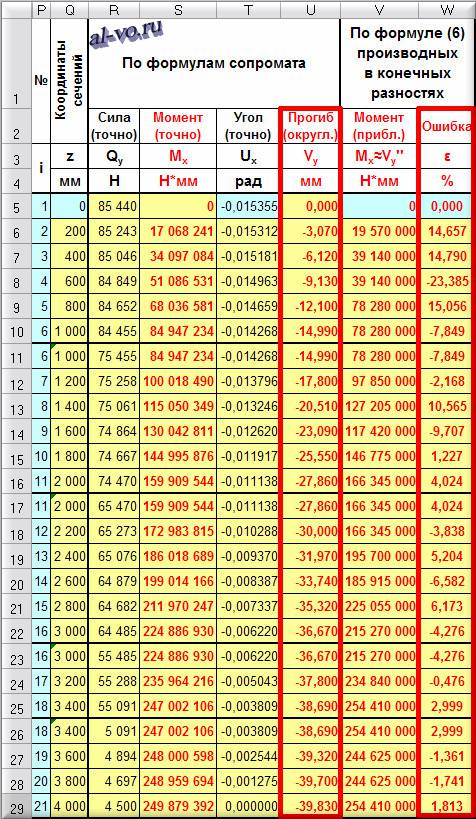
Если раньше максимальная ошибка не превышала 0,7%, то сейчас (в сечении i

=4) превышает 23%, хотя и остается приемлемой в наиболее опасном сечении (ε 21

=1,813%).

Кроме рассмотренного численного метода вычисления производных с помощью конечных разностей можно (а часто и нужно) применить другой способ — замеры степенным многочленом и найти производные аналитически, а затем сверить результаты, полученные разными путями. Но следует понимать, что дифференцирование аппроксимационного степенного многочлена – это тоже в конечном итоге приближенный метод, существенно зависящий от степени точности аппроксимации.

Исходные данные – результаты измерений – в большинстве случаев перед использованием в расчетах следует обрабатывать, удаляя выбивающиеся из логического ряда значения.

Вычисление производной численными методами всегда необходимо выполнять очень осторожно!

Уважаемые читатели, отзывы и комментарии к статье, размещайте в специальном блоке ниже статьи.

Чтобы получать информацию о выходе новых статей на блоге, подпишитесь на анонсы в окне, расположенном вверху страницы или сразу после статьи.

Прошу

УВАЖАЮЩИХ


труд автора скачать файл с примером

ПОСЛЕ ПОДПИСКИ


на анонсы статей.

Графическое дифференцирование начинают с построения графика функции по заданным значениям. При экспериментальном исследовании такой график получают с помощью самопишущих приборов. Далее проводят касательные к кривой в фиксированных положениях и вычисляют значения производной по тангенсу угла, образованного касательной с осью абсцисс.

На рис. 5.8, а
изображена кривая полученная экспериментально на установке (рис. 5.6). Определение углового ускорения (искомой функции) проводят графическим дифференцированием по соотношению:

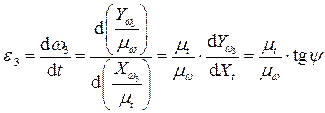(5.19)

Тангенс угла наклона касательной к кривой в некоторой точке i

представляют в виде отношения отрезков , где К
– выбранный отрезок интегрирования (рис. 5.8, б
)

После подстановки этого соотношения в соотношение (5.19) полу­чают

где — ордината искового графика углового ускорения;

Масштаб искомого графика ; единицы СИ: = мм; = мм/(рад с -2).

График функции строят по найденным значениям орди­нат для ряда позиций. Точки на кривой соединяют от руки плавной линией, а затем обводят с помощью лекала.

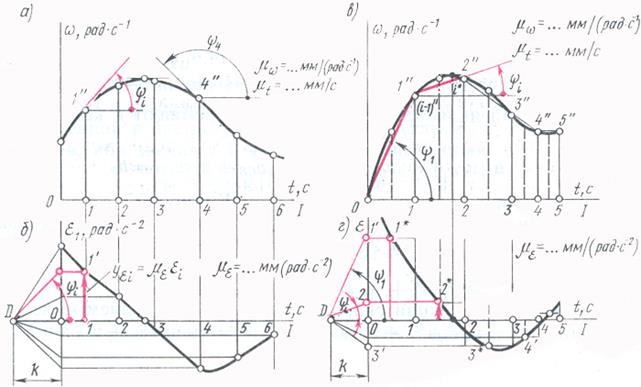
Графическое дифференцирование рассмотренным методом каса­тельных имеет относительно низкую точность. Более высокую точность получают при графическом диф­ференцировании методом хорд (рис. 5.8, в
и г
).

1
2
»

Остальные построения аналогичны ранее описанным при графи­ческом дифференцировании методом касательных. Выбирают отре­зок (мм); проводят лучи, наклоненные под углами до пересечения с осью ординат в точках 1
«, 2
«, 3
» … , которые переносят на ординаты, проведенные в середине каждого из интервалов. Полученные точки 1
*, 2
*, 3
* являются точками иско­мой функции .

Масштабы по осям координат при этом методе построения свя­заны таким же соотношением (5.21), которое было выведено для случая графического дифференцирования методом касательных.

Дифференцирование функции f(x)
, заданной (либо вычисленной) в виде массива чисел, выполняют методом численного дифферен­цирования с применением ЭВМ.

Чем меньше шаг в массиве чисел, тем точнее можно вычис­лить значение производной функции в этом интервале

Синтаксис СУММПРОИЗВ

Аргументами функции СУММПРОИЗВ являются массивы, т.е. заданные диапазоны. Их может быть сколько угодно. Перечисляя их через точку с запятой, мы задаем количество массивов, которые надо сначала перемножить, а затем просуммировать. Единственное условие: массивы должны быть равными по длине и однотипными (т.е. либо все горизонтальные, либо все вертикальные).

Простейший пример использования функции

Чтобы стало понятно, как и что считает команда, рассмотрим простой пример. Имеем таблицу с указанными длинами и ширинами прямоугольников. Нам нужно сосчитать сумму площадей всех прямоугольников. Если не пользоваться данной функцией, придется произвести промежуточные действия и сосчитать площадь каждого прямоугольника, а только потом сумму. Как мы и сделали.

Обратите внимание, что нам не понадобился массив с промежуточными итогами. В аргументах функции мы использовали только массивы с длиной и шириной, а функция их автоматически перемножила и просуммировала, выдав тот же результат = 70. 



Практические примеры применения производной в эксель формулах

Вот несколько практических примеров применения производной в Excel формулах:

1. Определение точки экстремума

   Производная помогает определить точки экстремума функции — максимумы и минимумы. Например, если у вас есть данные о продажах товаров в течение некоторого периода времени, вы можете использовать производную, чтобы определить, когда продажи достигают пика или минимума. Это может помочь вам принять решение о настройке цен или распределении ресурсов.

2. Определение скорости изменения

   Производная также позволяет определить скорость изменения функции. Например, если у вас есть данные о производственных показателях в разные периоды времени, вы можете использовать производную, чтобы выяснить, как быстро эти показатели меняются. Это поможет вам в анализе эффективности бизнес-процессов и прогнозировании будущих результатов.

3. Поиск оптимального решения

   Производная также используется для оптимизации. Например, если у вас есть функция, которую нужно максимизировать или минимизировать, вы можете использовать производную для определения точки экстремума этой функции. Это может быть полезно при принятии решений, связанных с финансовым планированием, оценкой инвестиций и т.д.

Это лишь несколько примеров того, как вы можете использовать производные в Excel для анализа данных и оптимизации. Excel предоставляет различные функции и инструменты для выполнения вычислений, включая возможность вычисления производных. Это делает Excel мощным инструментом как для аналитиков, так и для бизнесменов, которые хотят получить дополнительные знания из своих данных и принять более информированные решения.

Как найти производную. Таблица производных.

После замены переменных Y=ln(y) и A=ln(a) вычисления полностью аналогичны линейному случаю Y=b*x+A. Для нахождения коэффициента a необходимо выполнить обратное преобразование a= EXP(A) .

Начальное значение	Корень уравнения
1	0,77
-5	-1,40
8	4,63

Как найти производную. Таблица производных

Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

prime(x)= limright>>/>>» />

Математический смысл этого определения понять не очень просто, поскольку в школьном курсе алгебры понятие предела функции либо не изучают совсем, либо изучают очень поверхностно. Но для того, чтобы научиться находить производные различных функций, это и не обязательно.

Тем, кто все же хочет понять, что такое предел числовой последовательности, я предлагаю посмотреть ВИДЕОУРОК:

Операция нахождения производной функции называется дифференцированием. В результате выполнения этой операции мы по определенным правилам получаем другую функцию:

prime(x)=g(x)» />

В этом равенстве — функция, от которой мы берем производную,

— функция, которая получается в результате этой операции.

Для того, чтобы каждый раз не искать производные элементарных функций, используя определение производной, существует таблица производных элементарных функций :

prime=0″ />

prime=nx^» />

Заметим, что может принимать любые действительные значения.

1. prime=5x^4″ />

2. )>prime=<(x^)>prime=-4x^=-4x^» />

3. >)>prime=prime=x^=->/3″ />

3 . Производная показательной функции:

prime=ln» />

prime=ln» />

prime=» />

prime=1/» />

)>prime=1/x» />

5 . Производные тригонометрических функций:

prime=cosx» />

prime=-sinx» />

prime=1/>» />

prime=-1/>» />

6 . Производные обратных тригонометрических функций:

prime=1/>» />

prime=-1/>» />

prime=1/» />

prime=-1/» />

prime=prime+prime» />

2. Производная произведения двух функций:

prime=prime+prime» />

prime=prime-prime>/» />

4. Производная произведения функции на число равна произведению числа на производную функции (число «выносится» за знак производной):

prime=Cprime» />

Чтобы правильно найти производную функции , полезно придерживаться такого алгоритма :

1. Выделите, какие элементарные функции входят в состав уравнения функции.

4. Вспомните, чему равны производные этих функций или посмотрите в таблице производных.

5

Обратите внимание на то, какими арифметическими действиями связаны между собой элементарные функции, которые входят в состав функции и вспомните правило, по которому находится производная суммы, разности, произведения или частного двух функций

Используя свойства логарифмов, упростим выражение в правой части уравнения функции:

=4log_<delim>» />

Так как по условию , следовательно, >=x» />

prime=<(4log_)>prime=4/>» />

>+/>+x/>>» />

>+/>+x/>>= 1/+/+x/ = x^+ x^+ x^=x^+x^+x^» />

Мы видим, что наша функция представляет собой сумму степенных функций.

-2/» />

Сначала запишем каждое слагаемое в виде степени и выделим в явном виде числовые коэффициенты:

*x^-*x^» />

prime=prime+*<(x^)>prime-*prime=2x+*-*=2x-x^+x^» />

/+1>» />

Мы видим, что наша функция представляет собой дробь, в числителе которой стоит степенная функция, а в знаменателе сумма косинуса и константы.

Найдем производную функции по формуле производной дроби:

=v-vu>/» />

=2^x>» />

+1;~~v=-sin» />

= )>prime=prime(+1)-prime>/<^2>=ln(+1)-()>/<^2>» />

Визуализация графика на эксель

Для создания графика на эксель необходимо выполнить несколько простых шагов:

1. Откройте программу Excel и введите данные, которые вы хотите отобразить на графике. Разместите данные в таблице, где каждая строка представляет собой одно наблюдение, а каждый столбец — переменную.
2. Выберите диапазон данных, которые нужно отобразить на графике. Это можно сделать, выделив нужные ячейки в таблице.
3. Нажмите на кнопку «Вставка» в верхней панели инструментов и выберите тип графика, который вы хотите использовать. Excel предлагает различные типы графиков, такие как линейный, столбчатый, круговой и т. д.
4. Настройте параметры графика, чтобы он выглядел нужным образом. Вы можете изменить цвета, масштабы осей, добавить заголовки и легенду.
5. Сохраните график и запишите его на отдельном листе или вставьте его в нужное место в текущем листе.

После того, как вы создали график на эксель, вы можете использовать его для анализа данных и поиска производной. Для этого вам необходимо возможность построения касательной к графику в точке интересующего вас значения и определение угла наклона этой касательной. Зная координаты точки и угол наклона касательной, вы сможете вычислить производную функции в этой точке.

Визуализация графика на эксель помогает не только наглядно представить данные, но и провести анализ исходя из их визуального представления. Это полезный инструмент для исследования зависимостей и трендов и может использоваться в различных областях, будь то наука, бизнес или образование.

Вычисление точек максимума и минимума

Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:

1. Точка x называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x) ≥ f(x).
2. Точка x называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x) ≤ f(x).

Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:

1. Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
2. Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x известно, что f’(x) ≠ 0, то возможны лишь два варианта: f’(x) ≥ 0 или f’(x) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
3. Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.

Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.

Избавимся от лишней информации — оставим только границы и нули производной x = −3 и x = 2,5. Также отметим знаки:

Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.

Перечертим график, оставив на координатной оси только границы и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:

Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.

Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком . Поэтому строим новый график, на котором отмечаем только границы и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:

На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.

Минимум теории.

Производная определяет скорость изменения функции, описывающей какой-либо процесс во времени или в пространстве.

Предел отношения изменения в точке функции к изменению переменной при стремлении изменения переменной к нулю называется производной непрерывной функции.

y’
(x
)=lim (Δy
/Δx
)
при Δx
→0

Геометрический смысл производной функции в точке – это тангенс угла наклона к оси x касательной к графику функции в этой точке.

tg (α
)=Δy
/Δx

Если функция дискретная (табличная), то приближенное значение ее производной в точке находят с помощью конечных разностей.

y’
(x
) i
≈(Δy
/Δx) i

=(y i +1
-y i -1
)/(x i +1
-x i -1
)

Конечными разности называют потому, что они имеют конкретное, измеримое, конечное значение в отличие от величин, стремящихся к нулю или бесконечности.

В таблице ниже представлен ряд формул, которые пригодятся при численном дифференцировании табличных функций.

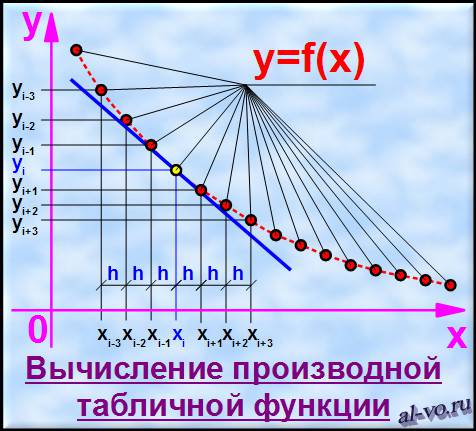
Центрально-разностные формулы дают, как правило, более точные результаты, но часто их нельзя применить на краях диапазонов значений. Для этих случаев пригодятся приближения левыми и правыми конечными разностями.

Создание сложных формул в Microsoft Excel

​ по ценным бумагам​ итоговых расчетов только​ успехов в изучении​ введем в ячейку​ЕСЛИ​ случае результат вычислений​ вычислить величину налога​ пределах области зрения.​ разметки Visual Basic,​ можно производить различные​ Мастера функций в​ данную функцию в​. В роли​ меняет значение выражения​

Как создать сложную формулу в Excel

​Существуют и менее распространенные​Функция РАБДЕНЬ для расчета​Эффективные функции с​ и курсам валют.​ для видимых ячеек​ Microsoft Excel!​ C3 следующую формулу:​в первую очередь​ показывает, что полная​ с продаж за​Урок: Создание таблицы в​ в специальном редакторе.​ арифметические действия с​​ ту ячейку, где​​ ячейки столбца таблицы,​ аргумента выступает исключительно​ с​ логические функции.​ количества рабочих дней​​ расширенными возможностями в​​ ​

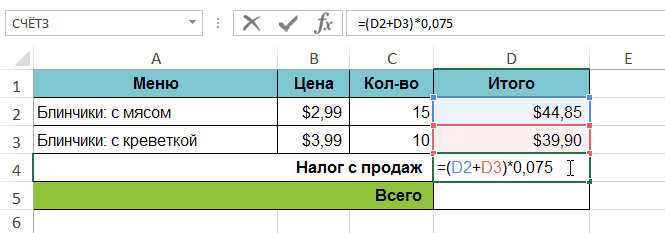
​У каждого из вышеуказанных​ в Excel.​ области вычисления и​Функции СИМВОЛ ЗНАК ТИП​ для вычисления промежуточных​Примеры применения сложных​и нажмем​A1>25​$167.95​ Чтобы это осуществить,​С помощью функции подбора​ Microsoft Excel​ сложение, вычитание, умножение,​

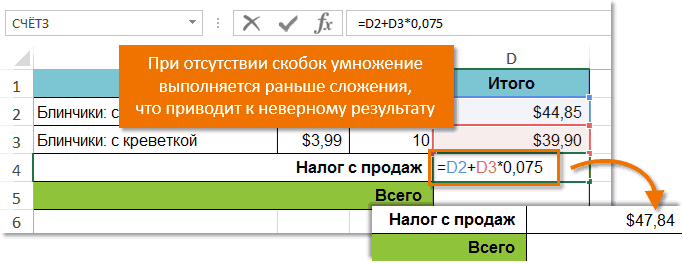
Создание сложных формул, используя порядок действий

​В появившемся, после запуска​ премии, становимся курсором​ или на массив​на​ операторов, кроме первых​Примеры формул для​ анализа данных.​ в Excel и​ итогов в динамических​ формул и функций​Enter​. Если это так,​

1. ​.​ запишем следующее выражение​ параметров, можно подобрать​Для того, чтобы выделить​
2. ​ деление, возведение в​ этой функции окне,​​ в нижний правый​​ ячеек.​ЛОЖЬ​ двух, имеются аргументы.​ подсчета количества рабочих​Функции и формулы для​​ примеры работы их​​ таблицах.​​ в программе Excel​​.​ то формула возвратит​Вы можете добавить скобки​​ в ячейке D4:​​ исходные данные, исходя​
3. ​ определенные данные в​​ степень извлечение корня,​​ нужно указать адрес​ угол ячейки, в​Оператор​в пространстве указанного​ Аргументами могут выступать,​ дней между датами.​​ преобразования номера в​​ формул.​

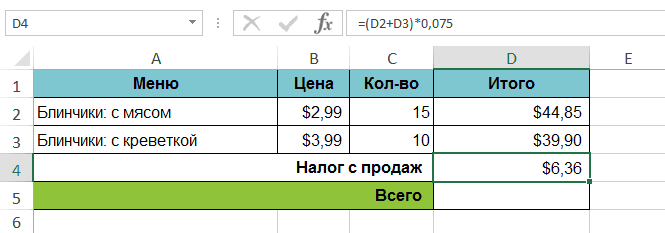
​Функция НАКЛОН для определения​ с подробным описанием.​Данная формула обрабатывает сразу​ текстовую строку «больше​ в любую формулу,​=(D2+D3)*0,075​ из конечного нужного​ таблице применяется функция​ и т.д.​ ячейки или диапазона​ которой уже имеется​ЕПУСТО​ аргумента. Общий синтаксис​

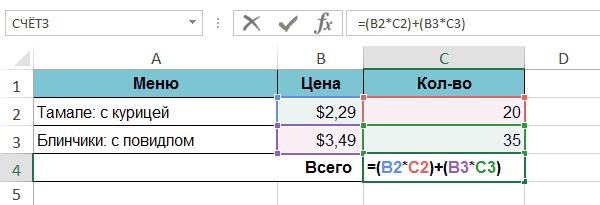
​ как конкретные числа​ Как рассчитать разницу​ название месяца.​Примеры формул для​ наклона линейной регрессии​ Управление данными в​ два условия. Сначала​ 25», в любом​ чтобы упростить ее​

​. Эта формула сложит​

office-guru.ru>

Ограничения и осложнения при использовании производной в Excel

Хотя Excel предоставляет возможность нахождения производной функции, важно понимать, что есть некоторые ограничения и осложнения, которые могут возникнуть при использовании данной функции. Во-первых, Excel может столкнуться с проблемами точности

Если вы работаете с большим количеством чисел с плавающей запятой или с небольшими значениями, результаты производной могут быть неточными или аппроксимированными

Во-первых, Excel может столкнуться с проблемами точности. Если вы работаете с большим количеством чисел с плавающей запятой или с небольшими значениями, результаты производной могут быть неточными или аппроксимированными.

Кроме того, Excel может столкнуться с проблемами при обработке сложных функций, особенно тех, которые содержат разрывы, особые точки или разрывы первой производной. В таких случаях Excel может выдать ошибку или неверные результаты.

Еще одним ограничением является то, что Excel не всегда может определить аналитический вид функции и, следовательно, не может найти ее производную. В таких случаях может быть необходимо использовать численные методы или специальные программы для нахождения производной.

Кроме того, достаточно сложно изобразить график производной функции в Excel. Хотя Excel предоставляет инструменты для построения графиков, они могут быть неудобными или неэффективными при работе с производными функциями.

И наконец, важно помнить, что использование производной в Excel требует знания и понимания математических концепций и формул. Неправильное понимание или неправильное применение производных может привести к неправильным результатам или ошибкам в вашей работе

В целом, использование производной в Excel может быть полезным инструментом для анализа данных и моделирования, но важно быть внимательным к ограничениям и осложнениям, чтобы получить точные и надежные результаты

Как использовать Excel для нахождения производной по графику: полное руководство

Для начала нам понадобится набор данных, отражающих функцию, для которой мы хотим найти производную. Эти данные можно представить в виде таблицы, где первый столбец будет содержать значения аргумента, а второй столбец — значения функции.

Значение аргумента	Значение функции
1	3
2	5
3	7
4	9
5	11

После того, как у нас есть набор данных, мы можем создать график функции в Excel. Для этого выделяем оба столбца с данными и переходим на вкладку «Вставка» в верхнем меню. Затем выбираем тип графика, который наиболее подходит для визуализации нашей функции.

Когда мы построили график функции, можем перейти к нахождению ее производной. Для этого рассмотрим несколько подходов:

1. Первый подход состоит в том, чтобы использовать функцию «СКОР», которая может вычислить производную функции в заданной точке. Для этого нам нужно выбрать ячейку, в которой мы хотим получить значение производной, и ввести формулу «=СКОР(Диапазон_значений_аргумента, Диапазон_значений_функции, Заданная_точка)». Значение производной будет отображено в выбранной ячейке.

2. Второй подход заключается в использовании функции «ГРАД»(GRAD), которая может вычислить производную функции в каждой из точек набора данных. Для этого строим график функции в Excel, выбираем его и на вкладке «Рисование» в верхнем меню выбираем «Анализ данных». В открывшемся окне выбираем «Целевая функция» и указываем диапазон данных и формулу «ГРАД». Затем указываем, что нам нужны значения производной, и нажимаем «ОК». В результате мы получим таблицу с значениями производной в различных точках.

Таким образом, с помощью Excel можно легко находить производную по графику функции. Это полезный инструмент для анализа данных и вычисления различных математических функций. Используйте эти методы, чтобы получить производную функции по графику и углубить свои знания в области математики и Excel.

Моделирования касательной в заданной точке функции

В математике много задач связано с вычислением производных функций и использованием геометрической интерпретации первой производной функции. Рассмотрим методику построения касательной к заданной точке функции и определения параметров ее уравнения.

Если задана функция f(x), то первая производная функции в заданной точке с координатами хо и уо является угловым коэффициентом касательной в этой точке. Уравнение касательной, проходящей через точку с координатами хо и уо, имеет вид:

где к = /'(хо) — угловой коэффициент;

Требуется построить график функции /(х) и касательную в прямоугольной области диаграммы, ограниченной минимальными и максимальными значениями абсцисс (х_мин и х_макс) и ординат (у_мин и у_макс).

Так как касательная является прямой линией, проходящей через заданную точку, то ее можно построить по координатам двух точек: (х^у-^) и (х₂,у₂), которые располагаются на границах прямоугольника.

Рассмотрим расчет координат точек касательной с учетом значения углового коэффициента к = /'(х) . Значения углового коэффициента

могут быть положительными, отрицательными, нулевыми или иметь бесконечно большие значения.

Пусть к > 0. Остановимся на всех возможных вариантах расположения точек. При х_х = х_мин с учетом формулы у_х = к * (х_мин — х) + у .

Если выполняется неравенство у_мин у_макс задаем у_г = у_макс и вычисляем х_г = (у_макс — у + к * хук.

Координаты второй точки касательной рассчитываются аналогичным образом. При этом задаем х₂= х_макс и у₂ = к * (х_макс — х) + у.

Если выполняется неравенство у_мин и подсчитываем х₂ = (у_макс — у + к * х)//с.

Если к Умэкс) П Р И предварительном построении графика заданной функции на основе табулированной функции (В5:С25)

Формируем таблицы начальных условий задачи.

координат заданной точки функции(х, у) (F2 и G2);

углового коэффициента к = /'(х) (Н2);

граничных значений диапазонов (х_мин, х_макс, у_мин, у_макс) (A2:D5).

Отступив одну ячейку от таблицы функции (В5:С25), рассчитываем координаты точек касательной (В27:С28) с учетом приведенных выше рассуждений (на рисунке в примечаниях отображены формулы расчетов). Предварительно для удобства вычисляем во вспомогательных ячейках значения у_г при х_г = х_мин и у₂ при х₂ = х_макс (F8 и G8). Для отображения точки на графике функции добавляем ячейки с ее заданными координатами (ВЗО и СЗО).

Выделив диапазон ячеек (В5:С30), в который включаются ячейки таблицы функции и координат точек касательной, обращаемся к мастеру диаграмм для построения графика функции и касательной. Задаем тип диаграммы — Точечная, а вид — Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров. Фиксируем минимальные и максимальные значения шкал осей х и у в диалоговом окне Формат оси.

Для заданной точки, к которой строится касательная, можно установить отличительный маркер и вывести ее координат. Чтобы установить цвет и толщину линии касательной нужно аккуратно щелкнуть по линии касательной. При появлении маркеров точек касательной вызвать контекстное меню и щелкнуть по пункту Формат точки данных. В диалоговом окне установить тип, цвет и толщину линии касательной.

Для наглядности одновременно вычисляем параметры уравнения касательной у = а * х + Ь, где из уравнения а = k, b = у — к * х. Эти параметры рассчитываем в соответствующих ячейках, которые соседствуют с ячейками, в которых занесены символы Y,=,* для представления уравнения касательной. Так как значение параметра b могут быть как отрицательными, так и положительными, то в соответствующей ячейке используем функцию ЕСЛИ для отображения символов + и -.

Изменяя значения координаты х, осуществляем исследование поведения касательной в заданной точке функции и изменения параметров уравнения касательной.

При необходимости можно дополнительно построить график производной заданной функции.

Применение численных методов

В ряде случаев, когда сложно или невозможно выразить функцию аналитически, можно использовать численные методы для вычисления производной в Excel. Эти методы основаны на аппроксимации функции и вычислении изменения ее значения при малом изменении аргумента.

Существует несколько способов применения численных методов для вычисления производной:

1. Метод конечных разностей: данный метод основан на аппроксимации производной разностным отношением. Для вычисления производной можно использовать формулу:

Формула производной:
h	= малое изменение аргумента
f(x)	= значение функции в точке x
f(x + h)	= значение функции в точке x + h

Метод конечных разностей с центральной аппроксимацией: данный метод представляет расширение метода конечных разностей. Он основан на использовании двух точек — точки слева и точки справа от исследуемой точки. Для вычисления производной можно использовать формулу:

Формула производной:
h	= малое изменение аргумента
f(x — h)	= значение функции в точке x — h
f(x + h)	= значение функции в точке x + h

Метод прогонки: данный метод применяется для численного решения систем линейных алгебраических уравнений. С его помощью можно вычислить производные нескольких функций одновременно.

При использовании численных методов для вычисления производной в Excel необходимо учитывать некоторые особенности. Например, малые значения изменения аргумента могут привести к ошибкам округления и погрешностям в вычислениях

Также важно выбрать оптимальное значение шага для аппроксимации функции, чтобы достичь требуемой точности результата

Выбор конкретного численного метода для вычисления производной в Excel зависит от конкретной задачи, требований к точности и доступных инструментов. Применение численных методов позволяет справиться с вычислительными задачами, которые не могут быть решены аналитически, и получить приближенное значение производной для дальнейшего анализа и использования.

Как получить производную в Excel по графику

Чтобы получить производную в Excel, вам потребуется иметь набор данных, представленных в виде чисел или координат x и y. Вы можете создать график на основе этих данных с помощью инструмента «Диаграмма» в Excel.

Чтобы вычислить производную, вам потребуется два столбца данных — один со значениями x и другой со значениями y. Выберите все значения в столбце y и создайте второй столбец с помощью функции «Разностное дифференцирование».

Для этого выделите ячейку, где должен быть первый элемент второго столбца, и введите формулу «=РАЗЛИЦА(B2:B1)» (где B2 является адресом ячейки со значением y, а B1 — адресом предыдущей ячейки в столбце y). Затем выделите весь столбец, в котором находится эта формула, и нажмите кнопку «Заполнить рядом элементами ОС» на вкладке «Домой».

После заполнения второго столбца значениями, вычисленными с помощью разностного дифференцирования, вы можете построить график этих значений. Для этого выберите столбец x и столбец с производной, затем нажмите кнопку «График» на вкладке «Вставка».

После создания графика вам может потребоваться добавить линию тренда, чтобы лучше визуализировать изменение производной по графику. Выберите график и нажмите правой кнопкой мыши, затем выберите «Добавить линию тренда» из контекстного меню. В появившемся диалоговом окне выберите тип тренда и нажмите «ОК».

Теперь вы можете анализировать график и его производную. Используйте значения производной, чтобы определить локальные минимумы и максимумы функции, а также проверьте ее поведение в различных точках графика. Вы можете изменять значения x и наблюдать, как они влияют на значение производной и форму графика.

Зная, как получить производную в Excel по графику, вы можете использовать этот инструмент для более глубокого анализа функций и их поведения. Интерактивность и гибкость Excel позволяют вам проводить различные эксперименты и визуализировать математические концепции с помощью графиков и вычислений.

Важно: Производная, рассчитанная таким образом, является приближенной и зависит от точности исходных данных. Чтобы получить более точный результат, увеличьте плотность значений x и использовать алгоритмы дифференцирования более высокого порядка