Как определить периодичность функции

Используйте формулу для расчета периода

Если вы хотите найти период по графику, вам нужно использовать математическую формулу, которая выражает периодическую функцию. Периодическая функция повторяется через равные интервалы времени и может быть описана с помощью синусоиды или косинусоиды.

Формула для расчета периода упрощается, если функция является синусоидой или косинусоидой. Если это не так, то вам нужно преобразовать функцию таким образом, чтобы она стала периодической.

Для расчета периода используется формула T = 2π/ω, где T — период, а ω — угловая скорость. Угловая скорость определяется как ω = 2π/T, где T — период. Вы можете использовать эту формулу, чтобы найти период для любой периодической функции.

Пример	Расчет периода
sin(x)	T = 2π
cos(2x)	T = π
sin(4x)	T = π/2

Если вы знаете угловую скорость, вы можете легко найти период. Например, если угловая скорость равна 2π, то период будет T = 2π/2π = 1.

Таким образом, формула для расчета периода позволяет легко и быстро найти период для любой периодической функции, используя угловую скорость.

Вопрос-ответ

Вопрос: Как найти период по графику?

Ответ: Для того чтобы найти период по графику, необходимо определить периодичность повторяющегося элемента на графике. Например, если график представляет собой функцию синуса, то период можно найти по формуле T = 2π/ω, где T — период, а ω — частота.

Вопрос: Как определить частоту по графику?

Ответ: Для того чтобы определить частоту по графику, можно воспользоваться формулой ω = 2π/T, где T — период. Эта формула позволяет определить частоту повторяющихся элементов на графике.

Вопрос: Можно ли определить период по графику, если он не является периодическим?

Ответ: Если график не является периодическим, то найти его период не удастся. Однако можно попробовать определить характер изменения функции на графике и использовать эту информацию для анализа данных.

Вопрос: Какой метод лучше всего подходит для определения периода по графику?

Ответ: Метод определения периода по графику зависит от типа функции, представленной на графике. Например, для функции синуса можно использовать формулы T = 2π/ω, ω = 2π/T, а для функции косинуса — T = 2π/ω, ω = 2π/T. Для других типов функций могут быть свои методы и формулы.

Вопрос: Как определить периодические колебания по графику?

Ответ: Периодические колебания можно определить по графику, если на нем есть повторяющиеся элементы. Например, если на графике представлена функция синуса, то периодические колебания можно определить по повторяемости волны. Для определения периода можно использовать формулы T = 2π/ω, ω = 2π/T.

Главная — Полезно — Простой способ определить период функции: 5 шагов для поиска по графику

Комментарии

Samantha78

5.0 out of 5.0 stars5.0

Анастасия Петрова
5.0 out of 5.0 stars5.0

Статья очень полезная, я научилась быстро и точно определять период по графику. Спасибо автору!

Иван
5.0 out of 5.0 stars5.0

Maxwell
5.0 out of 5.0 stars5.0

Статья действительно помогла мне разобраться в том, как находить период по графику. Особенно удобно было использовать эквалайзер и смотреть на фазовый сдвиг между каналами. Спасибо автору за такой подробный и понятный материал!

Nick1
5.0 out of 5.0 stars5.0

Полезная статья, сразу разобрался, как находить период по графику.

Евгения Сергеева
5.0 out of 5.0 stars5.0

Статья очень понятно объясняет, как находить период по графику. Очень пригодилось мне, так как я не очень сильна в математике. Сейчас я могу быстро анализировать графики и найти период. Но хотелось бы больше примеров, чтобы лучше понимать, как это работает в различных ситуациях.

Как определить периодичность функции без графика: методы и алгоритмы

Один из таких методов — метод последовательных разностей. Суть метода заключается в вычислении разности между значениями функции в соседних точках и проверке, имеет ли эта разность постоянное значение. Если разность между значениями функции постоянна на протяжении нескольких точек, то это может указывать на периодичность функции.

Другой метод — метод Фурье. Он основан на представлении функции в виде суммы синусоидальных компонент. При использовании алгоритма Фурье можно найти коэффициенты разложения функции и определить, включает ли разложение периодические компоненты. Если такие компоненты присутствуют, это указывает на периодичность функции.

Также можно использовать алгоритм корреляции для определения периодичности функции. Этот алгоритм сравнивает функцию с ее сдвинутой копией и измеряет степень сходства. Если функция имеет периодичность, возникает наибольшая корреляция при сравнении функции с самой собой со сдвигом на кратные длине периода.

И, наконец, одним из простых методов является анализ явных математических выражений функции на предмет наличия периодических компонент. Некоторые функции, например, тригонометрические или логарифмические, имеют известные периодические свойства и могут быть легко идентифицированы.

Метод	Описание
Метод последовательных разностей	Вычисление разности между значениями функции в соседних точках и проверка постоянства этой разности.
Метод Фурье	Разложение функции в сумму синусоидальных компонент и определение наличия периодических компонент.
Алгоритм корреляции	Сравнение функции с ее сдвинутой копией и измерение степени сходства для определения периодичности.
Анализ явных математических выражений	Идентификация периодических компонент в функции, основанная на знании ее явного математического выражения.

В зависимости от доступной информации и характеристик функции, можно выбрать один или несколько из этих методов для определения периодичности без графика.

По теме: методические разработки, презентации и конспекты

Периодический закон и периодическая система Д.И. Менделеева.

Обощающий урок по данной теме проводится в виде игры, с использованием элементов технологии педагогических мастерских….

Внеклассное мероприятие «Периодический закон и периодическая система химических элементов Д.И. Менделеева»

Внеклассное мероприятие раскрывает историю создания периодического закона и периодической системы Д.И. Менделеева. Информация изложена в стихотворной форме, которая способствует быстрому запоминанию м…

Приложение к внеклассному мероприятию «Периодический закон и периодическая система химических элементов Д.И. Менделеева»

Открытию закона предшествовала длительная и напряженная научная работа Д.И. Менделеева в течение 15 лет, а дальнейшему его углублению было отдано еще 25 лет….

Аргумента x, то она называется периодической, если есть число T, что для любого x F(x + T) = F(x). Это число T и называется периодом функции.

Периодов может быть и несколько. Например, функция F = const для любых значений аргумента принимает одно и то же значение, а потому любое число может считаться ее периодом.

Обычно интересует наименьший не равный нулю период функции. Его для краткости и называют просто периодом.

Классический пример периодических функций — тригонометрические: синус, косинус и тангенс. Их период одинаков и равен 2π, то есть sin(x) = sin(x + 2π) = sin(x + 4π) и так далее. Однако, разумеется, тригонометрические функции — не единственные периодические.

Относительно простых, базовых функций единственный способ установить их периодичность или непериодичность — вычисления. Но для сложных функций уже есть несколько простых правил.

Если F(x) — с периодом T, и для нее определена производная, то эта производная f(x) = F′(x) — тоже периодическая функция с периодом T. Ведь значение производной в точке x равно тангенсу угла касательной графика ее первообразной в этой точке к оси абсцисс, а поскольку первообразная периодически повторяется, то должна повторяться и производная. Например, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется неизменно.

Однако обратное не всегда верно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.

Если F(x) — периодическая функция с периодом T, то G(x) = a*F(kx + b), где a, b, и k — константы и k не равно нулю — тоже периодическая функция, и ее период равен T/k. Например sin(2x) — периодическая функция, и ее период равен π. Наглядно это можно представить так: умножая x на какое-нибудь число, вы как бы сжимаете график функции по горизонтали именно в столько раз

Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Однако ее период не будет простой суммой периодов T1 и T2. Если результат деления T1/T2 — рациональное число, то сумма функций периодична, и ее период равен наименьшему общему кратному (НОК) периодов T1 и T2. Например, если период первой функции равен 12, а период второй — 15, то период их суммы будет равен НОК (12, 15) = 60.

Наглядно это можно представить так: функции идут с разной «шириной шага», но если отношение их ширин рационально, то рано или поздно (а точнее, именно через НОК шагов), они снова сравняются, и их сумма начнет новый период.

Однако если соотношение периодов иррационально, то суммарная функция не будет периодической вовсе. Например, пусть F1(x) = x mod 2 (остаток от деления x на 2), а F2(x) = sin(x). T1 здесь будет равен 2, а T2 равен 2π. Соотношение периодов равняется π — иррациональному числу. Следовательно, функция sin(x) + x mod 2 не является периодической.

Повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (пери́ода
функции) на всей области определения.

Говоря более формально, функция называется периодической с периодом
T
≠
0
{\displaystyle T\neq 0}
, если для каждой точки
x
{\displaystyle x}

из её области определения точки
x
+
T
{\displaystyle x+T}
и
x
−
T
{\displaystyle x-T}
также принадлежат её области определения, и для них выполняется равенство
f
(x)
=
f
(x
+
T)
=
f
(x
−
T)
{\displaystyle f(x)=f(x+T)=f(x-T)}
.

Исходя из определения, для периодической функции справедливо также равенство
f
(x)
=
f
(x
+
n
T)
{\displaystyle f(x)=f(x+nT)}
, где
n
{\displaystyle n}

— любое целое число.

Однако если у множества периодов
{
T
,
T
>
0
,
T
∈
R
}
{\displaystyle \{T,T>0,T\in \mathbb {R} \}}
имеется наименьшее значение, то оно называется основным (или главным) периодом
функции.

Возрастающая и убывающая функция

О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x). Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2}, причем x_{1} > x_{2}, будет y(x_{1}) > y(x_{2}).

Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x). Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2}, причем x_{1} > x_{2}, будет y(x_{1}) < y(x_{2}).

Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0).

а) Если при x > 0 четная функция возрастает, то убывает она при x < 0

б) Когда при x > 0 четная функция убывает, то возрастает она при x < 0

в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x < 0

г) Когда нечетная функция будет убывать при x > 0, то она будет убывать и при x < 0

Ограниченность функции

Случай 1

Рассмотрим функцию $y=f\left(x\right)$ на интервале $\left(a,\; b\right)$. Будем выбирать на нём произвольные точки $x^{*} $ и сравнивать значения $y^{*} =f\left(x^{*} \right)$ с некоторым заданным числом $M>0$. На этом интервале функция считается ограниченной, если справедливо неравенство $\left|y^{*} \right|\le M$.

График такой функции расположен в полосе между горизонтальными прямыми, проведёнными через точки $y=M$ и $y=-M$.

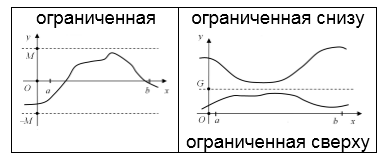
Пример 1

Рассмотрим функцию $y= \sin x$ и число $M=1$. Функция ограничена, так как значения $\left|\sin x\right|\le 1$ для любых $-\infty

Случай 2

На интервале $\left(a,\; b\right)$ функция считается ограниченной сверху или ограниченной снизу, если существует такое число $G$, что $y^{*} \le G$ или $y^{*} \ge G$ соответственно. При этом график функции располагается или под, или над горизонтальной прямой, проведённой через точку $y=G$.

Пример 2

Функция $y=\frac{1}{x} $ ограничена сверху на интервале $\left(-\infty ,\; 0\right)$, и ограничена снизу на интервале $\left(0,\; +\infty \right)$, причем в обоих случаях $G=0$, то есть соответствующие графики расположены ниже и выше оси $Ox$.

Четность и нечетность функции

Рассмотрим функцию $y=f\left(x\right)$ на интервале $\left(-a,\; a\right)$, симметричном относительно начала координат. Данная функция будет считаться четной на этом интервале, если справедливо равенство $f\left(-x\right)=f\left(x\right)$, и нечетной, если $f\left(-x\right)=-f\left(x\right)$. Если же ни одно из указанных условий не выполняется, то функция не относится ни к четным, ни к нечетным.

График четной функции симметричен относительно оси $Oy$, нечетной — относительно начала координат.

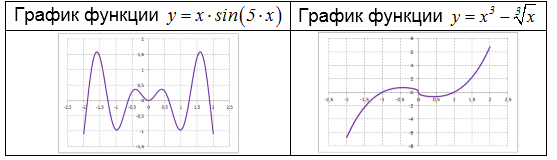
Задача 1

Проанализировать на четность (нечетность) функцию $y=x\cdot \sin \left(5\cdot x\right)$.

Заменим в функции $x$ на $-x$. Получим:

\

Следовательно, данная функция четная. Её график симметричен относительно оси $Oy$.

Задача 2

Проанализировать на четность (нечетность) функцию $y=x^{3} -\sqrt{x} $.

Заменим в функции $x$ на $-x$. Получим:

\{-x} =-\left(x^{3} \right)-\left(-\sqrt{x} \right)=-\left(x^{3} \right)+\sqrt{x} =-f\left(x\right). \]

Следовательно, данная функция нечетная. Её график симметричен относительно начала координат.

Периодичность функции

Рассмотрим функцию $y=f\left(x\right)$ на интервале $\left(a,\; b\right)$. Данная функция будет считаться периодической на этом интервале, если существует некоторое постоянное число $T>0$, для которого $f\left(x\pm T\right)=f\left(x\right)$ при $a

Задача 3

Найти период функции $y=\sin \left(2\cdot x+5\right)$ при $ -\infty

Условие периодичности имеет вид $\sin \left(2\cdot \left(x+T\right)+5\right)=\sin \left(2\cdot x+5\right)$. По формуле для разности синусов получим $\sin T\cdot \cos \left(2\cdot x+5+T\right)=0$. Сомножитель $\sin T$ не зависит от $x$, и поэтому уравнение $\sin T=0$ дает значение основного периода $T=\pi $. Из уравнения $\cos \left(2\cdot x+5+T\right)=0$ значение периода, независимого от $x$, получить невозможно.

Способы задания функции

Кроме графического и аналитического способов задания функции, использованных выше, существует еще и табличный.

При табличном способе в определенном порядке выписываются значения аргумента $x_{1} ,\; x_{2} ,\; \ldots ,\; x_{n} $ и соответствующие значения функции $y_{1} ,\; y_{2} ,\; \ldots ,\; y_{n} $. В таком виде часто получают функции во время измерительных экспериментов. Кроме того, таблицы значений разнообразных специальных функций мы можем видеть в справочниках.

Форма аналитического способа задания функции может быть явной, неявной и параметрической.

Если функция $y$ аргумента $x$ имеет вид уравнения, разрешенного относительно $y$, то есть $y=f\left(x\right)$, то такая форма аналитического задания называется явной. Примеры представлены в задачах выше.

Если аргумент $x$ и функция $y$ связаны между собой уравнением, не разрешенным относительно $y$, то есть в виде $F\left(x,\; y\right)=0$, то такая форма аналитического задания называется неявной. Например, $y^{2} +\cos \left(x+y\right)=0$.

Если соответствующие значения аргумента $x$ и функции $y$ связаны между собой через третью вспомогательную переменную (параметр) $t$, то есть $x=x\left(t\right)$ и $y=y\left(t\right)$, то такая форма аналитического задания называется параметрической. Например, $x=2\cdot tgt$, $y=5\cdot \cos t$.

Определение периодичности

Периодичность функции — это повторение определенного паттерна в ее значениях через заданный интервал. Определить периодичность функции можно с помощью следующих шагов:

1. Изучение графика функции. На графике можно обнаружить повторяющиеся участки и сделать предположение о периодичности функции.
2. Расчет разности между значениями функции для разных аргументов. Если разность между значениями равна определенному числу, это может указывать на периодичность функции.
3. Проверка функции на равенство значений при смещении аргумента на определенное число (период). Если функция возвращается к начальному значению, то это может указывать на периодичность.
4. Исследование функции на симметричность относительно оси абсцисс. Если функция симметрична, то она, скорее всего, периодична.
5. Построение таблицы значений функции для разных аргументов и поиск повторяющихся значений. Если значения функции повторяются через заданный интервал, это может указывать на периодичность.
6. Расчет производной функции и анализ ее свойств. Если производная функции имеет периодическую структуру, то и сама функция, скорее всего, периодична.

Если один или несколько шагов указывают на возможную периодичность функции, следует провести более детальный анализ, чтобы подтвердить или опровергнуть это предположение.

Простая физика — EASY-PHYSIC

В этой статье обсуждаем периодичность функций: как определить, периодична ли  функция, и каков ее период.

Функция периодична, если  некоторый набор ее значений повторяется раз за разом, и точки с одинаковыми значениями функции расположены на числовой оси с равными промежутками. Это расстояние и будем называть периодом. Периодичная функция может иметь и несколько периодов, самый маленький положительный из них будем называть основным.

Тогда, если мы знаем период, мы можем, зная все значения функции на протяжении данного периода, достроить функцию, либо узнать ее значения в любой точке числовой оси – то есть при любом аргументе.

Периодичная функция

Пример 1: функция имеет период, равный 2: и при . Найдите значение выражения .

Раз наша функция принимает форму части параболы на отрезке при периоде, равном 2, значит, такую же форму она будет иметь и на следующем отрезке – , и на отрезке .

Определение значения периодичной функции

Видно, что функция принимает одинаковые значения в точках, отстоящих друг от друга на 2, 4, 6  единиц и т.д., тогда . Найдем эти значения функции. В точке (-1) функция принимает значение , в точке (3,5) функция принимает значение .

Теперь найдем значение искомого выражения: .

Строго говоря, функция периодична, если есть такое число Т, что .

Попробуем научиться определять, периодична ли функция или нет. Для этого рассмотрим несколько примеров.

Пример 2. Проверим, периодична ли функция .

Установим, выполняется ли условие: , то есть ? Очевидно, что данное условие не выполняется. Значит, функция непериодична.

Пример 3. Проверим, периодична ли функция .

Функцию для удобства представим в виде: .

Установим, выполняется ли условие: , то есть ? Очевидно, что данное условие не выполняется: . Значит, функция непериодична.

Пример 4. Проверим, периодична ли функция . Если функция периодична, то будет выполняться условие: , то есть . Поскольку нам все равно, в какой точке числовой оси мы проведем свое исследование, то очень удобно начать с точки . Тогда  , или . Это означает, что либо  , либо ,  то есть либо ,  либо ,  а так как главным считается наименьший  положительный период, то .

Определение периода функции

В данном примере делать проверку необязательно, но проверка бывает очень полезна в более сложных задачах, поэтому сделаем ее здесь для тренировки: .

Пример 5. Определить периодичность функции .

Если Т – период, то .

В это равенство подставим какие-нибудь «удобные» точки, например, . Получим:

Далее есть два пути отыскания периода, первый – решение этого уравнения, второй – составление еще одного уравнения такого же вида. Если функция имеет период Т, то верно и следующее: . Подставим  «удобную» точку :

Пользуясь четностью косинуса  и нечетностью синуса можем записать:

Имеем систему:

Уравнения сложим, и получим

, откуда

, при получим  – ведь нам нужен наименьший период.

Теперь испробуем второй путь, решим это уравнение: . Из основного тригонометрического тождества:

Оставим в левой части только корень:

Возведем в квадрат:

Тогда либо , либо и .

Это уравнение имеет два решения, одно из которых (второе) – посторонний корень, появившийся при возведении в квадрат. Проверка подстановкой его в исходное уравнение позволит нам выявить его и отбросить. Таким образом, получаем:

и наименьшим будет период при , то есть .

Здесь также необходимо сделать проверку. Подставим полученный период в условие  :

, то есть

период данной функции — .

Определение периода функции

Пример 6. Определить периодичность функции и найти ее основной период.

Если Т – период, то

Подставим , имеем

,

Или , , наименьший период при , .

Проверим:

Определение периода функции

Пример 7. Определим период функции .

Запишем условие периодичности:

, если , то

, откуда  , . При , , при , . Проверкой можно показать, что периодом не является. Тогда . Действительно:

Определение периода функции

Пример 8. Доказать, что периодом функции является .

Тогда:

Пример 9. Доказать, что периодом функции является .

Тогда:

Если , то

, а  так как и —  одна и та же точка на единичной окружности, то равенство выполняется.

Удачи вам в учебе и надеюсь, эта статья вам помогла.

Способы задания функции

Кроме графического и аналитического способов задания функции, использованных выше, существует еще и табличный.

При табличном способе в определенном порядке выписываются значения аргумента $x_{1} ,\; x_{2} ,\; \ldots ,\; x_{n} $ и соответствующие значения функции $y_{1} ,\; y_{2} ,\; \ldots ,\; y_{n} $. В таком виде часто получают функции во время измерительных экспериментов. Кроме того, таблицы значений разнообразных специальных функций мы можем видеть в справочниках.

Форма аналитического способа задания функции может быть явной, неявной и параметрической.

Если функция $y$ аргумента $x$ имеет вид уравнения, разрешенного относительно $y$, то есть $y=f\left(x\right)$, то такая форма аналитического задания называется явной. Примеры представлены в задачах выше.

Если аргумент $x$ и функция $y$ связаны между собой уравнением, не разрешенным относительно $y$, то есть в виде $F\left(x,\; y\right)=0$, то такая форма аналитического задания называется неявной. Например, $y^{2} +\cos \left(x+y\right)=0$.

Если соответствующие значения аргумента $x$ и функции $y$ связаны между собой через третью вспомогательную переменную (параметр) $t$, то есть $x=x\left(t\right)$ и $y=y\left(t\right)$, то такая форма аналитического задания называется параметрической. Например, $x=2\cdot tgt$, $y=5\cdot \cos t$.

Возрастание и убывание функций

Посмотрим на график произвольной функции:

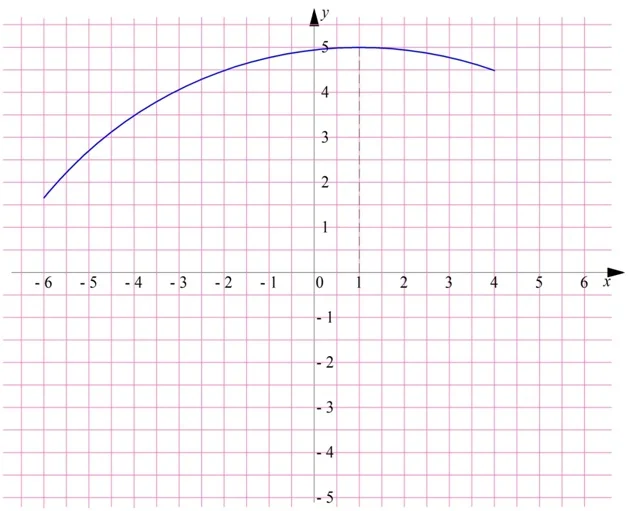
Видно, что область определения ф-ции – это промежуток .

На графике сначала ф-ция как бы «поднимается». При увеличении х растет значение у. Так происходит до точки (1; 5). После этого ситуация меняется, при увеличении аргумента значение ф-ции начинает падать. В математике принято говорить, что ф-ция возрастает на промежутке и функция убывает на промежутке . Можно сказать и иначе – ф-ция у является возрастающей функцией на множестве и убывающей функцией на множестве .

Рассмотрим это определение возрастающей функции подробнее. Построим произвольную возрастающую ф-цию и выберем на ней две точки со значениями аргумента х₁ и х₂. Также отметим значения ф-ции в этих точках, у(х₁) и у(х₂):

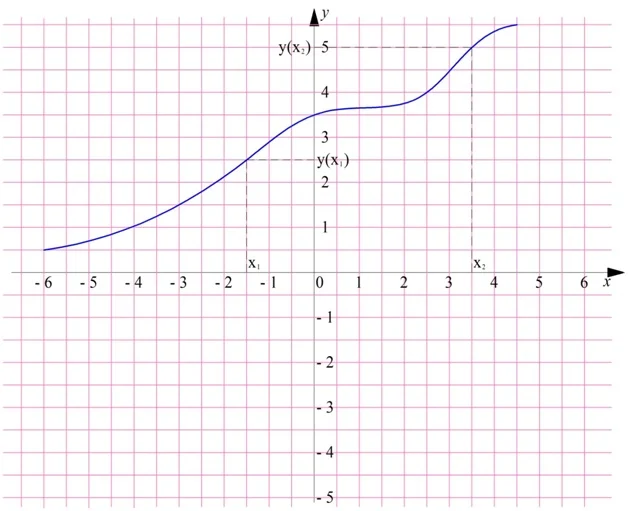
По определению, если х₁ меньше х₂, то и у(х₁) <у(х₂). Другими словами, из двух точек та, которая располагается левее (то есть имеет меньшее значение х), будет одновременно располагаться и ниже, (то есть иметь меньшее значение у).

Мы видим возрастание функции на промежутке . Однако она также будет возрастать и на любом другом промежутке, который является частью отрезка . Например, можно сказать, что она возрастает на промежутке или .

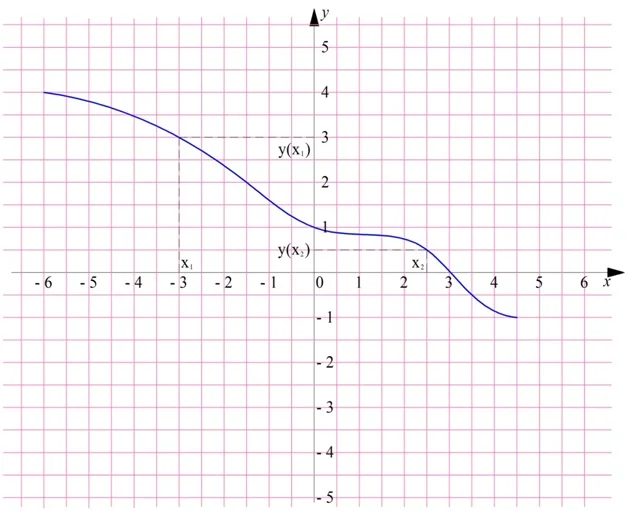
Аналогично дается и определение убывающей ф-ции:

По сравнению с определением возрастающей ф-ции изменился лишь один символ, в последнем неравенстве для у(х₁) и у(х₂) стоит знак «больше» а не меньше. Покажем пример убывания функции.

Заметим, что в приведенных определениях используются строгие неравенства со знаками «>»и «<». Однако в математике используются и нестрогие неравенства, содержащие знаки «≤» и «≥». С их использованием можно записать ещё 2 определения:

 

Приведем пример неубывающей ф-ции:

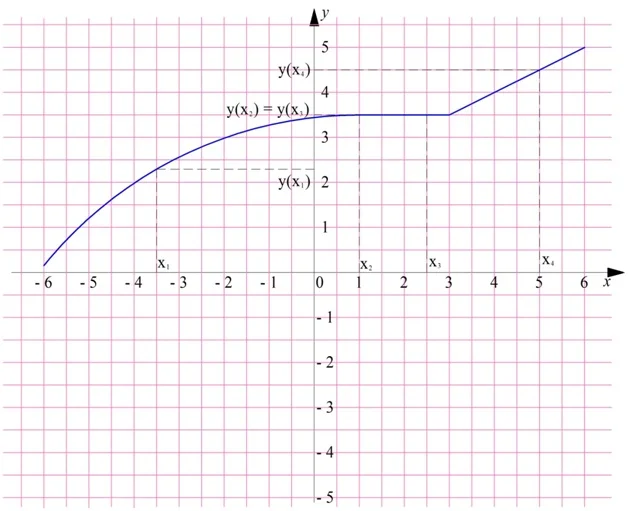
Здесь х₁<x₂<x₃<x₄. Видно, что, например, у(х₁) <у(х₂). Однако у(х₂) = у(х₃). Получается, что на графике ф-ции есть плоская «площадка» на промежутке . Для всех значений х из этого промежутка у = 3,5. Из-за этой площадки ф-цию нельзя считать строго возрастающей.

Теперь покажем пример невозрастающей ф-ции:

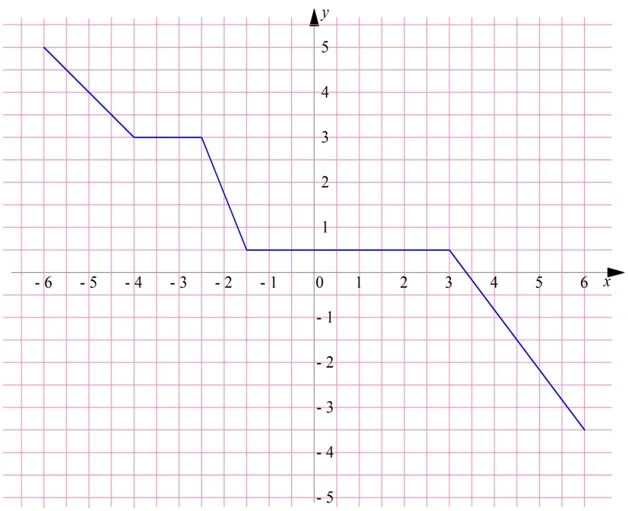
Здесь также есть плоские «площадки», из-за которых ф-цию нельзя считать просто убывающей.

Ясно, что всякая возрастающая ф-ция является неубывающей, а каждая убывающая ф-ция одновременно считается и невозрастающей.

В математике часто вместо всех этих терминов используют понятие монотонности. Дадим определение монотонной функции:

Если же ф-ция убывает или возрастает на промежутке (то есть не имеет плоской площадки), то говорят, что она строго монотонна.

Рассмотрим ф-цию, изображенную на рисунке:

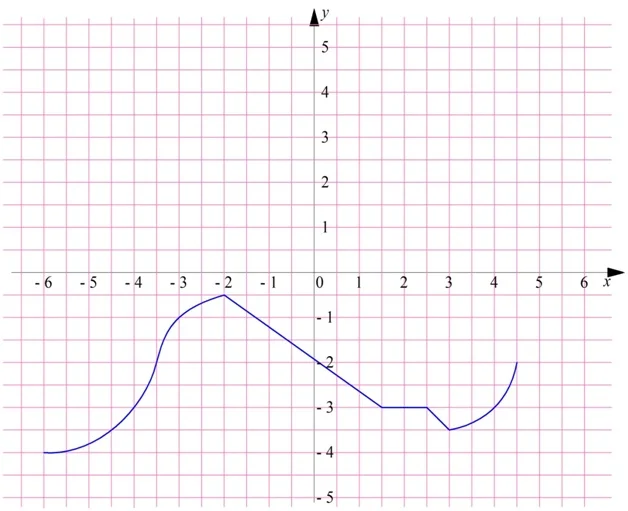
Ф-ция возрастает на промежутках и , а также убывает на промежутках и . Значит, на каждом из этих промежутков ф-ция строго монотонна. На отрезке ф-ция невозрастающая, поэтому здесь она просто монотонна. Любой промежуток, на котором ф-ция монотонна, называют промежутком монотонности.

Различают как промежутки убывания функции, так и промежутки возрастания функции.

Понятно, что если ф-ция строго монотонна, то она и просто монотонна. В большинстве школьных задач не важна строгость монотонности, поэтому слово «строго» часто опускают.

Во всех данных определениях рассматривалось поведение ф-ции на каком-то отдельном числовом промежутке. Одна и та же ф-ция может на одном числовом промежутке возрастать, а на другом убывать. Однако некоторые ф-ции сохраняют свой характер на всей своей области определения. Например, линейная ф-ция у = 2х – 3 возрастает на протяжении всей числовой прямой, то есть на промежутке (– ∞; + ∞):

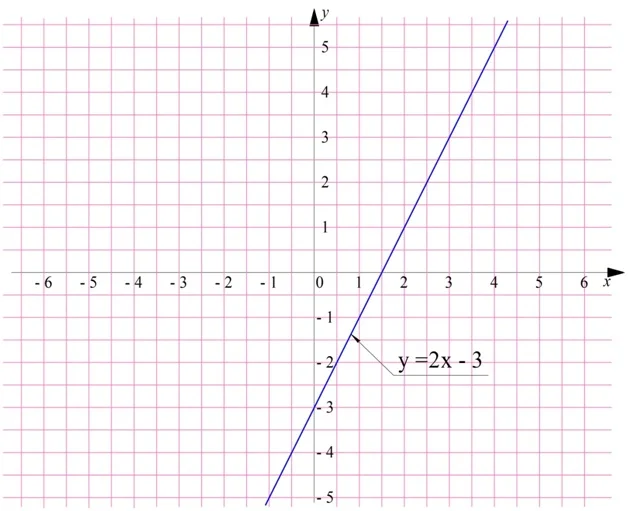
В большинстве случаев промежутки монотонности ф-ции очевидны, исходя из графика ф-ции. Однако и без их построения можно аналитически доказывать монотонность ф-ции.

Пример. Докажите, что ф-ция у = 2х – 3 возрастает на промежутке (– ∞; + ∞).

Решение. Выберем произвольные числа х₁ и х₂, причем х₁< х₂. Разность (х₂ – х₁) будет, очевидно, положительным числом. Найдем теперь разность (у(х₂) – у(х₁)):

у(х₂) – у(х₁) = (2х₂ – 3) – (2х₁ – 3) = 2х₂– 3 – 2х₁+ 3 = 2х₂ – 2х₁ = 2(х₂ – х₁)

Так как (х₂ – х₁) – положительное число, то и 2(х₂ – х₁), а значит, и (у(х₂) – у(х₁)) – тоже положительное число. Если же разность двух числе положительна, то уменьшаемое больше вычитаемого. Значит, у(х₂) > у(х₁). По определению получаем, что у = 2х – 3 – возрастающая ф-ция.

Свойства монотонных функций

Монотонные функции имеют ряд примечательных свойств, которые могут помогать при решении задач. Вспомним, что некоторые ф-ции могут при различных значениях аргументов принимать одинаковое значение. Например, таковой является степенная ф-ция у = х2:

у(2) = 4

у(– 2) = 4

С точки зрения графиков это означает, что горизонтальная линия может пересекать график ф-ции в нескольких точках:

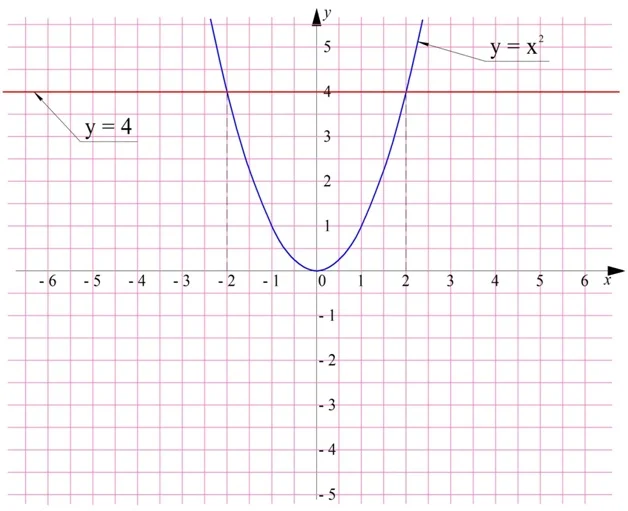
С другой стороны, это значит, что уравнение х2 = 4 имеет два корня, 2 и ( – 2).

Если же ф-ция строго монотонна, то такая ситуация невозможна. Любое ее значение может быть получено только при одном значении аргумента.

Действительно, если ф-ция монотонна, то любая горизонтальная прямая сможет пересечь ее график не более чем в одной точке:

Это также означает, что, если у(х) – строго монотонная ф-ция, а b– произвольное число, то уравнение у(х) = b имеет не более одного корня. Так, у уравнения х3 = 8 есть только один корень (он равен 2), потому что х3 – монотонная ф-ция.

Рассмотрим следующее свойство монотонных функций.

Действительно, ранее мы уже изучали сжатие и растягивание графиков. умножение ф-ции на постоянное число как раз и ведет к подобным преобразованиям. Ясно, что при этом не происходит изменение монотонности ф-ций:

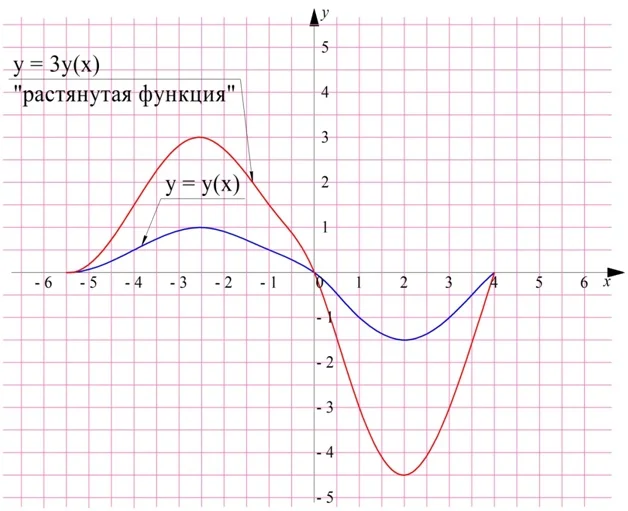
Например, парабола у = х2 возрастает на промежутке [0; + ∞), значит, и ф-ция у = 3х2 также возрастает на этом же промежутке:

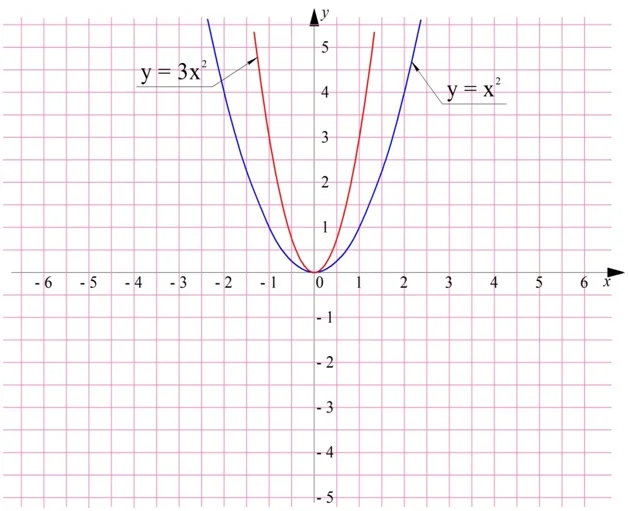
Проще говоря, при умножении ф-ции на положительное число ее промежутки монотонности не изменяются.

А что же произойдет при умножении ф-ции на отрицательное число. Она не только сожмется или растянется, но ещё и отобразится симметрично относительно оси Ох. В результате промежутки возрастания ф-ции превратятся в промежутки убывания, и наоборот.

Проиллюстрируем это на примере ф-ций у = х2 и у = – х2:

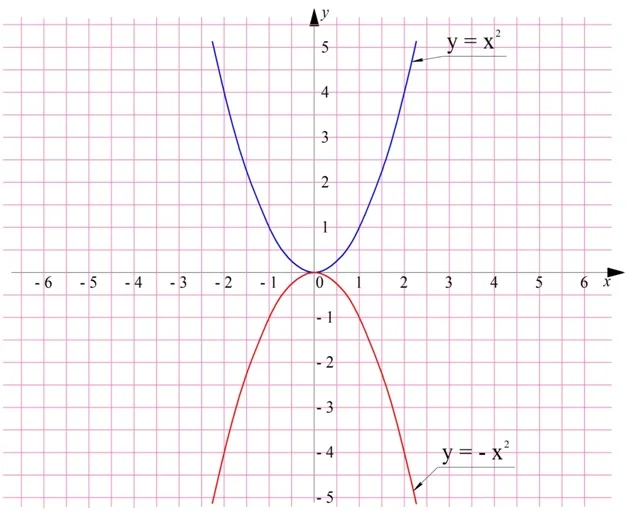
Видно, что на промежутке (– ∞; 0] ф-ция у = – х2 возрастает, в то время как обычная парабола убывает. На промежутке [0; + ∞)ситуация противоположная.

Если две ф-ции одновременно возрастают на одном промежутке, то и их сумма также будет возрастать на этом промежутке.

Например, ф-ции у = х5 и у = 4х возрастают на всей числовой прямой. Следовательно, возрастающей является и ф-ция у = х5 + 4х.

Пример. Решите уравнение

х7 + 2х – 3 = 0

Решение. Можно заметить, что число 1 является корнем этого уравнения. Действительно, подставим единицу в уравнение и получим верное равенство:

17 + 2•1 – 3 = 0

1 + 2 – 3 = 0

0 = 0

Докажем, что других корней уравнение не имеет. В его левой части стоит сумма двух возрастающих ф-ций, у = х7 и у = 2х – 3. Следовательно, и ф-ция у = х7 + 2х – 3 также является возрастающей на всей числовой прямой. Это значит, что исследуемое уравнение имеет не более 1 корня, то есть корень х = 1 – единственный.

Ответ: 1.

Пример. Докажите, что у уравнения

не более одного корня.

Решение.

Выражение в левой части имеет смысл только при положительных х. Ведь если х < 0, то под корнем окажется отрицательное число, а если х = 0, то ноль окажется в знаменателе. Другими словами, уравнение имеет смысл на промежутке (0; + ∞). При этом левая часть представляет собой сумму трех слагаемых:

Первое и третье из них являются возрастающими ф-циями. Второе слагаемое – это взятая со знаком «минус» ф-ция у = 2/х. Так как у = 2/х убывает на промежутке (0; + ∞), то у = – 2/х на нем же возрастает. В итоге получаем, что в левой части сумма трех возрастающих ф-ций, значит, и всё это выражение – возрастающая ф-ция. Из этого следует, что у уравнения есть не более одного корня. Попробуйте сами подобрать его.

суббота, 4 сентября 2021 г.

Урок 5. Периодичность тригонометрических функций

Из этого определения сразу следует, что если Т – период функции

– также периоды функций. Значит у периодической функции бесконечно много периодов.

Чаще всего (но не всегда) среди множества положительных периодов функции можно найти наименьший. Его называют основным периодом .

График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.

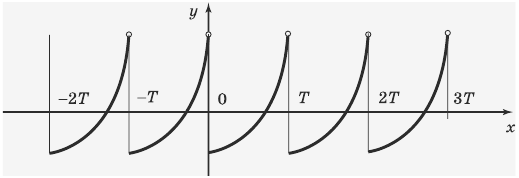
у = х – [х] , где [х] – целая часть числа. Если к произвольному значение аргумента этой функции добавить 1 , то значение функции от этого не изменится :

Следовательно, при любом значении х

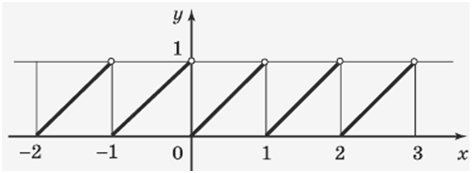
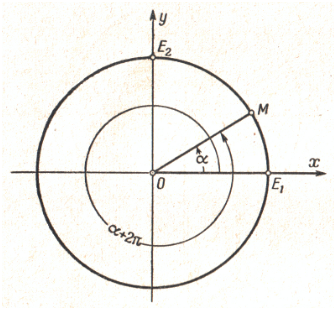
sin (α + 360 ° ) = sin α

Таким образом, функции sin α и cos α от прибавления к аргументу α одного полного оборота ( 2π или 360 ° ) не меняют своих значений.

где k – любое целое число.

Следовательно, функции sin α и cos α – периодические.

Наименьшее положительное число, от прибавления которого к любому допустимому значению аргумента не изменяется значение функции, называется периодом функции.

В самом деле, пусть α – произвольный угол, составленный с осью Ох подвижным радиусом ОМ единичной окружности.

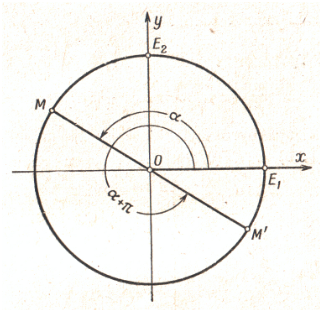
отсюда следует, что значения tg α и с tg α не изменяются, если к углу α прибавить любое число полуоборотов:

где k – любое целое число.

вычисляются по формуле

равен наименьшему числу, при делении которого на T ₁ и T ₂ получаются целые числа.

Найти период функции

не существует, так как такого числа, при делении которого на 2π и на 2 получались бы целые числа, нет.

Периода не существует.

Доказать следующее утверждение :

Так как тангенс – периодическая функция с минимальным периодом 20 ∙ 180 ° , то получим :

Доказать следующее утверждение :

Так как косинус – чётная и периодическая функция с минимальным периодом 2π , то получим :

сos (–13π) = сos 13π = сos (π + 6 ∙ 2π) = сos π = –1.

Доказать следующее утверждение :

Так как синус – нечётная и периодическая функция с минимальным периодом 20 ∙ 360 ° , то получим :

Найти основной период функции

Пусть Т основной период функции, тогда:

так как 2 πk период синуса, то получим :

sin (7х + 7 t ) = sin (7х + 2 πk ),

Найти основной период функции

Пусть Т основной период функции, тогда:

со s 0,3х = со s 0,3(х + t ) = со s (0,3х + 0,3 t )

так как 2 πk период косинуса, то получим :

Найти период функции :

y = 5 sin 2 x + 2 ctg 3х.

Наименьшее число, при делении которого на

Найти период функции :

Находим периоды слагаемых. Период функции

Очевидно, что период заданной функции равен

Найти период функции :

Периода у заданной функции не существует, так как нет такого числа, при делении которого на 2 и на π одновременно получались бы целые числа.

Найти период функции :

Приведём к общему знаменателю периоды :

Тогда наименьшее общее кратное (НОК) будет :

Теперь найдём период заданной функции :

Методы определения периодичности

Одним из наиболее распространенных методов является анализ гармонических колебаний. При этом используется преобразование Фурье, которое позволяет разложить функцию на сумму гармонических компонент с определенными амплитудами и частотами. Периодическая функция будет иметь резко выраженный пик в спектре амплитуд, соответствующий основной частоте соответствующего колебания.

Еще одним методом является анализ автокорреляции. Автокорреляционная функция позволяет найти лаги в функции, которые соответствуют периодическим закономерностям. Пиковые значения автокорреляционной функции указывают на наличие периодичных шаблонов в данных. Относительные значения лагов могут быть использованы для определения периода функции.

Существуют также статистические методы определения периодичности, такие как анализ сезонных временных рядов и вейвлет-преобразование. Анализ сезонных временных рядов позволяет выделить сезонные факторы или повторяющиеся шаблоны, которые могут свидетельствовать о периодичности данных. Вейвлет-преобразование использует вейвлет-функции для разложения сигнала на различные масштабы и частоты, что позволяет выявить периодичность в различных временных масштабах.

Комбинация этих и других методов может быть использована для более точного определения периодичности функций и временных рядов. При анализе реальных данных часто требуется использовать несколько методов и сравнивать их результаты для достижения наилучшей точности и надежности. После определения периода функции можно использовать его для прогнозирования будущих значений и дальнейшего анализа данных.