Функция y = sign(x)
Функция y = sign(x) обозначает знак числа x и определяется следующим образом:
y = sign(x) = {
-1, x 0
}
Свойства функции y = sign(x):
Функция является ступенчатой и постоянна на интервалах (-∞, 0), (0, +∞).
Функция не является непрерывной и не дифференцируемой в точке x = 0.
Построение графика функции y = sign(x):
График функции y = sign(x) представляет собой две горизонтальные линии: y = -1 на интервале (-∞, 0) и y = 1 на интервале (0, +∞). В точке x = 0 график функции имеет разрыв.
Примеры применения функции y = sign(x):
Использование в физике для определения направления силы или скорости.
Использование в анализе данных для определения направления изменения значения переменной.
В заключении можно отметить, что функции y = |x|, y = , y = {x} и y = sign(x) являются важными и широко используемыми математическими функциями. Знание и понимание свойств их графиков позволяет более глубоко понимать многие явления и процессы, которые возникают в нашей жизни и в различных областях знаний.
Периодические функции.
Число \(T\neq 0\) называют периодом функции \(f\), если для любого \(x\in D(f)\) значения \(x+T\) и \(x-T\) также принадлежат \(D(f)\) и выполняется равенство
$$
f(x-T)=f(x)=f(x+T).\nonumber
$$
Функцию, имеющую период \(T\), называют периодической с периодом \(Т\).
Отметим, что если \(T\) — период функции \(f\), то каждое число вида \(nT\), где \(n\in\mathbb{Z},\;n\neq 0\), также является периодом этой функции.
Примерами периодических функций могут служить тригонометрические функции. При этом число \(2\pi\) — наименьший положительный период функций \(\sin x,\;\cos x,\) a \(\pi\) — наименьший положительный период функций tg x и ctg x.
Пример 10
Доказать, что функция \(f(x)=\sin\alpha x\), где \(\alpha>0\) является периодической, и найти ее наименьший положительный период.
\(\triangle\) Предположим, что \(f\) — периодическая с положительным периодом T функция. Тогда для любых \(x\in\mathbb{R}\) должно выполняться равенство
$$
\sin\alpha x=\sin\alpha (x+T),\label{ref7}
$$
откуда при х = 0 получаем
$$
\sin\alpha T=0,\ T=\frac{k\pi}{\alpha},\nonumber
$$
где \(k\in\mathbb{N}\).
Таким образом, положительными периодами функции \(\sin\alpha x\) могут быть только числа \(k\pi/\alpha\), где \(k\in\mathbb{N}\). Заметим, что число \(\displaystyle \pi/\alpha\) не является периодом функции \(\sin\alpha x\), так как в противном случае при всех \(x\in\mathbb{R}\) выполнялось бы равенство \(\displaystyle \sin\alpha x=\sin\alpha(x+\pi/\alpha)=\sin(\pi+\alpha x)=-\sin\alpha x\), то есть \(\sin\alpha x=0\), что невозможно.
Число \(\displaystyle 2\pi/\alpha\) — период функции \(\sin \alpha x\), так как при любых \(x\in\mathbb{R}\) справедливо равенство \(\sin \alpha x=\displaystyle \sin \alpha(x+2\pi/\alpha)\).
Таким образом \(2\pi/\alpha\) — наименьший положительный период функции \(\sin\alpha x.\quad \blacktriangle\)
Приложения
Внешние ссылки
- (ru) В. М. Храпченко , “Симметричная функция” , в книге Михиля Хазевинкеля , Энциклопедия математики , Springer ,2002 г.
- (en) Эрик В. Вайстейн , , на сайте MathWorld.
Библиография
- Пьер Картье , « Классическая и современная теория симметричных функций », Seminaire Бурбаки , п о 597, 1982-1983, стр. 1-23
- (о) М. Голубицкий (о) и В. Guillemin , Устойчивые отображения и их особенность , Спрингер , Coll. » GTM » ( п о 14)1973, х + 209 п. ( Обзоры по математике , zbMATH ) , стр. 108 и далее.
- Серж Ланг , Алгебра
- (ru) Б.Л. ван дер Варден , Алгебра I , Спрингер,2003 г., 265 с.
- (ru) Б.Л. ван дер Варден , Алгебра II ,2003 г., 284 с.
- (en) Ян Г. Макдональд , Симметричные функции и многочлены Холла , Oxford University Press , сб. «Оксфордские математические монографии»,1979 г.( ISBN 0-19-853530-9 )
Монотонные функции.
Функцию \(f\) называют возрастающей (неубывающей) на множестве \(X\subset D(f)\), если для любых точек \(x_1 \in X, x_{2}\in X\) таких, что \(x_{1}\;<\;x_{2}\), выполняется неравенство \( f(x_1)\leq f(х_2)\).Если это неравенство является строгим \((f(x_{1})\;<\;f(x_{2}))\), то функцию \(f\) называют строго возрастающей на множестве \(X\).
Таким образом, функция \(f\) называется:
-
возрастающей (неубывающей) на множестве \(X\), если
$$
\forall x_{1}\in X\quad \forall x_{2}\in X:\;x_{1}\;<\;x_{2}\rightarrow f(x_{1})\leq f(x_{2});\nonumber
$$ -
строго возрастающей на множестве \(X\), если
$$
\forall x_{1}\in X\quad \forall x_{2}\in X:\;x_{1}\;<\;x_{2}\rightarrow f(x_{1})\;<\;f(x_{2}).\nonumber
$$
Аналогично функция \(f\) называется:
-
убывающей (невозрастающей) на множестве \(X\), если
$$
\forall x_{1}\in X\quad\forall x_{2}\in X:\;x_{1}\;<\;x_{2}\rightarrow f(x_{1})\geq f(x_{2});\nonumber
$$ -
строго убывающей на множестве \(X\), если
$$
\forall x_{1}\in X\quad\forall x_{2}\in X:\;x_{1}\;<\;x_{2}\rightarrow f(x_{1})>f(x_{2}).\nonumber
$$
Убывающие и возрастающие функции объединяют названием монотонные, а строго возрастающие и строго убывающие — названием строго монотонные.
Если \(X=D(f)\), то в этих определениях указание на множество \(X\) обычно опускают.
Пример 9
Доказать, что функция f строго возрастает на множестве X, если:
- \(f(x)=x^{3},\;X=\mathbb{R}\);
- \(f(x)=\sin x, X=\).
- Если \(0\leq x_{1}\;<\;x_{2}\), то \(x_{1}^{3}\;<\;x_{2}^{3}\), а если \(x_1\;<\;x_{2}\leq 0\), то \(0\leq-x_{2}\;<\;-x_{1}\), откуда
$$
(-x_{2})^{3}\;<\;(-x_{1})^{3}.\label{ref6}
$$
Так как \(x^{3}\) — нечетная функция, то неравенство \eqref{ref6} можно записать в виде \(-x_{2}^{3}\;<\;-x_{1}^{3}\), откуда \(x_{1}^{3}\;<\;x_{2}^{3}\). Наконец, если \(x_1\;<\;0\), а \(x_{2}>0\), то \(x_{1}^{3}\;<\;x_{2}^{3}\). Таким образом, неравенство \(x_{1}^{3}\;<\;x_{2}^{3}\) справедливо для любых \(x_{1}\in\mathbb{R},\;x_{2}\in\mathbb{R}\) таких, что \(x_{1}\;<\;x_{2}\). Поэтому \(x^3\) — строго возрастающая на \(\mathbb{R}\) функция. - Пусть \(\displaystyle -\frac{\pi}{2}\leq x_{1}\;<\;x_{2}\leq\frac{\pi}{2}\); тогда
$$
\sin x_{2}-\sin x_{1}=2\sin\frac{x_{2}-x_{1}}{2}\cos\frac{x_{2}+x_{1}}{2}>0,\nonumber
$$
так как \(0\;<\;\displaystyle \frac{x_{2}-x_{1}}{2}\;<\;\frac{\pi}{2},\quad -\displaystyle \frac{\pi}{2}\;<\;\frac{x_{2}+x_{1}}{2}\;<\;\frac{\pi}{2}\).Таким образом, неравенство \(\sin x_{2}>\sin x_{1}\) выполняется для \(x_{1},x_{2}\displaystyle \in\), если \(x_{2}>x_{1}\). Следовательно, функция \(\sin x\) строго возрастает на отрезке \(\displaystyle .\quad\blacktriangle\)
Модуль аргумента и модуль функции
Внимание: мелкие рисунки увеличиваются щелчком левой клавиши мыши.
Если Вы попали на эту страницу из поисковика, миновав предыдущие разделы темы «Графики функций и их преобразования», то рекомендую сначала повторить графики основных элементарных функций и общие правила преобразования графиков функций.
Модуль переменной (абсолютная величина значения) определяется следующим образом:
- если если
В контексте построения графиков это означает использование преобразования симметрии относительно осей координат.
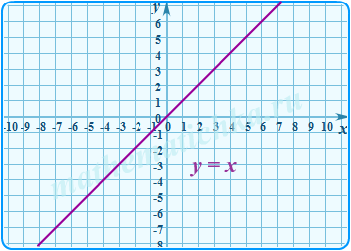
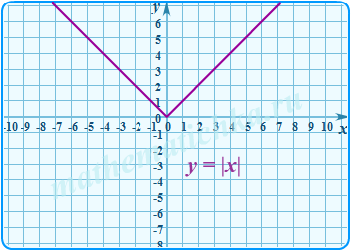
Iy = f(|x|)
- Построить график функции .
- Исключить его часть, расположенную в отрицательной половине оси абсцисс. (Например, просто стереть ластиком, если график был построен карандашом.)
- Построить левую ветвь графика (при отрицательных x) симметричным отображением его правой ветви относительно оси Oy.
II
- Построить график функции .
- Участок графика, расположенный ниже оси абсцисс (при отрицательных y) развернуть на верхнюю половину координатной сетки преобразованием симметрии относительно оси Ox.
Пример 1.
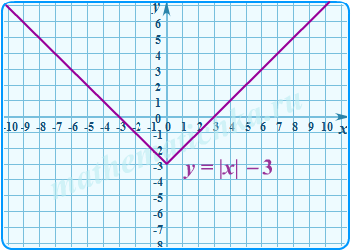
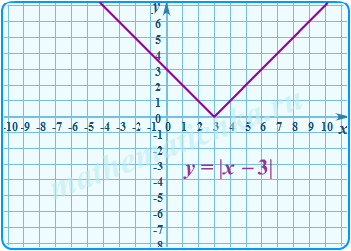
В этом примере оба графика получены из графика функции Первый — преобразованием Гf(x) → Гf(|x|), второй — преобразованием Гf(x) → Г|f(x)|.
Пример 2.
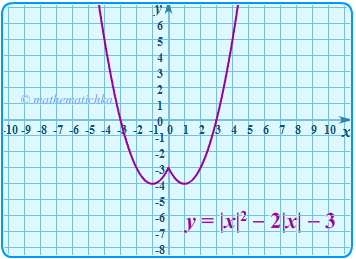
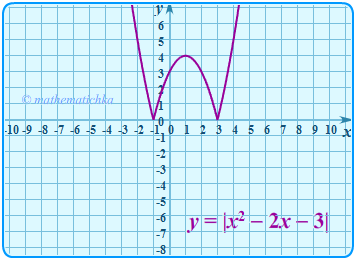
В этом примере оба графика получены из графика функции Первый — преобразованием Гf(x) → Гf(|x|), второй — преобразованием Гf(x) → Г|f(x)|.
Один из способов быстро и точно построить исходную параболу по характерным точкам показан в видео на канале Mathematichka.
IIIпоследовательность преобразований
- 1.
2.
3.
4.
5.
| 1. | 2. | 3. | 4. | 5. |
IV Равенство вида по определению не является функцией, так как допускает неоднозначность при вычислении значения y. Однако линию на координатной плоскости оно задает, и эту линию тоже можно построить, исходя из графика функции . Для этого нужно:
- Построить график функции .
- Исключить его часть, расположенную ниже оси абсцисс, поскольку указанное равенство возможно только для положительных значений f(x).
- Построить нижнюю часть линии (при отрицательных y) симметричным отображением относительно оси Ox.
- 6.
7.
8.
| 6. | 7. | 8. |
Пример 3.
Задан график функции . Построить кривые, удовлетворяющие уравнению, .
Заметим, что (значение четной степени, как и значение модуля, всегда неотрицательно). Поэтому, выделяя полный квадрат, преобразуем функцию к виду
и строим её график последовательными преобразованиями.
Строим график функции переносом на 1 вправо вдоль оси Ox, а затем переносом вниз на 6 единиц вдоль оси Oy.
Строим график функции с использованием преобразования симметрии относительно оси Oy.
Строим линии, удовлетворяющие уравнению с использованием преобразования симметрии относительно оси Ox.
- 1.
2.
3.
4. 5.
6.
| 1. | 2. | 3. | 4. |
| 5. | 6. |
Следующий график постройте самостоятельно, чтобы убедиться, что вы правильно поняли материал.
Пример 4.
Задан график функции . Построить график функции .
Показать ответ
Характеристики
Когда функции имеют действительные или комплексные значения, симметричные функции образуют подалгебру алгебры функций с n переменными, то есть:
- сумма двух симметричных функций остается симметричной функцией;
- произведение двух симметричных функций остается симметричной функцией.
Любая симметричная рациональная дробь (над коммутативным полем ) является частным двух симметричных многочленов.
Демонстрация
Позвольте быть симметричной рациональной дроби.
Fзнак равнопQ∈K(Икс1,…,Икснет){\ displaystyle F = {\ frac {P} {Q}} \ in K (X_ {1}, \ dots, X_ {n})}
Обратите внимание на любую перестановку .
s∈Sнет{\ displaystyle s \ in S_ {n}}Qs(Икс1,…,Икснет)знак равноQ(Иксs(1),…,Иксs(нет)){\ Displaystyle Q ^ {s} (X_ {1}, \ dots, X_ {n}) = Q (X_ {s (1)}, \ dots, X_ {s (n)})}
Следовательно, многочлен симметричен (который является многочленом) также, и .
Dзнак равно∏s∈SнетQs{\ Displaystyle D: = \ prod _ {s \ in S_ {n}} Q ^ {s}}НЕТзнак равноFD{\ Displaystyle N: = FD}Fзнак равноНЕТD{\ displaystyle F = {\ frac {N} {D}}}
Примеры применения функций
Функции y = |x|, y = , y = {x} и y = sign(x) находят применение во многих областях науки, техники и экономики. Например, функция y = |x| используется в физике для описания модуля вектора или амплитуды волн. Она также широко применяется в экономике для описания абсолютной величины изменений величин.
Функция y = , называемая функцией целой части, используется в комбинаторике и теории чисел для округления вниз до ближайшего целого числа. Она также может быть использована в экономических моделях для округления до целого числа, например, при расчете налогов.
Функция y = {x}, называемая функцией дробной части, используется в комбинаторике, теории чисел и теории вероятностей. Она также может быть использована в физике и технике при работе с периодическими сигналами и в криптографии для генерации случайных чисел.
Функция y = sign(x), называемая функцией знака, используется в анализе сигналов и теории управления для определения направления движения сигнала или системы. Она также может быть использована в физике и механике для определения направления движения тела.
В целом, функции y = |x|, y = , y = {x} и y = sign(x) являются важными и полезными математическими инструментами для решения различных задач в различных областях науки, техники и экономики.
Обратная функция.
Пусть задана числовая функция \(y=f(x),\;x\in D(f)\). Тогда каждому числу \(x_0\in D(f)\)соответствует единственное число \(y_{0}=f(x_{0})\in E(f)\) . Нередко приходится по заданному значению функции \(y_0\) находить соответствующее значение аргумента, то есть решать относительно \(x\) уравнение
$$
f(x)=y_{0},\quad y_{0}\in E(f).\label{ref8}
$$
Это уравнение может иметь не одно, а несколько и даже бесконечно много решений. Решениями уравнения \eqref{ref8} являются абсциссы всех точек, в которых прямая \(y=y_0\) пересекает график функции \(y=f(x)\).
Например, если \(f(x)=x^{2}\), то уравнение
$$
x^{2}=y_{0},\quad y_{0}>0,\nonumber
$$
имеет два решения: \(x_{0}=\displaystyle \sqrt{y_0}\) и \({\widetilde x}_0=\sqrt{y_0}\). Если \(f(x)=\sin x\), то уравнение
$$
\sin{x}=y_{0},\quad |y_{0}|\leq 1,\nonumber
$$
имеет бесконечно много решений вида \(x_n=(-1)^{n}x_{0}+\pi n\), где \(n\in\mathbb{Z}\;x_0\) — одно из решений этого уравнения.
Однако существуют функции, для которых уравнение \eqref{ref8} при каждом \(y_{0}\in E(f)\) однозначно разрешимо, то есть имеет единственное решение \(x_0\in D(f)\). Этим свойством обладают, например, следующие функции:
- \(f(x)=3x+4,\;D(f)=\mathbb{R}\);
- \(f(x)=x^{3},\;D(f)=\mathbb{R}\);
- \(f(x)=\displaystyle \frac{1}{x},\quad D(f)=\{x\in\mathbb{R},\;x\neq 0\}\).
Если функция \(f\) такова, что при каждое значение \(y_{0}\in E(f)\) она принимает только при одном значении \(x_{0}\in D(f)\) , то эту функцию называют обратимой. Для такой функции уравнение
$$
f(x)=y\nonumber
$$
можно при любом \(у\in Е(f)\)однозначно разрешить относительно \(x\), то есть каждому \(y\in Е(f)\) соответствует единственное значение \(x\in D(f)\).
Это соответствие определяет функцию, которую называют обратной к функции \(f\) и обозначают символом \(f^{-1}\).
Заметим, что прямая \(y=y_0\) для каждого \(y_{0}\in E(f)\) пересекает график обратимой функции \(y=f(x)\) в единственной точке \((x_0,\;y_0)\), где \(f(x_{0})=y_{0}\).
Обозначая, как обычно, аргумент обратной функции буквой \(x\), а ее значения — буквой \(y\), обратную для \(f\) функцию записывают в виде
$$
y=f^{-1}(x),\quad x\in D(f^{-1}).\nonumber
$$
Для упрощения записи вместо символа \(f^{-1}\) будем употреблять букву \(g\).
Отметим следующие свойства, которые показывают, как связаны данная функция и обратная к ней:
- если \(g\) — функция, обратная к \(f\), то и \(f\) — функция, обратная к \(g\); при этом
$$
D(g)=E(f),\quad E(g)=D(f),\nonumber
$$
то есть область определения функции \(g\) совпадает с множеством значений функции \(f\) и наоборот; - для любого \(x\in D(f)\) справедливо равенство
$$
g(f(x))=x,\nonumber
$$
а для любого \(х\in Е(f)\) справедливо равенство
$$
f(g(x))=x;\nonumber
$$ - график функции \(y=g(x)\) симметричен графику функции \(y=f(x)\) относительно прямой \(y=x\);
- если нечетная функция обратима, то обратная к ней функция также является нечетной;
- если \(f\) — строго возрастающая (строго убывающая) функция, то она обратима, причем обратная к ней функция \(g\) также является строго возрастающей (строго убывающей).
Рис. 9.9
Свойства 1) и 2) следуют непосредственно из определения обратной функции, 4) и 5) — из определений обратной и соответственно нечетной и строго монотонной функции.
Рис. 9.10
Рассмотрим свойство 3). Пусть точка \((x_{0},y_{0})\) принадлежит графику функции \(y=f(x)\), то есть \(y_{0}=f(x_0)\). Тогда \(x_{0}=g(y_{0})\), то есть точка \((x_{0},y_{0})\) принадлежит графику обратной функции \(g\). Так как точки \((x_{0},y_{0})\) и \((y_{0},x_{0})\) симметричны относительно прямой \(y=x\) (рис. 9.9), то график функции \(у=g(х)\) симметричен графику функции относительно этой прямой.
Рис. 9.11
На рис. 9.10 изображены графики взаимно обратных функций \(y=x^{2},\;x\geq 0\), и \(y=\sqrt{x}\), а на рис. 9.11 — графики взаимно обратных функций \(y=x^{2},\;x\leq 0\), и \(y=-\sqrt{x}\).
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.



Конспект урока «Четность и нечетность функций»
· повторить такое свойство функции, как чётность и нечётность.
Прежде давайте вспомним свойства функций, о которых мы уже говорили. Это: область определения функции, область значений функции, нули функции, промежутки знакопостоянства функции, промежутки монотонности функции.
Для того чтобы мы могли говорить о чётности, еще раз давайте повторим, что мы понимаем под областью определения функции.
Область определения функции – это все значения, которые может принимать аргумент.
Теперь вспомним, что

Теперь давайте разберёмся с этим определением по подробней. Первым условием является то, что область определения функции должна быть симметрична относительно икс равного нулю. Что это значит? Это значит, что если число А принадлежит области определения, то и число минус А тоже принадлежит области определения этой функции.

Второе условие чётности говорит о том, что:
Если посмотреть на график чётной функции, то можно увидеть, что он будет симметричен относительно оси ординат.
Если же нарушается первое условие, то есть область определения функции – не симметричное относительно x = 0 множество, то такая функция не обладает свойством чётности.
Теперь давайте вспомним какую функцию называют нечётной.
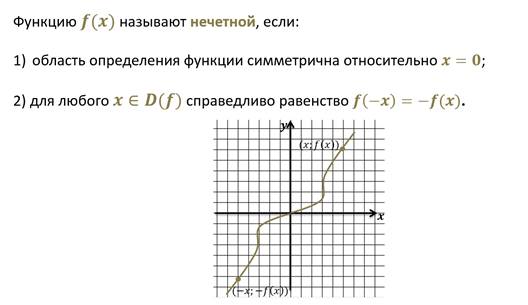
Если мы посмотрим на график нечётной функции, то нетрудно увидеть, что он симметричен относительно начала координат.
Мы с вами уже рассмотрели некоторые элементарные функции, их свойства и графики. А теперь давайте попробуем определить какие из этих функций являются чётными, нечётными, ни чётными, ни нечётными.
Если мы посмотрим на графики прямой пропорциональности, то увидим, что эти графики симметричны относительно начала координат.
Теперь давайте рассмотрим обратную пропорциональность.
Область определения этой функции – симметричная относительно x = 0 область, то есть говорить о чётности или нечётности этой функции можно.
Следующей мы рассмотрим линейную функцию.
То есть линейная функция не является ни чётной, ни нечётной.
Рассмотрим функцию y = │x│.
![]()
Тогда получим, что функция игрек равно модуль икс – чётная функция.
Область определения – вся числовая прямая.
![]()
то есть функция чётная.
Рассмотрим квадратичную функцию.
Область определения – вся числовая прямая.
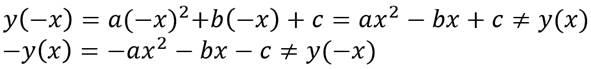
то есть квадратичная функция не является ни чётной, ни нечётной.
Теперь давайте рассмотрим функцию:
Область определения функции – промежуток 0; + ∞) – это не симметричное относительно точки x = 0 множество, то есть мы сразу можем написать, что о чётности или нечётности этой функции говорить нельзя.
![]()
то есть перед нами нечётная функция.
Теперь давайте решим несколько заданий.

Рассмотрим ещё один пример.


Сегодня на уроке мы повторили такое свойство функций как чётность. Вспомнили какая функция называется чётной, а какая – нечётной.
Исследование функций в примерах
Задача №1
Доказать, что функция \(y=x^2\) четная.
1. Найдем область определения: \(D(y):x\in(-\infty;+\infty)\) — симметрична относительно 0.
2. \(f(x)=x^2\)
\(f(-x)=x^2\)
\(f(x)=f(-x)\), значит функция четная.
Задача №2
Исследовать на четность и нечетность функцию \(f(x)=8x^3-7x.\)
1. Найдем область определения: \(D(f):x\in(-\infty;+\infty)\) — симметрична относительно 0.
2. \(f(x)=8x^3-7x\)
\(f(-x)=-8x^3+7x\)
\(f(x)\neq f(-x)\), значит функция не является четной.
\(-f(x)=-8x^3+7x\)
\(-f(x)=f(-x)\), значит функция нечетна.
Задача №3
Исследовать на четность и нечетность функции \(f_1(x)=\frac{x^2}{x-1}\) и \(f_2(x)=\frac4{x^2-1}\)
Рассмотрим первую функцию:
1. Найдем область определения: x — любое число, кроме 1. Она не симметрична относительно 0, значит\( f_1(x)\) относится к функциям общего вида, то есть не является ни четной ни нечетной.
Рассмотрим вторую функцию:
1. Найдем область определения: х — любое число кроме -1 и 1. Она симметрична относительно 0.
2. \(f_1(x)=\frac4{x^2-1}\)
\(f_1(-x)=\frac4{x^2-1}\)
Определение и значение симметричности относительно нуля
Симметрия относительно нуля является отражением равенства значений функции относительно нулевого значения на отрицательное и положительное значение. Такое свойство графика функции позволяет анализировать его особенности и предсказывать значения функции на основе симметричности.
Основное значение симметрии относительно нуля заключается в возможности упрощения математических расчетов и анализа функций. Зная значения функции на одном из отражающихся отрезков, мы можем легко получить значения функции на другом отрезке, использовав симметричность графика. Также симметричность позволяет нам легко определить симметричные точки графика и анализировать его поведение в окрестности нуля.
Важно отметить, что симметричность относительно нуля может наблюдаться не только у функций, но и у других математических объектов, таких как фигуры, геометрические формы и т.д. Использование симметрии помогает в их изучении и анализе и является ключевым элементом в решении различных задач и проблем
Применение графиков, симметричных относительно начала координат в реальной жизни
Графики, симметричные относительно начала координат, находят применение в различных областях жизни, где необходимо отобразить отношения между двумя переменными.
1. Экономика:
В экономической сфере графики, симметричные относительно начала координат, помогают визуализировать зависимость между различными показателями. Например, такие графики могут быть использованы для анализа зависимости между объемом продаж и затратами на производство.
2. Физика:
В физике графики, симметричные относительно начала координат, используются для отображения различных физических закономерностей. Например, график зависимости скорости тела от времени при равномерном прямолинейном движении будет симметричен относительно начала координат.
3. Математика:
В математике графики, симметричные относительно начала координат, используются для исследования и построения функций. Например, симметрия относительно начала координат может указывать на четной или нечетной характер функции.
4. Картография:
В картографии графики, симметричные относительно начала координат, могут использоваться для отображения географических объектов и их расположения относительно друг друга. Например, график симметричный относительно начала координат может описывать границы двух смежных стран.
В заключение, графики, симметричные относительно начала координат, являются удобным инструментом для визуализации и анализа отношений между переменными в различных областях жизни. Они позволяют наглядно представить зависимости и закономерности, что делает их полезными инструментами для исследования и анализа данных.
Понятие области определения функции
Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.
Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).
Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.
Из понятия функции сформулируем определение области определения функции.
Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.
Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = .
Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:
Например, все действительные числа от 2 до 5 включительно можно записать так:
Все положительные числа можно описать так:
Ноль не положительное число, поэтому скобка возле него круглая.








![Функции y=|x|, y=[x], y={x}, y=sign(x) и их графики: основные концепции и практическое применение - napishem.ru](http://mtrufa.ru/wp-content/uploads/f/2/9/f298aea3706a4fa6942a929b7af87168.jpeg)


















![Функции y=|x|, y=[x], y={x}, y=sign(x) и их графики: основные концепции и практическое применение](http://mtrufa.ru/wp-content/uploads/6/f/1/6f1a2a9481c4338c4d03d9c7c5367474.jpeg)


