Переполнение
Переполнение (англ. overflow) — это ситуация, когда значение, хранимое в переменной или регистре, превышает максимально допустимое значение для данного типа данных.
В Python, как и в других языках программирования, возможно переполнение при выполнении арифметических операций, например, при сложении или умножении чисел. В таких случаях, результатом операции может быть непредсказуемое значение или возникнет ошибка типа «OverflowError».
Чтобы предотвратить переполнение, необходимо заранее оценить промежуточные результаты арифметических операций и выбирать подходящий тип данных для хранения результатов. Также можно использовать специальные функции и библиотеки для работы с большими числами, такие как «Decimal» или «numpy».
Важно помнить, что в Python тип данных «int» не имеет ограничений на длину, поэтому переполнения возникают редко в сравнении с другими языками программирования
4.10. Как производятся арифметические операции в позиционных системах счисления?
Рассмотрим основные арифметические операции: сложение, вычитание, умножение
и деление. Правила выполнения этих операций в десятичной системе хорошо
известны это сложение, вычитание, умножение столбиком и
деление углом. Эти правила применимы и ко всем другим позиционным системам
счисления. Только таблицами сложения и умножения надо пользоваться особыми
для каждой системы.
Таблицы сложения легко составить, используя Правило Счета.
| Сложение в двоичной системе | Сложение в восьмеричной системе |
Сложение в шестнадцатиричной системе
При сложении цифры суммируются по разрядам, и если при этом возникает
избыток, то он переносится влево.
Пример 1. Сложим числа 15 и 6 в
различных системах счисления.
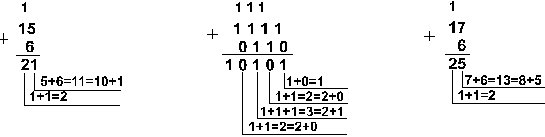
| Шестнадцатеричная: F16+616 |
Ответ: 15+6 = 2110 = 101012 = 258 = 1516. Проверка. Преобразуем полученные суммы к десятичному виду: 101012 = 24 + 22 + 2 = 16+4+1=21, 258 = 2. 81 + 5. 8 = 16 + 5 = 21, 1516 = 1. 161 + 5. 16 = 16+5 = 21. |
Пример 2.
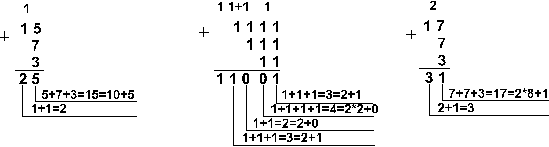
| Шестнадцатеричная: F16+716+316 |
Ответ: 5+7+3 = 2510 = 110012 = 318 = 1916. Проверка: 110012 = 24 + 23 + 2 = 16+8+1=25, 318 = 3. 81 + 1. 8 = 24 + 1 = 25, 1916 = 1. 161 + 9. 16 = 16+9 = 25. |
Пример 3.
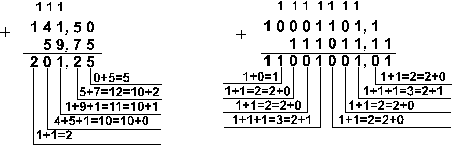
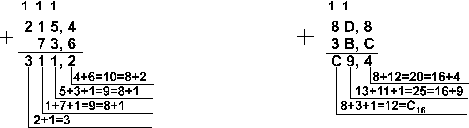
Ответ: 141,5 + 59,75 = 201,2510 = 11001001,012
= 311,28 = C9,416Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,012 = 27 + 26 + 23
+ 2 + 2-2 = 201,25
311,28 = 3. 82 + 181 + 1. 8
+ 2. 8-1 = 201,25
C9,416 = 12. 161 + 9. 16 + 4. 16-1
= 201,25
Пример 4. 2816
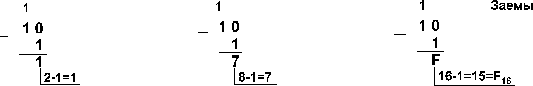Пример 5.2816
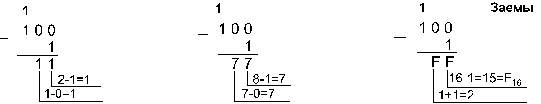Пример 6.
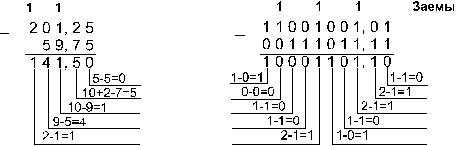
Ответ: 201,2510 — 59,7510 = 141,510
= 10001101,12 = 215,48 = 8D,816.
Проверка. Преобразуем полученные разности к десятичному виду:
10001101,12 = 27 + 23 + 22
+ 2 + 2-1 = 141,5;
215,48 = 2. 82 + 1. 81 + 5. 8
+ 4. 8-1 = 141,5;
8D,816 = 8. 161 + D. 16 + 8. 16-1
= 141,5.
Выполняя умножение многозначных чисел в различных позиционных системах
счисления, можно использовать обычный алгоритм перемножения чисел в столбик,
но при этом результаты перемножения и сложения однозначных чисел необходимо
заимствовать из соответствующих рассматриваемой системе таблиц умножения
и сложения.
| Умножение в двоичной системе |
Умножение в восьмеричной системе
|
Пример 7.
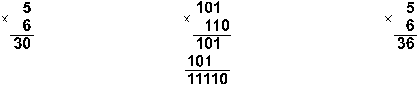Ответ: 5. 6 = 3010 = 111102 = 368.
Проверка. Преобразуем полученные произведения к десятичному виду:
111102 = 24 + 23 + 22 +
21 = 30;
368 = 381 + 68 = 30.
Пример 8. Перемножим числа 115 и 51.
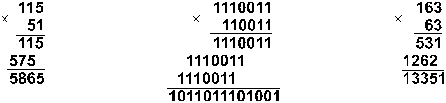Ответ: 115. 51 = 586510 = 10110111010012
= 133518.
Проверка. Преобразуем полученные произведения к десятичному виду:
10110111010012 = 212 + 210 + 29
+ 27 + 26 + 25 + 23 + 2
= 5865;
133518 = 1. 84 + 3. 83 + 3. 82
+ 5. 81 + 1. 8 = 5865.
Пример 9.
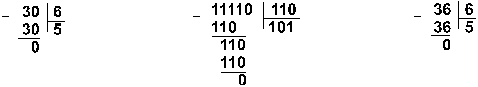Ответ: 30 : 6 = 510 = 1012 = 58.
Пример 10. Разделим число 5865 на
число 115.
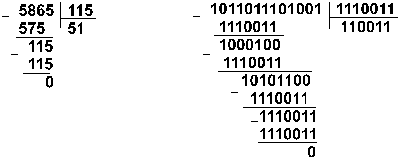
Восьмеричная: 133518 :1638
Ответ: 5865 : 115 = 5110 = 1100112 = 638.
Проверка. Преобразуем полученные частные к десятичному виду:
1100112 = 25 + 24 + 21
+ 2 = 51; 638 = 6. 81 + 3. 8
= 51.
Пример 11. Разделим число 35 на
число 14.
Восьмеричная: 438 : 168
Ответ: 35 : 14 = 2,510 = 10,12 = 2,48.
Проверка. Преобразуем полученные частные к десятичному виду:
10,12 = 21 + 2 -1 = 2,5;
2,48 = 2. 8 + 4. 8-1 = 2,5.
Виды
Существуют различные виды систем счисления:
- Непозиционные. В них значение не зависит от ее позиции.
- Позиционные. «Итог» зависит от того, где именно стоит тот или иной компонент.
- Однородные.
- Неоднородные.
Каждый вариант предусматривает свои ключевые особенности.
Позиционный тип
Здесь значение каждой цифры будет зависеть от ее разряда в числе. Пример – для человека привычна 10-я. Она является позиционной. 453 рассмотрено в виде примера. Тут 4 – это сотни, что указывает на 400, 5 – десятки (50), 3 – единицы (3). Чем больше разряд, тем выше окажется значение.
Непозиционный тип
Самый древний вариант. Каждый компонент – это отдельная величина. Она никак не зависит от разряда. В программировании не используется, поэтому рассматривать его более подробно не рекомендуется.
Однородный тип
Однородный вариант – это тот, в котором для всех позиций числа набор допустимых символов будет одинаковым. Пример – десятичная система. Для записи элемента можно использовать в каждом разряде только одну цифру. А именно – от 0 до 9. Запись 450 допускается (1-й разряд – 0, 2 – 5, 3-й – 4), а вот 4F5 – нет.
Смешанный тип
В нем в каждом разряде допускается разный набор других позиций. Пример – это измерение времени:
- в секундах – 60 символов;
- в часах – 24;
- в сутках – 365.
Теперь можно рассмотреть, какие системы встречаются в информатике чаще всего.
Таблицы истинности
При помощи тех же нулей и единиц создаются таблицы истинности логических выражений, в которых описаны всевозможные варианты.
Основные логические операции
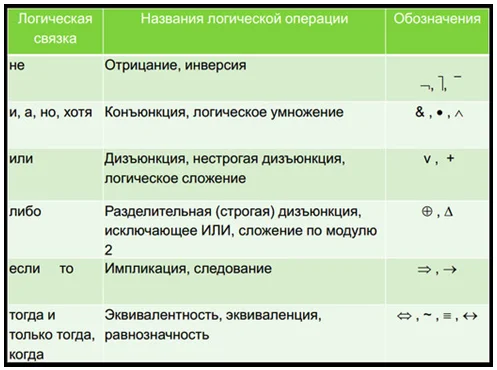
Например, конъюнкция является одной из логических операций. Она является истиной только в том случае, если два высказывания имеют истинные значения.
![Системы счисления. двоичная система счисления как основа компьютерной техники. [реферат №9808]](https://mtrufa.ru/wp-content/uploads/9/a/7/9a701e93fd85b43fa327cb9b9655a84e.jpeg)
Логические переменные таблицы истинности обозначают p и q, а их значения выражают при помощи 0 и 1, где 0 – ложь, 1 – истина:
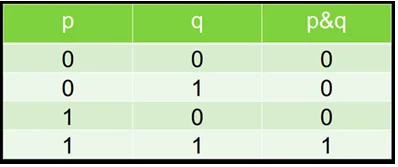
Фрагмент таблицы истинности для конъюнкции.
Так выражаются условия для всех логических операций.
Применяются таблицы истинности еще с начала 20 века в алгебре, логике, программировании.
Что делать с дробными выражениями
Работать с подобными числами тоже возможно. Способ перевода схож с описанным ранее, однако необходимо учитывать отдельные детали. В процессе перевода дробное число также делится на 3, однако если полученный результат не целый, к примеру 1,236. В таком случае записывается лишь число перед запятой (даже 0 учитывается). Затем полученные числа записываются уже после запятой в новой системе счисления, к примеру 0,21022 в троичной системе.
Если само выражение имеет как целую, так и дробную часть, то стоит выполнять раздельные перевод. Для начала возьмите целую часть, и поделитесь её описанным способом, затем рассчитайте дробную часть, и напишите её после запятой.
Определение системы счисления
Каждый символ или цифра представляет определенную величину, которая зависит от позиции этого символа в числе.
Системы счисления могут варьироваться в зависимости от количества используемых символов и правил представления чисел.
Самой распространенной системой счисления является десятичная система (с основанием 10), в которой используются десять цифр от 0 до 9.
В десятичной системе каждая цифра представляет значение, умноженное на соответствующую степень десяти.
Однако существуют и другие системы счисления, такие как двоичная (с основанием 2), восьмеричная (с основанием и шестнадцатеричная (с основанием 16).
В двоичной системе используются только две цифры — 0 и 1, а каждая цифра представляет значение, умноженное на соответствующую степень двойки.
Восьмеричная система основана на использовании восьми цифр — от 0 до 7, а шестнадцатеричная система — на использовании шестнадцати цифр — от 0 до 9 и от A до F.
Каждая система счисления имеет свои ограничения и применения.
Десятичная система применяется повсеместно в повседневной жизни, в то время как двоичная система широко используется в компьютерной технике, а шестнадцатеричная система — в программировании.
| Система счисления | Основание | Используемые цифры |
|---|---|---|
| Десятичная | 10 | 0-9 |
| Двоичная | 2 | 0-1 |
| Восьмеричная | 8 | 0-7 |
| Шестнадцатеричная | 16 | 0-9, A-F |
Понятие системы счисления
Наиболее распространенной системой счисления является десятичная система счисления, которая использует десять цифр от 0 до 9. В десятичной системе счисления каждая позиция числа обозначает определенную степень числа 10. Например, число 1234 в десятичной системе счисления может быть разложено на сумму продуктов: 1 * 10^3 + 2 * 10^2 + 3 * 10^1 + 4 * 10^0.
Однако, помимо десятичной системы счисления, существует множество других систем, таких как двоичная (использующая две цифры: 0 и 1), восьмеричная (использующая восемь цифр: 0-7) и шестнадцатеричная (использующая шестнадцать цифр: 0-9 и A-F).
Системы счисления широко применяются в информатике и компьютерных науках для представления данных и кодирования информации. Каждый числовой формат и кодировка имеют свою систему счисления, которая соответствует их специфическим требованиям и особенностям.
| Система счисления | База системы счисления | Цифры | Пример числа |
|---|---|---|---|
| Десятичная | 10 | 0-9 | 1234 |
| Двоичная | 2 | 0, 1 | 101010 |
| Восьмеричная | 8 | 0-7 | 764 |
| Шестнадцатеричная | 16 | 0-9, A-F | 3B2 |
Особенности системы счисления в информатике
Двоичная система счисления: В информатике часто используется двоичная система счисления, основанная на двух цифрах: 0 и 1. Двоичная система счисления особенно важна для работы с компьютерами, поскольку они могут только обрабатывать электрические сигналы, которые представляются в виде двоичных чисел. Цифры в двоичной системе счисления называются битами (binary digits).
Восьмеричная система счисления: Восьмеричная система счисления основана на восьми цифрах: 0, 1, 2, 3, 4, 5, 6 и 7. В информатике восьмеричная система счисления используется реже, но она удобна для представления больших двоичных чисел.
Шестнадцатеричная система счисления: Шестнадцатеричная система счисления основана на шестнадцати цифрах: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. Шестнадцатеричная система счисления широко применяется в информатике, особенно при работе с цветами, адресами памяти и другими значениями, которые могут быть представлены в виде больших двоичных чисел.
Выбор системы счисления в информатике зависит от контекста и требований конкретной задачи. Понимание особенностей каждой системы счисления помогает программистам эффективно работать с числовыми данными и разрабатывать программы, которые обрабатывают числа правильно и эффективно.
Позиционная система счисления: что это
— 2 0 умножить на 2. Коэффициент равен a
— 2 n-2 + … + a
- Простота запоминания и изображения чисел.
- Удобство совершения математических и логических операций.
- Миниатюрная запись огромных значений.
а остаток равен
- Обладает минимальными таблицами умножения, сложения.
- Представит любое число посредством двух состояний: единица и ноль.
- Помехоустойчивая по причине всего пары состояний.
- Проста в выполнении арифметических операций.
Полученный коэффициент снова делится на 2, а остаток является a
1.1.2. Двоичная система счисления
Если продолжить этот процесс деления, то на n-ом шаге мы получим набор цифр
которые являются частью двоичного представления исходного числа и соответствуют остатку от последовательного деления на 2.
100112Итак, чтобы перевести десятичное целое число в двоичную систему счисления, нужно разделить данное число и получившиеся целые части последовательно на 2, пока не получится часть, равная нулю. Исходное число в двоичной нотации составляется путем записи получающихся остатков один за другим, начиная с последнего.10.
Пример 4. Переведем десятичное число 11 в двоичную систему счисления. Описанная выше последовательность операций (алгоритм перевода) может быть представлена следующим образом:
Если мы запишем остаток от деления в направлении, указанном стрелкой, то получим: 11
= 1011n-1Пример 5. Если десятичное число достаточно велико, то более подходящей является следующая нотация вышеприведенного алгоритма:n-2= 101101011Восьмеричная система счисления — это позиционная система счисления, основанная на числе 8. Цифры восьмеричной системы счисления — 0, 1, 2, 3, 4, 5, 6, 7.n-1= 1011010111Например: 1063..
= 1 — 8 3 + 0 — 8 2 + 6 — 8 1 + 3 — 8 0 = 5631.
Таким образом, чтобы перевести восьмеричное целое число в десятичную систему счисления, мы должны перейти к расширенной системе счисления и вычислить значение полученного выражения.
Чтобы перевести целое десятичное число в восьмеричную систему счисления, необходимо разделить это число и полученные целые части на 8 последовательно, пока целая часть не будет равна нулю. Исходное число в новой нотации дополняется путем последовательной записи получившихся остатков, начиная с последнего.
Пример 6. Переведем десятичное число 103 в восьмеричную систему счисления.
База: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, C, C, D, E, F.10Здесь только десять из шестнадцати цифр имеют условное обозначение 0,…, 9. Первые пять букв латинского алфавита обычно используются для записи цифр с десятичными эквивалентами 10, 11, 12, 13, 14, 15.2.
Поэтому обозначение 3AF
36310означает:2
1.1.3. Восьмеричная система счисления
= 3 — 16 2 + 10 — 16 1 + 15 — 16 0 = 768 + 160 + 15 = 943
Пример 7. Переведем десятичное число 154 в шестнадцатеричную систему счисления.
Система, на которой основаны компьютеры, была изобретена гениальным немецким ученым Г.В. Лейбницем (до 19 века!). Он изобрел и описал СС, в которой все расчеты производятся с использованием d8Объяснение. Расширенная форма символики 579: 5*10 2 +7*10 1 +9*10 0 = 57910.
Источник
Обычно мы используем сокращенную нотацию чисел, т.е. без деления и умножения оснований.
А чтобы было проще, мы используем готовую таблицу коэффициентов, равных 2.
1.1.4. Шестнадцатеричная система счисления
Сначала запишите числа, равные двум, начиная с наибольшего:
Затем нужно вычесть из числа максимальную степень двойки и поставить 1, если в основании есть единица, или 0, если ее нет. Перевод 579
Обратный путь еще проще. Посчитайте количество цифр — это мощность от 2 д о-1. И так далее. И проще использовать одну и ту же таблицу:
Если оно на 1 больше, то число начинается и заканчивается 1, а внутри — сплошной 0.16Основание этой системы — 8, а числа в восьмеричной системе — 0-7. Эта система счисления является тематической и целочисленной. Он используется в областях, связанных с цифровыми технологиями, особенно с программным обеспечением Linux (права доступа, исполнение).
3AF16Это 16-ричная система целых чисел (шестнадцатеричные цифры 0-9 и буквы от A до F), используемая в приложениях низкоуровневого компьютерного программирования и документирования, поскольку она представляет собой 8-битный байт и для записи требуется 2 шестнадцатеричные цифры.10.
В стандарте Unicode используется 4 или более 16 символов SS.
Простая система счисления
У первобытных людей не было даже чисел, они количество предметов отображали равным количеством каких-либо значков. Такими значками могли быть зарубки, черточки, точки, а так же узелки на веревках.
Это самая простая система счисления. В этой системе счисления для записи чисел используется только одна цифра. Ее можно изобразить в виде палочки ?, кружочка , или любой другой фигуры. Тогда числа будут записываться примерно так:
|
1 |
? |
|
2 |
?? |
|
3 |
??? |
|
4 |
??? |
|
5 |
? ? ? ? ? и т. д. |
Такая система счисления использовалась, и до сих пор используется народами, не имеющими письменности.
Но иногда такой системой счисления пользуются и современные люди, например, отмечая зарубками количество прошедших дней, или карандашом отмечая черточками в тетради количество проданных товаров.
Позже, для облегчения счета, эти значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.
Но это удобно, пока числа небольшие. Вы только представьте себе число 1 000 записанное с помощью кучки камушков, а 1 000 000? Неудобно?
И люди начали изобретать системы счисления.
Перевод чисел
Данное действие можно считать самым простым из всех, относящихся к системам счисления.
Каждая цифра числа образует слагаемое, которое надо записать, а потом произвести необходимые арифметические действия.
Прежде чем перейти к конкретным рассуждениям, надо отметить, что приводимые в заданиях числа, обычно не превышают 102410 или ненамного больше этого значения.
Это связано с разумным ограничением сложности вычислений.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 2n | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| n2* | 1 | 10 | 100 | 1000 | 10000 | 100000 | … |
Любое из производимых действий будет замкнуто на эту таблицу!
В десятичную систему
Вне зависимости от обсуждаемой системы счисления, любое число можно разбить на разряды, каждый из которых вносит определенный вклад в значение числа.
Общей закономерностью является то, что чем правее стоит цифра, тем меньшее значение она подразумевает.
В качестве первого примера рассмотрим число 1111n
В качестве второго примера рассмотрим число 1234n
Общая формула для перевода:
a1*n
+ a2*n1
+ a3*n2
+ a4*n3
+ … + ak*nk–1
где n — основание системы счисления, k — номер разряда числа.
Из десятичной системы
1. Остаток от деления
Последовательно делим число на основание до тех пор, пока не получим частное, равное нулю.
Остатки записываем.
После завершения вычислений записываем значения остатков
в обратном порядке. Полученное число и будет ответом.
Разложим два числа: 23 и 64.
| Делимое | Остаток | Смысл действия |
| 23105210 | 11101 | 23/2 = 22/2 + 1 = 11 + 111/2 = 5 + 15/2 = 4/2 + 1 = 2 + 12/2 = 1 + 1/2 = 0 + 1 |
102
| Делимое | Остаток | Смысл действия |
| 64321684210 | 0000001 |
64/2 = 32 + 32/2 = 16 + 16/2 = 8 + 8/2 = 4 + 4/2 = 2 + 2/2 = 1 + 1/2 = 0 + 1 |
102
В некоторых учебниках (например, Босовой) предлагается таблицу записи располагать горизонтально, что очень удобно для сравнительно небольших чисел (11).
В верхней строке записывается число. Остаток от деления (в нашем случае на 2) записывается под ним, а целая часть частного — в следующей колонке.
| Делимое | 23 | 11 | 5 | 2 | 1 |
| Остаток | 1 | 1 | 1 | 1 |
102
Способом деления можно перевести число в любую систему счисления. Давайте переведем 44 в троичную систему.
| Делимое | 44 | 14 | 4 | 1 |
| Остаток | 2 | 2 | 1 | 1 |
103
Трудно сказать, насколько комфортно ощущают себя люди, производящие привычное деление столь необычным образом.
Лично я испытываю значительный дискомфорт, особенно при переводе не в двоичную систему.
Поэтому, давайте перейдем к другому, менее «магическому» способу.
2. Разложение
Как известно, любое число можно представить в виде суммы чисел.
Таким образом становиться ясно, что для этих вычислений нужно
Порядок действий на практике
Пример 1. Переведем 900 в семеричную систему.
Пример 2. Переведем 900 в пятеричную систему.
Пример 3. Переведем 900 в двоичную систему.
В связи с довольно большой трудоемкостью, данный метод едва ли можно назвать слишком простым
для двоичной системы. Но он вполне понятен и, из-за необходимости четкой записи, всегда может быть легко проверен.
В некоторых случаях, когда число очень мало отличается от степени основания, перевод может оказаться значительно более быстрым, чем другие способы.
Из двоичной в восьми- и шестнадцатеричную системы
Это действие является основным для многих заданий. К сожалению, большинство учебников предлагает зазубрить примерно следующий принцип.
Для перевода из двоичной системы счисления в восьмеричную следует разбить двоичное число по три разряда справа налево.
Необходимо заметить, что 8 = 23, а 16 = 24. Именно поэтому в приведенном правиле и используются группы по три разряда, а для перевода в 16-ричную потребуются уже 4 разряда.
Внимательный читатель может заметить, что еще осталось 4 = 22. То есть двоичную систему также легко можно преобразовать и в четверичную.
Отсюда же следует, что раз 9 = 32, то троичная система легко преобразуется в девятеричную, если разбить её число на пары.
Как это делается на практике.
Факультативный материал по переводу в четверичную систему.
24
Из восьми и шестнадцатеричной систем в двоичную
Все также, как и в предыдущем разделе, только каждая цифра восьмеричного числа
превращается в три двоичных цифры, а шестнадцатеричного — в четыре.
Типичной ошибкой является незаписывание ведущих нулей (10 вместо 010).
Буквально пара слов о системах счисления и математике: сколько в числе нолей в конце, столько раз оно делится без остатка на основание системы.
Системы счисления
Начнем с определения системы счисления. Система счисления — это совокупность правил записи чисел цифровыми знаками.
Системы счисления бывают позиционные и непозиционные. В настоящее время и в технике и в быту широко используются как
позиционные, так и непозиционные системы счисления. Рассмотрим сначала примеры непозиционных систем счисления.
В качестве классического примера непозиционной системы счисления обычно приводят римскую форму записи чисел. Там не
менее это не единственная непозиционная система счисления, используемая в настоящее время.
Сейчас, как и в глубокой древности, для записи числа используются так называемые «палочки». Эта форма записи чисел
наиболее понятна и требует для записи числа всего один символ. Число образуется суммой этих «палочек». Однако при записи
больших чисел возникают неудобства. Число получается громоздким и его трудно читать.
В следующем варианте непозиционной системы счисления стали использовать несколько символов (цифр). Каждая цифра
обозначает различное количеств единиц. Конечное число точно так же как и в предыдущем варианте образуется суммой цифр.
Наиболее яркий вариант использования такой системы счисления — это денежные отношения. Мы с ними сталкиваемся
каждый день. Здесь никому не приходит в голову, что сумма, которую мы выкладываем за продукты, может зависеть от того, в
каком порядке мы расположим монеты на столе! Номинал монеты или банкноты не зависит от того, в каком порядке она была
вынута из кошелька. Это классический пример непозиционной системы счисления.
Однако чем большее число требуется представить в такой системе счисления, тем большее количество цифр требуется для
этого. Позиционные системы счисления были придуманы относительно недавно для того, чтобы сэкономить количество цифр,
используемое для записи чисел.
Значение цифры в позиционной системе счисления зависит от её позиции в записываемом числе. В позиционной системе
счисления появляются два очень важных понятия — основание системы счисления и вес цифры. Дело в том, что в
позиционной системе счисления число представляется в виде формулы разложения:
pnnn-1n-12211-1-1-2-2-k-k
где p — основание системы счисления
pi — вес единицы данного разряда
ai — цифры, разрешённые в данной системе счисления.
При этом количество цифр в системе счисления зависит от основания. Количество цифр равно основанию системы счисления.
В двоичной системе счисления две цифры, в десятичной — десять, а в шестнадцатеричной — шестнадцать.
Число в любой позиционной системе счисления записываются в виде последовательности цифр:
nn-121-1-2-k
где ai — цифры данной системы счисления, а цифра, соответствующая единицам определяется по
положению десятичной запятой (или десятичной точки в англоязычных странах). Каждая цифра, использованная в записи числа,
называется разрядом.
Какие же системы счисления применяются в настоящее время? Первый ответ, который я ожидаю — это десятичная
система счисления. А ещё? Да, да не удивляйтесь! Мы широко используем и другие системы счисления! Достаточно посмотреть
себе на левую руку. Там мы увидим часы. Сколько минут помещается в часе? Шестьдесят! Сколько секунд помещается в минуте?
Шестьдесят! Налицо признаки шестидесятеричной системы счисления. Это наследование древней вавилонской системы счисления,
которую вместе с компасом и часами европейцы заимствовали от арабов.
А еще примеры? Да сколько угодно! Картушка компаса делится на восемь румбов. Чем не восьмеричная система счисления?
А давно ли в России отказались от полушек (четверть копейки) или грошей (половина копейки)? А следующее значение
монеты — две копейки! Чем не двоичная система счисления?
Рассмотрим подробнее системы счисления, наиболее часто используемые в цифровой технике.
Позиционные и непозиционные системы счисления
Системы счисления делятся на две большие группы: позиционные и непозиционные. Расскажем, что это значит и чем они различаются.
Непозиционные. Так называют системы, в которых не важна позиция цифры в числе. Где бы цифра ни находилась, она всегда имеет одно и то же значение. Самый яркий пример — унарная система счисления, она же единичная. Ее даже иногда выделяют в отдельный вид. В ней существует только одна цифра — 1. Поэтому, например, число 5 будет записываться как 11111. Если поменять единицы местами — ничего не изменится.
Непозиционные системы счисления считаются самыми древними. Они возникли, когда люди впервые начали что-то подсчитывать и использовали для этого палочки, узелки или собственные пальцы. Позже они начали «группировать» цифры в числа, и возникли позиционные системы счисления.
Второй пример непозиционной системы, менее очевидный, — римская запись. Символ X всегда будет означать десятку, а символ V — пятерку, в каком бы месте их ни поставили. Даже в числах вроде IV, где I перед V означает «-1», I всё равно будет единицей, а V — пятеркой. От положения цифры зависит только ее знак, но не ее вес.
Непозиционные системы используются редко. В них нет нуля, нет дробных чисел и других инструментов, которые бывают важны в современных вычислениях.
Позиционные. Сюда относятся десятичная, двоичная и большинство других современных систем счисления. В таких системах есть разряды, зависящие от позиции. Значение цифры меняется в зависимости от того, в каком месте она находится. Например, в числе 15 пятерка означает «пять единиц», а в числе 54 — «пять десятков».
Двоичная, восьмеричная и шестнадцатеричная система тоже позиционные. В целом такие системы используют чаще, чем непозиционные, за исключением некоторых узких сфер. Например, в некоторых комбинаторных расчетах используют непозиционную биномиальную систему — она основана на биноме Ньютона.
Позиционные системы счисления в свою очередь делятся на две категории — однородные и смешанные.
- Однородные системы — такие, в которых правила записи одинаковые для всех разрядов. В каждом разряде можно использовать один и тот же алфавит. Десятичная система именно такая. И в единицах, и в десятках, и в сотнях или тысячах мы пользуемся цифрами от 0 до 9.
- Смешанные системы — такие, где у разных разрядов различаются правила записи или даже основание. Например, система подсчета времени. У разряда «минуты» основание 60, и минуты можно обозначать числами от 0 до 59. На 60 число переходит в разряд «часы». А у разряда «часы» основание 24, и количество часов можно обозначать цифрами от 0 до 23. На 24 число переходит в разряд «сутки». И так далее.
Смешанные системы используют реже, чем однородные — исключением можно назвать разве что подсчет времени. Но, например, смешанной системой считается факториальная: 2! — это 2, 3! — уже 6, а 4! — 24. Видно, что основание меняется, а сама система нелинейная.
Алгоритмы перевода в системы счисления по разным основаниям
Алгоритм перевода чисел из любой системы счисления в десятичную
- Представить число в развернутой форме. При этом основание системы счисления должно быть представлено в десятичной системе счисления.
- Найти сумму ряда. Полученное число является значением числа в десятичной системе счисления.
Алгоритм перевода целых чисел из десятичной системы счисления в любую другую
- Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, меньше делителя.
- Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
- Составить число в новой системе счисления, записывая его, начиная с последнего остатка.
Алгоритм перевода правильных дробей из десятичной системы счисления в любую другую
- Последовательно умножаем данное число и получаемые дробные части произведения на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равна нулю или будет достигнута требуемая точность представления числа.
- Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
- Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Алгоритм перевода произвольных чисел из десятичной системы счисления в любую другую
Перевод произвольных чисел, т.е. содержащих целую и дробную часть, осуществляется в два этапа:
- Отдельно переводится целая часть.
- Отдельно переводится дробная.
- В итоговой записи полученного числа целая часть отделяется от дробной запятой.
Перевод чисел из двоичной системы счисления в систему счисления с основанием q=2n
Для облегчения решения задач заполним следующую таблицу:
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Если основание q-ричной системы счисления является степенью числа 2, то перевод чисел из q-ричной систему счисления в 2-ичную и обратно можно проводить по более простым правилам.
- Двоичное число разбить справа налево на группы по n в каждой.
- Если в левой последней группе окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов.
- Рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой в системе счисления с основанием q=2n
Двоичная арифметика
Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным правилам.
Сложение
Рассмотрим сложение чисел в двоичной системе счисления
В основе лежит таблица сложения одноразрядных двоичных чисел:
0+0=00+1=11+0=11+1=101+1+1=11
Важно обратить внимание на то, что при сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или больше основания системы счисления. Для двоичной системы счисления эта величина равна двум. Сложение многоразрядных двоичных чисел происходит в соответствие с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов с старшие.
Для двоичной системы счисления эта величина равна двум. Сложение многоразрядных двоичных чисел происходит в соответствие с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов с старшие.
Вычитание
Рассмотрим вычитание двоичных чисел. В основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда. В таблице заем обозначается 1 с чертой.
0-0=00-1=111-0=11-1=0
Умножение
В основе умножения лежит таблица умножения одноразрядных двоичных чисел:
0*0=00*1=01*0=01*1=1
Умножение многоразрядных двоичных чисел происходит в соответствии с приведенной таблицей умножения по обычной схеме, применяемой в десятичной системе счисления, с последовательным умножением множимого на очередную цифру множителя.
Деление
Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.
Зачем нужно переводить системы счисления?
Системы счисления являются важным инструментом в математике, информатике и других науках. Они позволяют нам записывать числа в различных форматах и переводить числа из одной системы счисления в другую.
Одним из основных применений перевода систем счисления является облегчение работы с большими числами. Например, в двоичной системе счисления для записи числа с 32-битным представлением потребуется всего 32 бита, в то время как в десятичной системе счисления требуется 10 раз больше бит.
Перевод систем счисления также необходим при работе с различными кодировками, например, в компьютерной графике и веб-разработке.
Кроме того, понимание систем счисления важно для понимания работы многих компьютерных алгоритмов и языков программирования. Иногда перевод систем счисления необходим для конвертации данных из одного формата в другой, например, для конвертации формата даты или времени в другой формат
Иногда перевод систем счисления необходим для конвертации данных из одного формата в другой, например, для конвертации формата даты или времени в другой формат.
В общем, перевод систем счисления является важным навыком, который полезен в различных областях науки и практической деятельности.