Урок 5. арифметические операции в системах счисления. сравнение чисел в различных системах счисления

Непозиционные системы

К непозиционным системам счисления относятся:

1. Единичная система, которая считается одной из первых. В ней вместо цифр использовались палочки. Чем их было больше, тем больше было значение числа. Встретить пример чисел, записанных таким образом, можно в фильмах, где речь идет о потерянных в море людях, заключенных, которые отмечают каждый день с помощью зарубок на камне или дереве.
2. Римская, в которой вместо цифр использовались латинские буквы. Используя их, можно записать любое число. При этом его значение определялось с помощью суммы и разницы цифр, из которых состояло число. Если слева от цифры находилось меньшее число, то левая цифра вычиталась из правой, а если справа цифра была меньше или равна цифре слева, то их значения суммировались. Например, число 11 записывалось как XI, а 9 — IX.
3. Буквенные, в которых числа обозначались с помощью алфавита того или иного языка. Одной из них считается славянская система, в которой ряд букв имел не только фонетическое, но и числовое значение.
4. в которой использовалось всего два обозначения для записи — клинья и стрелочки.
5. В Египте тоже использовались специальные символы для обозначения чисел. При записи числа каждый символ мог использоваться не более девяти раз.

Что такое двоичный код

Когда мы говорим о двоичном коде, мы должны сначала разобраться в понятии «бит». Бит (сокращение от binary digit) представляет собой самую маленькую единицу информации. Он может принимать значение либо 0, либо 1. Используя комбинацию битов, можно представлять различные виды информации: числа, символы (буквы, знаки препинания, спецсимволы и т. д.), изображения, звуки и т. д. 

Принцип работы современных компьютеров также имеет двоичную природу. Носителем информации в них является электрический заряд или импульс. Например, оперативная память содержит в себе множество ячеек, в которых этот заряд может либо отсутствовать, либо присутствовать, что соответствует 0 и 1. Комбинации таких ячеек с отсутствием или присутствием электрического заряда и являются физическим кодированием информации. Аналогично данные сохраняются на SSD, flash-картах. А вот на магнитных жестких дисках роль мельчайшего физического носителя информации играет ячейка из ферромагнетика, которая также принимает одно из двух состояний — намагниченное или ненамагниченное. Считывая информацию с жесткого диска специальной головкой, компьютер переводит это состояние в соответствующий электрический сигнал.

Иными словами, непосредственно в электронных вычислительных устройствах кодирование информации осуществляется с помощью бинарных пар состояний различных физических сущностей (электрического заряда или импульса, намагничивания и т. д.). А цифровой бинарный код — те самые 0 и 1 — это абстрактная двоичная запись таких состояний.

Двоичная система

Двоичная система счисления – позиционная система счисления с основанием 2. Также называется бинарной (binary). Она широко используется в вычислительной технике и других современных устройствах.

Двоичные системы счисления используют всего две цифры при записи информации – 0 и 1. Они появились еще в Древнем Китае, но современная binary system стала развиваться в 17 веке, а ее применение началось в середине 20-го века.

История развития

Томас Хэрриот, астроном и математик из Англии, в 1605 году впервые описал двоичное представление чисел, а Фрэнсис Бэкон, философ, создал шифр из двух символов – A и B.

В 1670-м году Хуан Карамюэль-и-Лобковиц, богослуживец из Испании, опубликовал разные способы представления чисел в системах счисления. В публикации было упомянуто и про двоичную интерпретацию.

Наиболее значительными в развитии binary system стали работы Готфрида Лейбница, математика из Германии. В 1703 году он описал двоичную арифметику – возможные математические операции с двоичными числами.

В 1838 году изобретатель из Америки Самюэл Морзе создал одноименный шифр, который включал в себя всего два символа – точку и тире. Они передавались по телеграфу в виде сигналов различной длины. Азбука Морзе – это не бинарная система в строгом понимании термина, но двоичный принцип в ней использовался. Именно с ней соответствующий вариант представления записей продемонстрировал свою значимость.

Чуть позже, в 1847 году, Джордж Буль, математик из Англии, создал «булеву алгебру». В ней появились такие понятия как «ложь» и «истина», а также определенные логические законы.

В 1937 году Клод Шеннон, инженер из Америки, объединил двоичный принцип, булеву логику и электрические схемы. Он же ввел понятие «бит» – минимального количества информации, где:

• 0 – это отсутствие тока, «ложь» (0 бит);
• 1 – наличие тока, «истина» (1 бит).

С того самого момента бинарная система счисления стала активно применяться в вычислительной технике, включая современные компьютеры.

Числа в binary system

Двоичным числом называется число, которое состоит из двоичных цифр. Их всего две – 0 и 1. В качестве записей в binary system могут использовать разные значения: «ток есть» и «тока нет», «истина» и «ложь» и так далее.

Ниже можно увидеть числа в двоичной системе, а также их интерпретации в других системах счисления:

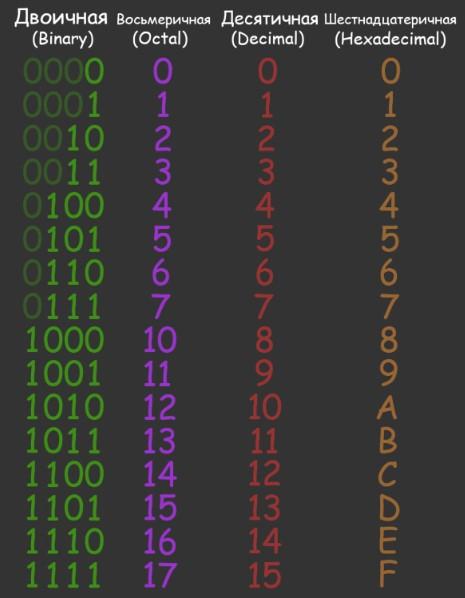
Эта таблица поможет лучше ориентироваться в расчетах и быстрее разобраться со способами представления чисел.

Любое натуральное число может быть закодировано в бинарном представлении. Оно будет представлять собой некоторую последовательность единиц и нулей.

Особенности

У двоичной системы счисления имеются как преимущества, так и недостатки. К ее слабым сторонам относят то, что она не понятна человеку на уровне интуиции. Также сюда можно отнести следующие моменты:

1. Неудобство работы с большими числами. Это вызвано длинной записью значения. Пример – RGB: 255₁₀, 255₁₀, 255₁₀. Здесь и далее нижний индекс будет указывать на основание системы. Значения RGB обычно записываются в шестнадцатеричной форме представления: FF₁₆, FF₁₆, FF₁₆. При переводе записи в бинарный вид получится 111111₂, 111111₂, 111111₂. Такая форма записи выглядит громоздко и непонятно.
2. Отсутствие реального применения в жизни (за исключением компьютеров и иной вычислительной техники).
3. Долгое вычисление вручную.

Двоичная система счисления для вычислительной техники – это некий стандарт. Из него следуют преимущества рассматриваемой формы представления информации:

• позиционная система предусматривает разряды;
• можно осуществлять различные арифметические действия;
• допустимо построение логики;
• подходит для шифрования данных;
• используется в качестве «родного» для компьютеров и других устройств.

Binary System – стандарт, используемый в ЭВМ. Он удобен при расчетах и занимает намного меньше пространства, чем остальные формы представления числовых записей.

Общепринятые системы счисления

Человечество в ходе своего развития со временем стало нуждаться в способах подсчета. Нужно было считать, например, количество добычи или убитых врагов из других племен. И эта нужда у древних людей только возрастала. Поначалу пользовались абстрактными понятиями типа «нисколько», «один», «много». Затем в употребление вошла «пара», означающая два каких-то предмета. Уже одно это нововведение существенно упростило жизнь древнему человеку.

Общепринятые системы счисления

В дальнейшем люди стали считать единицами, используя в качестве таковых пальцы на руках и ногах, зарубки на деревьях, кости зверей, узелки на веревках. Благодаря изобретению таких примитивных счетных машин человечество спустя тысячелетия смогло понять, что в древности люди умели не только считать, но также фиксировать результаты счета.

С течением времени возникла необходимость в символьном обозначении любого количества больше единицы. В итоге древними египтянами были впервые придуманы знаки, обозначающие 1, 5 и 10.

Система чисел, состоящая из определенных знаков (цифр), фактически и является системой счисления. Другими словами, это способ численного выражения с помощью принятых правил и специальных знаков, называемых цифрами.

Узнай, какие ИТ — профессии входят в ТОП-30 с доходом от 210 000 ₽/мес

Павел Симонов
Исполнительный директор Geekbrains

Команда GeekBrains совместно с международными специалистами по развитию карьеры
подготовили материалы, которые помогут вам начать путь к профессии мечты.

Подборка содержит только самые востребованные и высокооплачиваемые специальности и направления в
IT-сфере. 86% наших учеников с помощью данных материалов определились с карьерной целью на ближайшее
будущее!

Скачивайте и используйте уже сегодня:

Павел Симонов
Исполнительный директор Geekbrains

Топ-30 самых востребованных и высокооплачиваемых профессий 2023

Поможет разобраться в актуальной ситуации на рынке труда

Подборка 50+ бесплатных нейросетей для упрощения работы и увеличения заработка

Только проверенные нейросети с доступом из России и свободным использованием

ТОП-100 площадок для поиска работы от GeekBrains

Список проверенных ресурсов реальных вакансий с доходом от 210 000 ₽

Получить подборку бесплатно

pdf 3,7mb
doc 1,7mb

Уже скачали 27850

Любая система счисления принадлежит к одной из двух категорий:

Позиционные СС

Конкретное значение числа определяется не только цифрами, но и их позицией. Сюда относят арабскую систему, где первый разряд справа отведен для единиц, второй разряд справа — для десятков, третий разряд справа — для сотен и т. д. Таким образом, для записи числа 475 необходимо в крайней правой позиции расположить пятерку (пять единиц), после нее — семерку (семь десятков) и затем — четверку (четыре сотни). Позиционными считаются также системы счисления с основаниями (2, 8, 16).

Непозиционные СС

Значение числа определяется только знаком (цифрой). Для обозначения единиц, десятков, сотен и тысяч используются отдельные символы. Наиболее показательным представителем данной группы является римская система счисления. Здесь имеется еще одна отличительная особенность. Для записи очень больших чисел необязательно использовать весь набор знаков — на такие случаи существуют функции сложения и вычитания.

К примеру, число 475 римскими цифрами может выглядеть как CCCCXXXXXXXIIIII либо, в сокращенном виде, как CDLXXV. В последнем варианте используются именно вычитание и прибавление. Значение цифры, стоящей слева от большего числа, отнимается соответственно от этого числа. Если эта цифра стоит справа, то значение прибавляется.

Впервые позиционная система счисления была введена в Вавилоне. Примечательно, что она была шестнадцатеричная. К 19 веку распространение получила двенадцатеричная система.

Прежде чем разбирать, как записывается двоичная система счисления, определимся с терминами. Алфавит любой СС состоит из знаков, обозначающих отдельные цифры. Основанием называют значение, равное количеству знаков для кодирования чисел и представляющее собой целое число от 2 и выше.

Непозиционные СС

Когда рассматривается несколько разных СС, тип каждой из них обычно обозначается подстрочным знаком. По умолчанию, если не указано основание, число является десятичным. Позиция цифры в числе называется разрядом.

Что такое системы счисления

Для записи числа нужен символ. Это может быть как буква «β» (бета) греческого алфавита, так и | (чёрточка). Главное — чтобы символ всегда означал одно и то же количество, имел то же значение. Эти символы назвали цифрами.

Система счисления — это набор цифр, каждая из которых обозначает определённое количество. Системы счисления бывают позиционные и непозиционные. Разберём это на простых примерах.

Возьмём игральные кости и попробуем описать их значения чёрточками:

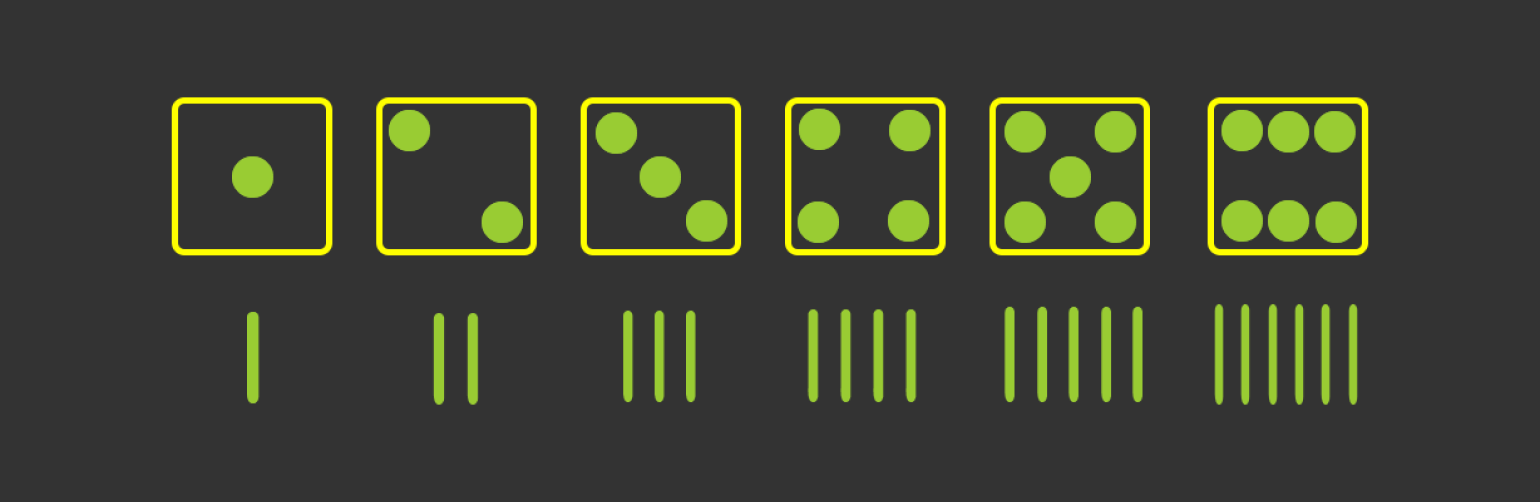
Изображение: Лев Сергеев для Skillbox Media

Перед нами — унарная (единичная) система счисления. Это значит, что в нашем распоряжении есть только один символ. Это не совсем удобно. Поступим по-другому: придумаем для каждого набора чёрточек свои символы. Например:

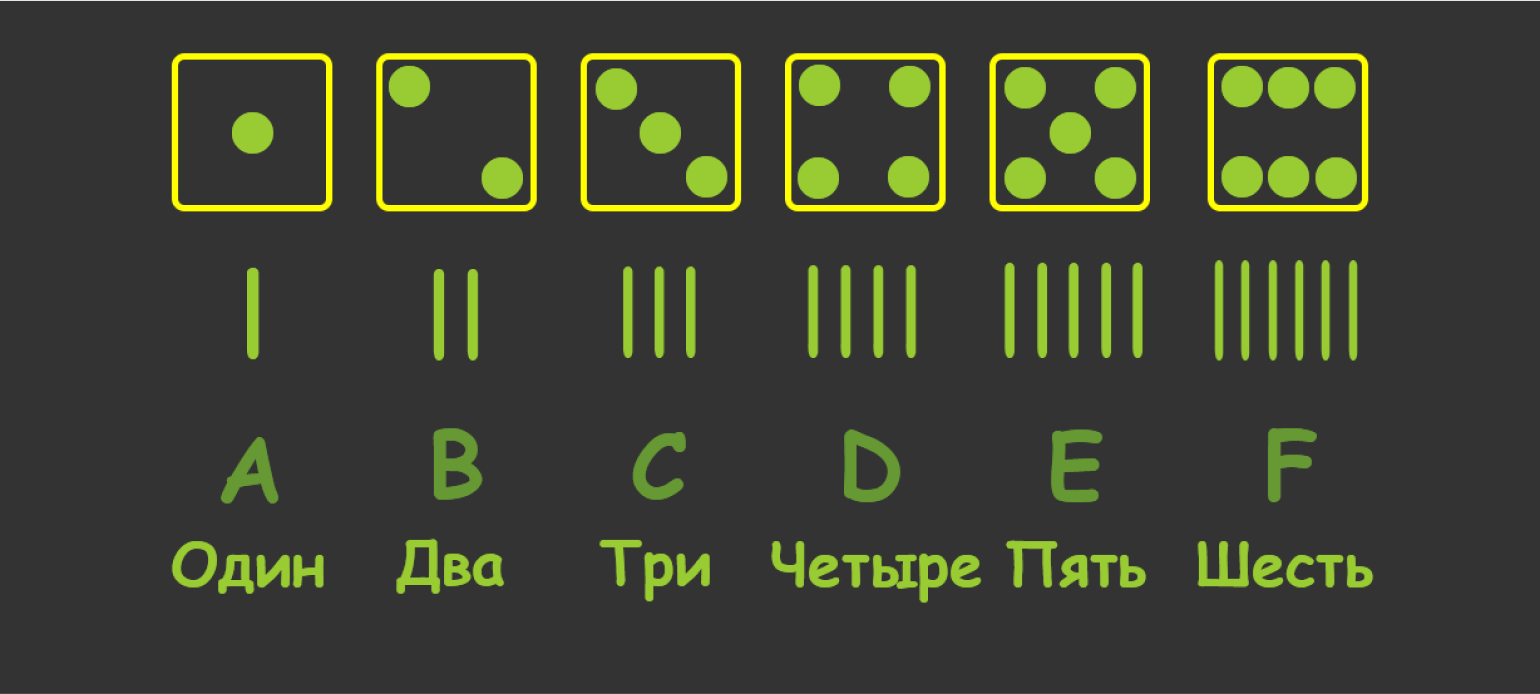
Изображение: Лев Сергеев для Skillbox Media

Символов теперь больше, а запись короче. Такую «кодировку» можно назвать шестеричной системой счисления, в которой 6 цифр:

• A = 1
• B = 2
• C = 3
• D = 4
• E = 5
• F = 6

Уже лучше, но данная система, как и единичная, — непозиционная. Это значит, что положение цифры в записи никак не связано с разрядностью (единицы, десятки, сотни, тысячи и так далее). Классический пример — римская форма записи:

Изображение: Лев Сергеев для Skillbox Media

Такая запись страшно затрудняет не только вычисления, но даже запись чисел, особенно больших, дробных или нерациональных — попытайтесь, например, записать «по-римски» число π (3,1415926535…).

Эту проблему решили позиционные системы счисления, самая популярная из которых — арабская. Разница — налицо. Достаточно посмотреть на запись числа 2023:

Изображение: Лев Сергеев для Skillbox Media

Если в первом случае поменять местами цифры M и X, значение числа не изменится — римляне считывали цифры от больших к меньшим.

Правда, у этого правила была пара исключений. Для удобства записи четвёрку записывали как IV, а девятку — как IX. Но в целом римская нумерация была непозиционной — точно так же, как древнеегипетская, греческая, вавилонская и прочие ветхозаветные.

А вот во втором случае, переставив цифры, мы получим совершенно разные результаты: 0223, 2320 и так далее.

Позиционные системы счисления имеют разряды. Их мы и меняли местами в примере выше. Разряд не может вмещать в себя число меньше или больше, чем основание системы. Основание — это количество цифр в системе счисления.

Изображение: Лев Сергеев для Skillbox Media

Пример позиционных систем:

Алгоритмы перевода в системы счисления по разным основаниям

Алгоритм перевода чисел из любой системы счисления в десятичную

1. Представить число в развернутой форме. При этом основание системы счисления должно быть представлено в десятичной системе счисления.
2. Найти сумму ряда. Полученное число является значением числа в десятичной системе счисления.

Алгоритм перевода целых чисел из десятичной системы счисления в любую другую

1. Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, меньше делителя.
2. Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
3. Составить число в новой системе счисления, записывая его, начиная с последнего остатка.

Алгоритм перевода правильных дробей из десятичной системы счисления в любую другую

1. Последовательно умножаем данное число и получаемые дробные части произведения на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равна нулю или будет достигнута требуемая точность представления числа.
2. Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
3. Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.

Алгоритм перевода произвольных чисел из десятичной системы счисления в любую другую

Перевод произвольных чисел, т.е. содержащих целую и дробную часть, осуществляется в два этапа:

1. Отдельно переводится целая часть.
2. Отдельно переводится дробная.
3. В итоговой записи полученного числа целая часть отделяется от дробной запятой.

Перевод чисел из двоичной системы счисления в систему счисления с основанием q=2n

Для облегчения решения задач заполним следующую таблицу: 

Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

Если основание q-ричной системы счисления является степенью числа 2, то перевод чисел из q-ричной систему счисления в 2-ичную и обратно можно проводить по более простым правилам.

1. Двоичное число разбить справа налево на группы по n в каждой.
2. Если в левой последней группе окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов.
3. Рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой в системе счисления с основанием q=2n

Двоичная арифметика

Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным правилам. 

Сложение

Рассмотрим сложение чисел в двоичной системе счисления

В основе лежит таблица сложения одноразрядных двоичных чисел: 
0+0=00+1=11+0=11+1=101+1+1=11

Важно обратить внимание на то, что при сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или больше основания системы счисления. Для двоичной системы счисления эта величина равна двум. Сложение многоразрядных двоичных чисел происходит в соответствие с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов с старшие. 

Для двоичной системы счисления эта величина равна двум. Сложение многоразрядных двоичных чисел происходит в соответствие с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов с старшие. 

Вычитание

Рассмотрим вычитание двоичных чисел. В основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда. В таблице заем обозначается 1 с чертой. 
0-0=00-1=111-0=11-1=0

Умножение

В основе умножения лежит таблица умножения одноразрядных двоичных чисел: 
0*0=00*1=01*0=01*1=1

Умножение многоразрядных двоичных чисел происходит в соответствии с приведенной таблицей умножения по обычной схеме, применяемой в десятичной системе счисления, с последовательным умножением множимого на очередную цифру множителя. 

Деление

Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.

Арифметические операции

Вне зависимости от того, в каком виде представлено число, с ним можно проводить привычные для нас вычисления. Это может быть деление и умножение, вычитание и сложение в системе счисления, которую вы выбрали. Конечно, для каждой из них действуют свои правила.

Так для двоичной системы разработаны свои таблицы для каждой из операций. Такие же таблицы используются и в других позиционных системах.

Заучивать их необязательно — достаточно просто распечатать и иметь под рукой. Также можно воспользоваться калькулятором на ПК.

Одна из важнейших тем в информатике — система счисления. Знание этой темы, понимание алгоритмов перевода чисел из одной системы в другую — залог того, что вы сможете разобраться в более сложных темах, таких как алгоритмизация и программирование и сможете самостоятельно написать свою первую программу.

Иногда бывает удобно хранить числа в памяти процессора в десятичном виде (Например, для вывода на экран дисплея). Для записи таких чисел используются
двоично-десятичные коды
. Не нужно путать двоично-десятичный код с .
Для записи одного десятичного разряда используется четыре двоичных бита. Эти четыре бита называются тетрадой. Иногда встречается название, пришедшее
из англоязычной литературы: нибл. При помощи четырех бит можно закодировать шестнадцать цифр. Лишние комбинации в двоично-десятичном коде являются
запрещенными. Таблица соответствия двоично-десятичного кода и десятичных цифр приведена ниже:

Двоично-десятичный код	Десятичный код
1	1
1	2
1	1	3
1	4
1	1	5
1	1	6
1	1	1	7
1	8
1	1	9

Остальные комбинации двоичного кода в тетраде являются запрещенными. Запишем пример двоично-десятичного
кода:

1258 = 0001 0010 0101 1000

В первой тетраде записана цифра 1, во второй — 2, в третьей — 5, а в последней тетраде записана цифра 8. В данном
примере для записи числа 1258 потребовалось четыре тетрады. Количество ячеек памяти микропроцессора
зависит от его разрядности. При 16-разрядном процессоре все число уместится в одну ячейку памяти.

589 = 0000 0101 1000 1001

В данном примере для записи числа достаточно трех тетрад, но ячейка памяти 16-разрядная. Поэтому старшая
тетрада заполняется нулями. Они не изменяют значение цифры. Если бы мы заполнили нулями младшую тетраду, то
число увеличилось бы в десять раз!

При записи десятичных чисел часто требуется записывать знак числа и десятичную запятую (в англоязычных странах точку). Двоично-десятичный код часто
применяется для набора телефонного номера или набора кодов телефонных служб. В этом случае кроме десятичных цифр часто применяются символы «*» или «#».
Для записи этих символов в двоично-десятичном коде применяются запрещенные комбинации

Достаточно часто в памяти процессора для хранения одной десятичной цифры выделяется одна ячейка памяти (восьми,
шестнадцати или тридцатидвухразрядная). Это делается для повышения скорости работы программы. Для того,
чтобы отличить такой способ записи двоично-десятичного числа от стандартного, способ записи десятичного
числа, как это показано в примере, называется упакованной формой
двоично-десятичного числа. Запишем те же
числа, что и в предыдущем примере в неупакованном двоично-десятичном коде для восьмиразрядного процессора:

1258 =00000001
00000010
00000101
00001000

В первой строке записана цифра 1, во второй — 2, в третьей — 5, а в последней строке записана цифра 8. В данном
примере для записи числа 1258 потребовалось четыре строки (ячейки памяти)

589 = 00000000
00000101
00001000
00001001

Суммирование двоично-десятичных чисел.

Суммирование двоично-десяичных чисел можно производить по правилам обычной двоичной арифметики, а затем
производить двоично-десятичную коррекцию
. Двоично-десятичная коррекция заключается в проверке каждой
тетрады на допустимые коды. Если в какой либо тетраде обнаруживается запрещенная комбинация, то это говорит
о переполнении. В этом случае необходимо произвести двоично-десятичную коррекцию. Двоично-десятичная
коррекция заключается в дополнительном суммировании числа шесть (число запрещенных комбинаций) с тетрадой,
в которой произошло переполнение или произошёл перенос в старшую тетраду. Приведём два примера.

Прямой код

Прямой код используется в двух вариантах.В первом (основной) — для записи только неотрицательных чисел:

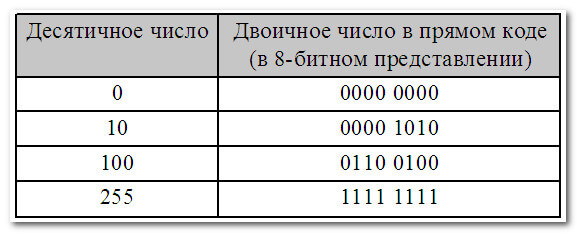В этом варианте (для восьмибитного двоичного числа) мы можем записать максимальное число 255 (всего чисел 256 — от 0 до 255)

Второй вариант — для записи как положительных, так и отрицательных чисел.В этом случае старший бит (в нашем случае — восьмой) объявляется знаковым разрядом (знаковым битом).При этом, если: — знаковый разряд равен 0, то число положительное — знаковый разряд равен 1, то число отрицательное

В этом случае диапазон десятичных чисел, которые можно записать в прямом коде составляет от — 127 до +127:

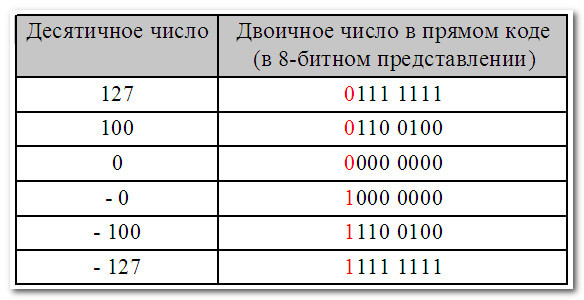Подводя итоги вопроса, не влезая в его дебри, скажу одно:Прямой код используется главным образом для представления неотрицательных чисел. Использование прямого кода для представления отрицательных чисел является неэффективным — очень сложно реализовать арифметические операции и, кроме того, в прямом коде два представления нуля — положительный ноль и отрицательный ноль (чего не бывает):

Побитовое И (&)

Побитовое И () выполняет булеву операцию конъюнкции над каждой парой битов, которые стоят на одинаковых позициях в двоичных представлениях операндов. Другими словами, результат равен 1, если оба соответствующих бита операндов равны 1; если же хотя бы один бит из пары равен , результирующий двоичный разряд равен .

Таблица истинности для этой операции выглядит так:

a	b	a & b
1
1
1	1	1

В следующем примере поразрядное И выполняется для чисел 38 и 3:

Выполнить код »
Скрыть результаты

Как видите, только в одной позиции биты обоих операндов равны 1. Из-за этого
все остальные биты результата обнуляются, что в итоге дает 000010.
Как результат, получаем 000010₂, или 2₁₀.

Преобразование десятичных чисел в двоичные

Одним из алгоритмов перевода десятичного числа в двоичное является деление нацело на 2 с последующим «сбором» двоичного числа из остатков деления. Например, для перевода десятичного числа 14 в двоичное представление необходимо выполнить следующие действия:

  14 / 2 = 7, остаток 0 — младший разряд двоичного числа
   7 / 2 = 3, остаток 1
   3 / 2 = 1, остаток 1
   1 / 2 = 0, остаток 1 — старший разряд двоичного числа

Таким образом, результат преобразования будет следующим: 14₁₀ = 1110₂

Преобразование дробных десятичных чисел в двоичные

Если в исходном числе есть целая часть, то она преобразуется отдельно от дробной. Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

• дробь умножается на основание двоичной системы счисления (2);
• в полученном произведении выделяется целая часть, которая принимается в качестве старшего разряда числа в двоичной системе счисления;
• в следующем шаге полученная в результате произведения дробная часть опять умножается на 2;
• алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений.

Например, для перевода дробного десятичного числа 206,625 в дробное двоичное число необходимо выполнить следующие действия:

• производим перевод целой части, где в итоге получаем 206₁₀ = 11001110₂;
• далее действуем в соответствии с алгоритмом перевода дробной части; целые части произведений, полученных в каждом шаге (выделены жирным шрифтом), являются разрядами искомой дробной части:

  0,625·2 = 1,25
  0,25·2  = ,5
  0,5·2   = 1,0

Таким образом, получаем значение дробной части 0,625₁₀ = 101₂ и в целом имеем результат: 206,625₁₀ = 11001110,101₂