Все о треугольниках

Свойства

Определение невырожденного треугольника в геометрии основано на том, что углы треугольника суммируются в 180 градусов, каждая сторона больше нуля, и сумма двух сторон всегда больше третьей стороны. Любая грань треугольника является отрезком, соединяющим две его вершины.

Примерами невырожденных треугольников могут служить треугольник со сторонами 3, 4 и 5, а также треугольник с углами 30, 60 и 90 градусов.

Равенство суммы углов треугольника 180 градусам.

Стандартное определение треугольника в геометрии — это фигура, образованная тремя сторонами и тремя вершинами. Каждая сторона соединяет две вершины, а каждый угол образуется двумя сторонами, исходящими из одной вершины. Углы треугольника также могут быть классифицированы как острые (меньше 90 градусов), прямые (равные 90 градусам) или тупые (больше 90 градусов).

Признак невырожденного треугольника — это условие, при котором сумма длин любых двух сторон треугольника всегда больше длины третьей стороны. Иначе говоря, треугольник должен быть «закрытой» фигурой, а не прямой линией или точкой.

Важным свойством невырожденного треугольника является равенство суммы углов треугольника 180 градусам. Это значит, что сумма всех внутренних углов треугольника равна 180 градусам. Например, если у нас есть треугольник с углами 60 градусов, 70 градусов и 50 градусов, то их сумма будет равна 180 градусам.

Сумма длин двух сторон треугольника всегда больше длины третьей стороны.

В геометрии треугольник представляет собой плоскую фигуру, образованную тремя отрезками, называемыми сторонами треугольника. Каждая сторона треугольника является гранью этой фигуры, а точки их пересечения – вершинами. Сумма длин двух сторон определенного треугольника всегда больше длины третьей стороны и служит важным признаком для определения невырожденного треугольника.

Позвольте рассмотреть пример, чтобы увидеть это свойство в действии. Предположим, что у нас есть треугольник с сторонами длиной 5, 7 и 10 единиц. Чтобы проверить, выполняется ли свойство суммы длин двух сторон, необходимо сложить длины двух самых коротких сторон:

Стороны треугольника	Сумма длин двух сторон
5, 7, 10	5 + 7 = 12

Как видим, сумма длин двух сторон треугольника равна 12. Затем сравниваем эту сумму с длиной третьей стороны:

Стороны треугольника	Сумма длин двух сторон	Длина третьей стороны
5, 7, 10	12	10

Как можно заметить, сумма длин двух сторон (12) больше длины третьей стороны (10), что подтверждает наше утверждение о том, что сумма длин двух сторон треугольника всегда больше длины третьей стороны.

Сумма длин двух сторон треугольника является важным свойством, она влияет на множество других характеристик треугольника, таких как его площадь, углы и отношения между сторонами.

Высоты треугольника пересекаются в одной точке — ортоцентре.

Одним из важных свойств треугольника является то, что все высоты треугольника пересекаются в одной точке, которая называется ортоцентром. Именно ортоцентр является точкой пересечения трех высот треугольника.

Ортоцентр имеет много геометрических свойств и является ключевой точкой в задачах треугольника. Он лежит внутри или на границе треугольника, в зависимости от его типа и положения высот. Более того, ортоцентр может быть использован для определения других важных элементов треугольника, таких как окружность Эйлера и описанная окружность.

Одно из основных свойств ортоцентра заключается в том, что отрезки, соединяющие ортоцентр с вершинами треугольника, перпендикулярны соответствующим сторонам. Это означает, что углы между сторонами треугольника и этими отрезками равны 90 градусам.

Еще одним важным признаком ортоцентра является его связь с площадью треугольника. Для любого треугольника, площадь треугольника ABC равна произведению половины основания BC на высоту, проведенную из вершины A:

SABC = 0.5 * BC * HA, где SABC — площадь треугольника ABC, BC — основание треугольника, HA — высота, проведенная из вершины A.

Таким образом, ортоцентр треугольника имеет большое значение и определение его свойств позволяет углубить понимание треугольника в геометрии. Благодаря своей особенной природе, ортоцентр является важным элементом в решении задач и определении основных характеристик треугольника.

[править] Свойства и особенности треугольников

Трём точкам пространства, не лежащим на одной прямой (и образуемому ими невырожденному треугольнику), обязательно соответствует одна и только одна плоскость. Это весьма уникально — так как меньшему количеству точек соответствуют прямая и точка, а уже четыре точки могут находится вне единой плоскости.

Треугольник — это часть плоскости, ограниченная минимально возможным количеством сторон. Любой многоугольник можно точно разбить на треугольники, лишь связав его вершины отрезками, не пересекающими его стороны. С некоторым приближением, на треугольники можно разбить поверхность любой формы, как на плоскости так и в пространстве. Процесс разбиения на треугольники называется триангуляция.

Существует раздел математики, целиком посвящённый изучению закономерностей треугольников — Тригонометрия.

Треугольник, когда не вырожден — всегда выпуклый многоугольник.

Для треугольника всегда существует одна вписанная и одна описанная окружность.

Число 9

Свойства треугольников не ограничиваются их сторонами и углами. На самом деле центр описанной окружности, центр вписанной окружности и ортоцентр треугольника — это все точки, тесно связанные с вершинами треугольника. Круг Нейпира — один из таких кругов, который можно построить, используя эти точки. Окружность проходит через вершины треугольника, а также через центр описанной окружности, и дает захватывающее представление о свойствах треугольника.

• В круге Нейпира центр описанной окружности является центром окружности. окружность.
• Радиус окружности равен расстоянию между центром описанной окружности и вершинами треугольника.
• Окружность пересекается со сторонами треугольника в трех различных точках.

Чтобы понять значение этих свойств, давайте подробнее рассмотрим число 9 в круге Нейпира.

9 баллов пересечения	Значение
3 вершины	Основные точки треугольника
3 точки пересечения со сторонами треугольника	Точки пересечения окружности со сторонами
1 центр окружности	Центр круга
1 incenter	Центр вписанного круга
1 ортоцентр	Точка пересечения высот

Как мы видим из таблицы выше, всего девять точки пересечения круга Нейпира. Каждый из этих пунктов имеет свое значение и значение, и все они способствуют нашему пониманию свойств треугольника и окружности.

В заключение, круг Нейпира — увлекательная тема в изучении треугольников. Свойства этого круга дают нам ценную информацию о свойствах треугольника и круга

В частности, число 9 в круге Нейпира важно, поскольку оно представляет собой общее количество точек пересечения в круге. Поняв свойства круга Нейпира и значение числа 9, мы сможем глубже понять геометрию и ее приложения

Основные величины и их формулы

Все геометрические фигуры имеют свои характеристики и собственную величину. Самыми распространёнными являются такие величины как площадь и периметр. Они используются в повседневной жизни, в строительстве и в других областях. Например, во время ремонта или нового строительства, количество необходимых материалов и объём работ не определить, не вычислив заранее площадь и периметр.

Периметр

Периметром называется замкнутая граница плоской геометрической фигуры, которая отделяет её внутреннюю область от внешней. Периметр есть у любой замкнутой геометрической фигуры:

На рисунке периметры выделены красной линией. Периметр окружности часто называют длиной.

Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.

Обозначается заглавной латинской P.

Площадь

Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой, то есть та часть плоскости, которая находится внутри периметра. Именно она даёт нам основную информацию о её размере. Любая плоская замкнутая геометрическая фигура имеет определённую площадь. 

На рисунке площади фигур окрашены различными цветами.

Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм2, см2, м2, км2 и т. д. S (square) — знак площади.

Вычисление периметра и площади

Периметр — это длина замкнутого контура геометрической фигуры. Можно, конечно, измерить линейкой длины всех сторон и сложить их. Но лучше воспользоваться специальными формулами для вычисления периметра, это значительно упростит задачу.

• Квадрат: периметр = 4 * сторона.
• Треугольник: периметр = сторона 1 + сторона 2 + сторона 3.
• Неправильный многоугольник: периметр = сумме всех сторон многоугольника.
• Круг: длина окружности = 2 * π * радиус = π * диаметр (где π – это число пи (константа, примерно равная 3,14), радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности, диаметр – это длина отрезка, проходящего через центр окружности и соединяющего любые две точки, лежащие на этой окружности).

Для вычисления площади фигуры также потребуется соответствующая формула. К разным фигурам применяются разные формулы. Для вычисления площади стандартных геометрических фигур можно воспользоваться следующими формулами:

• Параллелограмм: площадь = основание * высота
• Квадрат: площадь = сторона 1 * сторона 2
• Треугольник: площадь = ½ * основание * высота
• Круг: площадь = π * радиус² (где радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Квадрат радиуса – это значение радиуса, умноженное само на себя).

Итак, мы перечислили основные и самые распространённые геометрические фигуры и их свойства. Образовательная платформа iSmart поможет вашему ребёнок изучить основные геометрические фигуры, их виды, названия и свойства с помощью увлекательных заданий. Преимущества занятий на умных тренажёрах iSmart:

• интерактивные задания больше похожи на игру;
• их можно отрабатывать многократно и они не будут повторяться;
• платформа сформирует индивидуальную траекторию обучения на основе диагностики знаний;
• достаточно всего 20 минут занятий в день, чтобы в короткий срок увидеть прогресс в обучении.

Кроме того, занятия помогут вам освободить своё время, ведь ребёнок сможет заниматься самостоятельно, а родитель — получать отчёты и наблюдать за динамикой обучения. Метод обучения iSmart основан на последних научных практиках: микрообучение и поведенческий анализ.

Образовательная платформа iSmart предлагает подготовку к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.

Значение понятия «Невырожденный треугольник»

Невырожденный треугольник — это треугольник, который имеет конечные стороны и углы, а также положительную площадь. Такой треугольник является основным объектом изучения геометрии и математики.

Значит, треугольник, который не является невырожденным, будет иметь одну или несколько из следующих характеристик:

• Одна или несколько сторон имеют нулевую длину. В этом случае треугольник превращается в отрезок или точку.
• Одна или несколько сторон имеют отрицательную длину. Это может происходить, когда точки, задающие стороны треугольника, расположены в неправильном порядке.
• Сумма длин двух сторон меньше третьей стороны. Такой треугольник называется вырожденным, и он не может существовать в двумерном пространстве.
• Один или несколько углов равны 0 или 180 градусов. Такие углы называются вырожденными углами и не отличаются от прямой линии или плоскости.

Имея эти определения в виду, мы можем утверждать, что для треугольника с конечными сторонами и положительной площадью справедливо понятие «невырожденный треугольник». Это базовое понятие является основой для изучения свойств и характеристик треугольников в геометрии.

Основные характеристики невырожденного треугольника

Что значит невырожденный треугольник? Невырожденный треугольник — это треугольник, у которого все три стороны положительной длины и никакие три точки, задающие его вершины, не лежат на одной прямой.

Вот основные характеристики, которые отличают невырожденный треугольник:

• Три стороны: невырожденный треугольник имеет три стороны, каждая из которых имеет положительную длину и является отрезком прямой между двумя вершинами.
• Три вершины: треугольник имеет три вершины, которые являются точками пространства или плоскости. Вершины образуют углы друг с другом.
• Три угла: треугольник состоит из трех углов, которые образуются между сторонами. Сумма всех углов в невырожденном треугольнике равна 180 градусам.
• Площадь: невырожденный треугольник имеет площадь, которая можно вычислить с использованием формулы Герона или других методов.
• Периметр: периметр невырожденного треугольника — это сумма всех его сторон. Он также может быть вычислен с помощью известных значений длин сторон.

Невырожденный треугольник является одной из основных фигур в геометрии. Он имеет множество свойств и характеристик, которые могут быть использованы для изучения его свойств и применения в различных математических и физических задачах.

Различия невырожденного треугольника от вырожденного

Треугольник — это геометрическая фигура, состоящая из трех отрезков, которые соединяются между собой в трех точках. Однако не все треугольники являются невырожденными, и это имеет свои особенности и значения.

Невырожденный треугольник (также известный как обычный треугольник) — это треугольник, у которого все три стороны имеют разную длину и все три угла не равны нулю и не равны 180 градусов. Невырожденный треугольник значит, что он имеет достаточно размеров и формы, чтобы считаться полноценным и функциональным треугольником.

Основное отличие невырожденного треугольника от вырожденного заключается в его свойствах и определениях. Невырожденный треугольник имеет три разные стороны и три угла, которые в сумме равны 180 градусов. Каждая сторона невырожденного треугольника соединяет две точки, и каждый угол образуется между двумя сторонами. Такой треугольник может быть измерен и описан с помощью геометрических формул и правил.

В то же время, вырожденный треугольник имеет особые свойства и определения. Он представляет собой треугольник, у которого все три стороны соединены в одной точке, а все три угла равны нулю или 180 градусов. Это значит, что его стороны и углы не образуют полноценной фигуры у треугольника и не могут быть измерены с помощью геометрических формул.

Таким образом, различия между невырожденным и вырожденным треугольниками заключаются в их свойствах и определениях. Невырожденный треугольник является полноценной геометрической фигурой с тремя разными сторонами и углами в сумме, равной 180 градусов, в то время как вырожденный треугольник не обладает такими свойствами и не может быть измерен с помощью геометрических формул.

Центроид, центр окружности и ортоцентр треугольника

Треугольники — одна из самых важных фигур в математике. Они состоят из трех сторон, трех углов и трех вершин. Каждая вершина соединена стороной, а три стороны пересекаются в трех точках, называемых вершинами. Треугольник также является простейшим из существующих многоугольников, и поэтому он играет важную роль в различных областях математики, включая геометрию, тригонометрию и исчисление.

Один интересный аспект треугольников заключается в том, что они имеют три точки, которые значимы по разным причинам — центроид, центр описанной окружности и ортоцентр. Каждая из этих точек уникальна и может рассказать нам разные вещи о треугольнике и его свойствах.

• Центроид: Центроид — это точка, в которой пересекаются медианы треугольника. Медиана — это отрезок, соединяющий вершину с серединой противоположной стороны. Центроид также известен как центр тяжести треугольника, так как это точка, в которой треугольник может быть идеально сбалансирован на кончике карандаша. Центроид расположен на 2/3 пути от каждой вершины до середины противоположной стороны.
• Центр окружности: Центр описанной окружности — это точка, в которой биссектрисы сторон треугольник пересекается. Биссектриса — это отрезок, перпендикулярный стороне треугольника и проходящий через его середину. Центр описанной окружности важен, потому что это центр окружности, проходящей через все три вершины треугольника.
• Ортоцентр: ортоцентр — это точка пересечения высот треугольника. Высота – это отрезок, который выходит из вершины треугольника и перпендикулярен противоположной стороне. Ортоцентр важен, потому что он показывает нам, где встречаются высоты треугольника, и его можно использовать для определения площади треугольника.

Чтобы лучше понять эти три точки, мы можем посмотреть за следующей таблицей:

	Центроид	Центр окружности	Ортоцентр
Определение	Точка пересечения медиан треугольника	Точка пересечения серединных перпендикуляров к сторонам треугольника	Точка пересечения высот треугольника
Расположение	2/3 пути от каждой вершины до середины противоположной стороны	Внутрь для остроугольных треугольников, на треугольник для прямоугольных треугольников и снаружи для тупоугольных треугольников	Внутри для остроугольных треугольников, на треугольник для прямоугольных треугольников и снаружи для тупоугольных треугольников
Свойства	Центроид делит каждую медиану на два сегмента, причем сегмент, расположенный ближе к вершине, вдвое длиннее другого сегмента.	центр описанной окружности равноудален от трех вершин треугольника, а расстояние равно радиусу описанной окружности.	Ортоцентр — это пересечение высот треугольника, и его можно использовать для определения площадь треугольника.

Итак, центр тяжести, центр описанной окружности и ортоцентр — это три важные точки в треугольнике, которые могут дать представление о его свойствах и характеристики. Каждая из этих точек уникальна и определяется различными свойствами треугольника, такими как медианы, биссектрисы и высоты. Понимание этих моментов может быть полезным при решении задач по геометрии, исчислению и другим областям математики.

Значение понятия «Невырожденный треугольник»

Невырожденный треугольник — это треугольник, который имеет конечные стороны и углы, а также положительную площадь. Такой треугольник является основным объектом изучения геометрии и математики.

Значит, треугольник, который не является невырожденным, будет иметь одну или несколько из следующих характеристик:

• Одна или несколько сторон имеют нулевую длину. В этом случае треугольник превращается в отрезок или точку.
• Одна или несколько сторон имеют отрицательную длину. Это может происходить, когда точки, задающие стороны треугольника, расположены в неправильном порядке.
• Сумма длин двух сторон меньше третьей стороны. Такой треугольник называется вырожденным, и он не может существовать в двумерном пространстве.
• Один или несколько углов равны 0 или 180 градусов. Такие углы называются вырожденными углами и не отличаются от прямой линии или плоскости.

Имея эти определения в виду, мы можем утверждать, что для треугольника с конечными сторонами и положительной площадью справедливо понятие «невырожденный треугольник». Это базовое понятие является основой для изучения свойств и характеристик треугольников в геометрии.

Основные характеристики невырожденного треугольника

Что значит невырожденный треугольник? Невырожденный треугольник — это треугольник, у которого все три стороны положительной длины и никакие три точки, задающие его вершины, не лежат на одной прямой.

Вот основные характеристики, которые отличают невырожденный треугольник:

• Три стороны: невырожденный треугольник имеет три стороны, каждая из которых имеет положительную длину и является отрезком прямой между двумя вершинами.
• Три вершины: треугольник имеет три вершины, которые являются точками пространства или плоскости. Вершины образуют углы друг с другом.
• Три угла: треугольник состоит из трех углов, которые образуются между сторонами. Сумма всех углов в невырожденном треугольнике равна 180 градусам.
• Площадь: невырожденный треугольник имеет площадь, которая можно вычислить с использованием формулы Герона или других методов.
• Периметр: периметр невырожденного треугольника — это сумма всех его сторон. Он также может быть вычислен с помощью известных значений длин сторон.

Невырожденный треугольник является одной из основных фигур в геометрии. Он имеет множество свойств и характеристик, которые могут быть использованы для изучения его свойств и применения в различных математических и физических задачах.

Различия невырожденного треугольника от вырожденного

Треугольник — это геометрическая фигура, состоящая из трех отрезков, которые соединяются между собой в трех точках. Однако не все треугольники являются невырожденными, и это имеет свои особенности и значения.

Невырожденный треугольник (также известный как обычный треугольник) — это треугольник, у которого все три стороны имеют разную длину и все три угла не равны нулю и не равны 180 градусов. Невырожденный треугольник значит, что он имеет достаточно размеров и формы, чтобы считаться полноценным и функциональным треугольником.

Основное отличие невырожденного треугольника от вырожденного заключается в его свойствах и определениях. Невырожденный треугольник имеет три разные стороны и три угла, которые в сумме равны 180 градусов. Каждая сторона невырожденного треугольника соединяет две точки, и каждый угол образуется между двумя сторонами. Такой треугольник может быть измерен и описан с помощью геометрических формул и правил.

В то же время, вырожденный треугольник имеет особые свойства и определения. Он представляет собой треугольник, у которого все три стороны соединены в одной точке, а все три угла равны нулю или 180 градусов. Это значит, что его стороны и углы не образуют полноценной фигуры у треугольника и не могут быть измерены с помощью геометрических формул.

Таким образом, различия между невырожденным и вырожденным треугольниками заключаются в их свойствах и определениях. Невырожденный треугольник является полноценной геометрической фигурой с тремя разными сторонами и углами в сумме, равной 180 градусов, в то время как вырожденный треугольник не обладает такими свойствами и не может быть измерен с помощью геометрических формул.

Цилиндр и его свойства

Цилиндр – геометрическое тело, образованное двумя параллельными плоскостями, основаниями, и боковой поверхностью, являющейся цилиндрической поверхностью. Основания цилиндра имеют форму круга, а боковая поверхность представляет собой цилиндрическую оболочку между основаниями.

У цилиндра есть несколько свойств:

• Объем: объем цилиндра равен произведению площади основания на высоту. Формула для расчета объема цилиндра: V = πr2h, где π – математическая константа, r – радиус основания, h – высота цилиндра.
• Площадь боковой поверхности: площадь боковой поверхности цилиндра рассчитывается по формуле: Sб = 2πrh, где h – высота цилиндра, r – радиус основания.
• Площадь полной поверхности: площадь полной поверхности цилиндра складывается из площади двух оснований и боковой поверхности. Формула для расчета: Sп = 2πr2 + 2πrh.

Цилиндры используются в различных областях, например, для создания баков, цистерн, трубопроводов, а также в архитектуре, механике и других отраслях науки.

Четырёхугольник

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Другие свойства треугольника

Все треугольники имеют много различных свойств, которые могут быть определены по их сторонам и углам.

Прямоугольный треугольник — это такой треугольник, у которого один из его углов равен 90°.

У равнобедренного треугольника две стороны равны друг другу, а у его углов напротив равных сторон такое же значение.

Треугольник с разными сторонами и разными углами называется разносторонним.

Для треугольников существует несколько теорем, которые позволяют определить их свойства:

• Теорема синусов позволяет определить взаимосвязь между сторонами треугольника и синусами его углов.
• Теорема косинусов позволяет определить взаимосвязь между сторонами треугольника и косинусами его углов.
• Теорема Пифагора применима только к прямоугольным треугольникам и позволяет определить длину его гипотенузы по длинам катетов.

Треугольник также может быть описан вокруг окружности или вписан в окружность. Описанная окружность — это окружность, которая проходит через все вершины треугольника. Вписанная окружность — это окружность, которая касается сторон треугольника внутренним образом.

Другие свойства треугольника включают:

• Медианы, которые соединяют вершины треугольника со средними точками противоположных сторон.
• Высоты, которые опускаются из вершин треугольника на противоположные стороны и пересекаются в одной точке, называемой ортоцентром.
• Средняя линия, которая соединяет середины сторон треугольника.

Площадь треугольника можно вычислить с помощью различных формул, в зависимости от доступных данных о треугольнике:

• Формула Герона позволяет вычислить площадь треугольника по длинам его сторон.
• Формула основания и высоты позволяет вычислить площадь треугольника по его основанию и высоте.
• Формула синуса позволяет вычислить площадь треугольника по длинам двух его сторон и синусу угла между ними.
• Формула вписанной окружности позволяет вычислить площадь треугольника по радиусу вписанной окружности и длинам его сторон.
• Формула описанной окружности позволяет вычислить площадь треугольника по радиусу описанной окружности и длинам его сторон.

Также существуют отношения между длинами сторон и углами треугольника:

• Отношение длин сторон треугольника к его периметру называется относительной длиной.
• Отношение площадей двух треугольников, имеющих одну общую сторону, называется относительной площадью.
• Отношение синусов двух углов треугольника к длине стороны, напротив которой эти углы расположены, называется относительным синусом.

Таким образом, треугольник — это многоугольник, состоящий из трех сторон и трех углов. Существует три типа треугольников: равносторонний, равнобедренный и разносторонний. Каждый из них имеет свои уникальные свойства, определенные по длинам сторон и углам.

Что значит Невырожденный треугольник определение и свойстваНевырожденный треугольник —

Contents

Многоугольники

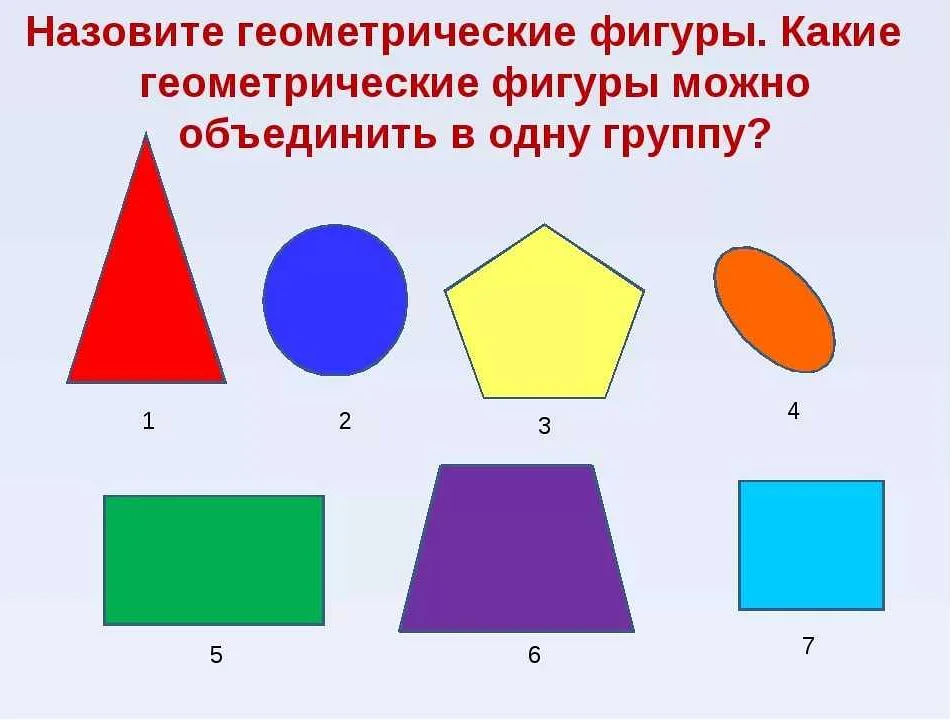
Многоугольник — это фигура, у которой есть три и более сторон и вершин. Один из примеров многоугольника — треугольник. Многоугольники могут иметь разное количество сторон и форму. Они могут быть правильными и неправильными, выпуклыми и невыпуклыми.

Неправильный многоугольник — это многоугольник, у которого не все стороны равны и не все углы между сторонами равны. Неправильные многоугольники могут иметь любое количество сторон и форму. Они могут быть выпуклыми или невыпуклыми. Примерами неправильных многоугольников могут являться правильный пятиугольник и любой другой многоугольник, у которого длины сторон и углы не равны.

Выпуклый многоугольник — это многоугольник, у которого все углы между сторонами меньше 180 градусов. Например, квадрат — это выпуклый многоугольник, потому что все его углы равны 90 градусов, и они меньше 180 градусов.

Невыпуклый многоугольник — это многоугольник, у которого есть углы между сторонами, равные или больше 180 градусов. Например, «звезда» — это невыпуклый многоугольник.

Также существует многоугольник, который называется правильный многогранник. Он имеет грани — правильные многоугольники. Примерами таких многогранников являются тетраэдр и октаэдр.

Итак, многоугольники разных форм и типов являются важной частью математики, и знание об этом может быть полезным не только для учеников, но и для различных профессий

Область применения алгоритма

Алгоритм проверки существования треугольника по длинам его сторон находит применение в различных областях, связанных с геометрией и вычислительной математикой. Ниже приведены основные области, в которых алгоритм может быть полезен:

• Геометрия и топология: Алгоритм активно применяется в геометрии для проверки возможности построения треугольника по заданным длинам сторон. Также он может использоваться для определения типа треугольника (равносторонний, равнобедренный, разносторонний) на основе длин его сторон. В топологии, алгоритм может использоваться для анализа формы и свойств треугольников и их сочетаний в различных структурах.
• Компьютерная графика и визуализация: В области компьютерной графики и визуализации алгоритм проверки существования треугольника может быть использован для предварительной обработки и фильтрации данных о треугольниках в 3D-моделях. Это позволяет улучшить производительность и качество визуализации, исключая некорректные, невозможные или неправильно заданные треугольники.
• Компьютерное моделирование: В компьютерном моделировании алгоритм может применяться для проверки корректности и согласованности моделируемых объектов, включая треугольники, в контексте физических или математических моделей и симуляций.
• Архитектура и конструирование: При проектировании и конструировании различных объектов и сооружений, алгоритм может быть полезен для проверки соответствия треугольников условиям стабильности и прочности, а также для контроля правильности изготовления и сборки треугольных элементов.

В целом, алгоритм проверки существования треугольника по длинам его сторон является важным инструментом в геометрическом анализе и различных приложениях, где требуется работа с треугольниками.

Какие еще методы могут использоваться для нахождения площади основания

В дополнение к классическим методам нахождения площади основания, есть и другие варианты, которые могут быть полезны в определенных ситуациях.

1. Использование геометрических фигур

Если форма основания не является прямоугольной или квадратной, можно разбить ее на более простые геометрические фигуры (например, треугольники, трапеции или круги). На основе этого можно найти площадь каждой фигуры и сложить их, чтобы получить общую площадь основания.

2. Использование метода Монте-Карло

Этот метод заключается в размещении точек на поверхности основания и подсчете количества точек, попавших внутрь фигуры основания. На основе этого можно определить отношение площади фигуры к площади общей поверхности. Чем больше точек используется, тем более точным становится результат.

3. Использование сканирующего лазера

Сканирующий лазер может использоваться для получения точных показаний размеров объекта, включая площадь основания. При этом нет необходимости делать сложные измерения вручную – все данные записываются автоматически в компьютер.

Вопрос-ответ

Вопрос: Как найти площадь основания прямоугольника?

Ответ: Площадь основания прямоугольника вычисляется как произведение его двух сторон.

Вопрос: Как найти площадь основания треугольника, если известны все его стороны?

Ответ: Площадь основания треугольника можно вычислить, используя формулу Герона: S = √p(p-a)(p-b)(p-c), где p – полупериметр треугольника, a, b и c – его стороны.

Вопрос: Как найти площадь основания круга?

Ответ: Площадь основания круга вычисляется по формуле S = πr², где r – радиус круга, π – математическая константа, примерно равная 3,14.

Вопрос: Как найти площадь основания призмы?

Ответ: Площадь основания призмы можно найти, зная форму основания. Например, для призмы с прямоугольным основанием площадь основания вычисляется как произведение его двух сторон.

Вопрос: Как найти площадь основания правильной треугольной пирамиды, если известна ее высота?

Ответ: Площадь основания правильной треугольной пирамиды можно найти, используя следующую формулу: S = (a²√3)/4, где a – длина стороны правильного треугольника, основания пирамиды. Затем умножаем полученную площадь на высоту пирамиды.

Главная — Советы — Простой и эффективный способ: как быстро найти площадь основания

Комментарии

Анна

5.0 out of 5.0 stars5.0

Екатерина
5.0 out of 5.0 stars5.0

Я всегда сталкиваюсь с проблемой вычисления площади основания объектов. Статья помогла мне разобраться в этом вопросе. Хорошо, что применение формулы и процесс вычисления расписаны по шагам, что облегчило мне задачу.

Ольга Смирнова
5.0 out of 5.0 stars5.0

Статья очень краткая и понятная. Теперь я знаю, как найти площадь основания. Спасибо!

Sapphire
5.0 out of 5.0 stars5.0

Как женщина, я часто оказываюсь в ситуации, когда нужно рассчитать площадь основания различных фигур — будь то круг, прямоугольник или треугольник. К сожалению, мои знания по математике и геометрии ограничены, и я не знаю, как найти площадь основания. Поэтому я рада, что наткнулась на эту статью. Статья помогла мне понять, что не нужно бояться главной формулы для рассчета площади основания — независимо от того, какая фигура у вас есть перед глазами. Все описано очень доступно и понятно. Я прочитала эту статью несколько раз, чтобы убедиться, что я точно понимаю, как найти площадь основания. Используя эту информацию, я смогла рассчитать площадь основания для нескольких примеров. Теперь у меня есть более четкое понимание того, что такое площадь основания, как ее рассчитывать и как это применять на практике. Большое спасибо за эту статью! Я уверена, что многие женщины, так же как и я, оценят ее доступность и понятность.

Елена Кузнецова
5.0 out of 5.0 stars5.0

Я уже давно хотела научиться находить площадь основания, но всегда боялась, что это сложно. Статья помогла мне понять, что это проще, чем кажется. Все описано доступно и понятно. Теперь я готова рассчитывать площадь оснований и делать это правильно!

Luna
5.0 out of 5.0 stars5.0

Статья понятная и полезная для решения задач по геометрии.

Одномерные фигуры

Одномерные фигуры это фигуры, у которых есть только одно измерение — длина. Эти фигуры могут быть представлены линиями или отрезками.

Примерами одномерных фигур являются:

• Отрезок — это часть прямой, которая ограничена двумя точками. Длина отрезка определяется расстоянием между этими точками.
• Линия — это бесконечно длинная фигура, состоящая из точек, которые лежат на одной прямой.
• Кривая — это линия, которая не является прямой и может иметь разные формы, такие как окружность, эллипс, парабола и другие.

Одномерные фигуры важны в математике и физике для описания перемещения и движения тел. Они также используются в геометрии для решения задач и построения различных графиков и диаграмм.