Какие числа называются целыми

Иррациональные числа в геометрии

Иррациональное значение можно встретить, вычисляя длину гипотенузы единичного равностороннего треугольника. Это такой треугольник, где оба катета равны единице. Если мы попробуем вычислить гипотенузу такого треугольника, то получим иррациональное число — √2.

Изображение: Лев Сергеев для Skillbox Media

Другой пример — вычисление длины окружности, которое невозможно без иррационального числа π (Пи). Для этого диаметр окружности умножается на число Пи: L = πD = 2πr, где L — длина окружности, D — диаметр, r — радиус. Из этого можно сделать вывод, что число Пи — это длина окружности, разделённая на её диаметр.

Практическое применение

Возможность разделить все числительные на парные и непарные широко используется в повседневной жизни. В зависимости от того, кратен ли двум порядковый номер месяца, по правилам дорожного движения может быть запрещена или разрешена стоянка в определенных зонах. Четные и нечетные недели помогают запомнить расписание вузов с многочисленной аудиторией.

В расписании железнодорожных поездов на кратности двум числа месяца завязаны маршруты с расписанием через день. Чтобы не нарушать установленный порядок, после 31 числа поезд может пропустить один выезд. Тот же принцип используется для нумерации вагонов — парность содержит информацию о направлении пути. В плацкартах и купе места с верхними полками всегда обозначены четным числом, а нижние — нечетным.

Вычислимые КБЧ.

Вычислимым КБЧ назовём такое, для которого существует алгоритм, выдающий
по порядку (справа налево) все цифры данного КБЧ (в заданной системе
счисления). Хотя общее количество КБЧ несчётное, количество вычислимых
КБЧ счётное (поскольку мы считаем, что алгоритм — это некий конечный
текст в конечном (или счётном) алфавите, а количество таких текстов — не
более чем счётное).

Понятно, что все конечные и периодические КБЧ являются вычислимыми.

Сумма, разность и произведение двух вычислимых чисел также являются
вычислимыми (поскольку они вычисляются справа налево, а после вычисления
очередной цифры к ней уже не приходится возвращаться).

Если основание системы счисления — простое число, то деление вычислимых
чисел и извлечение квадратного корня из вычислимого числа также являются
вычислимыми числами. (Возможно, что эти операции являются вычислимыми
для любой системы счисления, но это надо доказать.)

Преобразование в другую систему счисления иногда является вычислимым,
иногда нет.

Что запомнить

Мы разобрали, как устроены и как работают числа с плавающей точкой. Это тема гораздо шире и глубже, а её изучение может занять не один день. Поэтому давайте подведём итог и перечислим, что можно вынести из этой статьи:

• Числа с плавающей точкой — это приближённое представление вещественных чисел в программировании. Все правила их представления записаны в стандарте IEEE 754.
• Этот стандарт нужен, чтобы разные компьютерные архитектуры могли одинаково удобно и эффективно работать с вещественными числами.
• Числа с плавающей точкой бывают с одинарной точностью и двойной. Числа с одинарной точностью состоят из 32 битов: одного знакового бита, восьми битов для экспоненты и 23 битов для мантиссы. Числа с двойной точностью — из 64 битов: одного знакового бита, 11 битов для экспоненты и 52 битов для мантиссы.
• В стандарте IEEE 754 есть специальные значения, которые нужны для представления положительного и отрицательного нуля, бесконечностей и неопределённости.

Больше интересного про код в нашем телеграм-канале. Подписывайтесь!

Отсыпь и мне децимала!

Сна­чала нем­ного теории. Обоз­начим наше две ком­понен­ты, целую и дроб­ную часть чис­ла, как n и f, а само чис­ло будет пред­ста­вимо в виде

Для целой час­ти луч­ше все­го подой­дет зна­ковый тип 64-бит­ного целого, а для дроб­ной — без­зна­ковый, это упростит мно­гие опе­рации в даль­нейшем.

Це­лая часть в дан­ном слу­чае — мак­сималь­ное целое, мень­шее пред­став­ляемо­го чис­ла, дроб­ная часть — резуль­тат вычита­ния из это­го чис­ла его целой час­ти, пом­ножен­ной на 10 18 , и при­веден­ное к целому: f = (x – n) * 10 18 .

Це­лая часть для отри­цатель­ных чисел получит­ся боль­шей по модулю самого чис­ла, а дроб­ная часть будет не сов­падать с десятич­ной записью самого чис­ла, нап­ример для чис­ла –1,67 ком­понен­тами будут: n = –2 и f = 0,33 * 10 18 . Зато такая запись поз­воля­ет упростить и уско­рить алго­рит­мы сло­жения и умно­жения, пос­коль­ку не нуж­но вет­вле­ния для отри­цатель­ных чисел.

Свойства иррациональных чисел

У иррациональных чисел, как и у любых других, есть свои свойства. Давайте пройдёмся по каждому из них.

1. Если сложить иррациональное число с рациональным, получится иррациональное число:

π + 2 = 3,1415926535… + 2 = 5,1415926535…

√2 + 3 = 1,4142135623… + 3 = 4,4142135623…

Это же правило действует и при вычитании:

π − 3 = 3,1415926535… − 3 = 0,1415926535…

√7 − 1,645 = 2,6457513110… − 1,645 = 1,0007513110…

2. Если умножить иррациональное число на рациональное, получится иррациональное число:

π ∙ 8 = 3,1415926535… ∙ 8 = 25,1327412287…

√5 ∙ 3 = 2,2360679774… ∙ 3 = 6,7082039324…

3. Если вычесть одно иррациональное число из другого, может получиться рациональное или иррациональное число:

π − π = 3,1415926535… − 3,1415926535… = 0

√3 − √2 = 1,732050807… − 1,4142135623… = 0,3178372451…

4. При сложении или умножении двух иррациональных чисел может получиться рациональное или иррациональное число:

Работаем с иррациональными числами в Python

Выведем некоторые иррациональные значения в консоль на языке Python. Для этого нам понадобится математический модуль math, для работы с константами и извлечением корня, а также модуль и класс Decimal, для более точного исчисления. Импортируем эти объекты для начала работы:

В модуле math уже имеются для работы три константы — число Пи, два Пи и число Эйлера. Вывести их на экран довольно просто:

Вы можете заметить, что количество знаков после запятой всего 15, хотя эти значения иррациональны. Это связано с тем, что тип данных переменных является float, и большее значение он хранить не может.

Попробуем извлечь квадратный корень из 2 с помощью функции sqrt () модуля math и специального оператора возведения в степень **:

Оба способа работают одинаково, но вывод ограничивается 16 знаками. Чтобы увеличить точность, воспользуемся классом Decimal. Для этого поместим объект в переменную x, зададим ему параметр prec (precision — точность), например 10000, и вызовем метод sqrt () для этой переменной:

Мы получили 10 000 знаков после запятой при извлечении квадратного корня из 2. Таким же образом можно поиграться и с другими иррациональными значениями:

И напоследок вычислим иррациональное число Пи, используя характеристики нашей планеты. Длина окружности Земли составляет примерно 40 075,017 километров, а её диаметр — 12 756 километров. Зная формулу длины окружности L = πD, можно легко выйти на таинственное число Пи — π = L/D:

Операции над целыми числами.

1. Сумма целых чисел.

Для сложения двух целых чисел с одинаковыми знаками, необходимо сложить модули этих чисел и перед суммой поставить итоговый знак.

Пример:

(+2) + (+5) = +7.

2. Вычитание целых чисел.

Для сложения двух целых чисел с разными знаками, необходимо из модуля числа, которое больше вычесть модуль числа, которое меньше и перед ответом поставить знак большего числа по модулю.

Пример:

(-2) + (+5) = +3.

3. Умножение целых чисел.

Для умножения двух целых чисел, необходимо перемножить модули этих чисел и перед произведением поставить знак плюс (+), если исходные числа были одного знака, и минус (-) — если разного.

Пример:

(+2) ∙ (-3) = -6.

Когда умножаются несколько чисел, знак произведения будет положительным, если число неположительных сомножителей чётное, и отрицателен, если нечётное.

Пример:

(-2) ∙ (+3) ∙ (-5) ∙ (-3) ∙ (+4) = -360
(3 неположительных сомножителя).

4. Деление целых чисел.

Для деления целых чисел, необходимо поделить модуль одного на модуль другого и поставить перед результатом знак «+», если знаки чисел одинаковые, и минус, — если разные.

Пример:

(-12) : (+6) = -2.

Стандарт точечного плаванья

Ве­щес­твен­ные чис­ла с пла­вающей точ­кой, под­держан­ные на уров­не про­цес­сора, опи­саны спе­циаль­ным меж­дународ­ным стан­дартом IEEE 754. Основны­ми дву­мя типами для любых вычис­лений явля­ются single-precision (оди­нар­ной точ­ности) и double-precision (двой­ной точ­ности) floating-point (чис­ла с пла­вающей точ­кой). Наз­вания эти нап­рямую отра­жают раз­рядность бинар­ного пред­став­ления чисел оди­нар­ной и двой­ной точ­ности: под пред­став­ление с оди­нар­ной точ­ностью выделе­но 32 бита, а под двой­ную, как ни стран­но, 64 бита — ров­но вдвое боль­ше.

info

Кро­ме оди­нар­ной и двой­ной точ­ности, в новой редак­ции стан­дарта IEEE 754—2008 пре­дус­мотре­ны так­же типы рас­ширен­ной точ­ности, чет­верной и даже половин­ной точ­ности. Одна­ко в C/C++, кро­ме float и double, есть раз­ве что еще тип long double, упор­но не под­держи­ваемый ком­пани­ей Microsoft, которая в Visual C++ под­став­ляет вмес­то него обыч­ный double. Ядром про­цес­сора в нас­тоящий момент так­же, как пра­вило, пока не под­держи­вают­ся типы половин­ной и чет­верной точ­ности. Поэто­му, выбирая пред­став­ления с пла­вающей точ­кой, при­ходит­ся выбирать лишь из float и double.

В качес­тве осно­вания для экспо­нен­ты чис­ла по стан­дарту берет­ся 2, соот­ветс­твен­но, при­веден­ная выше фор­мула сво­дит­ся к сле­дующей:

Рас­клад в битах в чис­лах оди­нар­ной точ­ности выг­лядит так:

1 бит под знак	8 бит экспо­нен­ты	23 бита ман­тиссы

Для двой­ной точ­ности мы можем исполь­зовать боль­ше битов:

1 бит под знак	11 бит экспо­нен­ты	52 бита ман­тиссы

В обо­их слу­чаях если бит зна­ка равен 0, то чис­ло положи­тель­ное и 1 уста­нав­лива­ется для отри­цатель­ных чисел. Это пра­вило ана­логич­но целым чис­лам с той лишь раз­ницей, что в отли­чие от целых, что­бы получить чис­ло, обратное по сло­жению, дос­таточ­но инверти­ровать один бит зна­ка.

Пос­коль­ку ман­тисса записы­вает­ся в дво­ичном виде, под­разуме­вает­ся целая часть, уже рав­ная 1, поэто­му в записи ман­тиссы всег­да под­разуме­вает­ся один бит, который не хра­нит­ся в дво­ичной записи. В битах ман­тиссы хра­нит­ся имен­но дроб­ная часть нор­мализо­ван­ного чис­ла в дво­ичной записи.

info

Ман­тисса записы­вает­ся в дво­ичном виде, и отбра­сыва­ется целая часть, заведо­мо рав­ная 1, поэто­му никог­да не забыва­ем, что ман­тисса на один бит длин­нее, чем в она хра­нит­ся в дво­ичном виде.

Не нуж­но иметь док­тор­скую сте­пень, что­бы вычис­лить точ­ность в десятич­ных зна­ках чисел, которые мож­но пред­ста­вить этим стан­дартом: 2 23 + 1 = 16 777 216; это явно ука­зыва­ет нам на тот факт, что точ­ность пред­став­ления вещес­твен­ных чисел с оди­нар­ной точ­ностью дос­тига­ет чуть более семи десятич­ных зна­ков. Это зна­чит, что мы не смо­жем сох­ранить в дан­ном фор­мате, нап­ример, чис­ло 123 456,78 — неболь­шое, в общем‑то, чис­ло, но уже начиная с сотой доли мы получим не то чис­ло, что хотели. Ситу­ация усложня­ется тем, что для боль­ших чисел вида 1 234 567 890, которое прек­расно помеща­ется даже в 32-раз­рядное целое, мы получим пог­решность уже в сот­нях еди­ниц! Поэто­му, нап­ример, в C++ для вещес­твен­ных чисел по умол­чанию исполь­зует­ся тип double. Ман­тисса чис­ла с двой­ной точ­ностью уже пре­выша­ет 15 зна­ков: 2 52 = 4 503 599 627 370 496 и спо­кой­но вме­щает в себя все 32-раз­рядные целые, давая сбой толь­ко на дей­стви­тель­но боль­ших 64-раз­рядных целых (19 десятич­ных зна­ков), где пог­решность в сот­нях еди­ниц уже, как пра­вило, несущес­твен­на. Если же нуж­на боль­шая точ­ность, то мы в дан­ной статье обя­затель­но в этом поможем.

Те­перь что каса­ется экспо­нен­ты. Это обыч­ное бинар­ное пред­став­ление целого чис­ла, в которое нуж­но воз­вести 10, что­бы при перем­ножении на ман­тиссу в нор­мализо­ван­ном виде получить исходное чис­ло. Вот толь­ко в стан­дарте вдо­бавок вве­ли сме­щение, которое нуж­но вычитать из бинар­ного пред­став­ления, что­бы получить иско­мую сте­пень десят­ки (так называ­емая biased exponent — сме­щен­ная экспо­нен­та). Экспо­нен­та сме­щает­ся для упро­щения опе­рации срав­нения, то есть для оди­нар­ной точ­ности берет­ся зна­чение 127, а для двой­ной 1023. Все это зву­чит край­не слож­но, поэто­му мно­гие про­пус­кают гла­ву о типе с пла­вающей точ­кой. А зря!

Все свойства целых чисел

Daniel Jedzura/Shutterstock.com

Целые числа обладают некоторыми важными свойствами, которые необходимо знать, чтобы выполнять арифметические действия с ними:

замкнутость: выполняя сложение, вычитание или умножение целых чисел, в результате мы также получим целое число;

переместительность: неважно, в каком порядке мы складываем или умножаем целые числа, ведь результат будет одинаковым (4+2=2+4). Вычитание и деление целых чисел этим свойством не обладают;

распределительность: умножая целое число на сумму двух целых чисел, мы можем сначала умножить каждое слагаемое на это целое число, а затем сложить получившиеся произведения (3*(2+5)=3*2+3*5)

Это же свойство применимо к операциям деления целых чисел: (6+8):2=6:2+8:2;

разность знаков: умножая число со знаком «+» на число со знаком «–», мы всегда получаем произведение со знаком «–». Умножая числа с одинаковыми знаками, в результате получается положительное число (4*(–2)= –8; (–4)*(–2)=8);

сочетательность: складывая и умножая три целых числа (или больше трёх), мы также можем по-разному группировать их без изменения конечного результата, например, 6*(4*2)=(6*4)*2;

свойство нуля при сложении и вычитании: если мы прибавляем к целому числу ноль или вычитаем его, результат не меняется (5+0=5; 5–0=5);

свойство нуля при умножении и делении: умножая любое число на ноль, в результате мы получаем ноль (7*0=0). Делить на ноль нельзя; но при делении нуля на любое число частное равно нулю (0:7=0);

свойство противоположного элемента: сумма одинаковых чисел с разными знаками всегда равна нулю (9+(–9)=0);

свойство единицы при умножении и делении: если любое целое число умножить или разделить на 1, результат останется неизменным.

Основные свойства сложения, вычитания, умножения и деления целых чисел с примерами мы представили в виде таблицы:

Действие	Свойство	Пример
Сложение	Замкнутость	a+b∈Z
Переместительность	a+b=b+a
Сочетательность	a+(b+c)=(a+b)+c
Свойство нуля	a+0=a
Свойство противоположного элемента	a+(–a)=0
Вычитание	Замкнутость	a–b∈Z
Свойство нуля	a–0=a
Разность двух одинаковых целых чисел всегда равна нулю	a–a=0
Свойство вычитания целого числа из суммы двух чисел	(a+b)–c=a+(b–c)=(a–c)+b
Свойство вычитания суммы из целого числа	a–(b+c)=a–b–c
Умножение	Замкнутость	a*b∈Z
Переместительность	a*b=b*a
Сочетательность	a*(b*c)=(a*b)*c
Распределительность	a*(b+c)=a*b+a*c
Свойство единицы	a*1=a
Свойство нуля	a*0=0
Разность знаков	a*(–b)= –ab ⠀ (–a)*(–b)=ab
Деление	Распределительность	(a+b):c=a:c+b:c ⠀ (a–b):c=a:c–b:c
Разность знаков	a:(–b)= –c ⠀ (–a):(–b)=c
Любое целое число является делителем нуля	0:a=0
Любое целое число можно разделить на 1 и на само себя	a:1=a ⠀ a:a=1

Рациональные числа

Когда у нас было 7 мешков по 6 килограмм, с помощью умножения мы легко посчитали, что общий вес содержимого мешков составляет 42 килограмма. Представим себе, что мы высыпали всё содержимое всех мешков в одну общую кучу массой 42 килограмма. А потом передумали, и захотели распределить содержимое обратно по 7 мешкам. Сколько килограмм при этом попадет в один мешок, если будем распределять поровну? – Очевидно, что 6.

А если захотим распределить 42 килограмма по 6 мешкам? Тут мы подумаем о том, что те же общие 42 килограмма могли бы получиться, если бы мы высыпали в кучу 6 мешков по 7 килограмм. И значит при делении 42 килограмм на 6 мешков поровну получим в одном мешке по 7 килограмм.

А если разделить 42 килограмма поровну по 3 мешкам? И здесь тоже мы начинаем подбирать такое число, которое при умножении на 3 дало бы 42. Для «табличных» значений, как в случае 6 ·7=42 => 42:6=7, мы выполняем операцию деления, просто вспоминая таблицу умножения. Для более сложных случаев используется деление в столбик, которое будет рассмотрено в одной из следующих статей. В случае 3 и 42 можно «подбором» вспомнить, что 3 ·14 = 42. Значит, 42:3=14. В каждом мешке будет по 14 килограмм.

Теперь попробуем разделить 42 килограмма поровну на 5 мешков. 42:5=?
Замечаем, что 5 ·8=40 (мало), а 5·9=45 (много). То есть, ни по 8 килограмм в мешке, ни по 9 килограмм, из 5 мешков мы 42 килограмма никак не получим. При этом понятно, что в реальности разделить любое количество (крупы, например,) на 5 равных частей нам ничего не мешает.

Операция деления целых чисел друг на друга не обязательно дает в результате целое число. Так мы пришли к понятию дроби. 42:5 = 42/5 = 8 целых 2/5 (если считать в обыкновенных дробях) или 42:5=8,4 (если считать в десятичных дробях).

Обыкновенные и десятичные дроби

Обыкновенные дроби хороши тем, что, чтобы представить такой дробью результат деления любых двух целых чисел, нужно просто записать делимое в числитель дроби, а делитель в знаменатель. (123:11=123/11, 67:89=67/89, 127:53=127/53, …) Затем по возможности сократить дробь и/или выделить целую часть (эти действия с обыкновенными дробями будут подробно рассмотрены в следующих статьях). Проблема в том, что производить арифметические действия (сложение, вычитание) с обыкновенными дробями уже не так удобно, как с целыми числами.

Для удобства записи (в одну строку) и для удобства вычислений (с возможностью вычислений в столбик, как для обычных целых чисел) кроме обыкновенных дробей придуманы ещё и десятичные дроби. Десятичная дробь – это специальным образом записанная обыкновенная дробь со знаменателем 10, 100, 1000 и т.п. Например, обыкновенная дробь 7/10 – это то же, что и десятичная дробь 0,7. (8/100 = 0,08; 2 целых 3/10=2,3; 7 целых 1/1000 = 7, 001). Переводу обыкновенных дробей в десятичные и наоборот будет посвящена отдельная статья. Операциям с десятичными дробями – другие статьи.

Любое целое число может быть представлено в виде обыкновенной дроби со знаменателем 1. (5=5/1; −765=−765/1).

Определение: Все числа, которые могут быть представлены в виде обыкновенной дроби, называют рациональными числами. Множество рациональных чисел обозначают буквой Q.

При делении любых двух целых чисел друг на друга (кроме случая деления на 0) всегда получим в результате рациональное число. Для обыкновенных дробей есть правила сложения, вычитания, умножения и деления, позволяющие произвести соответствующую операцию с любыми двумя дробями и получить в результате также рациональное число (дробь или целое).

Множество рациональных чисел – это первое из рассмотренных нами множеств, в котором можно и складывать, и вычитать, и умножать, и делить (кроме деления на 0), никогда не выходя за пределы этого множества (то есть, всегда получая в результате рационально число).

Казалось бы, других чисел не существует, все числа рациональные. Но и это не так.

Признаки делимости чисел

Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.

Признак делимости на 10

Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.

Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.

В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.

Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.

Признак делимости на 5 и на 2

Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.

Примеры:

10 : 5 = 2

100 : 5 = 20

100 : 2 = 50

Признак делимости на 5

Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.

Примеры:

355 : 5 = 71

200 : 5 = 40

475 : 5 = 95

Признак делимости на 3

Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:

27 : 3 = 9

Признак делимости на 9

Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9

18 : 9 = 2

Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18.  Восемнадцать делится на девять, значит и 846 делится на 9:

Что такое динамическая типизация

Если вы пришли в python из другого языка, например, C++ или Java (для сравнения), то могли заметить, что здесь нет явного указания типизации. Не нужно перед названием переменной указывать, число будет в ней или символ. Это и называется динамическая типизация, когда не нужно явно указывать тип данных, а интерпретатор сам его определит. Возможно, в практике вам встретится такая конструкция:

Удивленные ею вы скажите: «Так вот же оно, явное указание типа переменной». Спешим вас разочаровать: Конструкция с указанием типа переменной после «:» не играет никакой роли для программы. Она нужна только для самого разработчика, чтобы последний не забывал, какие данные должны храниться здесь.

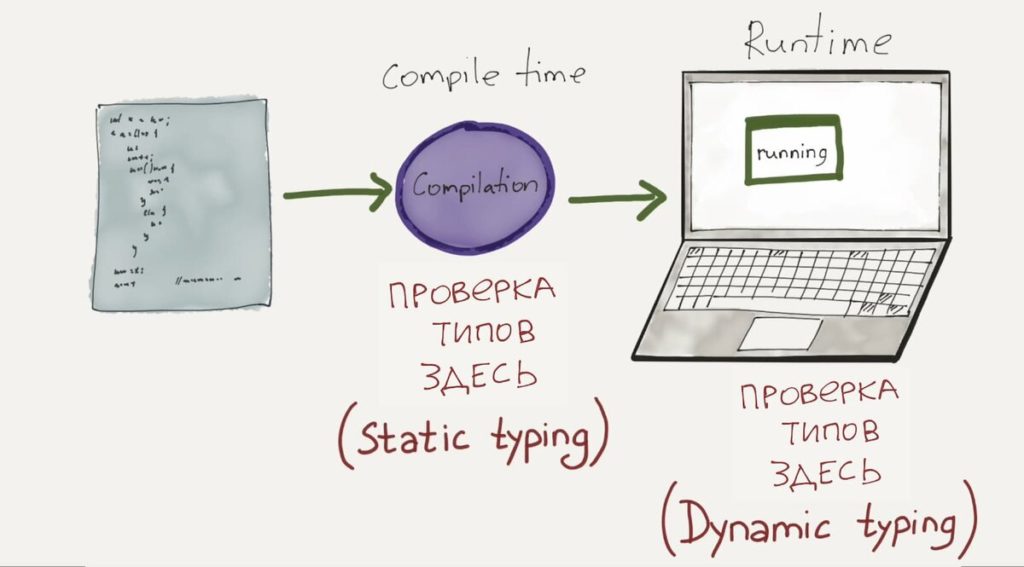
При динамике тип переменной определяется уже в процессе запуска программы

Кто придумал числа с плавающей точкой

1970-е годы, начало компьютерной революции. Учёные-программисты разрабатывают новые компьютеры и алгоритмы для вычислений, а также стараются всеми силами доказать, что их изобретения должны изменить мир.

Тогда все компьютеры работали по-разному: у них были собственные операционные системы, принципы организации памяти и способы представления данных. И это создавало проблему: нельзя было перенести программу с одного компьютера на другой, для этого каждый раз приходилось переписывать её под новую систему и «железо».

И если переделать пару функций было не так сложно, то подстраиваться под разные системы представления чисел было действительно мукой. Из-за этого иногда нужно было полностью менять поведение программы, что могло повлиять на её работоспособность и надёжность. В общем — проблема с представлениями чисел была поистине болезненной.

Такие компьютеры были в продаже в 1980-х годахФото:

Компания Intel решила помочь программистам со всего мира и создать единый стандарт представления вещественных чисел. Для этого была создана проектная группа из лучших инженеров. Но на пятки Intel наступали и другие компании — например, у той же DEC появилась похожая идея.

Началась настоящая гонка за лучшее решение: каждая компания фанатела исключительно от своей разработки и надеялась, что именно её примут как промышленный стандарт. А IT-гиганты IBM и Cray наблюдали за всем происходящим со стороны и ждали, пока появится победитель, — чтобы тут же реализовать его стандарт в своих компьютерах.

Сегодня из всех стандартов, возникших в то время, в живых остались только два: спецификация VAX от DEC и  от Intel. У каждой из них были как свои преимущества, так и недостатки.

Преимущества K-C-S:

• Десятичный формат. Он позволял представлять вещественные числа в десятичной записи, что очень удобно для человека, но так себе для компьютера.
• Высокая точность. Десятичное представление повышало точность вычислений и снижало возникновение ошибок при округлении — особенно для операций с большими числами.
• Меньше ошибок. Стандарт включал специальные значения, которые помогали легко избегать переполнения чисел и проще справляться с ошибками при вычислениях.

Преимущества VAX:

• Двоичный формат. Все числа записывались только в двоичном представлении, что повышало эффективность вычислений, особенно на компьютерах с VAX-архитектурой.
• Широкое распространение. Спецификацию VAX уже использовали на разных компьютерах того времени, что позволяло быстро адаптировать её под новые устройства.
• Высокая производительность. Спецификация VAX была оптимизирована под высокую скорость работы и требовала меньших вычислительных мощностей.

K-C-S	VAX
Десятичный формат	Двоичный формат
Высокая точность	Высокая производительность
Меньше ошибок	Широкая распространённость

Компания DEC пыталась сделать всё, чтобы VAX признали единым стандартом. Она даже пыталась убедить авторитетных учёных в том, что конкурирующий K-C-S никогда не станет таким же производительным и успешным. Однако у разработчиков из Intel были свои секретики: например, они знали, как ускорить свою спецификацию и обогнать DEC.

Что такое множество в математике и как оно обозначается

Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.

В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.

Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.

Границы совокупности обозначаются фигурными скобками { }.

Пример:

1. А = {а, в, с, у} – А состоит из четырех элементов.
2. Записать совокупность Z согласных букв в слове «калькулятор»:

Z = {к, л, т, р}, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.

Принадлежность элементов множеству обозначается знаком – Є.

Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.

Выделяют три вида множеств:

• конечные — совокупности, имеющие максимальный и минимальный предел (например, отрезок);
• бесконечные — не являющиеся конечными (например, числовые);
• пустые (обозначаются Ø) – не имеющие элементов.

Если две разные совокупности содержат одинаковые элементы, то одна из них (со всеми своими элементами) является подмножеством другой и обозначается знаком — ⊆.

Пример: А = {а, в, с, у} и В = {а, в, с, е, к} – все элементы А являются элементами совокупности В, следовательно А ⊆ В.

Если множества состоят из одинаковых элементов, их называют равными.

Пример: А = {23, 29, 48} и В = {23, 29, 48}, тогда А = В.

В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.

Обозначения

Множество чаще всего обозначают заглавными буквами латинского алфавита, а его элементы — строчными. При этом элементы заключаются в фигурные скобки.

Например, если наших друзей зовут Том, Джон и Лео, то мы можем задать множество друзей, элементами которого будут Том, Джон и Лео.

Обозначим множество наших друзей через заглавную латинскую букву F (friends), затем поставим знак равенства и в фигурных скобках перечислим наших друзей:

F = { Том, Джон, Лео }

Пример 2. Запишем множество делителей числа 6.

Обозначим через любую заглавную латинскую букву данное множество, например, через букву D

D

затем поставим знак равенства и в фигурных скобках перечислим элементы данного множества, то есть перечислим делители числа 6

D = { 1, 2, 3, 6 }

Если какой-то элемент принадлежит заданному множеству, то эта принадлежность указывается с помощью знака принадлежности ∈. К примеру, делитель 2 принадлежит множеству делителей числа 6 (множеству D). Записывается это так:

2 ∈ D

Читается как «2 принадлежит множеству делителей числа 6»

Если какой-то элемент не принадлежит заданному множеству, то эта не принадлежность указывается с помощью зачёркнутого знака принадлежности ∉. К примеру, делитель 5 не принадлежит множеству D. Записывается это так:

5 ∉ D

Читается как «5 не принадлежит множеству делителей числа 6»

Кроме того, множество можно записывать прямым перечислением элементов, без заглавных букв. Это может быть удобным, если множество состоит из небольшого количества элементов. Например, зададим множество из одного элемента. Пусть этим элементом будет наш друг Том:

{ Том }

Зададим множество, которое состоит из одного числа 2

{ 2 }

Зададим множество, которое состоит из двух чисел: 2 и 5

{ 2, 5 }

Множество натуральных чисел

К совокупности натуральных чисел (N) относятся цифры, используемые при счете — от 1 до бесконечности.

Натуральные числа используют для исчисления порядка предметов. Обязательное условие данной числовой группы — каждое следующее число больше предыдущего на единицу.

N = {9, 11, 13, 15……}.

Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.

Множество целых чисел

Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:

Z = {-112, -60, -25, 0, 36, 58, 256}.

Следовательно, N — подмножество Z, что можно записать как N ⊆ Z. Любое натуральное число можно назвать так же и целым.

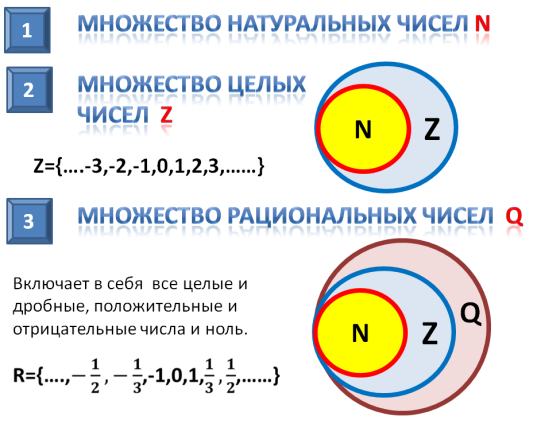
Множество рациональных чисел

Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:

Q={-½; 0; ½, 5; 10}.

Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:

5 = 5/1 = 10/2 = 25/5;

0,45 = 45/100 = 9/20.

Следовательно, N и Z являются подмножествами Q.

Строительство

Β-разложения обобщают десятичное разложение . Десятичные разложения являются уникальными , когда они конечны, бесконечные разложения не являются, так как , например, расширение десятичной единицы является . Β-развертки, даже конечные, не обязательно уникальны. Итак, если — золотое сечение , то 100 = 011. Канонический выбор для β-разложения действительного числа состоит в применении следующего жадного алгоритма , в основном из-за Реньи и сформулированного, например, Кристиан Фруни следующим образом:
1,000⋯знак равно,999⋯{\ displaystyle 1000 \ cdots = 0,999 \ cdots}βзнак равноφ{\ displaystyle \ beta = \ varphi}1+φзнак равноφ2{\ displaystyle 1+ \ varphi = \ varphi ^ {2}}

Либо положительное, либо нулевое действительное число. Пусть целое число такое, что . Мы просим:
Икс{\ displaystyle x}k{\ displaystyle k}βk≤Икс<βk+1{\ Displaystyle \ бета ^ {к} \ Leq х <\ бета ^ {к + 1}}

dkзнак равно⌊Иксβk⌋{\ displaystyle d_ {k} = \ lfloor x / \ beta ^ {k} \ rfloor} и ,рkзнак равно{Иксβk}{\ displaystyle r_ {k} = \ {x / \ beta ^ {k} \}}

и для  :
k>j>-∞{\ displaystyle k> j> — \ infty}

djзнак равно⌊рj+1β⌋{\ displaystyle d_ {j} = \ lfloor r_ {j + 1} \ beta \ rfloor} и .рjзнак равно{рj+1β}{\ displaystyle r_ {j} = \ {r_ {j + 1} \ beta \}}

Другими словами, это каноническое β-разложения из строится для принятия наибольшее целое число , таких как , затем принимать наибольшее целое число , например , как и так далее. Остальное отмечено . Этот выбор дает наибольшую последовательность в репрезентативном лексикографическом порядке . У нас есть
Икс{\ displaystyle x}dk{\ displaystyle d_ {k}}βkdk≤Икс{\ displaystyle \ beta ^ {k} d_ {k} \ leq x}dk-1{\ displaystyle d_ {k-1}}βkdk+βk-1dk-1≤Икс{\ displaystyle \ beta ^ {k} d_ {k} + \ beta ^ {k-1} d_ {k-1} \ leq x}dj{\ displaystyle d_ {j}}dβ(Икс){\ displaystyle d _ {\ beta} (х)}Икс{\ displaystyle x}

Иксзнак равно∑нет≤kdнетβнет{\ Displaystyle х = \ сумма _ {п \ leq k} d_ {п} \ бета ^ {п}}

и если <Икс≤1{\ Displaystyle 0 <х \ leq 1}

Иксзнак равно∑нет≥dнетβ-нет{\ displaystyle x = \ sum _ {n \ geq 0} d_ {n} \ beta ^ {- n}}.

В целочисленной базе мы получаем обычное представление числа; Вышеупомянутая конструкция расширяет алгоритм до нецелых значений основания β.