Как найти центр тяжести трапеции

Библиотека элементарных фигур.

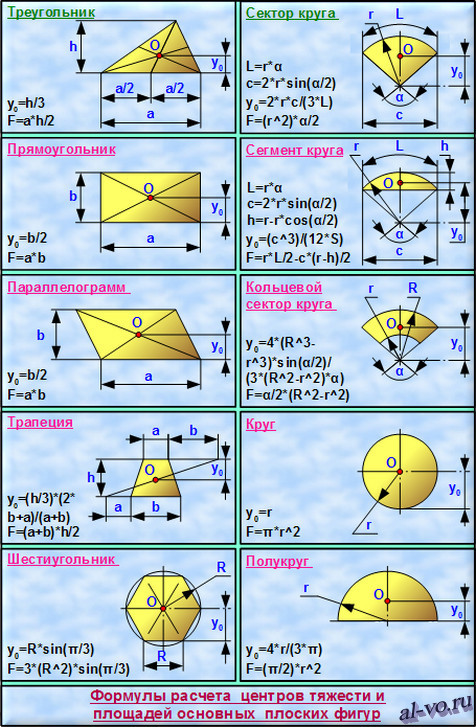
Для симметричных плоских фигур центр тяжести совпадает с центром симметрии. К симметричной группе элементарных объектов относятся: круг, прямоугольник (в том числе квадрат), параллелограмм (в том числе ромб), правильный многоугольник.

Из десяти фигур, представленных на рисунке выше, только две являются базовыми. То есть, используя треугольники и сектора кругов, можно скомбинировать почти любую фигуру, имеющую практический интерес. Любые произвольные кривые можно, разбив на участки, заменить дугами окружностей.

Оставшиеся восемь фигур являются самыми распространенными, поэтому они и были включены в эту своеобразную библиотеку. В нашей классификации эти элементы не являются базовыми. Прямоугольник, параллелограмм и трапецию можно составить из двух треугольников. Шестиугольник – это сумма из четырех треугольников. Сегмент круга — это разность сектора круга и треугольника. Кольцевой сектор круга — разность двух секторов. Круг – это сектор круга с углом α=2*π=360˚. Полукруг – это, соответственно, сектор круга с углом α=π=180˚.

Как найти центр трапеции

Трапецией называется четырехугольник, у которого только одна пара противолежащих сторон параллельна. Найти центр трапеции очень просто. Следуйте пошаговой инструкции ниже.

Вам понадобится

Карандаш, линейка

Инструкция

Возьмите линейку. С ее помощью найдите середину одного основания трапеции. Основание трапеции – это одна из параллельных сторон. Измерьте длину основания, разделите ее на два. Отмерьте от начала основания по ее длине найденную величину и поставьте точку.Так же измерьте и длину второго основания трапеции. В результате на двух параллельных сторонах у вас будут отметки точно на их серединах.

Соедините найденные в предыдущем шаге середины оснований прямой линией. Сделайте это с помощью карандаша и линейки.Теперь точки, обозначающие середины трапеции, соединены прямой.

Найдите середину прямой линии, которую вы провели в предыдущем шаге.Для этого с помощью линейки измерьте длину линии и разделите ее на два.От любого из оснований трапеции отмерьте по этой линии половину ее длины и поставьте точку.Эта точка является центром трапеции.

Видео по теме

Полезный совет

Чтобы проверить правильность расчетов, вырежьте трапецию из бумаги, проведите все вышеописанные действия, чтобы найти ее центр, и поместите трапецию на кончик карандаша или на зубочистку. Острие карандаша/зубочистки должно приходиться точно на центр трапеции.

Если центр трапеции найден верно, бумажная фигура не будет падать с кончика карандаша или с зубочистки.

Способы нахождения центра тяжести

Метод симметрии. Этот метод основан на том, что Если однородное тело имеет элемент симметрии (зеркало, вал или уровень центральной симметрии), то его центр тяжести должен находиться на этом элементе.

Действительно, предположим, что тело имеет уровень симметрии P. Тогда две его «половинки» имеют эквивалентные по модулю и совместному действию притяжения ɛ (ɛ vec g_ \) и ɛ (ɛ vec g_ \), с точками c₁ и в₂ (полуцентры тяжести) симметричны относительно плоскости зеркала (рис. 8.4).

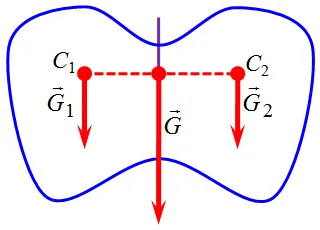
Рисунок 8.4. позиционная симметрия центра тяжести зеркала

Гравитация ĩ (ĩ vec g \), практикуемая во всем теле, является результатом линейной ĩ (ĩ vec g_ \) и ĩ (ĩ vec g_ \) и должна применяться вдоль линии, проходящей через центральную часть.₁ c₂ принадлежит уровню P. Поэтому центр тяжести тела на линии действия ⌘ (⌘ vec g_ \) находится на том же уровне.

Путем аналогичных рассуждений можно доказать, например, что центры тяжести образующих измерительных тел находятся на одной оси.

Пример. Пересечение диагоналей прямоугольника является его центром симметрии. Поэтому центр тяжести однородного («компактного») прямоугольника находится в точке пересечения его диагоналей (рис. 8.5).

Рисунок 8.5.Центр тяжести параллелограмма.

То же самое относится к прямоугольнику, составленному из двух пар брусков одинаковой длины и одинаковой плотности.

Если однородное тело имеет много уровней или осей симметрии, его центр тяжести находится на их пересечении. Это связано с тем, что он должен принадлежать каждому из этих уровней (осей).

Пример. Корабль с загруженными трюмами можно рассматривать как тело, разделенное на части. Сам корпус судна выступает в качестве одного из них, а некоторые позиции груза — в качестве других. Во время обрезки координаты центра изменяются — согласно (8.3a), положение центра тяжести всего грузового контейнера также изменяется. С его помощью можно добиться максимальной устойчивости лодки и избежать ее опрокидывания при сильных толчках. Напротив, неспособность зафиксировать вес может сделать центр тяжести нежелательным и опрокинуть лодку.

Для упрощения расчетов исследуемое тело делится на небольшое количество частей максимально простой формы.

Пример. Из квадрата клмн размером 60 см вырежьте квадрат MPQR со стороной 30 см (рис. 8.6 A). Найдите полученный центр тяжести.

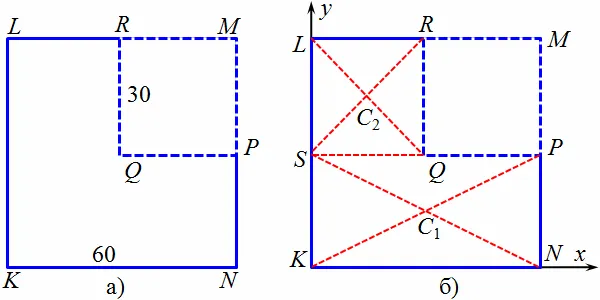
Разделите исходное тело на две части: прямоугольник kspn и квадрат slrq. Разрежьте исходное тело на две части: с₁ и в₂ — их центры тяжести. Введите систему координат в начало точки k, при этом ось x направьте вдоль стороны kn, а ось y — вдоль kl (рис. 8.6 b).

Исходя из вышеизложенного, c₁ пересечение диагоналей KSPN. В указанной системе координат x заканчивается на.₁ = 30 см и размещение y₁ = 15 см. Аналогично, c₂ (диагональное пересечение SLRQ) находится на расстоянии sq /2 = 15 см от оси y и ks + sl /2 = 45 см от оси x, x₂ = 15 см, y₂ = 45 см. площадь s₁ и с₂KSPN и SLPQ равны соответственно 60-30 = 1800 см2 и 30-30 = 900 см2. Используя формулу (8.3a), найдите координаты точки C — центра тяжести большого квадрата с разрезом:

Центр Тяжести своими словами для детей

Центр тяжести — это особое место внутри тела, где все силы тяжести действуют одновременно. Когда мы говорим о силах тяжести, мы имеем в виду то, что все тела притягиваются к Земле. Это происходит потому, что Земля имеет большую массу и она притягивает все вещи к себе.

Когда мы говорим о центре тяжести тела, мы говорим о точке, где все эти силы тяжести сосредоточены. Мы можем представить, что все силы тяжести, которые действуют на каждую часть нашего тела, собираются в одном месте. Это место и называется центром тяжести.

Давай представим, что у нас есть мяч. Мяч имеет массу и поэтому имеет силу тяжести, которая тянет его к Земле. Если мы возьмем мяч и повесим его на нитку, нитка будет тянуть мяч вниз. Если мы подвесим мяч за другую нитку, нитка снова будет тянуть мяч вниз. Но независимо от того, как мы подвесим мяч, мы всегда увидим, что нитка тянет его в одном и том же месте. И это место — центр тяжести мяча.

Таким образом, центр тяжести — это точка, где все силы тяжести сосредоточены. Он может находиться внутри или вне тела, в зависимости от его формы и распределения массы. Но в любом случае, центр тяжести играет важную роль в том, как тело движется и взаимодействует с окружающим миром.

Используемая литература:1. Бутенин Н. В., Лунц Я. Л., Меркин Д. Р. Курс теоретической механики. т. 1, 2; М., 1985 и предыдущие издания.2. Добронравов В. В., Никитин Н. Н. Курс теоретической механики. М., 1983.3. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики, ч. 1 – М.: 1954 и последующие издания, 342 с.4. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики, ч. 2. – М.: 1955 и последующие издания, 598 с.5. Тарг С. М. Краткий курс теоретической механики. М., 1986 и предыдущие издания.6. Яблонский А. А., Никифорова В. М. Курс теоретической механики. т. 1, 2; М., 1984 и предыдущие издания.7. Мещерский И. В. Сборник задач по теоретической механике. М., 1986 и предыдущие издания.8. Сборник задач по теоретической механике // Под ред. К. С. Колесникова. М., 1983.Значение термина Центр Тяжести на academic.ru

РАСЧЕТ ЦЕНТРА ТЯЖЕСТИ трапеции ПО КООРДИНАТАМ

Как же тогда рассчитывать центр тяжести трапеции?

Умные люди нашли формулу  расчета точки, но в ней исходные данные представлены в виде длин сторон трапеции.

Вот эта формула.

Она не удобна, когда нам известны только координаты трапеции. Но мы воспользуемся способом разбиения трапеции два треугольника, где для каждого из них  находим центр тяжести, а потом рассчитывая уже для двух точек(центров), находим окончательное решение.

Для каждого треугольника  центр будет рассчитыватся  по известной формуле

Но вот, когда мы будем рассчитывать окончательную точку, надо учитывать что мы, «стягивая» в центр тяжести каждый треугольник, стягиваем и всю массу поверхности которая лежала между этими координатами. 

Так как между площадью фигуры ( при одинаковой толщине)  и массой  связь линейная, то легко предположить что окончательный  расчет будет не таким

а  с учетом линейности между массой и площадью( а значит можно не высчитывать массу каждой новой точки, а учитывать лишь площадь каждого из двух треугольников)  формула  для трапеции будет такой

Причем эта формула будет работоспособна при любом произвольном многоугольнике,  единственное условие  что бы площади каждого из треугольника  не пересекались друг с другом.

Итак, у нас есть фигура с координатами 0:0 5:5 10:5 15:0

Несложно представить эту фигуру и определить что это равностороняя трапеция.

Кинематика. Кинематика точки. Способы задания движения точки.

Кинематика
–
раздел механики, в котором изучаются
движение материальных тел с геометрической
точки зрения, без учета массы и действующих
на них сил. Способы задания движения
точки: 1) естественный, 2) координатный,
3) векторный.

Кинема́тика
точки
—
раздел кинематики,
изучающий математическое описание движения
материпльных точек.
Основной задачей кинематики является
описание движения при помощи математического
аппарата без выяснения причин, вызывающих
это движение.

Естественный
сп
.
указывается траектория точки, закон ее
движения по этой траектории, начало и
направление отсчета дуговой
координаты: s=f(t)
– закон
движения точки. При прямолинейном
движении: х=f(t).

Координатный
сп
.
положение точки в пространстве
определяется тремя координатами, изменения
которых определяют закон движения
точки: x=f 1 (t),
y=f 2 (t),
z=f 3 (t).

Если
движение в плоскости, то два уравнения
движения. Уравнения движения описывают
уравнение траектории в параметрической
форме. Исключив из уравнений параметр t,
получаем уравнение траектории в обычном
виде:f(x,y)=0 (для
плоск-ти).

Векторный
сп
.
положение точки определяется ее
радиус-вектором, проведенным из
какого-либо центра. Кривая, которая
вычерчивается концом какого-либо
вектора, назыв. годографом
этого
вектора. Т.е. траектория – годограф
радиус-вектора.

Центры тяжести и моменты инерции основных простых фигур

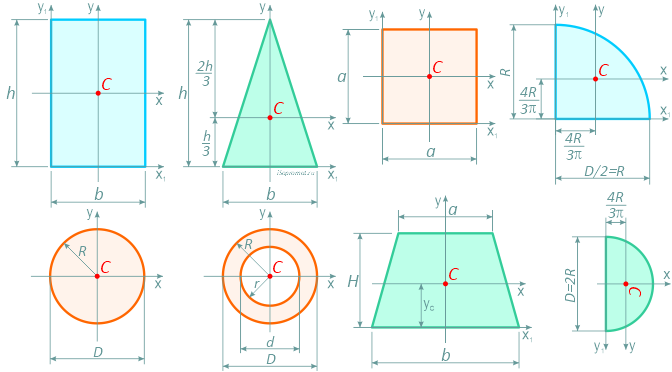
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.

Обозначения в формулах: C — положение центра тяжести фигуры; A — площадь сечения; I_x , I_y — осевые моменты инерции сечения относительно главных осей; I_x1 , I_y1 — осевые моменты инерции относительно вспомогательных (смещённых) осей; I_ρ — полярный момент инерции сечения; W_x , W_y — осевые моменты сопротивления; W_ρ — полярный момент сопротивления

Прямоугольник

Прямоугольник высотой h и шириной b.

Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.

Площадь

Центральные осевые моменты инерции прямоугольника Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку Осевые моменты сопротивления прямоугольного сечения

Квадрат

Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.

Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.

Площадь

Центральные осевые моменты инерции квадрата

Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку

Осевой момент сопротивления квадратного сечения

Треугольник равнобедренный

Равнобедренный треугольник высотой h и шириной основания b.

Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.

Площадь

Центральные осевые моменты инерции треугольника

Момент инерции относительно смещенной оси x₁, проходящей через его основание

Прямоугольный треугольник

Прямоугольный треугольник высотой h и шириной основания b.

Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.

Площадь

Центральные осевые моменты инерции прямоугольного треугольника Моменты инерции относительно смещенных осей x₁ и y₁, проходящих через точку, соединяющую его катеты

Трапеция

Равнобокая трапеция высотой H и шириной оснований: малого a и большого b. 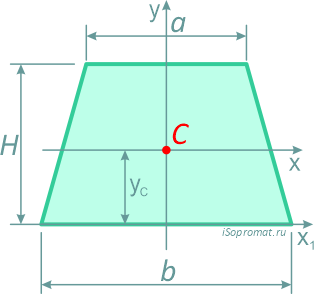Площадь трапеции

Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:

Круг

Круг диаметром D (d) или радиусом R (r) Площадь круга через его диаметр и радиус Центральные осевые и полярный моменты инерции круга 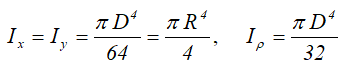Осевые и полярный моменты сопротивления

Четверть круга

Четверть круга диаметром D (d) или радиусом R (r) Площадь Центральные осевые моменты инерции четверти круга 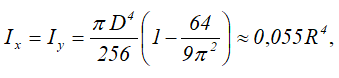Моменты инерции относительно смещенных осей x₁ и y₁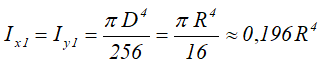

Кольцо

Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r) Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.

Площадь Центральные осевые и полярный моменты инерции кольца 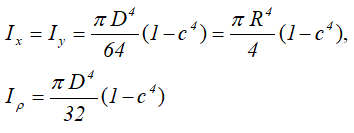Осевые и полярный моменты сопротивления

Тонкостенное сечение (труба)

Тонкостенный профиль (сечение трубы) средним радиусом R и толщиной стенки трубы t при R>>t Площадь

Центральные осевые и полярный моменты инерции трубного сечения Осевые и полярный моменты сопротивления

Пример определения координат центра тяжести сложной фигуры:

Пример задания

Теоретический материал лучше всего усваивается на практических заданиях. Не исключение и понятие о центре тяжести. Тема несложная, но при нахождении параметра желательно фигуру изобразить на рисунке.

Наиболее часто ученикам преподаватель предлагает решить задачу о нахождении центра масс сложного тела, но при этом достаточно симметричного. Например, пусть имеется диск из однородной пластины, в котором вырезан кусок треугольной формы. Необходимо найти центр равновесия оставшегося объекта.

Если нарисовать условие задачи, станет понятно, что треугольник прямоугольный, а центр масс находится на горизонтальной прямой, проходящей через середину диска. Пусть это будет ось x. Чтобы решить задачу, нужно разбить сложную фигуру на несколько частей, в каждой из которых можно найти искомую точку.

Симметрично удалённому треугольнику можно выделить аналогичную часть. В итоге останется круг с вырезанным внутри квадратом. Точка масс диска находится в центре. Для удобства её можно обозначить как x1. Вторая фигура — это треугольник. Точка равновесия у него находится на пересечении медиан. То есть на 1/3 высоты. Обозначить точку можно как x2.

Если масса треугольника равна М2, а круга М1, искомую координату можно определить по формуле: x = (m1x1 + m2x2) / m1 + m2. Далее, нужно найти, чему равняется сторона вырезанного треугольника. Из рисунка можно понять, что это расстояние будет r * √2, где r — радиус диска.

Теперь можно найти, чему будут равны x1 и x2. x1 будет равняться нулю, так как эту точку можно принять за начало координат. x2 же будет равняться 1/3 длины медианы. Высота фигуры совпадает с радиусом диска, значит: x2 = R/3.

В таких задачах самое сложное — это найти массы. Первую можно определить исходя из того, что она будет равняться массе диска минус значение квадрата. Так как фигура однородная, масса прямо пропорциональна площади. Тогда для первого участка m1 = σ * S = σ * (Sкруга — Sквадрата) = σ * (pR2 — 2R2) = σR2 * (p — 2), где: σ — поверхностная площадь. Соответственно, m2 = σ * Sтреугольника = σ * R2. Все найденные величины нужно подставить в формулу и найти ответ: x = ((r * σ * R2 /3)) / (σ * R2 * (p — 2) + σ * R2) = (r / 3 (p — 1)). Это и будет искомая координата.

38.Связь между координатным и векторным, координатным и естественным способами задания движения точки.

СВЯЗЬ
ВЕКТОРНОГО СПОСОБА С КООРДИНАТНЫМ И
ЕСТЕСТВЕННЫМ
выражается
соотношениями:

где —
орт касательной к траектории в данной
точке, направленный в сторону отсчета
расстояний, —
орт нормали к траектории в данной точке,
направленный в сторону центра кривизны
(см. рис. 3).

СВЯЗЬ
КООРДИНАТНОГО СПОСОБА С ЕСТЕСТВЕННЫМ
.
Уравнение траектории f(x, y)=z; f 1 (x,
z)=y получается из уравнений движения в
координатной форме посредством исключения
времени t. Дополнительным анализом
значений, которые могут принимать
координаты точки, определяется тот
участок кривой ,
который является траекторией. Например,
если движение точки задано уравнениями:
x=sin t; y=sin 2 t=x 2 ,
то траекторией точки является тот
участок параболы у=х 2 ,
для которого -1≤x≤+1, 0≤x≤1. Начало и
направление отсчета расстояний выбираются
произвольно, этим в дальнейшем определяется
знак скорости и величина и знак начального
расстояния s 0 .

Закон движения
определяется зависимостью:

знак + или —
определяется в зависимости от принятого
направления отсчета расстояний.

Скорость
точки
–
это кинематическая мера ее движения,
равная производной по времени от
радиус-вектора этой точки в рассматриваемой
системе отсчета. Вектор скорости
направлен по касательной к траектории
точки в сторону движения

Вектор
скорости (v)
—
это расстояние, которое тело проходит
в определенном направлении за единицу
времени

Обратите внимание, что
определение вектора
скорости
очень
похоже на определение скорости, за
исключением одного важного различия:
скорость тела не указывает направление
движения, а вектор скорости тела указывает
и скорость, и направление движения.
Следовательно, необходимы две переменные,
которые описывают вектор скорости тела:
скорость и направление. Физические
величины, у которых есть значение и
направление, называют векторными
величинами

Вектор
скорости
тела
может время от времени изменяться

Если
или его скорость, или направление
изменяются, скорость тела также меняется.
Постоянный вектор скорости подразумевает
неизменную скорость и неизменное
направление, тогда как термин «постоянная
скорость» подразумевает только неизменное
значение, не принимая во внимание
направление. Термин «вектор скорости»
часто используется попеременно с
термином «скорость»

Они оба выражают
расстояние, которое тело проходит в
единицу времени

Ускорение
точки
–
это мера изменения ее скорости, равная
производной по времени от скорости этой
точки или второй производной от
радиус-вектора точки по времени. Ускорение
характеризует изменение вектора скорости
по величине и направлению и направлено
в сторону вогнутости траектории.

Вектор ускорения

это отношение
изменения скорости к промежутку времени,
за который это изменении произошло.
Определить среднее ускорение можно
формулой:

где – вектор
ускорения
.

Направление
вектора ускорения совпадает с направлением
изменения скорости Δ = — 0 (здесь 0 –
это начальная скорость, то есть скорость,
с которой тело начало ускоряться).

В
момент времени t1 (см. рис 1.8) тело имеет
скорость 0 .
В момент времени t2 тело имеет скорость .
Согласно правилу вычитания векторов
найдём вектор изменения скорости
Δ = — 0 .
Тогда определить ускорение можно так:

Общие сведения

Пусть имеется физическое тело, на которое не оказывается влияние, то есть другие объекты не действуют или их силы воздействия скомпенсированы. Рассматриваемое тело будет находиться в состоянии прямолинейного движения или покоя. Для удобства можно принять, что объект неподвижен, например, пусть это будет лодка на поверхности воды.

Если к плавательному средству приложить силу, смещённую к началу лодки F1, судно начнёт поворачиваться в сторону направления воздействия. Если ее переместить в горизонтальной плоскости в другой конец судна, лодка начнёт также поворачиваться, но направление вращения изменится. Отсюда можно сделать вывод, что существует такая точка приложения силы, точнее, линия, при воздействии на которую лодка не изменит своего положения, то есть плавательное средство начнёт двигаться ускоренно поступательно. Допустим, это будет сила F3.

При этом точку воздействия можно перемещать по линии её направления, так как, согласно правилу, величина действия при этом не изменяется. В итоге получится точка, где пересекутся приложенные силы F3 и F4. Таких моментов можно приложить сколько угодно, при этом они все соединятся в одном месте. Точку пересечения линий действия сил, которые вызывают ускоренное поступательное движение тела, называют центром масс.

На лодку действует ещё одна сила — притяжения. На самом деле она воздействует на каждую частичку объекта, поэтому на тело одновременно оказывает влияние огромное количество моментов. Это множество и принято заменять их равнодействующей — то есть силой, приложенной к центру тяжести. В физике параметр обозначают как mg. Другими словами, это точка приложения равнодействующих сил тяжести.

Существует взаимосвязь между массой и тяжестью. Если тело разбить на кусочки и бросить их, скорость падения будет для всех тел одинаковой, так как ускорение не зависит от массы. При этом падающий объект движется поступательно.

Как использовать знания о центре тяжести

Знание о центре тяжести может быть полезным во многих областях, включая строительство, механику и дизайн. Например, зная, где находится центр тяжести объекта, вы можете рассчитать его устойчивость или понимать, как он будет вести себя в разных условиях.

В строительстве знание о центре тяжести может помочь избежать наклонов и опрокидываний зданий и сооружений, что может привести к катастрофе. Кроме того, знание о центре тяжести может помочь при создании новых конструкций, поскольку это может помочь определить наилучшее расположение материалов.

В механике знание о центре тяжести может помочь предсказать поведение объекта в движении. Например, если вы знаете, где находится центр тяжести автомобиля, вы можете рассчитать, как он будет реагировать на различные дорожные условия.

В дизайне знание о центре тяжести может помочь при создании более эргономичных и удобных в использовании продуктов. Например, знание о центре тяжести кресла может помочь создать кресло, которое меньше будет вибрировать или опрокидываться при перемещении.

Вопрос-ответ

Вопрос: Как определить центр тяжести модели?

Ответ: Центр тяжести модели можно определить путем размещения модели на плоской поверхности и нахождения точки, в которой она находится в равновесии.

Вопрос: Можно ли найти центр тяжести модели без использования специальных инструментов?

Ответ: Да, можно. Для этого необходимо разместить модель на плоской поверхности и последовательно произвести переносы ее тяжелых частей до тех пор, пока она не будет находиться в равновесии. Точка пересечения линий переноса является центром тяжести.

Вопрос: Можно ли определить центр тяжести модели, используя математические расчеты?

Ответ: Да, можно. Для этого необходимо знать массу, размеры и плотность материала модели. С помощью формул для центра тяжести можно провести расчеты и определить точку, в которой он находится.

Вопрос: Каким образом нахождение центра тяжести может помочь в создании устойчивых конструкций?

Ответ: Нахождение центра тяжести позволяет определить точку, в которой необходимо расположить опоры, чтобы конструкция была устойчива. Благодаря этому можно создавать более безопасные и надежные сооружения.

Вопрос: Существуют ли способы определения центра тяжести для необычных и сложных форм моделей?

Ответ: Да, существуют. Для этого можно использовать методы математического моделирования, такие как метод конечных элементов. С их помощью можно определить распределение массы внутри модели и точно определить центр тяжести.

Главная — Полезно — Основы моделирования: Как определить центр тяжести вашей модели?

Комментарии

Иван Иванов

5.0 out of 5.0 stars5.0

Статья очень полезна для меня как начинающего моделиста. Рекомендую всем ознакомиться!

Петр Петров
5.0 out of 5.0 stars5.0

Статья очень полезная! Отлично описаны методы нахождения центра тяжести модели. Благодарю автора за такой материал!

Алексей
5.0 out of 5.0 stars5.0

Я давно интересуюсь моделированием, но всегда была проблема в том, как правильно расположить центр тяжести модели. Эта статья помогла разобраться в этом вопросе. Хорошо описаны все шаги и объяснено, как это работает. Единственное, что хотелось бы добавить, это немного больше практических примеров и иллюстраций.

Дмитрий
5.0 out of 5.0 stars5.0

DarkKnight
5.0 out of 5.0 stars5.0

Как человек, который много лет занимается моделированием, я могу сказать, что эта статья — одна из лучших на эту тему. В ней всё очень логично и понятно описано, и всё, что там написано, действительно работает. Однако, я бы добавил немного дополнительной информации о том, как использовать это знание на практике. Например, можно было бы привести примеры тех моделей, где центр тяжести действительно играет важную роль, и объяснить, как варьирование веса влияет на летные характеристики.

Также, я считаю, что в статье следует уделить больше внимания на том, как правильно расставлять веса внутри модели. Ведь вес каждой детали тоже играет свою роль, и нередко одна-единственная мелочь может изменить центр тяжести настолько, что модель уже не будет летать. Хотелось бы видеть больше практических примеров и иллюстраций на эту тему.

В целом, статья очень хорошая и полезная для тех, кто хочет правильно располагать центр тяжести своей модели. Я думаю, что её стоит обязательно прочесть всем моделистам, и надеюсь, что авторы продолжат писать на эту тему и дополнят свою статью дополнительными примерами и иллюстрациями.

MaxPower
5.0 out of 5.0 stars5.0

Математические вычисления

При нахождении центра масса объекта, мы должны знать массу каждого его элемента, а также их координаты. Если все элементы имеют одинаковую массу, то вычисление ЦМ будет еще проще — достаточно просто усреднить координаты. Однако, если массы элементов разные, вычисления становятся сложнее.

Для нахождения центра тяжести объекта, нам нужно знать массу каждого элемента и силу тяжести, оказываемую на каждый элемент. Сила тяжести определяется как произведение массы на ускорение свободного падения, которое примерно равно 9,8 м/с^2 на поверхности Земли. С помощью этих данных, мы можем вычислить плечи сил тяжести для каждого элемента и затем найти их сумму. Центр тяжести это точка, в которой сумма плеч равна нулю.

Математические вычисления, связанные с нахождением ЦМ и ЦТ, требуют использования различных формул и алгоритмов. Они могут быть сложными для понимания и выполнения, особенно при работе с большими и сложными объектами. Однако, современные компьютерные программы и математические пакеты облегчают этот процесс, позволяя быстро и точно находить ЦМ и ЦТ для различных систем.

Таким образом, математические вычисления играют важную роль при работе с центром масса и центром тяжести. Они позволяют определить эти точки и использовать их для изучения и предсказания движения и поведения объектов. Кроме того, математические вычисления помогают инженерам и физикам создавать более эффективные и устойчивые конструкции, а также проводить анализы и исследования в различных областях науки и техники.

Что такое центр тяжести трапеции

Центр тяжести — это точка в теле или геометрической фигуре, в которой можно считать сосредоточенной всю массу или вес объекта. В контексте трапеции, центр тяжести является особым понятием, которое позволяет определить «среднюю» позицию массы фигуры.

Трапеция — это плоская фигура, которая состоит из четырех сторон, где две стороны параллельны, а другие две — непараллельны. Центр тяжести трапеции находится на оси симметрии фигуры и делит ее на две равные части относительно площадей.

Если мы представим трапецию как нерегулярную прямоугольную доску и попытаемся уравновесить ее, то точка, в которой находятся наши пальцы, будет соответствовать центру тяжести. Это наиболее устойчивое положение, в котором трапеция не наклоняется в одну сторону.

Математически центр тяжести трапеции можно найти с использованием формулы. Для прямоугольной трапеции, где стороны параллельны, центр тяжести находится на половине основания фигуры. Для нерегулярной трапеции, центр тяжести можно найти с помощью формулы, которая использует значения всех сторон и средние линии фигуры.

Заключение.

Пример в статье был выбран очень простым для того, чтобы легче было разобраться в методологии расчетов центра тяжести сложного сечения. Метод заключается в том, что любую сложную фигуру следует разбить на простые элементы с известными местами расположения центров тяжести и произвести итоговые вычисления для всего сечения.

Если сечение составлено из прокатных профилей – уголков и швеллеров, то их нет необходимости разбивать на прямоугольники и квадраты с вырезанными круговыми «π/2»- секторами. Координаты центров тяжести этих профилей приведены в таблицах ГОСТов, то есть и уголок и швеллер будут в ваших расчетах составных сечений базовыми элементарными элементами (о двутаврах, трубах, прутках и шестигранниках говорить нет смысла – это центрально симметричные сечения).

Расположение осей координат на положение центра тяжести фигуры, конечно, не влияет! Поэтому выбирайте систему координат, упрощающую вам расчеты. Если, например, я развернул бы в нашем примере систему координат на 45˚ по часовой стрелке, то вычисление координат центров тяжести прямоугольника, треугольника и полукруга превратилось бы в еще один отдельный и громоздкий этап расчетов, который «в уме» не выполнишь.

Представленный ниже расчетный файл Excel в данном случае программой не является. Скорее – это набросок калькулятора, алгоритм, шаблон по которому следует в каждом конкретном случае составлять свою последовательность формул для ячеек с яркой желтой заливкой
.

Итак, как найти центр тяжести любого сечения вы теперь знаете! Полный расчет всех геометрических характеристик произвольных сложных составных сечений будет рассмотрен в одной из ближайших статей в рубрике « ». Следите за новостями на блоге.

Для

получения
информации о выходе новых статей
и для
скачивания рабочих файлов программ



прошу вас подписаться на анонсы в окне, расположенном в конце статьи или в окне вверху страницы.

Несколько слов о бокале, монете и двух вилках, которые изображены на «значке-иллюстрации» в самом начале статьи. Многим из вас, безусловно, знаком этот «трюк», вызывающий восхищенные взгляды детей и непосвященных взрослых. Тема этой статьи – центр тяжести. Именно он и точка опоры, играя с нашим сознанием и опытом, попросту дурачат наш разум!

Центр тяжести системы «вилки+монета» всегда располагается на фиксированном
расстоянии по вертикали вниз
от края монеты, который в свою очередь является точкой опоры. Это положение устойчивого равновесия!
Если покачать вилки, то сразу становится очевидным, что система стремится занять свое прежнее устойчивое положение! Представьте маятник – точка закрепления (=точка опоры монеты на кромку бокала), стержень-ось маятника (=в нашем случае ось виртуальная, так как масса двух вилок разведена в разные стороны пространства) и груз внизу оси (=центр тяжести всей системы «вилки+монета»). Если начать отклонять маятник от вертикали в любую сторону (вперед, назад, налево, направо), то он неизбежно под действием силы тяжести будет возвращаться в исходное устойчивое состояние равновесия
(это же самое происходит и с нашими вилками и монетой)!

Кто не понял, но хочет понять – разберитесь самостоятельно. Это ведь очень интересно «доходить» самому! Добавлю, что этот же принцип использования устойчивого равновесия реализован и в игрушке ванька–встань-ка. Только центр тяжести у этой игрушки расположен выше точки опоры, но ниже центра полусферы опорной поверхности.

Всегда рад вашим комментариям, уважаемые читатели!!!

Прошу,

УВАЖАЯ


труд автора, скачивать файл


ПОСЛЕ ПОДПИСКИ


на анонсы статей.

Результат расчетов зависит не только от площади сечения, поэтому при решении задач по сопромату не обойтись без определения геометрических характеристик фигур
: статических, осевых, полярного и центробежного моментов инерции. Обязательно необходимо уметь определять положение центра тяжести сечения (от положения центра тяжести зависят перечисленные геометрические характеристики). К дополнению к геометрическим характеристикам простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольников, круга, полукруга
. Указаны центр тяжести и положение главных центральных осей, и определены относительно них геометрические характеристики при условии, что материал балки однородный.