Как посчитать стороны равнобедренного треугольника

Свойства треугольников с равными основаниями

Треугольник – это геометрическая фигура, которая имеет три стороны и три угла. Одним из важных элементов треугольника является его основание. Основание – это одна из сторон треугольника, на которую опирается высота. Если два треугольника имеют равные основания, то они могут иметь различные свойства.

Одно из свойств треугольников с равными основаниями заключается в том, что они могут иметь различные высоты. Высота – это перпендикуляр, опущенный из вершины треугольника на его основание. Если два треугольника имеют равные основания, но разные высоты, то они будут иметь различные площади.

Еще одно свойство треугольников с равными основаниями заключается в том, что они могут иметь различные боковые стороны. Боковые стороны – это стороны треугольника, не являющиеся его основанием. Если два треугольника имеют равные основания и равные боковые стороны, то они будут полностью равными.

Таким образом, свойства треугольников с равными основаниями могут быть различными в зависимости от высоты и боковых сторон. Однако, если два треугольника имеют равные основания и равные боковые стороны, то они будут полностью равными.

Как найти основание трапеции через высоту и основание?

Для нахождения основания трапеции через высоту и одно из оснований, нам нужно знать формулу для нахождения площади трапеции. Формула для площади трапеции состоит из умножения полусуммы оснований на высоту трапеции:

S = (a + b) * h / 2,

где S — площадь трапеции, a и b — основания трапеции, h — высота трапеции.

Таким образом, чтобы найти одно из оснований трапеции, нужно знать площадь, высоту и другое основание. Подставив известные значения в формулу для площади, можно найти нужное основание, перегруппировав уравнение:

a = (2 * S — b * h) / h.

Применим эти знания на примере. Предположим, у нас есть трапеция с площадью 36 квадратных сантиметров, высотой 8 сантиметров и основанием 12 сантиметров. Чтобы найти другое основание, используем формулу:

a = (2 * 36 — 12 * / 8 = 36 / 8 = 4.5.

Таким образом, другое основание этой трапеции равно 4.5 сантиметра.

Понятие обозначения треугольника в геометрии

В геометрии для обозначения треугольника используются различные символы и обозначения. Наиболее распространенным способом обозначения треугольника является указание вершин треугольника буквами.

Обычно в треугольнике используются заглавные буквы для обозначения вершин. Так, для треугольника ABC вершины обозначаются буквами A, B и C. При этом, вершины обычно указываются в определенном порядке. Например, вершина A может быть указана слева, вершина B – сверху, а вершина C – справа.

Если требуется указать возможные комбинации сторон и углов треугольника, для обозначения используются индексы. Например, сторона AB обозначается как AB, угол ABC обозначается как ∠ABC, а площадь треугольника ABC обозначается как S_ABC.

Кроме того, существуют и другие способы обозначения треугольника, используемые в специальных случаях или в определенных системах геометрической нотации. Например, в некоторых случаях треугольник может быть обозначен просто через точки, без использования букв или символов. Также, в некоторых текстах используются специальные обозначения для прямоугольных треугольников или треугольников с определенными свойствами.

Примеры решения треугольника ABC зная 1 сторону и 2 угла

\( Дано: \triangle ABC;\)

\( AC=\htmlClass{kAC}{8} см;\)

\( \angle A=\htmlClass{kA}{50} \degree;\)

\( \angle C=\htmlClass{kC}{50} \degree;\)

\( Найти: P _{\triangle ABC} ?\)

\( Решение:\)

\(P=AB+BC+AC\)

\(\angle B=180-\angle А- \angleС=180-\htmlClass{kA}{50}-\htmlClass{kC}{50}=\htmlClass{kB}{80}\degree\)

\(AB = {AC * sin(\angle C)\over sin(\angle B)} ={\htmlClass{kAC}{8} * sin( \htmlClass{kC}{50})\over sin( \htmlClass{kB}{80})}=\htmlClass{kAB}{6.223}см\)

\(BC = {AC * sin(\angle A)\over sin(\angle B)} ={\htmlClass{kAC}{8} * sin( \htmlClass{kA}{50})\over sin( \htmlClass{kB}{80})}=\htmlClass{kBC}{6.223}см\)

\(P=\htmlClass{kAB}{6.223}см+\htmlClass{kBC}{6.223}см+\htmlClass{kAC}{8}см=\htmlClass{kP}{20.446}см\)

\( Ответ:\htmlClass{kP}{20.446}см\)

Практическое применение основания треугольника в геометрии и других областях

Основание треугольника – это одна из важнейших характеристик этой геометрической фигуры. Оно определяется как любая из сторон треугольника, на которую опирается высота. Практическое применение основания треугольника можно найти в различных областях, начиная от геометрии и заканчивая архитектурой и инженерией.

В геометрии основание треугольника используется для вычисления его площади. Формула для расчета площади треугольника S = 1/2 * a * h, где a – основание, а h – высота, позволяет быстро и точно определить площадь треугольника.

В архитектуре и инженерии основание треугольника используется для создания прочных и устойчивых конструкций. Например, при проектировании мостов и зданий инженеры используют треугольные формы, так как они обладают высокой прочностью и устойчивостью.

Также основание треугольника находит применение в тригонометрии. Тригонометрические функции, такие как синус, косинус и тангенс, определяются отношением сторон треугольника. Основание треугольника играет важную роль в определении этих функций.

В целом, практическое применение основания треугольника в геометрии и других областях очень широко. Знание основных свойств треугольника и его элементов позволяет решать различные задачи и создавать устойчивые конструкции.

Дополнительные примеры нахождения основания трапеции через высоту и основание

При решении задач на нахождение основания трапеции по высоте и одной из оснований можно использовать формулу для расчета площади трапеции:

S = (a + b) * h / 2

где a и b – основания трапеции, h – высота трапеции.

Найдем значение одного из оснований, используя данную формулу и известные значения высоты и другого основания.

Пример 1:

Дано: высота трапеции h = 6 см, основание a = 10 см.

Необходимо найти значение основания b.

Для решения задачи используем формулу:

S = (a + b) * h / 2

Подставляем известные значения:

S = (10 + b) * 6 / 2

Решаем уравнение:

60 = 3b

b = 20 см

Ответ: основание трапеции b = 20 см.
Пример 2:

Дано: высота трапеции h = 8 м, основание b = 15 м.

Необходимо найти значение основания a.

Для решения задачи используем формулу:

S = (a + b) * h / 2

Подставляем известные значения:

S = (a + 15) * 8 / 2

Решаем уравнение:

S = 4a + 60

a = (S — 60) / 4

Ответ: основание трапеции a = (S — 60) / 4.

Таким образом, зная высоту и одно из оснований трапеции, можно легко найти значение другого основания, используя формулу для расчета площади.

Основные геометрические фигуры

Соединённые между собой точки образуют линии, а соединённые между собой линии — основные геометрические фигуры на плоскости.

Геометрические фигуры бывают плоские или двухмерные (2D) и объёмные пространственные, или трёхмерные (3D). Они ограничены замкнутой поверхностью своей наружной границы.

А если у геометрической фигуры все точки не находятся в одной плоскости, то она объёмная. К ним относятся шар, конус, цилиндр, сфера, пирамида и др.

Разберём плоские фигуры.

Треугольник

Треугольник — это фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки называются вершинами, а отрезки — сторонами.

Есть три вида треугольников:

Прямоугольный — когда один угол прямой, другие два меньше 90 градусов.
Остроугольный — когда градус его углов больше 0, но меньше 90 градусов.
Тупоугольный — когда один угол тупой, то есть больше 90 градусов, а два других — острые.

Треугольники имеют следующие свойства:

в треугольнике напротив большего угла лежит большая сторона и наоборот;
сумма углов треугольника всегда равна 180 градусам;
все углы равностороннего треугольника равны 60 градусам;
в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (но это изучается уже в старших классах).

Вершины треугольников обозначаются заглавными буквами латинского алфавита: A, B, C и др.

Примеры треугольников:

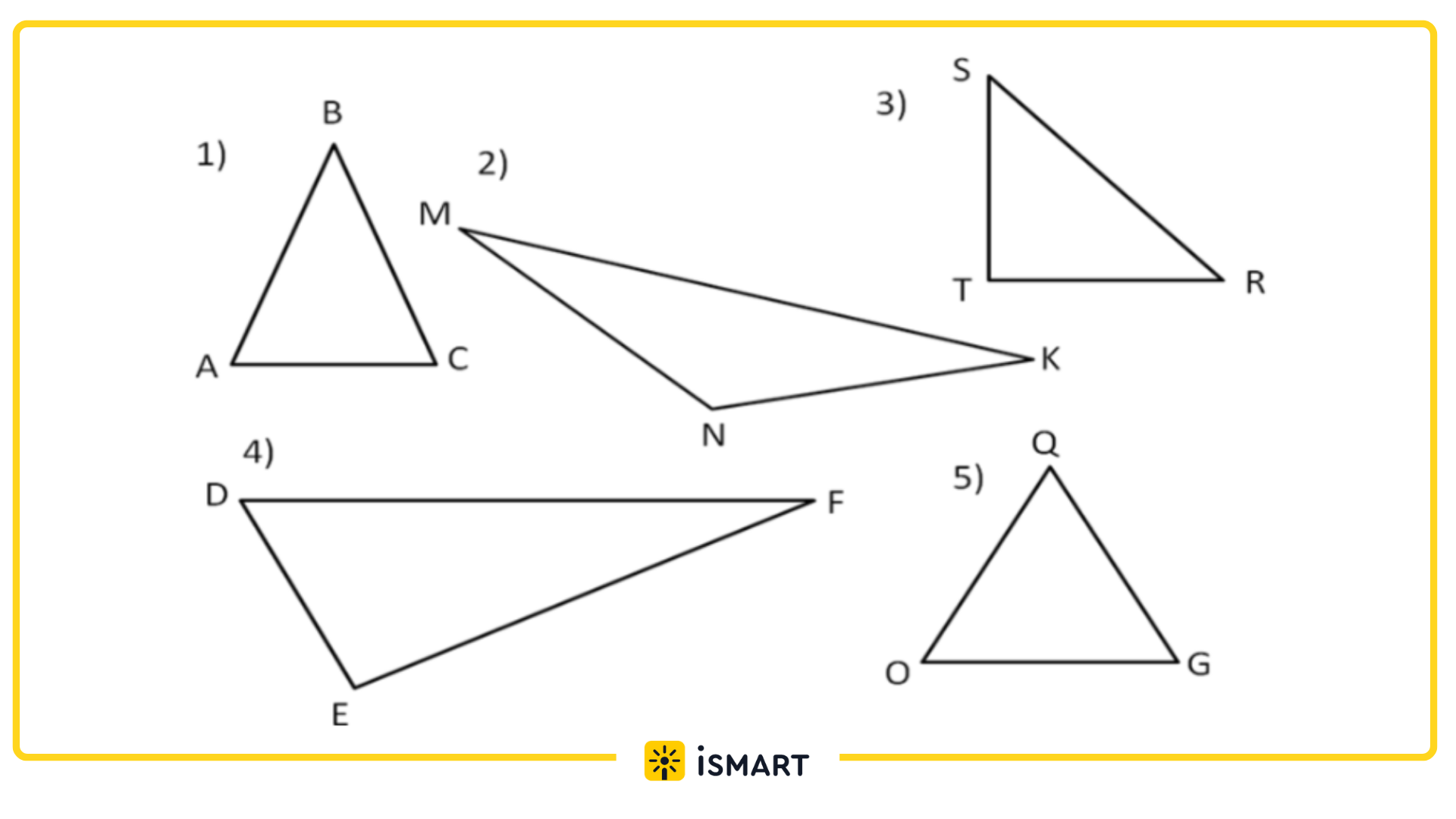
Окружность

Окружность — геометрическая фигура, образованная замкнутой кривой линией, все точки которой находятся на одинаковом от центра расстоянии.

Круг

Часть плоскости, находящаяся внутри окружности, называется кругом. То есть, окружность — это граница круга. А расстояние от центра окружности до любой точки на ней называется радиусом. Диаметр круга — это отрезок, который соединяет две точки на окружности и проходит через её центр. Диаметр круга равен двум его радиусам.

Прямоугольник

‍Прямоугольник — это фигура, состоящая из четырёх сторон и четырёх прямых углов, у которой:

противоположные стороны равны между собой;
диагонали равны и делятся в точке пересечения пополам;
около прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагоналей.

Квадрат

Квадрат — это тот же прямоугольник, у которого:

все стороны равны;
все углы равны и составляют 90 градусов;
диагонали равны и перпендикулярны;
центры вписанной и описанной окружности совпадают и находятся в точке пересечения его диагоналей.

Трапеция

Четырёхугольник, у которого две стороны параллельны, а две — нет, называется трапецией. Если сумма длин оснований трапеции равна сумме длин боковых сторон, в неё можно вписать окружность.

Параллелограмм и ромб

Параллелограмм — четырёхугольник, противоположные стороны которого попарно параллельны.

Ромб — это параллелограмм с равными сторонами.

Параллелограмм имеет следующие свойства:

противоположные стороны и углы равны;
сумма двух любых соседних углов равна 180 градусам;
диагонали пересекаются и точкой пересечения делятся пополам;
каждая диагональ делит фигуру на два равных треугольника.

Формулы треугольника ABC зная 1 сторону и 2 угла

Найдем угол B

Так как мы знаем значение угла A и угла С, а сумма всех углов всегда равна 180 градусов, то

\(\angle B=180-\angle А- \angleС=180-\htmlClass{kA}{50}-\htmlClass{kC}{50}=\htmlClass{kB}{80}\degree\)

Найдем сторону AB

Что бы найти сторону AB, необходимо знать длину стороны AC, а также углы С и B

\(AB = {AC * sin(\angle C)\over sin(\angle B)} ={\htmlClass{kAC}{8} * sin( \htmlClass{kC}{50})\over sin( \htmlClass{kB}{80})}=\htmlClass{kAB}{6.223}\)

Найдем сторону BC

Для нахождения стороны BC необходимо знать длину стороны AC, угол A и угол B

\(BC = {AC * sin(\angle A)\over sin(\angle B)} ={\htmlClass{kAC}{8} * sin( \htmlClass{kA}{50})\over sin( \htmlClass{kB}{80})}=\htmlClass{kBC}{6.223}\)

Найдем периметр P треугольника ABC

Периметр треугольника равен сумме длин всех его сторон

\(P=AB+BC+AC=\htmlClass{kAB}{6.223}+\htmlClass{kBC}{6.223}+\htmlClass{kAC}{8}=\htmlClass{kP}{20.446}\)

Найдем площадь S треугольника ABC

Зная периметр и длины всех сторон, рассчитаем площадь треугольника

\(S=\htmlClass{fontm}{ \sqrt{{P\over 2}*({P\over 2}-AC)*({P\over 2}-BC)*({P\over 2}-AB)}}=\htmlClass{fontm}{ \sqrt{{\htmlClass{kP}{20.446}\over 2}*({\htmlClass{kP}{20.446}\over 2}-\htmlClass{kAC}{8})*({\htmlClass{kP}{20.446}\over 2}-\htmlClass{kBC}{6.223})*({\htmlClass{kP}{20.446}\over 2}-\htmlClass{kAB}{6.223})}}=\htmlClass{kS}{19.068}\)

Найдем высоту H проведенную к стороне AC

Для нахождения высоты треугольника, понадобится его площадь и длина стороны AC

\(H={2 * S\over AC}={2 * \htmlClass{kS}{19.068}\over \htmlClass{kAC}{8}}=\htmlClass{kH}{4.767}\)

Примеры решения задач на определение основания

Рассмотрим несколько примеров, как можно найти основание прямоугольного треугольника.

Пример 1:

Известны катеты прямоугольного треугольника: один катет равен 3, а другой — 4. Найдем длину основания.

Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов. В данном случае гипотенуза равна √(3^2 + 4^2) = 5.

Длина основания равна половине произведения катетов, то есть (3 * 4) / 2 = 6.
Пример 2:

Известны гипотенуза прямоугольного треугольника, равная 10, и один из катетов, равный 6. Найдем длину основания.

Снова воспользуемся теоремой Пифагора. Квадрат второго катета равен квадрату гипотенузы минус квадрат первого катета (10^2 — 6^2 = 64). Следовательно, второй катет равен 8.

Длина основания вычисляется так же, как в предыдущем примере: (6 * / 2 = 24.
Пример 3:

Известны периметр прямоугольного треугольника, равный 24, и гипотенуза, равная 10. Найдем длину основания.

Периметр равен сумме длин всех сторон треугольника. В нашем случае это основание, гипотенуза и катет. Поэтому основание и катет в сумме дают 24 — 10 = 14.

Длина основания равна половине произведения катетов, то есть (14 * 10) / 2 = 70.

Это лишь несколько примеров решения задач на определение основания прямоугольного треугольника. В каждом конкретном случае следует использовать соответствующую теорему и применять известные формулы для нахождения основания.

Основные символы треугольника

В математике существуют несколько основных символов, которые используются для обозначения треугольников. Вот некоторые из них:

△ — этот символ обозначает треугольник. Он часто используется в геометрических формулах и определениях.
ABC — в этой записи каждая буква обозначает вершину треугольника. Например, треугольник ABC означает треугольник с вершинами A, B и C.
∆ — это символ также обозначает треугольник. Он используется для обозначения треугольника в некоторых математических формулах и теоремах.
∠ — данный символ обозначает угол. Он используется для обозначения угла, образованного двумя сторонами треугольника.

Эти символы часто используются в математических уравнениях, теоремах и определениях, чтобы обозначить треугольники и их свойства.

Свойства

Равнобедренный треугольник имеет две равные по значению боковые стороны a и основание b. Это позволяет рассчитать любые параметры треугольника, необходимые для решения задачи. Периметр равнобедренного треугольника равен удвоенной боковой стороне в сумме с основанием. (рис.88.1) P=2a+b

Высота, проведенная к основанию равнобедренного треугольника, делит его на два конгруэнтных прямоугольных треугольника, с половиной основания в качестве второго катета и боковой стороной как гипотенузой. Такая высота одновременно является и медианой и биссектрисой. Найти ее можно по теореме Пифагора из прямоугольного треугольника. (рис.88.2) h_b=m_b=l_b=√(a^2-(b/2)^2 )=√(4a^2-b^2 )/2

Остальные две высоты равны друг другу и считаются через формулу с произведением разностей полупериметров и сторон, где приравнены боковые стороны. (рис.88.8) h_a=(b√((4a^2-b^2)))/2a

Зная высоту, найти площадь равнобедренного треугольника можно, подставив полученное выражение в формулу, по которой площадь равна половине основания, умноженной на его высоту. S=hb/2=(b√(4a^2-b^2 ))/4

Углы в равнобедренном треугольнике распределяются следующим образом – углы при основании друг другу конгруэнтны, также как и боковые стороны, а в сумме все три угла дают 180 градусов, поэтому найти их можно двумя видами разности. α=(180°-β)/2 β=180°-2α

Если ни один из углов не дан, но есть все стороны, то можно воспользоваться теоремой косинусов, чтобы найти любой угол. cos⁡α=(b^2+c^2-a^2)/2bc=(b^2+a^2-a^2)/2ba=b^2/2ba=b/2a cos⁡β=(a^2+a^2-b^2)/(2a^2 )=(2a^2-b^2)/(2a^2 )

Медиана и биссектриса, опущенные на основание, вычисляются по формуле высоты, приведенной выше, а оставшиеся две медианы (равно как и две биссектрисы) равны друг другу, поскольку строятся на равных боковых сторонах. Вычислить медиану можно, упростив формулу произвольного треугольника. (рис. 88.3) m_a=√(2a^2+2b^2-a^2 )/2=√(a^2+2b^2 )/2

В формуле биссектрисы аналогично приравниваются боковые стороны, и ее становится возможным вычислить по упрощенной схеме. (рис. 88.4) l_a=√(ab(2a+b)(a+b-a) )/(a+b)=(b√(a(2a+b) ))/(a+b)

Средняя линия равнобедренного треугольника, параллельная основанию, равна его половине, а средние линии, параллельные боковым сторонам, равны между собой и также равны половинам самих боковых сторон. (рис. 88.5) M_b=b/2 M_a=a/2

Радиус окружности, вписанной в равнобедренной треугольник, является производной формулы для произвольного треугольника, и рассчитать его можно, зная боковую сторону и основание. (рис. 88.6) r=b/2 √((2a-b)/(2a+b))

Радиус окружности, описанной вокруг равнобедренного треугольника, также выводится из общей формулы и выглядит упрощенно следующим образом. (рис. 88.7) R=a^2/√(4a^2-b^2 )

Основание: определение и роль

Основание имеет ключевое значение в строительстве, инженерии и архитектуре. Оно обеспечивает стабильность и прочность всего сооружения. От качества основания зависит безопасность и долговечность строительных объектов.

Основное назначение основания — перераспределение нагрузки, которую оно получает от сверху на всю подстилающую площадку. Опоры и фундаменты передают нагрузку на основание, и если оно недостаточно крепкое или неравномерное, это может привести к деформации или разрушению сооружения.

Важно отметить, что несущая способность основания должна быть достаточной для поддержки всех нагрузок, включая вес сооружения, окружающие нагрузки (ветер, снег и т.д.) и динамические нагрузки (вибрация, землетрясение и т.д.). При проектировании зданий и сооружений необходимо тщательно анализировать и оценивать свойства основания, включая его геологическую структуру, грунтовую воду, устойчивость к деформациям и многие другие факторы. Выбор и расчет соответствующего фундамента или поддерживающей структуры зависит от таких данных

Выбор и расчет соответствующего фундамента или поддерживающей структуры зависит от таких данных

При проектировании зданий и сооружений необходимо тщательно анализировать и оценивать свойства основания, включая его геологическую структуру, грунтовую воду, устойчивость к деформациям и многие другие факторы. Выбор и расчет соответствующего фундамента или поддерживающей структуры зависит от таких данных.

Кроме того, при проведении строительных работ важно учесть возможные изменения основания в течение времени — например, связанные с периодическими повышениями уровня грунтовых вод или сезонными изменениями грунта

[править] Определения, связанные с треугольником

Окружности

Вписанная окружность — окружность, касающаяся всех трёх сторон треугольника. Она единственна. Центр вписанной окружности называется инцентром.
Описанная окружность — окружность, проходящая через все три вершины треугольника. Описанная окружность также единственна.
Вневписанная окружность — окружность, касающаяся одной стороны треугольника и продолжения двух других сторон.

Лучи, отрезки и точки

Медианой треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны (основанием медианы). Все три медианы треугольника пересекаются в одной точке. Эта точка пересечения называется центроидом или центром тяжести треугольника. Последнее название связано с тем, что у треугольника, сделанного из однородного материала, центр тяжести находится в точке пересечения медиан. Центроид делит каждую медиану в отношении 1:2, считая от основания медианы.

Высотой треугольника, проведённой из данной вершины, называется перпендикуляр, опущенный из этой вершины на противоположную сторону или её продолжение. Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.

Биссектрисой треугольника, проведённой из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам. Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности (инцентром).

Средней линией треугольника называют отрезок, соединяющий середины двух сторон этого треугольника.

В равнобедренном треугольнике биссектриса, медиана и высота, проведённые к основанию, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведённые из одной вершины, совпадают, то треугольник равнобедренный. Если треугольник разносторонний, то для любой его вершины биссектриса, проведённая из неё, лежит между медианой и высотой, проведёнными из той же вершины.

Серединные перпендикуляры(медиатриссы) к сторонам треугольника также пересекаются в одной точке, которая совпадает с центром описанной окружности.

Середины трёх сторон треугольника, основания трёх его высот и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности, называемой окружностью девяти точек.

В любом треугольнике центр тяжести, ортоцентр, центр описанной окружности и центр окружности девяти точек лежат на одной прямой, называемой прямой Эйлера.

Ортоцентр, инцентр, центроид (центр тяжести), а также некоторые другие точки называются замечательными точками треугольника.

Как пользоваться признаками равнобедренного треугольника при решении задач

Если дан равнобедренный треугольный треугольник, смело проводи высоту, получай два прямоугольных треугольника и решай задачу уже про прямоугольный треугольник;
Если дано, что два угла равны, то треугольник точно равнобедренный и можно проводить высоту и ….( Дом, который построил Джек… );
Если оказалось, что высота разделила сторону пополам, то треугольник – равнобедренный со всеми вытекающими бонусами;
Если оказалось, что высота разделила угол полам – тоже равнобедренный;
Если биссектриса разделила сторону пополам или медиана разделила угол, то это тоже бывает только в равнобедренном треугольнике.

Давайте посмотрим, как это проблематично.

Какие еще методы могут использоваться для нахождения площади основания

В дополнение к классическим методам нахождения площади основания, есть и другие варианты, которые могут быть полезны в определенных ситуациях.

1. Использование геометрических фигур

Если форма основания не является прямоугольной или квадратной, можно разбить ее на более простые геометрические фигуры (например, треугольники, трапеции или круги). На основе этого можно найти площадь каждой фигуры и сложить их, чтобы получить общую площадь основания.

2. Использование метода Монте-Карло

Этот метод заключается в размещении точек на поверхности основания и подсчете количества точек, попавших внутрь фигуры основания. На основе этого можно определить отношение площади фигуры к площади общей поверхности. Чем больше точек используется, тем более точным становится результат.

3. Использование сканирующего лазера

Сканирующий лазер может использоваться для получения точных показаний размеров объекта, включая площадь основания. При этом нет необходимости делать сложные измерения вручную – все данные записываются автоматически в компьютер.

Вопрос-ответ

Вопрос: Как найти площадь основания прямоугольника?

Ответ: Площадь основания прямоугольника вычисляется как произведение его двух сторон.

Вопрос: Как найти площадь основания треугольника, если известны все его стороны?

Ответ: Площадь основания треугольника можно вычислить, используя формулу Герона: S = √p(p-a)(p-b)(p-c), где p – полупериметр треугольника, a, b и c – его стороны.

Вопрос: Как найти площадь основания круга?

Ответ: Площадь основания круга вычисляется по формуле S = πr², где r – радиус круга, π – математическая константа, примерно равная 3,14.

Вопрос: Как найти площадь основания призмы?

Ответ: Площадь основания призмы можно найти, зная форму основания. Например, для призмы с прямоугольным основанием площадь основания вычисляется как произведение его двух сторон.

Вопрос: Как найти площадь основания правильной треугольной пирамиды, если известна ее высота?

Ответ: Площадь основания правильной треугольной пирамиды можно найти, используя следующую формулу: S = (a²√3)/4, где a – длина стороны правильного треугольника, основания пирамиды. Затем умножаем полученную площадь на высоту пирамиды.

Главная — Советы — Простой и эффективный способ: как быстро найти площадь основания

Я всегда сталкиваюсь с проблемой вычисления площади основания объектов. Статья помогла мне разобраться в этом вопросе. Хорошо, что применение формулы и процесс вычисления расписаны по шагам, что облегчило мне задачу.

Ольга Смирнова
5.0 out of 5.0 stars5.0

Статья очень краткая и понятная. Теперь я знаю, как найти площадь основания. Спасибо!

Sapphire
5.0 out of 5.0 stars5.0

Как женщина, я часто оказываюсь в ситуации, когда нужно рассчитать площадь основания различных фигур — будь то круг, прямоугольник или треугольник. К сожалению, мои знания по математике и геометрии ограничены, и я не знаю, как найти площадь основания. Поэтому я рада, что наткнулась на эту статью. Статья помогла мне понять, что не нужно бояться главной формулы для рассчета площади основания — независимо от того, какая фигура у вас есть перед глазами. Все описано очень доступно и понятно. Я прочитала эту статью несколько раз, чтобы убедиться, что я точно понимаю, как найти площадь основания. Используя эту информацию, я смогла рассчитать площадь основания для нескольких примеров. Теперь у меня есть более четкое понимание того, что такое площадь основания, как ее рассчитывать и как это применять на практике. Большое спасибо за эту статью! Я уверена, что многие женщины, так же как и я, оценят ее доступность и понятность.

Елена Кузнецова
5.0 out of 5.0 stars5.0

Я уже давно хотела научиться находить площадь основания, но всегда боялась, что это сложно. Статья помогла мне понять, что это проще, чем кажется. Все описано доступно и понятно. Теперь я готова рассчитывать площадь оснований и делать это правильно!

Luna
5.0 out of 5.0 stars5.0

Статья понятная и полезная для решения задач по геометрии.

Применение в науке и технике

Группа геометрических тел имеет широкое применение в науке и технике. Различные формы и свойства этих тел позволяют использовать их в разных областях.

Одним из наиболее распространенных применений геометрических тел является использование их в архитектуре и строительстве. Например, при проектировании зданий используются различные формы и комбинации геометрических тел для создания устойчивых и эстетически привлекательных конструкций.

Геометрические тела также находят применение в машиностроении. Например, при проектировании автомобилей используются геометрические тела для оптимизации обтекаемости, аэродинамики и прочности конструкции.

В науке геометрические тела применяются для моделирования и исследования различных физических явлений. Например, в физике геометрические тела используются для изучения тепловых процессов, взаимодействия света с веществом и других явлений.

Также геометрические тела находят применение в компьютерной графике и визуализации данных. Использование геометрических тел позволяет создавать реалистичные и детализированные изображения, а также эффективно представлять и анализировать различные виды данных.

Область применения	Примеры
Архитектура и строительство	Здания, мосты, туннели
Машиностроение	Автомобили, самолеты, суда
Наука	Физика, химия, биология
Компьютерная графика	Игры, анимация, визуализация данных

Группа геометрических тел в математике

В математике существует множество геометрических тел, которые можно классифицировать и объединять в различные группы. Эти тела обладают определенными свойствами и характеристиками, которые мы можем изучать и анализировать.

Одной из групп геометрических тел являются многогранники, или полиэдры. Они представляют собой трехмерные фигуры, ограниченные плоскими геометрическими фигурами, называемыми гранями. Многогранники могут быть правильными, когда все их грани равны и углы между ними одинаковы, или неправильными, когда грани различаются по форме и размерам.

Круглые тела, такие как сферы, цилиндры и конусы, также входят в группу геометрических тел. Они имеют форму, близкую к окружностям, и обладают особыми свойствами, такими как радиус, диаметр и высота.

Также в группу геометрических тел можно включить плоские фигуры, такие как треугольники, прямоугольники, квадраты и окружности. Хотя они не являются трехмерными, они все же имеют геометрические формы и характеристики, которые можно изучать и анализировать.

Все эти группы геометрических тел в математике имеют свои особенности и применения. Изучение и понимание этих тел помогает нам лучше разбираться в пространстве и формах, а также находить применение в различных областях науки и техники.