Как найти вектор
Процесс поиска вектора может зависеть от того, какой информацией вы располагаете и какой тип вектора вы пытаетесь найти. Вот несколько ситуаций и как к ним подойти:
Ответ: С двух точек зрения
Вектор смещения: Если у вас есть две точки в пространстве, A и B, и вы хотите найти вектор от A до B (также известный как вектор смещения), вы вычитаете координаты A из координат B. Если A = (x1, y1, z1) и B = (x2, y2, z2), то вектор AB = b — a = (x2 — x1, y2 — y1, z2 — z1). B. От величины и направления
Нахождение вектора на плоскости: Если вы знаете величину (длину) вектора и его направление (например, угол относительно оси x), вы можете найти вектор, используя тригонометрические функции для нахождения компонентов x и y. Если величина равна r, а угол равен θ, то вектор v = r cos(θ)i + r sin(θ)j, где i и j — единичные векторы в направлениях x и y соответственно.
Нахождение вектора в пространстве: Если вы знаете величину вектора и два угла (например, азимутальный угол φ и полярный угол θ в сферических координатах), вы можете найти вектор, используя формулы преобразования сферических координат в декартовы. Вектор v = r sin(θ) cos(φ)i + r sin(θ) sin(φ)j + r cos(θ)k, где i, j и k — единичные векторы в направлениях x, y и z соответственно.
C. Из перекрестного или точечного произведения
Если вам известно перекрестное или точечное произведение двух векторов, и вы знаете один из векторов, вы можете найти другой вектор, используя алгебраические методы. Обычно это включает в себя решение системы уравнений. D. Нормализация вектора
Поиск единичного вектора: Если у вас есть ненулевой вектор и вы хотите найти соответствующий единичный вектор (вектор длиной 1 в том же направлении), вы делите вектор на его величину. Если a — исходный вектор, то единичный вектор â = a / ||a||, где ||a|| — величина a. Помните, что метод, который вы используете, зависит от того, какой информацией вы располагаете. В некоторых случаях вам, возможно, придется использовать несколько методов в комбинации или выполнить дополнительные действия.
Геометрическая интерпретация векторов
Направление вектора определяется его ориентацией в пространстве. Оно указывает находится ли конечная точка вектора справа, слева, выше или ниже начальной точки.
Длина вектора определяется расстоянием между начальной и конечной точками. Если вектор имеет длину 0, то его называют нулевым вектором. Векторы, имеющие одинаковое направление, но разную длину, называются коллинеарными векторами.
- Сложение векторов: Для сложения двух векторов, их конечные точки соединяются, образуя треугольник или параллелограмм. Результатом сложения является вектор, который соединяет начальную точку первого вектора с конечной точкой второго вектора.
- Вычитание векторов: Для вычитания одного вектора из другого вектора, конечная точка вычитаемого вектора соединяется с начальной точкой вычитаемого вектора. Результатом вычитания является вектор, который соединяет начальную точку первого вектора с конечной точкой второго вектора.
- Умножение вектора на число: Умножение вектора на число приводит к изменению его длины, но не направления. Если число положительное, то увеличение длины вектора будет происходить в направлении вектора, если число отрицательное, то уменьшение длины будет происходить в противоположном направлении.
Геометрическая интерпретация векторов позволяет наглядно представлять сложные математические операции с векторами. Она широко применяется в физике, геометрии, компьютерной графике и других областях, где векторы играют важную роль.
Координаты середины отрезка
Если $A(x_1;y_1)$ и $B(x_2;y_2)$, то точка $M$ середина отрезка $AB$ имеет координаты $M\left(\dfrac{x_1+x_2}{2};\dfrac{y_1+y_2}{2}\right)$.
Доказательство
По теореме $\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}$.
Таким образом $\displaystyle\overrightarrow{OM}=\frac{\overrightarrow{OA}+\overrightarrow{OB}}{2}=\frac{(x_1;y_1)+(x_2;y_2)}{2}=\frac{(x_1+x_2;y_1+y_2)}{2}=\left(\frac{x_1+x_2}{2};\frac{y_1+y_2}{2}\right)$.
Таким образом точка $M$ имеет координаты $\displaystyle\left(\frac{x_1+x_2}{2};\frac{y_1+y_2}{2}\right)$.
Практика 2
В дополнение к функции нахождения точки пересечения, напишем «продвинутую» функцию, которая находит эту точку, определяет нахождение на каждом из отрезков, и определяет угол между направляющими векторами. Или же определяет, что прямые параллельны/совпадают.
//**********************************************************
// Тип пересечения прямых (p1,p2) и (p3,p4)
//**********************************************************
type
TxCrossLineResult = (
xclrEqual = -32// эквивалентны
,xclrParallel = -16// параллельны
,xclrOk = 0 // как минимум пересечение есть
,xclrFirst = 1 // попадает в первый отрезок
,xclrSecond = 2 // попадает во второй отрезок
,xclrBoth = 3 // попадает в оба
,xclrPerpend = 4 // перпендикулярны
// можно найти по маске через AND, но для полноты картины
,xclrFirstP = 5 // перпендикулярны и попадает в первый
,xclrSecondP = 6 // перпендикулярны и попадает в второй
,xclrBothP = 7 // перпендикулярны и попадает в оба
);
//**********************************************************
// Нахождение точки пересечения прямых (p1,p2) и (p3,p4)
// Определяет параллельность, совпадение,
// перпендикулярность, пересечение.
// Определяет, каким отрезкам принадлежит.
// Находит угол(рад.) от (p1,p2) к (p3,p4):
// отрицательное значение — против часовой
// положительное — по часовой
//**********************************************************
function CrossLines(const p1,p2,p3,p4: TxPoint;
var res: TxPoint; var Angle: Extended): TxCrossLineResult;
const
Prec = 0.0001;
var
a1, a2: Extended;
b1, b2: Extended;
c1, c2: Extended;
v: Extended;
begin
Angle := 0;
a1 := p2.y — p1.y;
a2 := p4.y — p3.y;
b1 := p1.x — p2.x;
b2 := p3.x — p4.x;
c1 := p2.x*p1.y — p1.x*p2.y;
c2 := p4.x*p3.y — p3.x*p4.y;
v := a1*b2 — a2*b1;
if abs(v) > Prec then
begin
Result := xclrOk;
res.X := -(c1*b2 — c2*b1)/v;
res.Y := -(a1*c2 — a2*c1)/v;
if CheckCrossPoint(p1,p2,res) then
Result := TxCrossLineResult(Integer(Result) +
Integer(xclrFirst));
if CheckCrossPoint(p3,p4,res) then
Result := TxCrossLineResult(Integer(Result) +
Integer(xclrSecond));
if (abs(a1*a2 + b1*b2) < Prec) then
Result := TxCrossLineResult(Integer(Result) +
Integer(xclrPerpend));
Angle := CalcCrossAngle(a1,b1,a2,b2);
end else
begin
Result := xclrParallel;
if ((abs(c1*b2 — c2*b1) < Prec) and
(abs(a1*c2 — a2*c1) < Prec))
then
Result := xclrEqual;
end;
end;
|
1 |
//********************************************************** TxCrossLineResult=( xclrEqual=-32// эквивалентны ,xclrParallel=-16// параллельны ,xclrOk=// как минимум пересечение есть ,xclrFirst=1// попадает в первый отрезок ,xclrSecond=2// попадает во второй отрезок ,xclrBoth=3// попадает в оба ,xclrPerpend=4// перпендикулярны // можно найти по маске через AND, но для полноты картины ,xclrFirstP=5// перпендикулярны и попадает в первый ,xclrSecondP=6// перпендикулярны и попадает в второй ,xclrBothP=7// перпендикулярны и попадает в оба ); functionCrossLines(constp1,p2,p3,p4TxPoint; varresTxPoint;varAngleExtended)TxCrossLineResult; const Prec=0.0001; var a1,a2Extended; b1,b2Extended; c1,c2Extended; vExtended; begin Angle=; a1=p2.y-p1.y; a2=p4.y-p3.y; b1=p1.x-p2.x; b2=p3.x-p4.x; c1=p2.x*p1.y-p1.x*p2.y; c2=p4.x*p3.y-p3.x*p4.y; v=a1*b2-a2*b1; ifabs(v)>Prec then begin Result=xclrOk; res.X=-(c1*b2-c2*b1)/v; res.Y=-(a1*c2-a2*c1)/v; ifCheckCrossPoint(p1,p2,res)then Result=TxCrossLineResult(Integer(Result)+ Integer(xclrFirst)); ifCheckCrossPoint(p3,p4,res)then Result=TxCrossLineResult(Integer(Result)+ Integer(xclrSecond)); if(abs(a1*a2+b1*b2)<Prec)then Result=TxCrossLineResult(Integer(Result)+ Integer(xclrPerpend)); Angle=CalcCrossAngle(a1,b1,a2,b2); endelse begin Result=xclrParallel; if((abs(c1*b2-c2*b1)<Prec)and (abs(a1*c2-a2*c1)<Prec)) then Result=xclrEqual; end; end;
|
Вектор и его характеристики
Направление: вектор указывает на то, в каком направлении происходит перемещение или воздействие. Направление может быть задано с помощью угла или с помощью указания на конкретные точки или объекты.
Величина: вектор также имеет величину, которая показывает, насколько велико перемещение или сила. Величину вектора можно измерять в единицах длины или силы, в зависимости от его назначения.
Нулевой вектор: это вектор с нулевой величиной. Он не имеет определенного направления и может быть представлен в виде точки на графике или в пространстве.
Сложение векторов: векторы могут складываться друг с другом, чтобы получить вектор, который является их суммой. Это выполняется путем сложения соответствующих компонент векторов по направлению и величине.
Умножение векторов: векторы также могут умножаться на скаляры (числа). Результатом такого умножения является новый вектор с измененной величиной, но с сохранением направления.
Направляющий вектор: это вектор, который указывает направление на прямую линию или на кривую. Направляющий вектор может быть найден, например, путем нахождения разности координат конечной и начальной точек на линии.
Векторы являются важным инструментом в различных областях, таких как физика, математика, инженерия и компьютерная графика. Они играют ключевую роль в описании движения тел, вычислении силы и величин, а также в решении задач, связанных с пространством и направлениями.
Длина вектора
Для вычисления длины вектора в трехмерном пространстве используется формула:
где x, y и z — координаты вектора в трехмерном пространстве.
Для вычисления длины вектора в двумерном пространстве используется формула:
где x и y — координаты вектора в двумерном пространстве.
Длина вектора всегда положительна или нулевая. Если длина вектора равна нулю, то вектор является нулевым вектором, у которого все компоненты равны нулю.
Вычисление длины вектора может быть полезно для определения его нормы, например, для нормализации вектора или для определения его масштаба.
Направление вектора
Вектор можно представить в виде отрезка, направленного от начала координат к конечной точке в пространстве. Направление вектора задается величиной и углом. Величина вектора показывает его длину, а угол определяет его направление относительно выбранной оси.
Векторное направление может быть задано абсолютно (в абсолютной системе координат), относительно другого вектора или относительно выбранной оси координат.
Для описания направления вектора могут использоваться различные обозначения. Например, в двумерном пространстве вектор может быть задан с помощью угла поворота относительно положительной оси абсцисс. В трехмерном пространстве направление вектора можно задать с помощью углов отклонения от осей координат.
Вектор, направленный по оси абсцисс, называется направляющим вектором. Он имеет координаты (1, 0, 0) в трехмерном пространстве. Направляющий вектор позволяет определить направление и длину других векторов при заданном начальном положении.
Направление вектора играет важную роль в физике, геометрии, механике и многих других областях науки и техники. Оно позволяет анализировать движение тел, моделировать системы и решать различные задачи.
Положительный и отрицательный вектор
Векторы могут быть разделены на две категории: положительные и отрицательные. Положительный вектор определен направленным отрезком, который указывает в определенном направлении. Он имеет положительное направление и обозначается положительным знаком (+) перед ним. Например, положительный вектор может указывать направление движения на оси координат.
Отрицательный вектор, напротив, указывает в противоположном направлении и имеет отрицательное направление. Он обозначается отрицательным знаком (-) перед вектором. Например, отрицательный вектор может указывать направление движения в противоположную сторону на оси координат.
Положительные и отрицательные векторы могут быть представлены численно или графически. Численное представление включает указание направления и длины вектора с помощью чисел. Графическое представление включает изображение вектора на декартовой системе координат или других графических средствах.
| Тип | Представление | Пример |
|---|---|---|
| Положительный вектор | Численное представление | +5 |
| Отрицательный вектор | Численное представление | -3 |
Точка пересечения 2 векторов
Координаты x,y я то нашел, спроецировав на плоскость вектора.
#1 12:45, 15 июня 2008
stl А что такое пересечение векторов?
#2 13:06, 15 июня 2008
Есть обобщенная задача — поиск двух БЛИЖАЙШИХ ТОЧЕК у двух отрезков в пространстве. Я щас не дома и не могу показать код, да и в двух словах алгоритм не опишешь. Гугли.
#3 13:30, 15 июня 2008
stl >Даны 2 вектора: x1,y1,z1; x2,y2,z2; Как найти точку пересечения? Элементарно: (0; 0; 0)
#4 13:43, 15 июня 2008
если честно , я не понял ваших ответов. Мне нужны не ближайшие точки, и причем тут 0,0,0 я тоже не понял.
2 вектора точно пересекаются в пространстве в какой-то точке. У векторов есть координаты начала и конца. Найти x,y точки пересечения легко — проецируем на экран, отбрасывая z, находим.
А как найти координату z, если она может потребоваться в дальнейшем?
#5 13:46, 15 июня 2008
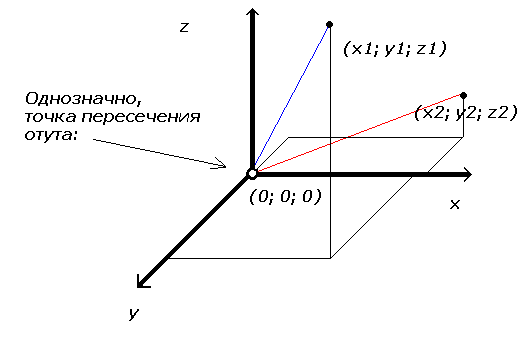
#6 13:52, 15 июня 2008
stl >2 вектора точно пересекаются в пространстве в какой-то точке. У векторов есть >координаты начала и конца.
У настоящих брутальных векторов координаты начала находятся в точке
- Tweedle Dee
- Постоялец
#7 13:57, 15 июня 2008
ты у каждого вектора указал лишь один набор координат. потому их от (0,0,0) и отсчитали вопрос надо правильней формулировать. тебя интересует пересение ОТРЕЗКОВ? ну так элементарно, пусть отрезки
(x1, y1, z1) — (x2, y2, z2) и (a1, b1, c1) — (a2, b2, c2) тогда уравнение первого x = x1*t + x2*(1 — t) y = y1*t + y2*(1 — t) z = z2*t + z2*(1 — t)
аналогично для второго x = a1*s + a2*(1 — s) y = b1*s + b2*(1 — s) z = c2*s + c2*(1 — s)
приравниваем x,y,z, получаем
x1 t + x2 (1 — t) = a1 s + a2 (1 — s) y1 t + y2 (1 — t) = b1 s + b2 (1 — s)
система из 2 уравнений с 2мя неизвестными, решаем, подставляем s и t во третьи уравнения, убеждаемся, что z-координаты совпали тоже (если нет, то и пересечения нет)
#8 14:09, 15 июня 2008
stl >У векторов есть координаты начала и конца А нету!
Вектор это упорядоченное конечное множество своих координат. Вектор может представлять множество отрезков, которые будут по длине равны абсолютному значению вектора и паралельны. И вот разница координат отрезков следовательно равна координатам вектора. Если проще, вектор — это не отрезок. Вектор — это точка. А его направление — это направление отрезка из начала координат в эту точку.
#9 14:10, 15 июня 2008
Tweedle Dee >ты у каждого вектора указал лишь один набор координат. потому их от (0,0,0) и отсчитали Он указал правильно а отсчитывают от нулей всегда.
#10 14:14, 15 июня 2008
>У настоящих брутальных векторов координаты начала находятся в точке Координаты у труЪ-математиков задаются либо (0; 0; 0) либо А вот — смахивает на неупорядоченное множество.
#11 14:24, 15 июня 2008
stl Короче объясняю. Такс. Если у тебя есть отрезок то вектор, который задаст множество отрезков, равных по модулю длине твоего отрезка и паралельных ему равен (x2 — x1; y2 — y1; z2 — z1). И любой отрезок, входящий в это множество будет равен , Отрезок, совпадающий с радиус-вектором на графике будет равен >. Где c1, c2, c3 — произвольные константы из множества декартовой степени 1/n пространства, которому принадлежит вектор, где n — мерность пространства. Например пространство R^3 возводим в декартовую степень 1/3 получаем R — множество действительных чисел (частный случай для трёхмерного пространства). x, y, z — координаты вектора, равные x2 — x1, y2 — y1 и z2 — z1 соответственно.
ПРАВКА: поумничал малость ПРАВКА: афрографея ПРАВКА: поумничал малость
- Sbtrn. Devil
- Постоялец
#12 15:21, 15 июня 2008
Векторы в пространстве — не пересекаются! Их пересечение возможно только при строгом и абсолютно точном соотношении параметров (как минимум, «лежат в одной плоскости»). Однако, поскольку в реальном мире имеют место квантовые флуктуации, а малейшего отклонения параметра достаточно для разрушения необходимого равенства (в случае компутера эта особенность физического мира симулируется неабсолютной точностью вычислений), то вероятность пересечения изничтожающе стремится к нулю.
А поэтому мораль такова: не надо математически эстетствовать, ибо жизнь сурова. А надо взять и найти, как предлагали в посте 2, ближайшие точки A и B обоих векторов. Если расстояние AB меньше некоторого епсилон (скажем, 0.001), то можно условно считать, что вектора пересеклись, и точка пересечения — середина AB. Если же больше епсилона — значит, не пересеклись.
- Alexander K
- Постоялец
Принадлежность точки отрезку
В общем случае, чтобы определить принадлежность точки отрезку, надо установить две вещи:
- Точка принадлежит прямой, проходящей через конечные точки отрезка. Для этого достаточно подставить значение X и Y в уравнение прямой и проверить получившееся равенство. В нашем случае, этот пункт уже выполнен, т.к. точка пересечения априори принадлежит обеим прямым.
- Проверить факт нахождения точки между концами отрезка.
Займемся пунктом 2. Данный факт можно установить двумя способами:
- Логически, т.е. (x1 <= x <= x2) ИЛИ (x1 >= x >= x2
(y1 = y >= y2).
). На случай «вертикальности» линии добавить проверку на Y:
- Арифметически. Сумма отрезков |x-x1| + |x-x2| должна быть равна длине отрезка |x1-x2
|y-y1| + |y-y2| = |y1-y2|
|. Аналогично, на случай «вертикальности» , добавить проверку:
//*****************************************************
// Проверка факта нахождения точки res между
// концами отрезка (p1,p2).
// Решение с помощью условных операторов и
// коэффициентов A=(y2-y1) B=(x1-x2).
// Выступают в качестве параметров, чтобы не тратить
// время на их подсчет, т.к. в вызывающей стороне
// они уже посчитаны
//*****************************************************
function CheckCrossPoint(const p1, p2, res: TxPoint;
const A,B: Extended): Boolean;
begin
Result :=
(((B<0) and (p1.X < res.X) and (p2.X > res.X)) or
((B>0) and (p1.X > res.X) and (p2.X < res.X)) or
((A<0) and (p1.y > res.Y) and (p2.Y < res.Y)) or
((A>0) and (p1.y < res.Y) and (p2.Y > res.Y)));
end;
//*****************************************************
// Проверить факт нахождения точки res между
// концами отрезка (p1,p2)
// Арифметическое решение без коэффициентов
//*****************************************************
function CheckCrossPoint(const p1, p2, res: TxPoint): Boolean;
begin
Result :=
(abs(p2.x-p1.x)>= abs(p2.x-res.x) + abs(p1.x-res.x)) and
(abs(p2.y-p1.y)>= abs(p2.y-res.y) + abs(p1.y-res.y));
end;
|
1 |
//***************************************************** functionCheckCrossPoint(constp1,p2,resTxPoint; constA,BExtended)Boolean; begin Result= (((B<)and(p1.X<res.X)and(p2.X>res.X))or ((B>)and(p1.X>res.X)and(p2.X<res.X))or ((A<)and(p1.y>res.Y)and(p2.Y<res.Y))or ((A>)and(p1.y<res.Y)and(p2.Y>res.Y))); end; functionCheckCrossPoint(constp1,p2,resTxPoint)Boolean; begin Result= (abs(p2.x-p1.x)>=abs(p2.x-res.x)+abs(p1.x-res.x))and (abs(p2.y-p1.y)>=abs(p2.y-res.y)+abs(p1.y-res.y)); end;
|
Практика показывает, что арифметический способ быстрее примерно в 3 раза. Когда-то я считал, что операции сравнения самые быстрые. Это давно уже не так.
Задача нахождения принадлежности точки P(x,y) отрезку, заданного двумя точками с координатами P1(x1, y1) и P2(x2, y2) подробно рассмотрена в отдельной статье.
Решение системы уравнений
Когда мы имеем два или более уравнений с неизвестными, мы можем использовать метод решения систем уравнений для нахождения их точек пересечения. Задача состоит в том, чтобы найти значения неизвестных, которые удовлетворяют всем уравнениям из системы.
Существует несколько методов решения систем уравнений, включая подстановку, метод Гаусса-Жордана, метод Крамера и метод Гаусса.
- Метод подстановки заключается в том, чтобы выразить одну переменную через другую и подставить это выражение в другое уравнение. Затем мы можем найти значение первой переменной и использовать его для нахождения значения второй переменной.
- Метод Гаусса-Жордана сводит систему уравнений к усеченной матрице и решает ее с помощью элементарных преобразований. Этот метод удобен для систем уравнений со множеством переменных.
- Метод Крамера использует определители матриц для нахождения значений неизвестных. Он можно применять только к системам уравнений с равным числом уравнений и неизвестных.
- Метод Гаусса использует элементарные преобразования для приведения системы уравнений к треугольному виду, что упрощает нахождение решения.
Выбор метода решения системы уравнений зависит от сложности системы и предпочтений решателя. Каждый из методов имеет свои преимущества и недостатки, и выбор метода может варьироваться в зависимости от ситуации.
| Метод | Преимущества | Недостатки |
|---|---|---|
| Подстановка | — Простой в использовании— Может быть применен к системам с любым количеством уравнений и неизвестных | — Может быть трудно применять к системам с большим количеством уравнений и неизвестных— Может быть неэффективен, если значения переменных неизвестны и требуется проводить множество подстановок |
| Гаусс-Жордан | — Позволяет решать системы уравнений с большим количеством переменных— Метод легко расширяется для решения более сложных систем уравнений | — Может потребоваться много времени и вычислительных ресурсов для больших систем уравнений |
| Крамер | — Прост в использовании— Есть точное решение для систем с равным количеством уравнений и неизвестных | — Требуется вычисление множества определителей, что может быть трудоемким для больших систем— Не может быть применен к системам с неравным числом уравнений и неизвестных |
| Гаусс | — Позволяет привести систему к треугольному виду и упростить ее решение— Может быть применен к системам с любым количеством уравнений и неизвестных | — Может потребоваться много вычислительных ресурсов для больших систем уравнений |
В зависимости от конкретной задачи и системы уравнений, один из этих методов может быть более предпочтительным
Важно изучить каждый из них и определить, какой метод наиболее подходит для решения вашей системы уравнений

















![Math-public:vektory-koordinaty-vektorov [президентский фмл №239]](http://mtrufa.ru/wp-content/uploads/b/8/b/b8b99b40d787f52273991ef0e41c48bb.jpeg)












