Презентация на тему: "егэ

Практический пример: нахождение угла между сторонами треугольника

Для начала, обозначим точку пересечения медианы BM с основанием AC как точку D. Также обозначим отрезки BD и DM как h и x соответственно.

Заметим, что медиана BM, проведенная из вершины B, делит сторону AC пополам, поэтому отрезок AD равен отрезку CD.

По теореме Пифагора для треугольника BDM, имеем:

BD² = BM² — DM²

Так как отрезок BD равен h и известны длины сторон AB и AC, которые обозначены как a и c соответственно, мы можем записать следующее:

a/2 = h + x

c/2 = h — x

Суммируя эти два уравнения, получим:

a/2 + c/2 = 2h

Выразив h, получим:

h = (a + c) / 4

Используя значение h, мы можем найти значение x, вычтя его из h:

x = h — x

Далее, подставляя найденные значения в формулу для BD², получим:

(a/2)² = BM² — ((a + c) / 4)²

Разрешая уравнение относительно BM², можно найти его значение. Затем, применяя теорему косинусов для треугольника ABC, выражая косинус угла между сторонами AB и AC через длины сторон и значение BM², мы можем найти искомый угол.

Таким образом, применяя вышеуказанные шаги, мы можем находить угол между сторонами треугольника, используя информацию о медиане и длинах сторон.

Практическое применение угла между сторонами

Угол между сторонами имеет множество практических применений в различных областях науки и техники. Ниже приведены некоторые из них:

Область применения	Примеры
Геометрия	Вычисление площади треугольника, нахождение координат вершин многоугольника, определение типа треугольника (остроугольный, тупоугольный, прямоугольный).
Навигация	Определение направления движения объекта по компасу на основе угла северного направления.
Архитектура	Расчёт угла между стенами здания для обеспечения оптимального освещения и воздухообмена.
Физика и механика	Определение угла наклона плоскости, с которой происходит телепортация, для точного вычисления расстояний и времени перемещения.
Инженерия	Разработка угловых датчиков для контроля положения мостов, строительных конструкций и автоматических систем.

Это лишь небольшой перечень примеров использования угла между сторонами. В реальности, угол является основным понятием в геометрии и имеет широкий спектр применений в практически всех научных и технических областях.

Медиана треугольника

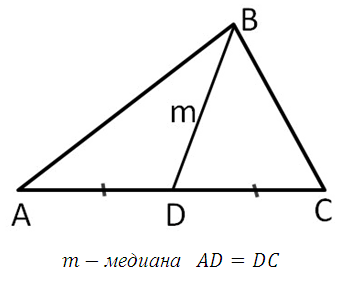
Медианой
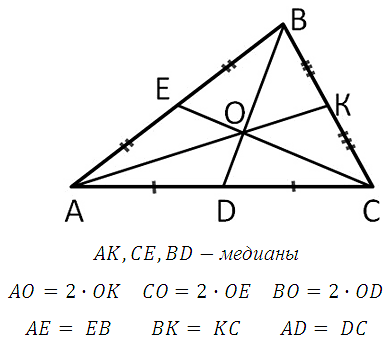
треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны (основанием медианы). Все три медианы треугольника пересекаются в одной точке. Эта точка пересечения делит каждую медиану в отношении 1:2 считая от основания медианы (этот факт следует помнить).

Высота треуголька

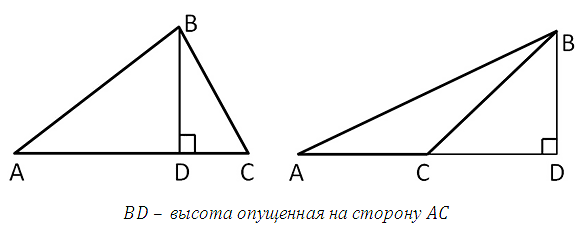
Высотой
треугольника, проведённой из данной вершины, называется перпендикуляр, опущенный из этой вершины на противоположную сторону или её продолжение.

Биссектриса треугольника

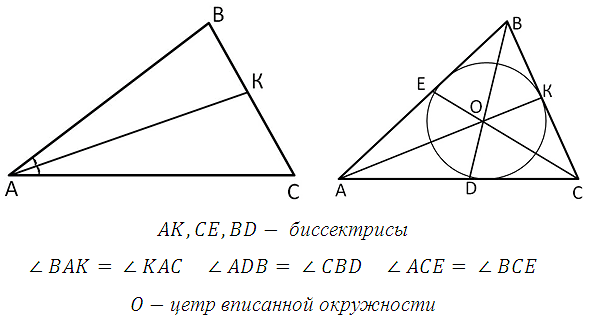
Биссектрисой
треугольника, проведённой из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам. Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности.

В равнобедренном треугольнике биссектриса, медиана и высота, проведённые к основанию, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведённые из одной вершины, совпадают, то треугольник равнобедренный.

Вспомним ещё одну теорему.

Теорема

:
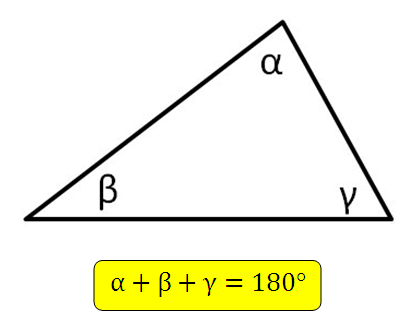
сумма углов треугольника равна 180 градусам

О следующем свойстве нужно сказать отдельно. Только с его помощью можно будетбыстро решить задачи, где речь идёт о медиане в прямоугольном треугольнике. Сначала сам факт:

Медиана в прямоугольном треугольнике, проведённая из

прямого угла к гипотенузе равна её половине

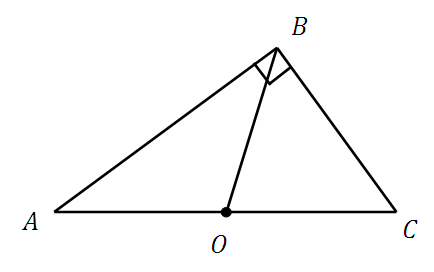
ОВ = 0,5АС АО = ОС = ОВ

То есть, треугольники АОВ и ВОС являются равнобедренными, и углы при их основаниях равны. Эти выводы (об углах) при решении ряда задач крайне необходимы.

Небольшое пояснение. Почему всё-таки медиана в данном случае равна половине гипотенузы? Здесь стоит вспомнить информацию о том, что любой треугольник построенный на диаметре окружности, вершина которого принадлежит этой окружности является прямоугольным, об этом подробно говорилось .

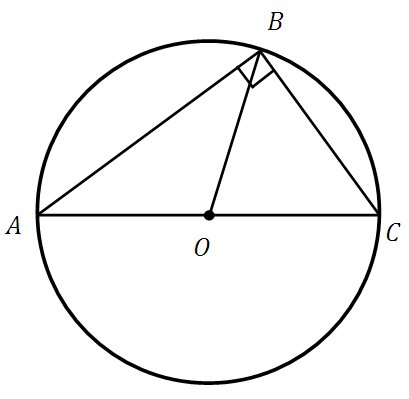
Посмотрите: АО, ОС и ОВ – это радиусы, они у окружности равны. И, конечно же, ОВ будет равно половине АС. Поэтому-то медиана в любом прямоугольном треугольнике проведённая к гипотенузе будет равна её половине.

Примечание
. В данном уроке изложены задачи по геометрии о медиане треугольника. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Почти наверняка курс будет дополнен
.

Задача. Найти угол между высотой и медианой прямоугольного треугольника

Решение
геометрической фигурыобразованной фигуры

Сначала достроим прямоугольный треугольник до прямоугольника.

В результате дополнительного построения катеты прямоугольного треугольника одновременно являются сторонами прямоугольника, а гипотенуза — его диагональю.

Сумма углов треугольника равна 180 градусам
Диагонали прямоугольника в точке пересечения делятся пополам
Диагонали прямоугольника равны

Величина одного из углов треугольника задана в условии задачи. Поскольку треугольник по условию прямоугольный, то мы можем найти величину третьего угла, зная, что сумма углов треугольника равна 180 градусам.

Поскольку угол CAB = 20°, то угол ABC = 180 — 90 — 20 = 70°

Таким образом, мы нашли градусную меру угла B в треугольнике ABC

Рассмотрим треугольник COA. Он равнобедренный, так как его стороны — это половины диагоналей прямоугольника. Это следует из свойств прямоугольника. Так как диагонали прямоугольника равны, а в точке пересечения они делятся пополам, то половины равных отрезков будут также между собой равны. Поскольку в равнобедренном треугольнике углы при основании равны, то:

∠OCA = ∠OAC = 20º

Рассмотрим треугольник BKC. CK является высотой треугольника ABC, проведенной к гипотенузе. Значит угол BKC — прямой, то есть равен 90 градусам, а сам треугольник BKC — прямоугольный. Поскольку треугольник BKC — прямоугольный, то угол BCK = 180 — 90 — 70 = 20°. (Это следует из того, что сумма углов треугольника 180 градусов, угол BKC — прямой, а величину угла B мы нашли ранее)

Поскольку угол BCA — прямой, то его градусная мера равна 90 градусов и, одновременно, равна сумме градусных мер составляющих его углов: BCK, KCO и OCA.

Величину угла BCK мы только что нашли, она составляет 20 градусов, величину угла OCA мы также нашли ранее и она тоже составляет 20 градусов.

Откуда:

20° + 20° + ∠KCO = 90°

∠KCO = 50°

Ответ
: Угол между медианой и биссектрисой заданного прямоугольного треугольника равен 50 градусов.

Аксиомы

Через любую точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну.
Через любую точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную данной, и притом только одну.
Если две прямые параллельны третьей прямой, то эти две прямые параллельны.
Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.
Любые три прямые имеют не более одной общей точки.
Через любую точку проходит более одной прямой.
Через любую точку проходит не менее одной прямой.
Через любые две точки можно провести прямую.
Через любые три точки проходит не более одной прямой.
Через любые три точки проходит не более одной прямой.

Как правильно измерить медиану и высоту

Для определения угла между высотой и медианой треугольника необходимо знать их точные значения. Измерение медианы и высоты может быть выполнено различными способами:

Использование правила Мерсенна

Правило Мерсенна позволяет определить длину медианы, исходя из известных сторон треугольника.

Для определения длины медианы, необходимо использовать формулу:

Медиана = (сторона треугольника) * (√3 / 2)

Полученное значение будет являться длиной медианы.

Использование теоремы Пифагора

Если известны длины сторон треугольника, можно применить теорему Пифагора.

Для определения длины высоты треугольника, необходимо использовать формулу:

Высота = √((a^2) — ((b^2) / 4))

Где a — сторона треугольника, b — медиана.

Использование таблицы значений

В некоторых случаях можно использовать готовую таблицу значений для определения длин медианы и высоты треугольника. В такой таблице перечислены значения медианы и высоты для различных типов треугольников с известными сторонами.

Нужно найти соответствующие значения в таблице и использовать их для определения длин медианы и высоты.

Важно помнить, что для корректного измерения медианы и высоты треугольника необходимо использовать правильные формулы или таблицы значений, а также правильно измерять стороны треугольника. Это поможет получить точные результаты и решить задачу нахождения угла между высотой и медианой

Геометрическое объяснение высоты треугольника

Высота треугольника имеет много важных свойств и применений в геометрии. Одно из основных свойств высоты треугольника заключается в том, что она делит основание на две отрезка пропорционально длинам прилегающих сторон треугольника.

Если длина высоты треугольника известна, можно использовать ее для вычисления площади треугольника. Площадь треугольника можно найти, умножив половину длины основания на длину высоты: Площадь = (1/2) * Основание * Высота.

Геометрическое объяснение высоты треугольника помогает нам лучше понять свойства и применение высоты

Это важное понятие играет важную роль в геометрии и на протяжении истории использовалось для решения различных задач и проблем, связанных с треугольниками

Свойства высоты треугольника

У высоты треугольника есть несколько свойств, которые помогают нам решать геометрические задачи. Рассмотрим некоторые из них:

Свойство 1: Высота треугольника является биссектрисой угла, образованного сторонами треугольника и проведенного к прямой, содержащей эту высоту.

Свойство 2: Высота треугольника делит противоположную сторону на два отрезка, пропорциональных остальным сторонам треугольника. Если высота образует отрезок равный x, то длины пропорциональных отрезков будут равны ax и bx, где a и b — это коэффициенты пропорциональности соответственно.

Свойство 3: Высоты треугольника пересекаются в одной точке — точке пересечения высот. Эта точка называется ортоцентром треугольника.

Использование данных свойств позволяет нам находить различные значения и отношения в треугольниках. Они являются основными инструментами решения задач, связанных с треугольниками.

Зависимость высоты от сторон и углов треугольника

1. Высота треугольника зависит от длины основания и соответствующего ей противоположного угла. Чем больше основание и угол при этом основании, тем длиннее высота.

Если основание треугольника увеличивается, а угол при этом основании остается неизменным, то высота также увеличивается.
Если основание треугольника остается неизменным, а угол при этом основании увеличивается, то высота также увеличивается.

Например, если увеличить основание треугольника и высота при этом основании не изменяется, то высота полученного треугольника будет такой же, как и высота исходного.

2. Высота треугольника зависит также от длины двух других сторон и смежных углов. Чем длиннее эти стороны, тем короче высота.

Если все стороны треугольника увеличиваются пропорционально, то высота также увеличивается.
Если сторона, противоположная углу, увеличивается, а прилежащие к ней стороны остаются неизменными, то высота уменьшается.

Таким образом, высота треугольника зависит от его сторон и углов, и изменение как одного из этих параметров, так и нескольких, может повлиять на её длину.

Примеры решения задач с высотой треугольника

Давайте рассмотрим несколько примеров решения задач с высотой треугольника:

Пример 1:

Дан треугольник ABC, в котором известны длины сторон: AB = 8 см, BC = 10 см и AC = 12 см. Найдите высоту треугольника, опущенную из вершины B.

Решение:

Для начала, найдем площадь треугольника ABC с помощью формулы Герона:

S = √(p(p — AB)(p — BC)(p — AC)), где p — полупериметр треугольника ABC.

В нашем случае, p = (AB + BC + AC) / 2 = (8 + 10 + 12) / 2 = 15.

Теперь, используя формулу площади треугольника S = 1/2 * AB * hB (где hB — высота, опущенная из вершины B), найдем hB:

hB = 2S / AB = 2 * √(15 * (15 — 8)(15 — 10)(15 — 12)) / 8 ≈ 6.71.

Ответ: высота треугольника, опущенная из вершины B, равна примерно 6.71 см.

Пример 2:

Дан равнобедренный треугольник ABC, в котором AB = AC = 6 см, а угол при вершине A равен 60 градусов. Найдите длину высоты, опущенной из вершины A.

Решение:

Так как у нас равнобедренный треугольник, высота, опущенная из вершины A, является биссектрисой угла при вершине A и медианой, проходящей через вершину A.

Используя теорему косинусов, найдем длину медианы MA:

MA = √(2 * AB² + 2 * AC² — BC²) / 2 = √(2 * 6² + 2 * 6² — 6²) / 2 = √(72) / 2 ≈ 4.24.

Теперь, используя свойство высоты, у нас есть два прямоугольных треугольника AMH и MAH, где H — точка пересечения медианы MA и высоты H.

Так как у нас равносторонний треугольник MAH, угол MHА равен 60 градусов. Значит, треугольник AMH — прямоугольный.

Таким образом, в треугольнике AMH, где AM = MA/2 = 4.24/2 = 2.12, МН (высота, опущенная из вершины A) является половиной гипотенузы AM, то есть МН = AM/2 = 2.12/2 = 1.06.

Ответ: длина высоты, опущенной из вершины A, равна примерно 1.06 см.

Надеюсь, эти примеры помогут вам лучше понять, как использовать высоту треугольника для решения задач в геометрии.

Углы

Вертикальные углы равны.
Если угол равен 45°, то вертикальный с ним угол равен 45°.
Если угол равен 108°, то вертикальный с ним равен 108°.
Сумма смежных углов равна 180°.
Если угол равен 60°, то смежный с ним равен 120°.
Если при пересечении двух прямых третьей прямой соответственные углы равны, то эти прямые параллельны.
Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны.
Если при пересечении двух прямых третьей прямой внешние накрест лежащие углы равны, то эти прямые параллельны.
Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна 180°, то эти прямые параллельны.
Если при пересечении двух прямых третьей прямой сумма внешних односторонних углов равна 180°, то эти прямые параллельны.
Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.
Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.
Если при пересечении двух прямых третьей прямой соответственные углы равны 37°, то эти две прямые параллельны.

Треугольники

Сумма углов любого треугольника равна 180° .
Сторона треугольника меньше суммы двух других сторон данного треугольника. (неравенство треугольника)
Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. (1 признак равенства треугольников)
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. (2 признак равенства треугольников)
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. (3 признак равенства треугольников)
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. (1 признак подобия треугольников)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны. (2 признак подобия треугольников)
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. (3 признак подобия треугольников)
Напротив равных углов лежат равные стороны.
Если два угла треугольника равны, то равны и противолежащие им стороны.
Площадь треугольника равна полупроизведению стороны на высоту, проведенную к этой стороне.
Площадь треугольника равна полупроизведению двух сторон треугольника на синус угла между ними.
Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, является медианой (то есть делит основание на две равные части) и высотой (перпендикулярна основанию).
Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
В прямоугольном треугольнике катет, лежащий напротив угла 30° равен половине гипотенузы.
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине этой гипотенузы.
Площадь прямоугольного треугольника меньше произведения его катетов.
Площадь прямоугольного треугольника равна половине произведения его катетов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. (теорема косинусов).
Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.
Стороны треугольника пропорциональны синусам противолежащих углов. (теорема синусов)
Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
Один из углов треугольника всегда не превышает 60°.
Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности.
Биссектрисы треугольника пересекаются в центре его вписанной окружности.

Полезные советы при нахождении угла

Нахождение угла между высотой и медианой треугольника может быть сложной задачей, но с помощью следующих советов вы сможете ее решить:

Изучите основные определения: перед тем, как начать решать задачу, необходимо понимать основные определения, связанные с треугольниками, такие как медиана, высота и угол. Убедитесь, что вы знаете, как эти понятия связаны друг с другом.
Используйте свойства треугольников: воспользуйтесь свойствами треугольников для нахождения отношений между сторонами и углами. Например, вы можете использовать теорему косинусов или теорему синусов.
Учтите, что высота и медиана делят треугольник пополам: помните, что высота и медиана делят треугольник на две равные части. Используйте эту информацию для определения связи между углом и отрезками высоты и медианы.
Используйте таблицу: создайте таблицу, в которой приведены известные вам данные, такие как значения сторон, углов и отрезков. Это поможет вам наглядно представить информацию и облегчит анализ задачи.
Пользуйтесь геометрическими построениями: при необходимости используйте геометрические построения, чтобы визуализировать задачу. Нарисуйте треугольник и отметьте на нем высоту и медиану, чтобы лучше понять ситуацию.

Следуя этим советам, вы сможете эффективно находить углы между высотой и медианой треугольника. Знание основных определений и свойств треугольников, а также использование геометрических построений и таблиц, поможет вам разобраться в подобных задачах.