Описанная окружность (егэ 2022)

Связь описанной окружности со вписанной окружностью, с ортоцентром и другими точками[править | править код]

Или через стороны треугольника:

d=OI=Ra3−a2b−ab2+b3−a2c+3abc−b2c−bc2−ac2+c3abc{\displaystyle d=OI=R{\sqrt {\frac {a^{3}-a^{2}b-ab^{2}+b^{3}-a^{2}c+3abc-b^{2}c-bc^{2}-ac^{2}+c^{3}}{abc}}}},

где R{\displaystyle R} — радиус описанной окружности (см. Окружность Фурмана).

Расстояние от центра O до ортоцентра H есть:p. 449

OH=R2−8R2cos⁡Acos⁡Bcos⁡C=9R2−(a2+b2+c2).{\displaystyle OH={\sqrt {R^{2}-8R^{2}\cos A\cos B\cos C}}={\sqrt {9R^{2}-(a^{2}+b^{2}+c^{2})}}.}

Для центроида G и центра девяти точек N имеем:

IG<IO,{\displaystyle IG<IO,}

2IN<IO,{\displaystyle 2IN<IO,}

OI2=2R⋅IN.{\displaystyle OI^{2}=2R\cdot IN.}

Произведение радиусов описанной и вписанной окружностей треугольника связано со сторонами a, b и c в виде: p. 189, #298(d):

rR=abc2(a+b+c).{\displaystyle rR={\frac {abc}{2(a+b+c)}}.}

Отношение радиусов вписанной и описанной окружностей треугольника :

rR=4S2pabc=cos⁡α+cos⁡β+cos⁡γ−1{\displaystyle {\frac {r}{R}}={\frac {4S^{2}}{pabc}}=\cos \alpha +\cos \beta +\cos \gamma -1}.

Если медиана m, высота h и внутренняя биссектриса t выходят из одной и той же вершины треугольника, около которого описана окружность радиуса R, тогда:p.122,#96

4R2h2(t2−h2)=t4(m2−h2).{\displaystyle 4R^{2}h^{2}(t^{2}-h^{2})=t^{4}(m^{2}-h^{2}).}

• Центр описанной окружности изогонально сопряжён с ортоцентром.
• Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности.
• В треугольнике есть три окружности, которые касаются двух сторон треугольника и описанной окружности. Такие окружности называют полувписанными или окружностями Веррьера. Отрезки, соединяющие вершины треугольника и соответствующие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке, называемой точкой Веррьера. Она служит центром гомотетии, которая переводит описанную окружность во вписанную. Точки касания окружностей Веррьера со сторонами лежат на прямой, которая проходит через центр вписанной окружности.

Полувписанная окружность

Теорема Тебо 3 утверждает (см. рис.):

Теорема Тебо 3

Пусть ABC{\displaystyle ABC} — произвольный треугольник, D{\displaystyle D} — произвольная точка на стороне BC{\displaystyle BC}, I1{\displaystyle I_{1}} — центр окружности, касающейся отрезков AD,BD{\displaystyle AD,BD} и описанной около ΔABC{\displaystyle \Delta ABC} окружности, I2{\displaystyle I_{2}} — центр окружности, касающейся отрезков CD,AD{\displaystyle CD,AD} и описанной около ΔABC{\displaystyle \Delta ABC} окружности. Тогда отрезок I1I2{\displaystyle I_{1}I_{2}} проходит через точку I{\displaystyle I} — центр окружности, вписанной в ΔABC{\displaystyle \Delta ABC}, и при этом I1III2=tg2⁡ϕ2{\displaystyle I_{1}I:II_{2}=\operatorname {tg} ^{2}{\frac {\phi }{2}}}, где ϕ=∠BDA{\displaystyle \phi =\angle BDA}.

Формула Карно утверждает, что в треугольнике ABC сумма расстояний от центра D описанной окружности до сторон треугольника ABC, взятых со знаком «-», когда высота из D на сторону целиком лежит вне треугольника (иначе со знаком «+»), будет равна R+r{\displaystyle R+r}, где r и R — радиусы вписанной и описанной окружностей:p.83.

Формула Карно: DG+DH−DF=R+r{\displaystyle DG+DH-DF=R+r}

Например для рисунка формула Карно примет вид: DG+DH−DF=R+r{\displaystyle DG+DH-DF=R+r}.

В другой формулировке формула Карно утверждает, что:

R+r=ka+kb+kc=12(dA+dB+dC),{\displaystyle R+r=k_{a}+k_{b}+k_{c}={\frac {1}{2}}(d_{A}+d_{B}+d_{C}),}

где ka,kb,kc{\displaystyle k_{a},k_{b},k_{c}} — расстояния от центра описанной окружности соответственно до сторон a,b,c{\displaystyle a,b,c} треугольника,
dA,dB,dC{\displaystyle d_{A},d_{B},d_{C}} — расстояния от ортоцентра соответственно до вершин A,B,C{\displaystyle A,B,C} треугольника.

Расстояние от центра описанной окружности например до стороны a{\displaystyle a} треугольника равно:

ka=a(2tgA);{\displaystyle k_{a}=a/(2tgA);}

расстояние от ортоцентра например до вершины A{\displaystyle A} треугольника равно:

dA=2ka=a(tgA).{\displaystyle d_{A}=2k_{a}=a/(tgA).}

Как найти радиус описанной окружности – треугольник

Произвольный треугольник

• Чтобы определить радиус окружности, описывающей треугольник, достаточно знать величину его сторон.
  R = m*l*k/4√p(p – m)*(p – l)*(p – k),
  p = (m + l + k)/2,
  m, l, k – стороны треугольника.
• Если известна длина стороны и градусная мера угла ей противолежащего, то радиус определяется следующим образом:
  Для треугольника MLK
  R = m/2sinM = l/2sinL = k/2sinK,
  M, L, K – его углы (вершины).
• При наличии площади фигуры также можно вычислить радиус окружности, в которую она помещена:
  R = m*l*k/4S,
  m, l, k – стороны треугольника,
  S – его площадь.

Равнобедренный треугольник

Если треугольник равнобедренный, то 2 его стороны равны между собой. При описывании такой фигуры радиус можно найти по такому соотношению:
R = m*l*k/4√p(p – m)*(p – l)*(p – k), но m = l
R = m 2 /√(4m 2 – k 2),
m, k – стороны треугольника.

Прямоугольный треугольник

Если один из углов треугольника прямой, а около фигуры описана окружность, то для определения длины радиуса последней потребуется наличие известных сторон треугольника.
R = (√m 2 + l 2)/2 = k/2,
m, l – катеты,
k – гипотенуза.

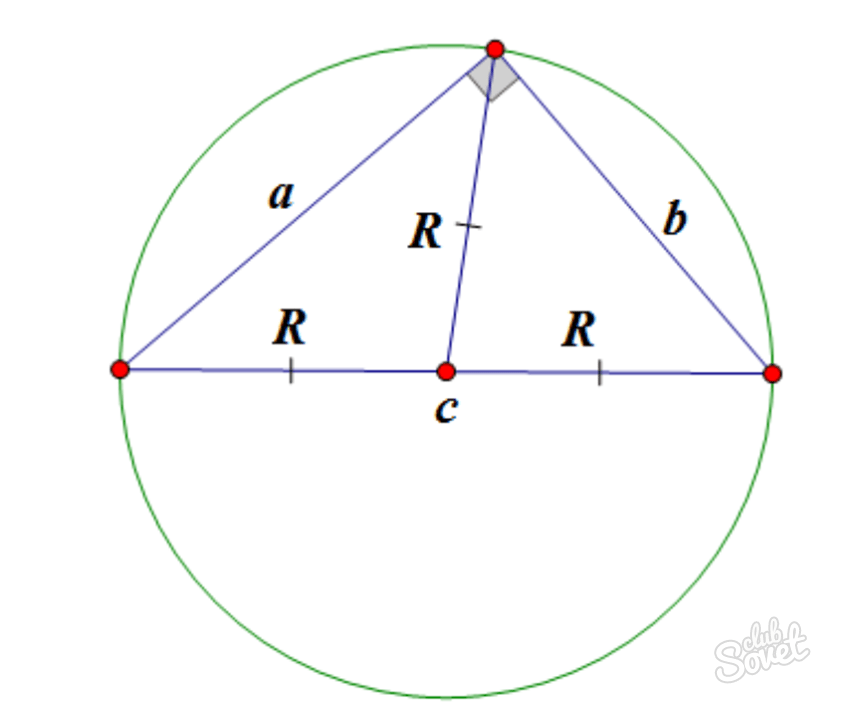
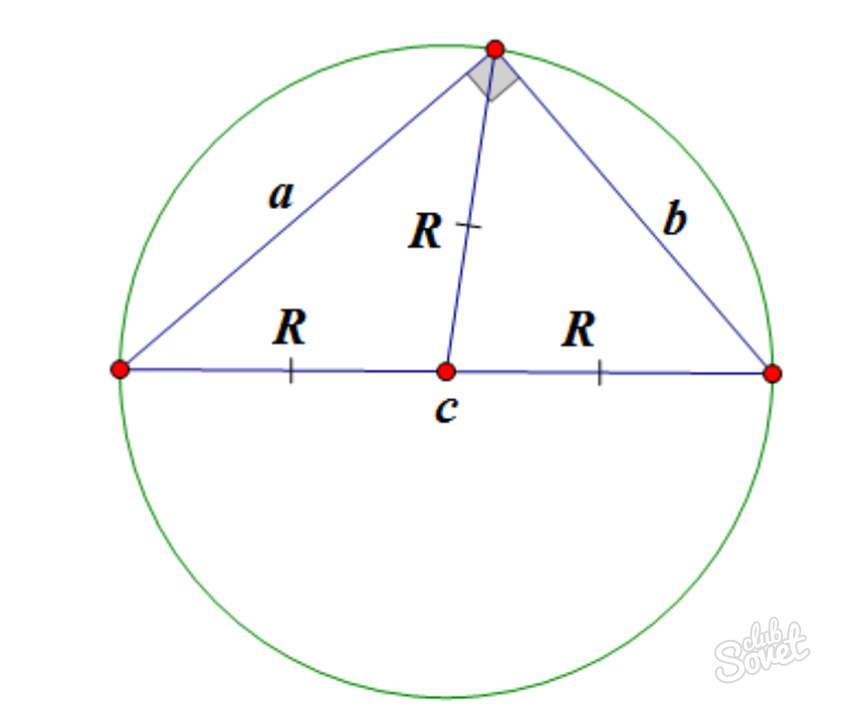
Как найти радиус окружности? Этот вопрос всегда актуален для школьников, изучающих планиметрию. Ниже мы рассмотрим несколько примеров того, как можно справиться с поставленной задачей.

В зависимости от условия задачи радиус окружности вы можете найти так.

Формула 1: R = Л / 2π, где Л — это а π — константа, равная 3,141…

Формула 2: R = √(S / π), где S — это величина площади круга.

Формула 1: R = В/2, где В — гипотенуза.

Формула 2: R = М*В, где В — гипотенуза, а М — медиана, проведенная к ней.

Как найти радиус окружности, если она описана вокруг правильного многоугольника

Формула: R = А / (2 * sin (360/(2*n))), где А — длина одной из сторон фигуры, а n — количество сторон в данной геометрической фигуре.

Как найти радиус вписанной окружности

Вписанной окружность называется тогда, когда она касается всех сторон многоугольника. Рассмотрим несколько примеров.

Формула 1: R = S / (Р/2), где — S и Р — площадь и периметр фигуры соответственно.

Формула 2: R = (Р/2 — А) * tg (а/2), где Р — периметр, А — длина одной из сторон, а — противолежащий этой стороне угол.

Как найти радиус окружности, если она вписана в прямоугольный треугольник

Формула 1:

Радиус окружности, которая вписана в ромб

Формула 1: R = 2 * Н, где Н — это высота геометрической фигуры.

Формула 2: R = S / (А*2), где S — это а А — длина его стороны.

Формула 3: R = √((S * sin А)/4), где S — это площадь ромба, а sin А — синус острого угла данной геометрической фигуры.

Формула 4: R = В*Г/(√(В² + Г²), где В и Г — это длины диагоналей геометрической фигуры.

Формула 5: R = В*sin (А/2), где В — диагональ ромба, а А — это угол в вершинах, соединяющих диагональ.

Радиус окружности, которая вписана в треугольник

В том случае, если в условии задачи вам даны длины всех сторон фигуры, то сначала высчитайте (П), а затем полупериметр (п):

П = А+Б+В, где А, Б, В — длин сторон геометрической фигуры.

Формула 1: R = √((п-А)*(п-Б)*(п-В)/п).

А если, зная все те же три стороны, вам дана еще и то можете рассчитать искомый радиус следующим образом.

Формула 2: R = S * 2(А + Б + В)

Формула 3: R = S/п = S / (А+Б+В)/2), где — п — это полупериметр геометрической фигуры.

Формула 4: R = (п — А) * tg (А/2), где п — это полупериметр треугольника, А — одна из его сторон, а tg (А/2) — тангенс половины противолежащего этой стороне угла.

А ниже приведенная формула поможет отыскать радиус той окружности, которая вписана в

Формула 5: R =А * √3/6.

Радиус окружности, которая вписана в прямоугольный треугольник

Если в задаче даны длины катетов, а также гипотенуза, то радиус вписанной окружности узнается так.

Формула 1: R = (А+Б-С)/2, где А, Б — катеты, С — гипотенуза.

В том случае, если вам даны только два катета, самое время вспомнить теорему Пифагора, чтобы гипотенузу найти и воспользоваться вышеприведенной формулой.

С = √(А²+Б²).

Радиус окружности, которая вписана в квадрат

Окружность, которая вписана в квадрат, делит все его 4 стороны ровно пополам в точках касания.

Формула 1: R = А/2, где А — длина стороны квадрата.

Формула 2: R = S / (Р/2), где S и Р — площадь и периметр квадрата соответственно.

Определение 2

Многоугольник, удовлетворяющий условию определения 1, называется описанным около окружности.

Рисунок 1. Вписанная окружность

Примечания[править | править код]

1. ↑
2. ↑
3. . Дата обращения: 29 апреля 2016.
4. , . Геометрические свойства кривых второго порядка. — 2-е изд., дополн.. — 2011. — С. 110.
5. , . Геометрические свойства кривых второго порядка. — 2-е изд., дополн.. — 2011. — С. 27—28.
6. ↑ , с. 175–209.
7. ↑ Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.: Учпедгиз, 1962. задача на с. 120—125. параграф 57, с.73.
8. (21 января 2017). Дата обращения: 22 июня 2020.  (англ.)
9. Smith, Geoff, and Leversha, Gerry, «Euler and triangle geometry», Mathematical Gazette 91, November 2007, 436—452.
10. Johnson, Roger A., Advanced Euclidean Geometry, Dover, 2007 (orig. 1929).
11. Longuet-Higgins, Michael S., «On the ratio of the inradius to the circumradius of a triangle», Mathematical Gazette 87, March 2003, 119—120.
12. ↑ Altshiller-Court, Nathan, College Geometry, Dover, 2007.
13. Мякишев А. Г. Элементы геометрии треугольника. Серия: «Библиотека „Математическое просвещение“». М.:МЦНМО,2002. c. 11, п. 5.
14. . Дата обращения: 15 марта 2009.
15. Стариков В. Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические науки: сборник научных трудов. Выпуск 1/ Гл. ред. Романова И. В. Чебоксары: ЦДИП «INet», 2014. С. 37-39
16. Здесь радиус окружности измеряется по сфере, то есть представляет собой градусную меру дуги большого круга, соединяющей точку пересечения радиуса сферы, проведённого из центра сферы через центр окружности, со сферой и вершину треугольника.
17. ↑ Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — 154 с.

Определения и свойства окружности

Введем несколько определений, связанных с темой окружности. Данные термины можно встретить на уроках в седьмом классе и других курсах по алгебре и геометрии.

1 Примечание 1

В распространенных случаях возникает путаница в понятиях окружности и круга. Заметим, что кругом может называться множество точек на плоскости, которые при построении ограничены окружностью, то есть данные точки расположены во внутренней области окружности.

Окружность обладает рядом свойств:

1. Если три точки на плоскости не принадлежат общей прямой, то через них допустимо построить единственную окружность.
2. Точка (С), в которой касаются две окружности, расположена на общей с центрами этих окружностей прямой (АВ).
3. Изопериметрическое неравенство: из всех замкнутых кривых на графике, имеющих одинаковую длину, окружность ограничивает область с максимальной площадью.

При решении самостоятельных работ и задач на некоторые окружности пригодятся следующие формулы, чтобы находить ключевые параметры:

Диаметр окружности можно высчитать таким образом:

Длина окружности в теории:

Радиус окружности можно узнать с помощью формулы:

Свойства треугольника

Сумма углов треугольника

Углы треугольника — это углы между его сторонами. Сумма углов треугольника всегда равна 180 градусам. Следовательно, если мы знаем два угла треугольника, мы всегда можем найти третий угол, вычитая сумму двух из 180.

Стороны треугольника и их соотношения

Стороны треугольника — это отрезки, соединяющие его вершины. В зависимости от соотношения длин сторон, треугольникы бывают разных типов:

• Равносторонний треугольник имеет три равные стороны;
• Равнобедренный треугольник имеет две равные стороны;
• Разносторонний треугольник имеет три разные стороны.

Площадь треугольника

Площадь треугольника — это мера его плоской фигуры, выражающая площадь заключенную между всеми его сторонами. Существует несколько формул для нахождения площади треугольника в зависимости от известных данных:

• Площадь треугольника можно найти, зная длины двух его сторон и угол между ними;
• При известной высоте треугольника и одной его стороне, площадь равна половине произведения этих величин;
• Если известны длины всех трех сторон, то для нахождения площади нужно использовать формулу Герона.

Примеры расчета диаметра описанной около треугольника окружности

Рассмотрим несколько примеров расчета диаметра окружности, описанной вокруг треугольника:

• Пример 1: Дан треугольник со сторонами 6, 8 и 10. Найдем диаметр окружности, описанной вокруг него.
• Решение: Используем формулу: d = a * sin(A) + b * sin(B) + c * sin(C), где d — диаметр, a, b, c — стороны треугольника, A, B, C — соответствующие углы. В нашем случае:
• d = 6 * sin(36,87°) + 8 * sin(53,13°) + 10 * sin(90°) ≈ 11,31
• Ответ: диаметр окружности ≈ 11,31

• Пример 2: Дан равнобедренный треугольник со стороной 5 и основанием 8. Найдем диаметр окружности, описанной вокруг него.
• Решение: Используем формулу: d = (a * √2) / 2, где d — диаметр, a — основание треугольника. В нашем случае:
• d = (8 * √2) / 2 = 4 * √2
• Ответ: диаметр окружности = 4 * √2

• Пример 3: Дан прямоугольный треугольник со сторонами 3, 4 и 5. Найдем диаметр окружности, описанной вокруг него.
• Решение: Используем формулу: d = c, где d — диаметр, c — гипотенуза треугольника. В нашем случае:
• d = 5
• Ответ: диаметр окружности = 5

Таким образом, расчет диаметра окружности, описанной вокруг треугольника, может осуществляться разными способами, в зависимости от данных о треугольнике.

Серединный перпендикуляр к отрезку

Определение 1
. Серединным перпендикуляром к отрезку
называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Теорема 1
. Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов

этого отрезка.

Доказательство
. Рассмотрим произвольную точку D
, лежащую на серединном перпендикуляре к отрезку AB
(рис.2), и докажем, что треугольники ADC
и BDC
равны .

Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC
и BC
равны, а катет DC
является общим. Из равенства треугольников ADC
и BDC
вытекает равенство отрезков AD
и DB
. Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1)
. Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

Доказательство
. Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E
находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E
и A
лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA
пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D
.

Докажем, что отрезок AE
длиннее отрезка EB
. Действительно,

Таким образом, в случае, когда точки E
и A
лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Теперь рассмотрим случай, когда точки E
и A
лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB
длиннее отрезка AE
. Действительно,

Полученное противоречие и завершает доказательство теоремы 2

Формулы

Радиус вписанной окружности в треугольник

1. Радиус вписанной окружности в треугольник, если известна площадь и все стороны:

Радиус вписанной окружности в треугольник, если известны площадь и периметр:

Радиус вписанной окружности в треугольник, если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

1. Радиус описанной окружности около треугольника, если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника, если известны все стороны и площадь:

Радиус описанной окружности около треугольника, если известны все стороны и полупериметр:

Площадь треугольника

1. Площадь треугольника вписанного в окружность, если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность, если известен полупериметр:

Площадь треугольника вписанного в окружность, если известен высота и основание:

Площадь треугольника вписанного в окружность, если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность, если известны две стороны и синус угла между ними:

\

Периметр треугольника

1. Периметр треугольника вписанного в окружность, если известны все стороны:

Периметр треугольника вписанного в окружность, если известна площадь и радиус вписанной окружности

Периметр треугольника вписанного в окружность, если известны две стороны и угол между ними:

Сторона треугольника

1. Сторона треугольника вписанного в окружность, если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в окружность, если известна сторона и два угла:

Средняя линия треугольника

1. Средняя линия треугольника вписанного в окружность, если известно основание:

Средняя линия треугольника вписанного в окружность, если известныдве стороны, ни одна из них не является основанием, и косинус угламежду ними

Высота треугольника

1. Высота треугольника вписанного в окружность, если известна площадь и основание:

Высота треугольника вписанного в окружность, если известен сторона и синус угла прилежащего к этой стороне, и находящегося напротив высоты:

\

Высота треугольника вписанного в окружность, если известен радиус описанной окружности и две стороны, ни одна из которых не является основанием:

Взаимное отношение хорд и их расстояний от центров

Изобразим окружность и ее элементы, согласно теореме:

Заметим, что радиус, обозначенный, как OC, расположен перпендикулярно к хорде AB, как показано на рисунке:

.

Попробуем доказать следующее:

.

Проведем прямую через точки А и В, которая соединит их с центральной точкой О. Заметим, что наклонные OA и OB равны и удалены от перпендикулярной прямой ОС. В результате:

AD = DB.

Предположим, что перпендикулярная прямая CD выходит из середины AB. В таком случае, точка C равноудалена относительно концов перпендикуляра. Из этого следует равенство хорд AC и CB. Таким образом:

.

Получаем, что перпендикуляр OC делит на две равные части дугу AB, что и требовалось доказать.

Начнем доказательство данного утверждения с того, что центральная точка равноудалена от концов хорды. В таком случае, она будет расположена на перпендикуляре, который восстановлен из середины хорды, что и требовалось доказать.

Перенесем данные на рисунок:

Запишем равенство двух хорд AB и CD:

AB = CD

Представим доказательство того, что данные хорды расположены на одинаковом расстоянии от центральной точки:

OE = OF

Если соединить между собой точки A и C, а также центральную точку O, получим пару треугольников AEO и COF, которые равны и являются прямоугольными. Объясним это равенством радиусов:

OA = OC.

Заметим также, что половины одинаковых хорд будут равны друг другу:

AE = CF.

В результате получим доказательство теоремы:

OE = = OF.

Воспользуемся предыдущим рисунком. Запишем, что хорды AB и CDравноудалены от центра:

OE = OF.

Попробуем подтвердить справедливость следующего равенства:

AB = CD.

Рассмотрим пару прямоугольных треугольников AEO и COF. Данные треугольники равны, исходя из равенства гипотенуз и катетов. Согласно условию:

OE = OF

Равенство радиусов:

OA = OC.

В результате получим, что:

AE = CF

Таким образом, теорема доказана:

AB = CD

Заметим, что хорда AB больше по сравнению с хордой AC:

AB > AC

Требуется доказать следующее:

OD < OE

Заметим, что OD расположен перпендикулярно относительно AB. Линия OF является наклонной. В таком случае:

OD < OF

Запишем, что:

OF < OE

В результате теорема доказана:

OD < OE

Типы заданий по СтатГраду с краткими ответами

Касательная, хорда, секущая, радиус

1. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 3, BC = 72. Найдите AK .

Ответ:

15

2. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 8, BC = 24. Найдите AK .

Ответ:

16

3. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 5, BC =15. Найдите AK.

Ответ:

10

4. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 2, BC =16. Найдите AK.

Ответ:

6

5. На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC . Ответ дайте в градусах.

Ответ:

36

6. На окружности отмечены точки A и B так, что меньшая дуга AB равна 92°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Ответ:

46

7. На окружности отмечены точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC . Ответ дайте в градусах.

Ответ:

28

8. На окружности отмечены точки A и B так, что меньшая дуга AB равна 152° . Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Ответ:

76

Центральные и вписанные углы

9. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 113°. Ответ дайте в градусах.

Ответ:

56,5

10. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 59°. Ответ дайте в градусах.

Ответ:

29,5

11. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 167°. Ответ дайте в градусах.

Ответ:

83,5

12. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 47°. Ответ дайте в градусах.

Ответ:

23,5

13. В угол C величиной 157° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.

Ответ:

23

14. В угол C величиной 18° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.

Ответ:

162

15. В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.

Ответ:

97

16. В угол C величиной 133° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.

Ответ:

47

Окружность, описанная вокруг многоугольника

17. Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.

Ответ:

9

18. Радиус окружности, описанной около равностороннего треугольника, равен 18. Найдите высоту этого треугольника.

Ответ:

27

19. Угол A трапеции ABCD с основаниями AD и BC , вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.

Ответ:

148

20. Угол A трапеции ABCD с основаниями AD и BC , вписанной в окружность, равен 81°. Найдите угол C этой трапеции. Ответ дайте в градусах.

Ответ:

99

21. Радиус окружности, описанной около квадрата, равен 16√2 . Найдите длину стороны этого квадрата.

Ответ:

32

22. Радиус окружности, описанной около квадрата, равен 28√2 . Найдите длину стороны этого квадрата.

Ответ:

56

23. Угол A четырёхугольника ABCD, вписанного в окружность, равен 112° . Найдите угол C этого четырёхугольника. Ответ дайте в градусах.

Ответ:

68

24. Угол A четырёхугольника ABCD, вписанного в окружность, равен 56° . Найдите угол C этого четырёхугольника. Ответ дайте в градусах.

Ответ:

124

25. Четырёхугольник ABCD описан около окружности, AB =12, BC = 6, CD =13. Найдите AD.

Ответ:

19

26. Четырёхугольник ABCD описан около окружности, AB =11, BC = 7, CD =12. Найдите AD.

Ответ:

16

27. Угол A четырёхугольника ABCD , вписанного в окружность, равен 37° . Найдите угол C этого четырёхугольника. Ответ дайте в градусах.

Ответ:

143

Способы расчета радиуса описанной окружности

Существуют различные способы расчета радиуса описанной окружности около треугольника, в зависимости от того, какие данные у нас есть.

Использование теорем

Существуют несколько теорем, которые помогают вычислить радиус описанной окружности в зависимости от известных параметров треугольника. Рассмотрим некоторые из них:

1. Теорема о центральном угле

Если мы знаем меру центрального угла, образованного двумя радиусами описанной окружности и стороной треугольника, то радиус описанной окружности можно вычислить по формуле:

R = (a / 2) * (1 / sin α),

где a – длина стороны треугольника, α – мера центрального угла.

2. Теорема синусов

Если мы знаем длины двух сторон треугольника и меру угла между ними, то радиус описанной окружности можно вычислить по формуле:

R = (a * b * c) / (4S),

где a, b и c – длины сторон треугольника, S – площадь треугольника.

3. Теорема косинусов

Если мы знаем длины всех трех сторон треугольника, то радиус описанной окружности можно вычислить по формуле:

R = (a * b * c) / (4S),

где a, b и c – длины сторон треугольника, S – площадь треугольника.

Примеры решения задач

Рассмотрим несколько примеров решения задач, связанных с вычислением радиуса описанной окружности.

Пример 1. Вычисление радиуса описанной окружности по теореме о центральном угле.

Дано: треугольник ABC, в котором AB = 6 см, BC = 8 см, угол BAC = 60°.

Решение:

1. Найдем длину стороны AC с помощью теоремы косинусов:

AC² = AB² + BC² – 2AB * BC * cos BAC AC² = 6² + 8² – 2 * 6 * 8 * cos 60° AC² = 100 AC = 10 см

2. Найдем меру центрального угла α:

α = 2 * arcsin (a / 2R) α = 2 * arcsin (5 / R)

3. Подставим известные значения в формулу для вычисления радиуса описанной окружности:

R = (a / 2) * (1 / sin α) R = (5 / sin α)

4. Пример 2. Вычисление радиуса описанной окружности по теореме синусов.

Дано: треугольник ABC, в котором AB = 5 см, BC = 7 см, угол BAC = 45°.

Решение:

1. Найдем длину стороны AC с помощью теоремы косинусов:

AC² = AB² + BC² – 2AB * BC * cos BAC AC² = 5² + 7² – 2 * 5 * 7 * cos 45° AC² = 24 AC = 2√6 см

2. Найдем площадь треугольника с помощью формулы Герона:

p = (AB + BC + AC) / 2 = (5 + 7 + 2√6) / 2 p = (12 + 2√6) / 2 = 6 + √6 S = √(p(p-AB)(p-BC)(p-AC)) S = √((6+√6)(6-5)(6-7)(6-2√6)) S = √(6√6 – 18) S = √6 * √(6 – 3√2)

3. Выразим радиус описанной окружности через длины сторон и площадь треугольника:

R = (a * b * c) / (4S) R = (5 * 7 * 2√6) / (4√6 * √(6 – 3√2)) R = (35 / (8√2 – 12))

Таким образом, радиус описанной окружности для данного треугольника равен (35 / (8√2 – 12)).

Часто задаваемые вопросы

Вопрос 1: Что такое радиус описанной окружности?

Ответ: Радиус описанной окружности – это расстояние от центра окружности до любой точки на ее окружности. Для треугольника радиус описанной окружности проходит через вершины треугольника и называется описанным радиусом.

Вопрос 2: Зачем нужно вычислять радиус описанной окружности?

Ответ: Вычисление радиуса описанной окружности является важным шагом в решении многих задач, связанных с треугольниками. Например, радиус описанной окружности позволяет определить длины сторон и углы треугольника, а также находить центр описанной окружности и другие параметры фигур.

Заключение

Вычисление радиуса описанной окружности – это важный шаг в решении задач, связанных с треугольниками. Для вычисления радиуса описанной окружности существуют различные формулы и теоремы, которые могут быть использованы в зависимости от известных данных о треугольнике. Например, для вычисления радиуса описанной окружности можно использовать теорему описанной окружности, формулу площади треугольника и длину его сторон, или теорему синусов.

Важно помнить, что вычисление радиуса описанной окружности является лишь одним из шагов в решении задач, связанных с треугольниками, и может быть использовано в сочетании с другими методами и формулами. Кроме того, для правильного вычисления радиуса описанной окружности необходимо точно знать данные о треугольнике и уметь применять соответствующие формулы и теоремы

Надеемся, что данная статья помогла вам лучше понять, как вычисляется радиус описанной окружности около треугольника, и какие формулы и теоремы могут быть использованы для этого.