Как убедиться в том, что треугольник является тупоугольным: методы и признаки

Применение конгруэнтности и Подобие треугольников

Соответствие и подобие треугольников имеют практическое применение в различных областях, таких как архитектура, инженерия и графический дизайн. Например, архитекторы используют конгруэнтность и сходство, чтобы убедиться, что разные части здания пропорциональны и идеально подходят друг к другу. Инженеры используют свойства треугольников для расчета устойчивости и прочности конструкций, таких как мосты и небоскребы. Графические дизайнеры используют принципы сходства и симметрии для создания гармоничных и визуально приятных макетов и композиций.

Понятия конгруэнтности и подобия треугольников также имеют образовательное значение, поскольку они развивают навыки критического мышления, решения проблем, и логические рассуждения. Они помогают учащимся развивать пространственное мышление, навыки визуализации и понимание красоты и симметрии геометрических фигур. Усвоив эти понятия, учащиеся смогут лучше разбираться в математике и применять свои знания к другим предметам и реальным ситуациям.

Сходства треугольников	Конгруэнтность треугольников
Треугольники с одинаковыми углами	Треугольники одинаковой формы и размера
Постулаты подобия AA (угол-угол) или SSS (сторона-сторона-сторона) могут быть использованы для доказательства сходства	SSS (сторона-сторона-сторона), SAS (сторона-угол-сторона) , и постулаты конгруэнтности ASA (Angle-Side-Angle) можно использовать для доказательства конгруэнтности
Подобные треугольники имеют соответствующие стороны в одинаковом соотношении	Конгруэнтные треугольники имеют соответствующие стороны и углы, равные по размеру

В целом, понятия конгруэнтности и подобия треугольников необходимы для изучения геометрии и имеют множество приложений и практических использует в различных областях. Понимая эти концепции и осваивая свойства треугольников, мы можем улучшить наше понимание мира природы и оценить красоту и симметрию математических фигур.

Определение геометрии

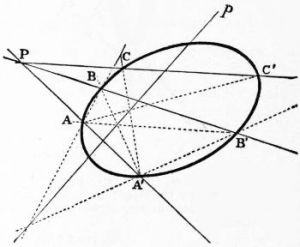
пример сложной геометрической задачи

Название «геометрия» происходит от греческих слов «гео» — земля и «метрео» — измеряю. Геометрия берёт свое начало именно с измерений на земле, вычисления площади плодородных участков. Также астрологи рассчитывали расположение различных небесных объектов и светил.

Геометрия не есть изолированная отрасль, не пересекающаяся с другими разделами математики. Дело состоит ровно наоборот. Многие задачи из алгебры, арифметики, математического анализа, теории дифференциальных уравнений, теоретической механики решаются как раз при помощи построений на плоскости и в пространстве, то есть путём применения геометрических методов. Более того, огромная часть уравнений решается геометрическим способом путем построений фигур или графиков функций.

Базовыми объектами в геометрии являются «точка», «луч», «прямая», «отрезок», «плоскость», «угол» и «фигура». Со своей стороны геометрия использует инструментарий алгебры и теории уравнений. Многие геометрические задачи на нахождение элементов фигур и площадей решаются путем сведения их к уравнениям. Геометрия также имеет дело и с числами, как и любая другая часть математики.

Треугольник Дали — что это?

Многие, столкнувшись с этим понятием, сначала думают, что это какое-то определение в геометрии, но это совсем не так. Треугольник Дали — это общее название трех мест, которые тесно связаны с жизнью знаменитого художника. «Вершинами» его являются дом, в котором Сальвадор Дали жил, замок, который он подарил своей жене, а также музей сюрреалистических картин. Во время экскурсии по этим местам можно узнать много интереснейших фактов об этом своеобразном креативном художнике, известном во всем мире.

Пожалуй, самой основной, простой и интересной фигурой в геометрии является треугольник. В курсе средней школы изучаются его основные свойства, однако иногда знания по этой теме формируются неполными. Виды треугольников изначально определяют их свойства. Но подобное представление остается смешанным. Поэтому сейчас разберем немного подробнее эту тему.

Виды треугольников зависят от градусной меры углов. Эти фигуры бывают остро-, прямо- и тупоугольными. Если все углы не превышают значения в 90 градусов, то фигуру смело можно назвать остроугольной. Если хотя бы один угол треугольника равен 90 градусам, то вы имеете дело с прямоугольным подвидом. Соответственно, во всех остальных случаях рассматриваемую называют тупоугольной.

Существует множество задач для остроугольных подвидов. Отличительной чертой является внутреннее местонахождение точек пересечения биссектрис, медиан и высот. В других случаях это условие может не выполняться. Определить тип фигуры “треугольник” нетрудно. Достаточно знать, например, косинус каждого угла. Если какие-нибудь значения меньше нуля, значит, треугольник в любом случае является тупоугольным. В случае нулевого показателя фигура обладает прямым углом. Все положительные значения гарантированно подскажут вам о том, что перед вами остроугольный вид.

Нельзя не сказать о правильном треугольнике. Это самый идеальный вид, где совпадают все точки пересечения медиан, биссектрис и высот. Центр вписанной и описанной окружности лежит также в одном месте. Для решения задач необходимо знать только одну сторону, так как вам углы изначально заданы, а две другие стороны известной. То есть фигура задается только одним параметром. Существуют Их главная особенность — равенство двух сторон и углов при основании.

Иногда встречается вопрос о том, существует ли треугольник с заданными сторонами. На самом деле вас спрашивают, подходит ли данное описание под основные виды. Например, если сумма двух сторон меньше третьей, то в реальности такой фигуры не существует вообще. Если в задании просят найти косинусы углов треугольника со сторонами 3,5,9, то здесь очевидный можно объяснить без сложных математических приемов. Предположим, вы хотите из пункта A попасть в пункт B. Расстояние по прямой равно 9 километрам. Однако вы вспомнили, что необходимо зайти в пункт C в магазин. Расстояние от А до С равно 3 километрам, а от С до В — 5. Таким образом получается, что, двигаясь через магазин, вы пройдете на один километр меньше. Но так как пункт C не расположен на прямой AB, то вам придется пройти лишнее расстояние. Здесь возникает противоречие. Это, конечно, условное объяснение. Математика знает не один способ доказательства того, что все виды треугольников подчиняются основному тождеству. Оно гласит о том, что сумма двух сторон больше длины третьей.

Любой вид обладает следующими свойствами:

1) Сумма всех углов равняется 180 градусам.

2) Всегда существует ортоцентр — точка пересечения всех трех высот.

3) Все три медианы, проведенные из вершин внутренних углов, пересекаются в одном месте.

4) Вокруг любого треугольника можно описать окружность. Также можно вписать круг так, чтобы он имел только три точки соприкосновения и не выходил за внешние стороны.

Теперь вы познакомились с основными свойствами, которыми обладают различные виды треугольников

В будущем важно понимать, с чем вы имеете дело при решении задачи

Как находится

Площадь любой фигуры измеряется в квадратных единицах (кв. метрах, кв. миллиметрах, кв. сантиметрах, кв. дециметрах и т. д.) Данную величину можно рассчитать разнообразными способами, в зависимости от вида треугольника. Площадь какой угодно фигуры с углами можно найти, если умножить ее сторону на перпендикуляр, опущенный на нее из противоположного угла, и разделив данную цифру на два. Также можно найти эту величину, если умножить две стороны. Потом умножить это число на синус угла, расположенного между данными сторонами, и разделить это получившееся на два. Зная все стороны треугольника, но не зная его углов, можно найти площадь еще и другим способом. Для этого нужно найти половину периметра. Затем поочередно отнять от данного числа разные стороны и перемножить полученные четыре значения. Далее найти из числа, которое вышло. Площадь вписанного треугольника можно отыскать, перемножив все стороны и разделив полученное число на которая описана вокруг него, умноженный на четыре.

Площадь описанного треугольника находится таким образом: половину периметра умножаем на радиус окружности, которая в него вписана. Если то его площадь можно найти следующим образом: сторону возводим в квадрат, умножаем полученную цифру на корень из трех, далее делим это число на четыре. Похожим образом можно вычислить высоту треугольника, у которого все стороны равны, для этого одну из них нужно умножить на корень из трех, а потом разделить данное число на два.

Центроид, центр окружности и ортоцентр треугольника

Треугольники — одна из самых важных фигур в математике. Они состоят из трех сторон, трех углов и трех вершин. Каждая вершина соединена стороной, а три стороны пересекаются в трех точках, называемых вершинами. Треугольник также является простейшим из существующих многоугольников, и поэтому он играет важную роль в различных областях математики, включая геометрию, тригонометрию и исчисление.

Один интересный аспект треугольников заключается в том, что они имеют три точки, которые значимы по разным причинам — центроид, центр описанной окружности и ортоцентр. Каждая из этих точек уникальна и может рассказать нам разные вещи о треугольнике и его свойствах.

Центроид: Центроид — это точка, в которой пересекаются медианы треугольника. Медиана — это отрезок, соединяющий вершину с серединой противоположной стороны. Центроид также известен как центр тяжести треугольника, так как это точка, в которой треугольник может быть идеально сбалансирован на кончике карандаша. Центроид расположен на 2/3 пути от каждой вершины до середины противоположной стороны.
Центр окружности: Центр описанной окружности — это точка, в которой биссектрисы сторон треугольник пересекается. Биссектриса — это отрезок, перпендикулярный стороне треугольника и проходящий через его середину. Центр описанной окружности важен, потому что это центр окружности, проходящей через все три вершины треугольника.
Ортоцентр: ортоцентр — это точка пересечения высот треугольника. Высота – это отрезок, который выходит из вершины треугольника и перпендикулярен противоположной стороне. Ортоцентр важен, потому что он показывает нам, где встречаются высоты треугольника, и его можно использовать для определения площади треугольника.

Чтобы лучше понять эти три точки, мы можем посмотреть за следующей таблицей:

	Центроид	Центр окружности	Ортоцентр
Определение	Точка пересечения медиан треугольника	Точка пересечения серединных перпендикуляров к сторонам треугольника	Точка пересечения высот треугольника
Расположение	2/3 пути от каждой вершины до середины противоположной стороны	Внутрь для остроугольных треугольников, на треугольник для прямоугольных треугольников и снаружи для тупоугольных треугольников	Внутри для остроугольных треугольников, на треугольник для прямоугольных треугольников и снаружи для тупоугольных треугольников
Свойства	Центроид делит каждую медиану на два сегмента, причем сегмент, расположенный ближе к вершине, вдвое длиннее другого сегмента.	центр описанной окружности равноудален от трех вершин треугольника, а расстояние равно радиусу описанной окружности.	Ортоцентр — это пересечение высот треугольника, и его можно использовать для определения площадь треугольника.

Итак, центр тяжести, центр описанной окружности и ортоцентр — это три важные точки в треугольнике, которые могут дать представление о его свойствах и характеристики. Каждая из этих точек уникальна и определяется различными свойствами треугольника, такими как медианы, биссектрисы и высоты. Понимание этих моментов может быть полезным при решении задач по геометрии, исчислению и другим областям математики.

Созвездие Треугольника

Точное происхождение названия этого созвездия неизвестно. Свое название оно получило на Древнем Востоке, его знали и использовали в навигации финикийские мореходы. Для них оно символизировало священный камень пирамидальной формы. Треугольник входил в число 48 классических созвездий античности. Древние греки считали, что это — перенесенная на небо дельта Нила, что указывает на египетские корни названия созвездия. Уже в Новое время на звездном небе были выделены созвездия Южного Треугольника и Наугольника.

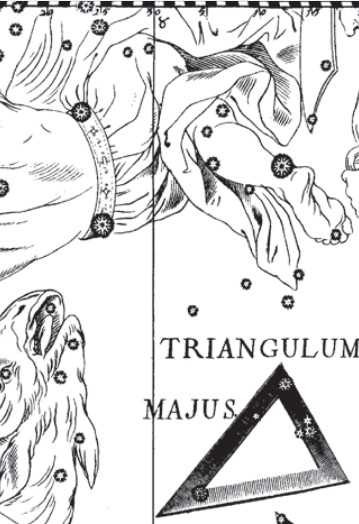Созвездие Треугольника. Иллюстрация из астрономического атласа «Уранография» Я. Гевелия

Пример решения задачи

В тупоугольном треугольнике АВС известно, что косинус тупого угла равен $-2/\sqrt{13}$. Сторона АС находится напротив тупого угла, $АВ=\sqrt{13}$, ВС=2. Необходимо найти внешнюю высоту треугольника АМ.
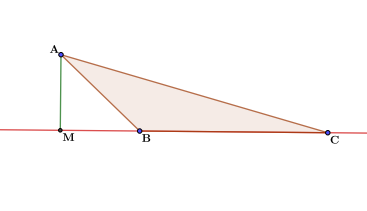Рис. 3. Рисунок к задаче.

Для решения любой задачи можно найти несколько способов. В данной ситуации можно пойти через площадь треугольников, достроить тупоугольный треугольник до прямоугольного или воспользоваться теоремой косинусов. Каждый из способов дает представление о том, как можно решать задачи с тупоугольным треугольником. Воспользуемся каждым из них.

Ответ в каждом случае должен быть одинаков. Но если округлять неточные ответы, то в одной задаче при одинаковых решениях можно получить разные величины. Будьте внимательны, результат не должен отличаться больше, чем на 1.

$$sin(ABC)=\sqrt{1-cos^2(ABC)}=\sqrt{13-4 \over13}=\sqrt{9 \over13}={3\over\sqrt{13}}$$

Теперь запишем две формулы площади, выразим через них высоту и найдем ее значение.

$$S={1\over2}*AM*BC$$

$$S={1\over2}*AB*BC sin(ABC)$$

$${1\over2}*AM*BC={1\over2}*AB*BC*sin(ABC)$$

$$AM*ВС=AB*BC*sin(ABC)$$

$$AM=AB*sin(ABC)$$

$$AM=\sqrt{13}*{3 \over \sqrt{13}}=3$$

$$cos(ABM)=cos(180-ABC)=-cos(ABC)$$

$$cos(ABM)=-cos(ABC)={2\over \sqrt{13}}$$

Тогда синус, как и в первом способе, выразим через основное тригонометрическое тождество.

$$Sin(ABM)=\sqrt{1-cos(ABM)^2}=\sqrt{13-4\over13}=\sqrt{9\over13}={3\over\sqrt{13}}$$

$$Sin(ABM)=AM/AB$$

$$AM=AB*sin(ABM)=\sqrt{13}*{3\over\sqrt{13}}=3$$

$$АС=\sqrt{AB^2+BC^2-2AB*BC*cos(ABC)}=$$

$$\sqrt {\sqrt{13}^2+2^2-2*\sqrt{13}*{-2\over\sqrt{13}}}=$$

$$\sqrt{13+4+8}=\sqrt{25}=5$$ – по теореме косинусов.

$${АС\over{sin(ABC)}}={AB\over{sin(ACB)}}$$ – по теореме синусов.

Значение синуса угла АВС определим по основному тригонометрическому тождеству.

$$ Sin(ABC)=\sqrt{1-cos^2(ABC)}=\sqrt{13-{4\over{4}}}=\sqrt{9\over{13}}={3\over\sqrt{13}}$$

Выразим искомый синус угла АСВ.

$$Sin(ACB)=AB*{sin(ABC)\over{AC}}$$

$$Sin(ACB)=(\sqrt{13}*{{3\over\sqrt{13}}\over{5}})={3\over5}$$

Выразим из треугольника АМС и найденного значения синуса сторону АМ.

$$Sin(ACB)={AM\over AC}$$

$$AM=sin(ACB)*AC$$

$$AM={3\over5}*{5}=3$$

Ответы всех трех способов совпали, а, значит, задача решена верно.

Что мы узнали?

Мы поговорили об определении тупоугольного треугольника. Узнали и посмотрели на практике, какие методы решения тупоугольных треугольников существуют, а также выяснили ,какие формулы и теоремы необходимо знать для успешного решения тупоугольного треугольника.

/5

Вопрос 1 из 5

Способы определить тип угла

Использование геометрических построений: Путем проведения перпендикуляра на одну из сторон треугольника можно определить, является ли угол прямым или острым. Если перпендикуляр пересекает сторону треугольника внутри него, то угол будет острый. Если перпендикуляр пересекает сторону треугольника на ее продолжении, то угол будет прямым.
Измерение угла: Используя геометрический инструмент – транспортир, можно измерить угол и определить его тип. Угол острый будет иметь меньшую меру 90 градусов, угол тупой – большую меру 90 градусов, а прямой угол – меру 90 градусов.
Использование формул: Если известны длины сторон треугольника, то можно использовать теорему косинусов, чтобы вычислить углы треугольника и определить их тип. Если квадрат одной из сторон треугольника суммируется с квадратом другой стороны, но меньше квадрата третьей стороны, то угол будет острым. Если квадрат одной из сторон треугольника суммируется с квадратом другой стороны, но больше квадрата третьей стороны, то угол будет тупым.
Определение угла по его свойствам: В некоторых случаях можно определить тип угла, исходя из его свойств. Например, угол, меньший 90 градусов, будет острым; угол, больший 90 градусов, будет тупым; угол, равный 90 градусов, будет прямым.

Используя эти способы, можно определить тип угла и классифицировать его в треугольнике. Знание типа угла позволяет лучше понять свойства и характеристики треугольника и использовать их в решении геометрических задач.

Как определить тупоугольный треугольник?

Чтобы определить, является ли треугольник тупоугольным, необходимо знать значения всех трех углов. Если один из углов превышает 90 градусов, то треугольник является тупоугольным. Для этого можно использовать такие способы:

1. Измерить углы с помощью транспортира: Примените транспортир и измерьте углы треугольника. Если один из углов превышает 90 градусов, то треугольник тупоугольный.

2. Использовать значения углов из существующих данных: Если вам известны значения углов треугольника, вы можете сложить значения углов и проверить, превышает ли их сумма 180 градусов. Если сумма углов больше 180 градусов и один из углов больше 90 градусов, то треугольник тупоугольный.

3. Использовать теорему косинусов: Если вам известны длины всех сторон треугольника, вы можете использовать теорему косинусов для определения углов треугольника. Если один из вычисленных углов больше 90 градусов, то треугольник тупоугольный.

Имея значение о том, является ли треугольник тупоугольным или нет, вы можете применять соответствующие методы и формулы для решения задач, связанных с этим типом треугольника.

Метод проверки углов

Проверка на тупоугольность треугольника основывается на измерении его углов. Тупоугольный треугольник имеет один из своих углов больше 90 градусов.

Для определения, является ли треугольник тупоугольным, необходимо измерить все три его угла. Сумма углов треугольника всегда равна 180 градусов. Если один из углов больше 90 градусов, то треугольник является тупоугольным. Для измерения углов можно использовать геодезический инструмент, например, угломер или геометрический транспортир.

Пример:

Допустим, мы измерили углы треугольника и получили следующие значения: угол A — 60 градусов, угол B — 100 градусов, угол C — 20 градусов.

Сумма углов: 60 + 100 + 20 = 180 градусов.

Измеренный угол B равен 100 градусов, что больше 90 градусов. Следовательно, данный треугольник является тупоугольным.

Используя метод проверки углов, можно определить, является ли треугольник тупоугольным или нет.

Расчет угловых величин

Угловые величины треугольника определяются суммой всех его углов. В случае тупоугольного треугольника, один из углов будет больше 90 градусов.

Вычислить углы треугольника можно с помощью известных значений его сторон и применения тригонометрических функций. Например, если известны длины всех сторон, можно воспользоваться теоремой косинусов, чтобы найти значения углов треугольника.

Если у вас есть длины двух сторон и противолежащего им угла, вы можете использовать теорему синусов для вычисления других двух углов треугольника.

В случае, если известны только длины сторон, но нет данных о величинах углов, можно воспользоваться теоремой косинусов или теоремой синусов для нахождения углов треугольника.

Если все углы треугольника меньше 90 градусов, то треугольник является остроугольным. Если один из углов равен 90 градусов, треугольник называется прямоугольным. А если хотя бы один из углов больше 90 градусов, треугольник считается тупоугольным.

Применение теоремы косинусов

Применение теоремы косинусов особенно полезно при работе с тупоугольными треугольниками. Тупоугольный треугольник – это треугольник, у которого один из углов превышает 90 градусов. В тупоугольном треугольнике косинус тупого угла отрицательный.

Для определения тупоугольного треугольника можно использовать теорему косинусов. Если квадрат одной из сторон треугольника равен сумме квадратов двух других сторон, то треугольник является тупоугольным. Данное утверждение можно записать в виде формулы:

a² = b² + c² — 2bc * cos(A)

b² = a² + c² — 2ac * cos(B)

c² = a² + b² — 2ab * cos(C)

где a, b, c – длины сторон треугольника, а A, B, C – соответствующие углы. Из этих формул можно определить углы и стороны тупоугольного треугольника, используя известные значения.

Применение теоремы косинусов позволяет расширить наши знания о треугольниках и использовать их для решения различных задач. Она особенно полезна при работе с тупоугольными треугольниками, позволяя определить их свойства и характеристики.

Вписанные треугольники

Как уже было сказано ранее, если круг проходит через все три вершины, то это называется описанной окружностью. Главным ее свойством является то, что она единственная. Чтобы выяснить, как должна располагаться описанная окружность тупоугольного треугольника, необходимо помнить, что ее центр находится на пересечении трех серединных перпендикуляров, которые идут к сторонам фигуры. Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном — за его пределами.

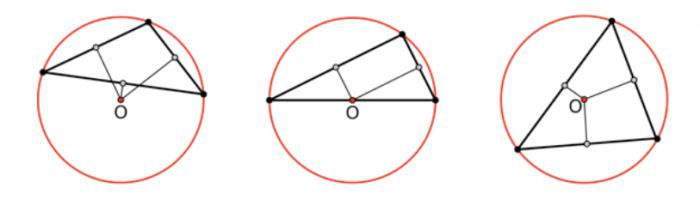
Зная, например, что одна из сторон тупоугольного треугольника равна его радиусу, можно найти угол, который лежит напротив известной грани. Его синус будет равен результату от деления длины известной стороны на 2R (где R — это радиус окружности). То есть sin угла будет равен ½. Значит, угол будет равен 150 о.

Если вам необходимо найти радиус описанной окружности тупоугольного треугольника, то вам пригодятся сведения о длине его сторон (c, v, b) и его площади S. Ведь радиус высчитывается так: (c х v х b) : 4 х S

Кстати, неважно, какого именно у вас вида фигура: разносторонний тупоугольный треугольник, равнобедренный, прямо- или остроугольный. В любой ситуации, благодаря приведенной формуле, вы можете узнать площадь заданного многоугольника с тремя сторонами

Теорема о неравенстве треугольников

Теорема о неравенстве треугольников — это фундаментальное понятие в геометрии, особенно в изучении треугольников. Он гласит, что сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. Эту теорему можно применить к любому треугольнику, независимо от его размера или формы.

Теорема может быть выражена математически как:

a + b > с

б + с > а

с + а > b

Связь с геометрией: Теорема о неравенстве треугольников является ключевым понятием в математическом предмете геометрии. Это помогает в понимании и анализе различных типов треугольников и их свойств. Она также используется при изучении геометрических фигур, таких как многоугольники и круги, поскольку треугольники являются самыми основными из всех многоугольников.
Применения: Теорема о неравенстве треугольников имеет много реальных мировые приложения, такие как навигация и картографирование. Он также используется в таких областях, как инженерия и архитектура, где необходимо рассчитать длину сторон треугольников в таких конструкциях, как мосты и здания.
Доказательство: существуют различные способы доказательства теоремы о неравенстве треугольников, включая алгебраические и геометрические методы. Алгебраическое доказательство включает использование свойств чисел и неравенств для доказательства теоремы. Геометрическое доказательство включает в себя построение треугольника и использование свойств углов и сторон, чтобы показать, что теорема верна.

В целом, теорема о неравенстве треугольника является важным понятием в геометрии, которое помогает понять Треугольники и их свойства. Он может применяться во многих реальных сценариях и имеет различные методы доказательства.