3 4 5 треугольник

Как треугольник используется в строительстве?

Треугольник используется в строительстве, чтобы убедиться, что что-то квадратное или что-то квадратное. Квадрат скорости представляет собой небольшой треугольный инструмент, используемый для обозначения углов стропила. Один из методов проверки квадрата комнаты или одной стены, перпендикулярной другой, состоит в том, чтобы измерить 3 фута вдоль одной стены и сделать отметку карандашом, чтобы они измеряли 4 фута вдоль другой стены и делали метку карандаша. Затем измерьте диагонально от метки карандаша до метки карандаша. Если число составляет 5 футов, две стены квадратные друг к другу.

Определение острого угла треугольника

Для определения острого угла треугольника можно использовать несколько методов. Ниже приведены некоторые из них:

1. Метод с использованием тригонометрии. По известным значениям сторон треугольника и применяя тригонометрические функции (например, синус), можно найти значения углов треугольника. Если значение угла меньше 90 градусов, то он является острым.
2. Метод с использованием теоремы Пифагора. Если квадрат длины наибольшей стороны треугольника меньше суммы квадратов двух других сторон, то треугольник является остроугольным, а наибольший угол в нем будет острым.
3. Метод с использованием формулы для вычисления площади треугольника. Если площадь треугольника больше нуля, то он является остроугольным. В этом случае все его углы будут острыми.

Определение острого угла треугольника имеет важное значение при решении задач геометрии, строительства, а также в других областях, где требуется работать с треугольниками

Значение валькнута как символа

Буквальное значение термина «валькнут» (valrknut) – «узел павших (воинов)».

Воины, убитые на поле боя, отправлялись в Вальхаллу (в скандинавской мифологии – огромный зал с потолком из позолоченных щитов и стенами из копьев.

Это сооружение находится в Асгарде – небесном городе, где обитают боги). Вальхаллой управляет верховный бог Один.

А так как валькнут наносился, в основном, при отправлении воинов «на встречу с Одином», то и знак этот стал отождествляться с этим божеством.

Символизм знака «валькнут» раскрывается в следующих тезисах:

• значение валькнута – объединение мира людей (Мидгарда), богов (Асгарда) и мертвых (Хельхейма);
• значение валькнута связано с мировым древом (ясенем) Иггдрассиль, которое охватывает собой все 9 миров, также ассоциируется с Одином, который на этом дереве пробыл повешенным 9 дней с целью постижения значения рун. Эта связь проявляется через 9 углов (в валькнуте 3 треугольника, у каждого из которых по 3 угла);
• значение символа также ассоциируется с 3 богинями судьбы – Урд («прошлое»), Верданди («настоящее») и Скульд («будущее»), поскольку в нем соединяются 3 треугольника.

Суммируя все приведенные трактовки, можно вывести такое значение «узла павших» — связь между мирами и временами.

Именно поэтому при помощи этого символа люди пытались (и пытаются) постичь скрытые знания.

Также знак используется в магических ритуалах. Для «простых» людей (не связанных с магией и тайными учениями) валькнут по своему значению символизирует единство духа, души и тела.

Применение такого талисмана позволяет гармонизировать свою жизнь. Однако подходит оберег валькнут отнюдь не ко всем жизненным ситуациям и не всем людям.

Как выглядит треугольник?

В выходной день Глеб с родителями ехали в парк. Мальчик заметил, что вдоль дороги стояла непонятная табличка, увидев которую, отец поехал очень медленно.

«Что это такое?» – поинтересовался ребенок. Папа рассказал, что это дорожный знак, который предупреждает о трудностях на пути. Глебу очень понравился знак, а особенно его форма. Отец продолжил рассказ о знаках: «Форма знака о многом говорит водителю, ведь при плохой видимости автолюбитель видит только форму, а не надпись. Поэтому все предупреждающие знаки – треугольные». «А что такое треугольные?» – не унимался мальчик. Найти ответ на этот и многие другие вопросы папе помог наш сегодняшний урок.

Вначале, давайте разберемся, что же такое треугольник и из чего он состоит.

В повседневной жизни нас окружает масса предметов имеющих треугольную форму. Например:

Часы, воздушный змей, кусочек торта, пиццы, арбуза, салатники, рамки для фотографий, пузырек парфюма – этот список можно продолжать бесконечно. Но что же такое треугольник?

Приведем примеры треугольников:

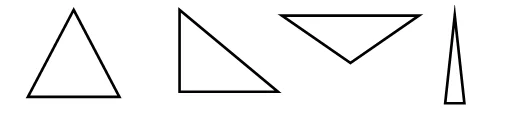
Исходя из определения, каждый рисунок состоит из трех отрезков. В геометрии такие отрезки называют сторонами треугольника.

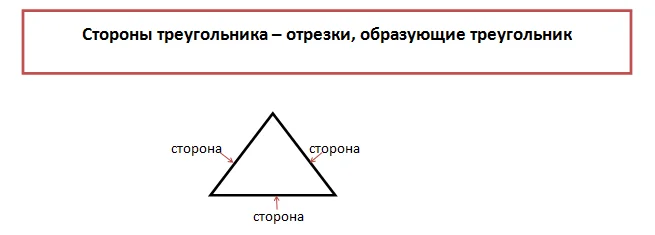
Кроме отрезков, составляющей частью фигуры являются три точки, которые принято называть вершинами.

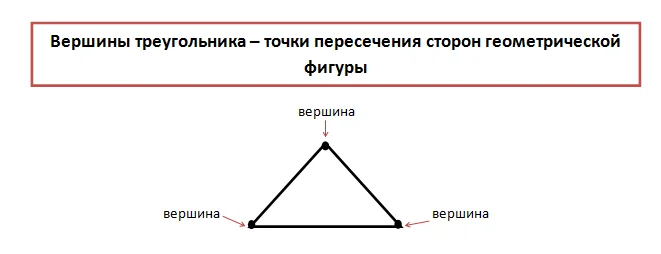
В геометрии, вершины треугольника принято обозначать заглавными буквами латиницы: A,C,D,B.

Начертим треугольник. Вершины, обозначим буквами A,C,D.

Данная геометрическая фигура имеет три вершины A,C,D и три стороны АС, CD, DА.

А как же на письме показать, что данная фигура является треугольником?

Очень интересным является то, что записывать название, можно перечисляя вершины в любом порядке.

Например: 

Можно записать: ∆NOK, ∆OKN, ∆KNО. Каждый вариант записи обозначает один и тот же треугольник и является верным.

Само название фигуры «Треугольник» предполагает, что в состав должны входить три угла. Так ли это?

Внимательно рассмотрим рисунок:

Действительно, мы видим три угла, которые отмечены дугами: ∠RFP,∠FPR, ∠PRF(мы уже знаем, что буква, обозначающая вершину угла всегда записывается в середине) или∠F, ∠P,∠R.

Углы образованные при пересечении двух прямых

При пересечении двух прямых образуются два вида углов:

• смежные;
• вертикальные.

Смежные углы

Определение

Два угла называются смежными, если они имеют общую вершину и одну общую сторону, а две другие стороны расположены на одной прямой и образуют развернутый угол. Смежные углы между собой дополняемые, так как являются продолжением один другого.

Свойства смежных углов

1. Сумма смежных углов равна 180°
2. Если оба смежных угла равны между собой, то они являются прямыми.
3. В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
4. Синусы смежных углов равны.
5. Косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.

Вертикальные углы

Определение

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Пример:

Пары углов 1 и 3; 2 и 4 – являются вертикальными

По свойству вертикальных углов:

\

\

Пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1 — являются смежными

По свойству смежных углов:

\

\

\

\

Смежные углы	Вертикальные углы
Два угла с общей стороной и вершиной называются смежными.	Когда две прямые пересекаются друг с другом, то пары противоположных углов, образованных при вершине, называются вертикальными углами.
Имеют общую сторону и общую вершину.	Имеют общую вершину, но не имеют общую сторону
Смежные углы не всегда равны по величине	Вертикально противоположные углы равны по величине

Разница между смежными и вертикальными углами

Решение задач на построение треугольника по трем элементам

Задача 1

Существует некая сторона треугольника ВС, к которой прилегают углы \alpha и \beta. Необходимо построить треугольник по трем известным элементам.

Решение

Пусть углы треугольника АВС соответствуют следующему условию:

К = \alpha

М = \beta

Можно составить план действий, согласно стандартному алгоритму:

1. Построить прямую а и отмерить на ней отрезок ВС.
2. Начертить угол К с вершиной В на стороне ВС.
3. Изобразить угол М с вершиной С на стороне ВС.
4. На пересечении лучей изображенных углов получить точку А, соединить ее с точками С и В для получения отрезков АС и АВ.

Построим треугольник:

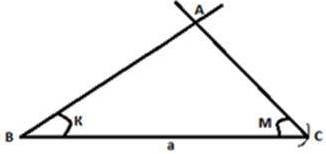
В процессе доказательства следует рассмотреть изображение треугольника. Можно прийти к выводу, что условия задачи выполнены. Заданные углы могут быть построены и в противоположную сторону, соответственно можно изобразить второй треугольник. Однако, так как он аналогичен первому, можно заключить, что задача имеет единственное решение. В том случае, когда углы \alpha и \beta равны или больше, чем 180 градусов, задача не имеет решения.

Задача 2

Даны три стороны треугольника АВ, АС и ВС. Необходимо построить треугольник.

Решение

В процессе анализа условий задания можно составить план решения:

1. Начертить прямую а и отметить на ней отрезок АВ.
2. Используя циркуль, изобразить пару окружностей. Одна из них имеет радиус АС и центр в точке А, а вторая — радиус ВС и центр в точке В.
3. Точку, где пересекаются данные окружности, можно обозначить С. Далее следует соединить точку С с точками А и В. В результате получаются отрезки АС и ВС.
4. Затем остается построить треугольник.

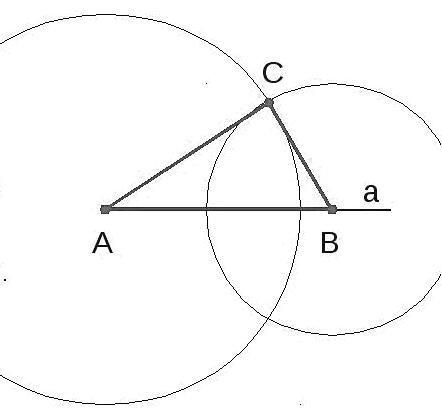
Полученная геометрическая фигура соответствует условиям задачи. Изображенные окружности обладают двумя точками пересечения, что позволяет построить еще один треугольник. Он будет аналогичен первому, поэтому у задачи есть одно единственное решение. С учетом того, что сумма двух сторон треугольника всегда больше третьей его стороны, можно заключить следующее: при невыполнении данного условия для заданных сторон задача не будет иметь решение.

Задача 3

У треугольника имеется две стороны АВ и АС, а также угол \alpha между ними. Требуется изобразить треугольник.

Решение

Порядок действий следующий:

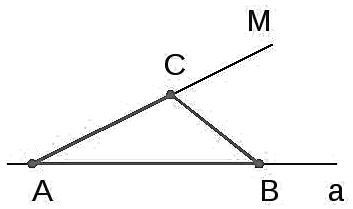
• начертить прямую а, отметить отрезок АВ;
• отмерить угол МАВ, соответствующий углу \alpha;
• отложить отрезок АС на прямой АМ;
• начертить третью сторону треугольника СВ, соединив точки В и С.

В результате получится треугольник:

Число 7

В алхимии число 7 символизирует завершение, совершенство и целостность. Это священное число, представляющее союз духовного и материального. Семь шагов алхимического преобразования включают прокаливание, растворение, разделение, соединение, ферментацию, дистилляцию и коагуляцию. Каждый шаг представляет собой отдельный аспект процесса преобразования и конечную цель достижения совершенства.

• Прокаливание: этот первый шаг включает сжигание вещества до пепла и его разрушение. на его основные компоненты.
• Растворение: пепел затем растворяется в воде, что символизирует высвобождение нечистот и негативных эмоций.
• Разделение: Затем раствор разделяется на различные компоненты, включая чистую эссенцию вещества.
• Соединение: чистая эссенция затем объединяется с другими веществами для создания чего-то новое.
• Ферментация: на этом этапе новое творение ферментируется и трансформируется с течением времени.
• Дистилляция: новое творение затем перегоняется, разделяя его на основные части.
• Коагуляция: основные части затем объединяются вместе, чтобы создать новое цельное вещество, которое более ценно, чем исходное.

Семь шагов алхимической трансформации также связаны с семью классическими планетами: Сатурном, Юпитером, Марсом, Солнцем, Венерой, Меркурием и Луной. Каждая планета представляет отдельный аспект процесса трансформации, от разрушения (Сатурн) до просветления (Солнце).

Шаг	Планета
Кальцинация	Сатурн
Растворение	Меркурий
Разделение	Марс
Соединение	Венера
Брожение	Юпитер
Дистилляция	Луна
Коагуляция	Солнце

Треугольник символизирует процесс трансформации в алхимии, где каждая точка представляет отдельный аспект процесса трансформации. Три точки могут представлять три элемента, используемых в алхимии: серу, ртуть и соль. Треугольник, обращенный вверх, представляет огонь, воздух и духовное царство, а треугольник, обращенный вниз, представляет воду, землю и материальное царство. Вместе они представляют союз духовного и материального, что является конечной целью алхимии.

Описание презентации Треугольники вокруг нас Здесь вы узнайте о треугольниках по слайдам

Цель проекта. Сегодня мы расскажем о треугольниках не только в геометрии но и вокруг нас. Мы расскажем о треугольниках в химии, в быту, в архитектуре, в живописи и в искусстве, в природе, в географии и в биологии и расскажем про египетский треугольник.

Треугольник Треуг льникоо (в евклидовом пространстве) — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Со времен «Начал» Евклида покоится на «трёх китах» – трёх признаках равенства треугольников. Первые упоминания о треугольнике и его свойствах мы находим в египетских папирусах, которым более 4000 лет. Там упоминается способ нахождения площади треугольника. Через 2000 лет в Древней Греции изучение свойств треугольника достигает высокого уровня – достаточно упомянуть теорему Пифагора. В XY – XYI веках появилось огромное количество исследований свойств треугольника. Эти исследования составили новый раздел в геометрии «Новая геометрия треугольника» . Лишь на рубеже XIX–XX вв. математики научились строить геометрию на основе более фундаментального и общего, чем равенство треугольников, понятия геометрического преобразования. Были открыты новые теоремы о свойствах треугольника и даже целая наука – тригонометрия. Фейербах, Эйлер, Морли и даже Наполеон внесли свой вклад в изучение треугольника

Треугольники в химии Химию изучают и посей день, но и в химии тоже есть треугольники, хотя они незаметны.

Треугольники в быту. Треугольники есть и в быту. Но они везде и в быту, и в химии, и так далее, но мы их и не замечаем, хотя они везде.

Треугольник в архитектуре Треугольник одна из важных частей при строительстве. Треугольник используется для: фасада таможни, фасада биржи, Исаакиевского собора. Так же используется при строительстве мостов и пирамид. Свойство жесткости треугольника широко используют в практике при строительстве железных конструкций. Треугольники делают конструкции надежными. При постройке крупных сооружений на широких и глубоких реках в теплое время года невозможно непосредственными измерениями определить расстояние между исходными пунктами и разбить оси опор. В этом случае прибегают к параллактическому или триангуляционному способам. С этой целью создают на берегах геодезическую опорную сеть, представляющую собой в плане систему треугольников

Треугольники в искусстве и живописи Треугольник присутствует в красивых ландшафтах и дизайнах. Не стоит забывать про красивы поделки из бумаги – оригами. Там тоже присутствует треугольник. Оригами тоже относится к искусству. В сфере рисования или же живописи, тоже присутствуют треугольники. Геометрические фигуры определяют внутреннее состояние: круг — спокойствие, квадрат — напряжение. а треугольник — сильное напряжение. Значит, художник «выплёскивает» своё психоэмоциональное со стояние на картину.

Треугольники в природе

Треугольники встречаются нам каждый день но мы не обращаем на это внимание. Если присмотреться можно увидит разновидных треугольников. Треугольники в биологии Это естественное происхождение треугольников

Они образованы от изменение структуры и привыкание к естественной среде

Треугольники в биологии Это естественное происхождение треугольников. Они образованы от изменение структуры и привыкание к естественной среде.

Египетский треугольник Это прямоугольный треугольник с соотношением сторон 3: 4: 5. Особенностью такого, треугольника, известной со времен античности, является то, что все три стороны состоят из целых чисел, а по теореме, обратной теореме Пифагора.

Окружности треугольника

Файл:Треугольник АВС и его окружности.png

Треугольник АВС и его окружности: вписанная (синяя), описанная (красная) и три вневписанных (зеленые)

Окружности, проходящие через вершины треугольника

• Описанная окружность (см. рис. справа) — окружность, проходящая через все три вершины треугольника. Описанная окружность всегда единственна, если треугольник не вырожден особым образом, т. е. две из трех его вершин не совпадают.
• Окружность Джонсона — окружность, проходящая через две вершины треугольника и через его ортоцентр. Радиусы всех трех окружностей Джонсона равны. Окружности Джонсона являются описанными окружностями треугольников Гамильтона, имеющих в качестве двух вершин две вершины данного остроугольного треугольника, а в качестве третьей вершины имеющих его ортоцентр.

Окружности, касающиеся сторон треугольника или их продолжений

Вписанная окружность (см. рис. справа) — окружность, касающаяся всех трёх сторон треугольника. Она единственна. Центр вписанной окружности называется инцентром
Отрезки, соединяющие точки касания вписанной окружности с вершинами, пересекаются в одной точке, называемой точкой Жергонна. Точка Жергонна изотомически сопряжена точке Нагеля (см. ниже).

.

Вневписанная окружность(см. рис. справа) — окружность, касающаяся одной стороны треугольника и продолжения двух других сторон. Таких окружностей в треугольнике три. Их радикальный центр — центр вписанной окружности срединного треугольника, называемый центром Шпикера или точкой Шпикера
Отрезки, соединяющие вершины с точками касания вневписанных окружностей с вершинами, пересекаются в одной точке, называемой точкой Нагеля.
.

Файл:Окружности Мальфатти.png

Окружности Мальфатти

Три окружности Мальфатти треугольника (см. рис. справа). Каждая из них касается двух сторон треугольника и двух других окружностей Мальфатти
Если провести три прямые, соединяющие центр каждой окружности Мальфатти с точкой касания между собой двух других, то они пересекутся в одной точке в точке Аджима-Мальфатти(=Ajima-Malfatti Point= http://faculty.evansville.edu/ck6/tcenters/recent/ajmalf.html).
.

Файл:Полувписанные окружности.png

Полувписанные окружности

• Три полувписанные окружности или окружности Веррьера (см. рис. слева). Каждая из них касается двух сторон треугольника и описанной окружности внутренним образом

  Отрезки, соединяющие вершины треугольника и соответствующие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке, называемой точкой Веррьера. Она служит центром гомотетии, которая переводит описанную окружность во вписанную.

• Лемма Веррьера. Точки касания окружностей Веррьера со сторонами лежат на прямой, которая проходит через центр вписанной окружности (инцентр).

Замечание

Вообще говоря, окружностей типа окружностей Веррьера, касающихся двух сторон треугольника и его описанной окружности, существует не три, а шесть: три внутренних и три внешних. Три последние касаются продолжений двух сторон треугольника и внешним образом описанной окружности. Для них можно ввести свою точку Веррьера.

Окружности, взаимно касающиеся друг друга внутри треугольника

• Три окружности Мальфатти попарно касаются друг друга внутри треугольника. (см. выше)
• Окружность девяти точек или окружность Эйлера касается вписанной окружности внутри треугольника в точке Фейербаха.

Окружности, взаимно касающиеся друг друга вне треугольника

• Три окружности Веррьера касаются описанной окружности вне треугольника.
• Окружность девяти точек или окружность Эйлера касается трех вневписанных окружностей вне треугольника внешним образом (Теорема Фейербаха, см. рисунок).

Файл:Circ9pnt3.svg

Иллюстрация к теореме Фейербаха. Точкой Фейербаха F считается наиболее близкая к вершине A отмеченная жирно точка на окружности

Окружность Аполлония касается трех вневписанных окружностей вне треугольника внутренним образом (см. рисунок)

Файл:Apollonius point.svg

Другие окружности

Файл:Окружность Ламуна.png

Окружность Ламуна

Центры описанных окружностей шести треугольников, на которые треугольник разбивается медианами, лежат на одной окружности, которая называется окружностью Ламуна.

Файл:Окружность Конвея.png

Окружность Конвея

Если от каждой вершины отложить наружу треугольника на прямых, содержащих стороны, отрезки, равные по длине противоположным сторонам, то получившиеся шесть точек лежат на одной окружности — окружности Конвея.

Примеры решения задач на нахождение угла по трем сторонам

Найдем угол А в треугольнике ABC, если известны длины сторон AB, BC и CA:

Известно, что: AB = 3 см, BC = 4 см и CA = 5 см.

Применим формулу косинусов: cos(A) = (b^2 + c^2 — a^2) / (2 * b * c),

где a, b, c — длины сторон треугольника, соответствующие углу A, B и C соответственно.

Подставив значения длин сторон, получим: cos(A) = (4^2 + 5^2 — 3^2) / (2 * 4 * 5) = 0,6.

Находим угол А: A = arccos(0,6) ≈ 53,13°.

Найдем угол B в треугольнике ABC, если известны длины сторон AB, BC и CA:

Известно, что: AB = 7 см, BC = 9 см и CA = 5 см.

Применим формулу косинусов: cos(B) = (a^2 + c^2 — b^2) / (2 * a * c),

где a, b, c — длины сторон треугольника, соответствующие углу A, B и C соответственно.

Подставив значения длин сторон, получим: cos(B) = (5^2 + 9^2 — 7^2) / (2 * 5 * 9) ≈ 0,83.

Находим угол B: B = arccos(0,83) ≈ 33,69°.

Найдем угол C в треугольнике ABC, если известны длины сторон AB, BC и CA:

Известно, что: AB = 8 см, BC = 6 см и CA = 10 см.

Применим формулу косинусов: cos(C) = (a^2 + b^2 — c^2) / (2 * a * b),

где a, b, c — длины сторон треугольника, соответствующие углу A, B и C соответственно.

Подставив значения длин сторон, получим: cos(C) = (8^2 + 6^2 — 10^2) / (2 * 8 * 6) ≈ -0,25.

Находим угол C: C = arccos(-0,25) ≈ 104,48°.

Вопрос-ответ

Вопрос: Как найти угол по трем сторонам?

Ответ: Для этого можно воспользоваться законом косинусов: cos(угол) = (a^2 + b^2 — c^2) / (2ab), где a, b и c — длины сторон треугольника. После подстановки известных значений в эту формулу можно вычислить угол.

Вопрос: Я не понимаю, как использовать закон косинусов. Можете объяснить подробнее?

Ответ: Конечно! Закон косинусов позволяет вычислить угол в треугольнике, если известны длины трех его сторон. Формула выглядит так: cos(угол) = (a^2 + b^2 — c^2) / (2ab), где a, b и c — стороны треугольника. Чтобы вычислить угол, нужно подставить в эту формулу известные значения и решить уравнение относительно угла. Главное — не забывайте, что угол должен быть выражен в радианах!

Вопрос: Что делать, если у меня нет информации о длине одной из сторон треугольника?

Ответ: В этом случае найти угол невозможно. Чтобы вычислить угол, необходимо знать длины всех трех сторон треугольника.

Вопрос: Можно ли использовать другие формулы для вычисления угла в треугольнике?

Ответ: Да, есть и другие формулы, например, формула синусов или формула тангенсов. Однако, формула косинусов является наиболее удобной и широко используется в геометрии.

Вопрос: А как найти площадь треугольника, если известны его стороны?

Ответ: Для вычисления площади можно воспользоваться формулой Герона: S = sqrt(p(p-a)(p-b)(p-c)), где p — полупериметр треугольника, a, b, c — его стороны. После вычисления полупериметра и подстановки известных значений в формулу, можно вычислить площадь треугольника.

Главная — Советы — Просто и быстро: как найти угол по трем сторонам с помощью нашего подробного руководства.

!Комментарии

AlexRider

5.0 out of 5.0 stars5.0

Интересная статья, помогла мне решить пару задач в школе

MaxPower
5.0 out of 5.0 stars5.0

Никогда не думал, что можно найти угол по трём сторонам. Статья раскрыла тему очень доступно и подробно. Конечно, для меня это было немного сложно, но с дополнительными примерами и объяснениями я смог разобраться. Очень удобно, что рассмотрены все возможные случаи, надеюсь использовать полученные знания в будущем.

AnnaBell
5.0 out of 5.0 stars5.0

Я давно искала информацию о том, как найти угол по трем сторонам, и наконец нашла эту статью. Было очень интересно и познавательно узнать о различных формулах и методах решения таких задач. Теперь я готова к новым заданиям.

Андрей Сидоров
5.0 out of 5.0 stars5.0

KateQueen
5.0 out of 5.0 stars5.0

Спасибо большое за эту статью! Я всегда была немного скептически настроена к математике, но прочитав ее, я поняла, что понимаю даже такой сложный и для меня непривычный термин, как «противоположный угол». На самом деле оказалось, что все формулы и методы для нахождения угла по трем сторонам, не такие страшные, как я думала, и их можно применять в решении многих задач.

Особенно меня порадовала обилие примеров и иллюстраций, которые объясняют каждый этап решения задачи. Я не ожидала, что всего за несколько минут я смогу найти угол по трем сторонам, но благодаря этой статье я получила новые знания и уверенность в будущих математических испытаниях. Спасибо еще раз!

Марина Кузнецова
5.0 out of 5.0 stars5.0

Полезная статья, спасибо! Никогда не знала, как найти угол по трем сторонам, теперь все ясно.

Сумма, разность и произведение синуса и косинуса

Нам осталось разобрать еще несколько формул. В этот раз они связаны с действиями, производимыми с самими функциями. Например, с произведением синуса и косинуса. 

Рассмотрим формулы:

\(sin\alpha+sin \beta =2sin(\frac{\alpha+\beta}{2})*cos(\frac{\alpha-\beta}{2})\)\(sin \alpha-sin \beta=2sin(\frac{\alpha-\beta}{2})*cos(\frac{\alpha+\beta}{2})\)\(cos \alpha+cos \beta =2cos(\frac{\alpha-\beta}{2})*cos(\frac{\alpha+\beta}{2})\)\(cos \alpha-cos \beta =-2sin(\frac{\alpha+\beta}{2})*sin(\frac{\alpha-\beta}{2})\)\(sin \alpha*sin \beta =\frac{1}{2}(cos(\alpha-\beta)-cos(\alpha+\beta))\)\(cos \alpha*cos \beta =\frac{1}{2}(cos(\alpha-\beta)+cos(\alpha+\beta))\)\(sin \alpha*cos \beta=\frac{1}{2}(sin(\alpha-\beta)+sin(\alpha+\beta))\)

Заметим, что в формулах разные аргументы. Если они не табличные, то посчитать значение выражения почти нереально. Поэтому, если это возможно, с помощью этих формул мы можем упростить выражение до табличных углов.

Например, попробуем преобразовать выражение \(sin(\frac{3\pi}{8})*cos(\frac{\pi}{8})\). 

Рассчитать значение не представляется возможным: в аргументе стоят нетабличные значения. Попробуем преобразовать это выражение с помощью формулы \(sin \alpha*cos\beta =\frac{1}{2}(sin(\alpha-\beta)+sin(\alpha+\beta))\):

\(sin(\frac{3\pi}{8})*cos(\frac{\pi}{8})=\frac{1}{2}(sin(\frac{3\pi}{8}-\frac{\pi}{8})+sin(\frac{3\pi}{8}+\frac{\pi}{8}))\)

Преобразуем выражения в аргументах синусов отдельно:

\(\frac{3\pi}{8}-\frac{\pi}{8}=\frac{3\pi-\pi}{8}=\frac{2\pi}{8}=\frac{\pi}{4}\)\(\frac{3\pi}{8}+\frac{\pi}{8}=\frac{3\pi+\pi}{8}=\frac{4\pi}{8}=\frac{\pi}{2}\)

Получаем выражение:

\(\frac{1}{2}(sin(\frac{3\pi}{8}-\frac{\pi}{8})+sin(\frac{3\pi}{8}+\frac{\pi}{8}))=\frac{1}{2}(sin(\frac{\pi}{4})+sin(\frac{\pi}{2}))\)

Теперь подставим значения из таблицы:

\(\frac{1}{2}(sin(\frac{\pi}{4})+sin(\frac{\pi}{2}))=\frac{1}{2}(\frac{\sqrt2}{2}+1)=\frac{1}{2}*\frac{2+\sqrt2}{2}=\frac{2+\sqrt2}{4}\)

Значение выражения найдено.

Подведем итог. Формулы тригонометрии необходимы для преобразования сложных выражений. А чтобы они были в одном месте, мы составили для вас таблицу.

Итак, мы разобрались, как преобразовывать выражения с тригонометрическими функциями. Какой следующий шаг? Правильно, решение уравнений.