Основные сведения о геометрических углах и их свойствах за 7 класс

Прямой угол

Прямой угол является особенным типом угла, потому что он образуется важными и часто используемыми фигурами, такими как прямоугольник и квадрат.

Прямой угол можно наблюдать в повседневной жизни. Например, когда рисуешь линейку о двух взаимно перпендикулярных линиях, угол между ними будет прямым углом. Также прямые углы можно увидеть на углах столов, книжных полках и коробках.

Прямой угол один из основных элементов геометрии и наук о природе. Он является базовым строительным блоком для других типов углов и помогает нам разобраться в пространстве и формах.

Что такое прямой угол

Прямой угол называется также прямым углом или прямым углом 90°.

В геометрии прямой угол является одной из основных единиц измерения углов. Он часто используется в задачах и конструкциях, связанных с изучением геометрии и пространственного моделирования.

Прямой угол является противоположностью других типов углов, таких как острый угол, тупой угол и растянутый угол. Острый угол меньше 90°, тупой угол больше 90°, а растянутый угол равен 180°.

Важно уметь распознавать прямой угол и использовать его в геометрических расчетах, поскольку он является основным строительным блоком для многих других геометрических форм и фигур. Прямой угол — это ключевой элемент в определении острого, прямого и тупого углов, и его понимание позволяет более глубоко и точно изучать геометрию и ее приложения

Прямой угол — это ключевой элемент в определении острого, прямого и тупого углов, и его понимание позволяет более глубоко и точно изучать геометрию и ее приложения.

Характеристики прямого угла

Острый угол — это одна из двух острот прямого угла. Он имеет значение меньше 90 градусов и обозначает остроту угла между положительной полуосью абсцисс (x) и прямой линией.

Тупой угол — это другая острота прямого угла. Он имеет значение больше 90 градусов и обозначает остроту угла между положительной полуосью ординат (y) и прямой линией.

Прямой угол встречается в различных областях науки и применяется для измерения углов и описания геометрических фигур.

Примеры прямых углов

• Угол в 90 градусов, который образуется, когда две прямые пересекаются и одна из них вертикальная, называется прямым углом. Например, угол между стеной и полом, угол между двумя сторонами прямоугольного треугольника.
• В круглом плане, прямыми углами образуются оси координат – горизонтальная и вертикальная оси, которые пересекаются в начале координат.
• В рулетке, каждый из секторов между числами от 0 до 36 образует прямой угол с центральной осью рулетки.
• В календаре, угол между двумя ближайшими часовыми делениями на циферблате также является прямым углом.

Это лишь некоторые примеры прямых углов. В геометрии и повседневной жизни таких примеров много.

Примеры применения угла по косинусу

1. Тригонометрия:

Угол по косинусу является одним из основных понятий тригонометрии. Он позволяет определить соотношение между сторонами прямоугольного треугольника и его углами. Формула косинуса, основанная на угле по косинусу, имеет вид: cos(A) = adjacent/hypotenuse, где adjacent — прилежащая сторона, а hypotenuse — гипотенуза треугольника.

2. Геометрия:

Угол по косинусу также находит применение в геометрии. Он используется для определения косинуса угла между двумя векторами. Косинус угла между векторами позволяет определить степень их схожести и направление.

3. Физика:

В физике угол по косинусу используется для анализа взаимодействия сил и определения механической энергии. Например, при работе с системами сил, зная угол между силой и перемещением, можно рассчитать работу силы. Формула для расчета работы учитывает косинус угла между силой и перемещением.

4. Инженерия:

В различных областях инженерии, таких как строительство, авиация, электротехника и другие, угол по косинусу используется для рассчета нагрузок, качества связей и определения эффективности систем. Например, при проектировании конструкции здания можно использовать угол по косинусу для определения величины нагрузки на опоры.

Это лишь несколько примеров применения угла по косинусу

В целом, это важное понятие, которое находит свое применение во многих сферах науки и техники, и позволяет решать разнообразные задачи

Определение тригонометрических функций через окружность[]

Пусть на плоскости задана прямоугольная система координат с началом в точке O{\displaystyle O} и с осями OX{\displaystyle {OX}} и OY{\displaystyle {OY}} . Возьмём в этой системе координат окружность с центром в точке O{\displaystyle O} и радиусом, равным единице. Пусть отрезок OA{\displaystyle {OA}} поворачивается на произвольный угол ϑ{\displaystyle \vartheta} вокруг центра O.{\displaystyle O.}

Синусом угла ϑ{\displaystyle \vartheta} называется отношение ординаты точки A{\displaystyle A} к длине отрезка OA.{\displaystyle {OA}.} Обозначают sin⁡ϑ=ACOA.{\displaystyle \sin\vartheta=\frac{AC}{OA}.} Так как длина отрезка OA{\displaystyle {OA}} равна 1{\displaystyle 1}, то sin⁡ϑ=AC.{\displaystyle \sin\vartheta={AC}.}

Косинусом угла ϑ{\displaystyle \vartheta} называется отношение абсциссы точки A{\displaystyle A} к длине отрезка OA.{\displaystyle {OA}.} Обозначают cos⁡ϑ=OCOA.{\displaystyle \cos\vartheta=\frac{OC}{OA}.} Так как длина отрезка OA{\displaystyle {OA}} равна 1, то cos⁡ϑ=OC.{\displaystyle \cos\vartheta={OC}.}

Тангенсом угла ϑ{\displaystyle \vartheta} называется отношение ординаты точки A{\displaystyle A} к абсциссе точки A{\displaystyle A}. Обозначают tgϑ=ACOC{\displaystyle \operatorname{tg}\,\vartheta=\frac{AC}{OC}} (в англоязычной литературе tan⁡ϑ).{\displaystyle \tan\vartheta ).} Так как AC=sin⁡ϑ{\displaystyle {AC}=\sin \vartheta} и OC=cos⁡ϑ,{\displaystyle {OC}=\cos\vartheta,} то tgϑ=sin⁡ϑcos⁡ϑ.{\displaystyle \operatorname{tg}\,\vartheta=\frac{\sin\vartheta}{\cos\vartheta}.}

Котангенсом угла ϑ{\displaystyle \vartheta} называется отношение абсциссы точки A{\displaystyle A} к ординате точки A{\displaystyle A}. Обозначают ctgϑ=OCAC{\displaystyle \operatorname{ctg}\,\vartheta=\frac{OC}{AC}} (в англоязычной литературе cot⁡ϑ).{\displaystyle \cot\vartheta ).} Так как AC=sin⁡ϑ{\displaystyle {AC}=\sin \vartheta} и OC=cos⁡ϑ,{\displaystyle {OC}=\cos\vartheta,} то ctgϑ=cos⁡ϑsin⁡ϑ.{\displaystyle \operatorname{ctg}\,\vartheta=\frac{\cos\vartheta}{\sin\vartheta}.} Котангенс равен обратному значению тангенса: ctgϑ=1tgϑ.{\displaystyle \operatorname{ctg}\,\vartheta=\frac{1}{\operatorname{tg}\,\vartheta}.}

Секансом угла ϑ{\displaystyle \vartheta} называется отношение длины отрезка OA{\displaystyle {OA}} к абсциссе точки A{\displaystyle A}. Обозначают sec⁡ϑ=OAOC.{\displaystyle \sec\vartheta=\frac{OA}{OC}.} Так как длина отрезка OA{\displaystyle {OA}} равна 1, то sec⁡ϑ=1OC.{\displaystyle \sec\vartheta=\frac{1}{OC}.} Секанс равен обратному значению косинуса: sec⁡ϑ=1cos⁡ϑ.{\displaystyle \sec\vartheta=\frac{1}{\cos\vartheta}.}

Косекансом угла ϑ{\displaystyle \vartheta} называется отношение длины отрезка OA{\displaystyle {OA}} к ординате точки A{\displaystyle A}. Обозначают cosecϑ=OAAC{\displaystyle \operatorname{cosec}\,\vartheta=\frac{OA}{AC}} (в англоязычной литературе csc⁡ϑ).{\displaystyle \csc \vartheta ).} Так как длина отрезка OA{\displaystyle {OA}} равна 1{\displaystyle 1}, то cosecϑ=1AC.{\displaystyle \operatorname{cosec}\,\vartheta=\frac{1}{AC}.} Косеканс равен обратному значению синуса: cosecϑ=1sin⁡ϑ.{\displaystyle \operatorname{cosec}\,\vartheta=\frac{1}{\sin\vartheta}.}

Из определения следует: если косинус угла равен нулю, то тангенс и секанс этого угла не существуют. Аналогично для котангенса и косеканса: если синус угла равен нулю, то котангенс и косеканс этого угла не существуют.

Построение прямого угла, прямоугольника, квадрата на клетчатой бумаге

Как вы заметили, король Луч и принцесса Точка любят чертить. Они приглашают нас, ребята, поучаствовать в этом увлекательном занятии. Вооружитесь тетрадью в клеточку, простым карандашом, угольником.

Задание: построить на бумаге в клеточку прямой угол, прямоугольник со сторонами 6 см и 3 см, квадрат со стороной 7 см.

Посмотрите, как получилось у принцессы. Сравните со своими чертежами. 

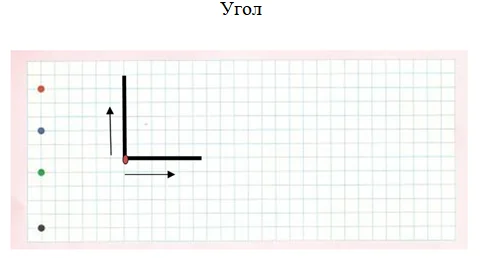
Ставим точку. Откладываем два луча при помощи угольника или линейки.

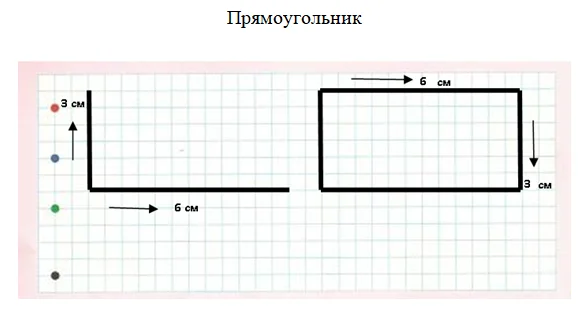
Ставим точку. Вверх – 3 см, вправо – 6 см. Помним, что противоположные прямоугольника стороны равны. Чертим их – 6 см и 3 см.

Квадрат

А это тетрадь короля. Он чертил квадрат. Сравните со своим чертежом.

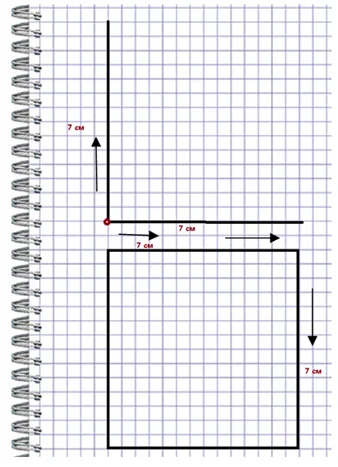
Ставим точку. Помним, что у квадрата все стороны равны. Откладываем вверх 7 см, вправо – 7 см. Чертим противоположные стороны по 7 см.

Молодцы, здорово получилось! Если такое занятие было для вас интересным и увлекательным, попробуйте начертить прямой угол, прямоугольник и квадрат на нелинованной бумаге. Сделать это будет гораздо сложнее. Здесь на помощь придет угольник: проверять прямой угол. Можно воспользоваться моделью прямого угла, которую мы изготовили.

Посмотрите, как это получилось у короля и Точки.

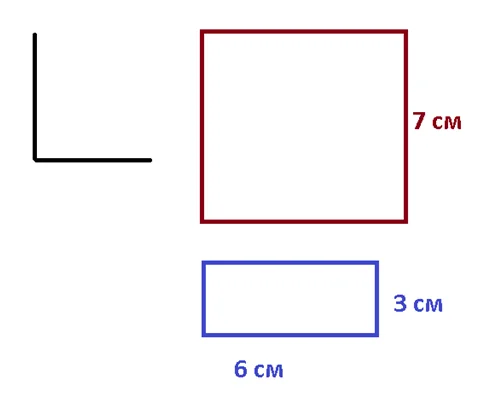
После нелегкого занятия король Луч и его дочка присели отдохнуть. Принцесса попросила рассказать интересную сказку. Давайте и мы послушаем!

Сказка

Жил-был на свете Прямоугольник. Фигура важная, спору нет! Люди ценили и уважали Прямоугольника, потому что при изготовлении многих вещей использовали эту фигуру. Всё хорошо у Прямоугольника, но одиноко как-то. Решил он найти своих родственников. Думает: «Если встречу родственников, сразу узнаю, потому что на меня должны быть похожи!».

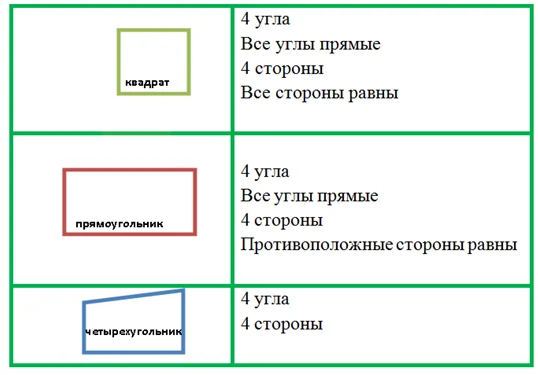
Однажды встретил Прямоугольник Квадрата и говорит: «Как тебя зовут? Очень ты, брат, на меня похож!». Отвечает Квадрат: «Если найдем  не меньше четырех общих признака, значит, родственники». Стали они друг друга рассматривать и обнаружили четыре сходства:

У каждого было по 4 угла, да все прямые, по 4 стороны, да стороны, которые одна напротив другой – одинаковой длины.

Обрадовались родственники, что нашли друг друга. Поспешили вместе отправиться дальше. Встретили однажды Четырехугольника и спрашивают: «Похож ты на нас. Уж не родня ли?».

Говорит им Четырехугольник: «Я был бы очень рад! Если найдем хотя бы два сходства, значит, родственники». Стали опять внимательно друг к другу приглядываться и увидели два общих признака:

1. 4 угла.
2. 4 стороны.

Обрадовались фигуры и решили не терять друг друга, держаться всегда рядом.

Понравилась вам сказка? Давайте повторим о фигурах все, что узнали. 

В сказочное королевство Геометрия мы вернемся еще не раз. А этот урок подошел к концу. Выберите смайлик вашего настроения.

Основные связи тригонометрических функций

А как найти тангенс или котангенс, если нам, например, известен косинус? Посмотрите на формулы №2, для того, чтобы найти тангенс, нужно знать и косинус, и синус:

$$\mathbf{tg(\alpha)=\frac{\sin(\alpha)}{\cos(\alpha)};}$$
$$\mathbf{ctg(\alpha)=\frac{\cos(\alpha)}{\sin(\alpha)};}$$

Но зная косинус, мы легко можем найти синус по основному тригонометрическому тождеству, а потом уже найти тангенс.

Пример 2
Найдите \(tg(\alpha)\) и \(ctg(\alpha)\), если \(\cos(\alpha)=\frac{\sqrt{10}}{10}\) и \(\alpha \in (\frac{3\pi}{2};2\pi)\).

Сначала находим значение синуса:
$$\sin^2(\alpha)+\cos^2(\alpha)=1;$$
$$\sin^2(\alpha)+\left(\frac{\sqrt{10}}{10}\right)^2=1;$$
$$\sin^2(\alpha)+\frac{1}{10}=1;$$
$$\sin^2(\alpha)=1-\frac{1}{10};$$
$$\sin^2(\alpha)=\frac{9}{10};$$
$$\sin(\alpha)=\pm\sqrt{\frac{9}{10}}=\pm\frac{3}{\sqrt{10}};$$
Так как по условию задачи \(\alpha \in (\frac{3\pi}{2};2\pi)\), что соответствует четвертой четверти на тригонометрической окружности, то \(\sin(\alpha)

Ответ: \(tg(\alpha)=-3;\) \(ctg(\alpha)=-\frac{1}{3}.\)

Как видите, чтобы найти тангенс или котангенс через косинус или синус, необходимо воспользоваться сразу двумя тригонометрическими формулами. Это не очень удобно, поэтому очень полезны тригонометрические формулы, связывающие тангенс с косинусом или котангенс с синусом напрямую:
$$\mathbf{tg^2(\alpha)+1=\frac{1}{\cos^2(\alpha)};}$$
$$\mathbf{ctg^2(\alpha)+1=\frac{1}{\sin^2(\alpha)};}$$

Вывод связи тангенса с косинусом и котангенса с синусом

Полезно знать, как они выводятся. Вывод, на самом деле, элементарный, с использованием основного тригонометрического тождества и определения тангенса через синус и косинус:
$$tg^2(\alpha)+1=\frac{1}{\cos^2(\alpha)};$$
$$\left(\frac{\sin(\alpha)}{\cos(\alpha)}\right)^2+1=\frac{1}{\cos^2(\alpha)};$$
Приводим левую часть к общему знаменателю:
$$\frac{\sin^2(\alpha)}{\cos^2(\alpha)}+\frac{\cos^2(\alpha)}{\cos^2(\alpha)}=\frac{1}{\cos^2(\alpha)};$$
$$\frac{\sin^2(\alpha)+\cos^2(\alpha)}{\cos^2(\alpha)}=\frac{1}{\cos^2(\alpha)};$$
В числителе у нас получилось основное тригонометрическое тождество:
$$\frac{1}{\cos^2(\alpha)}=\frac{1}{\cos^2(\alpha)};$$
Получилось верное равенство — формула доказана. Аналогично доказывается формула для котангенса и синуса. (В качестве упражнения докажите ее сами).

Если решать пример №2 по этим формулам, то решение заметно сокращается:
$$tg^2(\alpha)+1=\frac{1}{\left(\frac{\sqrt{10}}{10}\right)^2};$$
$$tg^2(\alpha)+1=10;$$
$$tg^2(\alpha)=9;$$
$$tg(\alpha)=\pm3;$$
Так как \(\alpha \in (\frac{3\pi}{2};2\pi)\), то тангенс будет отрицательным:
$$tg(\alpha)=-3;$$

Формулы приведения. Быстро и легко!

Тригонометрия.Формулы приведения.

Формулы приведения не нужно учить их нужно понять. Понять алгоритм их вывода.

Возьмем единичную окружность и расставим все градусные меры (0°; 90°; 180°; 270°; 360°) на ней.

Разберем в каждой четверти функции sin(a) и cos(a). Запомним, что функцию sin(a) смотрим по оси Y, а функцию cos(a) по оси X.

В первой четверти видно, что функция sin(a)>0, потому что ось Y положительна в этой четверти. И функция cos(a)>0, потому что ось X положительна в этой четверти.

Первую четверть можно описать через градусную меру, как (90-α) или (360+α).

Во второй четверти видно, что функция sin(a)>0, потому что ось Y положительна в этой четверти.
А функция cos(a)

В четвертой четверти видно, что функция sin(a)0, потому что ось X положительна в этой четверти.Четвертую четверть можно описать через градусную меру, как (270+α) или (360-α).

Теперь рассмотрим сами формулы приведения.

Запомним простой алгоритм:

• Четверть. (Всегда смотрите в какой вы четверти находитесь).
• Знак. (Относительно четверти смотрите положительны или отрицательный функции косинуса или синуса).
• Если у вас есть в скобочках (90° или π/2) и (270° или 3π/2), то функция меняется.

И так начнем разбирать по четвертям данный алгоритм.

Выясни чему будет равно выражение cos(90-α)

Рассуждаем по алгоритму:

• Четверть первая.
• В первой четверти знак у функции косинуса положительный.
• В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.

Будет cos(90-α) = sin(α).

Формулы приведения. Как запомнить?

Не пугайтесь, учить их не надо, как и многие другие формулы  в курсе математики. Лишней информацией голову забивать не нужно, необходимо  запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!»  – это значит, что  действительно,  это необходимо  именно выучить.

Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.

Перечислю лишь некоторые задачи, которые будут на ЕГЭ по математике, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:

• задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.
• задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
• задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
• стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.

И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.

Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?

Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от  0 до 450 градусов

Формулы приведения:

Угол альфа лежит пределах от 0 до 90 градусов.

Итак, необходимо уяснить «закон», который здесь работает:

Определите знак функции в соответствующей четверти.

Напомню их:

Запомните следующее:

Функция изменяется на кофункцию

Функция на кофункцию не изменяется

Что означает понятие — функция изменяется на кофункцию?

Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.

Теперь по представленному закону запишем несколько формул приведения самостоятельно:

Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:

• Угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Меняем функцию на кофункцию, так как у нас 270 градусов.
• Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов.
• Угол лежит во второй  четверти, синус во второй  четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов.

Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.

В статье на решение прямоугольного треугольника был отмечен такой факт  –  синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.

И наоборот – косинус одного острого угла в прямоугольном треугольнике равен синусу другого острого угла в нём. Вот вам и подтверждение этого с помощью формул приведения.

Конечно, определить  значения углов можно и без формул приведения, по тригонометрической окружности. И если вы умеете это делать, то очень хорошо. Но поняв, как работают формулы приведения, вы сможете делать это очень быстро.

В дальнейшем, применяя свойство периодичности, четности (нечётности) вы без труда определите значение любого угла: 10500, -7500, 23700 и любые другие. Статья об этом в будущем обязательно будет, не пропустите!

Когда в решениях задач буду использовать формулы приведения, то обязательно буду ссылаться на эту статью, чтобы вы всегда смогли освежить в памяти представленную выше теорию. На этом всё. Надеюсь, материал был вам полезен.

Какие понятия используются в геометрии?

В геометрии используются различные понятия, которые позволяют описывать и изучать геометрические фигуры и их свойства.

• Точка — это базовое понятие геометрии. Точка не имеет размеров и обозначается заглавной латинской буквой.
• Прямая — это бесконечное множество точек, которые лежат на одной линии. Прямую обозначают двумя точками или маленькой латинской буквой.
• Отрезок — это конечное множество точек на прямой, соединенных двумя конечными точками. Отрезок обозначается двумя точками над ним.
• Угол — это область между двумя лучами, имеющими общее начало. Угол измеряется в градусах (°) или радианах (рад).
• Треугольник — это фигура, образованная тремя отрезками, которые называются сторонами треугольника. Треугольник может быть разносторонним, равнобедренным или равносторонним.
• Полигон — это фигура, образованная отрезками, которые называются сторонами полигона. Полигон может быть треугольником, четырехугольником или многоугольником.
• Фигура — это геометрическое образование, которое имеет площадь и периметр. Фигуры могут быть плоскими или пространственными.

Это лишь некоторые из понятий, используемых в геометрии. Геометрия имеет много различных концепций и терминов, которые помогают понять и изучать геометрические объекты и их взаимодействие.

Измерение углов

Угловая мера

Угловая мера имеет свое важное место, она определяет отношение одного измерения углов на плоскости к другому, часто служа основой для строительства и математических вычислений. Угловая мера — это ключевой элемент геометрии, который помогает нам ориентироваться в мире и приводит нас к новым открытиям и пониманию форм

Это важный инструмент для создания и понимания структур, как в архитектуре, так и в науке. Угловая мера используется для сопоставления плоских углов. Два плоских угла считаются равными, если они полностью совмещаются, то есть их вершины и стороны совпадают. В любом направлении на плоскости можно построить один угол, равный данному. Если один угол может быть полностью включен внутрь другого так, что их вершины и одна из сторон совпадают, то первый угол будет меньше второго. Прилежащими называются два угла, у которых вершина и одна из сторон совпадают, однако их внутренние области не пересекаются. Угол, образованный несовпадающими сторонами двух прилежащих углов, будет являться комбинированным углом, составленным из данных углов.

Углы могут быть измерены в:

• радианах
• градусах — величина (градусная мера) угла, равная части развёрнутого угла.
• минутах — часть градуса.
• секундах — часть минуты.

Градусная мера угла обычно записывается в виде числа, которое указывает количество полных градусов, минут и секунд в угле. Например, угол 45 градусов 30 минут 20 секунд записывается как 45° 30′ 20″.

Для перевода градусов в минуты и секунды используется следующая формула:

1 градус = 60 минут.

1 минута = 60 секунд.

Таким образом, угол 45° можно представить как 45° * 60 минут = 2700 минут, или как 2700 минут * 60 секунд = 162000 секунд.

Градусная мера угла может быть положительной или отрицательной, в зависимости от направления вращения. Например, положительная градусная мера обозначает поворот против часовой стрелки, а отрицательная — по часовой стрелке. В градусной мере угол полного вращения равен 360°, в то время как в радианном измерении он равен 2π радианам.

Приборы для измерения углов

Для измерения углов существуют специальные измерительные приборы.

Транспортир представляет собой полукруглую пластину или полукруглый неподвижный выступ с делениями. Он обычно изготавливается из прозрачного пластика или металла. Чтобы построить угол с помощью транспортира, его нужно приложить к начальной точке угла, так чтобы центр транспортира совпал с вершиной угла. Затем можно провести линии через деления транспортира, чтобы определить величину угла.

Угломер представляет собой специальный инструмент для измерения углов. Он обычно состоит из двух подвижных линеек, которые можно установить в разные позиции для измерения различных типов углов. Угломеры могут быть аналоговыми или цифровыми, в зависимости от того, как они показывают измеренное значение угла.

Гониометр — это прибор для точного измерения углов в лабораторных условиях. Он обычно состоит из фиксированной основы и подвижной платформы, на которой устанавливаются примеры или объекты для измерения углов. Гониометры могут иметь тонкие шкалы и механизмы для поворота платформы с высокой точностью.

Кипрегель — это геодезический инструмент, используемый для измерения углов на местности. Он состоит из трёх ножек, которые можно установить на землю, и вертикального стержня с прикреплённым транспортиром для измерения углов. Кипрегели обычно используются геодезистами для измерения направления или углов между различными точками на местности.

Все эти инструменты предназначены для более точного и удобного измерения углов. Они используются в различных областях, включая строительство, геодезию, физику и другие науки. Применение правильного инструмента может значительно улучшить точность измерений и обеспечить более надежные результаты.

Определение косинуса

Косинус является одним из тригонометрических функций, которая определяется как отношение длины стороны прилегающего катета к длине гипотенузы в прямоугольном треугольнике.

Косинус обозначается символом cos и широко используется в математике, физике, геометрии и других науках. Он позволяет вычислять значения углов и решать различные задачи, связанные с треугольниками и циклическими процессами.

Углы в треугольнике могут быть описаны с помощью градусов или радианов. Косинус принимает значения в диапазоне от -1 до 1.

Определить значение косинуса можно с помощью таблицы значений, графика или специальных формул. Формула, наиболее часто используемая для определения косинуса, основывается на связи между косинусом и катетами прямоугольного треугольника:

Катет прилегающий	Гипотенуза	Косинус угла
Катет A	Гипотенуза c	cos(A) = A/c
Катет B	Гипотенуза c	cos(B) = B/c

Для определения значения косинуса по таблице необходимо знать значения длин катета и гипотенузы

Обратите внимание, что величина косинуса всегда будет находиться в диапазоне от -1 до 1

Знание косинуса и его свойств позволяет решать широкий круг задач, например, находить длины сторон треугольника или находить значения углов в треугольнике.