Диагонали четырехугольника - перпендикулярны тогда и только тогда, когда суммы квадратов

Диагонали четырехугольника — перпендикулярны или нет?

Одним из таких свойств является перпендикулярность диагоналей в некоторых случаях. Два отрезка называются перпендикулярными, если они образуют прямой угол, то есть угол между ними равен 90 градусам.

Существуют определенные условия, при которых диагонали четырехугольника являются перпендикулярными. Как правило, это касается некоторых особых классов четырехугольников, таких как квадрат или ромб.

Например, в квадрате все диагонали являются перпендикулярными. Также, в ромбе, диагонали, соединяющие его вершины, всегда перпендикулярны друг другу.

Однако, в общем случае, диагонали произвольного четырехугольника не являются перпендикулярными. Существует большое разнообразие четырехугольников, и возможные взаимное расположение их диагоналей весьма разнообразно.

Чтобы определить, перпендикулярны ли диагонали произвольного четырехугольника, необходимо провести дополнительные исследования, исполнять определенные условия или использовать известные свойства геометрических фигур.

Основные геометрические фигуры

Соединённые между собой точки образуют линии, а соединённые между собой линии — основные геометрические фигуры на плоскости.

Геометрические фигуры бывают плоские или двухмерные (2D) и объёмные пространственные, или трёхмерные (3D). Они ограничены замкнутой поверхностью своей наружной границы.

А если у геометрической фигуры все точки не находятся в одной плоскости, то она объёмная. К ним относятся шар, конус, цилиндр, сфера, пирамида и др.

Разберём плоские фигуры.

Треугольник

Треугольник — это фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки называются вершинами, а отрезки — сторонами.

Есть три вида треугольников:

Прямоугольный — когда один угол прямой, другие два меньше 90 градусов.
Остроугольный — когда градус его углов больше 0, но меньше 90 градусов.
Тупоугольный — когда один угол тупой, то есть больше 90 градусов, а два других — острые.

Треугольники имеют следующие свойства:

в треугольнике напротив большего угла лежит большая сторона и наоборот;
сумма углов треугольника всегда равна 180 градусам;
все углы равностороннего треугольника равны 60 градусам;
в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (но это изучается уже в старших классах).

Вершины треугольников обозначаются заглавными буквами латинского алфавита: A, B, C и др.

Примеры треугольников:

Окружность

Окружность — геометрическая фигура, образованная замкнутой кривой линией, все точки которой находятся на одинаковом от центра расстоянии.

Круг

Часть плоскости, находящаяся внутри окружности, называется кругом. То есть, окружность — это граница круга. А расстояние от центра окружности до любой точки на ней называется радиусом. Диаметр круга — это отрезок, который соединяет две точки на окружности и проходит через её центр. Диаметр круга равен двум его радиусам.

Прямоугольник

‍Прямоугольник — это фигура, состоящая из четырёх сторон и четырёх прямых углов, у которой:

противоположные стороны равны между собой;
диагонали равны и делятся в точке пересечения пополам;
около прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагоналей.

Квадрат

Квадрат — это тот же прямоугольник, у которого:

все стороны равны;
все углы равны и составляют 90 градусов;
диагонали равны и перпендикулярны;
центры вписанной и описанной окружности совпадают и находятся в точке пересечения его диагоналей.

Трапеция

Четырёхугольник, у которого две стороны параллельны, а две — нет, называется трапецией. Если сумма длин оснований трапеции равна сумме длин боковых сторон, в неё можно вписать окружность.

Параллелограмм и ромб

Параллелограмм — четырёхугольник, противоположные стороны которого попарно параллельны.

Ромб — это параллелограмм с равными сторонами.

Параллелограмм имеет следующие свойства:

противоположные стороны и углы равны;
сумма двух любых соседних углов равна 180 градусам;
диагонали пересекаются и точкой пересечения делятся пополам;
каждая диагональ делит фигуру на два равных треугольника.

Основные величины и их формулы

Все геометрические фигуры имеют свои характеристики и собственную величину. Самыми распространёнными являются такие величины как площадь и периметр. Они используются в повседневной жизни, в строительстве и в других областях. Например, во время ремонта или нового строительства, количество необходимых материалов и объём работ не определить, не вычислив заранее площадь и периметр.

Периметр

Периметром называется замкнутая граница плоской геометрической фигуры, которая отделяет её внутреннюю область от внешней. Периметр есть у любой замкнутой геометрической фигуры:

На рисунке периметры выделены красной линией. Периметр окружности часто называют длиной.

Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.

Обозначается заглавной латинской P.

Площадь

Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой, то есть та часть плоскости, которая находится внутри периметра. Именно она даёт нам основную информацию о её размере. Любая плоская замкнутая геометрическая фигура имеет определённую площадь.

На рисунке площади фигур окрашены различными цветами.

Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм2, см2, м2, км2 и т. д. S (square) — знак площади.

Вычисление периметра и площади

Периметр — это длина замкнутого контура геометрической фигуры. Можно, конечно, измерить линейкой длины всех сторон и сложить их. Но лучше воспользоваться специальными формулами для вычисления периметра, это значительно упростит задачу.

Квадрат: периметр = 4 * сторона.
Треугольник: периметр = сторона 1 + сторона 2 + сторона 3.
Неправильный многоугольник: периметр = сумме всех сторон многоугольника.
Круг: длина окружности = 2 * π * радиус = π * диаметр (где π – это число пи (константа, примерно равная 3,14), радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности, диаметр – это длина отрезка, проходящего через центр окружности и соединяющего любые две точки, лежащие на этой окружности).

Для вычисления площади фигуры также потребуется соответствующая формула. К разным фигурам применяются разные формулы. Для вычисления площади стандартных геометрических фигур можно воспользоваться следующими формулами:

Параллелограмм: площадь = основание * высота
Квадрат: площадь = сторона 1 * сторона 2
Треугольник: площадь = ½ * основание * высота
Круг: площадь = π * радиус² (где радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Квадрат радиуса – это значение радиуса, умноженное само на себя).

Итак, мы перечислили основные и самые распространённые геометрические фигуры и их свойства. Образовательная платформа iSmart поможет вашему ребёнок изучить основные геометрические фигуры, их виды, названия и свойства с помощью увлекательных заданий. Преимущества занятий на умных тренажёрах iSmart:

интерактивные задания больше похожи на игру;
их можно отрабатывать многократно и они не будут повторяться;
платформа сформирует индивидуальную траекторию обучения на основе диагностики знаний;
достаточно всего 20 минут занятий в день, чтобы в короткий срок увидеть прогресс в обучении.

Кроме того, занятия помогут вам освободить своё время, ведь ребёнок сможет заниматься самостоятельно, а родитель — получать отчёты и наблюдать за динамикой обучения. Метод обучения iSmart основан на последних научных практиках: микрообучение и поведенческий анализ.

Образовательная платформа iSmart предлагает подготовку к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.

Как описать четырехугольник окружностью?

Окружность, проходящая по всем вершинам четырехугольника, называется описанной окружностью. Если сумма противоположных углов равна 180°, то такой четырехугольник можно описать окружностью. В случае, если данное условие не выполняется, то такой четырехугольник невозможно описать окружностью.

Центр описанной окружности четырехугольника — это точка пересечения перпендикуляров, выходящих из середины сторон.

Мы уже рисовали описанную окружность для треугольника. Алгоритм для описания окружности для четырехугольника такой же. На рисунке хорошо видно, как из середины сторон мы провели перпендикуляры и нашли точку пересечения. С помощью штангенциркуля выставляем радиус от центра до любой вершины и круговым движением рисуем описанную окружность четырехугольника.

Найди ортодиагональные четырехугольники.

Вопрос-ответ:

Что означает понятие «перпендикулярно» в геометрии?

В геометрии, «перпендикулярно» означает, что две линии или отрезка образуют прямой угол, то есть угол, равный 90 градусов.

Как можно определить, что две линии перпендикулярны?

Для определения перпендикулярности двух линий необходимо убедиться, что угол между ними равен 90 градусов. Для этого можно использовать специальный инструмент — угольник или использовать геометрические свойства, например, если две линии пересекаются и образуют прямой угол, то они перпендикулярны.

Какие примеры можно привести для иллюстрации понятия перпендикулярности?

Примеры перпендикулярности можно встретить везде в повседневной жизни, например, угол стола и его ножек, угол дома и его фундамента, перекрестие дорог и т. д. В геометрии часто используют примеры перпендикулярности, чтобы объяснить свойства и теоремы.

Какова роль перпендикулярности в геометрии?

Перпендикулярность является важным понятием в геометрии, так как она образует основу для доказательств и выводов. Она позволяет определить прямые углы, разбить изначально сложные фигуры на более простые, а также использовать перпендикулярность для построения различных геометрических фигур.

Какие еще теоремы и свойства связаны с понятием перпендикулярности?

К перпендикулярности относятся также теорема о перпендикуляре к радиусу, теорема о перпендикуляре к хорде, свойство перпендикуляра в прямоугольном треугольнике и другие. Все эти свойства и теоремы позволяют проводить дальнейшие выводы и вычисления на основе перпендикулярности в геометрии.

Что значит перпендикулярно в геометрии?

Перпендикулярно в геометрии означает, что две линии или отрезка пересекаются под прямым углом. То есть, если провести отрезок или линию, которая перпендикулярна к другой линии, то они будут образовывать угол в 90 градусов.

Можете привести примеры перпендикулярных линий?

Конечно! Примеры перпендикулярных линий могут быть следующими: 1) Если провести отрезок, вертикальный линейка, и отрезок, горизонтальный линейка, то они будут перпендикулярными. 2) Или если провести прямые отрезки, один из которых идет вертикально вверх, а другой горизонтально вправо, то они также будут перпендикулярными.

Обыкновенный и необыкновенный лучи

Определение. У первого луча, с вектором (перенаправленным ровно основной плоскости), скорость не имеет зависимости от направлений и равняется лучевой скорости с перенаправлением коллинеарным оптической оси. Величины, которые можно отнести к этому лучу, будем выделяться индексом o.

Определение. Луч можно назвать необыкновенным, если у него электрический вектор прибывает в основной плоскости, его скорость будет зависеть от направления (основная ось в сечении эллипсоида изменяется при смещении направлений луча). Характеристики, относятся к этому лучу, выделяют индексом e. У отрицательных кристаллов есть соотношение скоростей: .

Основные утверждения и теоремы о диагоналях четырехугольника

Основной теоремой, связанной с диагоналями четырехугольника, является теорема о диагоналях, которая утверждает, что диагонали являются векторами, делящими его пополам и пересекающимися в одной точке. Это означает, что точка пересечения диагоналей является серединой каждой диагонали.

Другая важная теорема, связанная с диагоналями четырехугольника, — теорема о противоположных диагоналях. Она утверждает, что противоположные диагонали четырехугольника равны друг другу, то есть длины AC и BD равны длинам AD и BC соответственно.
Еще одно утверждение, касающееся диагоналей четырехугольника, является теорема о треугольниках. Она гласит, что треугольники ABD и BCD являются равными, а также треугольники ABC и ACD также равны. Это означает, что диагонали делят четырехугольник на четыре равных треугольника.

Помимо основных утверждений и теорем, есть и другие зависимости, касающиеся диагоналей четырехугольника. Например, если четырехугольник является выпуклым, то прямая, проходящая через середины диагоналей, является линией симметрии для четырехугольника. Также существует теорема о параллельности диагоналей, утверждающая, что если прямая, проходящая через середины противоположных сторон, параллельна одной из диагоналей четырехугольника, то она также параллельна и второй диагонали.

Шаг 1: Перпендикулярность: определение и свойства

Основное свойство перпендикулярных прямых заключается в том, что угол между ними равен 90 градусам. Это значит, что когда две перпендикулярные прямые пересекаются, они образуют прямой угол.

Перпендикулярные прямые обладают следующими свойствами:

Свойство	Описание
Определение	Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Угол	Угол между перпендикулярными прямыми равен 90 градусам.
Существование	Для любой данной прямой существует единственная перпендикулярная ей прямая.
Симметрия	Если прямая A перпендикулярна прямой B, то прямая B также перпендикулярна прямой A.
Третья прямая	Если прямая A перпендикулярна прямой B, и прямая B перпендикулярна прямой C, то прямая A также перпендикулярна прямой C.

Примеры перпендикулярных прямых включают:

— Вертикальные линии, такие как стены в здании, которые пересекают горизонтальные полы или потолки.

— Углы треугольников, где перпендикулярные прямые соответствуют боковым сторонам.

— Линии на карте, которые пересекают друг друга в прямых углах.

Понимание понятия перпендикулярности и его свойств поможет в решении задач геометрии, а также в построении и анализе различных фигур и объектов.

Геометрическое определение перпендикулярности

Геометрическое определение перпендикулярности можно проиллюстрировать на примере перпендикулярных отрезков. Если два отрезка пересекаются так, что образуется прямой угол, то они являются перпендикулярными. Данное определение также применимо к отрезкам, лучам и прямым линиям. Примером перпендикулярных прямых могут служить стороны прямоугольника или крест-анкер, где четыре прямые линии образуют углы в 90 градусов друг с другом.

Понятие перпендикулярности широко используется в геометрии и играет важную роль в решении различных задач. Например, перпендикулярные линии и плоскости часто используются для построения прямоугольных форм, ориентации объектов в пространстве и определения правильных углов. Знание определения перпендикулярности позволяет точно определить взаимное расположение линий и применять их в практических ситуациях.

Свойства перпендикулярных линий и отрезков

Одним из главных свойств перпендикулярных линий является то, что они образуют прямой угол. Прямой угол равен 90 градусам и может быть обозначен символом ⌫. Если две линии пересекаются и образуют прямой угол, то они называются перпендикулярными.

Еще одним свойством перпендикулярных линий и отрезков является то, что они имеют равные углы косинусы. Если две линии перпендикулярны, то косинусы углов, образованных этими линиями, равны 0. Это свойство может быть использовано для нахождения перпендикулярной линии или отрезка.

Еще одно важное свойство перпендикулярных линий и отрезков — то, что они не пересекаются. Если две линии пересекаются, то они не могут быть перпендикулярными. Это свойство помогает строить перпендикуляры и определять их положение в пространстве

Это свойство помогает строить перпендикуляры и определять их положение в пространстве.

Кроме того, перпендикулярные линии и отрезки могут использоваться для создания прямоугольников, параллелограммов и других геометрических фигур.

Итак, свойства перпендикулярных линий и отрезков — это образование прямого угла, равность углов косинусов, их непересечение и использование в построении различных фигур. Знание этих свойств поможет решать задачи и проводить геометрические конструкции.

Понятие взаимной перпендикулярности

Другими словами, если имеются две перпендикулярные линии А и В, и две перпендикулярные линии С и D, то можно сказать, что А перпендикулярна В, С перпендикулярна D, и А перпендикулярна С, и В перпендикулярна D. Таким образом, все линии в данной системе взаимно перпендикулярны друг другу.

Примером взаимной перпендикулярности может служить прямоугольник. В прямоугольнике все четыре стороны являются взаимно перпендикулярными, так как каждая из них образует прямой угол с соседними сторонами.

Видео:2. Уравнение плоскости примеры решения задач #1Скачать

Теорема о вписанной окружности

Теорема о вписанной окружности имеет множество важных следствий и свойств, которые широко применяются в геометрии и ее приложениях. В частности, она позволяет устанавливать равенства углов, длины отрезков и другие свойства четырехугольников без знания их сторон и углов.

Доказательство теоремы основано на наблюдении, что в двухпараллельном четырехугольнике сумма противоположных углов равна 180 градусам, а также на свойствах углов, образуемых хордами внутри окружности. Доказательство можно представить в виде следующей последовательности шагов:

Рассмотрим двухпараллельный четырехугольник ABCD, в котором угол A и угол C являются противоположными углами.
Проведем диагонали AC и BD четырехугольника ABCD.
Предположим, что существует окружность, проходящая через все вершины четырехугольника ABCD.
Так как окружность проходит через точки A и C, она будет проходить через точку пересечения диагоналей AC и BD (обозначим эту точку как O).
Так как угол A и угол C являются противоположными углами, из свойств пересекающихся хорд следует, что угол AOC будет являться остроугольным.
Но так как сумма углов треугольника AOC равна 180 градусам, то угол AOC не может быть остроугольным.
Противоречие! Значит, предположение о существовании окружности, проходящей через все вершины четырехугольника ABCD, неверно.
Таким образом, мы доказали теорему о вписанной окружности: в любом двухпараллельном четырехугольнике, в котором сумма противоположных углов равна 180 градусам, существует окружность, которая проходит через все вершины этого четырехугольника.

Теорема о вписанной окружности является важным инструментом в геометрии и широко применяется в различных областях, таких как аналитическая геометрия, теория алгоритмов и дизайн. Учение о вписанных окружностях помогает устанавливать различные свойства и интересные факты о фигурах, а также позволяет проводить точные и эффективные вычисления в различных задачах.

Виды четырехугольников

Выпуклый четырехугольник

Когда мы слышим слово «выпуклый», нам следует представить что-то, что выдается наружу или бугристое. Так вот, выпуклый четырехугольник — это такой четырехугольник, у которого все углы меньше 180 градусов. Если вы нарисуете эту фигуру на листе бумаги, то сможете провести любую прямую, пересекающую две стороны, и она будет целиком находиться внутри четырехугольника.

Пошаговое рисование выпуклого четырехугольника:

Возьмите лист бумаги и ручку.
Нарисуйте четыре точки, но так, чтобы они не образовывали букву «С».
Соедините точки, создавая четыре стороны. Убедитесь, что все углы меньше 180 градусов.
У вас на руках выпуклый четырехугольник!

Невыпуклый четырехугольник

В отличие от выпуклого четырехугольника, у невыпуклого четырехугольника есть хотя бы один угол, который превышает 180 градусов. Представьте себе бумажный самолетик, одна из его частей напоминает невыпуклый четырехугольник.

Пошаговое рисование невыпуклого четырехугольника:

Начните с листа бумаги и ручки.
Рисуйте четыре точки, но так, чтобы, например, три из них образовывали букву «U».
Соедините точки, чтобы получилась замкнутая фигура.
Готово! У вас есть невыпуклый четырехугольник.

Прямоугольник как особый случай четырехугольника

Прямоугольник — это четырехугольник, у которого все углы равны 90 градусам, а противоположные стороны равны и параллельны друг другу. Например, ваш компьютерный экран или книга часто имеют форму прямоугольника.

Как определить прямоугольник:

Посмотрите на фигуру. Есть ли у нее четыре угла?
Если да, проверьте, равны ли все углы 90 градусам.
Также убедитесь, что противоположные стороны одинаковы по длине и параллельны.
Если все условия соблюдены, перед вами прямоугольник!

С каждым видом четырехугольника связаны свои интересные особенности и задачи. Продолжим исследование, чтобы узнать больше!

Способы построения перпендикулярных прямых

Но как можно построить вертикальные линии? Что вам для этого нужно? Давайте рассмотрим все доступные нам методы.

Самое простое — использовать транспортир. Постройте прямую a и точку A, которая не лежит на этой прямой. Совместите значение 90 градусов с точкой так, чтобы нижняя часть транспортира как линейки полностью совпадала с линией, и сделайте надрез в отверстии транспортира. Соедините точку А с конным шерифом до пересечения с прямой линией.

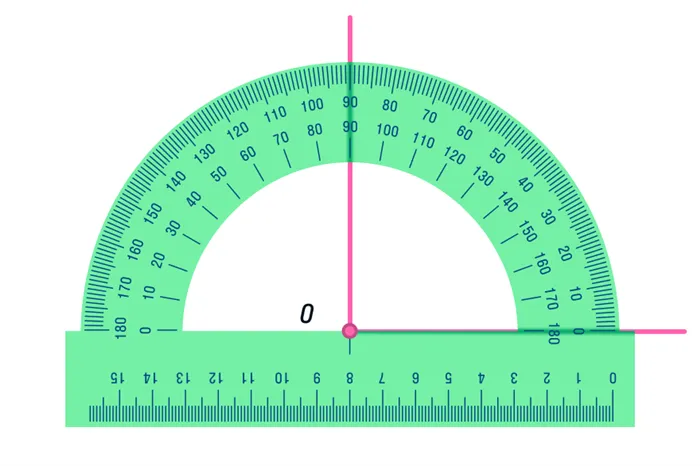
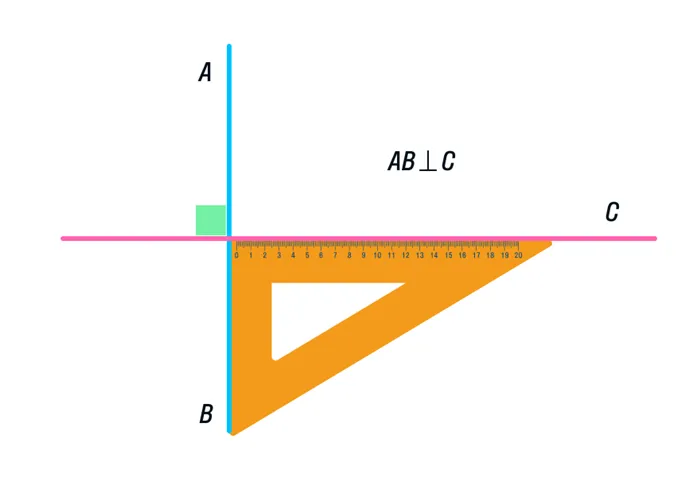
Но что делать, если транспортир забыт дома, а в наличии только линейка и транспортир? Внимательно рассмотрите рисунок и потренируйтесь рисовать дома.

Роль диагонали в измерении фигуры

Диагональ является одной из ключевых характеристик четырехугольника и играет важную роль в его измерении и геометрических свойствах. Диагональ – это отрезок, соединяющий две вершины многоугольника, не являющиеся соседними. В случае четырехугольника диагональ соединяет вершины, не лежащие на одной и той же стороне фигуры.

Рассмотрим роль диагонали в измерении и характеристиках четырехугольника:

Длина диагонали. Длина диагонали определяет расстояние между двумя вершинами четырехугольника, которые не связаны стороной. Это позволяет оценить размеры фигуры и ее геометрические свойства. Для определения длины диагонали часто используются различные методы, такие как использование теоремы Пифагора или применение тригонометрических функций.
Углы между диагоналями. В четырехугольнике, основанном на структуре его диагоналей, существуют определенные связи между углами, образованными диагоналями и сторонами фигуры. В зависимости от свойств четырехугольника, эти углы могут иметь разные величины и определять его форму и тип.
Разделение фигуры на треугольники. Диагонали четырехугольника делят его на два треугольника, каждый из которых может быть рассмотрен по отдельности. Это позволяет проводить более глубокий анализ фигуры и расчет различных характеристик каждого из треугольников.
Сравнение длин диагоналей. Диагонали четырехугольника могут иметь разные величины. Сравнение длин диагоналей позволяет определить, является ли четырехугольник ромбом, квадратом, прямоугольником или другим типом четырехугольника. Например, в ромбе все диагонали равны между собой, а в прямоугольнике диагонали являются взаимно перпендикулярными и равными.

Таким образом, диагональ играет значительную роль в измерении фигуры, определении ее формы и типа, а также в выявлении ее геометрических свойств. Знание длин диагоналей и углов между ними позволяет проводить детальный анализ и расчет различных характеристик четырехугольника.

Практическое применение диагоналей в дизайне

Диагональная композиция – это один из наиболее универсальных и эффективных способов организации пространства в дизайне. Она создает динамичность и движение, а также позволяет выделить важные элементы и акценты в макете.

Диагонали могут использоваться в различных видах дизайна – от веб-дизайна до графического и промышленного дизайна. Вот несколько практических применений диагоналей в дизайне:

Создание рамок и границ. Диагональные линии могут использоваться для создания рамок вокруг изображений или текста, что помогает выделить его и добавляет интересный визуальный эффект.
Создание переходов и градиентов. Диагональные линии могут быть использованы для создания плавных переходов цветов или тонов в градиентах.
Создание движения и направления. Диагональные линии могут добавлять ощущение движения или направления в дизайне, что делает его более динамичным и интересным для восприятия.
Выделение важных элементов. Диагональные линии могут быть использованы для выделения ключевых элементов в дизайне, таких как заголовки, кнопки или важная информация.
Создание графических элементов. Диагональные линии могут быть использованы для создания графических элементов, таких как карточки, рамки или фоны с текстурой.

Когда используется диагональная композиция, важно учитывать ее соотношение с другими элементами дизайна

Она должна быть гармоничной и не отвлекать внимание от важных информационных или функциональных элементов

Зная основные принципы и методы работы с диагоналями, дизайнеры могут создавать более интересные и эффективные макеты, которые будут привлекать внимание пользователей и подчеркивать важность содержимого

Критерии перпендикулярности диагоналей

Четырехугольник, у которого диагонали перпендикулярны, называется ортодиагональным. Для доказательства ортодиагональности четырехугольника можно использовать несколько критериев.

1. Первый критерий основан на использовании теоремы Пифагора. Если сумма квадратов диагоналей равна сумме квадратов их отрезков, соединяющих их с вершинами четырехугольника, то диагонали перпендикулярны.

2. Второй критерий базируется на том, что квадрат расстояния между серединами диагоналей равен половине суммы квадратов длин диагоналей. Если это равенство выполняется, то диагонали перпендикулярны.

3. Третий критерий предполагает использование векторов. Если вектор, соединяющий вершины противоположных углов, является радиус-вектором, то диагонали перпендикулярны.

4. Четвертый критерий основан на равенстве треугольников. Если две треугольника, образованные диагоналями и сторонами четырехугольника, равны между собой, то диагонали перпендикулярны.

Необходимо отметить, что в каждом критерии требуется доказать равенство некоторых элементов геометрических фигур, а также использовать свойства перпендикулярности и равенства треугольников. При выполнении этих условий можно доказать перпендикулярность диагоналей четырехугольника.

Свойства перпендикуляра к прямой

Свойство	Описание
1	Перпендикулярные прямые не пересекаются.
2	Все точки, лежащие на перпендикуляре к прямой, равноудалены от данной прямой.
3	Перпендикуляр к прямой является кратчайшим расстоянием от данной прямой до любой точки на плоскости.
4	Перпендикуляр к прямой одновременно является нормалью к данной прямой. Это означает, что у них пересекающиеся прямые образуют прямоугольник.

Перпендикулярность диагоналей четырехугольника

Для доказательства перпендикулярности диагоналей четырехугольника нам необходимо установить, что их попарные произведения наклонов равны и противоположны.

Пусть дан четырехугольник ABCD с вершинами A, B, C и D. Для удобства обозначим стороны и диагонали следующим образом:

AB — сторона, соединяющая вершины A и B

BC — сторона, соединяющая вершины B и C

CD — сторона, соединяющая вершины C и D

DA — сторона, соединяющая вершины D и A

AC — диагональ, соединяющая вершины A и C

BD — диагональ, соединяющая вершины B и D

Для доказательства перпендикулярности необходимо установить следующее:

AC * BD = -AB * CD

Так как в четырехугольнике ABCD диагонали пересекаются в точке O, а теорема о произведении наклонов гласит, что произведение попарных наклонов равно -1, то мы можем записать следующее равенство:

AC * BD = -AO * OC * -BO * OD = AO * OC * BO * OD = AB * CD

Таким образом, мы доказали, что произведение наклонов попарных диагоналей равно и противоположно друг другу, что подтверждает их перпендикулярность.