Рациональные методы устных вычислений

Сложение и вычитание: основы арифметики

В арифметике существует две основные операции — сложение и вычитание. Эти действия позволяют совершать различные операции с числами и решать математические задачи.

Сложение — это операция, которая позволяет объединять два или более числа для получения их суммы. В математике сложение обозначается знаком «+». Например, сумма чисел 2 и 3 обозначается как 2 + 3 = 5.

Чтобы сложить два числа, нужно записать их друг под другом, так чтобы единицы, десятки и сотни располагались в столбик. Затем сложите цифры в каждом столбике, начиная справа налево. Если сумма цифр в столбике больше или равна 10, запишите только единицы, а десятки запишите в следующий столбик.

Например, чтобы сложить числа 256 и 137, следует записать их столбиком:

	2	5	6
+	1	3	7
	3	8	3

В данном примере, сумма цифр в столбиках равна: 6 + 7 = 13 (единицы в столбике), 5 + 3 = 8 (десятки в столбике), 2 + 1 = 3 (сотни в столбике). Таким образом, сумма чисел 256 и 137 равна 383.

Вычитание — это операция, которая позволяет находить разность между двумя числами. В математике вычитание обозначается знаком «-«. Например, разность чисел 10 и 5 обозначается как 10 — 5 = 5.

Чтобы вычесть одно число из другого, нужно записать их друг под другом, так чтобы единицы, десятки и сотни располагались в столбик. Затем вычитайте цифры в каждом столбике, начиная справа налево. Если разность цифр в столбике меньше 0, возьмите 1 из столбика выше. Если разность равна 0 или больше, запишите ее в соответствующий столбик.

Например, чтобы вычесть число 537 из числа 829, следует записать их столбиком:

	8	2	9
—	5	3	7
	3	9	2

В данном примере, разность цифр в столбиках равна: 9 — 7 = 2 (единицы в столбике), 2 — 3 = -1 (десятки в столбике), 8 — 5 = 3 (сотни в столбике). Таким образом, разность чисел 829 и 537 равна 292.

Освоив основы сложения и вычитания, ученики смогут более эффективно решать задачи и применять полученные навыки в повседневной жизни.

Что делать первым: умножение или деление?

На уроках математики мы часто сталкиваемся с умножением и делением чисел. Иногда возникает вопрос, какое из этих действий следует выполнять первым. Ответ на этот вопрос зависит от конкретной ситуации. Рассмотрим несколько примеров:

1. Если задача содержит только умножение и деление:

   • Выполняйте действия в порядке, в котором они даны в задаче.
   • Если нет явного указания, выполните операции слева направо.

2. Если задача содержит умножение, деление и другие действия:

   • Выполняйте умножение и деление в порядке их появления в задаче.
   • Если есть скобки, выполните действия внутри скобок сначала.
   • Затем выполните умножение и деление с лева на право.
   • В конце выполните сложение и вычитание с лева на право.

3. Если задача содержит только умножение и деление без скобок:

   Выполняйте операции слева направо.

Важно помнить, что существуют математические правила, которые определяют порядок выполнения операций (например, умножение и деление выполняются раньше сложения и вычитания). Однако, в задачах могут быть дополнительные условия, поэтому всегда внимательно читайте и анализируйте их перед выполнением действий

Сколько действий есть в математике?

Математика – это наука, изучающая числа, их свойства и взаимоотношения, а также различные операции над ними.

В математике существуют различные действия, которые позволяют выполнять операции с числами. Основные действия в математике включают:

1. Сложение – операция, позволяющая складывать два или более числа, результатом которой является их сумма.
2. Вычитание – операция, позволяющая вычитать одно число из другого, результатом которой является разность.
3. Умножение – операция, позволяющая находить произведение двух или более чисел.
4. Деление – операция, позволяющая делить одно число на другое, результатом которой является частное.

В математике также существуют и другие действия, такие как возведение в степень, извлечение корня, нахождение остатка от деления и др., которые позволяют решать различные задачи и проводить более сложные вычисления.

Правильное выполнение действий в математике имеет большое значение, поскольку ошибки в расчётах могут привести к неверным результатам и неправильным выводам

Поэтому важно уметь выполнять все действия в правильной последовательности и использовать правила математики

Что такое деление?

Деление — это одно из основных арифметических действий, которое используется для разделения одного числа на другое. Оно позволяет найти количество равных частей, на которые может быть разделено исходное число.

Деление обозначается символом «/», который называется «делить» или «разделить». Результатом деления является число, называемое частным.

Процесс деления состоит из трех основных компонентов: делимого, делителя и частного.

• Делимое — число, которое будет делиться.
• Делитель — число, на которое будет делиться делимое.
• Частное — результат деления.

Выполнять деление можно как на бумаге, используя алгоритм деления, так и с помощью калькулятора или компьютера.

Деление имеет свои особенности и правила, которые помогают выполнить это действие корректно и получить правильный результат. Например, если делитель равен нулю, то деление невозможно, так как на ноль делить нельзя.

Основными понятиями при делении являются:

1. Частное — результат деления.
2. Остаток — число, которое остается после выполнения деления.

Частное может быть целым или десятичным числом, в зависимости от исходных данных. Остаток также может быть нулевым или отличным от нуля.

Деление является важным элементом математики и широко используется в повседневной жизни. Оно позволяет решать различные задачи и выполнять сложные вычисления.

Гаусс и устный счет

Карл Фридрих Гаусс

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить.  Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Как выбрать порядок действий?

Правильный выбор порядка действий в математике очень важен для получения верного результата. Особенно это касается умножения и деления — двух основных операций, которые мы используем для работы с числами.

Когда перед нами стоит задача, где требуется выполнить и умножение, и деление, мы должны придерживаться определенного порядка действий, чтобы ответ был правильным.

Правило гласит, что сначала выполняется умножение, а затем деление. То есть, если в математическом выражении есть и умножение, и деление, мы сначала выполняем умножение, а затем уже деление.

Если в выражении нет скобок, то выполнение умножения и деления осуществляется слева направо. То есть, читаем выражение слева на право и выполняем все умножения перед делением.

Например, если у нас есть выражение 8 * 4 / 2, сначала мы выполняем умножение 8 * 4 = 32, а затем деление 32 / 2 = 16.

Однако, если в выражении есть скобки, то сначала выполняются операции внутри скобок. Затем выполняются умножение и деление внутри скобок. И, наконец, выполняются умножение и деление вне скобок.

Например, в выражении (8 * 4) / 2 мы сначала выполняем операцию в скобках 8 * 4 = 32, затем деление 32 / 2 = 16.

Если же есть несколько операций умножения и деления подряд, то выполняются они слева направо.

Например, в выражении 8 * 4 / 2 * 5 мы сначала выполняем умножение 8 * 4 = 32, затем деление 32 / 2 = 16, и в конце умножение 16 * 5 = 80.

Резюмируя, чтобы выбрать порядок действий в умножении и делении, следует запомнить основное правило: сначала выполняется умножение, затем деление. Если есть скобки, то сначала выполняются операции внутри скобок.

Деление чисел в уме

Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.

Деление на однозначное число

При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.

Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:

6144:8=(5600+544):8=700+544:8

Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

64:8=8

6144:8=700+60+8=768

Деление на двузначное число

При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.

Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет , так как 5*6=30. Действительно, 1325*656=869200.

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления  может быть либо число 74, либо 79. Проверяем:

79*56=4424

Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»

Примеры умножения в столбик

Пример 1

Умножьте двузначное число на однозначное, например, 32 на 7.

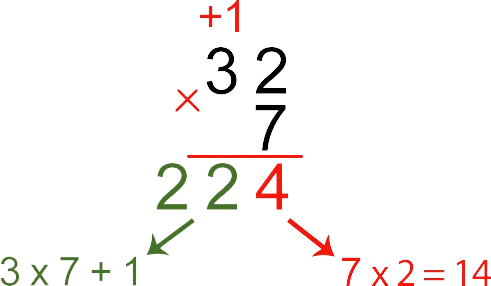
В этом случае второй множитель состоит только из одной цифры — единицы. Умножьте 7 на каждую цифру первого множителя по очереди. В данном случае произведение 7 и 2 равно 14. В ответе мы оставляем цифру 4 в ее текущем положении (единицы) и прибавляем единицу к результату умножения 7 на 3 (7⋅3+1=22).

Пример 2

Найдите произведение двузначного и трехзначного чисел: 416 и 23.

• Записываем множители друг под другом (в верхней строке – 416).
• Поочередно умножаем цифру 3 числа 23 на каждый разряд числа 416, получаем – 1248.
• Теперь умножаем 2 на каждую цифру 416, и полученный результат (832) записываем под числом 1248 со смещением на один разряд влево.
• Остается только сложить числа 832 и 1248, чтобы получить ответ, который равняется 9568.

Публикации по теме:

• Таблица сложения чисел
• Таблица умножения чисел
• Таблица деления чисел
• Таблица вычитания чисел
• Расчеты с процентами
• Чему равна промилле и как обозначается
• Простые и взаимно простые числа
• Позиционные системы счисления
• Квадраты натуральных чисел
• Кубы натуральных чисел
• Единицы измерения времени
• Единицы измерения длины
• Единицы измерения массы
• Единицы измерения объема
• Сложение двузначных, трехзначных и многозначных чисел столбиком
• Свойства сложения чисел с примерами
• Свойства вычитания чисел с примерами
• Свойства умножения чисел с примерами
• Свойства деления чисел с примерами
• Вычитание двузначных, трехзначных и многозначных чисел столбиком
• Что такое натуральные числа

Практическое применение умножения

Умножение — одна из основных операций в математике, которая находит произведение двух чисел. Эта операция имеет множество практических применений в повседневной жизни.

Умножение в торговле:

Умножение используется в торговле для определения общей стоимости товаров. Например, если цена одного товара составляет 100 рублей, а покупатель хочет приобрести 5 таких товаров, то общая стоимость будет равна 100 рублей * 5 = 500 рублей.

Умножение в строительстве:

В строительстве умножение применяется для вычисления площади поверхности или объема. Например, чтобы вычислить площадь комнаты со сторонами 4 метра и 5 метров, необходимо умножить эти два значения: 4 м * 5 м = 20 квадратных метров.

Умножение в финансовой сфере:

В финансовой сфере умножение используется для расчета процентов, дохода или ставок. Например, чтобы вычислить общую сумму с учетом процентов по займу, необходимо умножить начальную сумму займа на процентную ставку и на количество периодов.

Умножение в науке:

В науке умножение применяется для вычислений, моделирования и анализа данных. Например, при исследовании физических процессов или математических моделей, умножение используется для получения точных результатов.

Умножение в кулинарии:

В кулинарии умножение часто используется для настройки рецептов на нужное количество порций. Например, если в рецепте указано использование 2 яиц, а вы хотите приготовить блюдо на 4 порции, то необходимо умножить количество ингредиентов на 2 (2 * 2 = 4).

Умножение в спорте:

В спорте умножение может использоваться для расчета результатов, рекордов или статистики. Например, для определения скорости бегуна на дистанции 100 метров, необходимо разделить пройденное расстояние на время: скорость = расстояние / время.

Как видно из приведенных примеров, умножение неотъемлемая часть многих сфер нашей жизни, и его практическое применение намного шире, чем просто умножение двух чисел.

Как умножить тысячи на многозначное число

Здесь поможет система Якова Трахтенберга. Во время заключения нацистами математик нашёл способ счёта особо крупных чисел в уме.

Предупреждаю, что способ подойдёт только тем, кто наработал краткосрочную память на большой массив чисел. Поскольку вам придётся долго держать остаток в уме и параллельно делать десяток сложений.

Запомните метод как Принцип снежинки.

В качестве примера решим 5362∙2934. Алгоритм такой:

Представьте числа привычным столбиком.

1. Перемножьте конечные (2∙4) цифры сверху и снизу.

Предпоследнюю цифру при наличии держим в уме (0), последнюю отправляем в результат (8): ** *** **8.

2. Перемножьте предпоследнюю цифру верхнего числа на последнюю нижнего (6∙4) и наоборот (3∙2).

Сложите результаты с тем, что храните в уме (24+6+0=30).

Держим остаток (3), а последнее число ставим в итог слева от предыдущего (0): ** *** *08.

3. Умножьте вторую цифру верхнего числа на последнюю нижнего (3∙4) и наоборот (9∙2).

Сложите результаты (12+18=30), а к ним добавьте умноженные друг на друга третьи цифры (6∙3) и остаток в уме (30+18+3=51).

Получили десяток в уме (5) и третью с конца цифру (1): ** *** 108.

4. Умножьте первую цифру сверху на последнюю снизу (5∙4) и наоборот (2∙2).

Умножьте вторую цифру сверху на третью снизу (3∙3) и наоборот (9∙6).

Сложите четыре числа и пятое из ума (20+4+9+54+5=92).

Получили десяток в уме (9) и четвёртую с конца цифру (2): ** **2 108.

5. Умножьте первую цифру верхнего числа на третью нижнего (5∙3) и наоборот (2∙6).

Сложите результаты, а к ним добавьте умноженные друг на друга вторые числа (3∙9) и остаток в уме (15+12+27+9=63).

Получили десяток в уме (6) и пятую с конца цифру (3): ** *32 108.

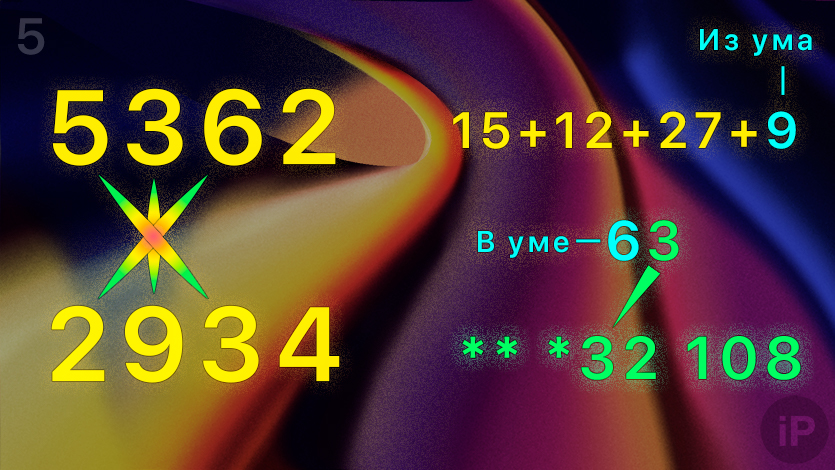
6. Умножьте первую цифру верхнего числа на вторую нижнего (5∙9) и наоборот (2∙3).

Сложите результаты с остатком в уме (45+6+6=57).

Получили десяток в уме (5) и пятую с конца цифру (7): ** 732 108.

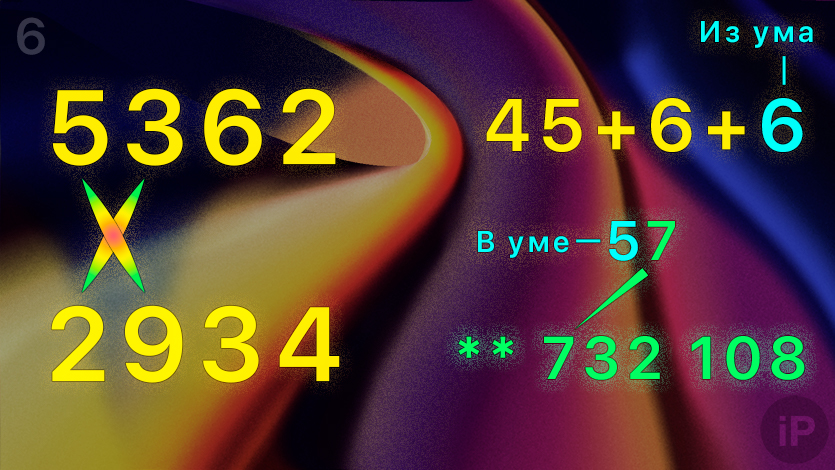
7. Умножьте первую цифру верхнего числа на первую нижнего (5∙2).

Сложите результат с остатком в уме (10+5=15).

Запишите всё число перед итоговым: 15 732 108.

Вы получили ответ.

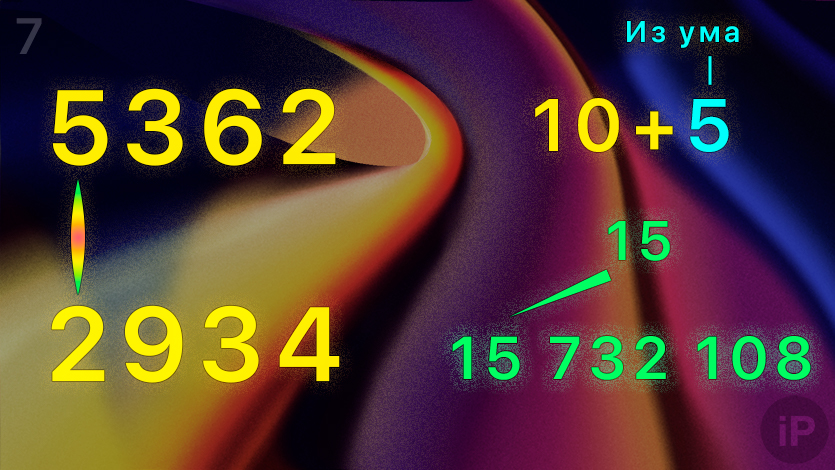
Если ваш множитель двух- или трёхзначный, то вместо недостающих цифр нижнего ряда подставляйте нули. В таком случае последним этапом будет тот, где вы умножаете максимальное количество пар.

Принцип снежинки намного проще, чем умножать столбиком. Вам не нужно держать в уме много крупных чисел сразу.

Важна только структура: запомните нарастающий порядок умноженных пар и что с чем нужно складывать.

Единственной сложностью останется запомнить результат, который вы постепенно выстраиваете.

Чаще тренируйте память вариантами проще, например, умножением двух- и трёхзначными числами в приложении Устный счёт.

И тогда сможете считать миллионы, не коснувшись бумаги.

iPhones.ru

Превращаем мозг в суперкомпьютер.

Павел

У меня 4 новых года: обычный, свой, WWDC и сентябрьская презентация Apple. Последний — самый ожидаемый, и ни капли за это не стыдно.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

8*4=8+8+8+8=32

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

Таблица умножения

Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

• 79*50=(70+9)*50=3500+450=3950
• 79*7=(70+9)*7=490+63=553
• 3950+553=4503

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11.

Проверим и умножим 54 на 11.

• 5+4=9
• 54*11=594

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

Возведение в квадрат

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Проверим! Возведем в квадрат число 75.

• 7*8=56
• 5*5=25
• 75*75=5625

Раньше все считали без калькуляторов

Что такое умножение?

Умножение — одна из основных арифметических операций, которая позволяет находить произведение двух или более чисел. В умножении присутствуют два множителя и результатом является их произведение, которое называется произведением.

Умножение обозначается знаком * или путем записи множителей друг за другом без знака умножения. Например, 3 * 4 или 3 · 4.

Основной способ умножения — посредством таблицы умножения. Таблица умножения позволяет запомнить результаты умножения чисел от 1 до 10, что упрощает выполнение умножения в уме.

Все числа, которые участвуют в умножении, называются множителями. Первый множитель называется множимым, а второй — множителем.

Пример умножения: 3 * 4 = 12. В данном примере число 3 является множимым, число 4 — множителем, а число 12 — произведением.

Умножение имеет несколько свойств:

• Ассоциативное свойство: (a * b) * c = a * (b * c), то есть порядок расстановки скобок при умножении не влияет на результат;
• Коммутативное свойство: a * b = b * a, то есть порядок множителей не влияет на результат;
• Дистрибутивное свойство: a * (b + c) = (a * b) + (a * c), то есть умножение распространяется на сумму.

Умножение имеет множество применений в различных областях науки, техники, экономики и других сферах деятельности. Оно является неотъемлемой частью математической основы и позволяет производить различные расчёты, анализировать данные и решать задачи.

Умножение многозначных чисел

Делить и умножать сложные числа проще всего столбиком. Для этого нужно разряды числа: сотни, десятки, единицы:

235 = 200 (сотни) + 30 (десятки) + 5 (единицы).

Это нам понадобится для правильной записи чисел при умножении.

При записи двух чисел, которые нужно перемножить, их записывают друг под другом, размещая числа по разрядам (единицы — под единицами, десятки под десятками). При умножении многозначного числа на однозначное трудностей не возникнет:

Правило умножения двухзначных чисел гласит, что сначала умножается первое из чисел на последнюю из цифр второго ряда (стоящую в разряде единиц), затем – оно же – на цифру из разряда десятков.

Запись ведется так:

• 3 х 5 = 15, записываем 5 (единицы), десятки (1) запоминаем;
• 2 х 5 = 10 и 1 десяток, который мы запомнили, всего 11, записываем 1 (десятки), сотни (1) запоминаем;
• поскольку дальше разрядов у нас в примере нет, записываем сотни (1 – которую запоминали).

Следующее действие – умножаем на вторую цифру (разряд десятков):

•  3 х 1 = 3;
• 2 х 1 = 2.

Поскольку умножали мы на цифру из разряда десятков, записывать начнем так же, с конца, начиная со второго места справа (там, где разряд десятков).

Запомнить правила умножения столбиком несложно:

1.  записывать столбиком умножение нужно по разрядам;

2. вычисления производить, начиная с единиц;

3. записывать итог по разрядам – если умножаем на цифру из разряда единиц – запись начинаем с последнего столбика, из разряда – десятков – с этого столбца и ведем запись.

Правило, действующее для умножения в столбик на двухзначное число, действует и для чисел с большим количеством разрядов.

Чтобы легче было запомнить правила записи примеров умножения многозначных чисел в столбик, можно сделать карточки, выделив разными цветами разные разряды.

Если производится в столбик умножение чисел с нулями на конце, их не принимают во внимание при вычислении, а запись ведут так, чтобы значащая цифра была под значащей, а нули остаются справа. После проведения вычислений их количество дописывают справа:

Математик Яков Трахтенберг разработал систему быстрого счета. Метод Трахтенберга облегчает умножение, если применять определенную систему вычислений. Например, умножение на 11. Для получения результата нужно прибавить цифру к соседней:

2,253 х 11 = (0 + 2) (2 + 2) (2 + 5) (5 + 3) (3 + 0) = 2 + 4 + 7 + 8 + 3 = 24,783.

Доказать истинность просто: 11 = 10 + 1

2,253 х 10 + 2,253 = 22,530 + 2,253 = 24,783.

Алгоритмы вычислений для разных чисел разные, но они позволяют производить вычисления быстро.

Видео «Умножение столбиком»

Вам нужна только математика начальной школы

Чтобы умножать без бумаги, нужно на уровне рефлекса освоить два навыка:

I. Знать таблицу умноженияII. Складывать числа

Пункты важны, потому что будете десятки раз повторять операции. Получается просто, но много.

Отточить умножение поможет приложение УмноЖатель

Уделяйте тренировке не больше пяти минут за подход. Потом запоминать сложнее, а после тройки долгих сессий цифры начнут раздражать.

Быстро складывать получится точно таким же постоянным запоминанием.

Почти нигде не просят знать таблицу сложения, а она есть. Если до десяти цифры знают почти все, то после этого порога начинается ступор.

На лету вспомнить, какое число будет в следующем десятке полезнее в жизни, чем любое другое вычисление. Поэтому качайте и запоминайте.

Ещё один способ сложения, которого некоторые стесняются – довод до десятка. Это когда к одному числу сначала добавляют до круглого значения часть из второго, а потом плюсуют остаток:

В этом способе нет ничего стыдного, он эффективен, и с практикой доводится до автоматизма.

Когда научитесь на лету умножать и складывать элементарные значения, вставайте на продвинутый уровень: расчёты четырёхзначных чисел.

Советы

1. Всегда записывайте цифры в соответствующих столбцах.
2. Не нужно забывать переносить цифры из разряда десятков в двузначных числах, в противном случае ответ получится неверным.
3. Сначала старайтесь практиковаться на простых числах, например, на двузначных.
4. При умножении многозначных чисел нужно выполнить такие действия: сначала умножить верхнее число на единицы нижнего числа, а затем добавить ноль и умножить на десятки, затем добавить два нуля и умножить на сотни, потом добавить три нуля и умножить на тысячи и так далее. В конечном результате следует все полученные цифры сложить.
5. Всегда нужно писать в конце 0 при умножении цифру, стоящую в разряде десятков второго числа, а при умножении на сотни нужно писать два нуля.

Вопросы и ответы

Вот несколько часто задаваемых вопросов и ответов, связанных с умножением в столбик:

Как умножать числа в столбик?

Умножение в столбик осуществляется путем пошагового перемножения цифр чисел, начиная справа, и последующим сложением полученных результатов в соответствующих позициях.

Как умножить двузначное число на однозначное число в столбик?

Для умножения двузначного числа на однозначное число в столбик, первоначально умножьте цифры однозначного числа на обе цифры двузначного числа, выравнивая результаты по позициям, затем сложите полученные произведения.

Как умножить число на 10, 100 или другую степень 10 в столбик?

Умножение числа на 10, 100 или другую степень 10 в столбик выполняется сдвигом цифр числа влево на количество позиций, равное количеству нулей в степени 10.

Как умножить большее число на меньшее число в столбик?

При умножении большего числа на меньшее число в столбик рекомендуется начать с умножения цифр меньшего числа на последнюю цифру большего числа, а затем перемножить цифры меньшего числа со следующей цифрой большего числа, при этом добавляя нули справа.

Как умножить числа с десятичными дробями в столбик?

Для умножения чисел с десятичными дробями в столбик перемножьте числа, игнорируя десятичные разделители. Затем определите количество цифр после десятичной запятой в каждом числе и добавьте столько десятичных разделителей в результирующем произведении.

Умножение в столбик является одним из методов для выполнения умножения чисел и может быть использовано для работы с различными типами чисел, включая целые числа, десятичные числа и числа с десятичными дробями.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

• Индикт — что это и чему он равен. Индикт — это средневековый период времени, равный 15 годам.
• Декада — это сколько дней. Декада состоит из 10 дней, калькулятор показывает количество дней в декаде.
• Сколько лет в тысячелетии. Введите количество тысячелетий, чтобы узнать, сколько в них лет.
• Сколько месяцев в веке. Введите количество веков, чтобы узнать, сколько в них месяцев.
• Перевести месяцы в года. Введите количество месяцев, калькулятор переведет их в года.
• Перевести годы в недели. Введите количество лет, калькулятор переведет их в недели.
• Перевести недели в дни. Введите количество недель, калькулятор переведет их в дни.
• Перевести дни в недели. Введите количество дней, калькулятор переведет их в недели
• Перевести академические часы в часы. Введите количество академических часов, калькулятор переведет их в часы.
• Перевести наносекунды в миллисекунды. Введите количество наносекунд, калькулятор переведет их в миллисекунды.

Как умножить тысячи на однозначное число

Чтобы получить ответ на, допустим, пример 3864∙7, вам поможет система Разбить-умножить, разбить-сложить.

Так выглядит алгоритм:

1. Разбиваем большое число на единицы, десятки, сотни и так далее.

2. Умножаем каждый кусочек на второе число.

3. Разбиваем результаты на простые группы одного размера.

20000 | 1000+5000 | 600+400 | 20+20 | 8

4. Складываем группы с конца.

20000 + 6000 + 1000 + 40 + 8

27048

Хотя на бумаге способ получается долгим, через несколько дней тренировка даст заметные результаты в скорости. У вас улучшится краткосрочная память, и вместимость чисел для сложения постепенно увеличится.

Важнее всего не потерять куски при последнем сложении. Этот этап доведёте до автомата постоянной практикой.

Отличие метода от привычного столбика в том, что мы постоянно дробим элементы на лёгкие частицы, которые быстро складываются.

Как умножать столбиком, если в примере два многозначных числа

Чтобы понять, как умножать в столбик многозначные числа, возьмем задание и рассмотрим алгоритм его решения. Предположим, нам нужно умножить 8063 на 207.

Решение:

1. Первое действие – записывать множители правильно. Первым записывается множитель, имеющий больше разрядов. В нашем случае – 8063. Под ним записывается второй множитель – 207. Не забываем о строгом соблюдении разрядов. Если нам придется решать примеры, в которых оба множителя имеют равное количество разрядов, записывать их можно в любом порядке.
2. Следующий шаг – перемножение единиц. Это значит, что умножаем 3 на 7, потом 6 на 7, и так далее все разряды первого множителя на единицы второго. Полученный результат будет считаться промежуточным. В некоторых источниках его называют неполным произведением.
3. Следующий этап – перемножение десятков. Так как во втором множителе мы имеем нуль в десятках, его просто пропускаем. Согласно правилам, при умножении на нуль все равно получим нуль.
4. Следующий этап – перемножение сотен. В итоге мы получим второе неполное произведение или второй промежуточный результат. Его нужно записать под первым промежуточным результатом таким образом, как показано ниже.В итоге мы получили два неполных произведения. Задания на умножение столбиком содержат столько промежуточных результатов, сколько разрядов во втором множителе. У нас получилось два, так как в десятках мы имеем нуль, и его пропускаем. Если бы вместо него была любая другая натуральная цифра, мы бы записали три неполных произведения друг под другом со сдвигом влево.
5. Завершающий этап – сложение всех полученных промежуточных результатов. Для этого не нужно переписывать их в отдельный пример. Достаточно просто вписать слева знак суммы – плюс и подвести дополнительную черту.Под чертой будем записывать полученное в итоге сложения семизначный результат, который и будет ответом.

Таким образом, можно записать выражение:

8063×207=1669041

Можно сказать, что для быстрого и верного решения заданий на умножение в столбик нужно на отлично знать таблицу умножения, помнить правила сложения в столбик, а также помнить основные математические термины.

Под основными терминами понимаются следующие:

• Однозначное число – это число, состоящее из одной цифры (например, 6).
• Двухзначная цифра – это та, в составе которой два натуральных числа (например, 28), и т.д.
• Разряд – это позиция, которую занимает число в комбинации с другими числами. Разряд отсчитывается с конца.
• Разряд единиц – это концовка любого многозначного числа. Перед ним находится разряд десятков, далее разряд сотен, и т.д.

Например, число 4657.

7 – разряд единиц;

5 – разряд десятков;

6 – разряд сотен;

4 – разряд тысяч.

Определение

Умножение – это арифметическое действие, в процессе которого перемножаются два составляющих – множители. Результат данного действия называется произведением.

Чтобы разобраться, как решать умножение в столбик, нужно помнить и основные правила этого математического действия.

1. Перестановка мест множителей не влияет на результат.\
2. Произведение трех и более множителей будет иметь идентичное значение, даже если любую группу заменить произведением.\
3. Умножение на нуль всегда дает нуль.

Есть еще одна категория примеров, на которую стоит обратить внимание. Это перемножение множителей, на конце каждого из которых есть нули

В таких примерах часто допускаются ошибки. Независимо от количества нулей на конце многозначных натуральных чисел, нужно действовать в последовательности, описанной на примере ниже.

Помогите с гугл таблицей. Нужно время умножить на число

можно формулой перевести ячейку времени в числовое значение минут. а потом умножать на стоимость минуты 70 грн/60.

путь немножко обходной, но рабочий

это не совсем точный коэффициент.

я не знаю, с какой погрешностью автору нужен расчет, но на 1 час 25 ошибка натекает уже больше 20 коп

Я вам результат скинула выше. Пишите время в коэффициентах, коэффициент рассчитывается обыкновенной пропорцией.

Например, 30 минут = 0,5 часа 25 минут = Х

Я думаю, что можно сделать доп ячейку с формулой перевода времени в коэффициент, пусть девочки подскажут

это не совсем точный коэффициент.

я не знаю, с какой погрешностью автору нужен расчет, но на 1 час 25 ошибка натекает уже больше 20 коп

есть туча способов. один из самых простых я написала словами, и формула для ячеек также есть на скрине.

можно и через перевод в коэффициент.

+ нужно, что ваятель сего еще разбирался как минимум в формате ячеек.

Благодарочка 1

перевод времени (формат времени) — прямо в количество часов (в числовом формате) для умножение на цену часа в грн

перевод времени (формат времени) — прямо в количество часов (в числовом формате) для умножение на цену часа в грн

работу за других выполнять не буду (хотя, на мой вкус и так уже сделала). Вам, автор, нужно поднатужиться и погуглить про формат ячеек (в частности числовой формат и формат времени), а потом использовать формулы, которые я уже Вам написала.

у Вас нет понимания, что 1,25 не равно 1 час 25 мин.

Благодарочка 1

работу за других выполнять не буду (хотя, на мой вкус и так уже сделала). Вам, автор, нужно поднатужиться и погуглить про формат ячеек (в частности числовой формат и формат времени), а потом использовать формулы, которые я уже Вам написала.

Итоги: правильный порядок действий в математике

Определение правильного порядка действий в математике является одной из основных тем изучения на уроках этого предмета. Правильная последовательность выполнения действий является важным правилом, которое позволяет получить правильный результат при решении математических примеров.

Важно помнить основное правило: умножение и деление выполняются перед сложением и вычитанием. Это правило называется правилом приоритета операций

Если в примере встречается умножение и деление, то эти операции выполняются в порядке, в котором они встречаются, слева направо. Например, в примере 4 * 2 / 8 + 6, сначала нужно выполнить умножение 4 * 2 = 8, затем деление 8 / 8 = 1, и, наконец, сложение 1 + 6 = 7.

В случае, если в примере присутствуют скобки, операции внутри скобок выполняются первыми. Например, в примере (4 + 2) * 3 / 2 — 5, сначала выполняется сложение в скобках 4 + 2 = 6, затем умножение 6 * 3 = 18, деление 18 / 2 = 9 и вычитание 9 — 5 = 4.

Если в примере встречаются разные операции с одинаковым приоритетом, то выполнение происходит слева направо. Например, в примере 8 + 4 — 2 + 6, сложение выполняется сначала 8 + 4 = 12, затем вычитание 12 — 2 = 10 и, наконец, сложение 10 + 6 = 16.

Правильный порядок действий в математике является основой для получения правильных результатов при решении примеров. Он позволяет избежать ошибок и улучшить навыки работы с числами

Поэтому важно уделить достаточно времени изучению этой темы и проводить много практических заданий для закрепления полученных знаний