Иррациональные неравенства

Возведение в иррациональную степень

Иногда возникает необходимость узнать значение степени числа с иррациональным показателем . При этом в практических целях обычно достаточно получить значение степени с точностью до некоторого знака. Сразу отметим, что это значение на практике вычисляется с помощью электронной вычислительной техники, так как возведение в иррациональную степень вручную требует большого количества громоздких вычислений. Но все же опишем в общих чертах суть действий.

Чтобы получить приближенное значение степени числа a
с иррациональным показателем , берется некоторое десятичное приближение показателя степени , и вычисляется значение степени . Это значение и является приближенным значением степени числа a
с иррациональным показателем . Чем более точное десятичное приближение числа будет взято изначально, тем более точное значение степени будет получено в итоге.

В качестве примера вычислим приближенное значение степени 2 1,174367…
. Возьмем следующее десятичное приближение иррационального показателя: . Теперь возведем 2
в рациональную степень 1,17
(суть этого процесса мы описали в предыдущем пункте), получаем 2 1,17 ≈2,250116
. Таким образом, 2 1,174367… ≈2 1,17 ≈2,250116
. Если взять более точное десятичное приближение иррационального показателя степени, например, , то получим более точное значение исходной степени: 2 1,174367… ≈2 1,1743 ≈2,256833
.

Список литературы.

• Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. МатематикаЖ учебник для 5 кл. общеобразовательных учреждений.
• Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 7 кл. общеобразовательных учреждений.
• Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
• Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 9 кл. общеобразовательных учреждений.
• Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
• Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).

Как известно, в математике существуют не только положительные числа, но и отрицательные. Если знакомство с положительными степенями начинается с определения площади квадрата, то с отрицательными всё несколько сложнее.

Это следует знать:

1. Возведением числа в натуральную степень называется умножение числа (понятие число и цифра в статье будем считать эквивалентными) само на себя в таком количестве, каков показатель степени (в дальнейшем будем использовать параллельно и просто слово показатель). 6^3 = 6*6*6 = 36*6 =216. В общем виде это выглядит так: m^n = m*m*m*…*m (n раз).
2. Нужно учитывать, что при возведении отрицательного числа в натуральную степень, оно станет положительным, если показатель чётный.
3. Возведение числа в показатель 0 даёт единицу, при условии, что оно не равно нулю. Ноль в нулевой степени считается неопределённым. 17^0 = 1.
4. Извлечением корня некой степени из числа называется нахождение такого числа, которое при возведении в соответствующий показатель даст искомое. Так, корень кубический из 125 равен 5, поскольку 5^3 = 125.
5. Если требуется возвести число в дробную положительную степень, то необходимо возвести число в показатель знаменателя и извлечь из него корень показателя числителя. 6^5/7 = корень седьмой степени из произведения 6*6*6*6*6.
6. Если требуется возвести число в отрицательный показатель, то необходимо найти цифру обратную данной. x^-3 = 1/x^3. 8^-4 = 1/8^4 = 1/8*8*8*8 = 1/4096.

Как возвести в отрицательную степень дробь

Запомните!

Чтобы возвести дробь в отрицательную степень нужно:

• «перевернуть» дробь;
• заменить отрицательную степень на
  положительную;
• возвести дробь в положительную степень.

Пример. Требуется возвести в отрицательную степень дробь.

Возведем дробь в положительную степень по правилу возведения дроби в положительную степень.
Т.е. возведем и числитель «», и знаменатель «» в третью степень.

Для более грамотного ответа запишем полученный результат в виде десятичной дроби.

Как возвести отрицательное число в отрицательную степень

Как и при возведении отрицательного числа в положительную степень, в первую
очередь необходимо определить конечный знак результата возведения в степень. Вспомним основные правила еще раз.

Запомните!

Отрицательное число, возведённое в
чётную степень, — число
положительное.

Отрицательное число, возведённое в
нечётную степень, — число
отрицательное.

Пример.

Перевернем число «» и заменим отрицательную степень
«» на положительную
«».

Так как степень «» — четная, значит, результат возведения в степень будет
положительный. Поэтому
убираем знак минуса при раскрытии скобок.

Далее откроем скобки
и возведем во вторую степень и числитель «», и знаменатель «».

Как возвести отрицательную дробь в отрицательную степень

Конечный знак результата возведения в степень отрицательной дроби определяется по тем же правилам, что и для целого отрицательного числа.

Запомните!

Отрицательная дробь, возведённая в
чётную степень, — дробь
положительная.

Отрицательная дробь, возведённая в
нечётную степень, — дробь
отрицательная.

По правилу возведения дроби в отрицательную степень перевернем дробь и заменим отрицательную степень «» на положительную
«».

Теперь определим конечный знак результата возведения в «» степень.

Степень «» — нечетная, значит, по правилу возведения отрицательного числа в степень дробь
останется отрицательной.

Нам остается только раскрыть скобки и возвести в степень и числитель «», и знаменатель
«» в третью степень.

Для окончательного ответа выделим целую часть из дроби.

Рассмотрим другой пример возведения отрицательной дроби в отрицательную степень.

Правило возведения отрицательного числа в степень гласит: если степень четная, значит, результат возведения
будет положительным.

Применение умножения отрицательных чисел в реальной жизни

Умножение отрицательных чисел имеет свои особенности и может быть полезным в различных ситуациях в реальной жизни. Вот несколько примеров применения этой операции:

1. Финансы: В бизнесе и личных финансах часто возникают ситуации, когда необходимо учесть долги или убытки. В таких случаях умножение отрицательных чисел может быть полезным инструментом для расчета общей суммы долга или убытка.

2. Физика: В физике отрицательные числа используются для обозначения направления. Например, скорость объекта может быть положительной, если он движется вперед, и отрицательной, если он движется назад. Умножение отрицательной скорости на время может помочь рассчитать пройденное расстояние.

3. Математика и алгебра: Умножение отрицательных чисел в математике и алгебре также имеет свои применения. Например, при работе с полиномами и многочленами, умножение отрицательных значений может помочь найти значения функций в определенных точках.

4. Программирование: В программировании отрицательные числа широко используются для представления различных значений и состояний. Умножение отрицательных чисел может помочь вычислить значения переменных или выполнить определенные действия в программе.

5. Моделирование и статистика: Во многих областях науки, таких как моделирование и статистика, умножение отрицательных чисел может помочь представить и проанализировать различные сценарии и результаты. Например, в моделировании финансовых рынков умножение отрицательных значений может помочь предсказать потенциальные убытки.

Все эти примеры демонстрируют, что умножение отрицательных чисел имеет множество практических применений. Понимание этой операции и ее использование может помочь в решении различных задач и проблем в реальной жизни.

Возведение числа в степень

Возведение числа в степень – операция не сложная. Оно связано с умножением подобно связи умножения и сложения. Запись an – краткая запись n-ого количество чисел «а» умноженных друг на друга.

Рассмотри возведение в степень на самых простых примерах, переходя к сложным.

Например, 42. 42 = 4 * 4 = 16
. Четыре в квадрате (во второй степени) равно шестнадцати. Если вам не понятно умножение 4 * 4
, то читайте нашу стать об умножении .

Рассмотрим еще одни пример: 5^3. 5^3 = 5 * 5 * 5 = 25 * 5 = 125
. Пять в кубе (в третьей степени) равно ста двадцати пяти.

Еще один пример: 9^3. 9^3 = 9 * 9 * 9 = 81 * 9 = 729
. Девять в кубе равняется семи сотням двадцати девяти.

Алгоритмы решения иррациональных неравенств

Далее \(f(x)\) и \(g(x)\) — это функции, зависящие от переменной \(x;\)

Будьте внимательны, в иррациональных неравенствах даже знак неравенства может кардинальным образом изменить алгоритм решения у одинаковых, на первый взгляд, неравенств. Также у студентов часто возникают сложности с выбором строгого или нестрогого знака неравенства, поэтому мы приведем алгоритмы в некоторых спорных случаях для строгих и нестрогих неравенств по отдельности.

Иррациональные неравенства вида \(\sqrt{f(x)} \le a\)

Если \(a \ge 0:\)
$$\sqrt{f(x)} \le a \quad \Rightarrow \quad
\begin{cases}
f(x) \le a^2, \\
f(x) \ge 0.
\end{cases}$$
Если \(a \lt 0:\) корней нет.

Иррациональные неравенства вида \(\sqrt{f(x)} \le g(x)\)

$${ \small \sqrt{f(x)} \le g(x) \quad \Rightarrow \quad
\begin{cases}
f(x) \le g^2(x), \\
f(x) \ge 0, \\
g(x) \ge 0.
\end{cases}}$$
$${ \small \sqrt{f(x)} \lt g(x) \quad \Rightarrow \quad
\begin{cases}
f(x) \lt g^2(x), \\
f(x) \ge 0, \\
g(x) \ge 0.
\end{cases}}$$

Иррациональные неравенства вида \(\sqrt{f(x)} \ge g(x)\)

$${ \small \sqrt{f(x)} \ge g(x) \quad \Rightarrow \quad
\left[
\begin{gathered}
\begin{cases}
f(x) \ge g^2(x) \\
g(x) \ge 0;
\end{cases}
\\
\begin{cases}
f(x) \ge 0, \\
g(x) \lt 0;
\end{cases}
\end{gathered}
\right.}$$
$${ \small \sqrt{f(x)} \gt g(x) \quad \Rightarrow \quad
\left[
\begin{gathered}
\begin{cases}
f(x) \gt g^2(x) \\
g(x) \ge 0;
\end{cases}
\\
\begin{cases}
f(x) \ge 0, \\
g(x) \lt 0;
\end{cases}
\end{gathered}
\right. }$$

Иррациональные неравенства вида \(\sqrt{f(x)} \ge \sqrt{g(x)}\)

$${ \small \sqrt{f(x)} \ge \sqrt{g(x)} \quad \Rightarrow \quad
\begin{cases}
f(x) \ge g(x), \\
g(x) \ge 0.
\end{cases}}$$

$${ \small \sqrt{f(x)} \gt \sqrt{g(x)} \quad \Rightarrow \quad
\begin{cases}
f(x) \gt g(x), \\
g(x) \ge 0.
\end{cases}}$$

Иррациональные неравенства вида \(\sqrt{f(x)} \le \sqrt{g(x)}\)

$${ \small \sqrt{f(x)} \le \sqrt{g(x)} \quad \Rightarrow \quad
\begin{cases}
f(x) \le g(x), \\
f(x) \ge 0.
\end{cases}}$$

$${ \small \sqrt{f(x)} \lt \sqrt{g(x)} \quad \Rightarrow \quad
\begin{cases}
f(x) \lt g(x), \\
f(x) \ge 0.
\end{cases}}$$

Иррациональные неравенства вида \(g(x)*\sqrt{f(x)} \ge 0\)

$${ \small g(x)*\sqrt{f(x)} \ge 0 \quad \Rightarrow \quad
\left[
\begin{gathered}
\begin{cases}
g(x) \ge 0, \\
f(x) \ge 0;
\end{cases}
\\
f(x) = 0.
\end{gathered}
\right. }$$

$${ \small g(x)*\sqrt{f(x)} \gt 0 \quad \Rightarrow \quad
\begin{cases}
g(x) \gt 0, \\
f(x) \gt 0;
\end{cases}}
$$

Иррациональные неравенства вида \(g(x)*\sqrt{f(x)} \le 0\)

$${ \small g(x)*\sqrt{f(x)} \le 0 \quad \Rightarrow \quad
\left[
\begin{gathered}
\begin{cases}
g(x) \le 0, \\
f(x) \ge 0;
\end{cases}
\\
f(x) = 0.
\end{gathered}
\right. }$$

$${ \small g(x)*\sqrt{f(x)} \lt 0 \quad \Rightarrow \quad
\begin{cases}
g(x) \lt 0, \\
f(x) \gt 0;
\end{cases}}
$$

Корни нечётной степени

Возведение левой и правой частей неравенства в нечётную степень не накладывает никаких ограничений. Это равносильная операция, например:
$${ \small \sqrt{f(x)} \ge g(x) \quad \Rightarrow \quad f(x) \ge g^3(x).}$$
При решении иррациональных неравенств с арифметическими корнями нечётной степени можете смело возводить в нечётную степень, на корни неравенства это никак не повлияет.

Как возвести в степень в Excel?

Перед поиском необходимой функции обратите внимание на математические законы:

1. Число «1» в любой степени будет оставаться «1».
2. Число «0» в любой степени будет оставаться «0».
3. Любое число, возведенное в нулевую степень, равняется единице.
4. Любое значение «А» в степени «1» будет равняться «А».

Примеры в Excel:

Вариант №1. Используем символ «^»

Стандартный и самый простой вариант – использовать значок «^», который получается при нажатии Shift+6 при английской раскладке клавиатуры.

ВАЖНО!

1. Чтобы число было возведено в нужную нам степень, необходимо в ячейке поставить знак «=» перед указанием цифры, которую вы хотите возвести.
2. Степень указывается после знака «^».

Мы возвели 8 в «квадрат» (т.е. ко второй степени) и получили в ячейке «А2» результат вычисления.

Вариант №2. С использованием функции

В Microsoft Office Excel есть удобная функция «СТЕПЕНЬ», которую вы можете активизировать для осуществления простых и сложных математических расчетов.

Функция выглядит следующим образом:

СТЕПЕНЬ(число;степень)

ВНИМАНИЕ!

1. Цифры для этой формулы указываются без пробелов и других знаков.
2. Первая цифра – значение «число». Это основание (т.е. цифра, которую мы возводим). Microsoft Office Excel допускает введение любого вещественного числа.
3. Вторая цифра – значение «степень». Это показатель, в который мы возводим первую цифру.
4. Значения обоих параметров могут быть меньше нуля (т.е. со знаком «-»).

Функции инженерного калькулятора

Калькулятор умеет работать со степенями и логарифмами. Находит синус, косинус, тангенс и котангенс, а также арксинус, арккосинус, арктангенс и арккотангенс. Поддерживает двоичные логарифмы, логарифмы по основанию. Может возвести число в 10-ю степень. Также, калькулятор позволяет просматривать число Эйлера и число Пи. Помимо этого поддерживаются стандартные арифметический действия, с помощью которых вы можете сложить и вычесть числа, умножить и разделить, а также извлечь квадратный корень онлайн.

Подробная инструкция и ознакомление с основными возможностями.

1. Найти корень. Чтобы найти квадратный корень числа, введите это число в калькулятор, а затем нажмите кнопку «√», которая находится в верхнем ряду основного блока, вторая справа. Допустим, если мы введем число 9, то после нажатия на эту кнопку получим число 3.
2. Возвести число в квадрат. Чтобы возвести число в квадрат онлайн вам необходимо воспользоваться кнопкой «X2», которая находится в левом блоке функций, в правой части третьего ряда снизу. В результате число, имевшееся на экране, будет возведено в квадрат. К примеру, на экране горит 3. В результате мы получим 9.
3. Возвести число в степень. Возвести число в степень можно с помощью кнопки «Xy» в правом верхнем углу калькулятора. Сначала введите число, которое нужно возвести, затем нажмите на эту кнопку и введите число самой степени. Например, если мы попробуем возвести 10 в степень 2, то получим 100.
4. Синус, косинус, тангенс, котангенс. Часто бывает так, что необходимо найти синус острого угла, косинус прямого угла, синус внешнего угла, а также тангенс или котангенс треугольника. На нашем калькуляторе данные вычисления можно производить с помощью кнопок «sin», «cos», «tg», «ctg». Приведем конкретный пример: допустим, нам требуется найти косинус угла в 90 градусов. Для этого, введем на калькуляторе цифру 90 и нажмем кнопку «cos» в левом блоке функций. В результате мы получим длинную цифру -0.4480736161291701. Это и есть косинус угла 90. Точно так же на нашем калькуляторе можно вычислить косинус угла 60, синус угла 90 и многое другое.
5. Арксинус арккосинус арктангенс арккотангенс. Вычисляются точно так же как и в предыдущем примере. Просто введите нужное число (градусы угла) и нажмите на одну из следующих кнопок соответственно: «asin», «acos», «atg», «actg».
6. Логарифм по основанию вычисляется с помощью кнопки logyx. Введите число, допустим 10. Затем нажмите на эту кнопку и введите основание. Допустим 2. После нажатия на кнопку равно, мы получим ответ: 3.321928094887.
7. Возвести 10 в n-ю степень. С помощью данной функции можно возвести число 10 в степень, которая горит на табло калькулятора. Для этого используем кнопку X2,  которая располагается во втором ряду снизу (в левом блоке). К примеру, у нас на экране горит цифра 2. В результате произойдет возведение 10 во 2-у степень, т.е. 10^2=100.
8. Превратить число в отрицательное или положительное. Иногда требуется превратить число в отрицательное или наоборот. Чтобы не вводить его заново, просто нажмите на кнопку «+/-»
9. Посмотреть число Пи и число Эйлера можно с помощью кнопок «П» и «е» в правом углу левого блока.
10. Простые математические действия осуществляются с помощью клавиш в правом (основном) блоке. «+» — сложение, «-» — вычитание, «x» – умножение и «÷» — умножение.
11. Функция памяти. Пользоваться функцией памяти в нашем онлайн калькуляторе очень просто. Допустим, вы получили какое-то число, которое нужно запомнить. Чтобы сделать это нажмите «M+». Когда это число вам понадобится, просто нажмите кнопку «MR» и оно выведется на экран. После этого вы сможете совершать с ним математические операции. Также, вы можете плюсовать или вычитать имеющееся число из числа, которое уже в памяти. Допустим, в памяти у вас число 10. А на экране число 2. Если вы нажмете кнопку «M-«, то из 10 вычтется 2 и в памяти останется число 8. Точно так же происходит с кнопкой «M+». Если вы хотите очистить память — нажмите «MC» и память станет пустой.
12. Разделить целое на текущее. Часто в инженерной работе требуется провести довольно тривиальное вычисление: узнать, сколько текущий показатель составляет от единого целого. Для этого в нашем инженерном калькулятор существует кнопочка 1/x. Она делит единицу на текущее число. Скажем, если на табло горит 5, то функция выведет 0.2.

Алгоритм извлечения квадратного корня

Вычислите квадратный корень из числа, которое называется подкоренное выражение. Чтобы извлечь квадратный корень, мы используем формулу, которая выражает степень корня:

Если в подкоренном выражении стоит отрицательное число, то результатом вычисления будет комплексное число. В этом случае перед корнем добавляется i, чтобы указать, что число является мнимым.

Для извлечения квадратного корня с множителем в подкоренном выражении, мы сначала вносим множитель в самый левый множитель перед корнем. Например, если у нас есть √3, то мы представляем это как 3 * √1.

Если перед корнем стоит отрицательное число, мы можем использовать вынесение знака из подкоренного выражения. Например, вычисление √(-9) можно представить как -√9.

Извлекаемый корень ищем с помощью следующего алгоритма:

1. Разбиваем подкоренное выражение на квадраты между множителями.
2. Внесите множитель перед корнем в самый левый множитель.
3. Если перед корнем стоит отрицательное число, выносим знак.
4. Вычисляем каждый квадратный корень отдельно.
5. Далее применяем определения квадратных корней, чтобы получить конечный результат.

Вот несколько примеров использования алгоритма:

1. Вычислим квадратный корень из 16. У нас есть подкоренное выражение без множителей, поэтому мы получаем √16 = 4.

2. Вычислим квадратный корень из 3. Мы представим его как 3 * √1 = 3. (Здесь √1 равно 1).

3. Вычислим квадратный корень из -9. Мы представим его как -√9. Окончательный результат -3.

Таким образом, алгоритм извлечения квадратного корня позволяет нам вычислять корни от различных чисел, представлять множители внутри корня и обрабатывать отрицательные числа.

Урок и презентация на тему: «Степень с отрицательным показателем. Определение и примеры решения задач»

Дополнительные материалы

Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Определение степени с отрицательным показателем

Мы хорошо знаем, что любое число в нулевой степени равно единице. $a^0=1$, $a≠0$.
Возникает вопрос, а что будет, если возвести число в отрицательную степень? Например, чему будет равно число $2^{-2}$?
Первые математики, задавшиеся этим вопросом, решили, что изобретать велосипед заново не стоит, и хорошо, чтобы все свойства степеней оставались прежними. То есть при умножении степеней с одинаковым основанием, показатели степени складываются.
Давайте рассмотрим такой случай: $2^3*2^{-3}=2^{3-3}=2^0=1$.
Получили, что произведение таких чисел должно давать единицу. Единица в произведении получается при перемножении обратных чисел, то есть $2^{-3}=\frac{1}{2^3}$.

Такие рассуждения привели к следующему определению.
Определение. Если $n$ – натуральное число и $а≠0$, то выполняется равенство:
$a^{-n}=\frac{1}{a^n}$.

Важное тождество, которое часто используется: $(\frac{a}{b})^{-n}=(\frac{b}{a})^n$.
В частности, $(\frac{1}{a})^{-n}=a^n$

Примеры решения

Решение. Рассмотрим каждое слагаемое по отдельности.
1. $2^{-3}=\frac{1}{2^3}=\frac{1}{2*2*2}=\frac{1}{8}$.
2. $(\frac{2}{5})^{-2}=(\frac{5}{2})^2=\frac{5^2}{2^2}=\frac{25}{4}$.
3. $8^{-1}=\frac{1}{8}$.
Осталось выполнить операции сложения и вычитания: $\frac{1}{8}+\frac{25}{4}-\frac{1}{8}=\frac{25}{4}=6\frac{1}{4}$.
Ответ: $6\frac{1}{4}$.

Пример 2. Представить заданное число в виде степени простого числа
$\frac{1}{729}$.

Решение. Очевидно, что $\frac{1}{729}=729^{-1}$.
Но 729 — не простое число, заканчивающиеся на 9. Можно предположить, что это число является степенью тройки. Последовательно разделим 729 на 3.
1) $\frac{729}{3}=243$; 2) $\frac{243}{3}=81$; 3) $\frac{81}{3}=27$; 4) $\frac{27}{3}=9$; 5) $\frac{9}{3}=3$; 6) $\frac{3}{3}=1$.
Выполнено шесть операций и значит: $729=3^6$.
Для нашей задачи:
$729^{-1}=(3^6)^{-1}=3^{-6}$.
Ответ: $3^{-6}$.

Пример 3. Представьте выражение в виде степени:
$\frac{a^6*(a^{-5})^2}{(a^{-3}*a^8)^{-1}}$.
Решение. Первое действие выполняется всегда внутри скобок, затем умножение
$\frac{a^6*(a^{-5})^2}{(a^{-3}*a^8)^{-1}}=\frac{a^6*a^{-10}}{(a^5)^{-1}}=\frac{a^{(-4)}}{a^{(-5)}}=a^{-4-(-5)}=a^{-4+5}=a$.
Ответ: $a$.

Пример 4. Докажите тождество:
$(\frac{y^2 (xy^{-1}-1)^2}{x(1+x^{-1}y)^2}*\frac{y^2(x^{-2}+y^{-2})}{x(xy^{-1}+x^{-1}y)}):\frac{1-x^{-1} y}{xy^{-1}+1}=\frac{x-y}{x+y}$.

Решение.
В левой части рассмотрим каждый сомножитель в скобках отдельно.
1.
$\frac{y^2(xy^{-1}-1)^2}{x(1+x^{-1}y)^2}=\frac{y^2(\frac{x}{y}-1)^2}{x(1+\frac{y}{x})^2}
=\frac{y^2(\frac{x^2}{y^2}-2\frac{x}{y}+1)}{x(1+2\frac{y}{x}+\frac{y^2}{x^2})}=\frac{x^2-2xy+y^2}{x+2y+\frac{y^2}{x}}=\frac{x^2-2xy+y^2}{\frac{x^2+2xy+y^2}{x}}=\frac{x(x^2-2xy+y^2)}{(x^2+2xy+y^2)}$.
2. $\frac{y^2(x^{-2}+y^{-2})}{x(xy^{-1}+x^{-1}y)}=\frac{y^2(\frac{1}{x^2}+\frac{1}{y^2})}{x(\frac{x}{y}+\frac{y}{x})}
=\frac{\frac{y^2}{x^2}+1}{\frac{x^2}{y}+y}=\frac{\frac{y^2+x^2}{x^2}}{{\frac{x^2+y^2}{y}}}=\frac{y^2+x^2}{x^2} *\frac{y}{x^2+y^2}=\frac{y}{x^2}$.
3. $\frac{x(x^2-2xy+y^2)}{(x^2+2xy+y^2)}*\frac{y}{x^2}=\frac{y(x^2-2xy+y^2)}{x(x^2+2xy+y^2)}=\frac{y(x-y)^2}{x(x+y)^2}$.
4. Перейдем к дроби, на которую делим.
$\frac{1-x^{-1}y}{xy^{-1}+1}=\frac{1-\frac{y}{x}}{\frac{x}{y}+1}=\frac{\frac{x-y}{x}}{\frac{x+y}{y}}=\frac{x-y}{x}*\frac{y}{x+y}=\frac{y(x-y)}{x(x+y)}$.
5. Выполним деление.
$\frac{y(x-y)^2}{x(x+y)^2}:\frac{y(x-y)}{x(x+y)}=\frac{y(x-y)^2}{x(x+y)^2}*\frac{x(x+y)}{y(x-y)}=\frac{x-y}{x+y}$.
Получили верное тождество, что и требовалось доказать.

В конце урока еще раз запишем правила действий со степенями, здесь показатель степени — это целое число.
$a^s*a^t=a^{s+t}$.
$\frac{a^s}{a^t}=a^{s-t}$.
$(a^s)^t=a^{st}$.
$(ab)^s=a^s*b^s$.
$(\frac{a}{b})^s=\frac{a^s}{b^s}$.

Задачи для самостоятельного решения

Калькулятор помогает быстро возвести число в степень онлайн. Основанием степени могут быть любые числа (как целые, так и вещественные). Показатель степени также может быть целым или вещественным, и также как положительным, так и отрицательным. Следует помнить, что для отрицательных чисел возведение в нецелую степень не определено и потому калькулятор сообщит об ошибке в случае, если вы всё же попытаетесь это выполнить.

Калькулятор степеней

Возвести в степень

Возведений в степень: 20880

Вычисление квадратного корня

Ранее для выполнения арифметических операций мы использовали метод «столбика». А как производить вычисление квадратного корня? Существует несколько приемов, мы рассмотрим простейший из них.

Очевидно, что чем больше число, тем больше и его квадрат. Например, 5 > 4, поэтому и 52> 42. Значит, справедливо и обратное утверждение: чем больше число, тем больше и его квадратный корень.

Убедиться в этом можно и с помощью графика функции у = х2. Будем отмечать на нем числа и их квадратные корни:

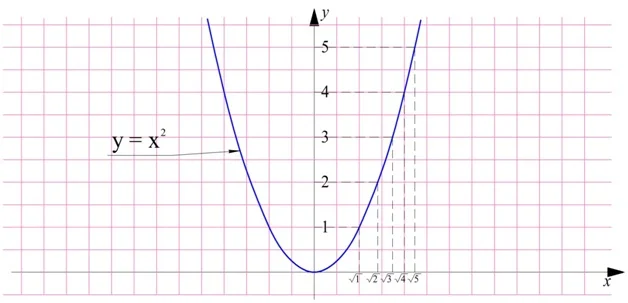
Видно, что чем выше на оси Оу располагается число, тем правее на оси Ох находится его квадратный корень.

Зная это свойство, легко оценить значение корня из любого числа. Продемонстрируем это на примере вычисления значение корня из 2. Нам известно, что

1 < 2 < 4

Значит, можно записать следующие неравенства:

Нам удалось определить, что корень из двух находится между единицей и двойкой, то есть

Теперь определим первую цифру после запятой для корня из двух. Будем возводить в квадрат десятичные дроби 1,1; 1,2; 1,3 и т. д, до тех пор пока не получим выражение, большее 2:

1,12 = 1,21

1,22 = 1,44

1,32 = 1,69

1,42 = 1,96

1,52 = 2,25

Теперь мы можем записать неравенства:

Получается, что корень имеет значение, находящееся между 1,4 и 1,5, то есть

Попытаемся определить ещё одну цифру после запятой:

1,412 = 1,999396

1,422 = 2,002225

Отсюда следует, что:

Продолжая подобные вычисления, можно вычислить любое количество знаков после запятой:

Конечно, на практике все вычисления выполняются компьютером, а не вручную. Однако программисты стремятся написать программы так, чтобы они работали как можно быстрее, то есть получали результат, выполняя меньшее количество вычислений. Поэтому на практике чаще используется метод бисекции (деления надвое), который отличается большей эффективностью. Для начала нужно найти очевидную оценку корня, например:

Получили, что корень из 2 находится между 1 и 2. Теперь найдем среднее арифметическое этих двух значений:

(1 + 2)/2 = 1,5

Возведем среднее арифметическое в квадрат:

1,52 = 2,25

Теперь мы можем записать неравенство

То есть искомое нами значение находится между 1 и 1,5. Снова найдем среднее этих двух оценок и возведем его в квадрат:

(1 + 1,5)/2 = 1,25

1,252 = 1,5625

Зная это, можем записать:

На каждом следующем шаге вычислений мы будем всё точнее определять оценки корня, при этом вычислений мы делаем не очень много.

Периодически могут встречаться задания, в которых надо грубо оценить значение квадратного корня.

Пример. Сколько целых чисел на координатной прямой располагается между

Решение: Ближайшие к числу 60 полные квадраты – это 64 и 49, поэтому можно записать:

Также можно оценить и корень из 140:

Получаем, что между корнями располагается четыре числа: 8, 9, 10 и 11:

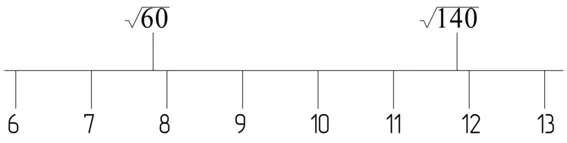
Ответ: 4

Умножение арифметических корней

Для умножения арифметических корней используйте формулу:

Примеры:

Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.

Если нет возможности извлечь корни из чисел, то поступаем так:

Если множителей больше двух, то решается примерно точно так, как и с двумя множителями:

Добрая напоминалочкаЧтобы решать примеры быстрее, не забывайте пользоваться таблицей квадратов.

Метод умножения показателей с множителями

Умножить множители. Множитель — число, которое стоит перед знаком корня. В случае отсутствия множителя, он, по умолчанию, считается единицей. Далее необходимо перемножить множители:

Пример 1: 3 2 × 10 = 3 ? 3 × 1 = 3

Пример 2: 4 3 × 3 6 = 12 ? 4 × 3 = 12

Умножить числа под знаком корня. Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:

Пример 1: 3 2 × 10 = 3 (2 × 10) = 3 20

Пример 2: 4 3 × 3 6 = 12 (3 × 6) = 12 18

Упростить подкоренное выражение. Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня. После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:

Пример 1: 3 20 = 3 (4 × 5) = 3 (2 × 2) × 5 = (3 × 2) 5 = 6 5

Пример 2: 12 18 = 12 (9 × 2) = 12 (3 × 3) × 2 = (12 × 3) 2 = 36 2

Метод умножения корней без множителей

Убедиться, что у корня одинаковые показатели (степени). Вспомним, что степень записывается слева над знаком корня. Если нет обозначения степени, это значит, что корень квадратный, т.е. со степенью 2, и его можно умножать на другие корни со степенью 2.

Пример 1: 18 × 2 = 36

Пример 2: 10 × 5 = 50

Пример 3: 3 3 × 9 3 = 27 3

Упростить подкоренные выражения. Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:

Пример 1: 36 = 6 . 36 — квадратный корень из шести (6 × 6 = 36) .

Пример 2: 50 = (25 × 2) = (5 × 5) × 2 = 5 2 . Число 50 раскладываем на произведение 25 и 2 . Корень из 25 — 5 , поэтому выносим 5 из-под знака корня и упрощаем выражение.

Пример 3: 27 3 = 3 . Кубический корень из 27 равен 3: 3 × 3 × 3 = 27 .

Умножение корней с одинаковыми показателями

Чтобы перемножить корни с одинаковыми показателями, нужно оставить тот же показатель корня, а подкоренные выражения перемножить.

√(81) × √(25) =
= √(81 × 25) =
= 9 × 5 =
= 45

Умножение корней с разными показателями

Чтобы перемножить корни с разными показателями, нужно сначала привести корни к общему показателю, а потом перемножить полученные корни с одинаковым показателем. Чтобы умножить корень на число, надо занести под знак корня это число, возведённое в степень с показателем, как у корня.

∛‎(729) × √(25) =
= √(81) × √(25) =
= √(81 × 25) =
= 9 × 5 =
= 45

Итог

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.

Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса…
» . Все понимают, что их дурят, но никто не понимает, в чем заключается обман.

С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.

Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».

Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:

За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.

Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.

Другая интересная апория Зенона повествует о летящей стреле:

Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.

В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь)

На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.