Инженерный калькулятор онлайн с самыми точными расчетами!

Извлечение квадратного корня из большого числа

Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

1. Определить «сотни», между которыми оно стоит.
2. Определить «десятки», между которыми оно стоит.
3. Определить последнюю цифру в этом числе.

Извлечь корень из большого числа можно разными способами — вот один из них.

Извлечем корень из √2116.

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

102 = 100

202 = 400

302 = 900

402 = 1600

502 = 2500

Мы видим что, 2116 больше 1600, но меньше 2500.

Это значит, что число 2116 находится между 402и 502.

41, 42, 43, 44, 45, 46, 47, 48, 49.

Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.

Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей

12 = 1

22 = 4

32 = 9

42 = 16 ⇒ 6

52 = 25 ⇒ 5

62 = 36 ⇒ 6

72 = 49 ⇒ 9

82 = 64 ⇒ 4

92 = 81 ⇒ 1

Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.

Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.

Число 43, возведенное в квадрат, даст число, на конце которого — 9.

Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.

Таким образом, у нас остаются два варианта: 442 и 462.

Далее вычисляем: 44 * 44 = 1936.

46 * 46 = 2116.

Ответ: √2116 = 46

Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.

Еще пример. Извлечем корень из числа √11664

Разложим число 11664 на множители:

11666 : 4 = 2916

2916 : 4 = 729

729 : 3 = 243

243 : 3 = 81

11664	4
2916	4
729	3
243	3
81	81

Запишем выражение в следующем виде:

Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.

Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.

• Вычислите значение квадратного корня: √36
• Вычислите значение квадратного корня: √64*36
• Вычислите значение квадратного корня:
• Вычислите значение квадратного корня:
• Вычислите значение квадратного корня:
• Вычислите значение выражения: 4√16 — 12
• Вычислите значение выражения: 5√9 — 8
• Вычислите значение выражения: 7√25 — 10
• Вычислите значение квадратного корня:
• Вычислите значение квадратного уравнения:
• Вычислите значение квадратного уравнения:
• Извлеките квадратный корень из числа √7056 удобным вам способом
  Как решаем:

  7056	4
  1764	4
  441	3
  147	3
  49	7
  7	7
  1

• Вычислите значение квадратного корня √0,81
  Ответ: √0,81 = 0,9
• Вычислите значение квадратного корня:

  Как решаем:
  = 0,09

• Вычислите значение выражения: 8√81 — 20
  Как решаем: 8√81 — 20 = 8 * 9 — 20 = 72 — 20 = 52
  Ответ: 8√81 — 20 = 52.
• Вычислите значение выражения: 13√100 — 15
  Как решаем: 13√100 — 15 = 13 * 10 — 15 = 130 — 15 = 115
  Ответ: 13√100 — 15 = 115.
• Вычислите значение выражения: √16 + 5√4
  Как решаем: √16 + 5√4 = 4 + 5 * 4 = 4 + 20 = 24 Ответ: √16 + 5√4 = 24.
• Вычислите значение выражения: √36 + 2√9
  Как решаем: √36 + 2√9 = 6 + 2 * 3 = 6 + 6 = 12
  Ответ: √36 + 2√9 = 12.
• Вычислите значение выражения: 2√16 — 3√25
  Как решаем: 2√16 — 3√25 = 2 * 4 — 3 * 5 = 8 — 15 = -7
  Ответ: 2√16 — 3√25 = -7.
• Вычислите значение выражения: 3√81 — 5√9
  Как решаем: 3√81 — 5√9 = 3*9 — 5 * 3 = 27 — 15 = 12
  Ответ: 3√81 — 5√9 = 12.
• Вынесите множитель из-под знака корень: √60
  Как решаем: √60 = √15 * √4 = 2√15
  Ответ: √60 = 2√15.
• Вынесите множитель из-под знака корень: √160
  Как решаем: √160 = √16 * √10 = 4√10
  Ответ: √160 = 4√10.
• Внесите множитель под знак корня: 6√7
  Как решаем: √62 * 7 = √36 * √7 = √252
  Ответ: 6√7 = √252.
• Внесите множитель под знак корня: 8√2
  Как решаем: 8√2 = √82 * 2 = √64 * √2 = √128 Ответ: 8√2 = √128.
• Внесите множитель под знак корня: 9√5
  Как решаем: 9√5 = √92 * 5 = √81 * √5 = √405
  Ответ: 9√5 = √405.
• Упростите выражение: (5 — √2)2
  Как решаем: (5 — √2)2 = 52 — 2 * 5 * √2 + (√2)2 = 25 — 10√2 + 2 = 27 — 10√2.
  Ответ: (5 — √2)2 = 27 — 10√2.
• Вычислите значение выражения: 3√49 — 3√25
  Как решаем: 3√49 — 3√25 = 3 * 7 — 3 * 5 = 21 — 15 = 6
  Ответ: 3√49 — 3√25 = 6.
• Вычислите значение квадратного корня: √484 * √576
  Как решаем: √484 * √576 = 22 * 24 = 528
  Ответ: √484 * √576 = 528.
• Вычислите значение квадратного корня: √625 * √81
  Как решаем: √625 * √81 = 25 * 9 = 225
  Ответ: √625 * √81 = 225.
• Найдите значение выражения: 3√100 — √144
  Как решаем: 3100 — 144 = 3 * 10 — 12 = 18
  Ответ: 3√100 — √144 = 18.

Функция квадратного корня

Каждому числу соответствует не более чем 1 арифметический квадратный корень. Поэтому формула

задает функцию. Исследуем ее.

Так как под знаком радикала может находиться лишь неотрицательное число, то областью определения корня является множество всех неотрицательных чисел. Такова же и область допустимых значений.

Построим график квадратного корня по точкам. Для этого вычислим ее значения в нескольких точках (указана точность до 0,1):

График функции квадратного корня будет выглядеть так:

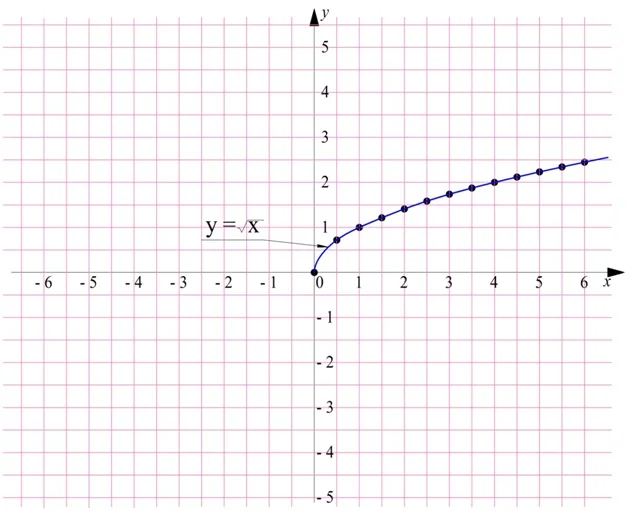
Отметим, что полученная линия чем-то напоминает обычную параболу функции у = х2, которую «положили набок», то есть повернули против часовой стрелки на 90°, а после убрали одну из ветвей:

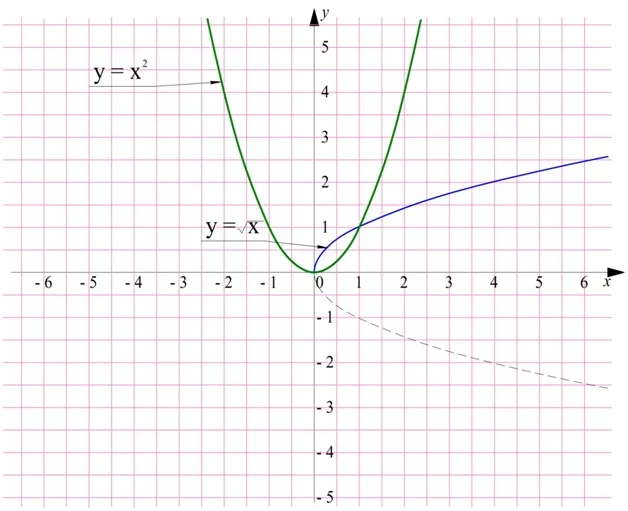
И это не случайность. Дело в том, что две эти функции являются обратными друг другу. Действительно, пусть с помощью графика параболы мы хотим найти значение величины а2. Стрелки показывают последовательность действий:

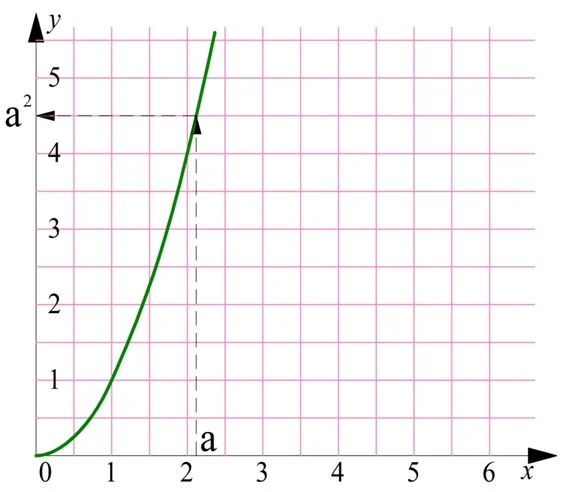
Мы должны найти а на оси Ох, построить от найденной точки вертикальную линию до пересечения с графиком, а потом провести горизонтальную линию. Но если нам надо вычислить корень из положительного числа b, то мы должны действовать в обратном порядке: найти b на вертикальной оси, провести горизонтальную линию до пересечения с параболой, и потом опустить перпендикуляр на горизонтальную ось:

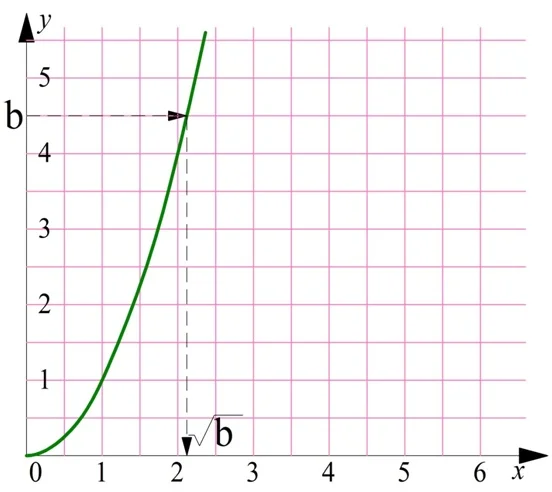
Получается, для вычисления обеих функций можно использовать один график! Но, так как традиционно аргумент функции обозначают буквой х, а саму функцию как у, а также ось Ох располагают горизонтально, то для получения графика обратной функции надо буквально повернуть график основной функции так, чтобы оси Ох и Оу поменялись местами:

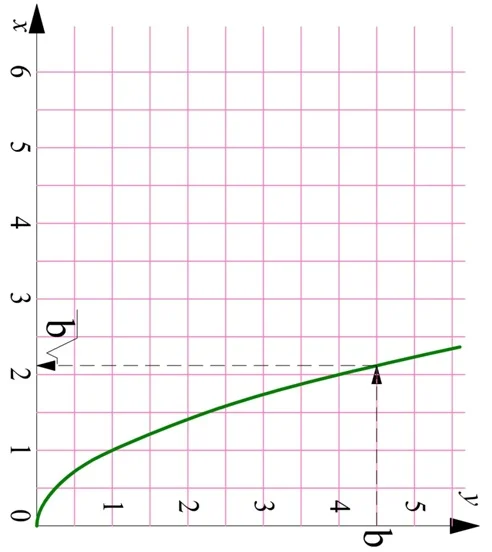
Действительно, в результате поворота получили уже знакомый график функции корня из х. Осталось лишь правильно переименовать оси и повернуть цифры в привычное положение.

Взаимное расположение этих графиков можно описать и иначе. Они симметричны относительно прямой линии, которую задает график у = х. Ведь если точка имеет координаты (а; b) принадлежит параболе у = х2, то, по определению корня, точка с обратными координатами (b; а) должна лежать на графике корня. Однако две такие точки будут симметричны относительно линии у = х:

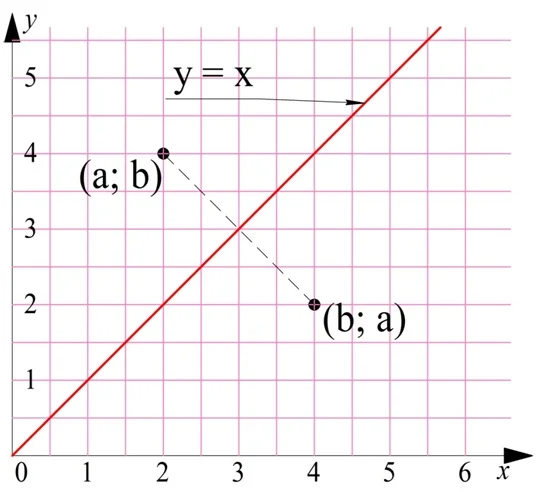
Соответственно, симметричны относительно этой прямой и графики обратных функций:

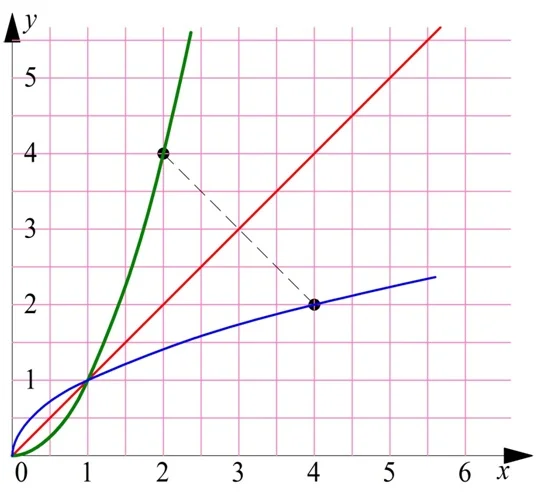
Исключительно для большей наглядности (чтобы была очевидна симметрия, о которой идет речь), повернем эту картинку на 45°:

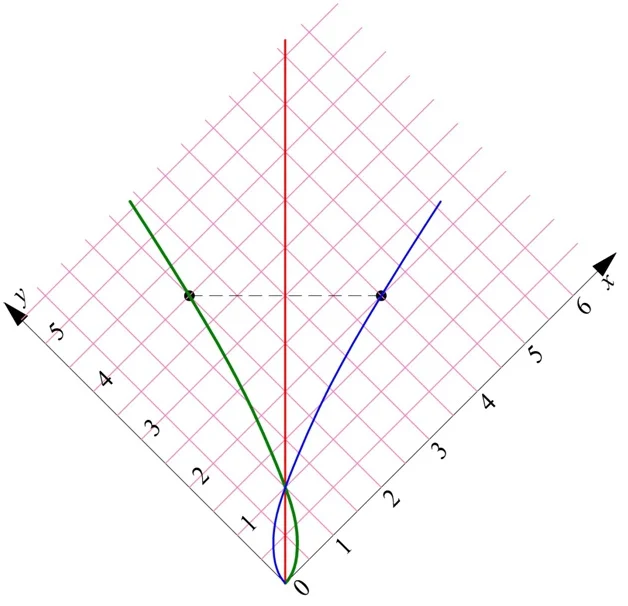
Полезные советы для успешного выполнения вычисления

Вычисление квадратного корня на калькуляторе Андроид может быть простым, если вы следуете нескольким полезным советам:

1. Убедитесь в правильном вводе числа.

Перед нажатием кнопки извлечения квадратного корня убедитесь, что вы правильно ввели число, из которого вы хотите извлечь корень. Дважды проверьте, чтобы избежать ошибок.

2. Ознакомьтесь с режимами калькулятора.

Ознакомьтесь с доступными режимами калькулятора на вашем устройстве. Возможно, ваш калькулятор имеет специальный режим для вычисления квадратного корня. Использование этого режима может значительно упростить процесс и сэкономить вам время.

3. Используйте скобки для сложных выражений.

Если вам нужно вычислить квадратный корень сложного выражения, используйте скобки, чтобы явно указать, какие части выражения должны быть вычислены первыми. Это поможет избежать ошибок и сделает вычисление более понятным.

4

Обратите внимание на точность и округление

Калькуляторы могут иметь разную точность при вычислении квадратного корня

Убедитесь, что вы понимаете, какая точность используется, и обратите внимание на результат. Если вам нужна более точная оценка, вы можете округлить результат до нужного числа знаков после запятой

5. Изучите дополнительные функции калькулятора.

Калькуляторы на Андроид могут иметь дополнительные функции, такие как вычисление степеней и процентов. Изучите эти функции и узнайте, как они могут быть полезны в вашей работе.

Следуя этим советам, вы сможете успешно выполнить вычисление квадратного корня на калькуляторе Андроид и продолжить свою математическую работу без проблем.

Способ вычисления квадратного корня на Андроид

1. Откройте калькулятор на вашем устройстве Андроид.
2. На данном экране вы должны увидеть основные математические функции, такие как сложение, вычитание и умножение.
3. Нажмите на кнопку, обозначенную символом «√» или «sqrt». Она может быть помечена как «корень» или «root».
4. После того, как вы нажмете эту кнопку, в интерфейсе калькулятора появится область для ввода числа, из которого вы хотите извлечь квадратный корень.
5. Введите число в это поле с помощью цифровых кнопок калькулятора или используйте клавиатуру вашего устройства Андроид.
6. После ввода числа нажмите на кнопку «=» или «равно» для получения результата.

Теперь вы должны увидеть на экране результат — квадратный корень из введенного вами числа. Если вы хотите вычислить квадратный корень из другого числа, просто повторите указанные выше шаги.

Вычисление квадратного корня на калькуляторе Андроид — это быстрый и удобный способ получить точный ответ на ваши математические вопросы

Не важно, вы используете калькулятор для повседневных вычислений или для более сложных задач, вы можете легко извлечь квадратный корень, следуя простым инструкциям выше

Изящное решение проблемы удобное для всех

Когда речь идет о вычислении квадратного корня на калькуляторе Андроид, на помощь приходит простое и удобное решение. Для этого необходимо запустить приложение калькулятора на своем устройстве и выполнить следующие простые шаги.

Шаг	Описание
1	Откройте калькулятор на своем устройстве Андроид.
2	На экране калькулятора вы увидите кнопки с различными математическими операциями.
3	Из списка доступных функций выберите «√» или «sqrt».
4	В поле ввода калькулятора введите число, из которого вы хотите извлечь квадратный корень.
5	Нажмите кнопку «равно» для получения результата.
6	На экране вывода калькулятора появится результат – квадратный корень из заданного числа.

Изящным решением проблемы является использование встроенной функции квадратного корня на калькуляторе Андроид. Оно позволяет легко и быстро извлекать квадратные корни из любых чисел, не требуя установки дополнительных приложений. Этот метод доступен для всех пользователей устройств Андроид и позволяет выполнять вычисления в любое удобное время.

Ввод команд с компьютерной клавиатуры

Для работы с калькулятором можно использовать любые цифровые клавиши: как цифровые клавиши находящиеся сверху, так и отдельные цифровые клавиши находящиеся справа.

Для ввода равно можно использовать клавишу ; Для стирания последнего знака используется клавиша (клавиша со стрелкой); Для ввода знака плюс используется клавиша сверху или на боковой клавиатуре; Для ввода знака минус используется клавиша сверху или на боковой клавиатуре; Для ввода знака умножения используется клавиша на боковой клавиатуре; Для ввода знака деления используется клавиша [ / ] на боковой клавиатуре; Для сброса калькулятора можно использовать клавиши , на верхней клавиатуре или на цифровой клавиатуре.

Понятие корня и его свойства

Корень — это число, при возведении в формуле в степень равным индексу корня, дает исходное число.

Например, корень числа 9 с индексом 2 равен 3, так как 3 в квадрате равно 9: √9 = 3. Корень числа 64 с индексом 3 равен 4, так как 4 в кубе равно 64: ∛64 = 4.

В математике часто используются несколько свойств корней:

1. Корень из суммы: корень от суммы двух чисел равен корню из первого числа, увеличенному на корень из второго числа. Например, √(a + b) = √a + √b.
2. Корень из разности: корень от разности двух чисел равен корню из первого числа, уменьшенному на корень из второго числа. Например, √(a — b) = √a — √b.
3. Корень из произведения: корень от произведения двух чисел равен корню из первого числа, умноженному на корень из второго числа. Например, √(a * b) = √a * √b.
4. Корень из деления: корень от деления двух чисел равен корню из первого числа, деленному на корень из второго числа. Например, √(a ÷ b) = √a ÷ √b.

Корни в математике широко применяются для решения уравнений, изучения геометрических фигур и в других областях математики.

Плюсы использования квадратного корня

Использование квадратного корня имеет свои преимущества в математике. Наверняка вы сталкивались с ситуацией, когда находились в объявлении идеального квадрата и вам нужно было найти значение числа, возводящегося в квадрат, чтобы получить данное число. В таком случае вам приходилось использовать корень как ответ на вопрос.

Представьте, что у вас есть выражение, в котором нужно извлечь корень из подкоренного числа. Например, в уравнении x^2 = 25, мы ищем значение x. Чтобы найти ответ, используйте квадратный корень: √25 = 5. Здесь мы можем сказать, что между символом корня и числом, подкоренное извлекаемое число 25, стоит большой знак «радикала». С помощью этого знака мы можем представить корень в виде символа √.

Маленькая цифра перед корнем сверху может быть использована для отметки степени корня. Например, когда вы возводите число под корнем в какую-то степень, такая цифра может указывать на степень корня. Например, √(3^2) = 3. Здесь цифра 2 перед корнем сверху говорит о том, что мы извлекаем корень из числа 3 во 2-й степени. Таким образом, мы можем возвести число под корнем в любую степень и получить ответ.

Другой плюс использования квадратного корня — возможность извлечения корня из числа, получившегося в результате умножения. Например, мы можем возвести число 3 во 2-ю степень и умножить на число 2, чтобы получить число 18. Затем мы можем взять корень из числа 18, используя символ корня: √(3^2 * 2) = √18. Вычислите эту операцию и получите ответ.

Также важно отметить, что внесение корня в выражение может помочь в решении уравнений. Например, когда мы решаем квадратное уравнение, мы ищем значения переменной x

Здесь корень может помочь нам найти ответы. Возьмем уравнение x^2 — 9 = 0. Мы можем искать ответ, используя вынесение корня: √(x^2) = √9. Здесь мы выносим корень под квадратным знаком из-под переменной x. Все ответы найдены, и мы можем найти решение уравнения.

Попробуйте сами использовать квадратный корень для решения различных примеров и задач. Используйте таблицей умножения и забывайте вносить маленькую цифру перед корнем сверху, чтобы найти ответы на вопросы. Не стоит бояться возводить числа в корень и извлекать корни из чисел — это может быть интересным и полезным упражнением для вашего математического развития.

Сведения о квадратном корне в производных математических операциях

Квадратный корень это операция обратная возведению в квадрат. Извлекая корень, мы находим число, которое при возведении в квадрат даст исходное число. Здесь мы разберем основные аспекты использования квадратного корня в математических операциях.

Маленькая цифра перед корнем сверху представляет собой индекс. В случае квадратного корня она указывает на степень, в которую нужно возвести число, чтобы получить исходное число. Например, корень во 2 степени () даст исходное число .

Используя корень с индексом 2, мы решаем уравнения вида , где — это корень, который мы ищем, а — это число, под корнем. Попробуйте решить примеры:

1. Найдите корень из числа 25.

   Ответ: √25 = 5

2. Найдите корень из числа 81.

   Ответ: √81 = 9

3. Найдите корень из числа 16.

   Ответ: √16 = 4

Во многих случаях важно учитывать, что корни могут иметь иррациональные значения, то есть они не могут быть выражены обычной десятичной дробью. Например, корень из числа 2 (√2) является иррациональным числом и не может быть точно представлен десятичным числом

Также, помимо извлечения корня, с квадратным корнем можно выполнять другие арифметические операции, такие как сложение, вычитание, умножение и деление. В таблице ниже приведены примеры этих операций:

Операция	Пример	Результат
Сложение	√4 + √9	2 + 3 = 5
Вычитание	√9 — √4	3 — 2 = 1
Умножение	√4 * √9	2 * 3 = 6
Деление	√9 / √4	3 / 2 = 1.5

Важно помнить, что перед квадратным корнем иногда стоит множитель, который необходимо вынести за пределы корня. Например, √(4 * x²) = 2 * √x

Используйте эти сведения о квадратном корне в производных математических операциях для решения уравнений, нахождения корней и выполнения других операций. Запомните определения и примеры, и пользуйтесь таблицей для удобства вычислений. Неверно вносить большой множитель под корень или забывать использовать индекс перед корнем. Чтобы научиться решать уравнения с корнями, попробуйте решить примеры самостоятельно и проверьте свои ответы. Наверняка с опытом вы станете все лучше и точнее в использовании квадратного корня в математических операциях.

Определение и основные понятия

Корень – это операция обратная возведению в степень. Если число а возведено в степень n равную b (an = b), то корнем n-й степени из числа b называется такое число а, что а n = b.

Другими словами, корень из числа b – это такое число а, возведение в n-ю степень которого дает число b.

Например:

Корень квадратный из числа 9 равен 3, так как 3 возвели в квадрат (32 = 9).

Корень кубический из числа 8 равен 2, так как 2 возвели в куб (23 = 8).

Чтобы обозначить корень, под числом ставят символ извлечения корня и указывают степень, с которой нужно извлекать корень.

Например:

√9 – корень квадратный из числа 9,

∛8 – корень кубический из числа 8.

Как использовать таблицу символов

Альтернативой этому варианту является использование специальной таблицы символов, имеющейся в ОС Виндовс, позволяющей использовать корень на клавиатуре. Выполните следующее:

В текстовом редакторе Word (а также в Excel) также имеется соответствующая таблица символов, которую можно использовать для наших задач. Вы можете найти её, перейдя во вкладку «Вставка», и нажав на «Символ» справа, а затем и кликнув на надпись «Другие символы» чуть снизу, это поможет вам в решении вопроса написании корня в Ворде.

Можно, также, использовать опцию «Формула» во вкладке «Вставка» по описанному в данном ролике алгоритму.

Калькулятор инженерный

Используйте инженерный калькулятор для сложных расчетов с применением тригонометрических функций. Команды вводятся с помощью мыши или клавиатуры. Инженерный калькулятор позволяет производить сложные расчеты с применением различных тригонометрических функций: синуса, косинуса, тангенса, котангенса. Калькулятор позволяет возводить числа в степень, вычислять логарифм числа. Основные команды (цифры, умножение, деление, сложение, вычитание, равенство, сброс) можно вводить как с помощью мышки, так и с помощью цифровой клавиатуры (верхней или боковой). Подробные инструкции по работе с инженерным калькулятором смотрите внизу страницы.

Примеры решения уравнений с корнем

Корень в математике часто используется при решении уравнений. Он помогает нам найти значения переменных, при которых уравнение является истинным.

Рассмотрим несколько примеров решения уравнений с корнем:

1. Пример 1:

   Решить уравнение x2 = 16.

   Для начала выделим корень из обеих сторон уравнения: √(x2) = √16.

   Получаем: x = ±4.

   Ответ: x = 4 или x = -4.

2. Пример 2:

   Решить уравнение 2×2 — 8 = 0.

   Выразим переменную под корнем: 2×2 = 8.

   Разделим обе стороны уравнения на 2: x2 = 4.

   Выделим корень из обеих сторон: √(x2) = √4.

   Получаем: x = ±2.

   Ответ: x = 2 или x = -2.

3. Пример 3:

   Решить уравнение 3√x = 9.

   Перенесем число 3 под корень: √x = 9/3.

   Выразим переменную из-под корня: x = (9/3)2.

   Сократим: x = 32.

   Получаем: x = 9.

   Ответ: x = 9.

Запомни, что корень позволяет нам найти значения переменных, которые удовлетворяют уравнению. В решении уравнений с корнем нужно быть внимательным и следить за выполнением всех математических операций.

| Квадраты и квадратные корни

К

Харис Алик

Харис увлеченно изучает информационные технологии и любит облегчать проблемы других во всех сферах жизни. В свободное время предпочитает читать и писать тексты. Он также любит стратегические игры и музыку. Коммуникабельный, амбициозный, креативный, ответственный, целеустремленный и мотивированный к работе человек. Социально активный, с большим опытом работы с молодежью, связями с общественностью и планированием проектов.

Последнее обновление: 4 апреля 2022 г.

5 / 5 ( 15 голоса
)

Этот калькулятор квадратного корня поможет вам найти главный квадратный корень, а также корни других действительных чисел.

Тем временем посмотрите другие калькуляторы, связанные с математикой, такие как Калькулятор логарифмов, Площадь трапеции, Конденсированные логарифмы, или, может быть, вы хотите узнать больше о тригонометрии, так что отправляйтесь к этому Калькулятору кофункций. Кроме того, мы рекомендуем вам узнать больше о постулате сложения сегментов.

Что такое квадратный корень?

Квадратным корнем называется выражение, в котором одно число умножается само на себя. Укоренение — это вычислительная операция, в которой у нас есть корни. В основном мы выражаем это знаком √. Натуральное число под корнем называется радиантом, а выражение выше корня — показателем степени. Мы часто используем его почти в каждом случае, написанном без экспоненты.

Символ « √ » для квадратного корня впервые был использован в печати в 1525 году в книге Кристофа Рудольфа «Косс».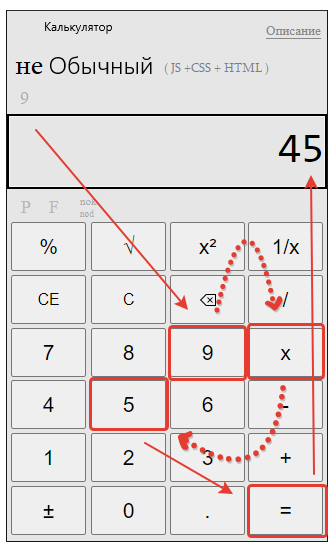

История

Эта таблица была составлена ​​между 1800 г. до н.э. и 1600 г. до н.э. Йельским вавилонянином, на ней показаны:
\sqrt{2}\text{и}\frac{\sqrt{2}}{2} = \frac{1}{\sqrt{2}}

разделены как 1; 24,51,10 и 0; 42,25,35 основано на 60 числах на квадрате, пересеченном двумя диагоналями. Они нашли процедуру определения стоимости этого. Они использовали вычисление приблизительного значения алгоритмов извлечения квадратного корня.

Для его расчета он использовал итерационный метод. В Йельском университете хранятся глиняные таблички с клинописными табличками 17 века до н.э., на которых находится процедура определения диагонали квадрата на странице 30.

Немецкий ученый Михаэль Штифель в 15 веке в своей книге Arthitmetica Integra использовал корневые символы. Обозначение корня, скорее всего, происходит от первой буквы латинского слова radix.

Продукт сначала вычисляется, а затем рутируется.

Как найти квадратный корень без калькулятора?

Чтобы найти квадратный корень из целого числа, вы также можете разделить целое число на числа, пока не получите ответ, который будет представлять собой число, которое вы разделили на .  Например, ,  16 разделить на 4 равно 4. 4 разделить на 2 равно 2 и так далее. Или просто используйте этот калькулятор квадратного корня.

Квадратный корень из отрицательного числа

Квадрат любого положительного и отрицательного числа дает положительный результат, а квадрат 0 равен 0. Таким образом, никакое отрицательное число не может иметь действительный квадратный корень.

Как упростить вычисление квадратных корней?

Упрощение квадратных корней кажется сложным, но на самом деле это не так. Чтобы упростить квадратный корень, вам просто нужно разложить число на множители и извлечь корни любых полных квадратов, которые вы найдете, из знака радикала. Как только вы запомните несколько типичных правильных квадратов и научитесь разлагать числа на множители, вы будете на пути к упрощению извлечения квадратного корня.

Совершенные квадраты — это квадраты следующих целых чисел:

Square	1	4	9	16	25	36
Result	1	2	3	4	5	6

Часто задаваемые вопросы

Квадратный корень из 2

Квадратный корень из 2 приблизительно равен 1,4142 — положительное действительное число.

Квадратный корень из 3

Квадратный корень из 3 — это положительное действительное число, которое при умножении само на себя дает число 3. Корень из 3 приблизительно равен 1,7320508075.

Является ли квадратный корень из 2 рациональным числом?

Да , 2 — рациональное число. Мы знаем, что рациональное число имеет форму p/q, где q не равно нулю.

Обязательно ознакомьтесь с нашим Калькулятором квадратных уравнений!

Способы набора корня на клавиатуре компьютера и ноутбука

Часто, чтобы поставить в текст радикал или запись с ним, используются сочетания букв. Sqrt, например, означает кв. корень, а cbrt – кубический. Но писать буквенные комбинации, слова неудобно. Кроме того, они не всем понятны.

Используем таблицу символов

Удобный инструмент, работающий в различных приложениях Microsoft Office, блокноте, – таблица символов.

Вызвать ее можно несколькими способами:

Далее найти значок корня, последовательно щелкнуть выделить, копировать и вставить в нужное место.

Код символа

Простой метод вставить корень – использовать код.

Алгоритм на компьютере:

В случае с ноутом сделать нужно так:

При работе с документом html, в программировании используются следующие значения:

Значок корня в уравнении

В документе можно написать не просто радикал, но и целое уравнение со степенью, неизвестным составляющим.

Самостоятельно уравнение с х, корнем из некоего числа записывается и через инструмент «Объект» в меню «Вставка». После нажатия на объект перейти в Microsoft equation 3.0, «Шаблоны дробей и радикалов». В открывшемся конструкторе записать уравнение.

Практическое применение корня

Корень в математике имеет множество практических применений в различных сферах нашей жизни. Ниже приведены несколько примеров, демонстрирующих, как мы можем использовать понятие корня в реальной жизни.

1. Строительство:

   При проектировании и строительстве зданий и сооружений, математики и инженеры часто используют корень. Например, для определения длины стороны квадрата или прямоугольника, требуется найти корень из числа площади. Также корень используется для определения расстояния между двумя точками в пространстве.

2. Финансы:

   В области финансов и банковского дела корень используется для расчета процентных ставок, сроков вкладов или займов. Например, для определения ежемесячного платежа по ипотеке, необходимо найти корень из суммы займа, процентной ставки и срока займа.

3. Наука:

   В различных научных исследованиях и экспериментах, корень используется для вычисления средних значений, определения зависимостей между переменными и анализа данных. Например, при изучении статистических данных о погоде, корень может использоваться для нахождения средней температуры за определенный период времени.

4. Информационные технологии:

   В области информационных технологий корень используется для определения сложности алгоритмов, расчета пропускной способности сети, а также для шифрования и декодирования информации. Корень также используется в задачах сжатия данных и обработке изображений.

Это лишь некоторые примеры практического использования корня в различных областях. Понимание понятия корня помогает нам в решении реальных задач и в повседневной жизни.

Запись иррациональных чисел с помощью квадратного корня

А теперь попробуй решить такое уравнение \( {{x}^{2}}=3\).

Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?

Начнем с самого начала – с нуля: \( {{0}^{2}}=0\) – не подходит.

Двигаемся дальше \( \displaystyle x=1\); \( \displaystyle {{1}^{2}}=1\) – меньше трех, тоже отметаем.

А что если \( \displaystyle x=2\)? 

Проверим: \( \displaystyle {{2}^{2}}=4\) – тоже не подходит, т.к. это больше трех.

С отрицательными числами получится такая же история.

И что же теперь делать? Неужели перебор нам ничего не дал?

Совсем нет, теперь мы точно знаем, что ответом будет некоторое число между \( \displaystyle 1\) и \( \displaystyle 2\), а также между \( \displaystyle -2\) и \( \displaystyle -1\).

Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными.

И что дальше?

Давай построим график функции \( \displaystyle y={{x}^{2}}\) и отметим на нем решения.

Попробуем обмануть систему и получить ответ с помощью калькулятора (как мы это делали в начале)!

Извлечем корень из \( \displaystyle 3\), делов-то!

Ой-ой-ой, выходит, что \( \sqrt{3}=1,732050807568\ldots \) Такое число никогда не кончается.

Как же такое запомнить, ведь на экзамене калькулятора не будет!?

Все очень просто, это и не надо запоминать, необходимо помнить (или уметь быстро прикинуть) приблизительное значение. \( \sqrt{3}\) и \( -\sqrt{3}\) уже сами по себе ответы.

Как найти корень числа без калькулятора

Нахождение корня числа без использования калькулятора может быть полезным навыком, особенно когда у вас нет доступа к калькулятору или компьютеру. Здесь описаны два простых подхода к нахождению корня числа без калькулятора: метод ближайших квадратов и метод деления пополам.

Метод ближайших квадратов:

1. Выберите два числа, которые находятся возле корня числа. Например, если нужно найти квадратный корень из 16, можно выбрать 4 и 5, так как 4^2 = 16 и 5^2 = 25.
2. Разделите число на одно из выбранных чисел. Например, 16/4 = 4.
3. Проведите этот шаг несколько раз, пока не получите достаточно точное приближение корня числа. Например, можно продолжать делить 4 на 4, получая 4/4 = 1, и затем делив 1 на 4, получая 1/4 = 0,25.

Метод деления пополам:

1. Выберите два числа, между которыми находится корень числа. Например, если нужно найти квадратный корень из 16, можно выбрать 4 и 5, так как 4^2 = 16 и 5^2 = 25.
2. Найдите среднее значение этих двух чисел. Например, (4 + 5)/2 = 4,5.
3. Если полученное среднее значение является точным корнем числа, то вы нашли ответ. В противном случае, выберите два числа между которыми находится среднее значение и продолжайте делить пополам до достижения нужной точности.

Оба этих метода позволяют находить корень числа без использования калькулятора. Они требуют некоторых математических операций и могут потребовать несколько итераций для достижения нужной точности.

Комплекс операций инженерного калькулятора

Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.

Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.

Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.

Ввод цифр производится в двух вариантах:

Умножение арифметических корней

Для умножения арифметических корней используйте формулу:

Примеры:

Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.

Если нет возможности извлечь корни из чисел, то поступаем так:

Если множителей больше двух, то решается примерно точно так, как и с двумя множителями: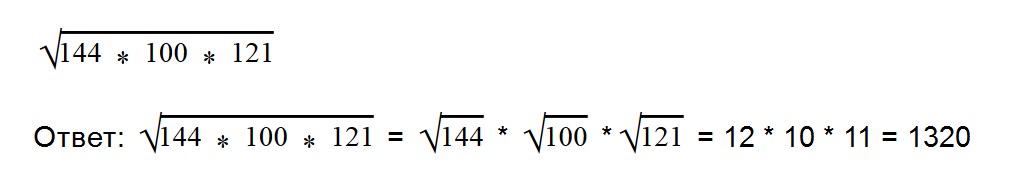

Добрая напоминалочкаЧтобы решать примеры быстрее, не забывайте пользоваться таблицей квадратов.

Метод умножения показателей с множителями

Умножить множители. Множитель — число, которое стоит перед знаком корня. В случае отсутствия множителя, он, по умолчанию, считается единицей. Далее необходимо перемножить множители:

Пример 1: 3 2 × 10 = 3 ? 3 × 1 = 3

Пример 2: 4 3 × 3 6 = 12 ? 4 × 3 = 12

Умножить числа под знаком корня. Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:

Пример 1: 3 2 × 10 = 3 (2 × 10) = 3 20

Пример 2: 4 3 × 3 6 = 12 (3 × 6) = 12 18

Упростить подкоренное выражение. Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня. После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:

Пример 1: 3 20 = 3 (4 × 5) = 3 (2 × 2) × 5 = (3 × 2) 5 = 6 5

Пример 2: 12 18 = 12 (9 × 2) = 12 (3 × 3) × 2 = (12 × 3) 2 = 36 2

Метод умножения корней без множителей

Убедиться, что у корня одинаковые показатели (степени). Вспомним, что степень записывается слева над знаком корня. Если нет обозначения степени, это значит, что корень квадратный, т.е. со степенью 2, и его можно умножать на другие корни со степенью 2.

Пример 1: 18 × 2 = 36

Пример 2: 10 × 5 = 50

Пример 3: 3 3 × 9 3 = 27 3

Упростить подкоренные выражения. Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:

Пример 1: 36 = 6 . 36 — квадратный корень из шести (6 × 6 = 36) .

Пример 2: 50 = (25 × 2) = (5 × 5) × 2 = 5 2 . Число 50 раскладываем на произведение 25 и 2 . Корень из 25 — 5 , поэтому выносим 5 из-под знака корня и упрощаем выражение.

Пример 3: 27 3 = 3 . Кубический корень из 27 равен 3: 3 × 3 × 3 = 27 .

Умножение корней с одинаковыми показателями

Чтобы перемножить корни с одинаковыми показателями, нужно оставить тот же показатель корня, а подкоренные выражения перемножить.

√(81) × √(25) =
= √(81 × 25) =
= 9 × 5 =
= 45

Умножение корней с разными показателями

Чтобы перемножить корни с разными показателями, нужно сначала привести корни к общему показателю, а потом перемножить полученные корни с одинаковым показателем. Чтобы умножить корень на число, надо занести под знак корня это число, возведённое в степень с показателем, как у корня.

∛‎(729) × √(25) =
= √(81) × √(25) =
= √(81 × 25) =
= 9 × 5 =
= 45