Преобразование рациональных выражений, виды преобразований, примеры

Решаем выражения с тригонометрической функцией

Часто в выражениях встречаются тригонометрические функции. Всего их в математике шесть:

• Синус;
• Косинус;
• Котангенс;
• Тангенс;
• Секанс;
• Косеканс.

Изучение тригонометрии начинается в 9-м классе, когда ученики уже подготовлены к сложным задачам. Большинство заданий представляются с sin и cos. Остальные функции встречаются значительно реже.

В математических примерах, которые содержат sin, cos, tg и др. функции, вычисление тригонометрической функции производится в первую очередь. Если это невозможно — осуществляется упрощение выражения до получения краткой формулы.

Задача. Решить:

\

Решение. Разложим 217 на 90 и 127. Т.к. по формуле приведения sin(90 + a) = cosa, получаем:

sin217 — sin (90 + 127) = cos127

Теперь заменяем полученной формулой наше слагаемое в знаменателе дроби:

\

Вспоминаем, что по тригонометрическому тождеству sin2a+ cos2 a= 1 (независимо от значения угла a). Поэтому одну часть слагаемого знаменателя (sin2127+ cos2127) преобразуем в единицу и получаем:

\

Ответ. 2

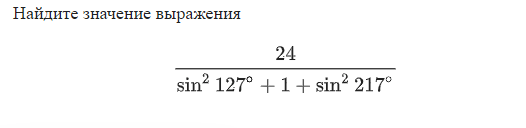
Важно: Не стоит бояться буквенных тригонометрических значений. Большинство примеров построено таким образом, чтобы функции можно было заменить более удобной для вычисления формулой

Поэтому вместо того, чтобы пытаться сразу решить пример, стоит обратить внимание на особенности функций и возможность их приведения к подходящей формуле

Задача. Решить:

\

Решение. Начинаем решение с разбора второй дроби

Обращаем внимание, что 192 = 48 • 2. А значит, корень этого числа можно представить в виде 2√48

Зная это и используя формулу косинуса двойного угла, преобразим наше выражение:

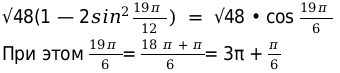
Теперь по формуле приведения решаем наш пример:

\

Ответ. — 6.

Алгоритм Евклида для вычисления НОД (наибольшего общего делителя)

Не всегда, сходу, можно понять какое число является наибольшим общим числителем, особенно если числа крупные, поэтому существует специальный алгоритм для выведения такого числа НОД.

Суть алгоритма такова: для нахождения НОД чисел а и b (где они целые и положительные числа, к тому же a больше b), выполняется ряд делений с остатком, получается ряд равенств, где деление останавливается в том случае если r_k+1=0, при этом r_k=НОД(a, b)

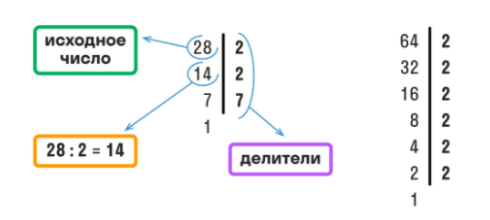
Пример. Рассчитаем НОД для 28 и 64.

Как находим:

Распишем простые множители для каждого числа и подчеркнем одинаковые

Д (28) = 2 * 2 * 7

Д (64) = 2 * 2 * 2 * 2 * 2 * 2

Найдем произведение одинаковых простых множителей и запишем ответ

НОД (28; 64) = 2 * 2 = 4

Ответ: НОД (28; 64) = 4

Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.

Когда использовать дроби?

Одной из основных сфер, в которых применяются дроби, является математика. Они позволяют точно представить любое вещественное число и выполнять арифметические операции с высокой точностью. Например, при решении уравнений или нахождении значений функций, дроби позволяют получить точные ответы.

В физике дроби используются для описания различных физических величин. Одна из самых известных дробей в физике — это отношение окружностей. Например, длина окружности делится на диаметр, что дает нам известное число π. Это позволяет точно вычислять площади, объемы и другие физические величины.

В экономике и финансах дроби используются для дробления и сравнения различных долей, процентов и долгов. Например, когда мы вычисляем проценты, мы используем отношение части к целому. Также дроби применяются при расчете финансового результата или при оценке доли акций или доли в собственности компании.

В повседневной жизни дроби применяются для разделения или комбинирования вещей и товаров. Например, при измерении объемов жидкостей или при подсчете денежных средств. Также дроби могут использоваться для представления времени, например, полуторачасовой отрезок времени.

Таким образом, дроби широко используются в различных сферах жизни и науки, чтобы представить доли, отношения или долги с помощью наглядного и точного математического представления.

Порядок действий в рациональных выражениях

Рассмотрим выражение:

$$\Big(\frac{2x-5y}{x+y}-\frac{x}{x+y} \Big):(x-5y)$$

В данном выражении можно найти разность дробей, а затем выполнить деление. В результате мы получим рациональную дробь.

Показать решение

Скрыть

Найдем разность дробей в скобках:$$\frac{2x-5y}{x+y}-\frac{x}{x+y}=\frac{\textcolor{darkgreen}{2x}-5y\textcolor{darkgreen}{-x}}{x+y}=\frac{\textcolor{darkgreen}{x}-5y}{x+y}$$

Выполним деление:$$\frac{x-5y}{x+y}:(x-5y)=\frac{\cancel{\textcolor{orange}{x-5y}}}{x+y} \cdot \frac{1}{\cancel{\textcolor{orange}{x-5y}}}=\frac{1}{x+y}$$

Порядок действий

В рациональных выражениях, так же как и в числовых выражениях, соблюдается порядок действий:

• Сначала считаются степени.
• Затем выполняются действия в скобках.
• Далее выполняется умножение и деление.
• В конце производится сложение и вычитание.

Пример 1

Представим в виде дроби выражение:$$2+y\overset{\textcolor{coral}{2}}-\frac{y+5}{x^2} \overset{\textcolor{blue}{1}}\cdot \frac{13}{2y+10}$$

$\textcolor{blue}{1)}$ Сначала выполняем умножение:$$\frac{y+5}{x^2} \cdot \frac{13}{2y+10}=\textcolor{darkgreen}{\frac{13}{2x^2}}$$

Показать решение

Скрыть

В знаменателе второй дроби вынесем общий множитель $\textcolor{orange}{2}$ за скобки:$$\frac{y+5}{x^2} \cdot \frac{13}{\textcolor{orange}{2}y+\textcolor{orange}{2}\cdot 5}=\frac{y+5}{x^2} \cdot \frac{13}{\textcolor{orange}{2}(y+5)}$$

Сократим и перемножим дроби:$$\frac{\cancel{\textcolor{purple}{y+5}}}{x^2} \cdot \frac{13}{2(\cancel{\textcolor{purple}{y+5}})}=\frac{1 \cdot 13}{x^2 \cdot 2}=\frac{13}{2x^2}$$

$\textcolor{coral}{2)}$ Теперь можно выполнить вычитание:$$2+y-\textcolor{darkgreen}{\frac{13}{2x^2}}=\frac{2x^2(2+y)-13}{2x^2}$$

Показать решение

Скрыть

Представим многочлен $\textcolor{coral}{2+y}$ в виде дроби: $\textcolor{coral}{\frac{2+y}{1}}$.

Приведем дроби к общему знаменателю $\textcolor{orange}{2x^2}$ и выполним вычитание: $$\textcolor{coral}{\frac{2+y}{1}}-\frac{13}{2x^2}=\frac{(2+y)\cdot \textcolor{orange}{2x^2}}{1\cdot \textcolor{orange}{2x^2}}-\frac{13}{2x^2}=$$ $$=\frac{2x^2(2+y)-13}{2x^2}$$

Пример 2

Упростим выражение:$$\Big(\frac{3x+1}{3x-1}\overset{\textcolor{blue}{1}}-\frac{3x-1}{3x+1} \Big)\overset{\textcolor{coral}{2}}: \frac{6x}{15x-5}$$

$\textcolor{blue}{1)}$ Выполним действие в скобках:$$\frac{3x+1}{3x-1}-\frac{3x-1}{3x+1}=\frac{12x}{(3x-1)(3x+1)}$$

Показать решение

Скрыть

Приведем дроби к общему знаменателю $(\textcolor{purple}{3x-1})(\textcolor{orange}{3x+1})$:$$\frac{(3x+1) \cdot (\textcolor{orange}{3x+1})}{(3x-1)\cdot (\textcolor{orange}{3x+1})}-\frac{(3x-1)\cdot (\textcolor{purple}{3x-1})}{(3x+1)\cdot (\textcolor{purple}{3x-1})}=$$ $$=\frac{(3x+1)^2-(3x-1)^2}{(3x-1)(3x+1)}$$

В числителе распишем «разность квадратов»:$$(\textcolor{blue}{3x+1})^\textcolor{coral}{2}-(\textcolor{darkgreen}{3x-1})^\textcolor{coral}{2}=((\textcolor{blue}{3x+1})+(\textcolor{darkgreen}{3x-1}))((\textcolor{blue}{3x+1})-(\textcolor{darkgreen}{3x-1}))$$

Раскроем скобки и произведем вычисления:$$(\textcolor{lightblue}{3x}\cancel{+1}+\textcolor{lightblue}{3x}\cancel{-1})(\cancel{3x}+\textcolor{orange}{1}\cancel{-3x}+\textcolor{orange}{1})=\textcolor{lightblue}{6x}\cdot \textcolor{orange}{2}=12x$$

Получаем:$$\frac{12x}{(3x-1)(3x+1)}$$

$\textcolor{coral}{2)}$ Произведем деление:$$\frac{12x}{(3x-1)(3x+1)}:\frac{6x}{15x-5}=\frac{10}{3x+1}$$

Показать решение

Скрыть

Заменим деление умножением, а вторую дробь перевернем. В числителе второй дроби вынесем общий множитель $\textcolor{orange}{5}$ за скобки:$$\frac{\textcolor{purple}{12x}}{(\textcolor{darkgreen}{3x-1})(3x+1)} \cdot \frac{\textcolor{orange}{5}(\textcolor{darkgreen}{3x-1})}{\textcolor{purple}{6x}}$$

Сократим дроби на $\textcolor{darkgreen}{3x-1}$ и на $\textcolor{purple}{6x}$: $$\frac{2}{3x+1} \cdot \frac{5}{1}=\frac{10}{3x+1}$$

{"questions":,"placeholder":0,"answer":0}},"step":1,"hints":}]}

Почему важно правильно представлять выражения в виде дробей?

Представление выражений в виде дробей позволяет работать с числами, которые не могут быть полностью представлены в виде конечной десятичной дроби. Например, число «пи» (π) является иррациональным, и его значение нельзя записать в виде десятичной дроби с конечным числом знаков после запятой. Однако, используя представление числа «пи» в виде дроби, мы можем получить более точные результаты при вычислениях.

Правильное представление выражений в виде дробей также упрощает работы с дробными исчислениями. Дроби позволяют точно выражать и вычислять доли и отношения, которые могут быть сложными или нецелыми числами. Например, дробь 3/4 означает, что у нас есть 3 части из 4 возможных, что является более точным и информативным, чем просто число 0.75.

Кроме того, правильное представление выражений в виде дроби позволяет удобно проводить арифметические операции с дробями. При сложении, вычитании, умножении и делении дробей мы можем использовать общие правила и приводить дроби к общему знаменателю, что упрощает вычисления и позволяет получать точные результаты.

Итак, правильное представление выражений в виде дробей имеет большое значение в математике и помогает нам точно и удобно работать с нецелыми числами и числовыми отношениями. Этот навык пригодится не только в школе и университете, но и в повседневной жизни, например, при решении финансовых задач или при работе с данными и статистикой.

Преобразования числителя и знаменателя рациональной дроби

Числитель и знаменатель считаются самодостаточными числовыми выражениями. Отсюда следует, что с ними можно производить различные преобразования, то есть в числителе или знаменателе разрешено заменять на тождественное равное ему выражение.

Чтобы провести тождественные преобразования, необходимо группировать и приводить подобные слагаемые, причем знаменатель заменять на более простое подобное ему выражение. Числители и знаменатели содержат многочлены, значит, что с ними можно производить преобразования, подобные для многочленов. Это могут быть и приведения к стандартному виду или представление в виде произведения.

Для начала необходимо привести к стандартному виду. Применим свойство степени, получим выражение вида

Необходимо выполнить преобразования знаменателя. Представляем его в виде произведения, то есть раскладываем на многочлены. Для этого производим группировку первого и третьего слагаемых, а второго с четвертым. Общий множитель выносим за скобки и получаем выражение вида

Видно, что полученное выражение имеет общий множитель, который и необходимо вынести за скобки, чтобы получить

Теперь подходим к произведению многочленов.

Данные преобразования необходимы для их использования в преобразованиях.

Значение числового выражения с корнями

Задача. Решить:

√ 2² • 2² • 3² = ?

Решение. Все действия под корнем одинаковы — умножение. Это дает нам право разделить выражение на множители. Получаем:

√2² • √2² • √3² = ?

Т.к. под квадратным корнем у нас числа, возведенные во вторую степень, получаем:

2 • 2 • 3 = 12

Решение без пояснений. √ 2² • 2² • 3² = √2² • √2² • √3² = 2 • 2 • 3 = 12

Ответ. 12

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Находим значение числовых выражений со степенями

Следующий математический знак, который имеет приоритет в процессе решения, — степени. Они представляют собой результат многократного умножения числа на себя. Само число является основанием степени. А количество операций умножения — ее показателем. Причем выражен он может быть не только целым числом, но и дробью, полноценным числовым выражением.

Начинается решение выражения со степенями с вычисления самих степеней. Если они представляют собой полноценное выражение (например: \), то его необходимо решить в нашем примере это будет: \.

Задача. Решите:

\[
3^{1 / 3} \cdot 7^{1 / 3} \cdot 21^{2 / 3}=?
\]

Решение. Чтобы решить это выражение со степенями, воспользуемся равенством:

\

Рассматривая пример слева направо, видим, что у первых двух множителей одинаковые степени. Это позволяет нам упростить выражение:

\[
(3 \cdot 7)^{1 / 3} \cdot 21^{2 / 3}=21^{1 / 3} \cdot 21^{2 / 3}
\]

Зная, что при умножении степени с одинаковыми показателями складываются, получаем следующее выражение:

\[
21^{1 / 3} \cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21
\]

Решение без пояснений: \[3^{1 / 3} \cdot 7^{1 / 3} \cdot 21^{2 / 3}=(3 \cdot 7)^{1 / 3} \cdot 21^{2 / 3}=21^{1 / 3} \cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21\]

Ответ. 21

Интересно: Этот же пример можно решить и другим способом, преобразовав число 21 в степени ⅔ в два множителя. В данном случае решение будет выглядеть следующим образом:

\[3^{1 / 3} \cdot 7^{1 / 3} \cdot 21^{2 / 3}=3^{1 / 3} \cdot 7^{1 / 3} \cdot(3 \cdot 7)^{2 / 3}=3^{1 / 3} \cdot 7^{1 / 3} \cdot 3^{2 / 3} \cdot 7^{2 / 3}=3^{1 / 3+2 / 3} \cdot 7^{1 / 3+2 / 3}=3^{1}+7^{1}=21\]

Ответ. 21

Задача. Решить:

\[
2^{-2 \sqrt{5}} \cdot 4^{\sqrt{5}-1}+\left((\sqrt{3})^{1 / 3}\right)^{6}
\]

Решение. В данном случает получить точные числовые значения показателей степеней не удастся. Поэтому искать значение выражения с дробями в виде степени будем снова через упрощение:

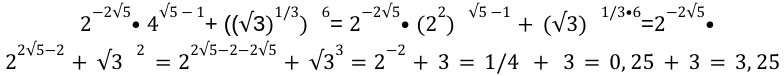
Ответ. 3,25

Выражения с дробями

Поиск значения выражения дробей начинается с их приведения к общему виду. В большинстве случаев проще представить все значения в виде обыкновенной дроби с числителем и знаменателем. После преобразования всех чисел необходимо привести все дроби к общему знаменателю.

Важно: Прежде чем найти выражение дробей, необходимо провести вычисления в их знаменателе и числителе отдельно. В данном случае действуют стандартные правила решения

Когда дроби приведены к единому знаменателю можно переходить к решению. Вычисление значений верхней строки (числителя) и нижней (знаменателя) производятся параллельно.

Задача. Решить:

\

Решение. Действуя по главному правилу, прежде чем найти значение числового выражения, преобразуем всего его части в простую дробь. Получаем:

\

Теперь выполняем вычисления в знаменателе и числителе и находим ответ:

\

Ответ. \

Примеры(2):

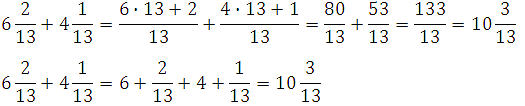
Задача. Решить:

\

Решение. В данном примере мы не можем извлечь корень из пятерки. Но мы можем воспользоваться формулой разложения корней:

\

Теперь можем придать нашему первоначальному выражению следующий вид:

\

Ответ. \.

Выражения с логарифмами

Как и степени, логарифмы (log), имеющиеся в выражении, вычисляются (если это возможно) в первую очередь. К примеру, зная, что \ мы можем сразу упростить выражение  \ до простого и понятного 2 + 5*6 = 32.

Со степенями логарифмы объединяет и порядок выполнения действий. Прежде чем искать значение выражения логарифмов, необходимо вычислить его основание (если оно представлено математическим выражением).

В случаях, когда полное вычисление логарифма невозможно, производится упрощение примера.

Задача. Решить:

\

Решение. Чтобы найти логарифм выражения, воспользуемся свойствами логарифмов и представим значение логарифмов со степенями:

Это позволит нам решить пример следующим образом:

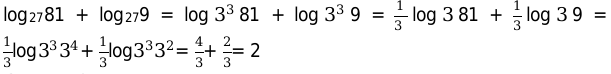
Ответ. 2

Работа с дробями в компьютерных программных системах

Для представления дробных чисел в программных системах существует несколько способов. Один из самых распространенных способов — использование десятичной дроби, которая может быть представлена в виде числа с плавающей точкой или десятичной десятичной записи.

В языке программирования C++, например, для работы с десятичными дробями используется тип данных float или double. В языке Python также есть встроенные типы данных float и decimal для работы с десятичными дробями.

Кроме десятичной дроби, в некоторых программных системах также используется простая дробь, которая представляет собой отношение двух целых чисел, числителя и знаменателя. Простые дроби удобны для точного представления рациональных чисел, таких как 1/3 или 5/8.

В языках программирования, поддерживающих рациональные числа, таких как Haskell или Lisp, можно использовать специальные типы данных для работы с простыми дробями. Например, в Haskell есть тип данных Rational, который позволяет манипулировать простыми дробями с высокой точностью и без округления.

При работе с дробными числами в компьютерных программных системах необходимо также учитывать возможность округления и потери точности при выполнении арифметических операций. В некоторых случаях может потребоваться использование специальных алгоритмов и библиотек для обеспечения точности вычислений с дробями.

Что такое дробные выражения

В процессе решения заданий и примеров по алгебре, физике, геометрии и другим наукам, предполагающим какие-либо расчеты с математическими величинами, нередко можно встретить дробные числа. С целыми числовыми значениями выполнять разнообразные действия достаточно просто. При вычитании, умножении, делении, сложении дробей возникают определенные сложности.

По этой причине целесообразно рассмотреть такое понятие как дробные выражения, а также приемы, позволяющие быстро упростить запись или решить задачу с ними. Начать стоит с определения дробного числа. В качестве примера допустимо рассмотреть следующую дробь:

\(\frac{7}{12}\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Заметим, что выше записана операция деления, то есть число 7 поделили на число 12 и зафиксировали выражение с применением дробной черты. Получим, что:

\(\frac{7}{12} = 7 \div 12\)

Частное пары числовых значений или выражений, где вместо знака деления использована черта, представляет собой дробное выражение.

Приведем несколько характерных примеров представления дробных выражений:

\(\frac{2+\frac{1}{3}}{\frac{5}{6}}\)

\(\frac{2х-4}{5уа^{3}+18}\)

\(\frac{4\frac{8}{19}-а}{1+\frac{b}{2+а}}\)

Чем отличаются от целых

Исходя из понятия дробных выражений, к данной категории следует причислять такие записи, не равные нулю, в составе которых присутствуют не только стандартные операции суммирования, вычитания, произведения, поиска частного, но и деление на выражение, содержащее переменные. Наглядно такие выражения можно представить следующим образом:

\(3х — \frac{3у}{2у+х}\)

\(\frac{2}{х}\)

\(\frac{2}{х^{2}-1}\)

\(7х \div 5у\)

\(х^{2} +\frac{у}{6}+\frac{2}{ х^{2} — у^{2} }\)

В свою очередь, целые выражения представляют собой записи, составленные из числовых значений и переменных с применением операций суммирования, разности, произведения, деления на какое-либо число, не равное нулю. В этом состоит разница между понятиями целых и дробных выражений. В качестве примеров для сопоставления можно привести записи с числами и неизвестными:

\(3х^{2}\)

\(х^{2}+ у^{2}\)

\((х^{2} – у)( х^{2} + у)\)

\(х^{2}у + ху^{2}\)

\(х\div 9\)

\(\frac{15х-3}{2}\)

Правило сокращения

Для того чтобы сократить, необходимо:

• Найти делитель наибольшего значения, который будет общим для знаменателя и числителя;
• Разделить числитель и знаменатель на него.

Примеры:

Дана такая дробь: \. сократим её.

Найдём такой делитель, при помощи применения алгоритма Евклида.

195 = 182 *1+13

182=13*14

Из чего следует, что НОД_(182,195)=13

Поэтому для сокращения дроби \, разделим числитель 182 и знаменатель 195 на 13 и получим равенство: \

Таким образом мы и получили несократимую дробь равную исходной.

Второй способ.

Второй способ основан на разложении числителя и знаменателя исходной дроби на простые множители, из которых позже все общие множители убираются.

Пример сокращения: \ для сокращения представим числитель и знаменатель дроби в виде простых множителей

\

Затем уберём все общие множители, как в числителе так и в знаменателе, \

Третий способ сокращения дроби.

Третий способ — способ последовательного сокращения. Применяя такой способ, сокращение происходит поэтапно, сокращая каждый раз на какой-либо очевидный общий множитель.

Пример: \

При сокращении такой дроби сразу можно увидеть, что и числитель и знаменатель деяться на 1000 в результате такого деления получается:

\

Следующим этапом мы видим, что оба значения и числителя, и знаменателя делятся на 2, получим несократимую дробь.

\

Как мы видим сокращение дроби не такой сложный процесс, главное подобрать удобный способ.

Как записывается натуральная дробь?

Натуральная дробь представляет собой отношение двух целых чисел: числителя и знаменателя. Числитель — это целое число, которое стоит перед знаком дроби, а знаменатель — это целое число, которое стоит после знака дроби.

Запись натуральной дроби производится следующим образом:

• Пишется числитель.
• Поставить знак дроби — это горизонтальная черта или дробная черта, которая указывает на то, что перед ней стоит числитель и после нее — знаменатель.
• Пишется знаменатель.

Например, запись натуральной дроби «половина» выглядит следующим образом:

1

—

2

Если знаменатель натуральной дроби равен 1, то запись может быть упрощена. Например, натуральная дробь «четыре целых» записывается как:

4

Также, если числитель равен нулю, то натуральная дробь считается равной нулю:

Примеры представления выражений в виде дробей

Представление выражения в виде дроби позволяет наглядно описать отношение двух величин и их соотношение. Рассмотрим несколько примеров:

Пример	Выражение	Дробь
Сумма двух чисел	4 + 3	7/1
Разность двух чисел	8 — 5	3/1
Произведение двух чисел	2 * 6	12/1
Частное двух чисел	15 / 3	5/1

В каждом из этих примеров мы можем представить результирующее выражение в виде дроби, где числитель будет равен значению самого выражения, а знаменатель — единице, поскольку знаменатель всегда равен 1 при представлении целых чисел в виде дробей. Таким образом, мы можем наглядно увидеть соотношение и отношение между числами.

Как представить выражение в виде дроби?

Выражение может быть представлено в виде дроби, если имеет числитель и знаменатель, разделенные дробной чертой. Числитель обозначает количество частей, которые нужно взять, а знаменатель обозначает количество одинаковых частей, на которые нужно разделить целое число или предметы.

Чтобы представить выражение в виде дроби, следует использовать теги и для создания таблицы с двумя строками и одним столбцом. В первой строке таблицы указывается числитель выражения, а во второй – знаменатель. Каждый элемент числителя или знаменателя может быть отдельной ячейкой таблицы.

Например, для выражения 3 + 1/2 можно представить в виде дроби следующим образом:

3

1/2

В данном случае числитель равен 3, знаменатель равен 2, и они разделены дробной чертой. Числитель и знаменатель отображаются в отдельных ячейках таблицы.

Представляя выражение в виде дроби, мы можем легко визуализировать и понять, какие части составляют целое число или предметы и как они делятся на равные части.

Как представить выражение в виде дроби?

Для представления выражения в виде дроби, нужно выполнить следующие шаги:

1. Определить числитель и знаменатель.
2. Записать числитель и знаменатель, разделив их чертой.

Рассмотрим пример: выражение 2 + 3/4.

Шаг 1: Определяем числитель и знаменатель. Числитель — это сумма 2+3, то есть 5. Знаменатель остается без изменений и равен 4.

Шаг 2: Записываем числитель и знаменатель, разделив их чертой. Получаем дробь 5/4.

Таким образом, выражение 2 + 3/4 представляется в виде дроби 5/4.

Дроби могут быть использованы для представления различных математических операций, таких как сложение, вычитание, умножение и деление. Они также могут быть использованы для представления нецелых чисел или результатов десятичных дробей в виде обыкновенной дроби.

Примечание: Если числитель в выражении является отрицательным числом, следует записать знак «-» перед дробью (например, -3/4).

Что такое дробь?

Числитель — это верхняя часть дроби, которая обозначает количество частей, которые мы рассматриваем.

Знаменатель — это нижняя часть дроби, которая обозначает общее количество частей, на которые мы делим целое число.

Например, в дроби 1/2, числитель равен 1, что означает, что мы рассматриваем одну часть целого числа. Знаменатель равен 2, что означает, что целое число разделено на две равные части.

Дроби могут быть положительными или отрицательными. В положительной дроби числитель и знаменатель положительные числа. В отрицательной дроби числитель или знаменатель (или оба) являются отрицательными числами.

Примеры дробей:

• 1/3 — Одна треть
• 2/5 — Две пятых
• 5/8 — Пять восьмых
• -3/4 — Минус три четверти

Примеры дробных выражений

Дробные выражения — это математические выражения, в которых числа представлены в виде дробей. Дробная форма позволяет более точно и удобно представлять десятичные числа и решать различные задачи.

Вот несколько примеров дробных выражений:

1. Простая дробь: ⅔
2. Смешанная дробь: 2 ½
3. Десятичная дробь: 0.75
4. Отрицательная дробь: -⅔
5. Дробь с отрицательным знаменателем: ⅓

Кроме простых примеров, дробные выражения могут содержать и арифметические операции:

Примеры дробных выражений с арифметическими операциями:

Выражение	Результат
⅔ + ⅓	1
⅔ — ⅓	⅓
⅔ × ⅓	2/9
⅔ ÷ ⅓	2

В этих примерах мы видим, что дробные выражения могут быть использованы для выполнения различных математических операций, таких как сложение, вычитание, умножение и деление дробей.

Основные понятия о натуральных дробях

Натуральная дробь представляет собой дробное число, где числитель и знаменатель являются натуральными числами.

Числитель — это верхняя часть дроби, обозначающая, сколько частей целого имеется.

Знаменатель — это нижняя часть дроби, обозначающая, на сколько частей целое разделено.

Например, в дроби 3/4 числитель равен 3, что означает, что имеется 3 части целого, а знаменатель равен 4, что означает, что целое разделено на 4 части.

Одной из характеристик натуральной дроби является единичная дробь. Это дробь, у которой числитель равен 1 и знаменатель равен любому натуральному числу. Например, 1/5, 1/8, 1/10 и т.д.

Существует также понятие правильной натуральной дроби. Правильная натуральная дробь характеризуется тем, что числитель меньше знаменателя.

Наибольшее целое число, которое можно получить из натуральной дроби, называется целой частью дроби. Целая часть представляет собой целое число исходной дроби, а остаток (дробная часть) — дробь, которая остается после отделения целой части.

Например, в дроби 5/3 целая часть равна 1, так как 5 можно разделить на 3 только один раз, а остаток будет равен 2/3.

Натуральные дроби могут быть использованы для представления долей и разделения целых чисел на части. Они широко используются в математике, науке и повседневной жизни.

Как решать дробные выражения

При поиске ответа на задачи с дробными выражениями необходимо учитывать важное свойство таких математических категорий. Суть его заключается в том, что при определенных значениях, которые принимает переменная, рассматриваемое выражение может не иметь смысла

Приведем несколько типичных примеров:

• \(\frac{2}{х}\) утрачивает логический смысл, если х принимает нулевое значение;
• \(3х — \frac{3у}{у-х}\) не обладает смыслом при равенстве значений х и у.

Исходя из вышесказанного, следует заключить, что смысл дробного выражения зависит от значений, которые принимают переменные, записанные в его составе. Смысловое условие выражено в отличии рассматриваемых переменных от нуля. Данное положение необходимо помнить, решая разнообразные примеры с дробными выражениями. С целью упростить понимание основного критерия следует сформулировать следующее понятие.

Допустимыми являются значения, характерные для переменных из некоторого дробного выражения, при которых это выражение приобретает смысл.

По итогам рассуждений целесообразно прийти к заключению о том, что процесс решения дробных выражений сводится к определению допустимых значений переменных, которые являются его составными компонентами. Рассмотрим рациональную дробь, где на месте в числителе и знаменателе записаны какие-либо многочлены. К данной категории дробей допустимо причислить следующие записи для наглядного примера:

\(х\div 6\)

\(\frac{15х-3}{2}\)

\(3х — \frac{3у}{у+х}\)

\(\frac{2}{х}\)

Заметим, что в случае рациональных дробей допустимы лишь те значения, которые принимают переменные, не обращающие знаменатель выражения в ноль. При решении заданий на дробные выражения применима инструкция поиска приемлемых значений переменных, входящих в состав дробного числа:

• сопоставление знаменателя рассматриваемой дроби, в котором записана переменная, к нулевому значению;
• вычисление корней полученного равенства, то есть таких значений переменных, которые приравнивают дробный знаменателю к нулю, лишая смысла выражение;
• устранение найденных значений из множества действительных чисел.

Дроби в математических операциях

Дробные числа часто используются в математических операциях. Они позволяют нам точно выражать части целого числа и выполнять операции с такими частями.

Во многих математических операциях мы можем столкнуться с дробями:

• Сложение и вычитание: при сложении или вычитании двух или более дробей мы приводим их к общему знаменателю, а затем складываем или вычитаем числители.
• Умножение: при умножении дробей мы умножаем числители между собой и знаменатели между собой.
• Деление: при делении одной дроби на другую мы умножаем первую дробь на обратную второй.

Например, если мы хотим сложить дроби 1/4 и 2/3:

Дробь	Десятичная запись	Шаги	Результат
1/4	0.25
2/3	0.6666…
Сложение		1/4 + 2/3 = 3/12 + 8/12 = 11/12	0.9166…

Таким образом, сумма 1/4 и 2/3 равна 11/12 или примерно 0.9166…

Дроби также используются в других математических операциях, таких как десятичная система счисления, проценты и т.д. Понимание основных понятий и правил работы с дробными числами поможет в решении различных математических задач.

Примеры решения задач

Задача 1

Сократить дробь 5/15

Решение: НОД дроби \(5/15
\) является 3. Разделив на 3 числитель и знаменатель, получаем \(1/5\)

Задача 2

Провести сокращение дроби 56/8.

Первым шагом превратим смешанную дробь в неправильную: \(56/8=46/8=(2*23)/(2*4)=23/4=53/4\)

Задача 3

Сократить неправильную дробь 86/42.

Решение: \((43*2)/(21*2)=43/21\)

Задача 4

Сократив дроби, найти значение выражения: 6/9+12/36

Решение: \(6/9+12/36=(2*3)/(3*3)+(1*12)/(3*12)=2/3+1/3=3/3\)

Результат примеры — неправильная дробь, в которой числитель равен знаменателю. Следовательно, ответом является 1.