Урок 2: логические операции

Введем выражение m k обозначающее поразрядную конъюнкцию m и k логическое и между соответствующими

Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число A, такое что выражение

(X & 15 ≠ 0) → ((X & 35 ≠ 0) → (X & A ≠ 0))

тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?

Для начала упростим выражение по закону

(X & 15 ≠ 0) → ((X & 35 ≠ 0) → (X & A ≠ 0))

(15 ≠ 0) → ((35 ≠ 0) → (A ≠ 0))

(15 = 0) ˅ (35 = 0) ˅ (A ≠ 0)

Теперь переведём 15 и 35 в двоичную систему счисления:

Выражение (15 = 0) ˅ (35 = 0) ˅ (A ≠ 0) должно быть истинно для любого натурального x. Проще говоря, если какое-то число при поразрядном умножении на 15 и на 35 не дают нуля, то при умножении на А это число также не должно давать нуля.

Рассмотрим произведение каждого разряда чисел 15 и 35 на единицу:

x	x & 1111 = 0	x & 100011 = 0	x & A ≠ 0
1	1
10	1
100	1	—
1000	1	—
10000	1	1	—
100000	1	—

В первом столбце указаны разряды (единицы, десятки и т.д.) Во втором столбце проверяется истинность выражения x & 1111 = 0, в третьем — истинность выражения x & 100011 = 0, в четвёртом столбце указано, критично ли значение А для этого разряда.

Посмотрите на первые две строки. x & 1111 = 0 ложно, x & 100011 = 0 ложно, значит x & A ≠ 0 обязательно должно быть истинно. А наименьший А, для которого произведение 1 и 10 не даст нуля — 11.

Что представляет собой данный ряд x0000xx000?

Данный ряд, записанный в формате x0000xx000, представляет собой последовательность символов, где «x» может быть заменено любым символом, а «0» обозначает пустое место или отсутствие символа.

Такое представление ряда может использоваться, например, в задачах программирования для обозначения определенных шаблонов или для обращения к определенной позиции в строке или массиве.

Причина, по которой используются символы «x» и «0», заключается в их четкой интерпретации: «x» обозначает любой символ, а «0» обозначает отсутствие символа или пустое место.

Примеры ряда в формате x0000xx000 могут выглядеть следующим образом:

Пример 1: a0000bc000
Пример 2: x0000yz000
Пример 3: 10000xx000

Такие ряды позволяют создавать универсальные шаблоны или схемы, которые могут быть применены в различных ситуациях, где необходимо указать определенное положение или паттерн символов.

Таким образом, ряд в формате x0000xx000 является универсальным обозначением для последовательности символов, где символ «x» может быть заменен любым символом, а «0» обозначает отсутствие символа.

Какое сочетание знаков продолжит ряд x0000xx000?

Ряд x0000xx000 представляет собой последовательность символов, где «x» — это место для одного из десяти возможных цифровых символов (от 0 до 9). Наша задача — определить, какое сочетание знаков продолжит данный ряд.

Расшифруем первую часть ряда «x0000». Здесь «x» может быть любой цифрой от 0 до 9, поэтому возможны десять вариантов: 00000, 10000, 20000, …, 90000.

Теперь перейдем ко второй части ряда «xx». Здесь «x» может быть любой цифрой от 0 до 9, поэтому существует сто возможных комбинаций: 00, 01, 02, …, 99.

Наконец, последняя часть ряда «000» фиксирована и не может измениться.

Окончательно, чтобы продолжить данный ряд, мы должны выбрать одну из десяти возможных комбинаций из первой части, одно из ста возможных сочетаний из второй части и фиксированную последнюю часть — «000». Таким образом, имеется 1 000 возможных вариантов продолжения данного ряда.

Например, одним из возможных вариантов продолжения ряда x0000xx000 может быть 5000045000, где первая часть — 50000, вторая часть — 45 и третья часть — 000.

Алгебра логики и решение задач

Несмотря на то, что логика, как наука о размышлении, существовала еще 5 в. До н.э., теперь это важная часть многих наук, а не только философии и риторики. Также логика существует, как отдельная наука уже более 200 лет.

Инструменты алгебры логики позволяют переводить словесные высказывания в сухие, объективные выражения, а с их помощью выполнять различные логические операции.Появился этот раздел математики 200 лет назад.

Стоит остановиться на базовых понятиях алгебры логики:

константы (0,1);
переменные;
формула;
знаки операций;
скобки.

Логическая переменная – обозначение логического выражения, которое может быть true (t, правда, истина, да, 1) – false (f, ложь, нет, 0).

Формула– символьный способ выражения операции между переменными при помощи специальных знаков и скобок ().

Логическое высказывание – утверждение, в котором говорится только правда или только ложь.

Образец таких предложений: «Луна – вертится вокруг Марса» – ложно, а «После зимы всегда приходит весна» – истинно.

Частицы «не», «или», если», «и» и другие, которые являются связующими элементами в обычной речи, позволяют создавать элементарные логические выражения.

Элементарные высказывания – те, к которым нельзя применить понятие истинности или ложности. Их обозначают различными символами (латинские буквы, цифры), знаками. Ими занимаются те сферы, к которым они относятся. Они входят в состав высказываний логики.

Из одних высказываний можно образовывать другие, в результате получая составные высказывания. И от того, являются исходные элементы составного конечного высказывания правдивыми или неправдивыми, а также какие логические связки использовались, будет правдой или ложью все высказывание в целом.

Чтобы образовать такое составное предложение в обычной жизни, используют связки И, ИЛИ, НЕ. А научный подход заменил их на конъюнкцию, дизъюнкцию, инверсию и более сложные операции. Все эти процессы выражают словесно, таблично (таблицы истинности) или графически (диаграммы Эйлера-Венна).

Простые выражения содержат лишь одно выражение (правдивое или нет), и не содержит никаких логических операций.

Сложные могут содержать от 2 и больше аргументов (простых выражений), которые между собой связаны логическими операциями.

Еще используют понятие «предикат» – содержит любое количество переменных без перечисления всех составляющих данных. Это предикат простых, отрицательных P(x)=(x<0) чисел.

Чтобы исключить лишнюю информацию, оставив только логические связи, используют таблицы истинности, наглядно демонстрирующие, правдиво или неправдиво конечное предложение, если учесть все значения входящих в его состав простейших частей.

Такая форма оформления и решения задач используется в построении электросхем, для решения различных логических задач, в булевой алгебре, программировании.

Поразрядная конъюнкция задачи 3

Лада Есакова, преподаватель информатики и математики, автор книги «Информатика. Полный курс подготовки к ЕГЭ».

Давайте разберем поразрядную конъюнкцию. Это задача, которая несколько лет была на ЕГЭ и на всех СтатГрадах, и она как-то исторически вызывает неприятные эмоции у учеников. На самом деле, ничего сложного.

Что такое поразрядная конъюнкция? Это перевод чисел в двоичную систему, а потом разряд с разрядом умножаем. Например, 7 х 4. 7 перевожу в двоичную систему – 1 1 1. 4 перевожу в двоичную систему – 1 0 0. И умножаю разряд с разрядом – 111 х 100=100.

Давайте порешаем задачи.

«Введем выражение М & К, обозначающие поразрядную конъюнкцию М и К (логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число А, такое, что выражение

Избавляемся от импликации. Формулу напоминать не буду, наверное, ее уже все знают наизусть.

Теперь мой любимый прием – известная часть пусть будет нулем (0), тогда искомая часть обязана быть единицей (1)

На какой-то момент я забываю про предметную область, я занимаюсь преобразованием до системы.

С нулем работать не очень приятно, поэтому сделаю отрицание и будет единица.

На что мне надо умножить 48, чтобы получились одни нули?

У X должны быть в первом разряде нули, чтобы обнулить единицы у 48, а остальное не важно

И те же самые X я должна умножить на 56 и не получить ноль. Чтобы не получить ноль, мне нужно здесь поставить единицу, чтобы она зацепила единицу от 56

Дальше может стоять что угодно. Все такие X являются решением этого уравнения.

Второе уравнение говорит, что все такие X (001…) нужно умножить на А и не получить ноль.

На первой и второй позиции у А может стоять что угодно. Три последние позиции тоже без разницы. Нужно поймать единственную единицу.

Если у А будет здесь единица, я умножу А и Х и ноль не получу. Вот такое А должно быть. Нужно найти наименьшее. Тогда остальные пусть будут нули.

Примеры аналогичных рядов сочетания символов

Ниже приведены несколько примеров аналогичных рядов сочетания символов, похожих на представленный в задании:

000000000
xx0000xx00
x0x0x0x0x0
000xx000xx
0x0x0x0x0x

В ряде символов можно заметить общие черты: группы одинаковых символов чередуются с символами, которые повторяются через определенное количество позиций.

Общая структура аналогичных рядов:
Описание
Пример

Группа одинаковых символов
000

Символ, повторяющийся через определенное количество позиций
xx

Такие ряды могут быть использованы для различных целей, например, в программировании, шифровании, или в качестве идентификаторов объектов. Фактическое значение символов будет зависеть от контекста, в котором они используются, поэтому точное объяснение значения и цели ряда с данной структурой без контекста невозможно.

В любом случае, эти примеры демонстрируют разнообразие возможных вариантов аналогичных рядов символов и демонстрируют их практическую применимость.

Электросхемы и таблицы истинности

При помощи «0» и «1» можно обозначить, светится ли лампочка, идет ли ток при параллельном или последовательном соединении проводов. Это настолько удобно, что у разных логических функций есть стандартные обозначения при построении электрических схем:

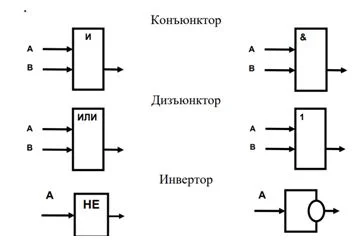
Переменными являются переключатели, а результат (горит лампа/идет ток) будет «1» – истина или «0» – ложь.

Для конъюнкции и инверсии подходит последовательное соединение, но во втором случае переключатель один, для дизъюнкции – параллельное.

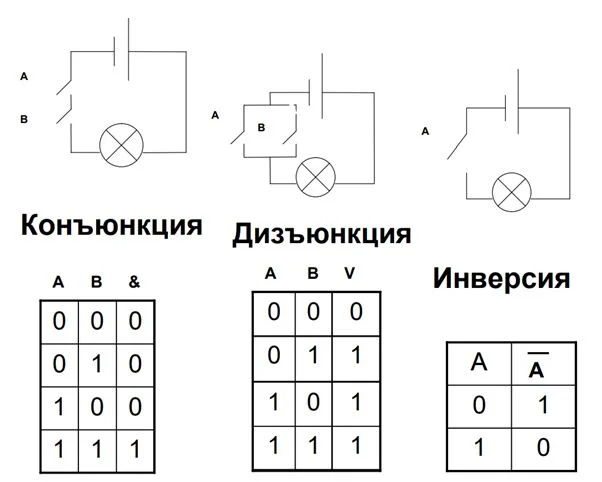
Это примеры простейших электросхем. Понимание простейших логических взаимосвязей, умение быстро строить и анализировать электроцепи позволяет строить, паять более сложные, многоуровневые схемы. Для автоматизации применяют различные программы, самый простой вариант – таблицы Excel.

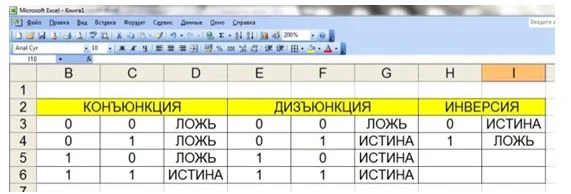
Практические примеры

Чтобы лучше понять, как работает ряд x0000xx000 и продолжить его, рассмотрим несколько практических примеров:

Пример 1:

Ряд x0000xx000 — это ряд, в котором некоторые символы заменены на «x». Чтобы найти продолжение ряда, нужно определить закономерность замены символов и продолжить ее. Например, если символы заменены на «x», «0» и «x», то следующим символом будет продолжение закономерности — «0». Таким образом, следующие символы ряда будут выглядеть как: x0000xx0000.
Пример 2:

Ряд x0000xx000 может иметь различные закономерности замены символов. Например, если первый символ заменен на «x», а второй и третий символы равны «0», то следующим символом будет «x». Если после него идут два нуля, то следующим символом будет «x». Таким образом, следующие символы ряда будут выглядеть как: x0000xx0000x.
Пример 3:

Закономерность в ряде x0000xx000 может быть связана с положением каждого символа. Например, если первая и третья позиции заменены на «x», а вторая и четвертая позиции равны «0», то следующим символом будет «x». Если после него идут два нуля, то следующим символом будет «x». Таким образом, следующие символы ряда будут выглядеть как: x0000xx0000x0.

Все эти примеры демонстрируют, что продолжение ряда x0000xx000 зависит от конкретной закономерности замены символов. Чтобы точно определить следующий символ, необходимо иметь дополнительную информацию или инструкцию, которая указывает на закономерность.

Используйте указанные примеры, чтобы развивать свои навыки анализа и поиска закономерностей в заданных сочетаниях символов.

О порядке логических операций

Лучше его представить списком. Логические операции выполняют в следующей последовательности: сначала идёт инверсия, затем конъюнкция, после этого дизъюнкция, после неё импликация, по её выполнении эквиваленция.

После них идут Штрих Шеффера и Стрелка Пирса. Первым может быть выполнено как то, так и другое.

Далее приведём несколько поучительных задач на построение таблиц истинности

Задачи 1 — 3

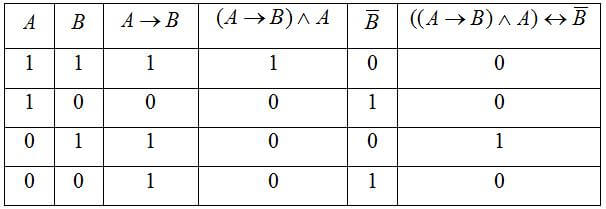
Сделать построение таблицы истинности для функции ((A→B) ∧ A) B

Решение:

1. Определяем сколько будет у нас столбцов. Количество переменных у нас 2, логических операций 4, число столбцов равно сумме 2+4 = 6.
2. Определяем, сколько будет у на строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций. У нас будет 2n+1 = 22 + 1= 5;
3. Заполняем первую строку. Прописываем символы переменные и логических операций;
4. В двух первых столбцах записываем возможные значения переменных;
5. В далее идущих столбцах записываем, какие значения принимают промежуточные функции;
6. В самом последнем из столбцов записываем итоговые значения функции.

В результате всего этого у нас должно получиться:

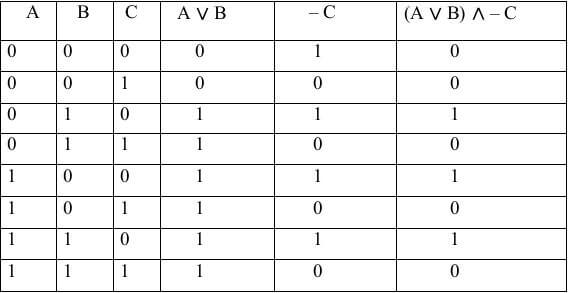
Провести построение таблицы истинности функции (A ∨ B) ∧ – C

Решение:

Определяем сколько будет столбцов. Количество переменных у нас 3, количество логических операций 3. Складываем то и другое: 3+3 = 5.
Определяем, количество строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций.В итоге будет 2n+1 = 23 + 1= 9;

Заполняем первую строку. Прописываем символы переменные и логических операций;
В два первые столбца вносим возможные значения наших переменных;
В далее следующие столбцы записываем, какие значения принимают промежуточные функции;
В последнем столбце записываем итоговые значения функции.

В итоге получим таблицу:

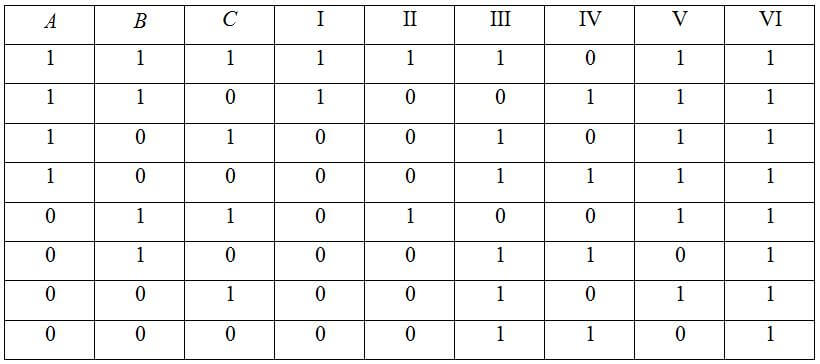
Сделать таблицу истинности для

(A ∧ B B ∧ C) ∨ (C → A)

Функция посложнее и таблица получится значительно больше, чем предыдущая.

Считаем столбцы. Количество переменных 3, количество логических операций 6. Значит столбцов будет 3+6=9;
Считаем строки. Их количество будет 23+1= 9;
Заполняем первую строку таблицы;
В первых столбцах записываем все допустимые значения наших переменных;
В остающихся столбцах пишем, какие наша функция принимает промежуточные значения
В последний столбец пишем итоговые значения данной нам функции.

В итоге у нас получается таблица:

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Какое сочетание знаков продолжит ряд x0000xx000?

Наконец, последняя часть ряда «000» фиксирована и не может измениться.

Сочетания знаков на выбор

В задачах, связанных с сочетаниями знаков, необходимо определить правильное продолжение ряда символов или найти закономерность в их последовательности. Знание основных правил и методов анализа позволяет успешно решать подобные задачи и предсказывать следующие сочетания.

Для анализа сочетаний знаков можно использовать различные подходы, включая логическое мышление, математическую модель или другие аналитические методы.

Приведенный ряд x0000xx000 представляет собой последовательность знаков, где «x» обозначает любой символ, а «0» — цифру ноль. Чтобы продолжить данный ряд, нужно найти закономерность в его структуре или определить условия, которым должно соответствовать следующее сочетание.

Возможные продолжения ряда x0000xx000:

x0000xx001
x0000xx010
x0000xx100
x0000xx011
x0000xx101
x0000xx110
x0000xx111

В данном случае значения «x» в продолжении ряда могут быть как «0», так и «1», поскольку эта часть строки является переменной и может принимать различные значения.

Ответ на вопрос о продолжении ряда зависит от предоставленной информации и контекста задачи. Поэтому, чтобы точно определить следующее сочетание, необходимы дополнительные данные или указания.

Практические примеры

Чтобы лучше понять, как работает ряд x0000xx000 и продолжить его, рассмотрим несколько практических примеров:

Пример 1:

Ряд x0000xx000 — это ряд, в котором некоторые символы заменены на «x». Чтобы найти продолжение ряда, нужно определить закономерность замены символов и продолжить ее. Например, если символы заменены на «x», «0» и «x», то следующим символом будет продолжение закономерности — «0». Таким образом, следующие символы ряда будут выглядеть как: x0000xx0000.
Пример 2:

Ряд x0000xx000 может иметь различные закономерности замены символов. Например, если первый символ заменен на «x», а второй и третий символы равны «0», то следующим символом будет «x». Если после него идут два нуля, то следующим символом будет «x». Таким образом, следующие символы ряда будут выглядеть как: x0000xx0000x.
Пример 3:

Закономерность в ряде x0000xx000 может быть связана с положением каждого символа. Например, если первая и третья позиции заменены на «x», а вторая и четвертая позиции равны «0», то следующим символом будет «x». Если после него идут два нуля, то следующим символом будет «x». Таким образом, следующие символы ряда будут выглядеть как: x0000xx0000x0.

Законы алгебры логики

В логике высказываний известно много общезначимых формул, которые также называются законами логики
высказываний. Основными законами являются следующие:

законы идемпотентности (повторение действия над объектом не изменяет его, латинский idem — «тот же
самый»
и potens — «способный»):
- $x \land x = x$
- $x \lor x = x$
$x \land 1 = x$ — $x$ и Истина всегда будет $x$
$x \lor 1 = 1$ — $x$ или Истина всегда будет Истина
$x \land 0 = 0$
$x \lor 0 = x$
$x \land \lnot x = 0$ – закон противоречия
$x \lor \lnot x = 1$ – закон исключения третьего
$\lnot \lnot x = x$ – закон снятия двойного отрицания
законы поглощения
- $x \land (y \lor x) = x$
- $x \lor (y \land x) = x$

Доказать эти и последующие законы можно с помощью построения таблиц истинности или
простейших логических рассуждений.
Следующая группа законов представляет взаимосвязь между логическими операциями:

$(x \equiv y) = (x \Rightarrow y) \land (y \Rightarrow x)$
$x \Rightarrow y = \lnot x \lor y$
законы Де Моргана
- $\lnot(y \lor x) = \lnot y \land \lnot x$
- $\lnot(y \land x) = \lnot y \lor \lnot x$

Замечательным следствием приведенных выше законов является следующий факт. Любую логическую формулу можно заменить
равносильной ей, но содержащую только две логические операции:

конъюнкцию «и» и отрицание «не»
дизъюнкцию «или» и отрицание «не»

Дальнейшее исключение логических операций, очевидно, невозможно, то есть приведенные пары представляют минимальный
базис для построения правильно построенных формул. Однако существует операция, с помощью которой можно представить
любую логическую связку. Эта операция получила название «штрих Шеффера» и определяется следующим образом:

$x$	$y$	$x \| y$
1
1
1
1	1

На основании этого определения можно ввести следующие законы, выражающие взаимосвязь операции «штрих Шеффера» и
других логических связок:

$\lnot x = x | x$ — связка «не» через «штрих Шеффера»
$x \land y = (x | y) | (x | y)$ — связка «и» через «штрих Шеффера»

Также следует отметить, что $x | y= \lnot (x \lor y)$.
К основным законам алгебры логики также относятся следующие:

коммутативные законы (от перестановки мест результат не меняется)
- $x \land y = y \land x$
- $х \lor y = y \lor x$
дистрибутивные законы (правила группировки)
- $x \land (y \lor z) = (x \land y) \lor (x \land z)$
- $x \lor (y \land z) = (x \lor y) \land (x \lor z)$
ассоциативные законы
- $x \land (y \land z) = (x \land y) \land z$
- $x \lor (y \lor z) = (х \lor y) \lor z$

С помощью законов логики можно осуществлять равносильные преобразования. Такие преобразования используются для
доказательств, приведения формул к заданному виду, упрощения формул.

Под сложностью формул обычно понимается количество символов, используемых для ее записи. То есть формула $\alpha$
проще
формулы $\beta$, если $\alpha$ содержит меньше букв и логических операций. Например, для формулы
$(\lnot (x \lor y) \Rightarrow x \lor y) \land y$
можно записать следующую цепочку преобразований, приводящих ее к более простому виду:

$(\lnot \lnot(x \lor y) \lor x \lor y) \land y = (x \lor y \lor x \lor y) \land y = (x \lor y) \land y = y$.

Сочетания знаков на выбор

Возможные продолжения ряда x0000xx000:

x0000xx001
x0000xx010
x0000xx100
x0000xx011
x0000xx101
x0000xx110
x0000xx111

Основные операции

Количество логических операций, которыми обычно оперирует логика 6:

Отрицание.
Умножение.
Сложение
Следование.
Дизъюнкция.
Равнозначность.

Остановимся на каждом из них детальнее, выясним как правильно они называются в алгебре логики, есть ли у них аналоги в обычной речи, в математике, и как их можно использовать в обычной жизни.

Отрицание или инверсия

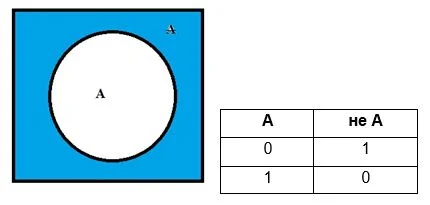
Операция отрицания или НЕлогическое, корректнее будет название инверсия.Конечное высказывание будет противоположным первоначальному (исходному). Применяется для одного выражения, которое может быть как сложным, так и элементарным.

На примере этой простейшей операции удобно показывать, насколько лаконичны и информативны таблицы истинности. Обозначим исходное высказывание буквой А, соответственно, окончательное будет не А (или НЕ, ‾, ˥ not А). А их ложность или правдивость напишем при помощи цифр 0 и 1.

Получается, если исходное значение правда, то новое будет ложь, и наоборот.

Умножение или конъюнкция &

Логическое И или умножение еще называют конъюнкцией. Финальное высказывание будет правдивым, только если его составляющие тоже правдивы. Во всех остальных случаях оно будет ложным. Применяется для двух и более аргументов, элементарных или сложных. Обозначение А и В; А ^ В; А &В; A and В.

Как видно, при помощи таблицы истинности из 15 ячеек можно описать то, на описание чего при помощи слов пришлось бы потратить минимум 5 полноценных предложений.

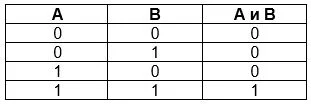
Логическое И в обычной жизни:

Хорошая певица должна быть талантливой и упорной (наличие только одного качества не позволит проявить миру свой талант).
По условиям задачи А – число меньше 30, В – число делиться на 3. Нужно найти решение А ˄ В.

Решение: Первое множество содержит числа 1,2,3….29. Второе – 3,6,9,…27. Решением будет множество на пересечении множеств А и В, что хорошо покажут диаграммы Эйлера-Венна. А ˄ В будет истинным для множества чисел 3,6,9,….27.

Сложение или дизъюнкция V

Логическое ИЛИ, сложение по-другому называют дизъюнкцией. Оно истинно всегда, кроме случая, если ложны все составные высказывания. Функция распространяется на простые и сложные исходные аргументы. Обозначение А или В; A v В; А ог В.

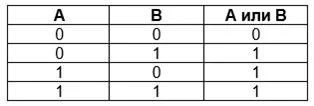
В обычной жизни нас окружает логическое ИЛИ:

«Чтобы сдать тесты на «отлично», нужно старательно готовиться ИЛИ должно повезти с билетом».
Есть задача с 2-мя условиями: А – число делится на 5, В – число делится на 2.

Решение: Первое множество чисел включает в себя 5, 10, 15…Второе – 10, 20, 30…Решение, при котором истинно Аv В – совокупность обеих множеств (5, 10, 15, 20, 25, 30…).

Следование или импликация

Для этого случая важно значение каждого выражения и даже его очередность, потому что первый аргумент считается условием, второй – следствием. Импликация будет ложной лишь в одном случае – если первое составляющее правдиво, а второе нет

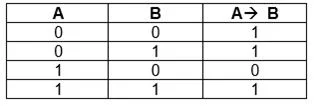
Такое логическое следование имеет аналог в обычной речи «если.. то», то есть одно событие зависит от другого. Символьно связи выражают следующим образом:

Логическое следование в обычной жизни:

Если пойти к врачу, можно выздороветь (но можно выздороветь и без похода к врачу, а можно и после визита в больницу не выздороветь).
По условию задачи, А – если число делится на 10, то В делится на 5.

Строгая дизъюнкция

Такая логическая операция выдаст истину, если любое из составляющих высказываний будет истинным, независимо очередности.

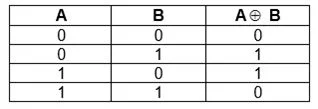
Это пример исключающей функции. Аналог в словесном выражении – «либо». Разница от простой дизъюнкции в том, что конечное выражение будет истинным, только если будет правдой одна переменная.

Эквиваленция или равнозначность

Операция, выдающая истину в случае, если обе исходные переменные истины или неправдивы.Обозначают А ~В, А В.

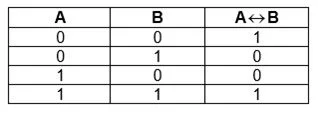
Словесная аналогия – «тогда и только тогда, когда», математическая – «необходимо и достаточно». Если сравнить таблицы истинности для предыдущих операций, очевидно, что она противоположна «исключающему ИЛИ», то ее можно посчитать так:

Пример эквивалентности из обычной жизни:

Если вечером на горизонте солнце темно-красного цвета, значит, завтра будет ветреный день.
В задаче 2 условия: А – сумма цифр числа равно 9, В – число делится на 9. АВ означает, что число делится на 9, если сумма цифр равна 9.

Способы представления булевой функции

С помощью формул можно получать огромное количество разнообразных функций, причём с помощью разных формул можно получить одну и ту же функцию. Иногда бывает весьма полезно узнать, как построить ту или иную функцию, используя лишь небольшой набор заданных операций или используя как можно меньше произвольных операций. Рассмотрим основные способы задания булевых функций:

Совершенная дизъюнктивная нормальная форма (СДНФ)
Совершенная конъюнктивная нормальная форма (СКНФ)
Алгебраическая нормальная форма (АНФ, полином Жегалкина)

Совершенная дизъюнктивная нормальная форма (ДНФ)

Простая конъюнкция — это конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза.Дизъюнктивная нормальная форма (ДНФ) — это дизъюнкция простых конъюнкций.Совершенная дизъюнктивная нормальная форма (СДНФ) — ДНФ относительно некоторого заданного конечного набора переменных, в каждую конъюнкцию которой входят все переменные данного набора.

Например, ДНФ является функция ¬abc ∨ ¬a¬bc ∨ ac, но не является СДНФ, так как в последней конъюнкции отсутствует переменная b.

Совершенная конъюнктивная нормальная форма (КНФ)

Простая дизъюнкция — это дизъюнкция одной или нескольких переменных, или их отрицаний, причём каждая переменная входит в неё не более одного раза.Конъюнктивная нормальная форма (КНФ) — это конъюнкция простых дизъюнкций.Совершенная конъюнктивная нормальная форма (СКНФ) — КНФ относительно некоторого заданного конечного набора переменных, в каждую дизъюнкцию которой входят все переменные данного набора.

Например, КНФ является функция (a ∨ b) ∧ (a ∨ b ∨ c), но не является СДНФ, так как в первой дизъюнкции отсутствует переменная с.

Алгебраическая нормальная форма (АНФ, полином Жегалкина)

Алгебраическая нормальная форма, полином Жегалкина — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции, а в качестве сложения — исключающее ИЛИ.

Примеры полиномов Жегалкина: 1, a, a⊕b, ab⊕a⊕b⊕1

Алгоритм построения СДНФ для булевой функции

Построить таблицу истинности для функции
Найти все наборы аргументов, на которых функция принимает значение 1
Выписать простые конъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 0, то она входит в конъюнкцию с отрицанием, а иначе без отрицания
Объединить все простые конъюнкции с помощью дизъюнкции

Алгоритм построения СКНФ для булевой функции

Построить таблицу истинности для функции
Найти все наборы аргументов, на которых функция принимает значение 0
Выписать простые дизъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 1, то она входит в дизъюнкцию с отрицанием, а иначе без отрицания
Объединить все простые дизъюнкции с помощью конъюнкции

Алгоритм построения полинома Жегалкина булевой функции

Есть несколько методов построения полинома Жегалкина, в данной статье рассмотрим наиболее удобный и простой из всех.

Построить таблицу истинности для функции
Добавить новый столбец к таблице истинности и записать в 1, 3, 5… ячейки значения из тех же строк предыдущего столбца таблицы истинности, а к значениям в строках 2, 4, 6… прибавить по модулю два значения из соответственно 1, 3, 5… строк.
Добавить новый столбец к таблице истинности и переписать в новый столбец значения 1, 2, 5, 6, 9, 10… строк, а к 3, 4, 7, 8, 11, 12… строкам аналогично предыдущему пункту прибавить переписанные значения.
Повторить действия каждый раз увеличивая в два раза количество переносимых и складываемых элементов до тех пор, пока длина не станет равна числу строк таблицы.
Выписать булевы наборы, на которых значение последнего столбца равно единице
Записать вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора записать единицу) и объединить их с помощью операции исключающего ИЛИ.

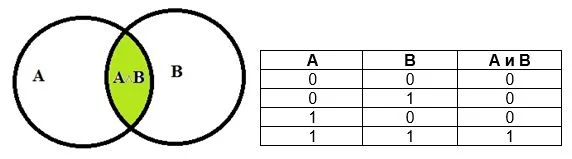
Диаграммы Эйлера-Венна

Тем, кто лучше воспринимает информацию в виде изображений, понравятся диаграммы Эйлера-Венна, которые показывают, как пересекаются множества между собой.

Число пересечений (областей) можно посчитать сразу, оно равно n = 2N, где N – число множеств. Так как значение двойки в степени растет очень быстро (4,8,16), обычно диаграммы используют для 2-3 множеств. Далее области пересечения будут сливаться, образуя неразличимые участки. Если множеств 2-3, то рисуют круги, если больше 4 – эллипсы. Этот «цветок» помещают в прямоугольную конструкцию, которую называют универсум U (универсальное множество).

Диаграммы позволяют наглядно увидеть результат большинства логических функций:

Конъюнкция множеств А и В:

Отрицание Ā:

Сложное выражение (Ā)∨(A∧B), составленное из элементарных Ā, A∧B и их комбинации, графическое выражение:

Примеры использования диаграмм Эйлера-Венна

Пример №1:

Есть 2 множества цифр и универсум:

А={4,5,6,7}

В={6,7,8,9}

U={0,4,5,6,7,8,9}

Пустой области ничего не принадлежит, опишем в табличном виде, какие цифры какой области принадлежит:

4.2 Логические операции

Расположите логические операторы в порядке значимости их приоритета (от наибольшего до наименьшего).

Ответ: not, and, or

Приведенная ниже таблица истинности показывает разные комбинации истинности и ложности значений, соединённых логическими операторами. Заполните таблицу, выбрав True или False, чтобы показать, является результатом такой комбинации истина или ложь.

True and False         false
True and True       true
False and True      false
False and False     false   
True or False       true
True or True        true
False or True       true
False or False      false
not True        false
not False               true

Допустим, что даны переменные a = 2, b = 4, c = 6. Заполните таблицу, выбрав True или False, чтобы показать, является результатом такой комбинации истина или ложь.

a == 2 or b > 2     true    
6 <= c and a > 3  false   
1 != b and c != 3   true    
a >= -1 or a <= b     true    
not (a > 2)      true
not (c <= 10)           false

Что будет выведено на экран в результате выполнения следующей программы?:

num1 = 34
num2 = 81
if num1 // 9 == 0 or num2 % 9 == 0:
    print('число', num1, 'выиграло')
else:
    print('число', num2, 'выиграло')

Ответ: число 34 выиграло

Какое значение будет выведено на экран после выполнения следующей программы, если с клавиатуры введено число 7?:

a = int(input())
if a >= 2 and a <= 17:
    b = 3
    p = a * a + b * b
else:
    b = 5
p = (a + b) * (a + b)
print(p)

Ответ: 100

Напишите программу, которая принимает целое число x и определяет, принадлежит ли данное число указанному промежутку.

x = int(input())

if -1 < x < 17:
    print('Принадлежит')
else:
    print('Не принадлежит')

Напишите программу, которая принимает целое число x и определяет, принадлежит ли данное число указанным промежуткам.

x = int(input())

if x <= -3 or x >= 7:
    print('Принадлежит')
else:
    print('Не принадлежит')

x = int(input())

if (-30 < x <= -2) or (7 < x <= 25):
    print('Принадлежит')
else:
    print('Не принадлежит')

Назовем число красивым, если оно является четырехзначным и делится нацело на 7 или на 17. Напишите программу, определяющую, является ли введённое число красивым. Программа должна вывести «YES», если число является красивым, или «NO» в противном случае.

x = int(input())

if (999 < x <= 9999) and ((x % 7 == 0) or (x % 17 == 0)):

    print('YES')
else:
    print('NO')

Напишите программу, которая принимает три положительных числа и определяет, существует ли невырожденный треугольник с такими сторонами.

a, b, c = int(input()), int(input()), int(input())

if a + b > c and a + c > b and b + c > a:
    print("YES")
else:
    print("NO")

Напишите программу, которая определяет, является ли год с данным номером високосным. Если год является високосным, то выведите «YES», иначе выведите «NO».

year = int(input())

if (year % 4 == 0 and year % 100 != 0) or year % 400 == 0:
    print('YES')
else:
    print('NO')

Даны две различные клетки шахматной доски. Напишите программу, которая определяет, может ли ладья попасть с первой клетки на вторую одним ходом. Программа получает на вход четыре числа от 1 до 8 каждое, задающие номер столбца и номер строки сначала для первой клетки, потом для второй клетки. Программа должна вывести «YES», если из первой клетки ходом ладьи можно попасть во вторую, или «NO» в противном случае.

a = int(input()) 
b = int(input()) 
aa = int(input())
bb = int(input())

if (a != aa and b == bb) or (b != bb and a == aa):
    print('YES')
else:
    print('NO')

Тут можно укоротить код.

Даны две различные клетки шахматной доски. Напишите программу, которая определяет, может ли король попасть с первой клетки на вторую одним ходом. Программа получает на вход четыре числа от 1 до 8 каждое, задающие номер столбца и номер строки сначала для первой клетки, потом для второй клетки. Программа должна вывести «YES», если из первой клетки ходом короля можно попасть во вторую, или «NO» в противном случае.

v = int(input())
h = int(input())
v_1 = int(input())
h_1 = int(input())

a = v_1 - v
b = h_1 - h
if (-1 <= a <= 1 ) and (-1 <= b <= 1):
    print('YES')
else:
    print('NO')

Введем выражение m k обозначающее поразрядную конъюнкцию m и k логическое и между соответствующими

Что представляет собой данный ряд x0000xx000?

Какое сочетание знаков продолжит ряд x0000xx000?

Алгебра логики и решение задач

Поразрядная конъюнкция задачи 3

Примеры аналогичных рядов сочетания символов

Электросхемы и таблицы истинности

Практические примеры

О порядке логических операций

Какое сочетание знаков продолжит ряд x0000xx000?

Сочетания знаков на выбор

Практические примеры

Законы алгебры логики

Сочетания знаков на выбор

Основные операции

Отрицание или инверсия

Умножение или конъюнкция &

Сложение или дизъюнкция V

Следование или импликация

Строгая дизъюнкция

Эквиваленция или равнозначность

Способы представления булевой функции

Совершенная дизъюнктивная нормальная форма (ДНФ)

Совершенная конъюнктивная нормальная форма (КНФ)

Алгебраическая нормальная форма (АНФ, полином Жегалкина)

Алгоритм построения СДНФ для булевой функции

Алгоритм построения СКНФ для булевой функции

Алгоритм построения полинома Жегалкина булевой функции

Диаграммы Эйлера-Венна

Примеры использования диаграмм Эйлера-Венна

4.2 Логические операции

Похожие записи:

Похожие записи: