Рассматриваемые вопросы:

Техники оверсемплинга

Оверсемплинг (или upsampling) — это метод, который позволяет увеличить количество образцов минорного класса в наборе данных, чтобы достичь баланса между классами и улучшить качество модели машинного обучения.

Существует несколько основных техник оверсемплинга:

1. Дублирование (Repetition): данная техника заключается в повторном добавлении случайных примеров минорного класса в набор данных. При этом примеры могут быть полностью идентичными уже существующим или немного модифицированными. Дублирование просто воспроизводит существующую информацию, не добавляя никаких новых сведений о классе.
2. Синтез новых примеров: в этом случае, новые примеры для минорного класса генерируются на основе уже существующих. Один из самых распространенных алгоритмов для синтеза новых примеров называется SMOTE (Synthetic Minority Over-sampling Technique). Он создает новые примеры, соединяя каждый экземпляр минорного класса с его k-ближайшими соседями.
3. Модификация признаков (Feature modification): при данном подходе, изменяются значения признаков минорного класса. Например, если у нас есть категориальный признак, то можно добавить новую категорию, которая будет представлять новые экземпляры минорного класса.
4. Комбинирование техник: также возможно применение комбинированных методов оверсемплинга. Например, можно применить сначала дублирование для увеличения размера минорного класса, а затем применить метод синтеза новых примеров.

Выбор конкретной техники оверсемплинга зависит от конкретного набора данных и проблемы, которую необходимо решить. Кроме того, следует учитывать потенциальные риски, такие как переобучение модели и увеличение шума в данных

Поэтому, перед применением оверсемплинга, важно тщательно изучить и проанализировать набор данных

Техники оверсемплинга являются одним из важных инструментов для борьбы с проблемой дисбаланса классов в задачах машинного обучения. Они позволяют эффективным образом улучшить результаты модели и получить более справедливые предсказания для минорного класса.

Voting and Averaging Based Ensemble Methods

Voting and averaging are two of the easiest examples of ensemble learning in machine learning. They are both easy to understand and implement. Voting is used for classification and averaging is used for regression.

In both methods, the first step is to create multiple classification/regression models using some training dataset. Each base model can be created using different splits of the same training dataset and same algorithm, or using the same dataset with different algorithms, or any other method. The following Python-esque pseudocode shows the use of same training dataset with different algorithms.

According to the above pseudocode, we created predictions for each model and saved them in a matrix called predictions where each column contains predictions from one model.

Majority Voting

Every model makes a prediction (votes) for each test instance and the final output prediction is the one that receives more than half of the votes. If none of the predictions get more than half of the votes, we may say that the ensemble method could not make a stable prediction for this instance. Although this is one of the more popular ensemble techniques, you may try the most voted prediction (even if that is less than half of the votes) as the final prediction. In some articles, you may see this method being called “plurality voting”.

Weighted Voting

Unlike majority voting, where each model has the same rights, we can increase the importance of one or more models. In weighted voting you count the prediction of the better models multiple times. Finding a reasonable set of weights is up to you.

Simple Averaging

In simple averaging method, for every instance of test dataset, the average predictions are calculated. This method often reduces overfit and creates a smoother regression model. The following pseudocode code shows this simple averaging method:

Weighted Averaging

Weighted averaging is a slightly modified version of simple averaging, where the prediction of each model is multiplied by the weight and then their average is calculated. The following pseudocode code shows the weighted averaging:

Корреляция (и ложная корреляция)

Корреляция — это явление, когда изменение одного показателя похоже на изменение другого показателя. Например, один растет, другой растет. Или один растет, другой падает — обратная корреляция. 

• Линейная корреляция — один показатель меняется, другой меняется пропорционально первому.
• Нелинейная корреляция — показатели меняются непропорционально друг другу, а, например, экспоненциально. Такие корреляции отслеживают с помощью специальных методов анализа.

Важно. Корреляция — это не причинно-следственная связь

Иногда оба показателя просто зависят от третьих факторов. Или связаны еще сложнее. Или между ними вообще нет связи, а корреляция появилась из-за совпадения.

Если ошибочно принимать корреляцию за причинно-следственную связь, можно прийти к ложным выводам. Классическая ошибка: «Когда ввели ремни безопасности, больше людей оказалось в больницах». Это звучит как аргумент против ремней, но фактически корреляция означает, что люди стали чаще выживать в ДТП, а значит, попадать в больницы.

Ложные корреляции могут быть опасными, а могут быть забавными. Есть целый проект, который собирает абсурдные коррелирующие друг с другом факторы — между ними нет связи, но графики очень похожи.

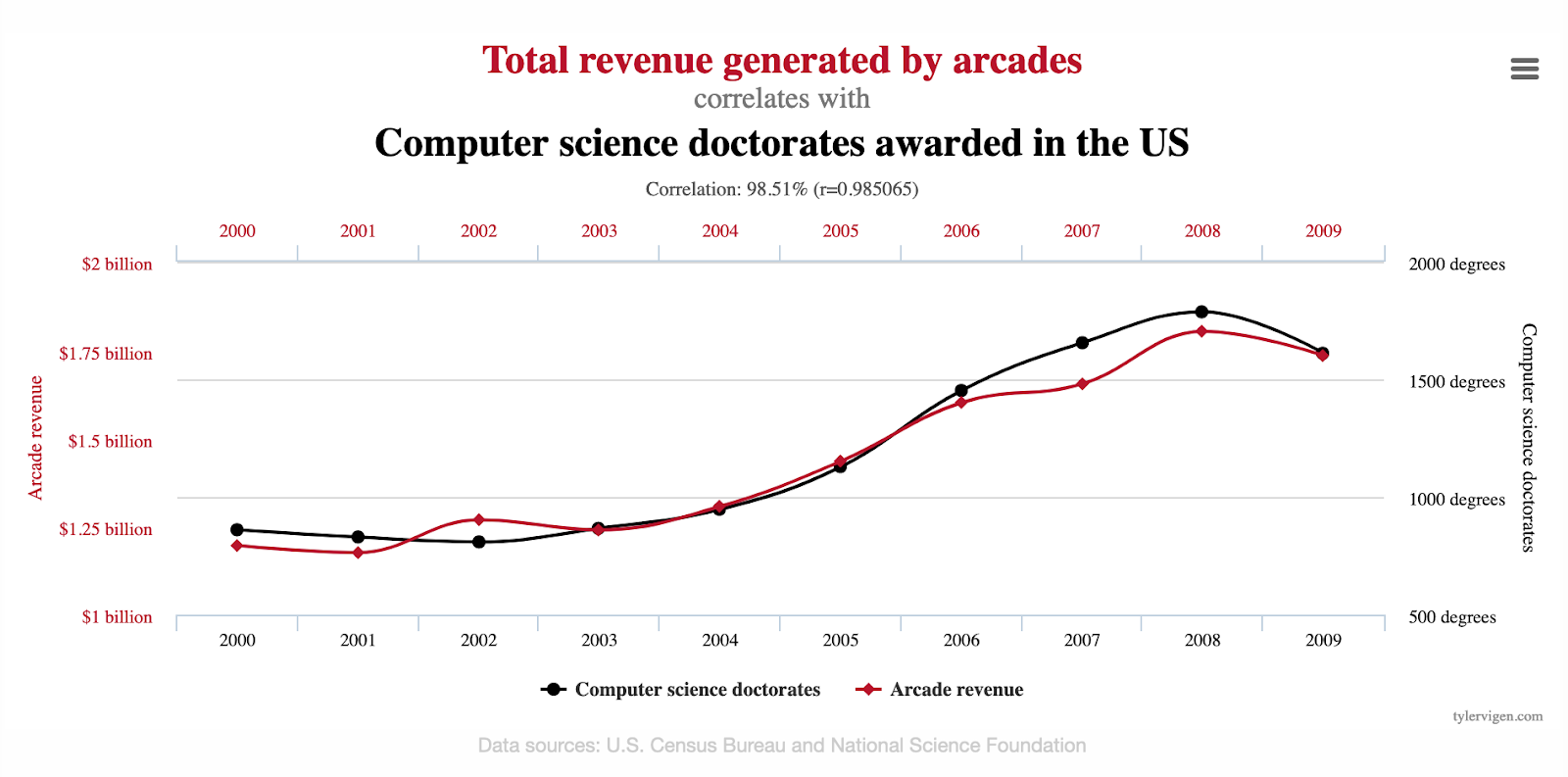Например, выручка от игровых автоматов очень четко коррелирует с количеством докторских по информатике в Америке

2.1 Частота дискретизации

Теорема Найквиста-Шеннона гласит, что аналоговый сигнал, имеющий ограниченный спектр, может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, если частота выборки (дискретизации) превышает максимальную частоту спектра сигнала более чем в 2 раза. Минимальная требуемая частота дискретизации называется частотой Найквиста.

Формула 2-1. Частота Найквиста

Где fsignal – это наивысшая частота входного сигнала.

Дискретизация сигнала с частотой выше частоты Найквиста называется оверсемплингом или дискретизацией с запасом по частоте. На практике обычно используют максимально возможную частоту дискретизации, чтобы получить как можно более точное представление измеряемого сигнала во временной области. Поэтому в большинстве случаев оцифрованный входной сигнал уже дискретизирован с запасом.

У микроконтроллеров AVR частота дискретизации АЦП определяется внутренней тактовой частотой и коэффициентом предделителя. Наименьший коэффициент дает наибольшую частоту дискретизации. Однако в определенный момент высокая тактовая частота АЦП будет уменьшать точность преобразования, то есть эффективное число разрядов (the Effective Number Of Bits ,ENOB) АЦП будет снижаться. Все АЦП имеют ограниченную полосу пропускания и АЦП микроконтроллеров AVR не исключение. Согласно техническому описанию, чтобы получить 10-ти разрядное разрешение, тактовая частота АЦП должна быть в диапазоне (50 – 200) кГц. Когда тактовая частота АЦП равна 200 кГц, частота дискретизации сигнала составляет ~ 15 kSPS (15 тысяч выборок в секунду), что ограничивает частоту входного сигнала до ~7.5 кГц. Тактовая частота АЦП микроконтроллеров AVR может иметь значение до 1 МГц, однако это будет снижать точность преобразований.

Принцип работы оверсемплинга

Оверсемплинг — это метод увеличения количества примеров положительного класса путем генерации новых данных, которые похожи на существующие примеры положительного класса. Принцип работы оверсемплинга заключается в том, чтобы сбалансировать дисбаланс классов в обучающем наборе данных.

Существуют различные методы оверсемплинга, такие как метод повторного выбора с заменой и генерация синтетических примеров.

1. Метод повторного выбора с заменой: в этом методе примеры положительного класса выбираются случайным образом из обучающего набора данных с заменой. То есть, один и тот же пример положительного класса может быть выбран несколько раз для включения в новый обучающий набор данных. Этот метод прост в реализации, но может привести к переобучению модели.
2. Генерация синтетических примеров: в этом методе новые примеры положительного класса генерируются путем комбинирования существующих примеров положительного класса. Например, для генерации нового примера можно взять два случайных примера положительного класса и сгенерировать новый пример, который будет являться их комбинацией. Этот метод более сложен в реализации, но может привести к созданию более разнообразного и репрезентативного обучающего набора данных.

Оверсемплинг позволяет улучшить качество модели машинного обучения, особенно в случаях, когда дисбаланс классов в обучающем наборе данных существенный

Однако, при использовании оверсемплинга необходимо быть осторожным и обратить внимание на возможность переобучения модели

Для определения оптимального количества оверсемплинга можно использовать различные метрики оценки качества модели, такие как точность, полнота и F1-мера. Также, возможно проведение кросс-валидации для оценки стабильности модели при разных значениях оверсемплинга.

Evaluation metrics: accuracy pitfall

Before diving into our example, let’s discuss the evaluation metrics. This is a critical choice for an imbalanced dataset.

For classification problems, we often use accuracy as the evaluation metric. It is easy to calculate and intuitive:

Accuracy = # of correct predictions / # of total predictions

But, it is misleading for highly imbalanced datasets. For the example of credit card fraud detection, we can set a model to always classify new transactions as legit. The accuracy could be high at 99.9% if 99.9% in the dataset is all legit.

What an ‘accurate’ model!

But, don’t forget that our goal is to detect fraud, so such a model is useless.

So for the imbalanced dataset, we must look at a broader picture of the prediction results. We could use other evaluation metrics such as Area Under the ROC Curve (AUC), F-score, Precision-Recall Curve.

Further learning: to learn about the common evaluation metrics, please check out 8 popular Evaluation Metrics for Machine Learning Models.

In this tutorial, we’ll use as the evaluation metric.

It’s a single metric that’s easy to use. AUC has the highest value of 1 when the classifier can predict 100% correctly.

We’ll calculate the AUC of using the original imbalanced dataset, versus the rebalanced datasets. So you can compare them and get an idea of the potential improvement of applying the imbalanced data techniques. Yet, please note that the improvement varies for different datasets or machine learning algorithms.

Now, let’s get to our example of imbalanced data.

Bootstrap Aggregating

The name Bootstrap Aggregating, also known as “Bagging”, summarizes the key elements of this strategy. In the bagging algorithm, the first step involves creating multiple models. These models are generated using the same algorithm with random sub-samples of the dataset which are drawn from the original dataset randomly with bootstrap sampling method. In bootstrap sampling, some original examples appear more than once and some original examples are not present in the sample. If you want to create a sub-dataset with m elements, you should select a random element from the original dataset m times. And if the goal is generating n dataset, you follow this step n times.

At the end, we have n datasets where the number of elements in each dataset is m. The following Python-esque pseudocode show bootstrap sampling:

The second step in bagging is aggregating the generated models. Well known methods, such as voting and averaging, are used for this purpose.

The overall pseudocode look like this:

In bagging, each sub-samples can be generated independently from each other. So generation and training can be done in parallel.

You can also find implementation of the bagging strategy in some algorithms. For example, Random Forest algorithm uses the bagging technique with some differences. Random Forest uses random feature selection, and the base algorithm of it is a decision tree algorithm.

Related: A Deep Learning Tutorial: From Perceptrons to Deep Networks

Какой должна быть заспамленность текста?

Начинающим авторам и копирайтерам бывает достаточно тяжело понять, какая именно частота повторений считается нормальной. А всё потому, что никакого единого стандарта заспамленности в природе не существует. Его попросту никто не устанавливал. Так что результаты проверок могут зависеть не только от качества написанного текста, но и от, выбранного для анализа, инструмента.

В большинстве случаев начинающим копирайтерам рекомендуют находиться в пределах от тридцати до шестидесяти процентов показателя заспамленности.

1. До 30% – это естественное содержание ключевых вхождений. Подобные тексты легко читаются и не вызывают отторжения от чрезмерных повторов и явных вставок «кривых» ключей.

2. От 30% до 60% – в промежутке между тридцатью и шестьюдесятью процентами находятся поисково-оптимизированные тексты. Они обработаны таким образом, чтобы в полной мере соответствовать ожиданиям поисковых алгоритмов, а это помогает получать более высокие оценки индекса качества сайта. 

3. Более 60% – явный переспам и злоупотребление ключевиками в тексте. Ни один поисковик не любит подобные статьи. В большинстве случаев, боты попросту не пропускают подобные творения в органическую выдачу. Более того, наличие таких статей может стать основанием для попадания сайта под фильтр.

RMSProp (running mean square)

Метод импульсов
с поправкой Нестерова – это достаточно очевидные эвристики. В последующем были
предложены более сложные и изощренные подходы. Например, довольно часто при
обучении нейронных сетей используют оптимизатор RMSProp. Его целью
является не только сглаживание псевдоградиента в стохастических алгоритмах, но
и нормализация скорости изменения вектора весов:

О чем здесь речь?
Часто в задачах многомерной оптимизации, когда число подбираемых весовых
коэффициентов не 2-3, а десятки, сотни, тысячи и более, частные производные по
функции потерь от каждого из них могут сильно различаться:

А это, в свою
очередь, приводит к сильному изменению одних весовых коэффициентов и
практически оставляет без изменения – другие:

Так вот, чтобы
нормализовать скорость адаптации весов вектора ,
Джефри Хинтон на своем курсе по Deep Learning (глубокое
обучение) предложил делать следующую перенормировку шага обучения:

(здесь деление
векторов во второй формуле выполняется поэлементно). Вначале мы похожим образом
вычисляем экспоненциальное скользящее среднее, но не по градиентам, а по
квадратам градиентов (здесь  —
поэлементное умножение соответствующих компонент векторов). А, затем, нормируем
текущий вектор градиента на корень квадратный из усредненных (по экспоненте)
квадратов градиентов на последних итерациях. (Здесь  —
небольшая константа для исключения деления на ноль). В результате, каждый
компонент вектора градиента  будет
поделен на пропорциональное значение из вектора  и,
таким образом, несколько нормирован. Благодаря этому выравнивается скорость
изменения коэффициентов в векторе :
значения с большими градиентами начинают меняться несколько медленнее, а
значения с малыми градиентами – несколько быстрее. В итоге это часто позволяет
увеличить сходимость псевдоградиентных методов.

Особенности применения upsampling в различных областях машинного обучения

Одной из областей, где применение upsampling является особенно важным, является медицина. В задачах диагностики или прогнозирования заболеваний часто возникает проблема дисбаланса классов, например, когда количество пациентов с определенным заболеванием значительно меньше, чем здоровых пациентов. Применение upsampling позволяет более равномерно представить оба класса и достичь более точных прогнозов.

В задачах компьютерного зрения, таких как распознавание объектов или сегментация изображений, применение upsampling может помочь улучшить качество работы модели. Например, при использовании сверточных нейронных сетей, увеличение размерности пространства признаков позволяет сохранить больше информации о деталях изображения и улучшить точность предсказания.

В области обработки естественного языка, upsampling также может быть полезным. Например, при выполнении задачи классификации текстов часто возникает проблема дисбаланса классов, когда количество текстов в одной категории существенно больше, чем в другой. Применение увеличения выборки позволяет более точно представить оба класса и повысить качество классификации.

Таблица ниже представляет сравнение различных методов увеличения выборки в машинном обучении:

Метод	Описание	Применение
Oversampling	Увеличение выборки путем добавления дополнительных образцов миноритарного класса	Борьба с дисбалансом классов
Undersampling	Уменьшение выборки путем удаления образцов мажоритарного класса	Борьба с дисбалансом классов
SMOTE	Генерация новых образцов путем интерполяции между существующими образцами	Борьба с дисбалансом классов
GANs	Генерация новых образцов путем обучения генеративных адверсариальных сетей	Увеличение выборки и генерация реалистичных данных

Таким образом, применение upsampling имеет свои особенности в различных областях машинного обучения. В каждом конкретном случае необходимо подбирать наиболее подходящий метод увеличения выборки, учитывая особенности задачи и доступные данные.

Oversampling vs upsampling

Any digital signal has a sample rate that defines its spectrum (low, high frequencies of a sound, in instance).

Upsampling is an increasing sampling rate on multiple or non-multiple ratios.

Oversampling is a multiple-ratio upsampling.

Though, these terms have no exact definition.

Upsampling may be done via interpolation (spline math function, as example).

But, multiple upsampling (oversampling) may be done by inserting zero samples. And, it may cause lesser non-linear distortions in proper applications than the interpolation.

On the other hand, non-multiple upsampling may be done via multiplication and dividing to integer ratio.

You can read the details below.

Сравнение upsampling с другими методами работы с несбалансированными данными

Сравнивая upsampling с другими методами, можно отметить следующие преимущества

Во-первых, upsampling позволяет использовать полный объем данных, что особенно важно при работе с ограниченным набором данных. В то время как downsampling может привести к потере информации, upsampling несбалансированных классов позволяет сохранять все существующие данные

Во-вторых, upsampling способствует увеличению количества примеров миноритарного класса путем копирования или генерации новых данных. Это позволяет модели получить больше информации о миноритарном классе и улучшить свою способность его распознавать.

В-третьих, upsampling может быть легко реализован во многих популярных фреймворках машинного обучения с помощью функций или модулей, предлагаемых эти фреймворками. Это делает его удобным и доступным методом для работы с несбалансированными данными.

Однако, upsampling имеет и некоторые недостатки. Во-первых, увеличение количества примеров миноритарного класса может привести к переобучению модели, особенно если данных миноритарного класса недостаточно, чтобы представлять полезную информацию. В таких случаях, downsampling или генерация синтетических данных может быть более предпочтительным методом.

Во-вторых, upsampling может замедлить время обучения модели, особенно при больших объемах данных. Увеличение количества примеров может увеличить время, необходимое для тренировки модели, и потребовать больше вычислительных ресурсов. Если время обучения является критическим фактором, то другие методы, такие как downsampling, могут быть более предпочтительными.

В итоге, выбор между upsampling и другими методами работы с несбалансированными данными зависит от конкретной задачи, имеющихся данных и требований модели

Важно учитывать их преимущества и недостатки, а также провести тщательную оценку и сравнение различных методов, чтобы выбрать наиболее эффективный подход к обработке несбалансированных данных

Уменьшение размерности

Даже грамотно отобранную выборку нужно «чистить» и уменьшать. Например, есть база пользователей — для каждого указаны пол, возраст, поведение, время захода на сайт, браузер, устройство и еще огромное количество показателей. Проанализировать их все слишком трудоемко и не всегда оправдано. В таких ситуациях требуется снижение размерности. Это уменьшение количества переменных, отбрасывание лишнего.

У снижения размерности есть два основных способа:

• отбор признаков — с помощью формул и векторных преобразований специалисты решают, какие признаки связаны с результатом или целевым показателем, а какие нет. Незначительные признаки отбрасывают;
• проекция признаков — показатели представляют на графике, а потом уменьшают размерность этого графика. Например, изначально он трехмерный — его делают двумерным. Некоторые точки трехмерного графика накладываются друг на друга и в двумерной версии выглядят как одна точка. Переменных становится меньше.

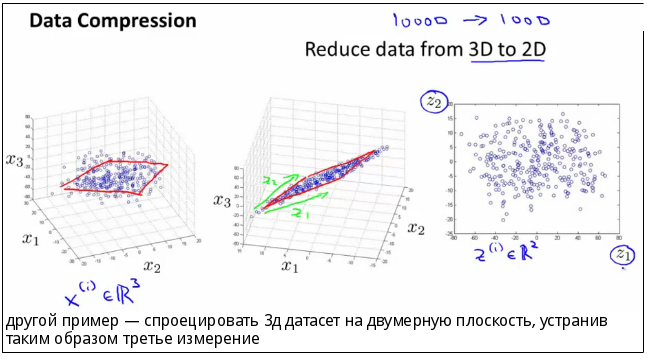Проекция признаков: из трехмерного пространства данные переводят в двумерные и тем самым уменьшают их количество. Источник

Внутри каждого способа есть разные стратегии, но основным считается так называемый метод главных компонент. Его используют чаще всего, причем для обоих способов.

Смещение, дисперсия и связь между ними

Показатели влияют на огромное количество факторов: от формы графика распределения до точности результатов анализа.

Смещение. Это то, насколько данные и выводы из них «смещены» относительно реальной ситуации. Например, в выборку попали только блондины. Аналитическая модель увидела, что показатель встречается часто, и сочла его важным. В итоге по результатам аналитики оказалось, что в магазин заходят только светловолосые люди. Но это ведь не так!

Или знаменитая «ошибка выжившего»: есть много случаев, когда дельфины спасали людей, но те, кого они не спасли, уже не могут ничего рассказать. Поэтому складывается ложное ощущение, что дельфины спасают людей всегда, или смещение.

Обычно сильное смещение получается при неверно составленной выборке или при неправильной обработке данных. Например:

• систематическая ошибка отбора — когда в выборку попадают случаи только с одним результатом, а с другим не попадают. Кстати, именно так работает ошибка выжившего. Еще есть шуточный пример: «интернет-опрос показал, что 100% населения пользуется интернетом»;
• эффект низкой базы — когда в качестве стартового берется самое низкое значение, и относительно него любое увеличение показателя кажется огромным. Обратная ситуация называется эффектом высокой базы;
• ошибка меткого стрелка — в выборку попадают только похожие друг на друга значения, поэтому разброс оказывается меньше, чем нужно;
• уменьшение выборки или периода — из выборки намеренно или случайно убирают важную категорию результатов либо «обрезают» рассматриваемый период.

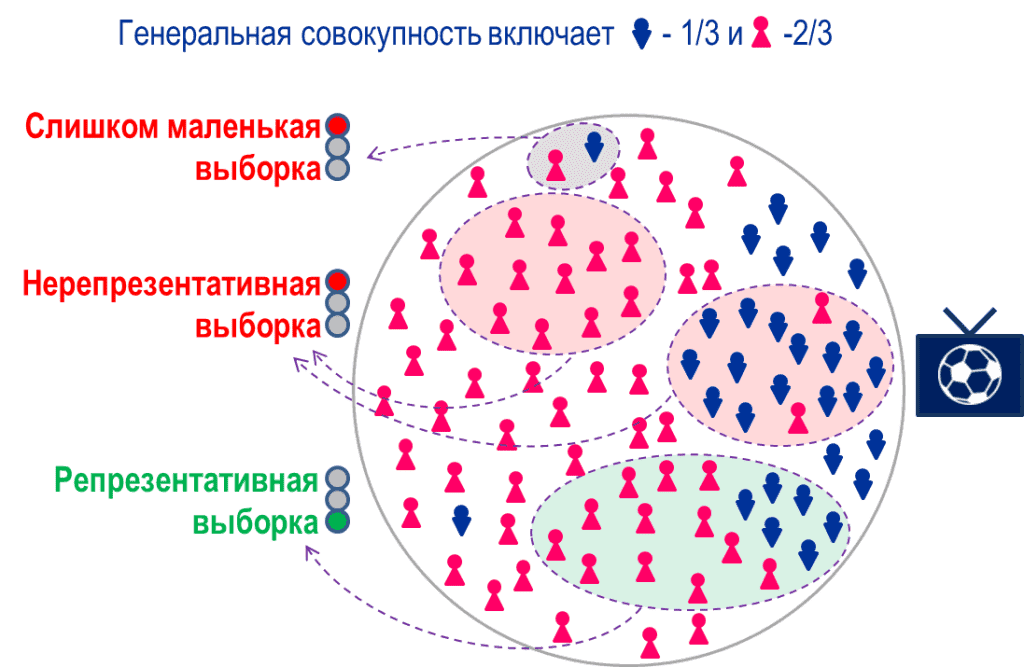Примеры неверно отобранных данных со смещением — получаются нерепрезентативные выборки. Источник

Смещение может возникать из-за намеренного манипулирования данными, а может быть результатом простой ошибки. Считается, что полностью избежать его почти невозможно.

Дисперсия. Это уровень разброса значений относительно определенной точки. В качестве точки может выступать среднее, медиана, истинное или целевое значение — зависит от ситуации. Если все данные в выборке близки к этой точке — дисперсия низкая. Тогда говорят, что у данных высокая кучность. А если результаты «разбросаны» в большом диапазоне относительно точки, дисперсия высокая. 

Показательный пример — мишень. Плохой стрелок стреляет с высокой дисперсией, а хороший стрелок бьет близко к центру мишени, и дисперсия получается низкая.

Дилемма смещения и дисперсии. Смещение и дисперсия обратно зависимы. Если мы корректируем выборку, чтобы уменьшить смещение, растет дисперсия. Если же стараемся уменьшить дисперсию, растет смещение. 

Так происходит, потому что малый разброс дает более низкую объективность: повышается риск, что в выборку попадут только условные блондины. А если разброс высокий, попадут все, но зато такую выборку сложнее анализировать, и в результатах может получиться мешанина.

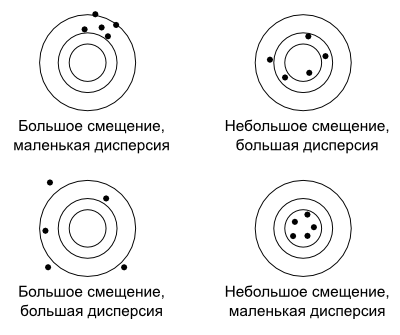Разные варианты соотношения смещения и дисперсии — наглядная демонстрация. Источник

Поэтому одна из задач дата-сайентиста — найти компромисс, баланс между смещением и дисперсией, чтобы получить близкий к истине результат.